Abstract
In this paper, the dual hesitant fuzzy rough set (DHFRS) is studied from the viewpoint of assessment deviations. Firstly, according to the relationship between intuitionistic fuzzy set and vague set, the DHFRS is transferred into a fuzzy set, where the membership of any given element to it has multi-grouped values. By the idea of bootstrap sampling, a group of four sets are generated to describe the membership degree on DHFRS, where the elements of the aforementioned sets are all considered as assessment values. Secondly, the generated sets are dealt with by assessment deviation theories, and specifically, two variables are proposed to describe the systematic and random deviations of the sets. Thirdly, the true-value of the membership degree of any elements to the set is estimated by a deviation-based dual hesitant fuzzy rough weighted aggregating operator. Fourthly, a dual hesitant fuzzy rough pattern recognition approach based on assessment deviation theories is proposed. Finally, an urban traffic modes recognition example is given to illustrate the validity of the proposed theories on DHFRSs.
1. Introduction
Rough set, first described by Pawlak [1], is a formal approximation of a crisp set in terms of a pair of sets, which gives the lower and the upper approximations of an original set. In rough set theory, the lower and the upper approximations are defined by an equivalence relation. In classical rough set theory, the equivalence relation is described by crisp values. Nowadays, it has been described as fuzzy sets [2], intuitionistic fuzzy sets [3] or hesitant fuzzy sets (HFS) [4], etc.
Moreover, as an extension of fuzzy set, HFS allows the membership degree of an element to a set to have several possible values. Yang et al. [5] firstly explored the fusions of HFSs and rough sets, and proposed some constructive and axiomatic approaches on hesitant fuzzy rough set (HFRS), where the HFRS is presented to approximate the hesitant fuzzy target through a hesitant fuzzy relation. Afterwards, Liang and Liu [6] proposed a risk decision making method based on decision-theoretic rough sets under hesitant fuzzy environment. It is noteworthy that Liang and Liu [6] both think and work creatively. Especially, it introduced HFSs into decision-theoretic rough sets and explored their decision mechanisms. Furthermore, Zhang et al. [7] noticed the connection between HFRS and intuitionistic fuzzy rough set, and proposed a novel rough set called dual hesitant fuzzy rough set (DHFRS). DHFS, proposed by Zhu et al. [8], comprised not only the multi-grouped membership degrees, but also the multi-grouped non-membership degrees of an element to a set. By using a dual hesitant fuzzy relation, Zhang et al. [7] firstly defined the lower and upper dual hesitant fuzzy rough approximation operators with respect to a dual hesitant fuzzy approximation space, and introduced some properties of this model.
According to the concept “depth” proposed by Hardy [9], “mathematical ideas are arranged somehow in strata, the ideas in each stratum being linked by a complex of relations both among themselves and with those above and below, the lower the stratum, the deeper the idea”. Obviously, DHFRS is a “deep” extension of rough set while classical fuzzy rough set [10], intuitionistic fuzzy rough sets [11] and HFRS [5] are all special cases of DHFRS. Therefore, it is fundamentally worthwhile to study on DHFRS. This paper is sparkled by the aforementioned works and the dual hesitant fuzzy rough information is studied from the viewpoint of assessment deviations. In assessment deviation analysis, any given value is composed of the true-value plus some deviation values. Just like measurement errors, deviations can be classified into three kinds: systematic deviations, random deviations, and gross deviations [12]. Firstly, the DHFRS is transferred to a set of four sets which are used to describe the degree of an element to a set; and then, to determine the deviations of the sets apart from the true-value, differentiated strategy is used. The four sets are weighted according to two parameters, where one quantifies the systematic deviations of the four sets, while the other one quantifies the random deviations of them; subsequently, the true-value of the membership degree of an element to a set is estimated by an operator; furthermore, a dual hesitant fuzzy rough pattern recognition approach based on assessment deviation theories is proposed.
The rest of this paper is organized as follows. In Section 2, the concepts and the fundamental properties of DHFSs and DHFRSs are reviewed. In Section 3, some assessment deviation analyses on DHFRSs are given, and a mathematical model to point estimate the true-value of the membership degree of an element to a set on DHFRSs is proposed. In Section 4, a dual hesitant fuzzy rough pattern recognition approach based on assessment deviation theories is also proposed. In Section 5, an urban traffic modes recognition example is given to illustrate the validity of the newly proposed dual hesitant fuzzy rough pattern recognition approach on DHFRSs. Finally, some conclusions are given in Section 6.
2. Preliminaries
In this section, the concepts and the fundamental properties on HFSs, DHFSs and DHFRSs are reviewed.
Definition 1.
[4,13] Let X be a non-empty set, and a hesitant fuzzy set (HFS) on X be in terms of a function that when applied to X returns a subset of .
Xia and Xu [14] expressed the HFS by a mathematical symbol , where is a finite subset of the set , denoting the possible membership degrees of the element to the set E. For convenience, is called a hesitant fuzzy element (HFE).
For any two HFEs and , Torra [13] defined the union and the intersection of them, which are denoted as , , respectively, where and denote the sth largest value in and , respectively. is denoted as cardinal function, . Especially, when and are two one-element sets, denote , , then, it gets , . When , the existed methods usually extend the shorter one until both of them have the same cardinal number.
As an extension of HFS, Zhu et al. [8] defined the DHFS as follows.
Definition 2.
[8] Let U be a non-empty and finite universe of discourse, then a DHFS on U is described as
where and are two finite subsets of the set , denoting the possible membership degrees and non-membership degrees of the element to the set , respectively, with the conditions , and for all , , , , . For convenience, the pair is called a DHF element (DHFE), and is denoted as . The set of all DHFSs on U is denoted by DHF .
Inspired by the aforementioned two definitions, Zhang et al. [7] defined the dual hesitant fuzzy relation as follows.
Definition 3.
[7] Let U, V be two non-empty and finite universes. A DHF subset of the universe is called a DHF relation from U to V, namely, is given by , where are two finite subsets of the set , denoting the possible membership degrees and non-membership degrees of the relationship between x and y, respectively, with the conditions: and , , where for all , , , . In particular, if , we call a DHF relation on U.
Furthermore, Zhang et al. [7] defined the lower and upper DHF approximations on rough set as follows.
Definition 4.
[7] Let U, V be two non-empty and finite universes, and be a DHF relation from U to V. The triple is called a DHF approximation space. For any , the lower and upper approximations of with respect to are two DHF sets of U, which are defined as
where , , , and . and are, respectively, called the lower and upper approximations of with respect to . The pair is called the DHF rough set of with respect to .
The union and intersection on HFSs which were introduced in Torra [13], Torra and Narukawa [4], Xia and Xu [14] are defined as follows.
Definition 5.
Let U be a nonempty and finite universe of discourse. For any two HFSs and on U, and for all , the union and intersection of and is denoted as and , where
3. Mathematical Methodologies
In this section, the dual hesitant fuzzy rough (DHFR) information is studied from the viewpoint of assessment deviations, and a series of research results on DHFRSs are proposed.
3.1. Assessment Deviation Analysis on DHFRSs
In general, to describe the membership and non-membership degrees of an element to a set in DHF setting, DHFRS gives a lower and an upper DHF approximations which are defined by HFSs. In the following, it will be proved that the lower and upper approximations can be re-defined by four sets, and any element in the sets is used to describe the aforementioned membership degree.
Taking U, V defined in Definition 4, for example, assuming that be a DHF relation from U to V, for any , and are two DHF sets of U whose structures are shown as Equations (2) and (3). Denote
According to the relationship between vague sets and intuitionistic fuzzy sets [15], and can be re-defined as
where
From a statistical point of view, , , , and all can be considered as sets of observation points generated by bootstrap sampling, which are used to describe the membership degree of to x. In the following subsection, by analysing the assessment deviations between the observation points and the true-value of the membership degree, a dual hesitant fuzzy rough weighted aggregating (DHFRWA) operator is proposed.
3.2. Novel Findings on DHFRSs
The systematic and random assessment deviations of DHFRS are defined as follows.
Definition 6.
Let U, V be two non-empty and finite universes, and be a DHF relation from U to V. For any , a set of four approximations of the membership degree of to x is obtained as , where , , , . Denote the true-value of the membership degree of to x as . Then, the Hamming, Euclidean, and the generalized systematic assessment deviations of apart from are denoted as
where is cardinal function, , is the jth largest values in ; whereas i, , = 1, 2, 3, 4, and . Besides, it is noteworthy that holds in most cases. To operate them correctly, one should extend the shorter one until the cardinal numbers of them are the same. The random assessment deviations of 1, 2, 3, 4) are denoted as
In order to better understand the systematic and random assessment deviations on DHFRSs, please refer to Figure 1. In Figure 1, denotes any given DHFS, x denotes any given fuzzy concept.
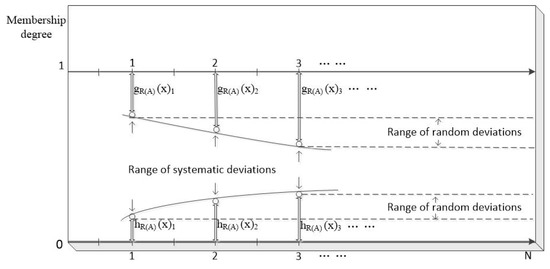
Figure 1.
The sketch map of systematic and random assessment deviations.
In the following, by referring to the measurement error theories [12], a DHFRWA operator is proposed to aggregate the four sets on DHFRS.
Definition 7.
Let U, V be two non-empty and finite universes, and be a DHF relation from U to V. For any , a set of four approximations of the membership degree of to x is obtained as . The given systematic and random assessment deviations of 1, 2, 3, 4) apart from are denoted as and , respectively. Then, a generalized deviation index of is denoted as , and two DHFRWA operators based on assessment deviations are denoted as
where . It is noteworthy that 1, 2, 3, 4) doesn’t always hold, to operate them correctly, one should extend the shorter one until all of them are the same.
Definition 8.
Let and be two fuzzy concepts, and a be an arbitrary element. Let , , be two HFEs representing the membership degrees of a to and , respectively. Then, the possibility that is superior to considering that a belongs to is denoted as
where is a Heaviside step function denoted as
is cardinal function, , 1, 2) is the jth largest values in . Besides, in case that , one should extend the shorter one until both of them are the same.
In order to better understand the novel findings on DHFRSs, please refer to Figure 2.
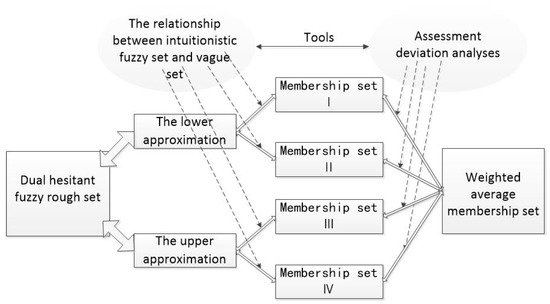
Figure 2.
The Information conversion from DHFRS to weighted average membership set.
4. Main Results
Based on the aforementioned mathematical methods, a novel pattern recognition approach on DHFRs is proposed as follows.
4.1. Novel Pattern Recognition Approach on DHFRs
In this subsection, a novel DHFR pattern recognition approach is proposed. Firstly, the weighted membership degree sets of an object to different patterns are obtained by the DHFRWA operator proposed in the previous subsection; subsequently, according to the comparative results of any two degree sets generated by Definition 7, an pattern recognition result is obtained. In the following, the approach is demonstrated by a mathematical model.
Suppose that there is a pattern recognition problem as follows. Let the universe be the pattern set, the universe be the symptom set, and be an intuitionistic fuzzy relation from U to V. Suppose that there is an object , who has some symptoms in the universe V which is described as , where and are two finite subsets of the set , representing the possible membership and non-membership degrees of to the symptom . Then, an approach is proposed to determine the suitable pattern in U that belongs to.
Step 1 According to Equations (2) and (3), we calculate the lower and upper approximations and of DHFSs with respect to .
Step 2 By Definition 5, for any , a set is obtained to describe the membership degree of to .
Step 3 By Equation (19) or Equation (20), a series of weighted membership degree sets are obtained as 1, 2, ⋯, m).
Step 4 By Equation (21), for any 1, 2, ⋯, m, and are compared, and the optimal pattern recognition that belongs is obtained.
4.2. Supplement Explanations
- (1)
- In classical intuitionistic fuzzy rough environments [16], Definitions 5 and 6 can be simplified as follows.
Theorem 1.
Let U, V be two non-empty finite universes, and be an intuitionistic fuzzy relation from U to V, where , , denoting the membership degree and non-membership degree of the relationship between x and y, respectively, and , . For any intuitionistic fuzzy set on V, where , , denoting the membership degree and non-membership degree of y to A, respectively, and , , the lower and upper approximations of A with respect to are two intuitionistic fuzzy sets on U, which are denoted as , , where , , , and . Then, it gets , where , , , .
By Theorem 1, the following conclusions can be obtained:
- (2)
- In classical hesitant fuzzy rough environments [17], Definitions 5 and 6 can be simplified.
Theorem 2.
Let U, V be two non-empty finite universes, and be a hesitant fuzzy relation from U to V, where is a finite subset of the set , denoting the possible membership degrees of the relationship between x and y. For any hesitant fuzzy set on V, where is a finite subset of the set , denoting the membership degrees of y to , then, the lower and upper approximations of with respect to are two intuitionistic fuzzy sets on U, which are denoted as , , where , , . Then, it gets , where , .
By Theorem 2, the following conclusions can be obtained:
- (i)
- (ii)
- (3)
- There are some important properties for Equations (19) and (20), which are as follows.
Theorem 3.
For any , . Denote
Then, by borrowing from Definition 7, it gets that
- (i)
- If , then, the variance of is larger than which of ;
- (ii)
- If , then, the variance of is smaller than which of ;
- (iii)
- If , then, the comparing between the variances of and is inconclusive.
- (iv)
By Theorem 3, decision-makers can operate flexibility in choose Equation (19) or Equation (20) to aggregate , and .
In the following section, a travel choice problem is studied to show the effectiveness of the proposed pattern recognition approach.
5. Illustrative Example
In this example, a traffic mode recognition problem in a certain district is studied where a new travel mode, i.e., a kind of shared electric bicycle will be domained into this district. In the studied district, residents go to work and live mainly relying on subway travel which locates within 5 km from the their home or work units. At present, there are four kinds of travel modes which residents choose to go to the station. For convenience, the modes are denoted as , where stands for “bicycle”, stands for “electric bicycle”, stands for “shared bicycle”, stands for “bus”. More details about “shared bicycle”, please refer to Schuijbroek et al. [18] and Chemla et al. [19]. Which classical traffic mode would be affected by the greatest extent when the shared electric bicycles are put into the studied market? In the following, the question is analysed and solved by the novel pattern recognition approach.
It is noteworthy that bicycles are made available for shared use to individuals on a very short term basis in Mode . At present, there are mainly five factors which affect residents’ choice behaviour. Also for convenience, the five factors are denoted as , where stands for “travel time”, stands for “travel expenses”, stands for “weather factor”, stands for “comfortability”, stands for “safety”, respectively. Besides, and are explained further as follows. Firstly, the sunk cost of a bicycle and electric bicycle are around 500 Yuan, 2000 Yuan, respectively, while the sunk cost of the shared bicycle and bus are all zero. Secondly, the travel cost of these four modes is 0 Yuan/h, 0.2 Yuan/h, 0.9 Yuan/h and 2 Yuan/time, respectively. Thirdly, the deposit for the mode is 100 Yuan but zero for the other modes. Consistent with social investigations, all the four traffic modes , , , have their own advantages and disadvantages under the aforementioned five factors in the studied district. For example, shows better performances than under the factors and , while shows better performances than under the factors and . Another example is that shows better performances than under the factors and , while shows better performances than under the factor .
In order to quantify the effect of these four traffic modes under five factors, our team make a lot effort in social investigation from positive and negative sides. Thereafter, dual hesitant fuzzy sets are used to aggregate the investigated information. Formally, denote as the knowledge-based relationship between A and F. Then, based on the aggregated investigated information, is obtained, where
In this study, the shared electric bicycle is denoted as . Also by questionnaire survey and interview designed, the dual hesitant fuzzy relationship between and F is obtained as
when is put into the market, which traffic mode would be affected by the greatest extent? In the following, the aforementioned problem is solved by using the novel pattern recognition method.
Step 1 By Definition 4, the lower and upper approximations of each with respect to can be obtained as
Step 2 By Definition 5, for any 1, 2, ⋯, 5), a series of membership sets are obtained as follows:
Step 3 Take , by Equation (19), a series of weighted membership degree sets are obtained as follows:
Step 4 For any , and are compared. From the comparison results, it can be obtained that . Therefore, when the shared electric bicycles are put into the market, electric bicycle would be affected by the greatest extent among the four kinds of classical traffic modes, followed closely by classical shared bicycle.
6. Conclusions
In this paper, the assessment deviations on DHFRSs are studied, and the said innovation points are as follows.
- (i)
- According to the relationship between intuitionistic fuzzy set and vague set, the DHFRS is transferred into a fuzzy set where the membership of any given element to it has multi-grouped values. And then, by the idea of bootstrap sampling, four sets are generated from the DHFRS information, where the elements of any of the sets are considered as observation values of the aforementioned membership degree.
- (ii)
- By differentiated strategy, the four sets on DHFRSS are weighted by their assessment deviations apart from the real-value of the membership degree on DHFRS, where the bigger the assessment deviation, the smaller the weight of its related set on DHFRS; the smaller the assessment deviation, the bigger the weight of its related set on DHFRS.
- (iii)
- The assessment deviations on the four sets are mainly determined by two parameters, where one quantifies the systematic deviations of the four sets, and the other one quantifies the random deviations of the sets. And then, the true-value of the membership degree of an element to the set on DHFRS is estimated by a deviation-based DHFRWA operator.
- (iv)
- A dual hesitant fuzzy rough pattern recognition approach based on the assessment deviation analysis is proposed, and an illustrative example is given to verify the effectiveness of this approach on DHFRSs.
In addition, there are many other methods to compare HFSs beyond Equation (17), and most of them use the thoughts of “Analytic Hierarchy Process” for reference [20]. However, since the Analytic Hierarchy Process is not the essence of this paper, it is not elaborated here.
Acknowledgments
The authors are thankful to the editor Grace Wang, and the anonymous reviewers for their insightful and constructive suggestions and helpful comments in improving this paper. The Fangwei Zhang’s work is partially supported by NNSF of China (51508319, 61374195, 51409157), the research program of the National Special Authorized Social Science Fund of China (07@ZH005), the Nature and Science Fund from Zhejiang Province Ministry of Education (Y201327642). The Jihong Chen’s work is partially supported by NNSF of China (51409157).
Author Contributions
Fangwei Zhang conceived that the DHFRS could be transferred into a fuzzy set where the membership of any given element to it has multi-grouped values; Yuhua Zhu generated four sets from the DHFRS information by using bootstrap sampling theories; Jihong Chen and Ziyi Zhuang analyzed the example data; Yuhua Zhu and Qiang Li wrote the paper; Fangwei Zhang and Jiaru Li revised the manuscript according to reviewer comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DHFRS | Dual hesitant fuzzy rough set |
| HFS | Hesiant fuzzy set |
| HFRS | Hesitant fuzzy rough set |
| DHFE | Dual hesitant fuzzy element |
References
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets. Syst. 1986, 20, 87–96. [Google Scholar]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the The 18th IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Yang, X.B.; Song, X.N.; Qi, Y.S.; Yang, J.Y. Constructive and axiomatic approaches to hesitant fuzzy rough set. Soft Comput. 2014, 18, 1067–1077. [Google Scholar]
- Liang, D.C.; Liu, D. A novel risk decision making based on decision-theoretic rough sets under hesitant fuzzy information. IEEE Trans. Fuzzy. Syst. 2015, 23, 237–247. [Google Scholar]
- Zhang, H.D.; Shu, L.; Liao, S.L.; Xiawu, C.R. Dual hesitant fuzzy rough set and its application. Soft Comput. 2015. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S.; Xia, M.M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 1–13. [Google Scholar] [CrossRef]
- Hardy, G.H. A Mathematician’s Apology; Cambridge University Press: Cambridge, UK, 1992; pp. 27–28. [Google Scholar]
- Dubois, D.; Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 1990, 17, 191–209. [Google Scholar]
- Zhou, L.; Wu, W.Z. On generalized intuitionistic fuzzy approximation operators. Inf. Sci. 2008, 178, 2448–2465. [Google Scholar]
- Fink, K. Knowledge Potential Measurement and Uncertainty; Deutscher University-Verlag: Wiesbaden, Germany, 2004; pp. 189–191. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar]
- Xia, M.M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets. Syst. 1996, 79, 403–405. [Google Scholar]
- Sun, B.; Ma, W.; Liu, Q. An approach to decision making based on intuitionistic fuzzy rough sets over two universes. J. Oper. Res. Soc. 2013, 64, 1079–1089. [Google Scholar]
- Zhang, H.D.; Shu, L.; Liao, S.L. Hesitant fuzzy rough set over two universes and its application in decision making. Soft Comput. 2015. [Google Scholar] [CrossRef]
- Schuijbroek, J.; Hampshire, R.C.; van Hoeve, W.J. Inventory rebalancing and vehicle routing in bike sharing systems. Eur. J. Oper. Res. 2017, 257, 992–1004. [Google Scholar]
- Chemla, A.D.; Meunier, F.; Calvo, R.W. Bike sharing systems: Solving the static rebalancing problem. Discrete Optim. 2013, 10, 120–146. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).