A Comparative Study of Some Soft Rough Sets

Abstract

Through the combination of different types of sets such as fuzzy sets, soft sets and rough sets, abundant hybrid models have been presented in order to take advantage of each other and handle uncertainties. A comparative study of relationships and interconnections of some existing hybrid models has been carried out. Some foundational properties of modified soft rough sets (MSR sets) are analyzed. It is pointed out that MSR approximation operators are some kinds of Pawlak approximation operators, whereas approximation operators of Z-soft rough fuzzy sets are equivalent to approximation operators of rough fuzzy sets. The relationships among F-soft rough fuzzy sets, M-soft rough fuzzy sets and Z-soft rough fuzzy sets are surveyed. A new model called soft rough soft sets has been provided as the generalization of F-soft rough sets, and its application in group decision-making has been studied. Various soft rough sets models show great potential as a tool to solve decision-making problems, and a depth study of the connections among these models contributes to the flexible application of soft rough sets based decision-making approaches.

1. Introduction

Various types of uncertainties exist in real life situations, which calls for useful mathematic tools to meet various information process demands. Usually complicated problems take place with uncertainties, and most of these complex situations can not be handled by adopting classical mathematic methods, considering the fact that with classical mathematic tools all notions are requested to be strict. Up to now, abundant mathematic tools such as fuzzy set theory [1] and rough set theory [2,3] have already been developed and proved to be useful in handling several kinds of the problems that contain uncertainties, and all of these theories share a common inherent difficulty, which is mainly the inadequacy of the parametrization tool [4,5]. However, it is noticed that, without proper parametrization tools, sometimes a practical problem can not be described in a way as much as information collected from different aspects could be taken into account. To handle this issue and to enrich mathematical methodologies for coping with uncertainties, soft set theory was initially proposed by Molodtsov [4] in 1999, which considers every specific object from different attributes’ aspects, in this way, this new model goes beyond all other existing mathematical tools to avoid the above-mentioned difficulties. After soft set theory comes out, in the past few years, there appears a continuous growth of interest in studying theoretical aspects of soft set theory, as well as the practical applications of soft sets.

Abundant mathematical models have already been designed in order to model and process vague concepts, among which it is noteworthy that fuzzy set theory and rough set theory have already drawn worldwide attention from researchers. The development of these two theories makes contributions to handle lots of complicated problems in engineering, economics, social science, et al. The main character of fuzzy set theory is that it describes a vague concept by using a membership function, and the allowance of partial memberships contributes to providing an appropriate framework to represent and process vague concepts. The character of rough set theory relies on handling vagueness and granularity in information systems by indirectly describing a vague concept through two exact concepts called its lower and upper approximations. In Pawlak’s rough set model, the equivalence relation is a vital concept, by replacing the equivalence relation with a fuzzy similarity relation, fuzzy rough sets and rough fuzzy sets have been proposed [6].

The combinations of soft sets, rough sets and fuzzy sets have been extensively studied to benefit each other and to take the best advantage of them. Research on generalization models of soft sets is promising since usually the generalized models are not short of parameter tools, that is, all of the generalized soft set models usually keep the most important feature of soft set theory in considering issues from various aspects. The history of research on extending soft sets applying fuzzy set theory goes beyond fifteen years already since Maji et al. introduced fuzzy soft sets in [7]. Therefore far, the soft sets have been extended to intuitionistic fuzzy soft sets [8], interval-valued intuitionistic fuzzy soft sets [5,9], vague soft sets [10], soft interval sets [11] and many other hybrid soft sets models. The history of research on the generalization of soft sets by using rough set theory is relatively short. To introduce parametrization tools to rough set theory, Feng et al. [12,13] initially put forward the concept of soft rough sets and soft rough fuzzy sets, in which a soft set looks for the lower and upper approximations of a subset of the universe. Afterwards, Meng et al. [14] proposed soft fuzzy rough set, in which model the fuzzy soft set has been adopted into granulate the universe. Benefitting from similarity measures induced by soft sets and soft fuzzy sets, Qin et al. [15] provided several soft fuzzy rough set models through introducing confidence threshold values. Recently, Shabir et al. [16] noticed that Feng et al.’s soft rough sets [12] suffer from some unexpected properties such as the upper approximation of a non-empty set might be empty and a subset set X might not be contained in its upper approximation. To resolve this problem, Shabir et al. [16] modified their soft rough sets and introduced the modified soft rough set (MSR set), which has already been extended to fuzzy soft sets [17], and Z-soft rough fuzzy sets was proposed, and its application in decision-making problems was analyzed.

The exploitation of soft sets and hybrid soft sets models in decision-making shows a great development in the recent years [18,19,20,21,22]. The utilization of soft rough sets models in decision-making shows a promising prospect. Different decision-making approaches have been put forth based on MSR set [20], Z-soft rough fuzzy sets [17], Z-soft fuzzy rough set [21], and other soft rough sets models [23,24]. If the researchers could have a thorough knowledge of the connections among various soft rough sets, we believe that decision-making approaches under framework of soft rough sets could be applied in a more flexible and reliable way. However, the relationships among these hybrid sets have not been systematically studied so far. Furthermore, we notice that a soft set S can be looked upon an information system $I_S$. Based on this information system, we can establish Pawlak rough approximations and rough fuzzy approximations. What is the relationship between soft rough approximations (soft rough fuzzy approximations) in S and Pawlak rough approximations (rough fuzzy approximations) in $I_S$? Additionally, soft set and formal context are mathematically equivalent. The relationships among soft rough approximation operators and derivation operators used in formal concept analysis (FCA) are also interesting issues to be addressed. In this paper, we will concentrate on the discussion of these problems. The paper is structured as follows: Section 2 revises several basic concepts of soft sets, fuzzy sets and rough set. Section 3 studies relationships among several soft rough sets. The properties of MSR approximation operators and different connections between MSR approximation operators and F-soft rough approximation operators are analyzed. It is shown that MSR approximation operators and a kind of Pawlak approximation operators are equivalent, while Z-soft rough fuzzy approximation operators and a kind of rough fuzzy approximation operators are equivalent. The relationships among F-soft rough fuzzy sets, M-soft rough fuzzy sets and Z-soft rough fuzzy sets have also been investigated. Section 4 discusses the relationship between F-soft rough sets and modal-style operators in formal concept analysis. Section 5 proposes a new generalization of F-soft rough set, which is called a soft rough soft set, and a simple application of soft rough soft sets in group decision-making has been studied. Eventually, Section 6 concludes the paper by presenting some remarks and future works.

2. Preliminaries

Here, several concepts of fuzzy sets, soft sets and rough sets are briefly reviewed. Please refer to [1,2,4,7] for details.

An advantageous framework has been offered by fuzzy set theory [1] to handle vague concepts through the allowance for partial memberships. Let U be the universe set. Define a fuzzy set $\mu$ on U by its membership function $\mu :U\to [0,1]$. $\mu (x)$ indicates the degree to which x belongs to the fuzzy set $\mu$ for all $x\in U$. In what follows, we denote the family of all subsets of U by $P(U)$ and the family of all fuzzy sets on U by $F(U)$. The operations of fuzzy sets can be found in [1].

Molodtsov [4] introduced the concept of soft set. Let U be the universe set and E the set consisted of all parameters that is related to U. Hence, a soft set is defined as below:

Definition 1.

A pair $(F,A)$ is called a soft set over U, where $A\subseteq E$ and F is a mapping given by $F:A\to P(U)$ [4].

The soft set is characterized by a parameter set and a function defined on the parameter set. For every parameter $e\in A$, $F(e)$ is said to be the e-approximate elements and, correspondingly, the soft set can be viewed as a parameterized family of subsets of U.

A soft set $(F,A)$ is called a full soft set if ${\cup }_{e\in A}F(e)=U$ [12]; ${\tilde{N}}_{(U,A)}=(N,A)$ is called a relative null soft set (with respect to the parameter set A), if $N(e)=\varnothing$ for all $e\in A$; ${\tilde{W}}_{(U,B)}=(W,B)$ is called a relative whole soft set (with respect to the parameter set B) if $W(e)=U$ for all $e\in B$ [25]. Maji et al. in [7] introduced the concept of fuzzy soft set.

Definition 2.

Let $(U,E)$ be a soft space. A pair $(F,A)$ is called a fuzzy soft set over U, where $A\subseteq E$ and F is a mapping defined as $F:A\to F(U)$ [7].

The fuzzy soft set is also characterized by a parameter set and a function on the parameter set, whereas a fuzzy set on U takes place of a crisp subset of U corresponds to each parameter. It follows that, to a certain degree, a soft set can also be viewed as a special kind of fuzzy soft set.

Pawlak introduced rough set theory in [2], the application of which is based on a structure called information system.

Definition 3.

An information system is a pair $I=(U,A)$ of non-empty finite sets U and A, where U is a set of objects and A is a set of attributes; each attribute $a\in A$ is a function $a:U\to V_a$ , where $V_a$ is the set of all values (called domain) of attribute a [3].

Soft sets and information systems are closely related [13,26,27]. $S=(F,A)$ is assumed to be a soft set over U and $I_S=(U,A)$ an information system induced by S. For any attribute $a\in A$, a function $a:U\to V_a=\{0,1\}$ is defined by $a(x)=1$ if $x\in F(a)$; or else $a(x)=0$. In this way, every soft set could be viewed as an information system. In what follows, $I_S$ is called the information system induced by soft set S.

By contrast, suppose the information system, $I=(U,A)$. It uses a parameter set as

$$\begin{array}{c}\hfill B=\{(a,v_a);a\in A\wedge v_a\in V_a\},\end{array}$$

and it follows that through setting $F(a,v_a)=\{x\in U;a(x)=v_a\}$ for each $a\in A$ and $v_a\in V_a$, a soft set $(F,B)$ can be defined, which is the soft set induced by I.

Let U be the universe of discourse and R be an equivalence relation on U. $(U,R)$ is called Pawlak approximation space. For each $X\subseteq U$, the upper approximation $\overline{R}(X)$ and lower approximation $\underline{R}(X)$ of X with respect to $(U,R)$ are defined as [2]:

$$\overline{R}(X)=\{x\in U;{[x]}_R\cap X\ne \varnothing \},$$

(1)

$$\underline{R}(X)=\{x\in U;{[x]}_R\subseteq X\}.$$

(2)

X is so-called definable in $(U,R)$ if $\underline{R}(X)=\overline{R}(X)$, or else X is a rough set. Thus, in rough set theory, a rough concept is characterized by a couple of exact concepts, namely, its lower approximation and upper approximation. $Po{s}_R(X)=\underline{R}(X)$ and $Ne{g}_R(X)=U-\overline{R}(X)$ are the R-positive region and R-negative region of X, respectively. Furthermore, $Bn{d}_R(X)=\overline{R}(X)-\underline{R}(X)$ is called the R-boundary region.

Up to now, various types of extension models of the Pawlak rough set have been proposed to enrich the theory and to meet different application demands [28,29]. In [12], by the combination of soft set, rough set and fuzzy set theory, soft rough sets and soft rough fuzzy sets were introduced. To make them easy to be distinguished from other models mentioned in the current work and also to facilitate the discussion, these two notions are called F-soft rough sets and F-soft rough fuzzy sets.

Definition 4.

Let $S=(f,A)$ be a soft set over U. $P=(U,S)$ is called a soft approximation space. Two operations can be defined based on P as follows [12]:

$${\underline{apr}}_P(X)=\{u\in U;\exists a\in A(u\in f(a)\subseteq X)\},$$

(3)

$${\overline{apr}}_P(X)=\{u\in U;\exists a\in A(u\in f(a),f(a)\cap X\ne \varnothing )\}.$$

(4)

For all $X\subseteq U$, ${\underline{apr}}_P(X)$ and ${\overline{apr}}_P(X)$ are respectively called the F-lower and F-upper soft rough approximations of X in S. X is F-soft definable in P if ${\underline{apr}}_P(X)={\overline{apr}}_P(X)$, or else X is a F-soft rough set.

It is noted that we can present ${\underline{apr}}_P(X)$ and ${\overline{apr}}_P(X)$ in a more concise manner [13]:

$${\underline{apr}}_P(X)=\cup \{f(a);a\in A\wedge f(a)\subseteq X\},$$

(5)

$${\overline{apr}}_P(X)=\cup \{f(a);a\in A\wedge f(a)\cap X\ne \varnothing \}.$$

(6)

In this definition, the soft set S is regarded as the elementary knowledge on the universe. F-lower and F-upper soft rough approximation operators are not dual to each other, that is, ${\underline{apr}}_P(X^c)={({\overline{apr}}_P(X))}^c$ usually does not hold, where the complement of set X is computed by $X^c=U-X$. If the condition ${\cup }_{a\in A}f(a)=U$ holds in a soft set $S=(f,A)$ over U, this soft set is a full soft set [12]. In this case, $\{f(a);a\in A\}$ comes into being a cover of the universe U. It is pointed out that ${\underline{apr}}_P$, ${\overline{apr}}_P$ and covering rough approximations [30] are closely related but fundamentally different [13]. Additionally, if $\{f(a);a\in A\}$ forms a partition of U, we will call $S=(f,A)$ a partition soft set [13,31].

It is pointed out by Shabir et al. [16] that ∃$x\in U$ s.t. $x\in Ne{g}_P(X)=U-{\overline{apr}}_P(X)$ for all $X\subseteq U$, if $S=(f,A)$ is not a full soft set. In other words, $x\notin {\overline{apr}}_P(X)$ for all $X\subseteq U$. Thus, $X\subseteq {\overline{apr}}_P(X)$ and some basic properties of rough set do not hold in general. Based on these observations, modified soft rough sets (MSR sets) was defined as follows.

Definition 5.

Let $(f,A)$ be a soft set over U and $\phi :U\to P(A)$ be a map defined as $\phi (x)=\{a\in A;x\in f(a)\}$. Then, $(U,\phi )$ is called MSR-approximation space and for any $X\subseteq U$, its lower MSR approximation ${\underline{X}}_{\phi }$ and upper MSR approximation ${\overline{X}}_{\phi }$ are defined as [16]:

$${\underline{X}}_{\phi }=\{x\in U;\forall y\in X^c(\phi (x)\ne \phi (y))\},$$

(7)

$${\overline{X}}_{\phi }=\{x\in U;\exists y\in X(\phi (x)=\phi (y)).$$

(8)

X is MSR definable if the condition ${\underline{X}}_{\phi }={\overline{X}}_{\phi }$ holds, or else X is a MSR set.

Mathematically speaking, $(U,\phi )$ can be looked upon a soft set over A. In [32], $(U,\phi )$ was considered as a pseudo soft set that is induced by $(f,A)$, afterwards a decision-making method related to pseudo soft set was provided.

3. Relationships among Several Soft Rough Sets

3.1. Relationships between F-Soft Rough Approximations and MSR Approximations

The notion of MSR set is the modification of a F-soft rough set, and some inherent connections between these two models should exist, which have not drawn enough attention from scholars yet. In this subsection, a theoretical analysis of F-soft rough sets and MSR sets will be provided, and some connections between F-soft rough approximations and MSR approximations will be pointed out.

It is noted that Ref. [16] ${\underline{apr}}_P(X)\subseteq {\underline{X}}_{\phi }$ for any $X\subseteq U$ and the containment may be proper. Furthermore, in general, ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ or ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$ does not hold. Now, we provide an example:

Example 1.

Let $A=\{a,b,c,d\}$ be a parameter set and $U=\{x_1,x_2,x_3,x_4,x_5,x_6\}$ the universe. Suppose that $S=(f,A)$ is a soft set over U, in which $F(a)=\{x_1,x_6\}$, $F(b)=\{x_3\}$, $F(c)=\varnothing$, $F(d)=\{x_1,x_2,x_5\}$.

(1) By the definition, ${\overline{apr}}_P(U)={\cup }_{a\in A}f(a)=\{x_1,x_2,x_3,x_5,x_6\}$. It follows that $x_4\notin {\overline{apr}}_P(U)$ and hence $x_4\notin {\overline{apr}}_P(X)$ for any $X\subseteq U$.

(2) Let $X=\{x_3,x_4,x_5\}$. By direct computation, we know that ${\overline{apr}}_P(X)=\{x_1,x_2,x_3,x_5\}$, ${\overline{X}}_{\phi }=\{x_2,x_3,x_4,x_5\}$. Thus, ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$, or ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ does not hold.

However, only a shallow impression can be obtained noticing the above-mentioned conclusions in [16], and no details have been provided discussing the properties of and connections among ${\overline{apr}}_P(X)$, ${\overline{X}}_{\phi }$, ${\underline{apr}}_P(X)$ and ${\underline{X}}_{\phi }$. The questions still remain: is there any possibility ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ or ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$ that holds? Which features will be requested if these conditions need to be established? Now, we will pay attention to these questions and provide answers.

A general assumption for Theorems 1–3 and Corollaries 1 and 2 is presented as below:

Let $S=(f,A)$ be a soft set over U and $P=(U,S)$ a soft approximation space.

Theorem 1.

S is a full soft set iff ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ for any $X\subseteq U$.

Proof. 

$(\Rightarrow )$. It is assumed that S is a full soft set and $X\subseteq U$. For all $x\in {\overline{X}}_{\phi }$, ∃$y\in X$ s.t. $\phi (x)=\phi (y)$. By $y\in U={\cup }_{a\in A}f(a)$, ∃$a\in A$ s.t. $y\in f(a)$. Then, $y\in X\cap f(a)$ and $X\cap f(a)\ne \varnothing$. By $y\in f(a)$ we obtain $a\in \phi (y)=\phi (x)$ and hence $x\in f(a)$. Consequently, $x\in {\overline{apr}}_P(X)$. Thus, ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$.

$(\Leftarrow )$. Suppose that, for all $X\subseteq U$, the condition ${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ holds. It can be observed that $x\in {\overline{\{x\}}}_{\phi }\subseteq {\overline{apr}}_P(\{x\})=\cup \{f(a);f(a)\cap \{x\}\ne \varnothing \}=\cup \{f(a);x\in f(a)\}$, for any x in U.

Thus, ∃$a\in A$ s.t. $x\in f(a)$. S is a full soft set by the arbitrary of x. ☐

Theorem 2.

${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$ for any $X\subseteq U$ iff for any $a,b\in A$, $f(a)\cap f(b)=\varnothing$ whenever $f(a)\ne f(b)$.

Proof. 

$(\Leftarrow )$. Assume that for any $a,b\in A$, $f(a)\cap f(b)=\varnothing$ whenever $f(a)\ne f(b)$. Let $X\subseteq U$. For any $x\in {\overline{apr}}_P(X)$, attribute $a\in A$ exists s.t. $x\in f(a)$ and $f(a)\cap X\ne \varnothing$. Thus, we know that there exists $y\in U$ s.t. $y\in f(a)\cap X$. For any $b\in A$, if $f(a)\ne f(b)$, then $f(a)\cap f(b)=\varnothing$ and hence $x\notin f(b)$ by $x\in f(a)$. Thus, $\phi (x)=\{b\in A;f(b)=f(a)\}$. Similarly, we have $\phi (y)=\{b\in A;f(b)=f(a)\}$ and hence $\phi (x)=\phi (y)$. By $y\in X$, we know that $x\in {\overline{X}}_{\phi }$ and consequently ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$.

$(\Rightarrow )$. Assume that ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$ for any $X\subseteq U$. For any $a,b\in A$, if $f(a)\cap f(b)\ne \varnothing$, ∃$x\in U$ s.t. $x\in f(a)\cap f(b)$. By $x\in f(a)$, we conclude that

$$\begin{array}{c}\hfill f(a)\subseteq \cup \{f(c);x\in f(c)\}=\cup \{f(c);\{x\}\cap f(c)\ne \varnothing \}={\overline{apr}}_P(\{x\})\\ \hfill \subseteq {\overline{\{x\}}}_{\phi }=\{y\in U;\phi (y)=\phi (x)\}.\end{array}$$

Meanwhile, if $\phi (y)=\phi (x)$, then $a\in \phi (x)=\phi (y)$ and hence $y\in f(a)$. Therefore, $f(a)=\{y\in U;\phi (y)=\phi (x)\}$. Similarly, by $x\in f(b)$, we have $f(b)=\{y\in U;\phi (y)=\phi (x)\}$ and hence $f(a)=f(b)$. ☐

Theorems 1 and 2 shows that ∃ containment relationships between ${\overline{X}}_{\phi }$ and ${\overline{apr}}_P(X)$ if some specific conditions hold. Based on these two theorems, we can have a clear idea about under which conditions the containment relationships can be held. Furthermore, by Theorems 1 and 2, we obtain

Corollary 1.

Let $f(e)\ne \varnothing$ for each $e\in A$. S is a partition soft set iff ${\overline{apr}}_P(X)={\overline{X}}_{\phi }$ for any $X\subseteq U$.

Corollary 2.

S is a full soft set iff $X\subseteq {\overline{apr}}_P(X)$ for any $X\subseteq U$.

Proof. 

It is assumed that S is a full soft set. For all $X\subseteq U$, it is obvious that $X\subseteq {\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$ by Theorem 1. On the contrary, assume that $X\subseteq {\overline{apr}}_P(X)$ for any $X\subseteq U$. For each $x\in U$,

$$\begin{array}{c}\hfill x\in \{x\}\subseteq {\overline{apr}}_P(\{x\})=\cup \{f(a);f(a)\cap \{x\}\ne \varnothing \}=\cup \{f(a);x\in f(a)\}.\end{array}$$

Thus, ∃$a\in A$ s.t. $x\in f(a)$. Consequently, S is a full soft set as required. ☐

Theorem 3.

${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$ for any $X\subseteq U$ iff for any $x\in U$, ∃$a\in A$ s.t. $f(a)=\{y\in U;\phi (y)=\phi (x)\}$.

Proof. 

$(\Rightarrow )$. Suppose that ${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$ for all $X\subseteq U$. For any $x\in U$, let $X=\{y\in U;\phi (y)=\phi (x)\}$. It follows that

$$\begin{array}{c}\hfill {\underline{X}}_{\phi }=\{u\in U;\exists y\in X(\phi (u)=\phi (y))\}=\{u\in U;\phi (u)=\phi (x)\}=X.\end{array}$$

By $x\in X$ and ${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$, then $x\in {\underline{apr}}_P(X)$ and hence ∃$a\in A$ s.t. $x\in f(a)$ and $f(a)\subseteq X$.

On the other hand, for any $y\in X$, we have $\phi (y)=\phi (x)$, therefore $a\in \phi (x)=\phi (y)$. Then, $y\in f(a)$ and hence $X\subseteq f(a)$. Thus, $f(a)=X=\{y\in U;\phi (y)=\phi (x)\}$.

$(\Leftarrow )$. Assume that $X\subseteq U$ and $x\in {\underline{X}}_{\phi }$. For each $y\in U$, if $\phi (x)=\phi (y)$, we have $y\in X$ by $x\in {\underline{X}}_{\phi }$. It follows that $\{y\in U;\phi (y)=\phi (x)\}\subseteq X$ and ∃$a\in A$ such that $f(a)=\{y\in U;\phi (y)=\phi (x)\}$. Thus, $x\in f(a)$ and $f(a)\subseteq X$. It follows that $x\in {\underline{apr}}_P(X)$ and consequently ${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$. ☐

By Theorem 3, we obtain a clear mind about the necessary conditions for ${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$ to be held, which has not been discussed in other literature yet. The connections between F-soft rough approximations and MSR approximations have been discussed in detail through the theorems presented above.

Keeping in mind that all of the theoretical research should serve practical applications. It is noted that F-soft rough sets and MSR sets group decision-making approaches have been put forward in [20,31], respectively. Based on the analysis about the connections of F-soft rough approximations and MSR approximations, the relationships between decision schemes by using these two different hybrid models could be further discussed in the future, and the decision results obtained by the two decision schemes may have some inherent relationship.

3.2. The Relationships between MSR Approximations and Pawlak’s Rough Approximations

After the notion of MSR sets was put forward, it was applied to different circumstances to cope with practical problems. However, since there is systematic research on its relationship with Pawlak’s rough sets up to now, the rationality of MSR sets may be questioned by scholars from a theoretical point of view.

Let $S=(f,A)$ be a soft set. S induces an information system $I_S=(U,A)$. According to Pawlak [2], A determines an indiscernibility relation $R_S$ on U given by

$$R_S=\{(x,y)\in U\times U;\forall a\in A(a(x)=a(y))\}.$$

(9)

Clearly, $(U,R_S)$ is a Pawlak approximation space. The equivalence class determined by the equivalence relation $R_S$ that contains x is denoted by ${[x]}_{R_S}$. What is the relationship between Pawlak’s rough approximations in $(U,R_S)$ and F-soft rough approximations (MSR approximations) induced by soft set S? This section offers the discussion of this problem.

Theorem 4.

Let $S=(f,A)$ be a partition soft set over U and $P=(U,S)$ a soft approximation space. Define an equivalence relation R on U by

$$R=\{(x,y)\in U\times U;\exists a\in A(\{x,y\}\subseteq f(a)\}.$$

(10)

Then, for all $X\subseteq U$, ${\underline{apr}}_P(X)=\underline{R}(X)$ and ${\overline{apr}}_P(X)=\overline{R}(X)$ [13,31].

Theorem 5.

Let $S=(f,A)$ be a partition soft set over U and $I_S=(U,A)$ the information system induced by soft set $S=(f,A)$. Then, $R_S=R$, where R is determined by Equation (10).

Proof. 

Let $x,y\in U$ and $(x,y)\in R$. By the definition, ∃ $a\in A$ s.t. $\{x,y\}\subseteq f(a)$. It follows that $a(x)=1=a(y)$. For any $b\in A-\{a\}$, if $f(b)=f(a)$, then $\{x,y\}\subseteq f(a)=f(b)$ and hence $b(x)=1=b(y)$; if $f(b)\ne f(a)$, then $f(b)\cap f(a)=\varnothing$ and hence $x\notin f(b)$, $y\notin f(b)$. Then, $b(x)=0=b(y)$. Thus, $c(x)=c(y)$ for each $c\in A$. Consequently, $(x,y)\in R_S$.

Conversely, let $x,y\in U$ and $(x,y)\in R_S$. By $x\in U={\cup }_{a\in A}f(a)$, ∃$a\in A$ s.t. $x\in f(a)$. It follows that $a(y)=a(x)=1$ and hence $y\in f(a)$. Consequently, $\{x,y\}\subseteq f(a)$ and thus $(x,y)\in R$. ☐

By Theorems 4 and 5, in cases when a partition soft set is used as the underlying soft set, F-soft rough sets in $(U,S)$ could be identified with Pawlak’s rough sets in $(U,R_S)$. For MSR sets, we have the following results.

Theorem 6.

Let $S=(F,A)$ be a soft set over U and $I_S=(U,A)$ be the information system induced by soft set $S=(F,A)$.

(1) 

For any $x\in U$, ${[x]}_{R_S}=\{y\in U;\phi (x)=\phi (y)\}$.

(2) 

For any $X\subseteq U$, ${\underline{X}}_{\phi }=\underline{R_S}(X)$.

(3) 

For any $X\subseteq U$, ${\overline{X}}_{\phi }=\overline{R_S}(X)$.

Proof. 

(1) Let $x,y\in U$ and $y\in {[x]}_{R_S}$. Then, $a(x)=a(y)$ for each $a\in A$. For any $b\in \phi (x)$, we have $x\in f(b)$ and hence $b(x)=1$. We can observe that $b(y)=b(x)=1$ and $y\in f(b)$. Thus, $b\in \phi (y)$ and hence $\phi (x)\subseteq \phi (y)$. Similarly, we have $\phi (y)\subseteq \phi (x)$ and consequently $\phi (x)=\phi (y)$.

On the contrary, suppose that $\phi (x)=\phi (y)$. For any $a\in A$, if $a(x)=1$, then $x\in f(a)$ and hence $a\in \phi (x)=\phi (y)$. Thus, $y\in f(a)$ and $a(y)=1$; if $a(x)=0$, then $x\notin f(a)$ and hence $a\notin \phi (x)=\phi (y)$. Thus, $y\notin f(a)$ and $a(y)=0$. Then, $a(x)=a(y)$ for any $a\in A$ and hence $y\in {[x]}_{R_S}$.

(2) Let $X\subseteq U$ and $x\in {\underline{X}}_{\phi }$. For any $y\in {[x]}_{R_S}$, we have $\phi (x)=\phi (y)$ by (1). By $x\in {\underline{X}}_{\phi }$, we have $\phi (x)\ne \phi (z)$ whenever $z\in X^c$. Thus, $y\in X$ by $\phi (x)=\phi (y)$. Then, ${[x]}_{R_S}\subseteq X$ and hence $x\in \underline{R_S}(X)$. We conclude that ${\underline{X}}_{\phi }\subseteq \underline{R_S}(X)$.

On the contrary, assume that $x\in \underline{R_S}(X)$. It follows that ${[x]}_{R_S}\subseteq X$. For any $y\in X^c$, we have $y\notin X$ and hence $y\notin {[x]}_{R_S}$. Thus, $\phi (x)\ne \phi (y)$ by (1). Consequently, $x\in {\underline{X}}_{\phi }$ and hence $\underline{R_S}(X)\subseteq {\underline{X}}_{\phi }$.

(3) Let $X\subseteq U$ and $x\in {\overline{X}}_{\phi }$. It follows that ∃$y\in X$ s.t. $\phi (x)=\phi (y)$. Thus, $y\in {[x]}_{R_S}$. Consequently, ${[x]}_{R_S}\cap X\ne \varnothing$ and hence $x\in \overline{R_S}(X)$.

Conversely, suppose that $x\in \overline{R_S}(X)$. Thus, ${[x]}_{R_S}\cap X\ne \varnothing$. It follows that there exists $y\in X$ s.t. $y\in {[x]}_{R_S}$. Consequently, $\phi (x)=\phi (y)$ and hence $x\in {\overline{X}}_{\phi }$. ☐

Theorem 6 shows that MSR approximation operator is a kind of Pawlak rough approximation operator. The two mathematic models that correspond with these approximation operators have been interconnected by this theorem, which could be regarded as a theoretical proof for the rationality of MSR sets. Benefitting from the notion of MSR set, Zhan et al. provided the definition of Z-soft rough fuzzy set in a recent work [17] .

Definition 6.

Let $(f,A)$ be a soft set over U and $(U,\phi )$ the MSR approximation space. For any fuzzy set $\mu \in F(U)$, the Z-lower and Z-upper soft rough approximations of μ are denoted by ${\underline{\mu }}_{\phi }$ and ${\overline{\mu }}_{\phi },$ respectively, which are fuzzy sets on U given by [17]:

$${\underline{\mu }}_{\phi }(x)=\wedge \{\mu (y);y\in U\wedge \phi (x)=\phi (y)\},$$

(11)

$${\overline{\mu }}_{\phi }(x)=\vee \{\mu (y);y\in U\wedge \phi (x)=\phi (y)\},$$

(12)

for each $x\in U$, and the operators ${\underline{\mu }}_{\phi }$ and ${\overline{\mu }}_{\phi }$ are the Z-lower and Z-upper soft rough approximation operators on a fuzzy set, respectively. Specifically, if ${\underline{\mu }}_{\phi }={\overline{\mu }}_{\phi }$, μ is a Z-soft definable; or else μ is a Z-soft rough fuzzy set.

By Theorem 6 (1), the following corollary could easily be achieved:

Corollary 3.

Let $S=(F,A)$ be a soft set over U and $I_S=(U,A)$ the information system induced by soft set $S=(F,A)$. Then,

(1) 

${\underline{\mu }}_{\phi }(x)=\wedge \{\mu (y);y\in {[x]}_{R_S}\},and$

(2) 

${\overline{\mu }}_{\phi }(x)=\vee \{\mu (y);y\in {[x]}_{R_S}\}$

for any $\mu \in F(U)$, $x\in U$.

By Corollary 3, Z-lower and Z-upper soft rough approximation operators are equivalent to Dubois and Prade’s lower and upper rough fuzzy approximation operators in [6]. Benefitting from this corollary, the researchers may refer to both of the theories’ aspects and the applications of rough fuzzy sets to better study the development of Z-soft rough sets. Furthermore, the utilization of rough set theory in decision system has been extensively studied during the past few decades. Through discussing the connections between F-soft rough set and and Pawlak rough set, as well as the connections between MSR approximation operators and Pawlak rough approximation operators, the exploitation of various soft rough sets models in decision-making may be studied in a more logic and systematic way in the future.

3.3. The Relationships among Several Soft Rough Fuzzy Sets

A soft rough fuzzy set can be viewed as an extension model of a soft rough set, where the approximations of a fuzzy set in a soft approximation space are characterized. There are several distinct soft rough fuzzy set models in the literature. In the current part, the connections between soft rough fuzzy set and rough fuzzy set will be discussed, as well as the relationships among several soft rough fuzzy sets.

Soft rough approximation operators on fuzzy sets were initially proposed by Feng et al. in [12].

Definition 7.

Let $S=(f,A)$ be a full soft set over U and $P=(U,S)$ a soft approximation space. The lower and upper soft rough approximations of a fuzzy set, $\mu \in F(U)$, with respect to P are noted as ${\underline{sap}}_P(\mu )$ and ${\overline{sap}}_P(\mu )$, respectively, which are defined by [12]:

$${\underline{sap}}_P(\mu )(x)=\wedge \{\mu (y);\exists a\in A(\{x,y\}\subseteq f(a))\},$$

(13)

$${\overline{sap}}_P(\mu )(x)=\vee \{\mu (y);\exists a\in A(\{x,y\}\subseteq f(a))\},$$

(14)

for all $x\in U$. The operators ${\underline{sap}}_P$ and ${\overline{sap}}_P$ are the F-lower and F-upper soft rough approximation operators on fuzzy sets. If ${\underline{sap}}_P(\mu )={\overline{sap}}_P(\mu )$, μ is said to be F-soft definable, or else μ is called a F-soft rough fuzzy set.

Note that ${\underline{sap}}_P$ and ${\overline{sap}}_P$ are dual to each other, i.e., ${\overline{sap}}_P({\mu }^c)={({\underline{sap}}_P(\mu ))}^c$ for every $\mu \in F(U)$. It has already been figured out that rough fuzzy sets in Pawlak approximation space $(U,R)$ can be identified with F-soft rough fuzzy sets in soft approximation space $(U,S)$ when the underlying soft set S is a partition soft set [13].

Meng et al. [14] noted that ${\overline{sap}}_P$ is a generalization of ${\overline{apr}}_P$, i.e., ${\overline{sap}}_P(X)={\overline{apr}}_P(X)$ if $X\in P(U)$. On the contrary, ${\underline{sap}}_P$ is a not a generalization of ${\underline{apr}}_P$. Considering this issue, Meng et al. presented another soft rough fuzzy set model in [14].

Definition 8.

Let $S=(f,A)$ be a full soft set over U and $P=(U,S)$ a soft approximation space. The lower soft rough approximation ${\underline{sap}}_P^{\prime }(\mu )$ and upper soft rough approximation ${\overline{sap}}_P^{\prime }(\mu )$ of the fuzzy set $\mu \in F(U)$ are fuzzy sets in U defined as [14]:

$${\underline{sap}}_P^{\prime }(\mu )(x)={\vee }_{x\in f(a)}{\wedge }_{y\in f(a)}\mu (y),$$

(15)

$${\overline{sap}}_P^{\prime }(\mu )(x)={\wedge }_{x\in f(a)}{\vee }_{y\in ,f(a)}\mu (y)$$

(16)

for all $x\in U$. μ is called soft definable if the condition ${\underline{sap}}_P^{\prime }(\mu )={\overline{sap}}_P^{\prime }(\mu )$ holds; or else μ is a soft rough fuzzy set. For avoiding confusion with other soft rough fuzzy set models, it will be called M-soft rough fuzzy set in the following parts.

It is proved that [14] ${\underline{sap}}_P^{\prime }$ and ${\overline{sap}}_P^{\prime }$ are dual to each other, and ${\underline{sap}}_P^{\prime }$ is a generalization of ${\underline{apr}}_P$, i.e., ${\underline{sap}}_P^{\prime }(X)={\underline{apr}}_P(X)$ for any $X\subseteq U$.

Theorem 7.

Let $S=(f,A)$ be a partition soft set over U, $P=(U,S)$ a soft approximation space, and $(U,R)$ a Pawlak approximation space, where R is given by Equation (10). For each $\mu \in F(U)$, ${\underline{sap}}_P^{\prime }(\mu )=\underline{R}(\mu )$ and ${\overline{sap}}_P^{\prime }(\mu )=\overline{R}(\mu )$.

Proof. 

Assume that $\mu \in F(U)$ and $x\in U$. For each $y\in {[x]}_R$, ∃$a\in A$ s.t. $\{x,y\}\subseteq f(a)$. Suppose that $b\in A$ and $x\in f(b)$. We note that $(f,A)$ is a partition soft set. By $x\in f(a)\cap f(b)$, it follows that $f(a)\cap f(b)\ne \varnothing$ and hence $f(a)=f(b)$. Hence,

$$\begin{array}{c}\hfill {\underline{sap}}_P^{\prime }(\mu )(x)={\vee }_{x\in f(a)}{\wedge }_{z\in f(a)}\mu (z)={\wedge }_{z\in f(a)}\mu (z)\le \mu (y).\end{array}$$

Consequently, ${\underline{sap}}_P^{\prime }(\mu )(x)\le \wedge \{\mu (y);y\in {[x]}_R\}=\underline{R}(\mu )(x)$.

Conversely, suppose that $x\in f(a)$. For each $y\in f(a)$, since $\{x,y\}\subseteq f(a),$ we get $y\in {[x]}_R$.

$$\begin{array}{c}\hfill \mu (y)\ge \wedge \{\mu (z);z\in {[x]}_R\}=\underline{R}(\mu )(x),\end{array}$$

hence ${\wedge }_{y\in f(a)}\mu (y)\ge \underline{R}(\mu )(x)$. Consequently,

$$\begin{array}{c}\hfill {\underline{sap}}_P^{\prime }(\mu )(x)={\vee }_{x\in f(a)}{\wedge }_{z\in f(a)}\mu (z)\ge \underline{R}(\mu )(x),\end{array}$$

and ${\overline{sap}}_P^{\prime }(\mu )=\overline{R}(\mu )$ can be proved similarly. ☐

By this theorem, the (classical) rough fuzzy sets in Pawlak approximation space $(U,R)$ and M-soft rough fuzzy sets in soft approximation space $(U,S)$ are equivalent when the underlying soft set S is a partition soft set. It is shown by Corollary 3 that Z-soft rough fuzzy sets could be regarded as a kind of rough fuzzy set, which indicates that there also exist some fantastic relationships between these two distinct models. The following theorem demonstrates the correlation between Z-soft rough approximation operators and M-soft rough approximation operators.

Theorem 8.

Let $S=(f,A)$ be a full soft set over U, $P=(U,S)$ a soft approximation space and $\mu \in F(U)$:

(1) 

${\underline{sap}}_P^{\prime }(\mu )\subseteq {\underline{\mu }}_{\phi }$,

(2) 

${\overline{\mu }}_{\phi }\subseteq {\overline{sap}}_P^{\prime }(\mu )$.

Proof. 

(1) Let $x\in U$, $a\in A$, $x\in f(a)$. For any $y\in U$, if $y\in {[x]}_R$, then $\phi (x)=\phi (y)$. It follows that $a\in \phi (x)=\phi (y)$ and hence $y\in f(a)$. Then, ${[x]}_R\subseteq f(a)$ and hence ${\wedge }_{y\in f(a)}\mu (y)\le \wedge \{\mu (y);y\in {[x]}_R\}={\underline{\mu }}_{\phi }(x)$. Consequently, we conclude that

$$\begin{array}{c}\hfill {\underline{sap}}_P^{\prime }(\mu )(x)={\vee }_{x\in f(a)}{\wedge }_{y\in f(a)}\mu (y)\le {\underline{\mu }}_{\phi }(x)\end{array}$$

and hence ${\underline{sap}}_P^{\prime }(\mu )\subseteq {\underline{\mu }}_{\phi }$.

(2) Let $x\in U$, $a\in A$ and $x\in f(a)$. By (1), we have ${[x]}_R\subseteq f(a)$ and hence ${\overline{\mu }}_{\phi }(x)=\vee \{\mu (y);y\in {[x]}_R\}\le {\vee }_{y\in f(a)}\mu (y)$. It follows that

$$\begin{array}{c}\hfill {\overline{\mu }}_{\phi }(x)\le {\wedge }_{x\in f(a)}{\vee }_{y\in f(a)}\mu (y)={\overline{sap}}_P^{\prime }(\mu )(x)\end{array}$$

and hence ${\overline{\mu }}_{\phi }\subseteq {\overline{sap}}_P^{\prime }(\mu )$. ☐

It is noted that F-soft rough approximation operators ${\underline{apr}}_P(\mu )$, ${\overline{apr}}_P(\mu )$ can be expressed equivalently as [15]:

$$\begin{array}{c}\hfill {\underline{sap}}_P(\mu )(x)=\wedge \{\mu (y);\exists a\in A(\{x,y\}\subseteq f(a))\}={\wedge }_{x\in f(a)}{\wedge }_{y\in f(a)}\mu (y),\\ \hfill {\overline{sap}}_P(\mu )(x)=\vee \{\mu (y);\exists a\in A(\{x,y\}\subseteq f(a))\}={\vee }_{x\in f(a)}{\vee }_{y\in f(a)}\mu (y).\end{array}$$

Therefore, we have the following corollary:

Corollary 4.

Let $S=(f,A)$ be a full soft set over U and $P=(U,S)$ a soft approximation space. For any $\mu \in F(U)$,

$$\begin{array}{c}\hfill {\underline{sap}}_P(\mu )\subseteq {\underline{sap}}_P^{\prime }(\mu )\subseteq {\underline{\mu }}_{\phi }\subseteq \mu \subseteq {\overline{\mu }}_{\phi }\subseteq {\overline{sap}}_P^{\prime }(\mu )\subseteq {\overline{sap}}_P(\mu ).\end{array}$$

Meng et al. [14] presented a kind of soft fuzzy approximation space, where a fuzzy soft set is regarded as the elementary knowledge on the universe and used to granulate the universe.

Definition 9.

Let $\mathcal{F}=(f,A)$ be a fuzzy soft set over U. The pair $SF=(U,\mathcal{F})$ is called a soft fuzzy approximation space. For a fuzzy set $\mu \in F(U)$, the lower and upper soft fuzzy rough approximations of μ with respect to $SF$ are denoted by ${\underline{Apr}}_{SF}(\mu )$ and ${\overline{Apr}}_{SF}(\mu )$, respectively, which are given by [14]:

$${\underline{Apr}}_{SF}(\mu )(x)={\wedge }_{a\in A}((1-f(a)(x))\vee ({\wedge }_{y\in U}((1-f(a)(y))\vee \mu (y)))),$$

(17)

$${\overline{Apr}}_{SF}(\mu )(x)={\vee }_{a\in A}(f(a)(x)\wedge ({\vee }_{y\in U}(f(a)(y)\wedge \mu (y)))),$$

(18)

for all $x\in U$. The operators ${\underline{Apr}}_{SF}$ and ${\overline{Apr}}_{SF}$ are called the lower and upper soft fuzzy rough approximation operators on fuzzy sets.

It is proved that [14] ${\underline{Apr}}_{SF}$ and ${\overline{Apr}}_{SF}$ are extensions of ${\underline{sap}}_{SF}$ and ${\overline{sap}}_{SF}$, respectively, i.e., if $\mathcal{F}=(f,A)$ is a soft set, then ${\underline{Apr}}_{SF}(\mu )={\underline{sap}}_{SF}(\mu )$ and ${\overline{Apr}}_{SF}(\mu )={\overline{sap}}_{SF}(\mu )$ for any $\mu \in F(U)$.

Theorem 9.

Suppose that $\mathcal{F}=(f,A)$ is a fuzzy soft set over U and $SF=(U,\mathcal{F})$. Let $R_{\mathcal{F}}$ be the fuzzy relation on U given by $R_{\mathcal{F}}(x,y)={\vee }_{a\in A}(f(a)(x)\wedge f(a)(y))$. For each $\mu \in F(U)$,

(1) 

${\underline{Apr}}_{SF}(\mu )=\underline{R_{\mathcal{F}}}(\mu )$,

(2) 

${\overline{Apr}}_{SF}(\mu )=\overline{R_{\mathcal{F}}}(\mu )$.

By this theorem, the soft fuzzy rough approximation presented in Definition 9 is a kind of Dubois and Prade’s fuzzy rough approximation in [6]. We note that $R_{\mathcal{F}}(x,y)$ describes a kind of similarity between x and y, and $R_{\mathcal{F}}$ is symmetric but $R_{\mathcal{F}}(x,x)\ne 1$ in general.

The utilization of Z-soft rough fuzzy set in decision-making has already been studied in [17]. Through discussing the connections among different soft rough fuzzy set models, we can further explore the applications of the other two kinds of soft rough fuzzy sets models in decision-making, enrich the decision mechanisms and pay attention to the selection of the most suitable mechanism according to environments. The soft fuzzy rough approximation operators on fuzzy sets proposed by Meng et al. [14] have the potential to be utilized to handle decision-making problems, discussion on the connections between which and fuzzy rough approximation operators confirm the rationality of this model from the theoretical perspective and lays the foundation for subsequent practical applications.

4. $\mathit{F}$-Soft Rough Sets and Modal-Style Operators in FCA

FCA [22,33,34] provides a methodology for knowledge description and summarization. In this section, several absorbing connections between F-soft rough sets and modal-style operators in FCA will be discussed. Formal concept analysis is carried out based on a formal context specifying which objects posses what properties or attributes. A formal concept is formulated as a pair of two sets, one is consists of objects and another consists of properties or attributes, and these two sets are connected by two set-theoretic operators. A complete lattice called concept lattice is constituted by the set of all formal concepts, which reflects the correlation of generalization and specialization for formal concepts.

Definition 10.

A formal context $(G,M,I)$ consists of two sets G and M and a relation I between G and M. The elements of G are called the objects and the elements of M are called the attributes of the context. $(g,m)\in I$ indicate that the object g has the attribute m, or the attribute m is possessed by the object g [33].

Let $(G,M,I)$ be a formal context. For $A\subseteq G$, $B\subseteq M$, Duntsch and Gediga [6] defined a pair of modal-style operators $△,▽$ as follows:

$$A^{△}=\{m\in M;\exists g\in A((g,m)\in I)\},$$

(19)

$$A^{▽}=\{m\in M;\forall g\in G((g,m)\in I\to g\in A)\},$$

(20)

$$B^{△}=\{g\in G;\exists m\in B((g,m)\in I)\},$$

(21)

$$B^{▽}=\{g\in G;\forall m\in M((g,m)\in I\to m\in B)\}.$$

(22)

Recently, the granular computing based concept lattice theory has received much attention [35].

Rough set theory, soft set theory and concept lattices have similar basis data description. Mathematically speaking, the notions of soft set and formal context are equivalent. Furthermore, both a formal context and a soft set can be considered as a two-valued information system.

Theorem 10.

Let $S=(F,A)$ be a soft set over U. A formal context $C_S=(U,A,I_S)$ is induced by S, where $I_S$ is provided as

$$\begin{array}{c}\hfill I_S=\{(x,a)\in U\times A;x\in F(a)\}.\end{array}$$

Conversely, let $C=(U,A,I)$ be a formal context. A set-valued mapping $F_C:A\to P(U)$ is defined by

$$\begin{array}{c}\hfill F_C(a)=\{x\in U;(x,a)\in I\}\end{array}$$

for all $a\in A$, and $S_C=(F_C,A)$ is a soft set. Moreover, we have $S_{C_S}=S$ and $C_{S_C}=C$.

Proof. 

Only the proof for $S_{C_S}=S$ and $C_{S_C}=C$ will be provided here. Suppose that $S=(F,A)$ is a soft set over U and $a\in A$. For any $x\in U$, from the definition, we obtain that

$$\begin{array}{c}\hfill x\in F_{C_S}(a)\iff (x,a)\in I_S\iff x\in F(a).\end{array}$$

That is, $F_{C_S}(a)=F(a)$ for all $a\in A$. Thus, $F_{C_S}=F$, whence $S_{C_S}=S$.

Next, assume that $C=(U,A,I)$ is a formal context, $x\in U$ and $a\in A$. Then, by definition,

$$\begin{array}{c}\hfill (x,a)\in I_{S_C}\iff x\in F_C(a)\iff (x,a)\in I.\end{array}$$

Therefore, we conclude that $C_{S_C}=C$ as required. ☐

Theorem 11 shows the relationship among operators △, ▽ and soft rough approximation operators.

Theorem 11.

Let $S=(F,A)$ be a soft set over U. For any $X\subseteq U$, ${\underline{apr}}_P(X)=X^{▽△}$, ${\overline{apr}}_P(X)=X^{△△}$.

Proof. 

(1) For any $x\in {\underline{apr}}_P(X)$, ∃$a\in A$ s.t. $x\in f(a)\subseteq X$. Then, $x\in a^{△}$ and $a^{△}\subseteq X$. Therefore, $a\in X^{▽}$ and consequently $x\in a^{△}\subseteq X^{▽△}$. We conclude that ${\underline{apr}}_P(X)\subseteq X^{▽△}$.

Conversely, if $x\in X^{▽△}$, then ∃$a\in X^{▽}$ s.t. $x\in a^{△}$. Then, $x\in f(a)$ and $f(a)\subseteq X$. Thus, $x\in \{f(c);f(c)\subseteq X\}={\underline{apr}}_P(X)$ and hence $X^{▽△}\subseteq {\underline{apr}}_P(X)$.

(2) For any $x\in {\overline{apr}}_P(X)$, ∃$a\in A$ satisfying $x\in f(a)$ and $f(a)\cap X\ne \varnothing$. It follows that $x\in a^{△}$ and $a^{△}\cap X\ne \varnothing$. Thus, $a\in X^{△}$ and consequently $x\in a^{△}\subseteq X^{△△}$.

Conversely, ∃$a\in X^{△}$ s.t. $x\in a^{△}$ if $x\in X^{△△}$. Then, $x\in f(a)$ and $f(a)\cap X\ne \varnothing$. Consequently, $x\in \{f(c);f(c)\cap X\ne \varnothing \}={\overline{apr}}_P(X)$.

FCA has become increasingly popular among various methods of conceptual data analysis, knowledge representation and decision-making. Depth study on the connections of soft rough sets theory and FCA contributes to the reference and fusion for decision-making approaches in these two different fields.

5. A New Generalization of F-Soft Rough Set: Soft Rough Soft Sets

In this section, by extending the notion of F-soft rough set, a new generalization model called soft rough soft set will be proposed. In this new model, we use a soft set is as the elementary knowledge to compute the approximations of soft set. In this way, parameterized tools can be used to the greatest extent. Some basic properties of the new proposed model are discussed. A multi-group decision-making approach based on soft rough soft sets has been provided.

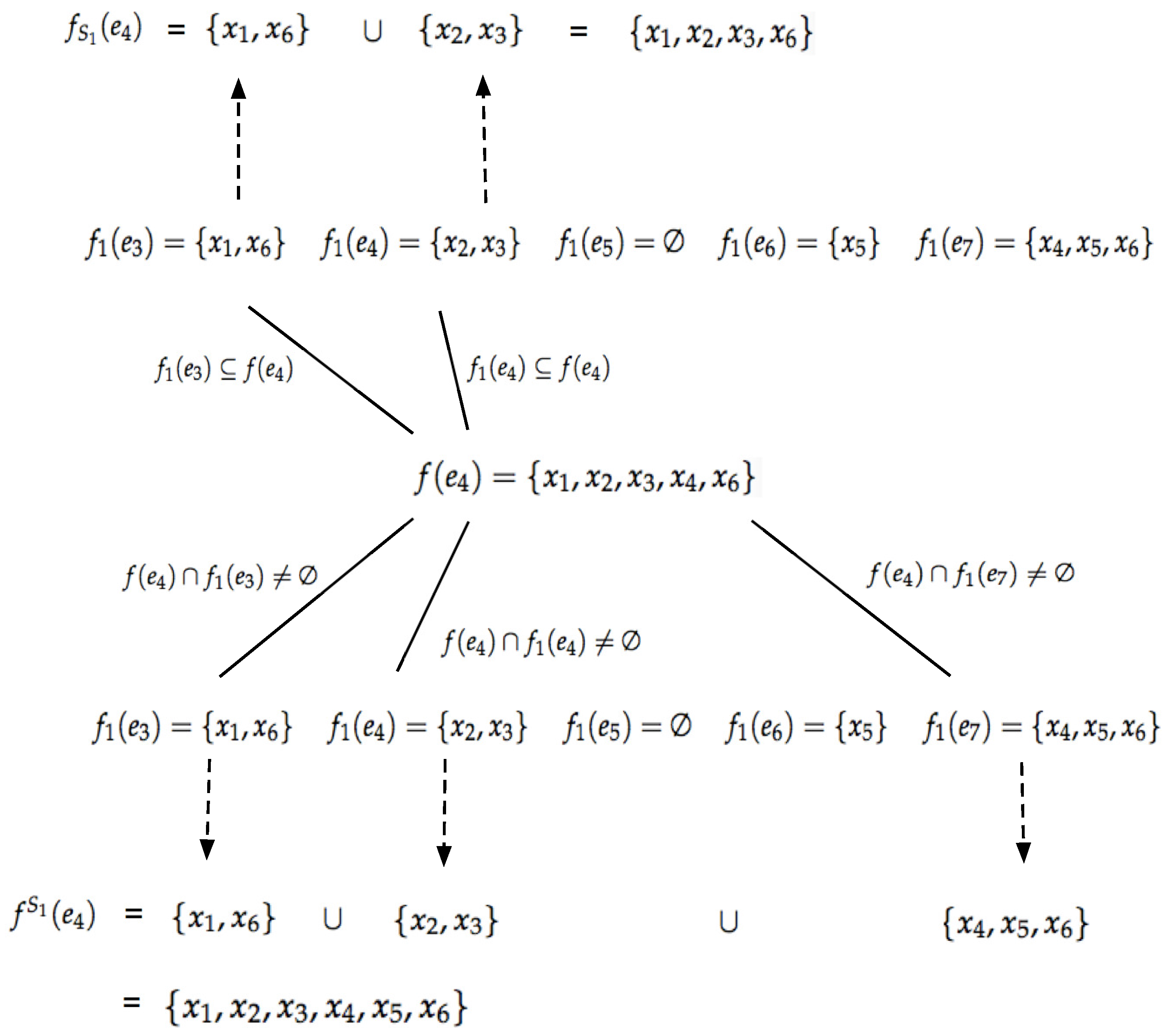
Definition 11.

Let U be the universe set and A, $A_1$ be parameter sets. Let ${\mathcal{S}}_1=(f_1,A_1)$ be a full soft set over U and $(U,{\mathcal{S}}_1)$ be a soft approximation space. Let $\mathcal{S}=(f,A)$ be a soft set over U. The lower and upper soft rough approximations of $\mathcal{S}$ in $(U,{\mathcal{S}}_1)$ are denoted by ${\underline{sapr}}_{S_1}(\mathcal{S})=(f_{S_1},A)$ and ${\overline{sapr}}_{S_1}(\mathcal{S})=(f^{S_1},A)$, which are soft sets over U defined by:

$$\begin{array}{c}\hfill f_{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq f(e)]\},\\ \hfill f^{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap f(e)\ne \varnothing ]\},\end{array}$$

for all $e\in A$. ${\underline{sapr}}_{S_1}$, ${\overline{sapr}}_{S_1}$ are the lower and the upper soft rough approximation operators on soft set $\mathcal{S}$, respectively. If ${\underline{sapr}}_{S_1}(\mathcal{S})={\overline{sapr}}_{S_1}(\mathcal{S})$, the soft set $\mathcal{S}$ is soft definable, or else $\mathcal{S}$ is so-called a soft rough soft set.

Example 2.

Suppose that the universe set $U=\{x_1,x_2,x_3,x_4,x_5,x_6\}$ and the parameters set $E=\{e_1,e_2,e_3,e_4,e_5,e_6,e_7\}$. Let $A=\{e_1,e_2,e_3,e_4\}\subseteq E$ and $A_1=\{e_3,e_4,e_5,e_6,e_7\}\subseteq E$. Let ${\mathcal{S}}_1=(f_1,A_1)$ be a full soft set and $\mathcal{S}=(f,A)$ be a soft set over U as shown by

Table 1. Soft set $(f_1,A_1)$.

	U	x1	x2	x3	x4	x5	x6
A
e3		1	0	0	0	0	1
e4		0	1	1	0	0	0
e5		0	0	0	0	0	0
e6		0	0	0	0	1	0
e7		0	0	0	1	1	1

and

Table 2. Soft set $(f,A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	0	1	0	1
e2		0	1	1	0	0	0
e3		0	0	0	1	1	1
e4		1	1	1	1	0	1

, respectively. In the soft approximation space $(U,{\mathcal{S}}_1)$, by Definition 11, we get the lower soft rough approximation ${\underline{sapr}}_{S_1}(\mathcal{S})=(f_{S_1},A)$ and the upper soft rough approximation ${\overline{sapr}}_{S_1}(\mathcal{S})=(f^{S_1},A)$ of soft set $\mathcal{S}=(f,A)$, as shown by

Table 3. Soft set $(f_{S_1},A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	0	0	0	0	1
e2		0	1	1	0	0	0
e3		0	0	0	1	1	1
e4		1	1	1	0	0	1

and

Table 4. Soft set $(f^{S_1},A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	1	1	1	1
e2		0	1	1	0	0	1
e3		1	0	0	1	1	1
e4		1	1	1	1	1	1

, respectively. In order to facilitate the readers to understand, Figure 1 is given to show the process of computing $f_{S_1}(e_4)$ and $f^{S_1}(e_4)$ from $f(e_4)$.

Proposition 1.

Let ${\mathcal{S}}_1=(f_1,A_1)$ be a full soft set over U and $(U,{\mathcal{S}}_1)$ be a soft approximation space. Let $\mathcal{S}=(f,A)$ be a soft set over U. The following properties hold:

(1) 

${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq \mathcal{S}\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})$,

(2) 

${\underline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})={\tilde{N}}_{(U,A)}={\overline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})$,

(3) 

${\overline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})={\tilde{W}}_{(U,A)}={\underline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})$.

Proof. 

The lower and upper soft rough approximations of ${\tilde{N}}_{(U,A)}=(N,A)$ in $(U,{\mathcal{S}}_1)$ are denoted by ${\underline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})=(N_{S_1},A)$ and ${\overline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})=(N^{S_1},A)$; the lower and upper soft rough approximations of ${\tilde{W}}_{(U,A)}=(W,A)$ in $(U,{\mathcal{S}}_1)$ are denoted by ${\underline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})=(W_{S_1},A)$ and ${\overline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})=(W^{S_1},A)$.

(1a) For all $x\in U,e\in A$, if $x\in f_{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq f(e)]\}$, then we obtain $x\in f(e)$, so $f_{S_1}(e)\subseteq f(e)$;

(1b) For all $e\in A$, if $x\in f(e)$, since $(f_1,A_1)$ is a full soft set, we obtain that $\exists e^{\prime }\in A_1$, s.t. $x\in f_1(e^{\prime })$, then $x\in f_1(e^{\prime })\cap f(e)\ne \varnothing$, then $x\in \{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap f(e)\ne \varnothing ]\}$, that is, $x\in f^{S_1}(e)$ and $f(e)\subseteq f^{S_1}(e)$ for all $e\in A$.

Hence, we know that $f_{S_1}(e)\subseteq f(e)\subseteq f^{S_1}(e)$ for all $e\in A$, that is, ${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq \mathcal{S}\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})$.

(2a) By the definition of relative null soft set, we know $N(e)=\varnothing$ for all $e\in A$. For all $e\in A$, we have $N_{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq N(e)]\}=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq \varnothing ]\}=\varnothing =N(e)$, that is, ${\underline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})={\tilde{N}}_{(U,A)}$;

(2b) By the definition of relative null soft set, we know $N(e)=\varnothing$ for all $e\in A$. For all $e\in A$, we have $N^{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap N(e)\ne \varnothing ]\}=\varnothing =N(e)$, that is, ${\overline{sapr}}_{S_1}({\tilde{N}}_{(U,A)})={\tilde{N}}_{(U,A)}$.

(3a) By the definition of relative whole soft set, we know $W(e)=U$ for all $e\in A$. For all $e\in A$, we have $W^{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap W(e)\ne \varnothing ]\}=U=W(e)$, that is, ${\overline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})={\tilde{W}}_{(U,A)}$.

(3b) By the definition of relative whole soft set, we know $W(e)=U$ for all $e\in A$. Since $(f_1,A_1)$ is a full soft set over U, for all $e\in A$, we have $W_{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq W(e)]\}=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq U]\}=U=W(e)$, that is, ${\underline{sapr}}_{S_1}({\tilde{W}}_{(U,A)})={\tilde{W}}_{(U,A)}$. ☐

Proposition 2.

Suppose that ${\mathcal{S}}_1=(f_1,A_1)$ is a full soft set over U and $(U,{\mathcal{S}}_1)$ is a soft approximation space. Let $\mathcal{S}=(f,A)$, $\mathcal{T}=(g,A)$ be two soft sets over U. The following properties hold:

(1) 

$\mathcal{S}\subseteq \mathcal{T}\Rightarrow {\underline{sapr}}_{S_1}(\mathcal{S})\subseteq {\underline{sapr}}_{S_1}(\mathcal{T})$,

(2) 

$\mathcal{S}\subseteq \mathcal{T}\Rightarrow {\overline{sapr}}_{S_1}(\mathcal{S})\subseteq {\overline{sapr}}_{S_1}(\mathcal{T})$,

(3) 

${\underline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\underline{sapr}}_{S_1}(\mathcal{S})\cap {\underline{sapr}}_{S_1}(\mathcal{T})$,

(4) 

${\underline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\underline{sapr}}_{S_1}(\mathcal{S})\cup {\underline{sapr}}_{S_1}(\mathcal{T})$,

(5) 

${\overline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\overline{sapr}}_{S_1}(\mathcal{S})\cup {\overline{sapr}}_{S_1}(\mathcal{T})$,

(6) 

${\overline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})\cap {\overline{sapr}}_{S_1}(\mathcal{T})$.

Proof. 

The lower and upper soft rough approximations of $\mathcal{S}$ in $(U,{\mathcal{S}}_1)$ are denoted by ${\underline{sapr}}_{S_1}(\mathcal{S})=(f_{S_1},A)$ and ${\overline{sapr}}_{S_1}(\mathcal{S})=(f^{S_1},A)$; the lower and upper soft rough approximations of $\mathcal{T}$ in $(U,{\mathcal{S}}_1)$ are denoted by ${\underline{sapr}}_{S_1}(\mathcal{T})=(g_{S_1},A)$ and ${\overline{sapr}}_{S_1}(\mathcal{T})=(g^{S_1},A)$.

(1) If $\mathcal{S}\subseteq \mathcal{T}$, then for all $e\in A$, we have $f(e)\subseteq g(e)$. Assume that $x\in f_{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq f(e)]\}$. From $f(e)\subseteq g(e)$, we obtain $x\in \{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime })\subseteq g(e)]\}=g_{S_1}(e)$. Therefore, we get $f_{S_1}(e)\subseteq g_{S_1}(e)$ for all $e\in A$, i.e., ${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq {\underline{sapr}}_{S_1}(\mathcal{T})$;

(2) If $\mathcal{S}\subseteq \mathcal{T}$, then for all $e\in A$, we have $f(e)\subseteq g(e)$. Assume that $x\in f^{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap f(e)\ne \varnothing ]\}$, from $f(e)\subseteq g(e)$, we obtain $\exists e^{\prime }\in A_1$, s.t. $x\in f_1(e^{\prime }),f_1(e^{\prime })\cap g(e)\ne \varnothing$, so $x\in g^{S_1}(e)=\{x\in U:\exists e^{\prime }\in A_1[x\in f_1(e^{\prime }),f_1(e^{\prime })\cap g(e)\ne \varnothing ]\}$, it follows that $f^{S_1}(e)\subseteq g^{S_1}(e)$ for all $e\in A$, i.e., ${\overline{sapr}}_{S_1}(\mathcal{S})\subseteq {\overline{sapr}}_{S_1}(\mathcal{T})$;

(3) It is obvious that $\mathcal{S}\cap \mathcal{T}\subseteq \mathcal{S}$ and $\mathcal{S}\cap \mathcal{T}\subseteq \mathcal{T}$. From property (1), we obtain ${\underline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\underline{sapr}}_{S_1}(\mathcal{S})$ and ${\underline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\underline{sapr}}_{S_1}(\mathcal{T})$. Thus, ${\underline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\underline{sapr}}_{S_1}(\mathcal{S})\cap {\underline{sapr}}_{S_1}(\mathcal{T})$.

(4) It is obvious that $\mathcal{S}\cup \mathcal{T}\supseteq \mathcal{S}$ and $\mathcal{S}\cup \mathcal{T}\supseteq \mathcal{T}$. From property (1), we obtain ${\underline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\underline{sapr}}_{S_1}(\mathcal{S})$ and ${\underline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\underline{sapr}}_{S_1}(\mathcal{T})$. Thus, ${\underline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\underline{sapr}}_{S_1}(\mathcal{S})\cup {\underline{sapr}}_{S_1}(\mathcal{T})$.

(5) It is obvious that $\mathcal{S}\cup \mathcal{T}\supseteq \mathcal{S}$ and $\mathcal{S}\cup \mathcal{T}\supseteq \mathcal{T}$. From property (2), we obtain ${\overline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\overline{sapr}}_{S_1}(\mathcal{S})$ and ${\overline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\overline{sapr}}_{S_1}(\mathcal{T})$. Thus, ${\overline{sapr}}_{S_1}(\mathcal{S}\cup \mathcal{T})\supseteq {\overline{sapr}}_{S_1}(\mathcal{S})\cup {\overline{sapr}}_{S_1}(\mathcal{T})$.

(6) It is obvious that $\mathcal{S}\cap \mathcal{T}\subseteq \mathcal{S}$ and $\mathcal{S}\cap \mathcal{T}\subseteq \mathcal{T}$. From property (2), we obtain ${\overline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})$ and ${\overline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\overline{sapr}}_{S_1}(\mathcal{T})$. Thus, ${\overline{sapr}}_{S_1}(\mathcal{S}\cap \mathcal{T})\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})\cap {\overline{sapr}}_{S_1}(\mathcal{T})$. ☐

Proposition 3.

Let ${\mathcal{S}}_1=(f_1,A_1)$ be a full soft set over U and $(U,{\mathcal{S}}_1)$ be a soft approximation space. Let $\mathcal{S}=(f,A)$ be a soft set over U. The following properties hold:

(1) 

${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq {\underline{sapr}}_{S_1}({\overline{sapr}}_{S_1}(\mathcal{S}))$,

(2) 

${\overline{sapr}}_{S_1}(\mathcal{S})\supseteq {\overline{sapr}}_{S_1}({\underline{sapr}}_{S_1}(\mathcal{S}))$.

Proof. 

From property (1) in Proposition 1, it is obvious that ${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq \mathcal{S}\subseteq {\overline{sapr}}_{S_1}(\mathcal{S})$. From property (1) and (2) in Proposition 2, we get ${\underline{sapr}}_{S_1}(\mathcal{S})\subseteq {\underline{sapr}}_{S_1}({\overline{sapr}}_{S_1}(\mathcal{S}))$ and ${\overline{sapr}}_{S_1}(\mathcal{S})\supseteq {\overline{sapr}}_{S_1}({\underline{sapr}}_{S_1}(\mathcal{S}))$, respectively. ☐

In [12], a group decision-making approach based on F-soft rough sets was proposed; however, if we carefully check their decision scheme, it is not hard to find that they actually use the tool of a soft rough soft set since the best alternatives provided by each specialist gather together to form a soft set and they compute the upper and lower soft rough approximations (soft sets) on the preliminary evaluation soft set during the decision process. That is, although the concept has not been formally proposed, the application of soft rough soft sets has already appeared in literature. From another perspective, the decision-making problem that can be solved by F-soft rough sets in [12] can also be solved by using soft rough soft sets. It is necessary to propose the concept for soft rough soft sets as well as its application to introduce parameter tools to the universe description, that is, make it feasible to describe objects in the universe from different aspects at the same time, information obtained from different aspects be able to be handled as a whole before the approximations of a soft set are computed, and allow the flexibility to make operations such as the restricted intersection “∩” [25] on soft sets whose soft rough approximations need to be computed; in this way, soft rough soft sets have the potential to be applied in more complex decision-making situations to meet demands of applications in real life cases. As follows, we provide a simple application of soft rough soft sets in decision-making.

Let $G=\{T_1,T_2,...,T_p\}$ and $A_1=\{e_1^{\prime },e_2^{\prime },...,e_q^{\prime }\}$ be two groups of specialists to evaluate all the candidates $U=\{x_1,x_2,...,x_m\}$. In group G, each specialist is asked to point out if the candidates satisfy benefit properties in $A=\{e_1,e_2,...,e_n\}$ or not. In this way, a serious of evaluations provided by specialists are obtained as $(g_1,A)$, $(g_2,A)$, $(g_3,A)$, ⋯, $(g_p,A)$. Afterwards, the evaluation made by group G could be obtained by $S=(f,A)=(g_1,A)\cap (g_2,A)\cap (g_3,A)\cap \cdots (g_p,A)$. Meanwhile, in another group $A_1=\{e_1^{\prime },e_2^{\prime },...,e_q^{\prime }\}$, the specialists are under time pressure, and a lack of patience, or, because of some other issues, each specialist only points out the best alternatives; however, we have no clear idea about which properties are under their consideration. The best alternatives chosen by specialists in group $A_1$ form another soft set $S_1=(f_1,A_1)$. We say the assessments provided by group G are more reliable since the assessments provided by them are more specific than group $A_1$. However, in order to make full use of information provided by the two independent groups, we can compute the lower soft rough approximation on $(f,A)$ in soft approximation space $(U,S_1)$. If $x_i\in f_{S_1}(e_j)$, from the axiomatic definition of soft rough soft sets, we know that the best alternatives of one or more specialists in $A_1$ are totally contained in $f(e_j)$, that is, the best alternatives chosen by some specialists in $A_1$ certainly occupy property $e_j$, which indicates that this benefit property $e_j$ considered by group G may also be very important to group $A_1$. The final decision is to select the alternative that occupies the most number of beneficial properties that may be important for both groups.

The steps of this soft rough soft sets based multi-group decision-making approach can be listed as:

Step 1. Input the evaluations on alternatives $U=\{x_1,x_2,...,x_m\}$ provided by specialists group $G=\{T_1,T_2,...,T_p\}$ as $(g_1,A)$, $(g_2,A)$, $(g_3,A)$, ⋯, $(g_p,A)$.

Step 2. Input the best alternatives selected by specialists group $A_1$ as $S_1=(f_1,A_1)$.

Step 3. Compute the group evaluation made by the specialists in G as $S=(f,A)=(g_1,A)\cap (g_2,A)\cap (g_3,A)\cap \cdots (g_p,A)$.

Step 4. Compute the lower soft rough approximation of $(f,A)$ in $(U,S_1)$, i.e. $(f_{S_1},A)$.

Step 5. Compute the score of alternatives of each $x_j$ ($j=1,2,\cdots ,m$) as $s(x_j)={\sum }_{i=1}^n{f}_{S_1}(e_i)(x_j)$, and the decision result is $x_k$ if it satisfies $s(x_k)=ma{x}_{j=1,2,\cdots ,m}s(x_j)$.

Example 3.

Suppose that a factory needs to purchase the best machine from $U=\{x_1,x_2,...,x_6\}$ according to evaluations provided by two specialists groups G and $A_1$, which form a multi-group decision-making problem. $G=\{T_1,T_2,T_3,T_4\}$ consists of four specialists and each of them provides assessments on machines in U with respect to beneficial properties $A=\{e_1=lowprice,e_2=highendurance,e_3=advancedtechnology$, $e_4=goodcompatibility\}$. Each specialist in G points out if the machines satisfy properties in A or not. In this way, a serious of evaluation soft sets provided by specialists are obtained as $(g_1,A)$, $(g_2,A)$, $(g_3,A)$, $(g_4,A)$ (see

Table 5. Soft set $(g_1,A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	1	1	0	1
e2		0	1	1	0	0	0
e3		0	0	0	1	1	1
e4		1	1	1	1	0	1

,

Table 6. Soft set $(g_2,A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	0	1	0	1
e2		1	1	1	0	0	0
e3		0	0	0	1	1	1
e4		1	1	1	1	0	1

,

Table 7. Soft set $(g_3,A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	0	1	0	1
e2		0	1	1	0	0	0
e3		1	0	0	1	1	1
e4		1	1	1	1	0	1

and

Table 8. Soft set $(g_4,A)$.

	U	x1	x2	x3	x4	x5	x6
A
e1		1	1	0	1	0	1
e2		0	1	1	0	0	0
e3		0	0	1	1	1	1
e4		1	1	1	1	0	1

as their tabular representations) and the group evaluation of G can be computed by $(f,A)=(g_1,A)\cap (g_2,A)\cap (g_3,A)\cap (g_4,A)$ (see also Table 2 as the tabular representation for $(f,A)$). Meanwhile, each specialist in another specialist group $A_1=\{e_3^{\prime },e_4^{\prime },e_5^{\prime },e_6^{\prime },e_7^{\prime }\}$ only points out the best machines according to his/her own cognition, which form soft set $(f_1,A_1)$ (replace $e_3^{\prime }-e_7^{\prime }$ by $e_3-e_7$ and see also Table 1 for its tabular representation). The lower soft rough approximation of $(f,A)$ in $(U,S_1)$ can be easily computed as $(f_{S_1},A)$ (see also Table 3 for its tabular representation). It is easy to obtain that $s(x_1)=s(x_2)=s(x_3)=2$, $s(x_4)=s(x_5)=1$ and $s(x_6)=3$, hence $x_6$ should be the machine purchased by the factory since it satisfies largest number of beneficial properties that are important to two groups.

As is mentioned at the beginning of this section, soft rough soft set is an extension model of F-soft rough set. Sometimes, in a practical situation, the universe set that needs to be granulated is presented from different attributes’ aspects simultaneously. In other words, the parameter tools are necessary not only for the knowledge presentation, but also for the universe description. The new model provides a framework for dealing with these kinds of problems and the exploration of its potential use in decision-making is promising. Compared to F-soft rough sets, soft rough soft sets introduce parameter tools to the universe description and a soft set (instead of a subset of the universe) is approximated. Compared to rough soft set [12], a soft set instead of an equivalence relation has been adopted in soft rough soft sets to compute the approximations of soft sets [36,37]. In this section, only a small application attempt of soft rough soft sets in decision-making has been provided, which is far from enough to meet various demands in real life situations. More flexible and effective approaches need to be developed in the future.

6. Conclusions

This paper has presented a comparative study of some existing soft rough set models, and new discoveries on the relationships among various hybrid sets have been summarized in

Table 9. Summary on relationships among various hybrid models.

Various Hybrid Models	Relationships
F-soft rough approximations and modified soft rough approximations (MSR approximations)	${\overline{X}}_{\phi }\subseteq {\overline{apr}}_P(X)$, ${\overline{apr}}_P(X)\subseteq {\overline{X}}_{\phi }$, ${\underline{X}}_{\phi }\subseteq {\underline{apr}}_P(X)$, if some specific conditions hold, respectively (see Theorems 1–3)
F-soft rough sets in $(U,S)$ and Pawlak’s rough sets in $(U,R_S)$	F-soft rough sets in $(U,S)$ could be identified with Pawlak’s rough sets in $(U,R_S)$, when the underlying soft set is a partition soft set (see Theorems 4 and 5)
MSR approximations and Pawlak’s rough approximations	MSR approximation operator is a kind of Pawlak rough approximation operator (see Theorem 6)
Z-lower, Z-upper soft rough approximation operators and Dubois and Prade’s lower and upper rough fuzzy approximation operators in [6]	Z-lower and Z-upper soft rough approximation operators are equivalent to Dubois and Prade’s lower and upper rough fuzzy approximation operators in [6] (see Corollary 3)
The (classical) rough fuzzy sets and M-soft rough fuzzy sets	The (classical) rough fuzzy sets in Pawlak approximation space $(U,R)$ and M-soft rough fuzzy sets in soft approximation space $(U,S)$ are equivalent when the underlying soft set S is a partition soft set (see Theorem 7)
Z-soft rough approximation operators and M-soft Rough approximation operators and F-soft rough approximation operators	${\underline{sap}}_P(\mu )\subseteq {\underline{sap}}_P^{\prime }(\mu )\subseteq {\underline{\mu }}_{\phi }\subseteq \mu \subseteq {\overline{\mu }}_{\phi }\subseteq {\overline{sap}}_P^{\prime }(\mu )$ $\subseteq {\overline{sap}}_P(\mu )$ (see Theorem 8 and Corollary 4)
The soft fuzzy rough approximation in Definition 9 and Dubois and Prade’s fuzzy rough approximation in [6]	The soft fuzzy rough approximation is a kind of Dubois and Prade’s fuzzy rough approximation in [6] (see Theorem 9)
F-soft rough set and soft rough soft set	Soft rough soft set is an extension of F-soft rough set

. It has been shown that the Z-soft rough fuzzy set is a kind of rough fuzzy set. Therefore, decision-making approaches based on rough fuzzy sets have the potential to be addicted to more specific situations in which Z-soft rough fuzzy sets should be applied to solve the problem. Various soft rough set models have shown great potential in coping with decision-making problems. Some potential applications of connections among various soft rough set models in decision-making have been briefly discussed in the current work. For instance, benefitting from the connections between F-soft rough approximations and MSR approximations that have been discussed, it is possible to further study the relationships between the decision results made by using soft rough sets and MSR sets. In future works, deeper and more specific research on the applications of these connections in decision-making will be conducted.