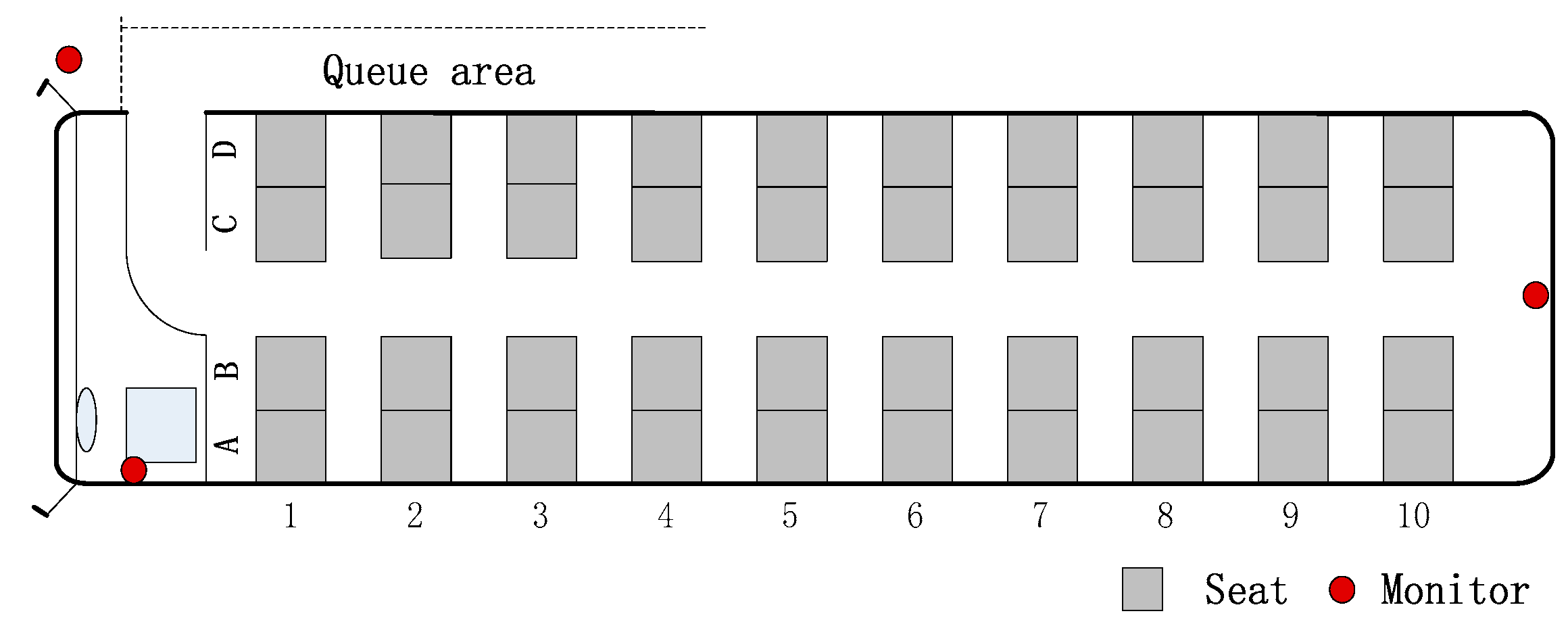1. Introduction
Airlines, under increasing competition pressure, are driven to optimize their operations by maximizing their efficiency and profitability. A feasible method is to reduce the airplane turn time, which includes the time to unload an airplane after its arrival and to prepare it for departure again. Turn time processes include boarding/deboarding, refueling, handling of catering, and the off-loading and loading of baggage. Shortening the time required in any of these sections will improve efficiency. Considering the boarding and deboarding processes are the main contribution to an airplane’s turn time, improvement in either one or both of these two parts provides the potential to reduce the turn time.
Adopting a fast and friendly boarding/deboarding strategy benefits the airlines, airport operators, and the passengers [
1], see
Figure 1. Airlines obtain revenue when the airplane is in the air, so they make every effort to minimize the time that their flights stay on the ground. A conservative estimation of a one-minute reduction in the turn time saves
$30 for an active airplane staying on the ground [
2]. Thus, each minute saved in the turn time of a flight can accumulate to produce considerable annual savings. These savings could inspire the airlines to make better utilization of airplanes, i.e., they may offer additional flights. Reduction of airplane turn time can also benefit the airport operators in three aspects: First, it could mitigate the flight delays caused by inefficient ground service, less redundant ground time could allow for scheduling more flights; Second, it makes a more efficient utilization of the equipment on the ground, such as the boarding bridge; Third, it increases the level of service at the airport by reducing the passengers’ waiting time at the departure hall. For passengers, they would enjoy a quick and friendly strategy for less individual boarding/deboarding time and avoid frustrating stoppages.
The currently used boarding strategies perform rather poorly concerning boarding time; flow stoppage occurs in a real boarding process. Such intermittent delays are caused by two kinds of interference: One is aisle interference, which occurs when a passenger is blocked by another passenger in the aisle. The other is seat interference, which happens when a window or middle seat passenger is blocked by other passengers who are already sitting in the same half-row. Efforts have been made to reduce those two interferences in boarding time, and most of them are based on simulation works, either by discrete modeling [
3,
4,
5,
6] or by continuous modeling [
7,
8]. Various optimal boarding strategies are proposed to reduce boarding time. In [
9], the author presented the most time-saving strategy by applying a Markov Chain Monte Carlo optimization algorithm. In addition, new strategies are also proposed by using linear or nonlinear programming approaches [
10,
11] based on an assumption that a minimization of the number of interferences leads to a minimal boarding time. In [
5,
12], the authors emphasized the importance of luggage storage space in stowing the luggage, and they assigned seats to the passengers by considering the number of luggage pieces with which they were traveling.
Though research on the optimal boarding problem has become a bit of a hot topic in the last few years, an obvious shortage is that most of the works are based on simulation analysis and seldom on validation works. Actually, deviation exists between computer simulation and the real process. An example of such deviation is that passengers are basically assumed to be homogeneous in simulations, which is too simple to describe the complex dynamic of the boarding process arising from individual differences. It is, therefore, important to know the real performance of some optimal strategies by experimental test. A primary work was done in [
13] as the authors conducted an experimental comparison of airplane boarding in a mock Boeing 757 fuselage, with twelve rows of six seats and a single aisle. The author found a significant reduction in boarding time with the optimized Steffen strategy over the other three traditional strategies, i.e., the block strategy, the window-to-aisle strategy, and random strategy.
In contrast with the experiment using a mock airplane fuselage in [
13], here, we designed a surrogate experimental test. Instead of boarding participants onto a real or mock airplane, we had them board a school bus, as there are similarities between passengers boarding these two means of transport. The purpose of our experiment was to evaluate various strategies in boarding time and other qualities such as time stability and time gap. Seven strategies were selected, including Random, Free, Back-to-front, Window-to-aisle, Steffen, Steffen-lug, and CRBF (column rotated in a back to front order, see
Section 2.3 for details). In addition, we evaluated two structured deboarding strategies proposed in [
6,
14], as the authors claimed that deplaning passengers in a structured manner reduces the deboarding time. Moreover, how the passengers’ seat preference influences the free boarding time is another interest of our work. By organizing participants to board in a free manner and then carrying out a poll on their seat preferences, we attempted to find the decision making mechanism behind the free boarding process. Based on the experimental results, we could further build or verify the free boarding simulation model, such as utilizing the rules of Boltzmann statistics to describe passengers’ preference on seats in a free boarding process [
15].
The remaining parts of the paper are organized as follows. In
Section 2, a surrogate experimental test is introduced. In
Section 3, we present some screenshots to identify the causes of boarding and deboarding time delay. In
Section 4, we evaluate various boarding and deboarding strategies by extracting data from the video recordings, and how the seat preference affects the free boarding process is also discussed. In
Section 5, conclusions and future works are given.
2. Design of a Surrogate Experimental Test
The equivalent experiment was conducted by organizing passengers to board a school bus instead of a real or mocked airplane. This makes sense because there exists similarities between passenger boarding of these two facilities for four reasons: (1) Seat layout in both facilities are similar, in which seats are symmetrically distributed on both sides of a single aisle, see
Figure 2; (2) The aisles are relatively narrow in both facilities which compels the passengers to move in a following manner, that is to say, they do not try to pass others in the boarding and deplaning process; (3) Passengers suffer from aisle and seat interferences in both processes; (4) Passengers will take some time to store (retrieve) luggage in the overhead bins, which is the main cause of boarding (delighting) time delay.
2.1. Seat Layout and Dimensions
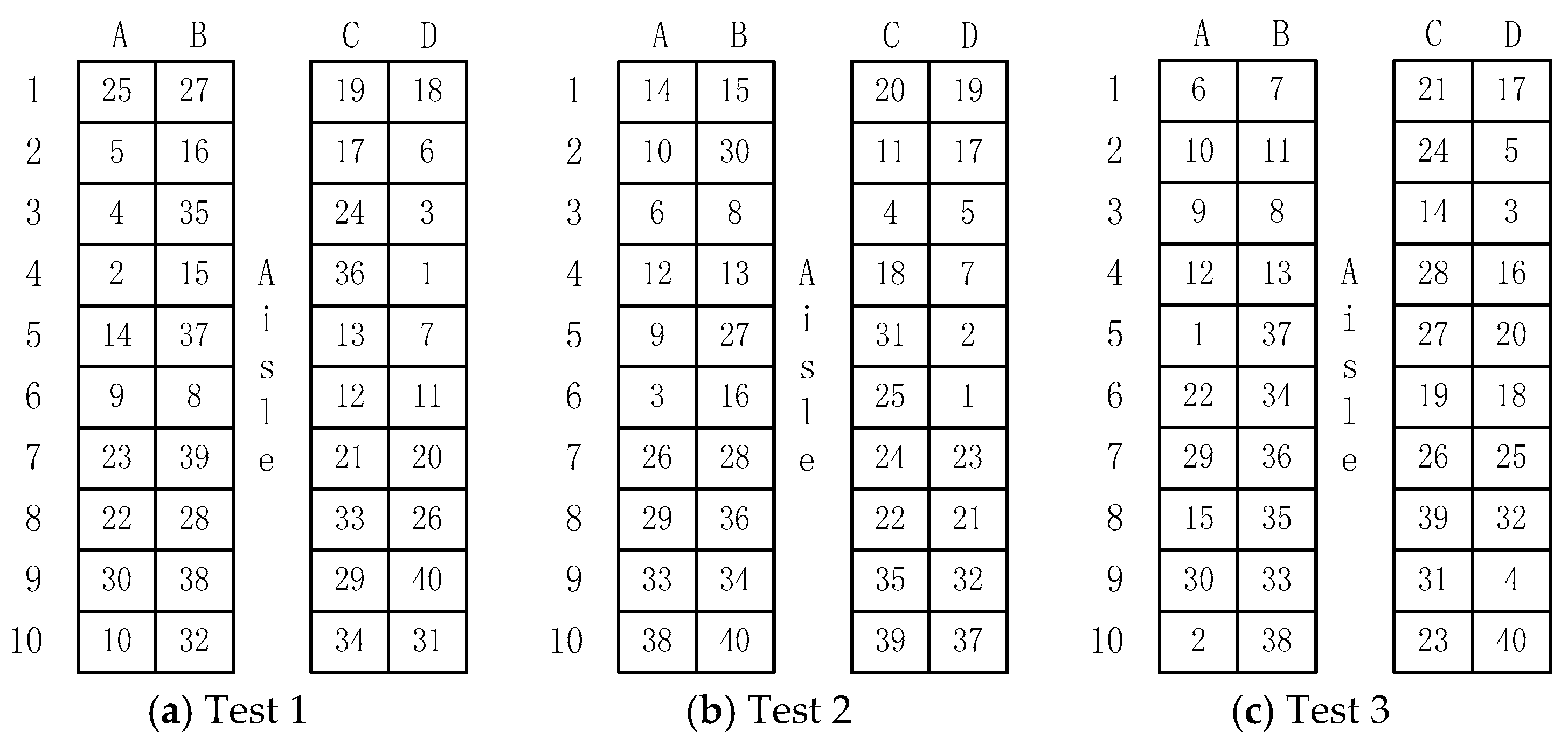
The maximum passenger capacity of the selected school bus was 45 passengers, and only 40 were selected in the experiment. The layout of available seats and the location of monitors are shown in
Figure 3, in which ten rows of four seats are symmetrically distributed on a single, central aisle. The seats are indicated by letters from A to D, and the rows are numbered from 1 in the front to 10 in the rear of the bus.
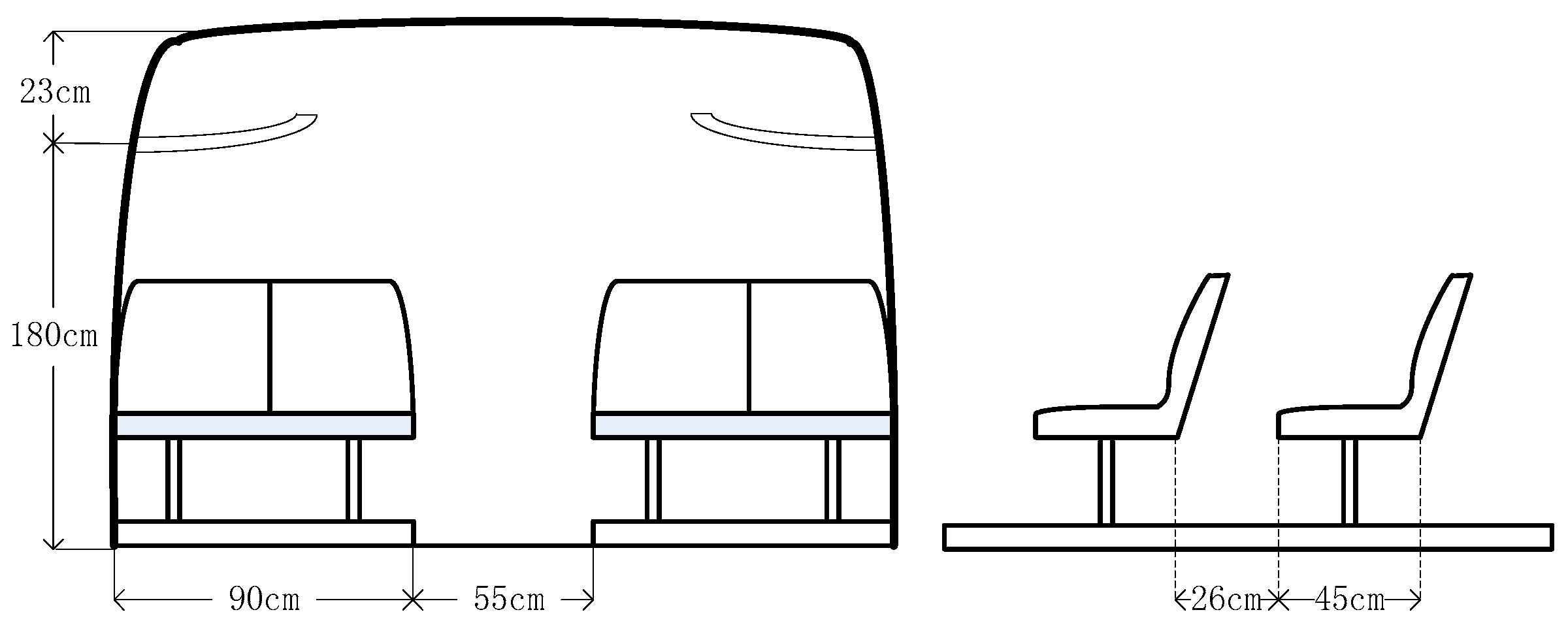
The dimensions of interior space of the school bus is shown in
Figure 4. The school bus cabin was almost 235 cm in width, 203 cm in height, and contained an affiliated overhead bin with a height of 23 cm. Each seat had a standard 45 cm width and was spaced by 71 cm from the seat in the next row. The aisle was 55 cm wide and only allowed one passenger to pass in a common situation.
2.2. Characteristics of Participants
We employed 40 college students with ages ranging from 22 to 30. Male and female students participated in almost equal number. Participants were randomly assigned 0, 1, or 2 pieces of luggage, and the luggage distribution is listed in
Table 1. The external dimensions of baggage was about 45 cm (height)
30 cm (width)
15 cm (thickness). It needs to be emphasized that the number of luggage carried by an individual remained unchanged in the repeated experiments.
2.3. Boarding and Deboarding Strategies
The purpose of our experiment was to evaluate the boarding strategies, including those that have been used in practice and those that have appeared in scientific literature. Seven boarding strategies and three deboarding strategies were tested and their abbreviations are listed in
Table 2. Correspondingly, these strategies are transplanted to fit the bus seat layout, and their configurations are exhibited in
Figure 5.
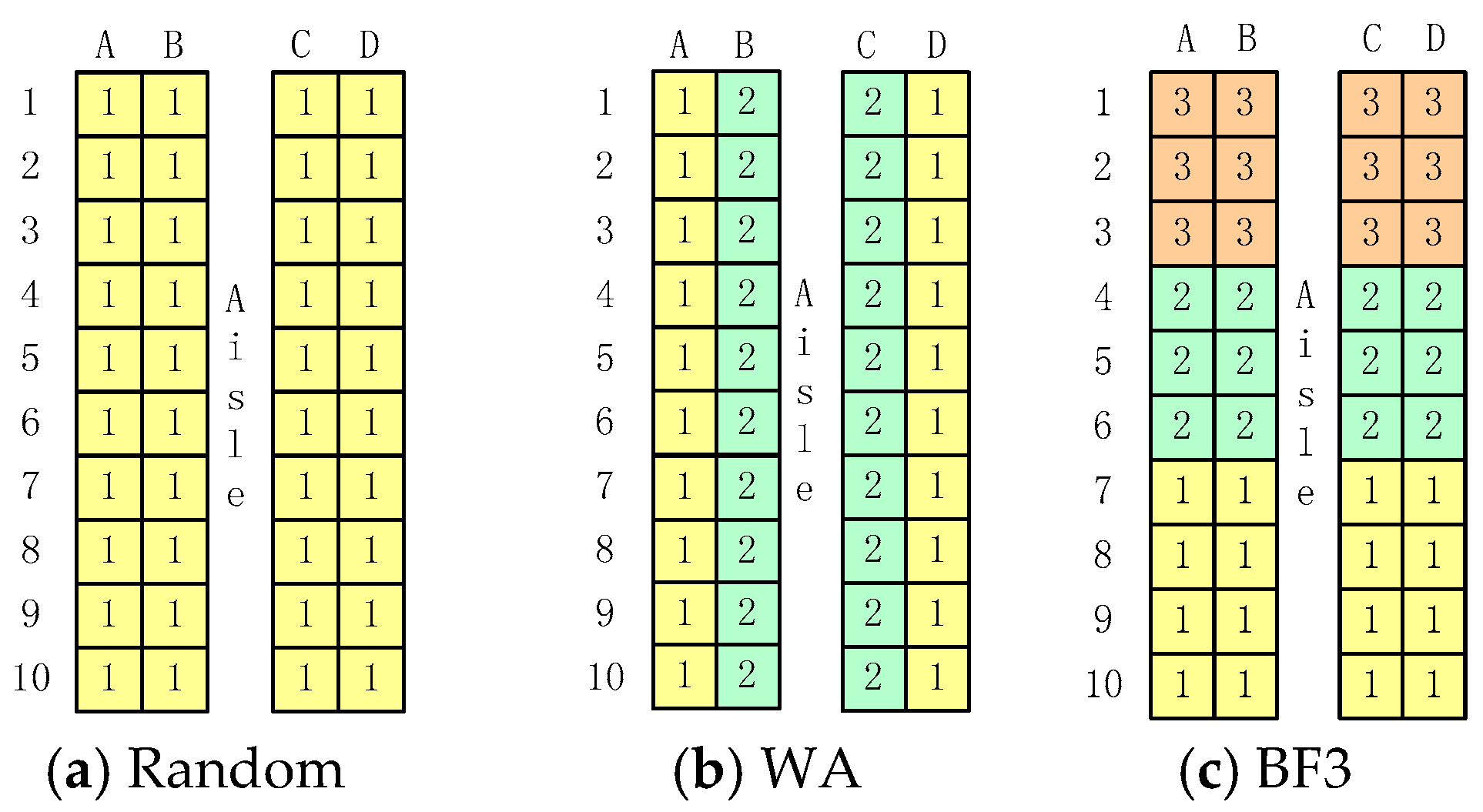
Random strategy: All participants are allowed to board in one group; each one of them is preassigned to a particular seat and enters the bus in no predefined order (see
Figure 5a).
WA strategy: Participants are divided into two groups according to the type of seats, aisle or window seat. The group with window seats board first, followed by the group with aisle seats; within each group, participants are essentially random (see
Figure 5b).
BF strategy: Participants are divided into several groups along the aisle (three groups in our experiment, indicated by BF3) and board in a back to front order; passengers are essentially random in each group (see
Figure 5c).
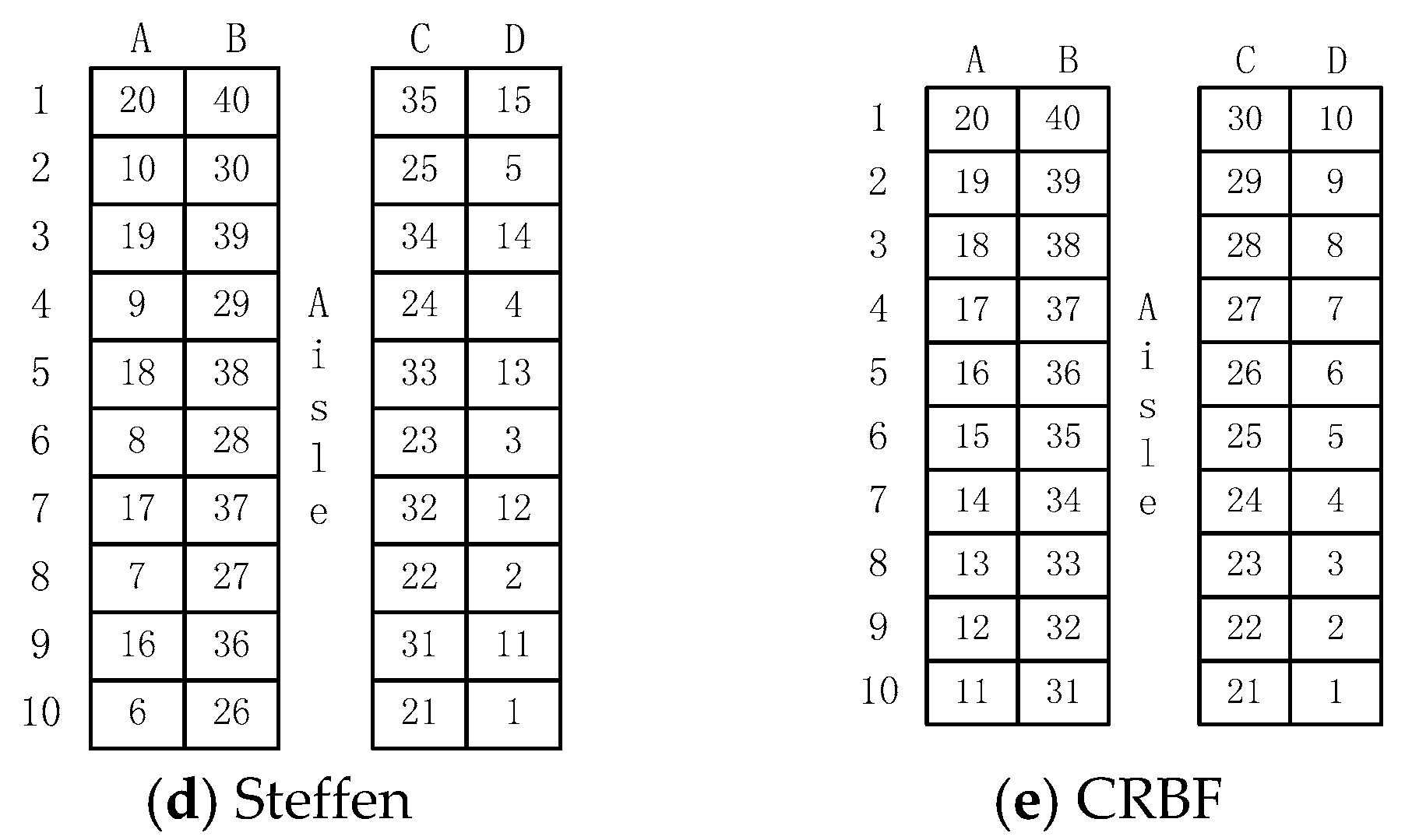
Steffen strategy: This method has the passengers lining up in a prescribed order that incorporates, in a specific way, boarding from the back to the front and from the windows to the aisle. Adjacent passengers in line are sitting two rows apart from each other in corresponding seats (e.g., 10D, 8D, 6D, 4D, 2D), so there is a total of eight successive groups (see
Figure 5d).
CRBF strategy: This strategy evolves from the Steffen strategy; one major improvement is that it allows for passengers who are sitting together to be adjacent in line (e.g., 10D, 9D, 8D, 7D, 6D). As seen in
Figure 5e, there are a total of four successive groups distinguished by columns. Within each group, passengers are boarded in a back to front order. Here, we name this strategy as CRBF (Column rotated in a back to front order).
Steffen-lug strategy: This method was first proposed in Reference [
5] based on the Steffen strategy. The most prominent characteristic of this method is that the seats of passengers are assigned considering the number of luggage pieces they carry. Passengers are divided into eight successive groups and board the bus in a way that is similar to the Steffen strategy; within each group, passengers with more luggage enter the bus first.
Free boarding strategy: This strategy is adopted by some budget airlines, such as Southwest in the United States and EasyJet in the UK. Rather than providing assigned seats, they do not offer any numbered tickets. The passengers choose their favorite seats and are free to sit in any available seats when entering the bus.
As an extension of this work, we also tested three deplaning strategies. Unstructured deplaning is the most used strategy adopted by airline companies, in which passengers leave the airplane without any instruction. It has been suggested in [
6,
14] that structured deplaning strategies may reduce the deplaning time. To what extent these structured deboarding strategies will quicken the deplaning process was also the focus of our attention. Here, we tested two structured deboarding strategies and their rules are summarized as follows.
AW strategy: Participants are divided into two groups, see
Figure 5b. The group with aisle seat deplanes first followed by the group with the window seat, namely in an order of 2→1. Within each group, participants leave freely.
FB strategy: Participants are divided into three groups (indicated by FB3), see
Figure 5c. The groups of participants deboard in a front to back order, namely in an order of 3→2→1. Within each group, participants leave freely.
2.4. Procedure
The test of each of the above boarding or deboarding strategies was repeated two or three times. In each experiment, participants were first required to queue in a line outside of the bus gate. Randomness was guaranteed by varying the sequence order with every test, this largely reduced the probability that participants deliberately stood in the same location of the line or in the same boarding group. Then, for those strategies with preassigned seats, each participant was given a ticket with a unique seat number, for example, number ‘6D’ meant he/she would sit in row 6, column D. The tickets were handed out to the participants according to the boarding strategy being tested. For example, tickets were randomly dispensed to the participants in the random strategy. However, for the Steffen strategy, the first participant in the waiting line was assigned a ticket with seat number ‘10D’, the second participant with a seat number ‘9D’, and the last participant with a seat number “1B”. Finally, participants were allowed to board after the ticket assignment work was finished.
Note that the ticket check procedure on the ground was neglected in our experiments. One could suggest that adding the ticket check procedure would make the test more appropriately imitate the real process. In actuality, modern electronic technology nearly makes no delay in reading the ticket at the check desk. Moreover, it has been confirmed by [
16] that each strategy has a critical ticket check time. Increasing the delay between successive airplane entries below the critical level will not increase the average boarding time. Usually, the ticket check time is below its critical time, and this makes no apparent difference in those two conditions. Therefore, we chose not to include this step in our experiment so as not to obscure the pure effect of sequencing on boarding time.
4. Experiment Results
4.1. Boarding and Deboarding Time
The boarding and deboarding time were recorded for these seven strategies, and the results are shown in
Table 3. The timing started when the first participant started to board the bus and ended when the last participant settled himself into his seat. The deboarding time was the time interval for all participants to leave the bus after the deboarding started.
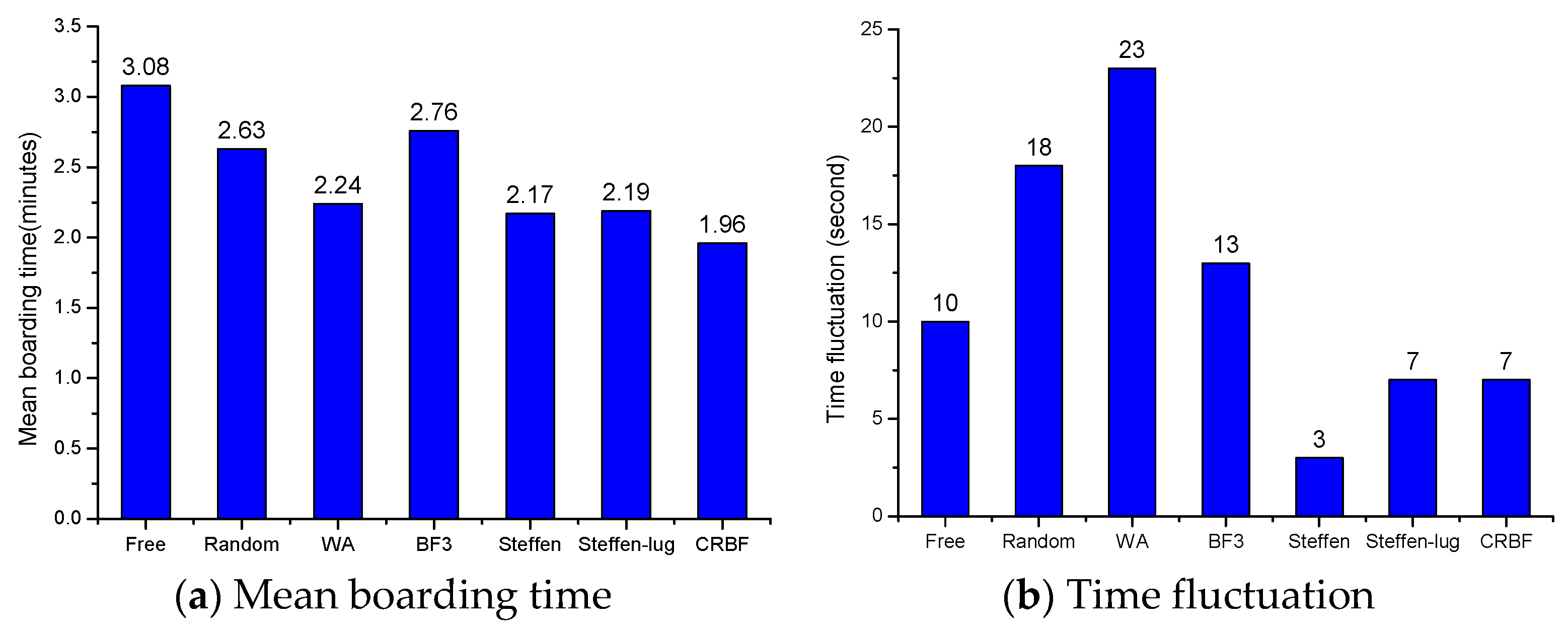
According to the results in
Table 3, we plot the mean boarding time of each strategy in
Figure 9a, as well as their boarding time variance in
Figure 9b. Here, the variance of boarding time is the time difference between the maximum and minimum boarding time in the repeated tests.
Note from
Figure 9a, the three strategies that saved the most time are the Steffen, Steffen-lug, and CRBF, which agrees well with the simulation work done by [
5]. A common feature of these three strategies is that they define an exact sequence of passengers and every passenger has to board at a given position that is planned in advance. They totally eliminate the seat interferences, and as much as possible aisle interferences. Moreover, they allow passengers to stow their luggage in the aisle simultaneously, for example, three and four participants are spotted storing their luggage simultaneously in
Figure 10a,b, respectively. The experimental results, see
Figure 9b, prove that a time effective strategy also has time stability. Indeed, boarding the passenger in an exact order makes the above three strategies tolerant of the time fluctuations induced by sequence randomness, or in other words, the stability is achieved.
It was seen in our experiments and other research, i.e., in references [
3,
4,
5,
6], that the BF strategy is not necessarily effective in reducing boarding time and is even detrimental with random boarding. It is argued in [
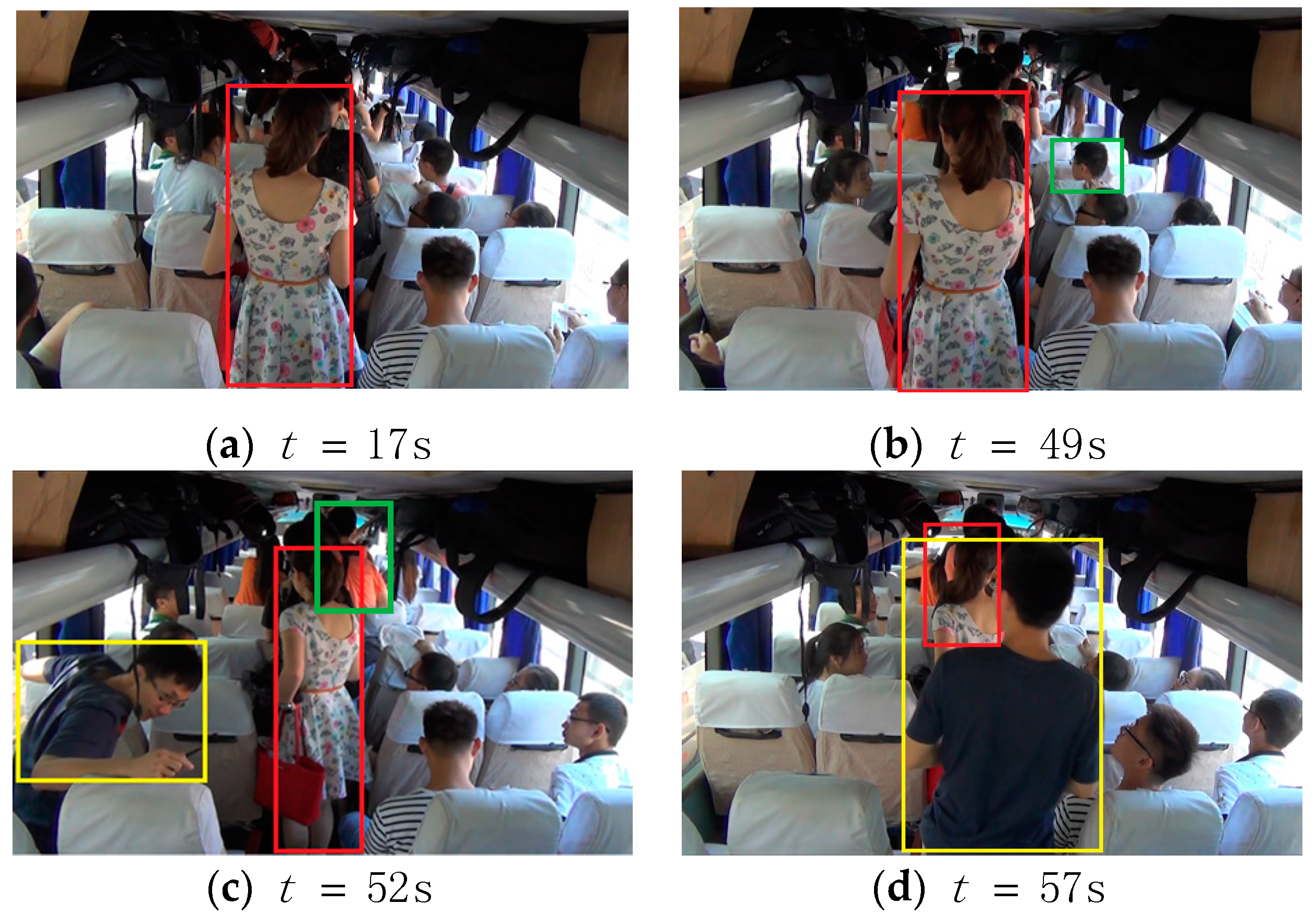
3] that the BF strategy was ineffective because it caused local congestion in the airplane. This kind of local congestion in BF3 can be found easily in
Figure 11. Taking the first boarding group for example, passengers were constrained to sit in the back of the cabin. When the participant in the red rectangular box was storing his luggage at
, he blocked his fellow passengers in the same group. Such interference occurs frequently in the back of the aisle, at
as another example. Due to the length of the aisle along the four rows and the size of the participants, not all of the 16 participants in the first group were able to store their luggage and sit down, some of them needed to queue. What makes this worse is the aisle and seat interference makes the queue move slowly, which triggers a chain of blocks in the aisle. Clearly, a movable bottleneck existed in the aisle and shifted to the head of the aisle during the boarding process.
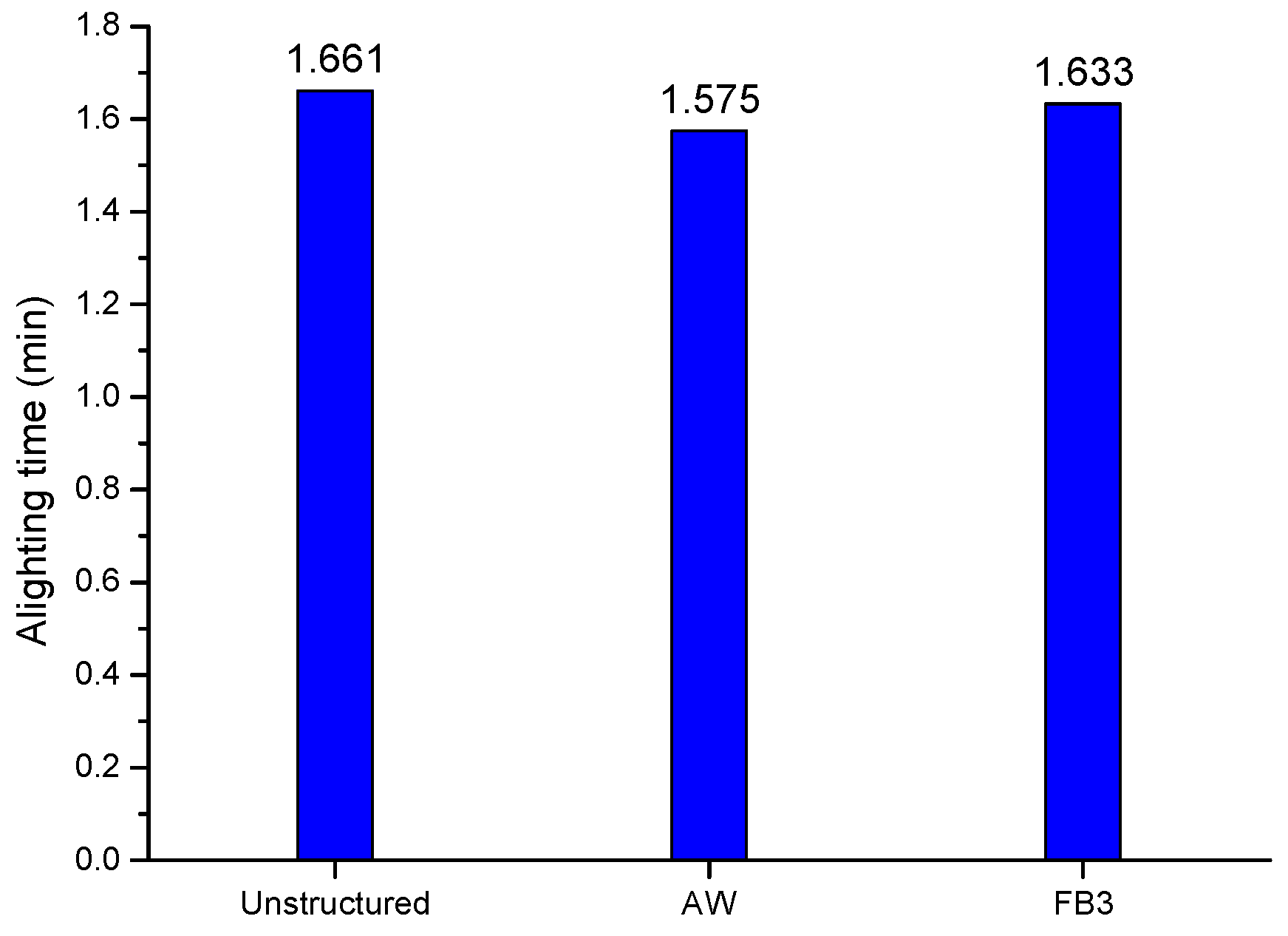
Though the structured strategies are used in the deboarding process, no apparent efficiency is achieved in reducing the deboarding time, see
Figure 12. This result is far from with simulation work done by [
6,
14], as they claimed that adopting the AW strategy could considerably reduce the deboarding time. Inconsistency comes from two main reasons. First, the effect of system size on the alighting time. The 40 participants in our experiment are much smaller than the approximately 150 passengers in a simulation model, which will largely weaken the difference between those structures. Second, but more importantly, there was nearly no time delay when passengers retrieved their luggage, because the bags carried by participants were small and portable. In such cases, participants left the bus successively, and thus mitigated the advantage of deplaning in order. In actuality, blocks occur frequently in a real deboarding process that is why the simulation model set the amount of time when retrieving luggage. Though they failed to reduce the deboarding time, these two strategies make the deboarding much more orderly. In addition, they appear fairer as they allow the groups to deplane with the first to board being the last to deboard.
Here, we want to emphasize the importance of the number of pieces of luggage, as well as their size and weight on the boarding and deboarding time. The stowing and retrieving of luggage are the main causes of time delay. If the airline allows passengers to take luggage, the differences between various boarding strategies are apparent, and those strategy that consider luggage distribution in the cabin show the most time-savings, i.e., Steffen-lug. If less or no luggage is allowed when boarding, there is no need to improve boarding strategy as they have almost equal performance.
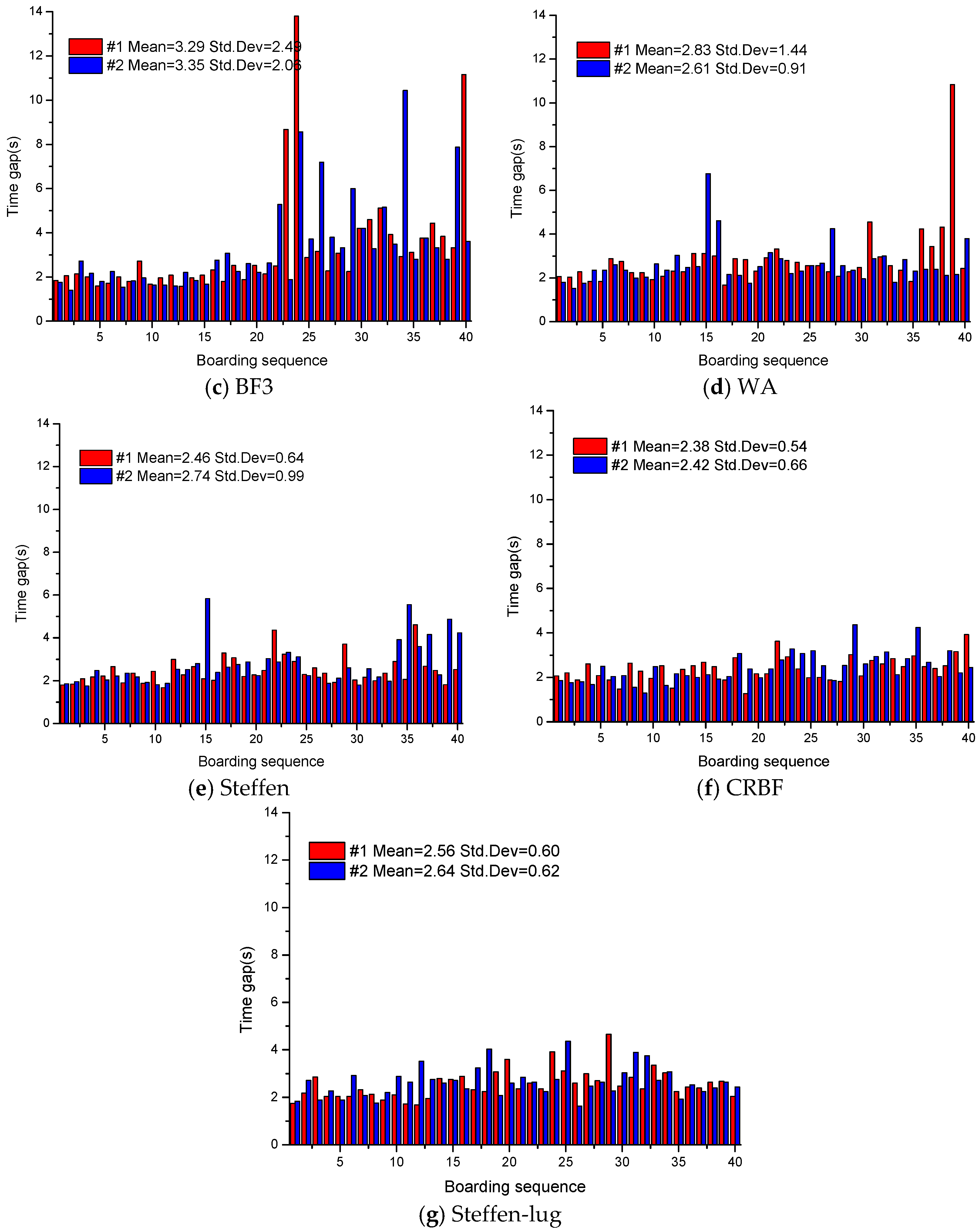
4.2. Time Gap
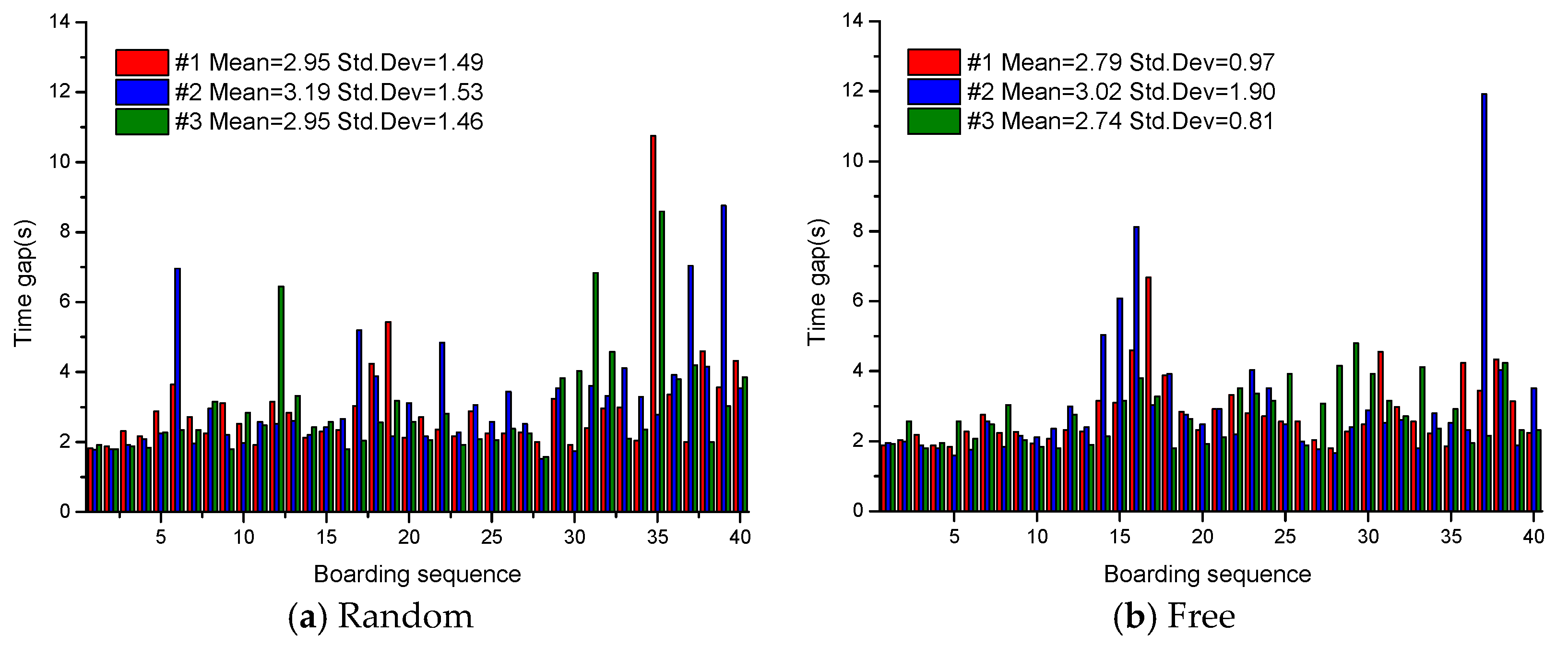
In order to further test the formation and diffusion of the aisle congestion caused by seat and aisle interference, we recorded the time gap of each participant getting through the bus gate in
Figure 13. The time gap is the time interval for two successive participants getting through the bus gate. A steady stream of passengers would be preferred since gaps would indicate flow stoppage. One could except that if no congestion occurs in the aisle, the distribution of the time gap should be stable. An abrupt increment of the time gap is caused by the transition of aisle congestion to the gate; the longer the time it takes a participant to go through the gate, the more severe is the congestion in the aisle.
A quick conclusion can be made that the time gap fluctuations were considerably smaller for those strategies boarding quickly, such as Steffen, Steffen-lug, and CRBF. In those strategies, participants got through the bus gate smoothly, less than 3 s per participant. In contrast, some of the participants took a long time to get through the gate, such as in the Free, Random, and BF3 strategies.
4.3. Seat Preference in Free Boarding
Passengers prefer to select their favorite seats when they travel, especially in a tight and stressful environment like airplane cabins or bus carriages. Their preferences on the seats might be conditioned by a range of factors, such as distance to the entrance, the seat type (aisle or window seat), and the degree of crowding. The window seats are good for sightseeing and sleeping and less affected by seatmates. Passengers in the aisle seat would enjoy an extra benefit of stretching their legs occasionally without disturbing their seatmates. The front seats in a bus are preferred by most of the passenger because they are easy to exit from, and they avoid the noise and vibration of a rear-engine bus. The above differences could be reflected in the free boarding experiments in
Figure 14, in which the number indicates the queue order in the waiting line. An intuitive conclusion confirms the preferences among different seat types; in general, participants preferred the head and window seats in boarding.
To further reveal the characteristics of passenger preference on seat layout, we carried out a poll of 40 respondents on their seat preferences. They were required to select their favorite three seats and the most disliked three seats in a bus seat layout as shown in
Figure 2. The survey results are shown in
Table 4. For simplicity, they are classed into two divisions for their ‘position’ features. In the first division, cabin seats are divided into head seats (from rows 1 to 3), middle seats (from rows 4 to 7) and rear seats (from rows 8 to 10); in the second division, cabin seats are divided into window seats (columns A and D) and aisle seats (columns B and C).
Apparently, in
Table 4, the respondents prefer the head and middle seats, rather than the seats in the rear of the cabin; compared with the aisle seats, they prefer to choose the window seat. This rightly explains the reason why free boarding is time-consuming in our experiment. Participants boarding the bus at an early time will probably select the seat in the head of the bus, this will cause local congestion in the front aisle, and thereby block the subsequent passengers from boarding the bus. This is confirmed in
Figure 13, the boarding interval suddenly increased. Of course, it can be seen from
Figure 8 that the time function of the free strategy was less volatile, which implies a stable preference on seats.
Note that the free boarding was the worst strategy in our experimental test. This is somewhat different with its real performance in practice. In the real boarding process, passengers ‘rush’ to board the airplane to select their favorite seats, however, this activity was mitigated by fatigue as the passengers in our test had to board several times, thus slowing down the pace of boarding. As mentioned above, in a free boarding process, passengers are only allowed to take some handy belongings, which will greatly reduce the storage time.