Towards a New Proposal for the Time Delay in Gravitational Lensing
Abstract
:1. Introduction
2. Standard Analysis
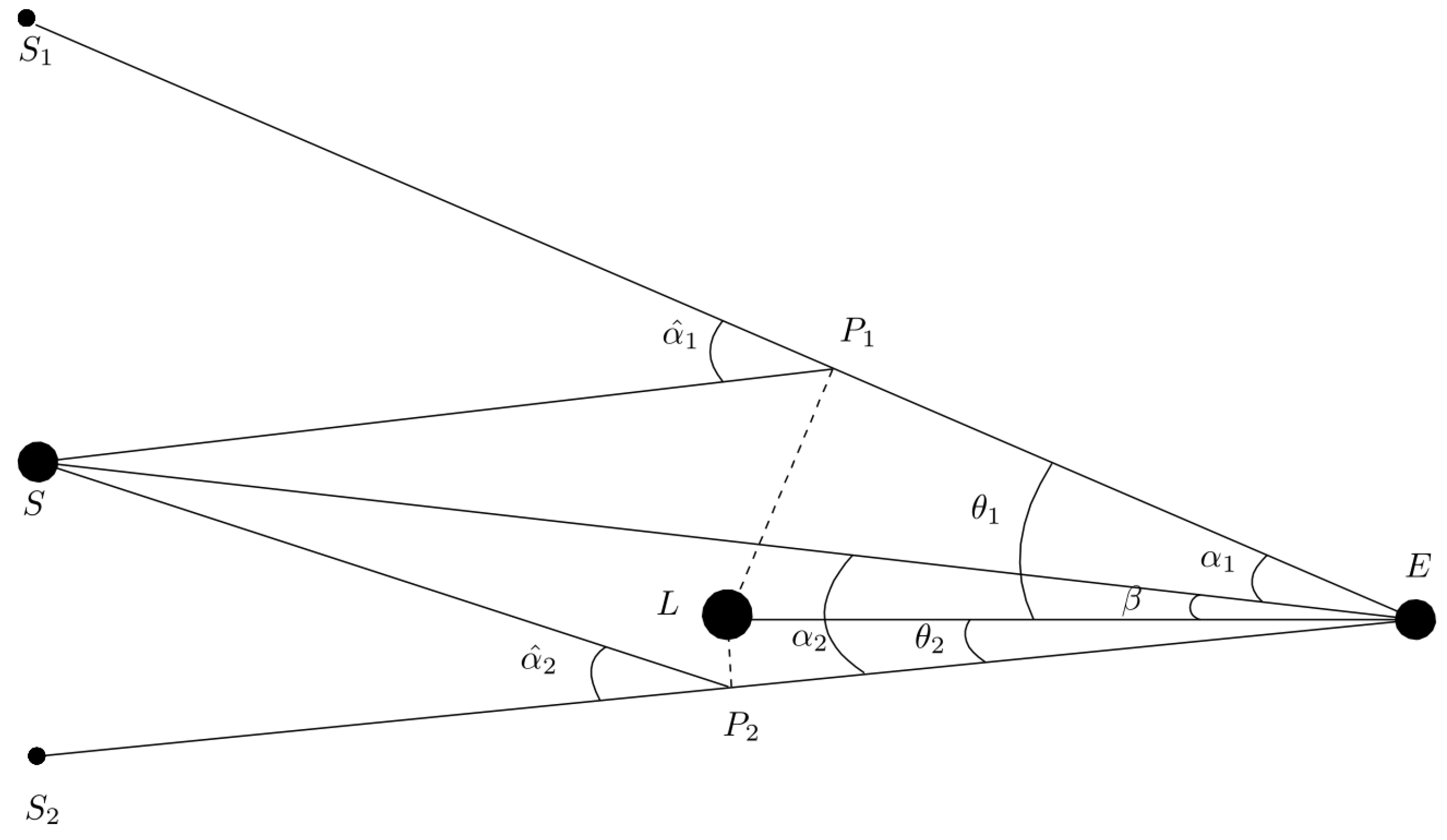
2.1. Basics of Gravitational Lensing
- The Shapiro delay, or potential time delay, caused directly by the motion of the light through the gravitational potential of the lens
- The geometric delay, caused by the increased length of the total light path from the source to the earth.
2.2. The Shapiro Time Delay in Minkowski Metric
2.3. Geometric Time Delay
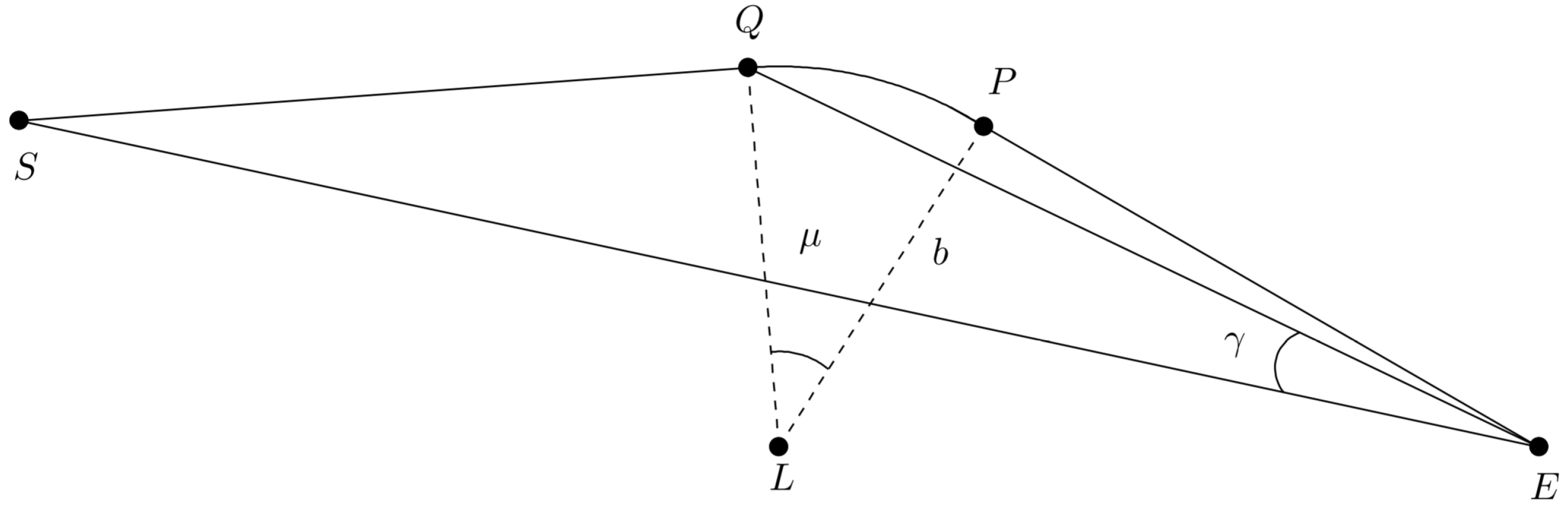
3. An Easy Extension
3.1. The Extension of
3.2. The Shapiro Time Delay in RW Metric
4. Cosmological Born-Oppenheimer Approximation for Time Delay
The Idea
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
Appendix A.1. Christoffel Symbols
Appendix A.2. Coefficients of the Expansion
References
- Blasi, A.; Maggiore, N. Massive deformations of rank-2 symmetric tensor theory (a.k.a. BRS characterization of Fierz–Pauli massive gravity). Class. Quantum Gravity 2017, 34, 015005. [Google Scholar] [CrossRef]
- Blasi, A.; Maggiore, N. Massive gravity and Fierz—Pauli theory. Eur. Phys. J. C 2017, 77, 614. [Google Scholar] [CrossRef]
- Blasi, A.; Braggio, A.; Carrega, M.; Ferraro, D.; Maggiore, N.; Magnoli, N. Non-Abelian BF theory for 2+1 dimensional topological states of matter. New J. Phys. 2012, 14, 013060. [Google Scholar] [CrossRef]
- Blasi, A.; Ferraro, D.; Maggiore, N.; Magnoli, N.; Sassetti, M. Symanzik’s method applied to the fractional quantum hall edge states. Ann. Phys. 2008, 17, 885. [Google Scholar] [CrossRef]
- Amoretti, A.; Blasi, A.; Caruso, G.; Maggiore, N.; Magnoli, N. Duality and dimensional reduction of 5D BF theory. Eur. Phys. J. C 2013, 73, 2461. [Google Scholar] [CrossRef]
- Amoretti, A.; Braggio, A.; Maggiore, N.; Magnoli, N. Thermo-electric transport in gauge/gravity models. Adv. Phys. X 2017, 2, 409. [Google Scholar] [CrossRef]
- Amoretti, A.; Braggio, A.; Caruso, G.; Maggiore, N.; Magnoli, N. Holography in flat spacetime: 4D theories and electromagnetic duality on the border. JHEP 2014, 1404, 142. [Google Scholar] [CrossRef]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison-Wesley: San Francisco, CA, USA, 2004; p. 513. [Google Scholar]
- Efstathiou, G.; Bond, J.R. Cosmic confusion: Degeneracies among cosmological parameters derived from measurements of microwave background anisotropies. Mon. Not. R. Astron. Soc. 1999, 304, 75. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Suyu, S.H.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Rusu, C.E.; Sluse, D.; Treu, T.; Wong, K.C.; Auger, M.W.; Ding, X.; et al. H0LiCOW—I. H0 Lenses in COSMOGRAIL’s Wellspring: Program overview. Mon. Not. R. Astron. Soc. 2017, 468, 2590. [Google Scholar] [CrossRef]
- Sluse, D.; Sonnenfeld, A.; Rumbaugh, N.; Rusu, C.E.; Fassnacht, C.D.; Treu, T.; Suyu, S.H.; Wong, K.C.; Auger, M.W.; Bonvin, V.; et al. H0LiCOW—II. Spectroscopic survey and galaxy-group identification of the strong gravitational lens system HE0435-1223. Mon. Not. R. Astron. Soc. 2017, 470, 4838. [Google Scholar] [CrossRef]
- Rusu, C.E.; Fassnacht, C.D.; Sluse, D.; Hilbert, S.; Wong, K.C.; Huang, K.H.; Suyu, S.H.; Collett, T.E.; Marshall, P.J.; Treu, T.; et al. H0LiCOW—III. Quantifying the effect of mass along the line of sight to the gravitational lens HE 0435-1223 through weighted galaxy counts. Mon. Not. R. Astron. Soc. 2017, 467. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Auger, M.W.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Halkola, A.; Rusu, C.E.; Sluse, D.; Sonnenfeld, A.; et al. H0LiCOW—IV. Lens mass model of HE 0435-1223 and blind measurement of its time-delay distance for cosmology. Mon. Not. R. Astron. Soc. 2017, 465, 4895. [Google Scholar] [CrossRef]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. H0LiCOW—V. New COSMOGRAIL time delays of HE 0435-1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model. Mon. Not. R. Astron. Soc. 2017, 465, 4914. [Google Scholar] [CrossRef]
- Refsdal, S. On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon. Not. R. Astron. Soc. 1964, 128, 307. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H0 tension? Phys. Rev. D 2017, 96, 043503. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin, Germany, 1992. [Google Scholar]
- CASTLES Catalogue. Available online: https://www.cfa.harvard.edu/castles (accessed on 24 September 2017).
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008; p. 593. [Google Scholar]
- Alchera, N.; Bonici, M.; Maggiore, N.; Panizzi, L.; Università di Genova, Genova, Italy. In progress. 2017.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alchera, N.; Bonici, M.; Maggiore, N. Towards a New Proposal for the Time Delay in Gravitational Lensing. Symmetry 2017, 9, 202. https://doi.org/10.3390/sym9100202
Alchera N, Bonici M, Maggiore N. Towards a New Proposal for the Time Delay in Gravitational Lensing. Symmetry. 2017; 9(10):202. https://doi.org/10.3390/sym9100202
Chicago/Turabian StyleAlchera, Nicola, Marco Bonici, and Nicola Maggiore. 2017. "Towards a New Proposal for the Time Delay in Gravitational Lensing" Symmetry 9, no. 10: 202. https://doi.org/10.3390/sym9100202
APA StyleAlchera, N., Bonici, M., & Maggiore, N. (2017). Towards a New Proposal for the Time Delay in Gravitational Lensing. Symmetry, 9(10), 202. https://doi.org/10.3390/sym9100202



