Some Algebraic Polynomials and Topological Indices of Generalized Prism and Toroidal Polyhex Networks

Abstract

A topological index of graph G is a numerical parameter related to G, which characterizes its topology and is preserved under isomorphism of graphs. Properties of the chemical compounds and topological indices are correlated. In this report, we compute closed forms of first Zagreb, second Zagreb, and forgotten polynomials of generalized prism and toroidal polyhex networks. We also compute hyper-Zagreb index, first multiple Zagreb index, second multiple Zagreb index, and forgotten index of these networks. Moreover we gave graphical representation of our results, showing the technical dependence of each topological index and polynomial on the involved structural parameters.

1. Introduction

Chemical reaction network theory is an area of applied mathematics that attempts to model the behavior of real world chemical systems. Since its foundation in the 1960s, it has attracted a growing research community, mainly due to its applications in biochemistry and theoretical chemistry. It has also attracted interest from pure mathematicians due to the interesting problems that arise from the mathematical patterns in structures of material.

Cheminformatics is an emerging field in which quantitative structure-activity (QSAR) and Structure-property (QSPR) relationships predict the biological activities and properties of nanomaterial. In these studies, some physcio–chemical properties and topological indices are used to predict bioactivity of the chemical compounds [1,2,3,4,5].

The branch of chemistry which deals with the chemical structures with the help of mathematical tools is called mathematical chemistry. Chemical graph theory is the branch of mathematical chemistry that applies graph theory to mathematical modeling of chemical phenomena. In chemical graph theory, a molecular graph is a simple graph (having no loops and multiple edges) in which atoms and chemical bonds between them are represented by vertices and edges respectively.

A graph $G$ with vertex set V(G) and edge set E(G) is connected if there exists a connection between any pair of vertices in G. The distance between two vertices u and v is denoted as $d(u,v)$ and is the length of shortest path between u and v in graph G. The number of vertices of G, adjacent to a given vertex v, is the “degree” of this vertex and will be denoted by $d_v.$ For details on basics of graph theory, any standard text such as [6] can be of great help.

A topological index is actually designed by transforming a chemical structure into a number. These topological indices associate certain physico–chemical properties like boiling point, stability, strain energy, etc. of chemical compounds. Graph theory has been of considerable use in this area of research. In 2013, Shirdel et al. [7] proposed the “hyper-Zagreb index”, which is a degree-based index as

$$HM\left(G\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]}^2$$

In 2012, Ghorbani and Azimi [8] proposed two new variants of Zagreb indices; first multiple Zagreb index $P{M}_1\left(G\right)={\displaystyle {\displaystyle \prod }_{uv\in E\left(G\right)}}\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]$ and second multiple Zagreb index $P{M}_2\left(G\right)={\displaystyle {\displaystyle \prod }_{uv\in E\left(G\right)}}\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right].$ Recently in 2015, Furtula and Gutman [9] introduced another topological index called the forgotten index or F-index

$$F\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}\left[{\left({\mathrm{d}}_u\right)}^2+{\left({\mathrm{d}}_v\right)}^2\right]}.$$

For more detail on the “F-index”, we refer to the articles [10,11,12].

The first Zagreb polynomial of G is defined as

$$M_1\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]}.$$

The second Zagreb polynomial of G is defined as

$$M_2\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right]}.$$

The forgotten polynomial of a graph G is defined as

$$F\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[{\left({\mathrm{d}}_u\right)}^2+{\left({\mathrm{d}}_v\right)}^2\right]}.$$

In this article, we compute the first Zagreb polynomial, the second Zagreb polynomial and the forgotten polynomial of generalized prism and toroidal polyhex networks. We also compute some degree-based topological indices of these networks. Recently authors computed M-polynomials and related topological indices for Nanostar dendrimers [13], titania nanotubes [14], circulant graphs [15], polyhex nanotubes [16], and generalized prism and toroidal polyhex networks [17]. The structures of Nanostar dendrimers, titania nanotubes, and polyhex nanotubes differ from fullerenes geometrically. Basic structural units of titania nanotubes are rectangles arranged differently for different types, whereas basic units of polyhex nanotubes are hexagons concatenated in different ways for different types. Nanostar dendrimers are macromolecules built in a tree-like structure. These materials have many applications in electronics, chemical processing, optics, and energy management and are used in flat panel display screens, hydrogen storage, robotics and artificial muscles, chemical sensors, and photography. Our results will help to determine physico–chemical properties like the heat of formation, strain energy, strength and fracture toughness of these materials.

2. Results and Discussions

In this part we give our main computational results.

2.1. Computational Aspects of Generalized Prism

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle or, in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called $C_n.$ The number of vertices in $C_n$ equals the number of edges, and every vertex has degree 2; that is, every vertex has exactly two edges incident with it. Figure 1 is a cycle of length 10.

Figure 1. Cycle graph $C_{10}$.

For a cycle $C_n,$ we have $V(C_n)=\{x_i:1\le i\le n\},$ and $E(C_n)=\{x_i{x}_{i+1}:1\le i\le n-1\}\cup \left\{x_n{x}_1\right\}.$

A path graph $P_m$ is a graph whose vertices can be listed in the order $v_1, v_2,\cdot \cdot \cdot , v_m$ such that the edges are $\{v_i, v_{i+1}\},$ where $i=1,2,\cdots , m-1$. Equivalently a path with at least two vertices is connected and has two terminal vertices (vertices that have degree 1), while all others (if any) have degree 2. Figure 2 shows a path graph $P_4$.

Figure 2. Path graph $P_4$.

For a path $P_m$, we have $V(P_m)=\{y_j:1\le j\le m\}$ and $E(P_n)=\{x_j{x}_{j+1}:1\le j\le n-1\}.$

The Cartesian product $G\square H$ of graphs G and H is a graph such that the vertex set of $G\square H$ is the Cartesian product $V(G)\times V(H)$ and any two vertices $\left(u,u\prime \right)$ and $\left(v,v\prime \right)$ are adjacent in $G\square H$ if and only if either u = v and $u\prime$ is adjacent with v′ in H, or u′ = v′ and u is adjacent with v in G.

Let $P_{\{n,m\}}$ be the generalized prism graph that is obtained by Cartesian product of a cycle $C_n$ with a path $P_m$ as shown in Figure 3. Then $V\left(P_{\{n,m\}}\right)=\left\{(x_i,y_j):1\le i\le n,1\le j\le m\right\}$ and $\begin{array}{l}E\left(P_{\{n,m\}}\right)=\left\{(x_i,y_j)(x_{i+1},y_j):1\le i\le n-1,1\le j\le m\right\}\cup \left\{(x_n,y_j)(x_1,y_j):1\le j\le m\right\}\\ \cup \left\{(x_i,y_j)(x_i,y_{j+1}):1\le i\le n,1\le j\le m-1\right\}.\end{array}$

Figure 3. The generalized prism $P_{\{n,m\}}$.

The generalized prism $P_{\{n,m\}}$ has been studied extensively in recent years. Kuo et al. [18] and Chiang et al. [19] studied distance-two labelings of $P_{\{n,m\}}$. Siddiqui et al. [20] counted some topological indices of $P_{\{n,m\}}.$ Deming et al. [21] gave complete characterization of the Cartesian product of cycles and paths for their incidence chromatic numbers. Gravier et al. [22] showed the link between the existence of perfect Lee codes and minimum dominating sets of $P_{\{n,m\}}$. Lai et al. [23] determined the edge addition number for the Cartesian product of a cycle with a path. Chang et al. [24] established upper bounds and lower bounds for global defensive alliance number of $P_{\{n,m\}}.$

Theorem 1.

Let $P_{\{n,m\}}$ be the generalized prism. Then the first Zagreb polynomial, second Zagreb polynomial, and forgotten polynomial of $P_{\{n,m\}}$ are

• $M_1\left(P_{\{n,m\}},x\right)=2mn{x}^8-5n{x}^8+2n{x}^7+2n{x}^6,$
• $M_2\left(P_{\{n,m\}},x\right)=2mn{x}^{16}-5n{x}^{16}+2n{x}^{12}+2n{x}^9,$
• $F\left(P_{\{n,m\}},x\right)=2mn{x}^{32}-5n{x}^{32}+2n{x}^{25}+2n{x}^{18}.$

Proof. 

Let $P_{\{n,m\}}$ be the generalized prism with defining parameters m and n. The number of vertices and edges in generalized prism $P_{\{n,m\}}$ are nm and n(2m − 1) respectively. There are three types of edges in $P_{\{n,m\}}$ based on degrees of end vertices of each edge. The first edge partition $E_1(P_{\{n,m\}})$ contains $2n$ edges uv, where $d_u=d_v=3$. The second edge partition $E_2(P_{\{n,m\}})$ contains $2n$ edges uv, where $d_u=3,d_v=4.$ The third edge partition $E_3(P_{\{n,m\}})$ contains $2mn-5n$ edges uv, where $d_u=d_v=4.$ Then;

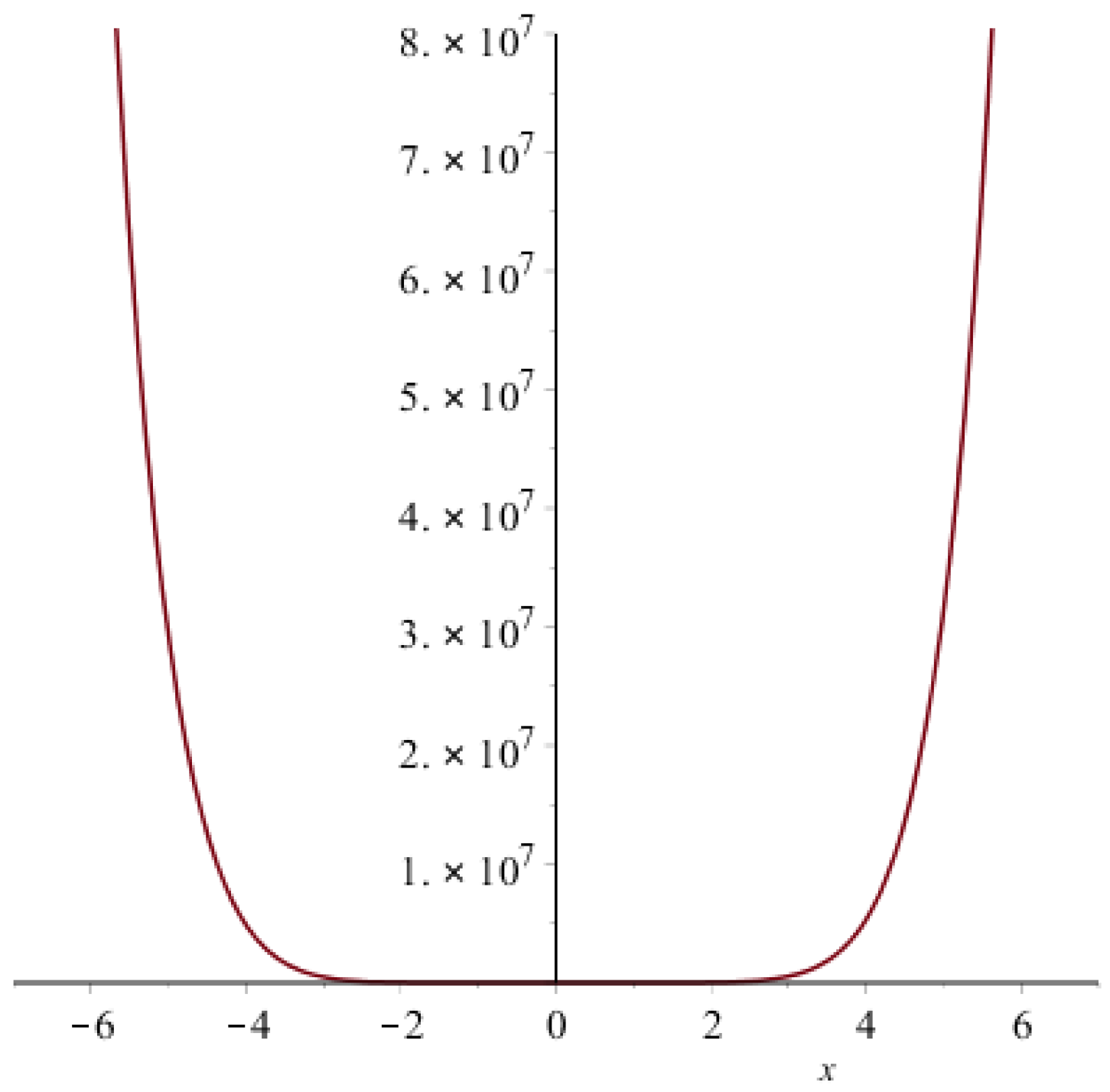
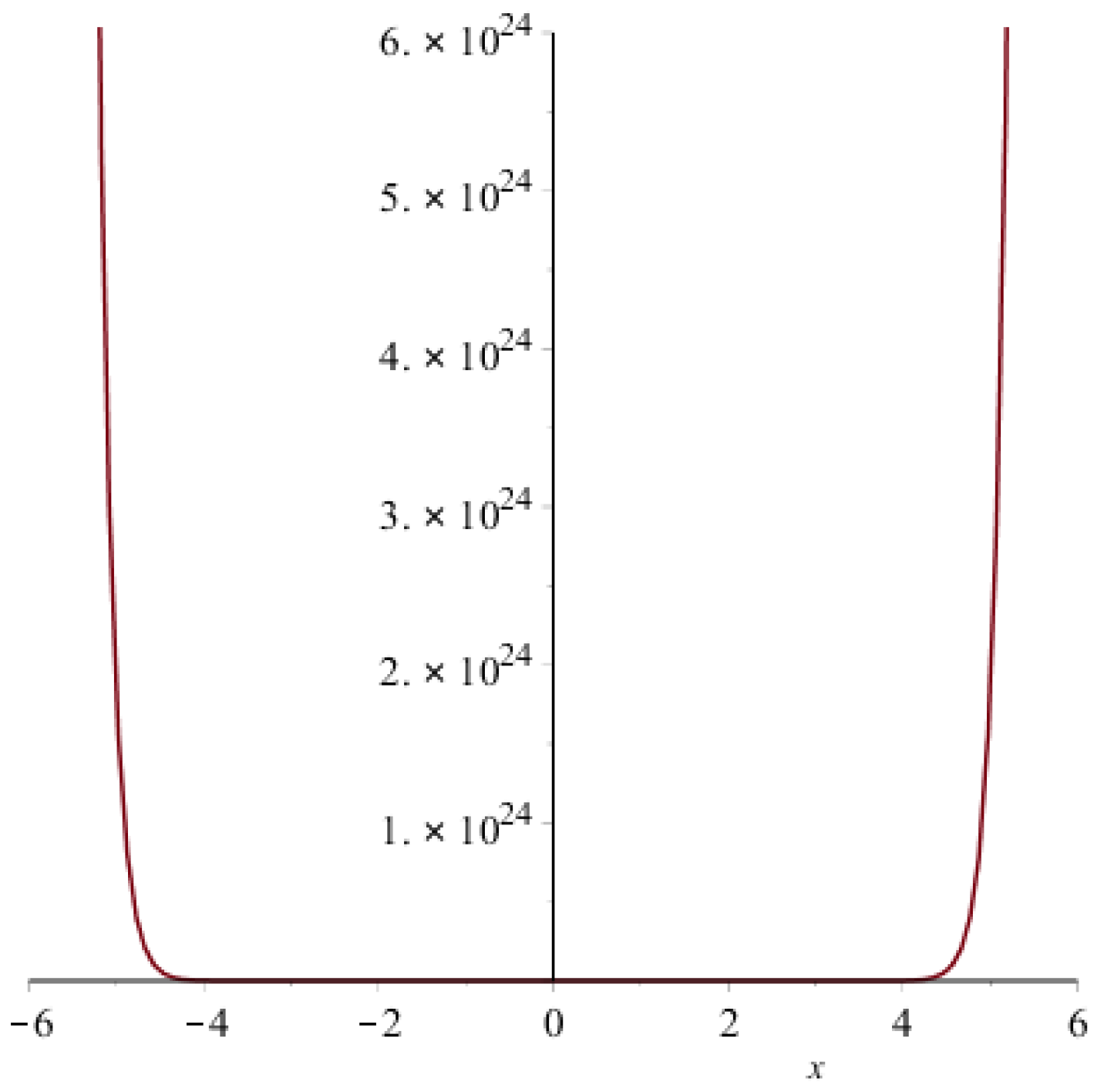
• by definition, the first Zagreb polynomial is;

  $$\begin{array}{ll}{M}_1\left(P_{\{n,m\}},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u+d_v\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u+d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u+d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u+d_v\right]}\\ & =\left|E_1\left(P_{\{n,m\}}\right)\right|x^6+\left|E_2\left(P_{\{n,m\}}\right)\right|x^7+\left|E_3\left(P_{\{n,m\}}\right)\right|x^8\\ & =2mn{x}^8-5n{x}^8+2n{x}^7+2n{x}^6.\end{array}$$
  Following Figure 4 is the graph of first Zagreb polynomial $P_{\{7,8\}}.$
  

  Figure 4. Graph of the first Zagreb polynomial of $P_{\{7,8\}}$.
• Now, by definition, the second Zagreb polynomial is;

  $$\begin{array}{ll}{M}_2\left(P_{\{n,m\}},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u\times d_v\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u\times d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u\times d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(P_{\{n,m\}}\right)}}{x}^{\left[d_u\times d_v\right]}\\ & =\left|E_1\left(P_{\{n,m\}}\right)\right|x^9+\left|E_2\left(P_{\{n,m\}}\right)\right|x^{12}+\left|E_3\left(P_{\{n,m\}}\right)\right|x^{16}\\ & =2mn{x}^{16}-5n{x}^{16}+2n{x}^{12}+2n{x}^9.\end{array}$$
  The graph of the second Zagreb polynomial of generalized prism is in Figure 5.
  

  Figure 5. Graph of the second Zagreb polynomial of $P_{\{7,8\}}$.
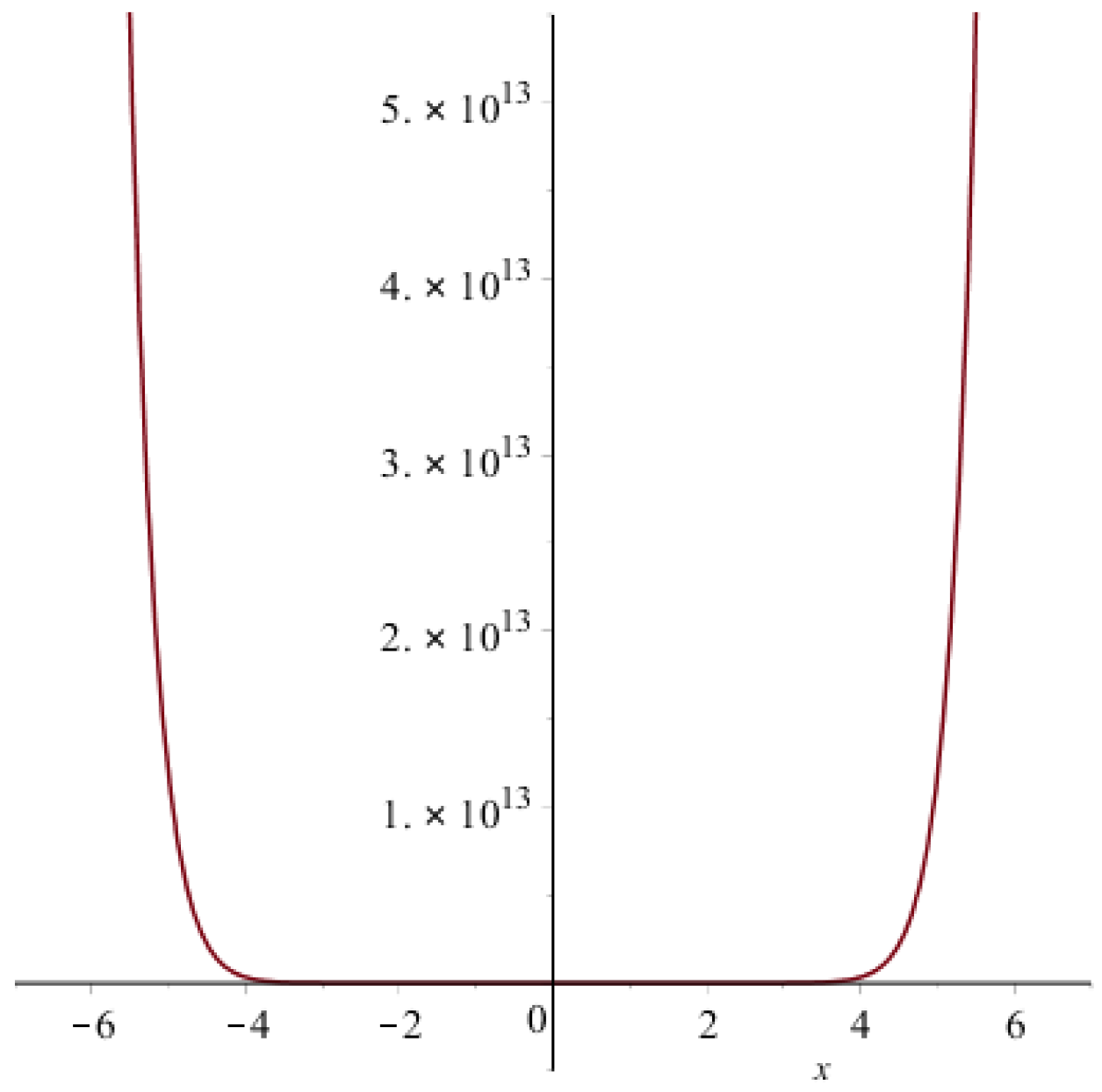
• By definition, the forgotten polynomial is:

  $$\begin{array}{ll}F\left(P_{\{n,m\}},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(P_{\{n,m\}}\right)}}{x}^{\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(P_{\{n,m\}}\right)}}{x}^{\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(P_{\{n,m\}}\right)}}{x}^{\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(P_{\{n,m\}}\right)}}{x}^{\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}\\ & =\left|E_1\left(P_{\{n,m\}}\right)\right|x^{18}+\left|E_2\left(P_{\{n,m\}}\right)\right|x^{25}+\left|E_3\left(P_{\{n,m\}}\right)\right|x^{32}\\ & =2mn{x}^{32}-5n{x}^{32}+2n{x}^{25}+2n{x}^{18}.\end{array}$$
  The graph of the forgotten polynomial of $P_{\{7,8\}}$ is given in Figure 6 below,
  

  Figure 6. Graph of the forgotten polynomial of $P_{\{7,8\}}$.

Proposition 1.

Let $P_{\{n,m\}}$ be the generalized prism. Then the hyper-Zagreb index, first multiple Zagreb index, second multiple Zagreb index, and forgotten index of $P_{\{n,m\}}$ are

• $HM\left(P_{\{n,m\}}\right)=-150n+128mn,$
• $P{M}_1\left(P_{\{n,m\}}\right){=6}^{2n}\times 7^{2n}\times 8^{2mn-5n},$
• $P{M}_2\left(O_{\{n,m\}}\right)=9^{2n}\times {12}^{2n}\times {16}^{2mn-5n},$
• $F\left(P_{\{n,m\}}\right)={324}^n+{625}^n+{36}^{n(2m-5)}.$

Proof. 

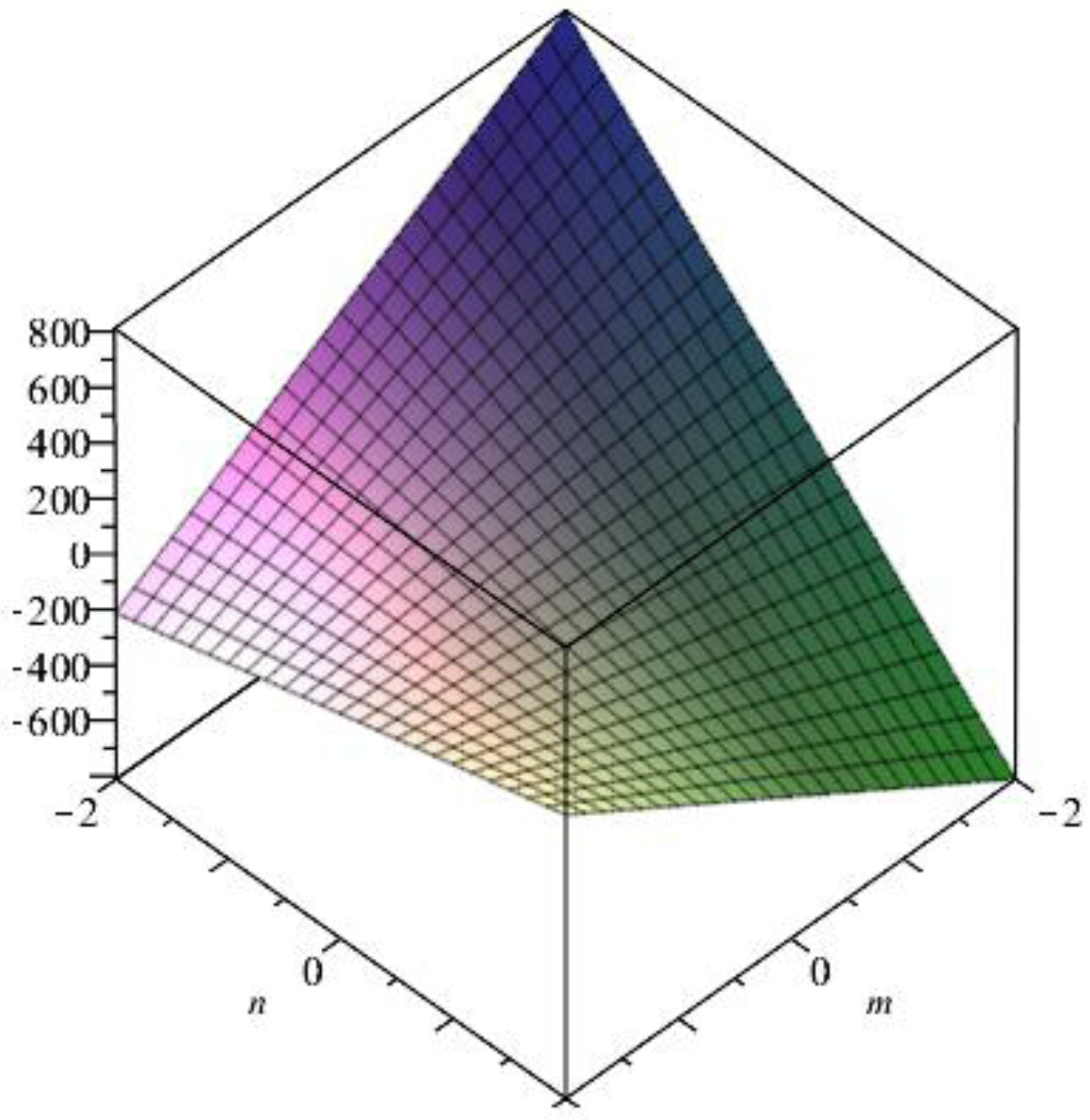
• By definition of the hyper-Zagreb index,

  $$\begin{array}{ll}HM\left(P_{\{n,m\}}\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(P_{\{n,m\}}\right)}}{\left[d_u+d_v\right]}^2\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(P_{\{n,m\}}\right)}}{\left[d_u+d_v\right]}^2+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(P_{\{n,m\}}\right)}}{\left[d_u+d_v\right]}^2+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(P_{\{n,m\}}\right)}}{\left[d_u+d_v\right]}^2\\ & =36\left|E_1\left(P_{\{n,m\}}\right)\right|+49\left|E_2\left(P_{\{n,m\}}\right)\right|+64\left|E_3\left(P_{\{n,m\}}\right)\right|\\ & =36\left(2n\right)+49\left(2n\right)+64\left(2mn-5n\right)\\ & =-150n+128mn.\end{array}$$
  The Figure 7 is 3D plot of the Hyper Zagreb index of generalized prism.
  

  Figure 7. 3D plot for the hyper-Zagreb index.
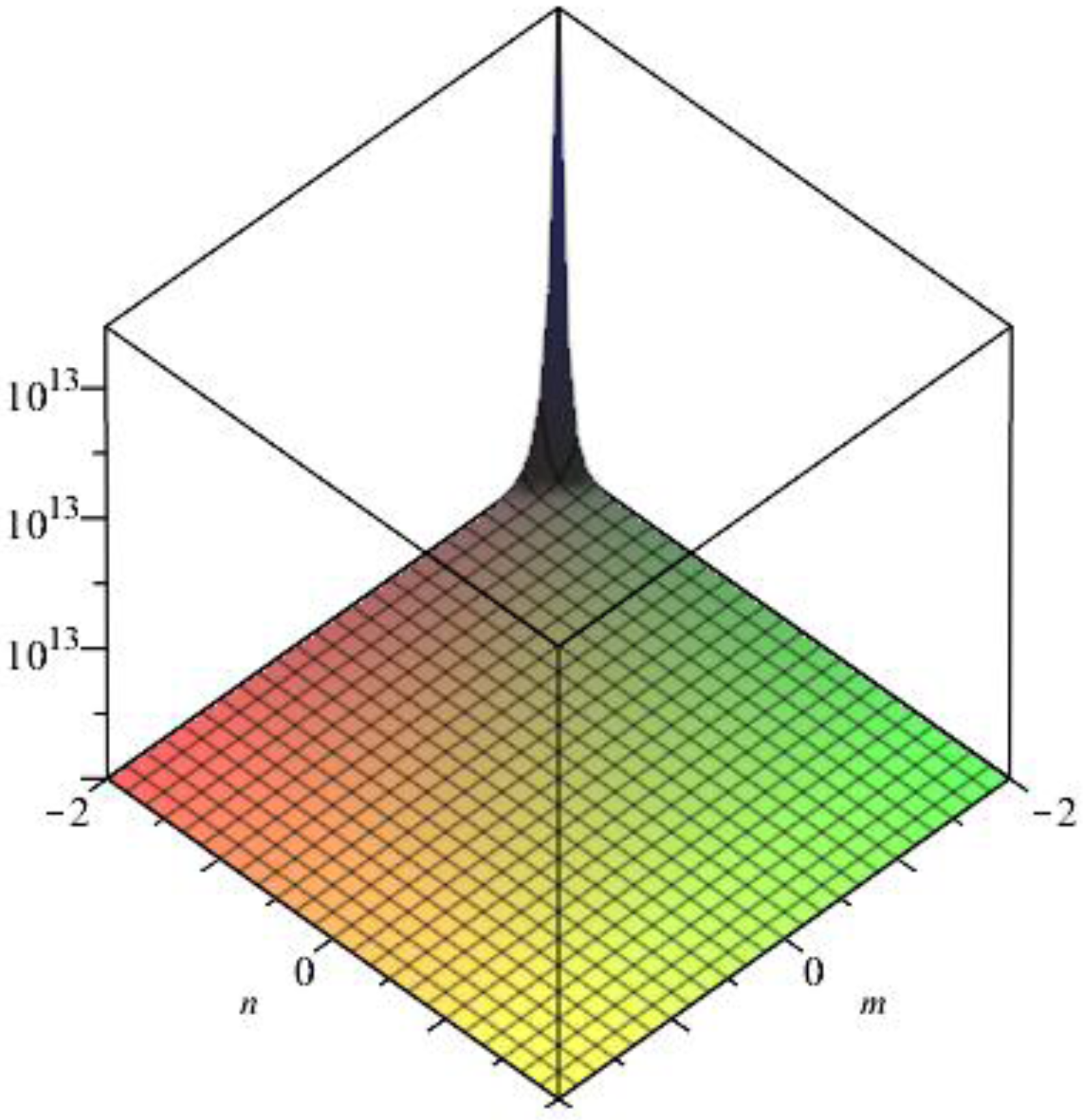
• By the definition of the first multiple Zagreb index,

  $$\begin{array}{ll}P{M}_1\left(P_{\{n,m\}}\right)& ={\displaystyle {\displaystyle \prod }_{uv\in E\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]\\ & ={\displaystyle {\displaystyle \prod }_{uv\in E_1\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_3\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u+{\mathrm{d}}_v\right]\\ & =6^{\left|E_1\left(P_{\{n,m\}}\right)\right|}\times 7^{\left|E_2\left(P_{\{n,m\}}\right)\right|}\times 8^{\left|E_3\left(P_{\{n,m\}}\right)\right|}\\ & =6^{2n}\times 7^{2n}\times 8^{2mn-5n}.\end{array}$$
  3D plot of the multiple-Zagreb index of generalized prism is shown in Figure 8.
  

  Figure 8. 3D plot for the first multiple-Zagreb index.
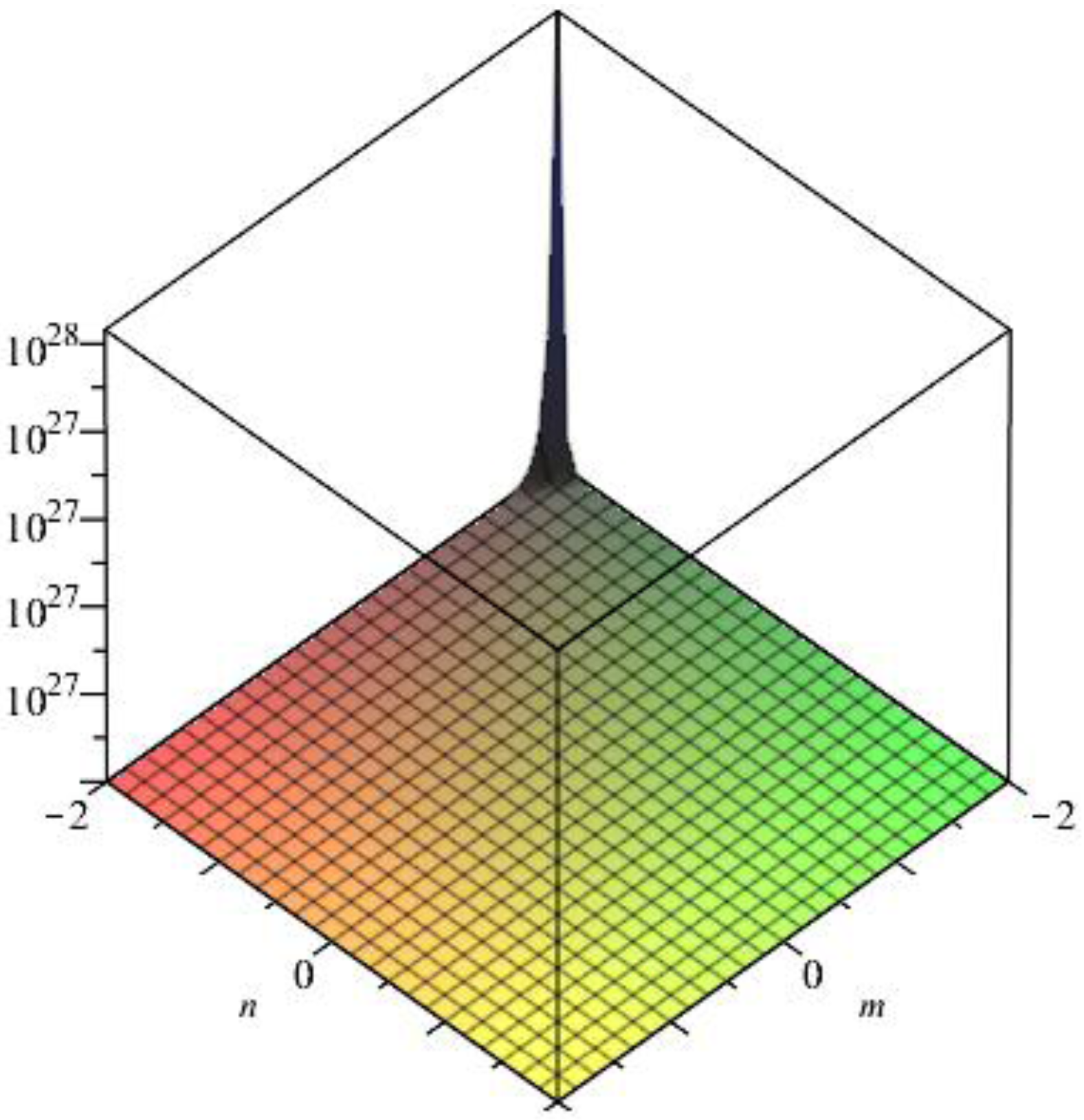
• By the definition of the second multiple Zagreb index,

  $$\begin{array}{ll}P{M}_2\left(P_{\{n,m\}}\right)& ={\displaystyle {\displaystyle \prod }_{uv\in E\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right]\\ & ={\displaystyle {\displaystyle \prod }_{uv\in E_1\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_3\left(P_{\{n,m\}}\right)}}\left[{\mathrm{d}}_u\times {\mathrm{d}}_v\right]\\ & =9^{\left|E_1\left(P_{\{n,m\}}\right)\right|}\times {12}^{\left|E_2\left(P_{\{n,m\}}\right)\right|}\times {16}^{\left|E_3\left(P_{\{n,m\}}\right)\right|}\\ & =9^{2n}\times {12}^{2n}\times {16}^{2mn-5n}.\end{array}$$
  3D plot for the second multiple-Zagreb index of generalized prism is given in Figure 9.
  

  Figure 9. 3D plot for the second multiple-Zagreb index.
• By the definition of the forgotten index,

  $$\begin{array}{ll}F\left(P_{\{n,m\}}\right)& ={\displaystyle {\displaystyle \prod }_{uv\in E\left(P_{\{n,m\}}\right)}}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]\\ & ={\displaystyle {\displaystyle \prod }_{uv\in E_1\left(P_{\{n,m\}}\right)}}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(P_{\{n,m\}}\right)}}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_3\left(P_{\{n,m\}}\right)}}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]\\ & ={18}^{\left|E_1\left(P_{\{n,m\}}\right)\right|}\times {25}^{\left|E_2\left(P_{\{n,m\}}\right)\right|}\times {31}^{\left|E_3\left(P_{\{n,m\}}\right)\right|}\\ & ={324}^n+{625}^n+{36}^{n(2m-5)}.\end{array}$$
  3D plot for the second multiple-Zagreb index of generalized prism is given in Figure 10.
  

  Figure 10. 3D plot of the forgotten index.

2.2. Computational Aspects of Toroidal Polyhex

The discovery of the fullerene molecules has stimulated many interests in other possibilities for carbons. Many properties of fullerenes can be studied using mathematical tools such as graph theory. A fullerene can be represented by a trivalent graph on a closed surface with pentagonal and hexagonal faces, such that its vertices are carbon atoms of the molecule. Two vertices are adjacent if there is a bond between corresponding atoms. In [25], authors considered fullerene’s extension to other closed surfaces and showed that only four surfaces, sphere, torus, Klein bottle and projective (elliptic) plane, are possible. The spherical and elliptic fullerenes have 12 and 6 pentagons respectively. There are no pentagons in the toroidal’s and the Klein bottle’s fullerenes [26].

A toroidal fullerene (toroidal polyhex), obtained from 3D Polyhex Torus Figure 11, is a cubic bipartite graph embedded on the torus such that each face is a hexagon. The torus is a closed surface that can carry the graph of the toroidal polyhex in which all faces are hexagons and the degree of all vertices is 3. The optical and vibrational properties of toroidal carbon nanotubes can be found in [27]. There have appeared a few works in the enumeration of perfect matchings of toroidal polyhexes by applying various techniques, such as transfer-matrix and permanent of the adjacency matrix. Ye et al. [28] have studied a k-resonance of toroidal polyhexes. Classification of all possible structures of fullerene Cayley graphs is given in [29] by Kang. The atom-bond connectivity index (ABC) and geometric–arithmetic index (GA) of the toroidal polyhex are computed in [30] by Baca et al. In [31], authors computed distance-based topological indices of eight infinite sequences of 3-generalized fullerenes.

Figure 11. Polyhex Torus.

In [32], authors presented a new extension of the generalized topological indices (GTI) approach to represent topological indices in a unified way.

Let L be a regular hexagonal lattice and ${}^{n}P_m$ be a $m\times n$ quadrilateral section (with m hexagons on the top and bottom sides and n hexagons on the lateral sides; n is even), cut from the regular hexagonal lattice L. First identify two lateral sides of ${}^{n}P_m$ to form a cylinder, and finally identify the top and bottom sides of ${}^{n}P_m$ at their corresponding points. From this we get a toroidal polyhex $H_{\{m,n\}}$ with mn hexagons.

The set of vertices of the toroidal polyhex is:

$$V(H_{\{m,n\}})=\{v_j^i,v_j^i:0\le i\le n-1,0\le j\le m-1\}.$$

The set of edges of the toroidal polyhex is splitted into mutually disjointed subsets; such that for even $i$, such that $0\le i\le n-2,$ we have $A_i=\{u_j^i{v}_j^i:0\le j\le m-1\}$ and ${A^{\prime }}_i=\{v_j^i{u}_{j+1}^i:0\le j\le m-1\}$, and for $i$ odd and $1\le i\le n-1,$ we have $B_i=\{v_j^i{u}_j^i:0\le j\le m-1\}$ and ${B^{\prime }}_i=\{u_j^i{v}_{j+1}^i:0\le j\le m-1\}$, and for $0\le i\le n-1$ we have $C_i=\{v_j^i{u}_j^{i+1}:0\le j\le m-1\},$ where i is taken modulo n and j is taken modulo m.

Hence $E(H_{\{m,n\}})={\displaystyle \underset{i=0}{\overset{\frac{n}{2}-1}{\cup }}\left(A_{2i}\cup {A^{\prime }}_{2i}\cup B_{2i+1}\cup {B^{\prime }}_{2i+1}\right)}{\displaystyle \underset{i=0}{\overset{n-1}{\cup }}{C}_i}.$ We can easily observe from Figure 12 that the number of vertices in $H_{\{m,n\}}$ are 2mn and the number of edges in $H_{\{m,n\}}$ are 3mn. Note that there is only one type of edge in a toroidal polyhex, based on degrees of end vertices of each edge. The edge partition $E_1(H_{\{m,n\}})$ contains 3mn edges uv, where $d_u=d_v=3.$

Figure 12. 2D lattice graph of toroidal polyhex.

Theorem 2.

Let $H_{\{m,n\}}$ be the toroidal polyhex. Then the first Zagreb polynomial, second Zagreb polynomial, and forgotten polynomial of $H_{\{m,n\}}$ are;

• $M_1\left(H_{\{m,n\}},x\right)=3mn{x}^6,$
• $M_2\left(H_{\{m,n\}},x\right)=3mn{x}^9,$ and
• $F\left(H_{\{m,n\}},x\right)=mn{x}^{18}.$

Proposition 2.

Let $H_{\{m,n\}}$ be the toroidal polyhex. Then the hyper-Zagreb index, first multiple Zagreb index, second multiple Zagreb inde, x and forgotten index of $H_{\{m,n\}}$ are;

• $HM\left(H_{\{m,n\}}\right){=108}^{mn},$
• $P{M}_1\left(H_{\{m,n\}}\right){=216}^{mn},$
• $P{M}_2\left(H_{\{m,n\}}\right){=729}^{mn},$
• $F\left(H_{\{m,n\}}\right){=5832}^{mn}.$

3. Conclusions and Discussion

In this article, we computed closed forms of topological indices for a generalized prism and toroidal polyhex. We also gave closed forms of some well-known polynomials concerning these structures. Further, we gave graphs (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) for the computed polynomials and topological indices to correlate these indices with involved parameters of structure. These results can play a vital role in industry and pharmacy. It is important to remark that the methodology described above can be employed in recently developed nanomaterials, nanotubes, and polymers [33,34,35]. Some examples are Boron nanotubes, aluminosilicate/aluminugerminate, SiO₂—layered structure and titania nanotubes.