Broken versus Non-Broken Time Reversal Symmetry: Irreversibility and Response
Abstract
:1. Introduction
2. Standard Picture for Irreversible Relaxation to Equilibrium
3. Time Reversible Dissipative Dynamics
4. The Dissipation Function
4.1. Time-Dependent Perturbations
4.2. Fluctuation Relations: Symmetry in Dissipative Dynamics
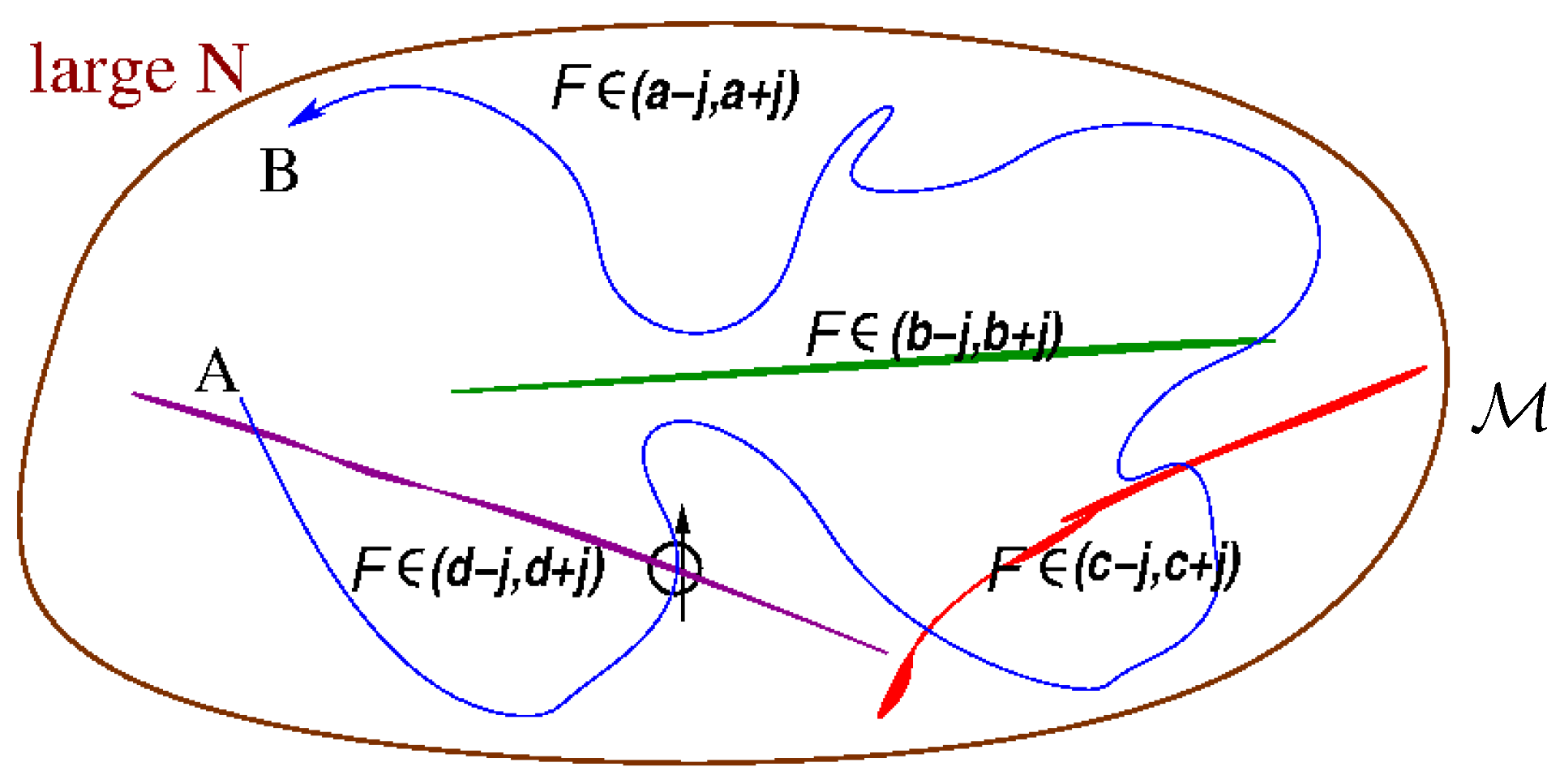
4.3. t-Mixing and Irreversibility
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
- For completeness, we report some mathematical derivations, as given in Ref. [24]. For the phase-space average of any observable , the following holds:where we have used to complete the final step.
- We give here some guidelines to obtain Equation (23):By using the midpoint rule on the term in squared brackets, we eventually reach:so thatFor a more detailed explanation, we refer to Ref. [24].
References
- Cohen, L. The history of noise. IEEE Signal Process. Mag. 2005, 22, 20–45. [Google Scholar] [CrossRef]
- Cercignani, C. The Boltzmann Equation and Its Applications; Spriger-Verlag: Berlin, Germany, 1987. [Google Scholar]
- Lebowitz, J. Boltzmann’s Entropy and Time’s Arrow. Phys. Today 1993, 46, 32–38. [Google Scholar] [CrossRef]
- Hoover, W.G.; Posch, H.; Holian, B.L. Is Boltzmann Entropy Time’s Arrow’s Archer? Phys. Today 1994, 47. [Google Scholar] [CrossRef]
- Goldstein, T. Typicality and Notions of Probability in Physics. In Probability in Physics; Ben-Menahem, Y., Hemmo, M., Eds.; Springer-Verlag: Berlin, Germany, 2012. [Google Scholar]
- Khinchin, A. Mathematical Foundations of Statistical Mechanics; Dover Publications: New York, NY, USA, 1949. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Castiglione, P.; Falcioni, M.; Lesne, A.; Vulpiani, A. Chaos and Coarse Graining in Statistical Mechanics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Cerino, L.; Cecconi, F.; Cencini, M.; Vulpiani, A. The role of the number of degrees of freedom and chaos in macroscopic irreversibility. Physica A 2016, 442, 486–497. [Google Scholar] [CrossRef]
- Pitowsky, I. Typicality and the Role of the Lebesgue Measure in Statistical Mechanics. In Probability in Physics; Ben-Menahem, Y., Hemmo, M., Eds.; Springer-Verlag: Berlin, Germany, 2012. [Google Scholar]
- Penrose, R. The Road to Reality: A Complete Guide to the Laws of the Universe; Jonathan Cape: London, UK, 2004. [Google Scholar]
- Albert, D.Z. Time and Chance; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilibrium Liquids; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Chibbaro, S.; Rondoni, L.; Vulpiani, A. Reductionism, Emergence and Levels of Reality. The Importance of Being Borderline; Springer: New York, NY, USA, 2014. [Google Scholar]
- Jepps, O.; Rondoni, L. Deterministic thermostats, theories of nonequilibrium systems and parallels with the ergodic condition. J. Phys. A Math. Theor. 2010, 43, 1–42. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of second law violations in shearing steady flows. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef] [PubMed]
- Bonaldi, M.; Conti, L.; De Gregorio, P.; Rondoni, L.; Vedovato, G.; Vinante, A.; Bignotto, M.; Cerdonio, M.; Falferi, P.; Liguori, N.; et al. Nonequilibrium Steady-State Fluctuations in Actively Cooled Resonators. Phys. Rev. Lett. 2009, 103, 010601. [Google Scholar] [CrossRef] [PubMed]
- Conti, L.; Lazzaro, C.; Karapetyan, G.; Bonaldi, M.; Pegoraro, M.; Thakur, R.-K.; De Gregorio, P.; Rondoni, L. Thermal noise of mechanical oscillators in steady states with a heat flux. Phys. Rev. E 2014, 90, 032119. [Google Scholar] [CrossRef] [PubMed]
- Bonella, S.; Ciccotti, G.; Rondoni, L. Time reversal symmetry in time-dependent correlation functions for systems in a constant magnetic field. EPL 2014, 108, 60004. [Google Scholar] [CrossRef]
- De Grood, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 2011. [Google Scholar]
- Gabrielli, D.; Jona-Lasinio, G.; Landim, C. Onsager Symmetry from Microscopic TP Invariance. J. Stat. Phys. 1999, 96, 639–652. [Google Scholar] [CrossRef]
- Gaspard, P. Multivariate fluctuation relations for currents. New J. Phys. 2013, 15, 115014. [Google Scholar] [CrossRef]
- Searles, D.J.; Rondoni, L.; Evans, D.J. The steady state fluctuation relation for the dissipation function. J. Stat. Phys. 2007, 128, 1337–1363. [Google Scholar] [CrossRef]
- Jepps, O.G.; Rondoni, L. A dynamical-systems interpretation of the dissipation function, T-mixing and their relation to thermodynamic relaxation. J. Phys. A 2016, 49, 154002. [Google Scholar] [CrossRef]
- Rondoni, L.; Evans, D.J.; Searles, D.J.; Williams, S.R. On typicality in nonequilibrium steady states. J. Stat. Phys. 2016, in press. [Google Scholar]
- Evans, D.J.; Searles, D.J. The Fluctuation Theorem. Adv. Phys. 2002, 51, 1529. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J.; Williams, S.R. On the Fluctuation Theorem for the Dissipation Function and Its Connection with Response Theory. J. Chem. Phys. 2008, 128, 014504. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II, Nonequilibrium Statistical Mechanics; Springer Verlag: Heidelberg, Germany, 1985. [Google Scholar]
- Colangeli, M.; Rondoni, L. Equilibrium, fluctuation relations and transport for irreversible deterministic dynamics. Physica D 2012, 241, 681–691. [Google Scholar] [CrossRef]
- Barbour, J.; Koslowski, T.; Mercati, F. Identification of a Gravitational Arrow of Time. Phys. Rev. Lett. 2014, 113, 181101. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, S.; Tumulka, R.; Zanghí, N. Is the Hypothesis about a Low Entropy Initial State of the Universe Necessary for Explaining the Arrow of Time? 2016; arXiv:1602.05601. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dal Cengio, S.; Rondoni, L. Broken versus Non-Broken Time Reversal Symmetry: Irreversibility and Response. Symmetry 2016, 8, 73. https://doi.org/10.3390/sym8080073
Dal Cengio S, Rondoni L. Broken versus Non-Broken Time Reversal Symmetry: Irreversibility and Response. Symmetry. 2016; 8(8):73. https://doi.org/10.3390/sym8080073
Chicago/Turabian StyleDal Cengio, Sara, and Lamberto Rondoni. 2016. "Broken versus Non-Broken Time Reversal Symmetry: Irreversibility and Response" Symmetry 8, no. 8: 73. https://doi.org/10.3390/sym8080073
APA StyleDal Cengio, S., & Rondoni, L. (2016). Broken versus Non-Broken Time Reversal Symmetry: Irreversibility and Response. Symmetry, 8(8), 73. https://doi.org/10.3390/sym8080073






