1. Introduction
An ordinary planar mirror generates a plane symmetric image of an object, that is, for an arbitrary point of an object and its mirror image, the line segment connecting them crosses the mirror plane at the midpoint in the right angle. Although the concept of the mirror symmetry has been generalized in many directions in mathematics and physics [
1,
2], the original mirror symmetry with respect to a planar mirror is simple and well understood from a mathematical point of view.
When we see the object and its mirror image, however, what we perceive does not necessarily obey this physical law, because what we perceive is the result of image processing in our brains, and hence optical illusion arises [
3,
4]. In particular, it was discovered recently that there are cylindrical objects whose mirror images appear to be quite different from what we usually expect [
5,
6]. Those cylinders seem to defy the law of optical physics. This phenomenon is called ambiguous cylinder illusion.
In this paper, we propose a new concept of symmetry, which we call “anomalous mirror symmetry” (“anomalous symmetry” for short). The anomalous symmetry is a modification of mirror symmetry, but it does not obey the law of optical physics. Hence, it cannot be realized in a purely physical manner. However, we show that anomalous symmetry can be generated if we employ ambiguous cylinder illusion. We characterize the class of cylinders whose mirror images generate anomalous symmetry and moreover the same anomaly is preserved even if the objects are rotated around a vertical axis.
From a mathematical point of view, we solve a problem of finding a pair of mirror symmetric space curves whose projections coincide with a pair of given point symmetric planar curves. The problem of finding symmetric space curves from given planar curves have been studied in many setting. For example, Hong
et al. [
7] showed that both the symmetric space curves and the camera poses can be reconstructed from their perspective images. Sawada
et al. [
8,
9] constructed an algorithm for finding a pair of mirror symmetric space curves and the associated mirror from a pair of planar curves. The present problem is similar to them in the sense that we construct symmetric space curves, but simpler because the mirror pose is given.
The paper is organized in the following way. In
Section 2, we review the nature of mirror symmetry and introduce a concept of anomalous symmetry. In
Section 3, we review a method to generate ambiguous cylinders. In
Section 4, we apply this method to design solids that produce the anomalous symmetry.
Section 5 gives examples of anomalously symmetric objects and
Section 6 gives concluding remarks together with future work.
2. Mirror Symmetry and Anomalous Symmetry
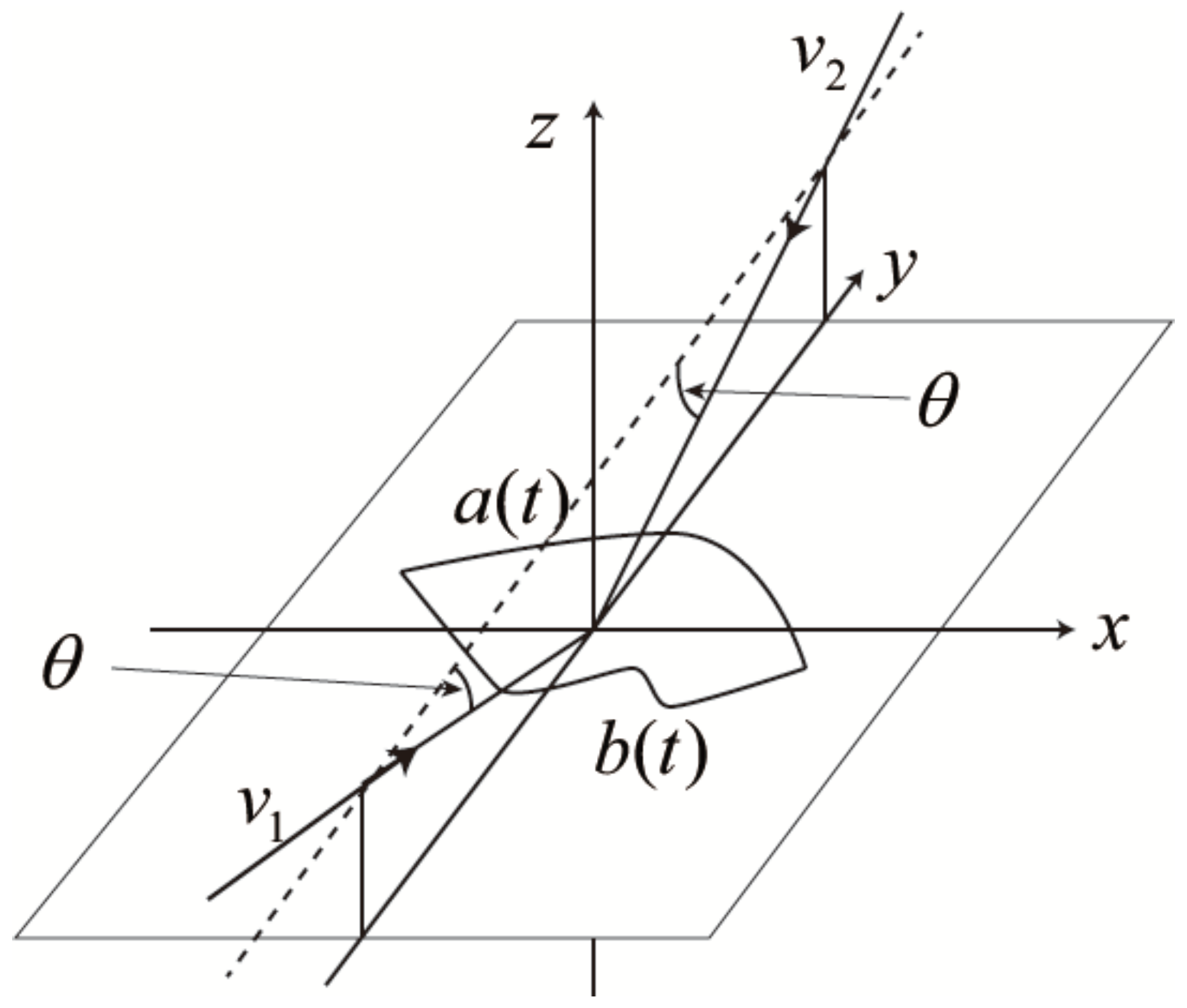
As shown in
Figure 1, we consider an
Cartesian coordinate systems, in which the
plane is horizontal and hence the
z axis is vertical.
Let O be an object and be its mirror image with respect to a mirror placed in the plane. Then, any point on O is mapped to the point . Thus, the y coordinate is reversed while the x and z coordinates are kept unchanged. Hence, we call the y-reversal mirror image. We extend the meaning of the term “y-reversal” for any translated version of . In other words, we refer to “y-reversal” to represent the posture of with respect to O, and do not care about the position of . Similarly we name the x-reversal mirror image for the image generated by a mirror in the plane, and its translated version.
We are interested in a class of objects whose y-reversal mirror images appear to be x-reversal.
An example is shown in
Figure 2. There is a cylinder whose section appears to be an arrow, and a vertical mirror stands behind it. However, the mirror image of the cylinder is anomalous in the sense that the left part and the right part appear to be reversed. Let us consider an
coordinate system such that the mirror is contained in the
plane. Then, the mirror image of the cylinder should be
y-reversal, but the actual mirror image in
Figure 2 appears to be
x-reversal.
If we rotate this cylinder around a vertical axis, the apparent shape of the section changes as shown in
Figure 3. Note that in all postures of the cylinder, the corresponding mirror images are
x-reversal instead of
y-reversal.
Note that the concept of anomalous symmetry is mathematically equivalent to line symmetry with respect to a vertical line. However, we use the term “anomalous mirror” symmetry in order to emphasize that it is physically impossible by a planar mirror.
It might be interesting to note that one of typical errors made by human subjects in predicting motion and orientation in the mirror image is similar to what we call anomalous symmetry. For example, Savardi
et al. [
10] and Bianchi
et al. [
11] made experiments in which they showed motion of an object to subjects and asked them to predict the motion and orientation in its mirror image. They reported that a typical error in estimation is line symmetric with respect to a vertical line instead of mirror symmetric.
The goal of this paper is to characterize the class of cylinders with this anomalous symmetry. For this purpose we review geometric aspects of the class of optical illusion called ambiguous cylinders in the next section.
3. Ambiguous Cylinders
Let
and
be two real-valued continuous functions defined for
, and let us define three-dimensional vectors,
where
t is a parameter. The vectors
and
represent planar curves on the
plane, and they are monotone in the
x direction.
As shown in
Figure 1, suppose that we see those curves along two view directions
and
. They are parallel to the
plane, and are slanted downward by the same angle
θ,
, with respect to the horizontal plane in mutually opposite directions in the
y axis. This means that the two viewpoints are both at infinity. This is a good approximation of actual perspective projection if the viewpoint is sufficiently far from the objects.
We are interested in finding a space curve that coincides with when it is seen along and that coincides with when it is seen along . This space curve can be determined uniquely in the following way. For any , and are in the plane , which is parallel to the plane. Hence the line passing through and parallel to and the line passing through and parallel to are both in this plane, and consequently they have a point of intersection. Let this point of intersection be denoted by . As t moves in , traces a space curve. This is the curve that we wanted to get.
The curve is just a space curve, and it is not necessarily be perceived as the planar curves and when it is seen in the corresponding view directions.
However, the human brains prefer right angles in interpreting retinal images as three-dimensional objects; this property is typically observed in Ames’s room illusion [
3], and is usually understood as a priori constraint for right angles [
12,
13,
14]. We can use this nature of the brains to guide viewers to perceive the planar curves
and
when they see the space curve
in the following way.
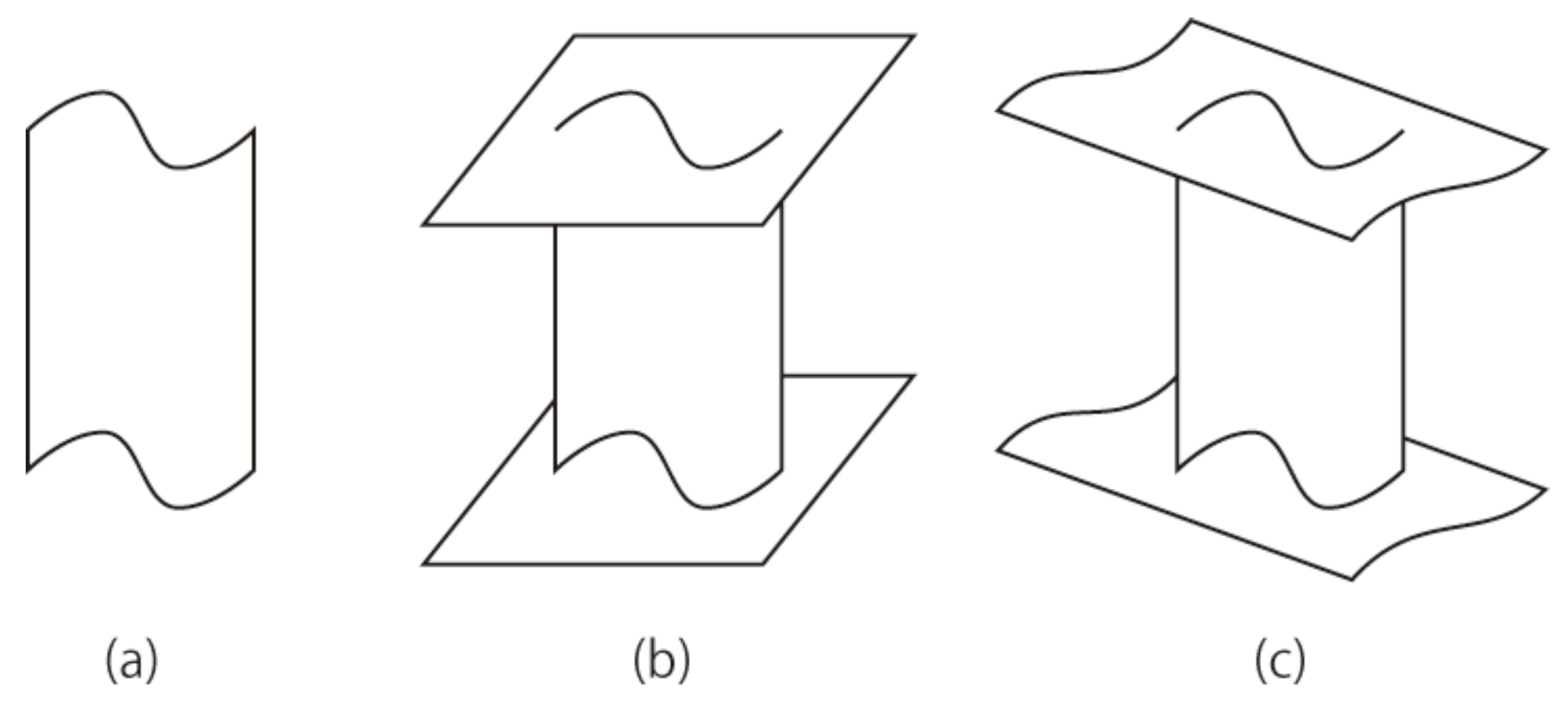
Let l be a vertical line segment, that is, l is parallel to the z axis. Suppose that we move l in a space in such a way that its orientation is fixed and its upper terminal point traces along the curve . Let the surface swept by l be S.
As shown in
Figure 4a, the resulting surface
S has the same vertical length as the length of
l. In this case we are apt to interpret the upper edge
as the intersection of
S and a plane perpendicular to
l as shown in
Figure 4b because of the preference of right angles; we usually do not consider it as the intersection of
S and a curved surface as shown in
Figure 4c although it is mathematically possible.
Therefore, we can expect that when the surface
S is seen along the view directions
and
, the upper edge
appears to be the planar curves
and
, respectively. Moreover, if we place a vertical mirror parallel to the
plane, the two views of
S are obtained simultaneously, the direct view corresponds to
and the mirror image corresponds to
. For the solid in
Figure 2, we applied the above method twice to the upper curve and the lower curve, resulting in the closed cylinder. This is the mathematical trick to generate ambiguous cylinder illusion.
4. Creation of Anomalous Mirror Symmetry
Our goal is to construct a method for designing the ambiguous cylinders that create anomalous symmetry. For this purpose we replace the pair of x-monotone curves and with a pair of closed curves.
Let and be two continuous functions defined in such that and . Hence and altogether form a closed curve on the plane. Similarly, let and be two continuous functions defined in such that and . Hence and constitute another closed curve on the plane. We want to construct a closed space curve that appears to be the closed curve composed of and when it is seen in the view direction , and that appears to be the closed curve composed of and when it is seen in the view direction , and it generates anomalous symmetry when we place a mirror parallel to the plane.
We apply the method for constructing an ambiguous cylinder twice, once to the pair
and
, and once more to the pair
and
. In order to create anomalous symmetry, the curves should satisfy
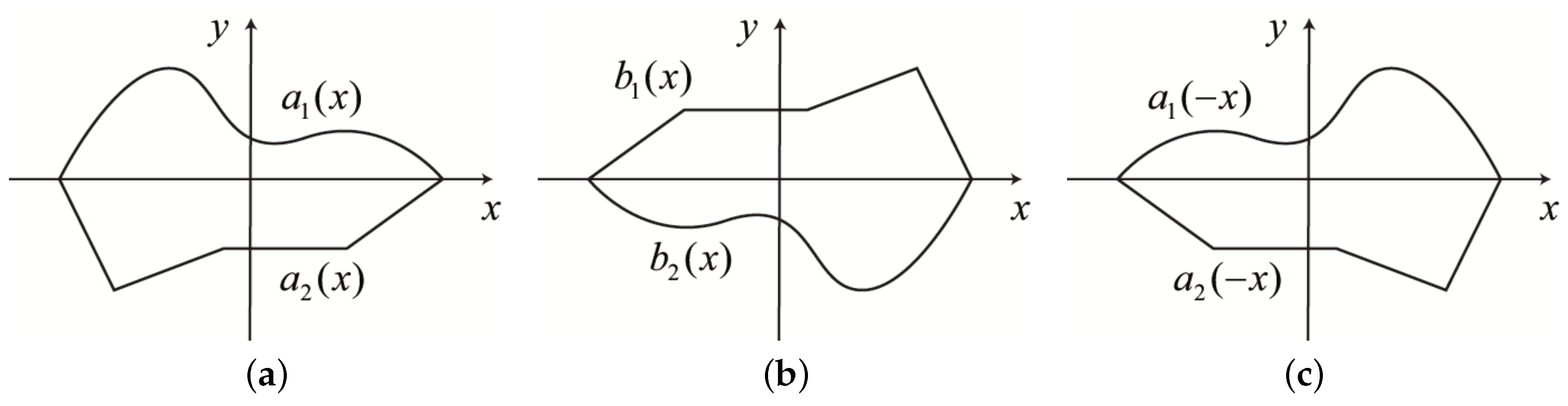
This is because, as shown in
Figure 5, the two appearances corresponding to the two view directions
and
should be point symmetric with respect to the origin as the center of the symmetry; if they are point symmetric as shown in
Figure 5a,b, the mirror parallel to the
plane will generate a normal image that is
y-reversal to
Figure 5b, resulting in the curve shown in
Figure 5c, which is
x-reversal to the curve in
Figure 5a, that is, which generates anomalous symmetry.
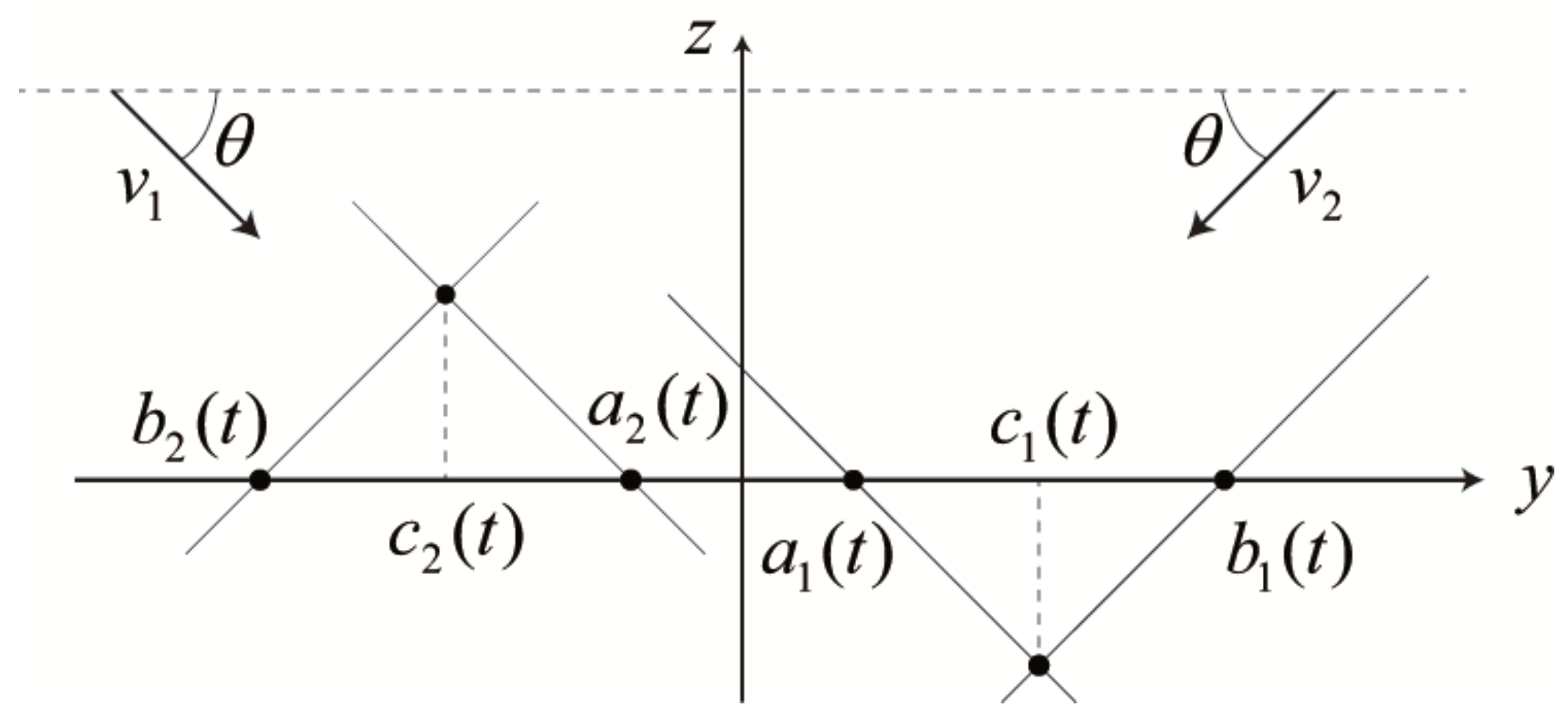
In
Figure 6 we show the intersection of the scene by a plane
parallel to the
plane. As shown in this figure, the space curve
that appears
when it is seen in the view direction
, and that appears
when it is seen in the view direction
, can be represented as
where
. Similarly, we get
Substituting Equations (
1) and (2), we get the explicit representation of the pair of space curves:
Note that we can choose a pair of functions
and
arbitrary. Once we choose them, the space curves
and
are determined by Equations (
5) and (6), which create anomalous symmetry.
Next, we consider the conditions such that the anomalous symmetry property is preserved even if the cylinder is rotated around the
z axis. Fortunately it turns out that no additional conditions are necessary; the closed curve given by Equations (
5) and (6) automatically satisfies the desired property. That is, the next proposition holds.
Proposition. The closed curve given by Equations (
5) and (6) does not destroy the anomalous symmetry property even if it is rotated around the
z axis.
Proof. The rotation around the
z axis does not destroy the anomalous symmetry property if the space curve is line symmetric with respect to the
z axis. That is,
where
and
represent the
y and
z coordinates of vector
. Actually the conditions Equations (
7) and (8) are satisfied by
and
defined by Equations (
5) and (6). Thus the anomalous symmetry property is preserved when the curve is rotated around the
z axis. (End of proof)
Recall that the object shown in
Figure 2 preserves the anomalous symmetry property when it is rotated around a vertical axis, as shown in
Figure 3. The above proposition implies that this is not accidental. When we rotate such an object around a vertical axis, we can enjoy an unordinary change of the appearance of the object that always keeps anomalous symmetry. This visual effect might be used as a means for new artistic presentation.
It is interesting to note that a similar non-accidental nature is observed by Sawada
et al. [
8] in the context of reconstructing 3D symmetric curves from 2D projected curves.
5. Examples
We applied our method to various figures whose upper and lower boundaries are both monotone in the x direction. The following are examples.
Figure 7 shows a shape of a fish. Let
and
be the upper boundary curve and the lower boundary curve, respectively, of this shape. We applied our method to this pair of curves, and constructed a solid object by first making a short cylinder whose edge curve consists of
and
, second making surfaces which cap the top and the bottom of the cylinder, and finally filling material in it.
The resulting object is shown in
Figure 8.
Figure 8a is a picture of the resulting solid in the original posture and its mirror image. The panels (b), (c) and (d) of this figure show the same object rotated around a vertical axis clockwise step by step in this order.
Figure 9 is a shape of a car, and
Figure 10 shows the object constructed from this shape.
Figure 11 is a shape of a ship, and
Figure 12 shows the object constructed from this shape. In both
Figure 10 and
Figure 12, (a) is the original posture, and (b), (c), (d) are the results of rotation.
From these examples, we can observe that the mirror image of an object appears to be the x-reversal mirror image instead of the y-reversal, not only in its original posture but also in its rotated versions. Thus, we achieve the anomalous mirror symmetry.
6. Concluding Remarks
We introduced a new concept called “anomalous mirror symmetry”, which is not consistent with the law of optical physics, but which can be perceived subjectively because of optical illusion. We characterized this symmetry and constructed a method for designing the class of space curves and the associated cylindrical surfaces that create anomalous symmetry.
The concept of anomalous symmetry we have introduced in this paper might be just one example of many possible new symmetries. The mirror symmetry with respect to a planar mirror is well studied from optical physics point of view. However, if we consider optical illusion, we may be able to extend the concept of mirror symmetry in many directions. The anomalous mirror symmetry introduced in this paper is such that the y-reversal image appears to be x-reversal. In general, for any pair of mirrors A and B, we might be able to define anomalous mirror symmetry in such a way that the mirror image with respect to the mirror A appears to be a mirror image with respect to the mirror B. To study those extensions is one of our future problems.