Multiple Minimum Support-Based Rare Graph Pattern Mining Considering Symmetry Feature-Based Growth Technique and the Differing Importance of Graph Elements

Abstract

Frequent graph pattern mining is one of the most interesting areas in data mining, and many researchers have developed a variety of approaches by suggesting efficient, useful mining techniques by integration of fundamental graph mining with other advanced mining works. However, previous graph mining approaches have faced fatal problems that cannot consider important characteristics in the real world because they cannot process both (1) different element importance and (2) multiple minimum support thresholds suitable for each graph element. In other words, graph elements in the real world have not only frequency factors but also their own importance; in addition, various elements composing graphs may require different thresholds according to their characteristics. However, traditional ones do not consider such features. To overcome these issues, we propose a new frequent graph pattern mining method, which can deal with both different element importance and multiple minimum support thresholds. Through the devised algorithm, we can obtain more meaningful graph pattern results with higher importance. We also demonstrate that the proposed algorithm has more outstanding performance compared to previous state-of-the-art approaches in terms of graph pattern generation, runtime, and memory usage.

1. Introduction

Data mining has been actively researched because of its useful applications such as classifying malicious information on web pages [1], mining consumer attitude and behavior [2], detecting or diagnosing important information [3,4], and other various mining applications [5,6,7,8,9]. As one of the interesting areas in data mining, frequent pattern mining [10,11,12] has been proposed, and numerous approaches related to this have been suggested [13,14]. However, traditional frequent pattern mining methods only focusing on databases composed of simple items have limitations that do not deal with complex types of data with graph forms such as network data [15,16,17]. It is essential to mine such complex data because recent data obtained from real world applications has become increasingly massive and complicated. To overcome these limitations, frequent graph pattern mining has been proposed and a variety of related methods have been studied [18,19,20,21] by developing novel techniques for performance improvement or effectively integrating graph mining with other mining fields.

Meanwhile, previous approaches of frequent graph pattern mining still have limitations because they cannot consider the following important issues in the real world: (1) the rare item problem [22] showing that items or patterns with low support values as well as ones with high supports may have meaningful information; and (2) the different importance problem [9] signifying that graph elements derived from real world applications have different importance or weight values depending on their characteristics. For this reason, to solve the limitations of the previous approaches and process these important issues in the graph pattern mining, we propose a new method that can mine Weighted Rare Graph patterns (WRGs) considering both different importance and multiple minimum support thresholds according to the features of elements, called WRG-Miner. Moreover, by conducting various performance evaluation tests, we also demonstrate that the proposed algorithm has better mining performance than previous state-of-the-art algorithms in terms of graph pattern generation, execution time, and memory usage.

The remainder of this paper is organized as follows. In Section 2, we introduce related work with several important previous studies. In Section 3, details of the proposed algorithm and its techniques are described. In Section 4, performance evaluation results among our method and previous state-of-the-art approaches are provided. Finally in Section 5, we conclude this paper.

2. Related Work

Since the concept of frequent pattern mining was proposed [10], a variety of methods have been actively researched. Apriori [10] is the first algorithm for mining frequent patterns from databases with simple items, where its mining process is based on a level-wise manner. Thereafter, to solve the inefficiency of the Apriori algorithm, a tree-based pattern growth algorithm, FP-growth [11], was devised. Using its own special tree structure, called FP-tree, the algorithm achieved better performance than that of Apriori. Satisfying the anti-monotone property during the mining process is one of the most important conditions in frequent pattern mining because this property can contribute to enhancing algorithm performance by suppressing any useless pattern generation in advance. The anti-monotone property signifies that if a certain pattern is infrequent, all of its possible super patterns are also infrequent. Therefore, we can prune such invalid patterns in advance by employing this property.

In frequent pattern mining, multiple minimum support threshold-based various research [18,19,22,23] has been conducted to solve the rare item problem. MSApriori [22] is an initial solution based on a level-wise manner. After that, a tree search-based algorithm, CFP-growth [18], and its advanced version, CFP-growth++ [23], were proposed. Although they make it possible to mine rare patterns applying multiple minimum support thresholds, they cannot consider different importance characteristics and their coverages are limited to simple itemset-based databases. Algorithms in the literature [24,25,26,27] are tree-based frequent pattern mining approaches considering importance of items’ own, but they cannot solve the rare item problem and process complex data such as graph databases.

As one of the fundamental graph mining algorithms, Gaston [20] is known as the most efficient method in terms of runtime speed. The algorithm, which is an effective integration of multiple enumeration methods for path, free-tree, and cyclic graph forms, improves its mining performance by utilizing its own special techniques and list-based data structure. FGM-MMS [19] mines frequent and rare graph patterns by applying multiple minimum support constraints in a graph mining environment, but it still has a problem that cannot consider different importance or weights for each element within graphs.

3. Mining Weighted Rare Graph Patterns from Graph Databases with Multiple Minimum Support Thresholds

In this section, we describe techniques for applying multiple minimum support thresholds and importance characteristics of graph elements into a frequent graph mining environment and explain strategies for preventing fatal problems such as pattern losses that can be caused in the mining process. In addition, we also show how the proposed algorithm is performed through its overall operational procedure.

3.1. Preliminaries

The following definitions and contents are fundamental preliminaries for more easily understanding frequent graph pattern mining.

Definition 1. (Graph pattern) Let G be a graph pattern composed of multiple elements, where there are two element types, vertex and edge. That is, G has a set of vertices, V_G = {v₁, v₂, …, v_m}, and a set of edges, E_G = {e₁, e₂, …, e_n}. Note that we consider a simple, labeled, undirected graph form in this paper to help understand the contents of our approach more easily, but it is trivial to apply other graph forms in this approach through several additional considerations.

Definition 2. (Support of a graph pattern) Let GDB = {Gtr₁, Gtr₂, …, Gtr_k} be a given graph database composed of multiple graph transactions, Gtrs, and G be a graph pattern. Then, a support of G, Sup(G) is calculated as follows:

$$IncG\left(G,Gt{r}_k\right)= \{\begin{array}{c} 1, if G \in Gt{r}_k \\ 0, otherwise\end{array}$$

(1)

$$Sup\left(G\right)= {\displaystyle \sum }_{Gt{r}_k \in GDB}IncG\left(G,Gt{r}_k\right)$$

(2)

Equation (1) is a function for determining whether G is included into each graph transaction, Gtr_k, as a sub graph pattern. That is, Sup(G) obtained from Equation (2) presents how many times G appears in GDB. Hence, in traditional frequent graph pattern mining, if Sup(G) is higher than or equal to a given minimum support threshold, G is considered as a frequent graph pattern. Consequently, the main goal of frequent graph pattern mining is to find all of the possible graph patterns such that each of their supports is not lower than the threshold.

Definition 3. (Degree of a graph pattern) Every graph has one of the three graph forms, path, free-tree, and cyclic graph, where their coverage is path ⊆ free-tree ⊆ cyclic graph. That is, a cyclic graph includes path and free-tree forms; a free-tree contains a path form. In the case of a path, all of its vertices except for both of its ends have degree 2, while both ends have degree 1. In other words, assuming that a given graph pattern, G is a path with n vertices, the following conditions are satisfied:

$$Deg\left(v_k\right)= 2 \left(2\le k \le n-1\right); Deg\left(v_1\right)= Deg\left(v_n\right)=1;\left|V_G\right|=\left|E_G\right|+1$$

(3)

Deg means a degree of a corresponding vertex, and v₁ and v_n are the first and last vertices, respectively. |V_G| and |E_G| signify the number of vertices and edges in G, respectively, where |V_G| is also equal to n. In the case of free-tree, one or more vertices must have degree 3 or more and all of its edges have no cyclic relation. That is, if G is a free-tree, it satisfies the following conditions:

$$Deg\left(v_k\right)\ge 3 \left(\exists v_k\in V_G\right); \left|V_G\right|=\left|E_G\right|+1$$

(4)

Once a cyclic relation occurs in a path or free-tree, the corresponding graph pattern becomes a cyclic graph. In other words, if G has one or more cyclic relations, i.e., cyclic edges, the following condition holds:

$$\left|V_G\right|\le \left|E_G\right|$$

(5)

3.2. Applying Symmetry Feature-Based Performance Improving Technique into the Graph Pattern Growth Process

Recall that all of the possible graph forms generated from graph miners must be one of the three graph types: path, free-tree, and cyclic graph. The mining procedure of the proposed algorithm employs a pattern growth framework based on a depth-first search (DFS) manner. In other words, an initial step of the graph pattern growth starts from a certain vertex and it is continually expanded by adding both an edge and a vertex or a cyclic edge. Therefore, the initial state of every graph pattern is always a path form. According to the shape and characteristics of graphs with a path form, we can consider their symmetry features in order to improve our mining performance in the graph pattern growth for paths. If a path is expanded as a longer path again, we can consider its expansion operation as two orientations: expansion at the first or last node in the path. Hence, if there is no limitation in the path expansion, a large number of duplicated graph patterns can be generated. To prevent such a problem, we employ a technique based on the symmetry features of graph patters with a path form. We consider the symmetry model of a path as three types: the whole symmetry, the start symmetry, and the end symmetry. Using these symmetry models, we can effectively control the growth process for the path form without any duplication of path expansion. Given a path, P = {v₁-e₁-v₂-e₂-…-e_n-1-v_n}, each symmetry type can be denoted as follows:

$$\begin{gathered} the whole symmetry=v_1–e_1–v_2–e_2–\dots –v_{n-1}–e_{n-1}–v_n \\ the start symmetry=v_1–e_1–v_2–e_2–\dots –v_{n-1} \\ the end symmetry=v_2–e_2–\dots –e_{n-1}–v_n \end{gathered}$$

(6)

Each of the symmetry types can have one of the three states: Neutrality, True, and False. Neutrality is set when the string corresponding to each type is symmetric; otherwise, it is set to True or False. True is set when the corresponding string is the lowest and False is assigned when the reverse string is the lowest, where the comparison is based on a lexicographical order. Through the above settings, we can easily decide what orientation leads to correct results of the graph pattern growth. If the whole symmetry is Neutrality, we do not need to select which one is correct because the corresponding path is symmetric and we just choose either the start or end node to expand the path. Otherwise, the expansion occurs at the last node corresponding to the True condition or the first one corresponding to the False condition. In addition, the start and end symmetry information can be effectively used as follows. After a path expanding operation is performed, the whole symmetry of the previous path becomes the start or end symmetry of the current one; the whole symmetry of the current path can be easily obtained from the start or end symmetry of the previous one. 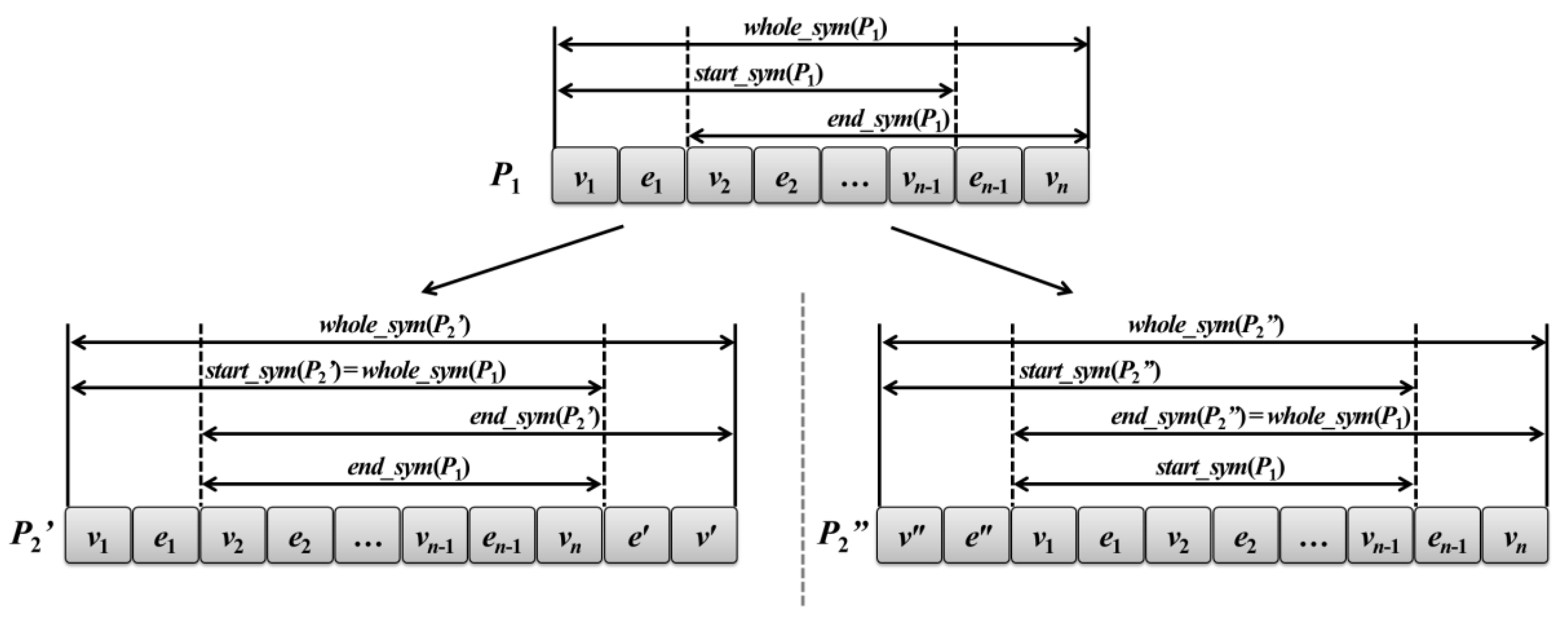Figure 1 is the relations of these symmetry models for helping clearer understanding of the above contents. In the figure, whole_sym, start_sym, and end_sym mean the whole, start, and end symmetry models, respectively. Let P₁ be a given path and P₂′ and P₂″ be paths expanded from P₁. The symmetry models of P₁ are shown in the top of the figure. In the case of P₂′, a new edge and vertex, e′ and v′, have been inserted at the end of P₁. In this case, start_sym(P₂′) is equal to whole_sym(P₁). whole_sym(P₂′) can be easily computed by end_sym(P₁) because we have only to compare the edges and vertices next to both end of end_sym(P₁), v₁ and e₂, and e′ and v′. In contrast, end_sym(P₂″) is equal to whole_sym(P₁), and whole_sym(P₂″) is obtained from start_sym(P₁). It is important to consider these three symmetry models in the growth step because we can easily determine whether or not a path is symmetric without computational overheads.

Through this symmetry method, the proposed algorithm can conduct its mining operations more efficiently.

Figure 1. Graph pattern growth of the path form and corresponding relations of the symmetry models.

Figure 1. Graph pattern growth of the path form and corresponding relations of the symmetry models.

3.3. Employing Element Importance and Multiple Minimum Support Thresholds in Frequent Graph Pattern Mining

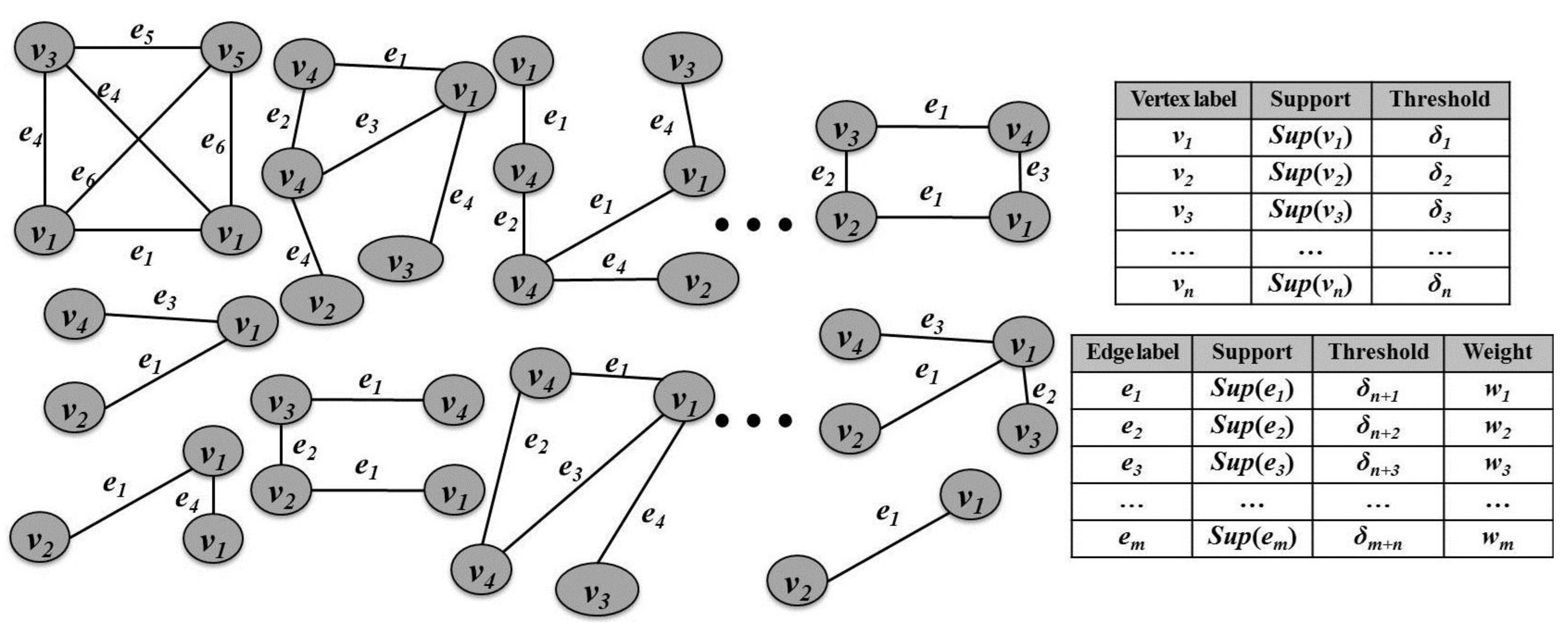
Figure 2 shows an example of a graph database including the information of multiple minimum support thresholds and edge weights. To apply different importance for each element composing graphs, we consider mining graph patterns from graph databases that assign a different weight value to each edge of the graphs. Since edges are important factors allowing us to determine correlations among vertices, edge weights are also valuable because they can be used to distinguish different importance of edges. As a result of the proposed algorithm, we can obtain a set of graph patterns considering both supports and weights of edges connected among nodes. The weighted support of a graph pattern is calculated as follows.

Figure 2. Example of a graph database with weight and multiple minimum support information.

Figure 2. Example of a graph database with weight and multiple minimum support information.

Definition 4. (Weighted support of a graph pattern) Let V_G = {v₁, v₂, …, v_m}, E_G = {e₁, e₂, …, e_n}, and W_G = {w₁, w₂, …, w_n} be a set of vertices in a graph pattern, G, a set of edges in G, and a set of edge weights in G. Then, the weighted support of G, Wsup(G) is calculated as follows:

$$Avg\left(W_G\right)= \raisebox{1ex}{${\sum }_{w_k \in W_G}{w}_k$}\!\left/ \!\raisebox{-1ex}{$\left|W_G\right|$}\right.$$

(7)

$$Wsup\left(G\right)=Sup\left(G\right)\text{ * }Avg\left(W_G\right)$$

(8)

If Wsup(G) is not lower than a given minimum support threshold, G is regarded as a weighted frequent graph pattern.

In order to consider the rare item problem in the graph pattern mining area, we need multiple minimum support thresholds for each element (vertex and edge) composing a given graph database.

Definition 5. (Minimum element support threshold)) Let GDB = {Gtr₁, Gtr₂, …, Gtr_k} be a given graph database composed of multiple graph transactions, Gtrs, V_GDB = {v₁, v₂, …, v_x} be a set of separate vertices included in GDB, and E_GDB = {e₁, e₂, …, e_y} be a set of separate edges in GDB. Then, a minimum element support threshold for each element (v or e), δ_i (1 ≤ i ≤ x + y) is set as a value specified by a user.

If a weighted support of any element is lower than the corresponding δ value, it becomes a useless one. Consequently, the threshold of a graph pattern is determined as follows.

Definition 6. (Minimum graph support threshold) Given a graph pattern, G, a set of vertices in G, V_G = {v₁, v₂, …, v_n}, and a set of edges in G, E_G = {e₁, e₂, …, e_m}, a set of δ values in G including V_G and E_G, T_G, can be denoted as T_G = {δ₁, δ₂, …, δ_n+m}. Then, a minimum graph support threshold for G, MGST(G), is computed as follows:

$$MGST\left(G\right)=Min\left(T_G=\left\{{\text{δ}}_1,{\text{ δ}}_2,\dots ,{\text{ δ}}_{n+m}\right\}\right)$$

(9)

Therefore, if Wsup(G) is lower than MGST(G), it becomes an invalid graph pattern.

By calculating the threshold for a graph pattern in the above manner, we can consider the rarity of the graph’s each element. In other words, only weighted frequent graph patterns satisfying their own MGST conditions are finally regarded as valid results.

3.4. Maintaining the Correctness of the Proposed Algorithm

Through the aforementioned conditions, we can obtain a set of graph patterns that completely consider both the weight and rarity of elements. However, if we simply apply such conditions into the mining process without any additional considerations, fatal pattern losses can be caused since these conditions violate the anti-monotone property (or the downward closure property). Therefore, to guarantee not only the efficiency of the proposed algorithm but also its correctness, we employ (1) an overestimated weight method and (2) an underestimated minimum support method. In the first method, the maximum edge weight within a given graph database, called MaxW, is used instead of the real average weight factor used in Definition 4. That is, given a graph pattern, G, multiplying Sup(G) by MaxW, called Wsup_over(G), is first applied in the mining process. Through such an overestimation method, we can maintain the anti-monotone property and prevent unintended pattern losses by the weight constraints. In the second method, among all the thresholds in Definition 5, we set the least value that does not violate the property and apply it into the mining process. Let L = {δ₁, δ₂, …, δ_x} be a list of all the elements’ δ values in GDB that are sorted in the descending order of their values. Then, starting from the last element in the list, we check whether or not the overestimated weighted support of the element is higher than its own δ value. If there is the first element satisfying this condition, its δ value becomes an underestimated minimum support threshold, called Least Minimum Support (LMS).

If any graph pattern does not satisfy the LMS condition, the pattern and all of its possible supersets become useless ones; hence, it can permanently be pruned in advance. Note that graph patterns obtained through the above conditions are candidate patterns, not final results. Among them, only partial ones satisfying the corresponding MGST conditions in Definition 6 finally become valid results.

3.5. WRG-Miner Algorithm

Figure 3 shows the overall procedure of the proposed algorithm. After finding sets of valid vertices and edges, V and E, from a given graph database, GDB (lines 1–2), the algorithm performs graph pattern growth processes for mining a set of WRGs, S, with respect to each vertex of V, v_i (lines 3–5). In this phase, WRG-Miner continues to expand graphs for each edge, e_i, considering their current states (lines 6–9). For each expanded graph, G’, if the overestimated weighted support of the graph is smaller than LMS, it is permanently pruned (line 10). If the graph pattern’s real weighted support is not lower than its corresponding MGST value, it is regarded as a valid result and the algorithm outputs it (line 11). Once the graph pattern has an overestimated weighted support higher than or equal to LMS, growth operations for the pattern are recursively conducted regardless of whether it is really outputted or not (lines 12–13). After finishing all the recursive processes, we can obtain a complete set of WRGs, S.

Figure 3. Procedure of Weighted Rare Graph (WRG)-miner.

Figure 3. Procedure of Weighted Rare Graph (WRG)-miner.

4. Performance Evaluation

4.1. Experimental Settings

In this section, the proposed algorithm is compared to: FGM-MMS, which is a state-of-the-art graph mining algorithm based on multiple minimum support constraints; Gaston, which is a well-known fundamental graph mining algorithm; and Gaston*, which is an obtimized version of Gaston implemented by us to mine weighted frequent graph patterns with respect to real datasets, DTP and PTE [20], and synthetic datasets—we call them Syn-1 and Syn-2, respectively—generated by a graph dataset generator based on the IBM generator (IBM, New York, NY, USA). Edge weight ranges of the real and synthetic datasets were randomly set between 0.6–0.9 and 0.5–0.8, respectively. All the algorithms were written in C++ and executed in an environment with 3.33 GHz CPU, 3 GB RAM, and Windows 7 OS. In the next sub-section, we provide analysis results of the performance comparison among our WRG-miner and the state-of-the-art algorithms, FGM-MMS, Gaston and Gaston*.

4.2. Experimental Results of the Proposed Algorithm

To set the δ value for each element of graph datasets, the methodology employed in the literature [18,19,22] was applied. That is, for each element, e_i, δ_i = MAX(β × Sup(e_i), LS), where LS is the lowest one among all the δ values and is set to the same as the threshold of Gaston for reasonable comparisons. β = 1/α (0 < β ≤ 1, 1 ≤ α) is a variable that represents how closely the real support of each element is related to its own threshold value. That is, as β becomes closer to 1, δ is more likely to be assigned as a value more similar to Sup(e_i) rather than LS.

Figure 4 and Figure 5 show results of pattern generations for the synthetic and real datasets. In the results of the synthetic datasets, the proposed algorithm extracts the smallest number of graph patterns; meanwhile, in the results of the real datasets, Gaston* generates the smallest patterns. From the results, we can determine that the multiple minimum support factor is more effective in the synthetic datasets. As shown in Figure 5, the number of patterns is changeable according to the α settings. On the other hand, such tendency is not significant in Figure 4. Figure 6 and Figure 7 are runtime performance results of the algorithms. Similarly to the results of Figure 4 and Figure 5, our WRG-Miner has better mining efficiency at lower α values. Multiple minimum support framework-based FGM-MMS and WRG-Miner guarantee better performance than those of the others. Especially in Figure 6, our algorithm shows the fastest runtime speed in every case. Meanwhile, Gaston always shows the worst result, which is the same regardless of α since it cannot consider the rarity of graph patterns. Although FGM-MMS has good performance at lower α values, it falls behind the proposed algorithm in every case since it does not consider element importance different from one another and has to mine all of the possible rare graph patterns regardless of their importance degrees. The last test is memory performance evaluation. As shown in Figure 8 and Figure 9, the proposed algorithm also shows the best results in almost all cases. At lower α settings, WRG-miner consumes smaller memory compared to the others. On the other hand, Gaston and Gaston* spend constant memory in mining graph patterns because they do not consider any condition for the multiple minimum support framework.

Figure 4. (a) Pattern generation results of Syn-1; (b) Pattern generation results of Syn-2.

Figure 4. (a) Pattern generation results of Syn-1; (b) Pattern generation results of Syn-2.

Figure 5. (a) Pattern generation results of DTP; (b) Pattern generation results of PTE.

Figure 5. (a) Pattern generation results of DTP; (b) Pattern generation results of PTE.

Figure 6. (a) Runtime results of Syn-1; (b) Runtime results of Syn-2.

Figure 6. (a) Runtime results of Syn-1; (b) Runtime results of Syn-2.

Figure 7. (a) Runtime results of DTP; (b) Runtime results of PTE.

Figure 7. (a) Runtime results of DTP; (b) Runtime results of PTE.

Figure 8. (a) Memory usage results of Syn-1; (b) Memory usage results of Syn-2.

Figure 8. (a) Memory usage results of Syn-1; (b) Memory usage results of Syn-2.

Figure 9. (a) Memory usage results of DTP; (b) Memory usage results of PTE.

Figure 9. (a) Memory usage results of DTP; (b) Memory usage results of PTE.

5. Conclusions

In this paper, we proposed a new approach that mined useful graph patterns with high importance and rarity by considering multiple thresholds and weights different from each element of the graphs. In addition, by devising the techniques for preventing unintended graph pattern losses occurring in the process of applying such conditions, we also guaranteed the correctness of our algorithm. The result of performance evaluation in this paper reported that our method outperformed the previous state-of-the-art methods in terms of pattern generation efficiency, runtime, and memory usage. The proposed algorithm and techniques can also be applied into other advanced mining areas such as stream pattern mining, uncertain pattern mining, and representative pattern mining, because of their advantages and contributions in the graph mining area. These extended works are scheduled to be studied in our future work.