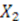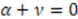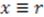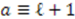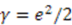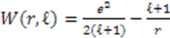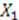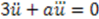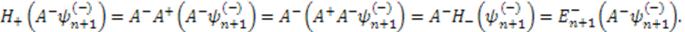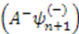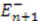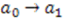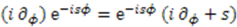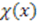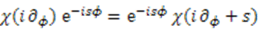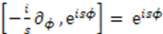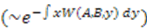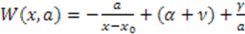Supersymmetric Quantum Mechanics and Solvable Models
1. Introduction
 .
.2. Supersymmetric Quantum Mechanics
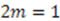 . For the harmonic oscillator, the Hamiltonian [9]
. For the harmonic oscillator, the Hamiltonian [9]  is factorized into
is factorized into 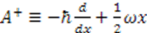 and
and 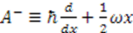 . Similarly, in the SUSYQM formalism [10,11] a general Hamiltonian
. Similarly, in the SUSYQM formalism [10,11] a general Hamiltonian  is written as a product of
is written as a product of 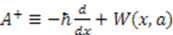 and
and 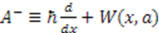 , where the function
, where the function 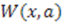 is known as the superpotential. The product
is known as the superpotential. The product 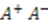 is then given by
is then given by 
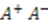 indeed reproduces the Hamiltonian
indeed reproduces the Hamiltonian 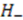 above, provided the potential
above, provided the potential 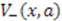 is related to the superpotential
is related to the superpotential 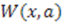 by
by 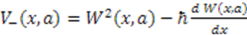 . The product
. The product 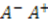 produces another Hamiltonian
produces another Hamiltonian 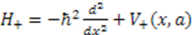 with
with 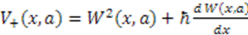 . To see the underlying supersymmetry of this formalism, let us construct a generator
. To see the underlying supersymmetry of this formalism, let us construct a generator 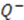 and its adjont
and its adjont 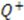 by:
by: 
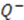 and
and 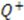 generate the following supersymmetry algebra:
generate the following supersymmetry algebra: 

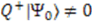 or
or 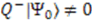 , and hence signals the spontaneous breaking of the supersymmetry. We therefore require that
, and hence signals the spontaneous breaking of the supersymmetry. We therefore require that 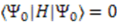 to preserve unbroken supersymmetry.
to preserve unbroken supersymmetry.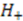 and
and 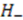 are intertwined; i.e.,
are intertwined; i.e., 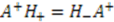 and
and  . This leads to the following relationships among their eigenvalues and eigenfunctions [12]
. This leads to the following relationships among their eigenvalues and eigenfunctions [12] 
 and its adjoint
and its adjoint  , their eigenvalues are either zero or positive [13]. The ground state eigenvalue of one of these Hamiltonians must be zero in order to have unbroken supersymmetry. Without loss of generality, we choose that Hamiltonian to be
, their eigenvalues are either zero or positive [13]. The ground state eigenvalue of one of these Hamiltonians must be zero in order to have unbroken supersymmetry. Without loss of generality, we choose that Hamiltonian to be  . Thus, we have
. Thus, we have 
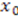 is an arbitrary point in the domain and
is an arbitrary point in the domain and 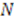 is the normalization constant that depends on the choice of
is the normalization constant that depends on the choice of 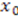 . Thus, if
. Thus, if 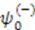 is a normalizable groundstate, we have a system with unbroken supersymmetry. Its groundstate
is a normalizable groundstate, we have a system with unbroken supersymmetry. Its groundstate 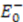 is zero and the operator
is zero and the operator 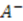 annihilates the corresponding eigenstate
annihilates the corresponding eigenstate 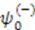 . For all higher states of
. For all higher states of 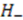 , as indicated in Equation (5), there is an one-to-one correspondence with the states of
, as indicated in Equation (5), there is an one-to-one correspondence with the states of 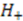 .
. 2.1. Example
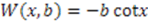 , defined over the domain
, defined over the domain 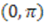 . Corresponding partner potentials are given by
. Corresponding partner potentials are given by 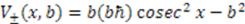 . This is a rather complicated potential, and rarely analyzed in quantum mechanics courses. However, for
. This is a rather complicated potential, and rarely analyzed in quantum mechanics courses. However, for 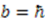 , the potential
, the potential 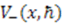 reduces to the infinite square well, with the bottom of the potential at
reduces to the infinite square well, with the bottom of the potential at 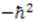 and zero groundstate energy. We know that the corresponding eigenstates are given by
and zero groundstate energy. We know that the corresponding eigenstates are given by 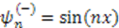 and eigenvalues
and eigenvalues 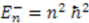 . Thus, using the familiarity with the relatively simpler potential
. Thus, using the familiarity with the relatively simpler potential 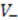 , we are able to derive all of the eigenvalues and eigenfunctions of
, we are able to derive all of the eigenvalues and eigenfunctions of 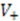 . Then the inter-relations expressed through Equation (5) enable us to determine eigenvalues and eigenfunctions of
. Then the inter-relations expressed through Equation (5) enable us to determine eigenvalues and eigenfunctions of  .
.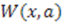 .
.3. Shape Invariance in Supersymmetric Quantum Mechanics
 of a system obeys the condition
of a system obeys the condition 
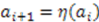 , the system is called shape invariant [5,22,23,24]. Various forms of the function
, the system is called shape invariant [5,22,23,24]. Various forms of the function 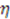 define classes of shape invariance. The most commonly discussed classes are:
define classes of shape invariance. The most commonly discussed classes are: 
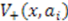 and
and  differ only by values of parameter
differ only by values of parameter 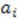 and additive constants
and additive constants  . In particular,
. In particular, 

3.1. Determination of Eigenvalues
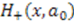 and
and 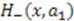 differ only by the constant
differ only by the constant  . We already know that
. We already know that 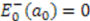 . Let us determine the first excited state of
. Let us determine the first excited state of 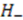 ; i.e.,
; i.e., 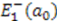 . Hence, using
. Hence, using 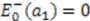 [33], we find that the energy
[33], we find that the energy 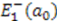 of the first excited state of
of the first excited state of 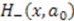 and
and 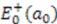 of the groundstate of
of the groundstate of 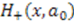 both are given by
both are given by  . Similarly, to determine
. Similarly, to determine  , we use the isospectrality condition (5) to relate it to
, we use the isospectrality condition (5) to relate it to 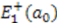 . But by the shape invariance condition (9),
. But by the shape invariance condition (9), 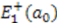 =
= 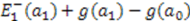 . Following the method used for determining
. Following the method used for determining 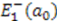 , we find
, we find 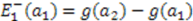 , and hence,
, and hence, 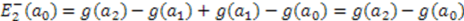 . Extending this argument to higher excited states of
. Extending this argument to higher excited states of 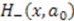 , we get
, we get
3.2 Determination of Eigenfunctions
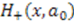 and
and 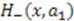 only differ by the constant
only differ by the constant  , they must have common eigenfunctions. Hence, from Equation (6), we have
, they must have common eigenfunctions. Hence, from Equation (6), we have 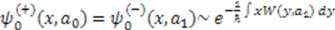 . Then the isospectrality condition (5), requires
. Then the isospectrality condition (5), requires 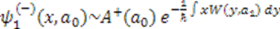 . Iterating this procedure, we obtain
. Iterating this procedure, we obtain 
4. Shape Invariance and Potential Algebra
4.1. Building the Algebra

 , and
, and 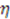 is a function that models the change of parameter
is a function that models the change of parameter 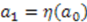 . For example, if the change of parameter is a translation,
. For example, if the change of parameter is a translation, 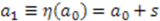 .
.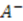 and
and 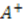 to build the generators of the potential algebra. To transform the above shape invariance condition into an exact commutator, we replace operators
to build the generators of the potential algebra. To transform the above shape invariance condition into an exact commutator, we replace operators 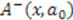 and
and 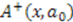 by
by
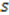 is a constant parameter,
is a constant parameter, 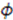 is an auxiliary variable, and
is an auxiliary variable, and 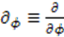 . The function
. The function 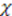 will be appropriately chosen to emulate the relationship between parameters
will be appropriately chosen to emulate the relationship between parameters 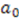 and
and 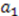 . Thus, to generate
. Thus, to generate  , we multiplied the operator
, we multiplied the operator 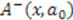 from right by
from right by 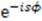 and replaced the parameter
and replaced the parameter 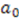 by the differential operator
by the differential operator 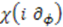 . If we now compute the commutator between operators
. If we now compute the commutator between operators  and
and  , we find [36]
, we find [36]

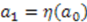 , these mappings require that the function
, these mappings require that the function 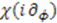 satisfy
satisfy
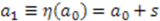
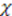 that models it is the identity function
that models it is the identity function
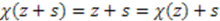 , which gives the desired change of parameters.
, which gives the desired change of parameters.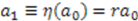
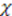 is the exponential
is the exponential
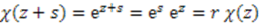 where we denoted
where we denoted 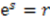 .
.
 iterations. These potentials appear also in connection with the dressing chain formalism [37]. To satisfy the cyclic parameter change, the function
iterations. These potentials appear also in connection with the dressing chain formalism [37]. To satisfy the cyclic parameter change, the function 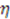 should obey
should obey  . The projective map
. The projective map 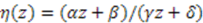 with specific constraints [38] on the parameters
with specific constraints [38] on the parameters 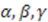 , and
, and 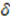 satisfies such a condition [27]. The function
satisfies such a condition [27]. The function 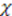 satisfying Equation (16) in this case is given by
satisfying Equation (16) in this case is given by
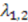 are solutions of the equation
are solutions of the equation 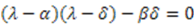 and
and 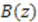 is an arbitrary periodic function of
is an arbitrary periodic function of 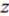 with period
with period  .
.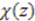 . For example taking
. For example taking
 .
.  and
and  , the shape invariance condition (12) becomes:
, the shape invariance condition (12) becomes:
 and
and 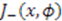 generates an operator
generates an operator 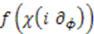 that has no
that has no  -dependence. If we now define a third operator
-dependence. If we now define a third operator 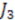 in terms of the operator
in terms of the operator 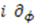 , the shape invariance condition becomes simply one of the commutation relations of the potential algebra. In particular, if we define
, the shape invariance condition becomes simply one of the commutation relations of the potential algebra. In particular, if we define
 is an arbitrary constant, the three commutators among these generators are given by [39]
is an arbitrary constant, the three commutators among these generators are given by [39]

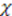 such that
such that 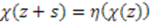 for arbitrary parameters
for arbitrary parameters 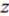 and
and 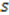 , we can associate an algebra [40]generated by
, we can associate an algebra [40]generated by




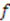 in Equation (29) is given by the shape invariance condition (24), while the function
in Equation (29) is given by the shape invariance condition (24), while the function 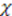 satisfies the compatibility equation:
satisfies the compatibility equation: 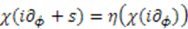 , where
, where 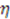 models the change of parameter
models the change of parameter 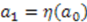 of Equation (24).
of Equation (24).
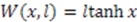 , through
, through 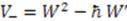 , where
, where 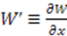 . Its supersymmetric partner
. Its supersymmetric partner 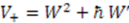 is given by
is given by
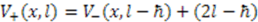 . Therefore, in terms of
. Therefore, in terms of 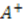 and
and 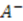 operators, the shape invariance (24) for the Pöschl-Teller II potential reads
operators, the shape invariance (24) for the Pöschl-Teller II potential reads
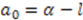 and
and 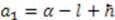 , where
, where  is an arbitrary positive constant greater than
is an arbitrary positive constant greater than  so that
so that 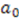 is a positive quantity;
is a positive quantity; 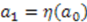 is thus given by
is thus given by 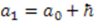 . This is a translational change of parameter
. This is a translational change of parameter 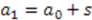 with the translation parameter
with the translation parameter 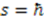 . Translation implies that the function
. Translation implies that the function 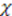 satisfying (16) is the identity function
satisfying (16) is the identity function  ;
;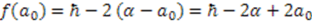 . Then, the function
. Then, the function 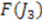 is given by
is given by 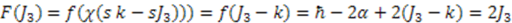 if we choose the arbitrary constant
if we choose the arbitrary constant 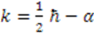 ;
;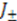 and
and 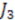 as prescribed by Equations (25) and (27), we obtain the differential realization of the algebra’s generators:
as prescribed by Equations (25) and (27), we obtain the differential realization of the algebra’s generators:
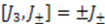 , and
, and  . Thus, shape invariance of this system implies that the system has a potential algebra given by
. Thus, shape invariance of this system implies that the system has a potential algebra given by 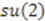 [?, 41, 42].
[?, 41, 42]. 4.2. Obtaining the Energy Spectrum from Algebra Representations

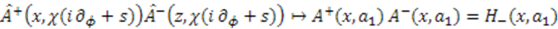 . Consequently, the spectrum of the operator
. Consequently, the spectrum of the operator 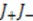 gives the spectrum of the Hamiltonian. To find the concrete values for the energy, we need to know the action of individual operators
gives the spectrum of the Hamiltonian. To find the concrete values for the energy, we need to know the action of individual operators  and
and  respectively on a set of eigenvectors of the operator
respectively on a set of eigenvectors of the operator 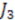 . In this general case,
. In this general case,  ,
,  and
and 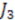 commute with the Casimir operator given by
commute with the Casimir operator given by
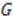 (defined up to an additive constant) such that
(defined up to an additive constant) such that
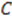 does indeed commute with
does indeed commute with  ,
,  and
and 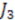 [41]. In a basis in which
[41]. In a basis in which 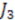 and
and 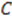 are diagonal,
are diagonal, 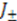 play the role of raising and lowering operators, respectively. Operating on an arbitrary eigenstate
play the role of raising and lowering operators, respectively. Operating on an arbitrary eigenstate 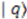 we have
we have
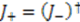 .
. , and observing that
, and observing that 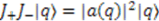 , we see that in order to find the energies of the system one must find the coefficients
, we see that in order to find the energies of the system one must find the coefficients 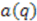 . If we apply the third commutation relation of Equation (23) to
. If we apply the third commutation relation of Equation (23) to 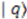 , we obtain using Equation (36)
, we obtain using Equation (36) 
 and the corresponding values
and the corresponding values 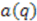 . Let us say
. Let us say 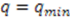 corresponds to the lowest state in a given representation of the algebra. This implies that
corresponds to the lowest state in a given representation of the algebra. This implies that 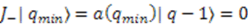 , which means
, which means  . From Equation (38) we get
. From Equation (38) we get
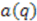

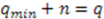 leads to
leads to
 determines the dimension of the representation. For example, let us consider the two cases presented in Figure 1.
determines the dimension of the representation. For example, let us consider the two cases presented in Figure 1.  . Case (a) corresponds to a finite, and (b) to an infinite representation of the potential algebra.
. Case (a) corresponds to a finite, and (b) to an infinite representation of the potential algebra.
 . Case (a) corresponds to a finite, and (b) to an infinite representation of the potential algebra.
. Case (a) corresponds to a finite, and (b) to an infinite representation of the potential algebra.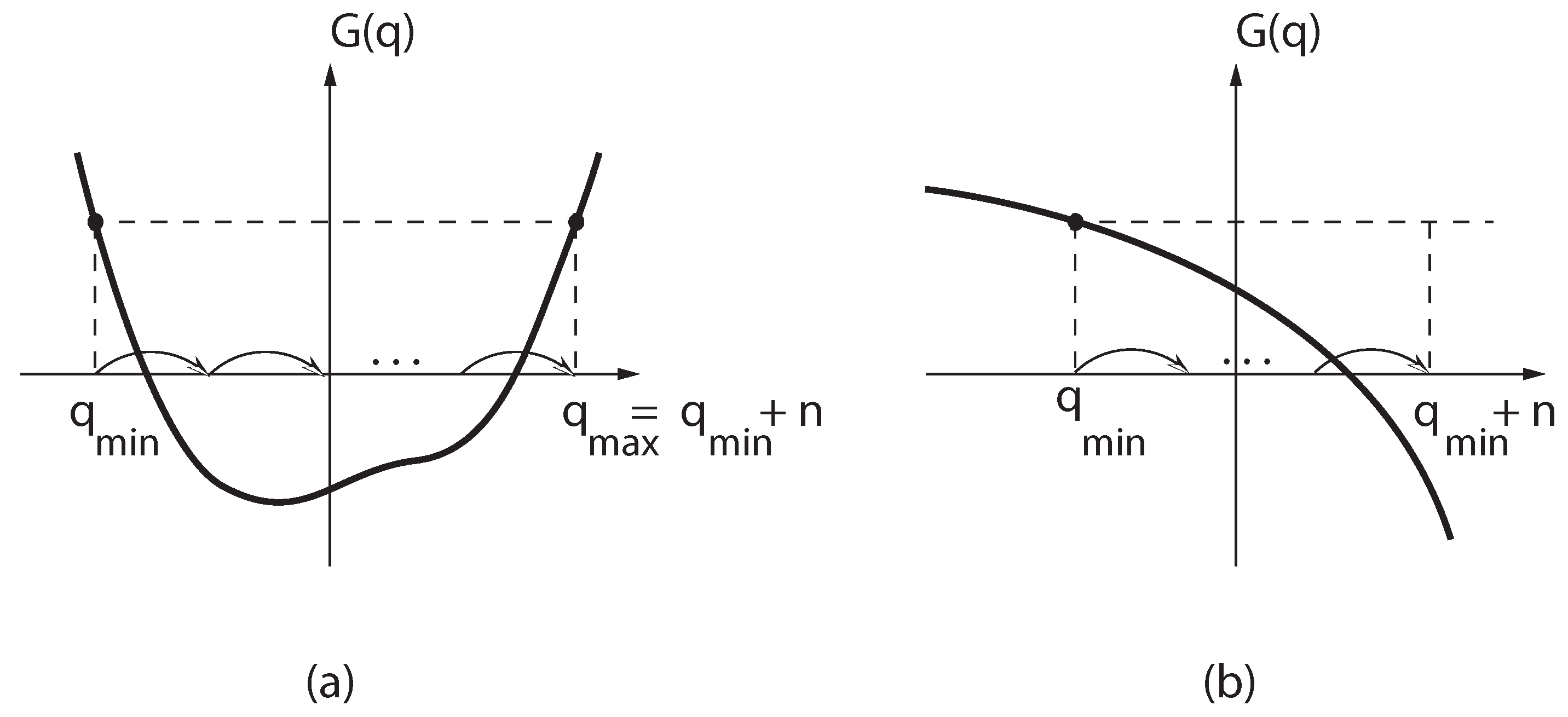
 vs.
vs.  graph corresponding to
graph corresponding to 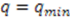 , and moving in integer steps parallel to the
, and moving in integer steps parallel to the  -axis to the point corresponding to
-axis to the point corresponding to 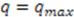 . At the end points,
. At the end points, 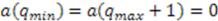 , and we get a finite representation. If
, and we get a finite representation. If  is decreasing monotonically, as in Figure 1b, there exists only one end point at
is decreasing monotonically, as in Figure 1b, there exists only one end point at 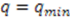 . Starting from
. Starting from  the value of
the value of  can be increased in integer steps up to infinity. In this case we have an infinite dimensional representation. As in the finite case,
can be increased in integer steps up to infinity. In this case we have an infinite dimensional representation. As in the finite case,  labels the representation. The difference is that here
labels the representation. The difference is that here  takes continuous values. Similar arguments apply for a monotonically increasing function
takes continuous values. Similar arguments apply for a monotonically increasing function  . Having the representation of the algebra associated with a characteristic model, we obtain, using Equation (41), the complete spectrum of the system.
. Having the representation of the algebra associated with a characteristic model, we obtain, using Equation (41), the complete spectrum of the system. . Consider the simple choice
. Consider the simple choice 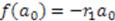 , where
, where 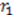 is a constant. This choice generates self-similar potentials studied in references [44,26,25]. In this case, combining Equation (18) with Equation (28) yields:
is a constant. This choice generates self-similar potentials studied in references [44,26,25]. In this case, combining Equation (18) with Equation (28) yields:
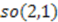 Lie algebra.
Lie algebra.
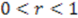 , which leads to
, which leads to  . From the monotonically decreasing profile of the function
. From the monotonically decreasing profile of the function  , it follows that the unitary representations of this algebra are infinite dimensional. If we label the lowest weight state of the operator
, it follows that the unitary representations of this algebra are infinite dimensional. If we label the lowest weight state of the operator 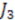 by
by  , then
, then  . Without loss of generality we can choose the coefficients
. Without loss of generality we can choose the coefficients 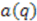 to be real. Then one obtains from (38) for an arbitrary
to be real. Then one obtains from (38) for an arbitrary 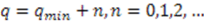

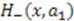 is given by
is given by

5. How Do We Find Additive Shape Invariant Superpotentials?
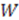 . For this section, we will restrict ourselves to considering cases of translational shape invariance. Before we embark on solving this equation, let us first note that quantum mechanical potentials generally have terms of two very different orders: One “large" and another “small". For example, the classical and quantum potentials for the radial oscillator system are
. For this section, we will restrict ourselves to considering cases of translational shape invariance. Before we embark on solving this equation, let us first note that quantum mechanical potentials generally have terms of two very different orders: One “large" and another “small". For example, the classical and quantum potentials for the radial oscillator system are 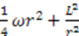 and
and 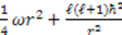 respectively. To make the transition from the quantum to the classical system, one takes the limit
respectively. To make the transition from the quantum to the classical system, one takes the limit  with the constraint that
with the constraint that 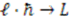 . Thus, the quantum Hamiltonian can be written as
. Thus, the quantum Hamiltonian can be written as 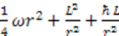 . This shows that in quantum mechanics, the potential generally has one small term that depends on
. This shows that in quantum mechanics, the potential generally has one small term that depends on  [43]. In SUSYQM, since the potential is given by
[43]. In SUSYQM, since the potential is given by 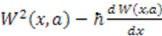 , the derivative term always brings in a factor of
, the derivative term always brings in a factor of  , even if the superpotential is independent of
, even if the superpotential is independent of  . In the following analysis, as we determine how to solve Equation (9) to find shape invariant superpotentials, we will consider the cases of
. In the following analysis, as we determine how to solve Equation (9) to find shape invariant superpotentials, we will consider the cases of  -independent and
-independent and  -dependent superpotentials separately.
-dependent superpotentials separately. 5.1. Known ![Symmetry 04 00452 i001]() -Independent Shape Invariant Superpotentials
-Independent Shape Invariant Superpotentials
 , which we call “conventional” superpotentials. In Table 1 we list the known “conventional" superpotentials that meet this criterion.
, which we call “conventional” superpotentials. In Table 1 we list the known “conventional" superpotentials that meet this criterion.| Name | Superpotential |
|---|---|
| Harmonic Oscillator | 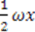 |
| Coulomb | 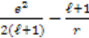 |
| -D oscillator | 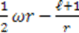 |
| Morse | 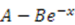 |
| Rosen-Morse I | 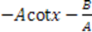 |
| Rosen-Morse II | 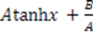 |
| Eckart | 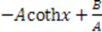 |
| Scarf I | 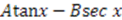 |
| Scarf II | 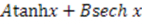 |
| Gen. Pöschl-Teller | 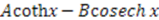 |
5.2. New Proof of Completeness of the Conventional Shape-Invariant Superpotentials
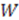 on
on 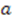 and
and  is through the linear combination
is through the linear combination 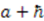 ; therefore, the derivatives of
; therefore, the derivatives of 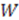 with respect to
with respect to 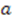 and
and  are related by:
are related by: 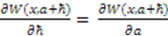 . Since Equation (7) must hold for an arbitrary value of
. Since Equation (7) must hold for an arbitrary value of  , if we assume that
, if we assume that 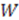 does not depend explicitly on
does not depend explicitly on  , we can expand in powers of
, we can expand in powers of  , and the coefficient of each power must separately vanish. Expanding the right hand side in powers of
, and the coefficient of each power must separately vanish. Expanding the right hand side in powers of  yields
yields 


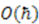 and
and 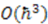 are satisfied, all others automatically follow. Therefore, we proceed to find all possible solutions to the two partial differential equations:
are satisfied, all others automatically follow. Therefore, we proceed to find all possible solutions to the two partial differential equations: 


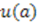 ,
,  , and
, and 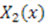 that satisfiy Equation (50). We will ignore the case when both
that satisfiy Equation (50). We will ignore the case when both  , and
, and 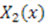 are constants, as this corresponds to a flat potential with no
are constants, as this corresponds to a flat potential with no  -dependence. We will also ignore the case in which
-dependence. We will also ignore the case in which  , and
, and 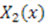 are linearly dependent on each other; i.e.,
are linearly dependent on each other; i.e., 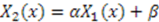 . In this case,
. In this case, 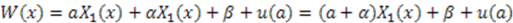 . If we redefine
. If we redefine 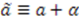 , this case becomes equivalent to a superpotential with a shifted parameter and constant
, this case becomes equivalent to a superpotential with a shifted parameter and constant 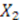 which will be considered shortly. We can therefore assume that
which will be considered shortly. We can therefore assume that 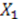 and
and 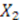 are linearly independent of each other without loss of generality. Note that from here onward, we will use lower case Greek letters to denote constants that are independent of both
are linearly independent of each other without loss of generality. Note that from here onward, we will use lower case Greek letters to denote constants that are independent of both 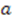 and
and  .
.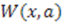 , we first focus on determining
, we first focus on determining 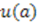 . To do so, we take two derivatives of (50) with respect to
. To do so, we take two derivatives of (50) with respect to 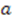 . This leads to the following differential equation:
. This leads to the following differential equation:
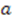 and
and  respectively. Since
respectively. Since  , this simplifies to:
, this simplifies to: 

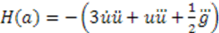 is a function of
is a function of 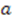 , and is independent of
, and is independent of  . Since
. Since 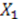 and
and 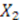 are linearly independent, we find that there are only three possible ways for the left-hand-side of Equation (54) to be independent of
are linearly independent, we find that there are only three possible ways for the left-hand-side of Equation (54) to be independent of  :
: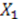 is a constant and
is a constant and 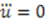 ;
; 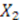 is a constant and
is a constant and 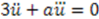 ;
; 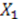 nor
nor 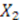 are not constants, but
are not constants, but 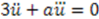 and
and 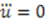 .
. 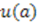 . Then we can determine
. Then we can determine  and
and 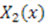 for these three cases. This we do by taking two derivatives of (50), this time one with respect to
for these three cases. This we do by taking two derivatives of (50), this time one with respect to 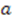 and another with respect to
and another with respect to  . This yields:
. This yields:

5.2.1. Case 1: X1 Is a Constant and ![Symmetry 04 00452 i245]()
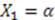 . Since
. Since 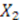 cannot be a constant as well, Equation (54) requires
cannot be a constant as well, Equation (54) requires 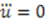 . This leads to
. This leads to 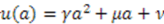 for some arbitrary constants
for some arbitrary constants  ,
, 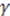 ,
, 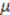 , and
, and 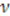 . Inserting
. Inserting 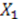 and
and 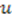 into Equation (52) yields
into Equation (52) yields 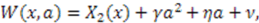 where
where  .
.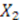 by inserting the above
by inserting the above 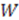 into Equation (50). This yields
into Equation (50). This yields

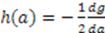 .
.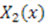 is independent of
is independent of 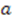 , and the left side of (57) is a sum of four linearly independent functions of
, and the left side of (57) is a sum of four linearly independent functions of 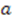
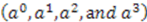 , and the term
, and the term 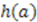 on the right-hand-side is independent of
on the right-hand-side is independent of  , the coefficient of each power of
, the coefficient of each power of 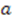 must separately be independent of
must separately be independent of  . The linear term in
. The linear term in 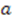 therefore requires that
therefore requires that 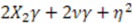 be independent of
be independent of  . Since a constant
. Since a constant 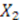 leads to a trivial solution, we must have
leads to a trivial solution, we must have  The remaining
The remaining  -dependent terms on the left side of (57),
-dependent terms on the left side of (57), 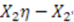 must be a constant:
must be a constant:
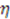 and
and 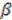 .
. 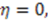
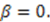 In this case,
In this case, 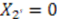 , which is a trivial solution;
, which is a trivial solution; 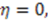
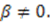 In this case,
In this case, 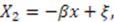 so
so 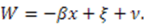 Defining
Defining 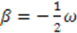 yields the harmonic oscillator superpotential;
yields the harmonic oscillator superpotential; 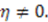 The solution is then
The solution is then 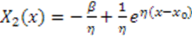 ,
, 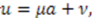
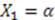 . Therefore,
. Therefore, 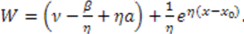 For
For 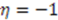 , this yields
, this yields  , where
, where  and
and 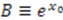 . This is the Morse superpotential. Note that
. This is the Morse superpotential. Note that 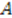 decreases as
decreases as 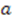 increases, and hence signals a finite number of eigenstates [48].
increases, and hence signals a finite number of eigenstates [48]. 5.2.2. Case 2: ![Symmetry 04 00452 i280]() Is Constant
Is Constant
 ; then Equation (54) requires
; then Equation (54) requires 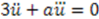 . This yields
. This yields 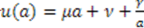 . We now insert this form of
. We now insert this form of 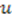 and
and  into (56) to get an ordinary differential equation in
into (56) to get an ordinary differential equation in  for
for 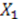 :
:


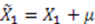 . This leads to
. This leads to 
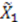 depend on the constant
depend on the constant 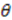 .
.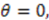 In this case,
In this case, 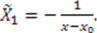 The whole superpotential is then given by
The whole superpotential is then given by 
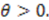 In this case, we have either
In this case, we have either 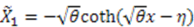 (Eckart) or
(Eckart) or 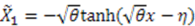 (Rosen-Morse II). In the first case, the superpotential is given by
(Rosen-Morse II). In the first case, the superpotential is given by 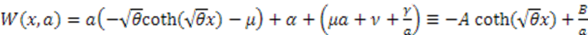 , where we have set
, where we have set 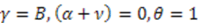 and
and 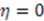 . This is the well known Eckart potential. Similarly, the other solution with
. This is the well known Eckart potential. Similarly, the other solution with 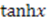 generates Rosen-Morse II;
generates Rosen-Morse II;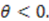 In this case, we obtain
In this case, we obtain  . An analysis similar to the previous case generates the superpotential for Rosen-Morse I.
. An analysis similar to the previous case generates the superpotential for Rosen-Morse I. 5.2.3. Case 3: ![Symmetry 04 00452 i308]() and
and ![Symmetry 04 00452 i280]() Are not Constant, but
Are not Constant, but ![Symmetry 04 00452 i309]() and
and ![Symmetry 04 00452 i245]()
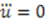 , and
, and 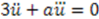 , we have
, we have 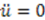 . Therefore
. Therefore 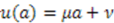 . In this case, Equation (56) yields
. In this case, Equation (56) yields


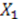 as Case 2. However, in this case,
as Case 2. However, in this case, 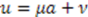 (this is equivalent to choosing
(this is equivalent to choosing  in Case 2) and
in Case 2) and 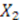 is not constant. Instead, in each case we must plug our solutions for
is not constant. Instead, in each case we must plug our solutions for 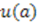 and
and  into Equation (50), which yields
into Equation (50), which yields
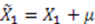 , which yields
, which yields 
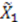 and
and 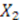 are independent of
are independent of 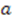 , the terms linear in
, the terms linear in 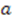 and the terms independent of
and the terms independent of 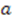 on the left side of this equation must each separately be independent of
on the left side of this equation must each separately be independent of  . Therefore,
. Therefore, 

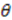 , we get different superpotentials:
, we get different superpotentials: 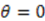 . We again get
. We again get 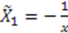 , where with an appropriate choice for the origin we have set
, where with an appropriate choice for the origin we have set  . Equation (65) for
. Equation (65) for 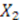 becomes
becomes
 . With the identification
. With the identification 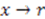 ,
,  ,
, 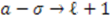 , we get
, we get 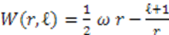 , the superpotential for the 3D-harmonic oscillator;
, the superpotential for the 3D-harmonic oscillator; 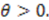 As seen before,
As seen before, 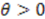 implies that
implies that 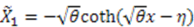 or
or 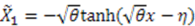 . By translation and scaling of
. By translation and scaling of  , we can simplify the first solution to
, we can simplify the first solution to 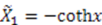 . Substituting
. Substituting 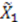 in Equation (65), we get
in Equation (65), we get
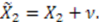 The solution to the homogeneous equation is
The solution to the homogeneous equation is  , and the particular solution is
, and the particular solution is 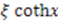 . Hence
. Hence 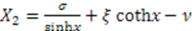 . Thus, the superpotential is given by
. Thus, the superpotential is given by 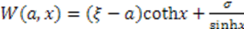 , the General Pöschl-Teller potential given in Table 1. The second solution generates the Scarf II potential;
, the General Pöschl-Teller potential given in Table 1. The second solution generates the Scarf II potential;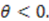 A similar analysis for this case leads to Scarf I as the corresponding shape invariant superpotential.
A similar analysis for this case leads to Scarf I as the corresponding shape invariant superpotential.  -independent solutions to the additive shape invariant condition.
-independent solutions to the additive shape invariant condition. 5.3. ![Symmetry 04 00452 i001]() -Dependent Superpotentials
-Dependent Superpotentials
 . However, a new class of superpotentials was discovered by Quesne [50,51]. It has been shown [46] that these “extended" superpotentials obey the shape invariance condition in the form of Equation (7) only when
. However, a new class of superpotentials was discovered by Quesne [50,51]. It has been shown [46] that these “extended" superpotentials obey the shape invariance condition in the form of Equation (7) only when 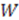 is allowed to depend explicitly on
is allowed to depend explicitly on  . While this dependence is frequently ignored by the conventional notation that sets
. While this dependence is frequently ignored by the conventional notation that sets 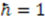 , we will show that this constraint results in important consequences for the energy spectrum of the resulting potentials. In each case, the new potential is isospectral with a potential that arises from one of the “conventional" superpotentials listed in Table 1. Authors of [52,53,54] have added an infinite number of potentials that belong in this class, and extended shape invariant potentials continue to be objects of intense research [55,56].
, we will show that this constraint results in important consequences for the energy spectrum of the resulting potentials. In each case, the new potential is isospectral with a potential that arises from one of the “conventional" superpotentials listed in Table 1. Authors of [52,53,54] have added an infinite number of potentials that belong in this class, and extended shape invariant potentials continue to be objects of intense research [55,56]. explicitly. To do so, we expand the superpotentials in powers of
explicitly. To do so, we expand the superpotentials in powers of  . Hence, we define
. Hence, we define 
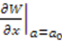 and
and 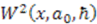 . We obtain
. We obtain

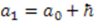 ,
, 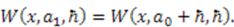 Expanding in powers of
Expanding in powers of 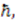


 . After some significant algebraic manupulation we find that the following equation must be true separately for each positive integer value of
. After some significant algebraic manupulation we find that the following equation must be true separately for each positive integer value of 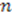 :
: 
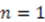 , we obtain
, we obtain 
 -independent
-independent 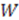 ’s. We have already found a set of solutions for Equation (70) that includes all known
’s. We have already found a set of solutions for Equation (70) that includes all known  -independent superpotentials. The extended cases [50,51] are solutions to (69) as well, as shown in [46]. Note that Equation (69) provides a consistency condition for all
-independent superpotentials. The extended cases [50,51] are solutions to (69) as well, as shown in [46]. Note that Equation (69) provides a consistency condition for all  -dependent potentials; however, these are not easy to solve to determine new potentials.
-dependent potentials; however, these are not easy to solve to determine new potentials.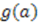 is given by
is given by

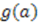 , and hence the energy of the system, is given entirely in terms of the
, and hence the energy of the system, is given entirely in terms of the  -independent part of the superpotential. Hence, the eigenvalues are not affected by the
-independent part of the superpotential. Hence, the eigenvalues are not affected by the  -dependent extension of the superpotential.
-dependent extension of the superpotential. -independent term of the superpotential
-independent term of the superpotential  . Therefore, each of the expanded potentials is isospectral with its corresponding conventional potential. Future possibilities for finding new shape-invariant superpotentials fall into one of two categories:
. Therefore, each of the expanded potentials is isospectral with its corresponding conventional potential. Future possibilities for finding new shape-invariant superpotentials fall into one of two categories:  is required to satisfy Equation (70), which is equivalent to Equation (50) for
is required to satisfy Equation (70), which is equivalent to Equation (50) for  -independent
-independent 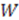 ’s,
’s,  is not required to satisfy Equation (48). Rather, the additional constraints for an extended
is not required to satisfy Equation (48). Rather, the additional constraints for an extended 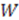 are supplied by Equation (69). It therefore may be possible to find an
are supplied by Equation (69). It therefore may be possible to find an  -dependent superpotential whose
-dependent superpotential whose  -independent term
-independent term  is not equivalent to a conventional superpotential. Intriguingly, it therefore may still be possible to discover shape-invariant systems with new energy spectra.
is not equivalent to a conventional superpotential. Intriguingly, it therefore may still be possible to discover shape-invariant systems with new energy spectra.6. Summary and Conclusions
 , this condition can be written as a set of local partial differential equations [45,46,47]. The solution to these equations showed that the list of such superpotentials was indeed complete. In this manuscript, we have presented a more straightforward proof of this result.
, this condition can be written as a set of local partial differential equations [45,46,47]. The solution to these equations showed that the list of such superpotentials was indeed complete. In this manuscript, we have presented a more straightforward proof of this result. ) must obey [46,47]. We have also discussed the constraints placed on the energy spectra of these extended potentials as well as possibilities for finding additional as-yet-undiscovered cases of additive shape invariance.
) must obey [46,47]. We have also discussed the constraints placed on the energy spectra of these extended potentials as well as possibilities for finding additional as-yet-undiscovered cases of additive shape invariance.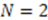 for cyclic and limiting cases for multiplicative). It remains to be shown whether the shape invariance condition for these classes can be transformed from a difference-differential equation into a set of partial differential equations and be subjected to similar analysis.
for cyclic and limiting cases for multiplicative). It remains to be shown whether the shape invariance condition for these classes can be transformed from a difference-differential equation into a set of partial differential equations and be subjected to similar analysis.Acknowledgements
References and Notes
- Darboux, G. Leçons sur la Théorie Général des Surfaces, 2nd ed; Gauthier-Villars: Paris, France, 1912. [Google Scholar]
- Schrödinger, E. A method of determining quantum-mechanical eigenvalues and eigenfunctions. Proc. R. Ir. Acad. 1940, A46, 9–16. [Google Scholar]
- Schrödinger, E. Further studies on solving eigenvalue problems by factorization. Proc. R. Ir. Acad. 1941, A46, 183–206. [Google Scholar]
- Schrödinger, E. The factorization of the hypergeometric equation. Proc. R. Ir. Acad. 1941, A47, 53–54. [Google Scholar]
- Infeld, L.; Hull, T.E. The factorization method. Rev. Mod. Phys. 1951, 23, 21–68. [Google Scholar]
- Witten, E. Dynamical breaking of supersymmetry. Nucl. Phys. 1981, B185, 513–554. [Google Scholar]
- Solomonson, P.; Van Holten, J.W. Fermionic coordinates and supersymmetry in quantum mechanics. Nucl. Phys. 1982, B196, 509–531. [Google Scholar]
- Cooper, F.; Freedman, B. Aspects of supersymmetric quantum mechanics. Ann. Phys. 1983, 146, 262–288. [Google Scholar]
- Note the constant
has been added to the usual harmonic oscillator potential to insure that the groundstate energy of the system remains at zero. This constant allows us to factorize the Hamiltonian
as a product of operators
and
.
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry in Quantum Mechanics; World Scientific: Singapore, 2001. [Google Scholar]
- Gangopadhyaya, A.; Mallow, J.; Rasinariu, C. Supersymmetric Quantum Mechanics: An Introduction; World Scientific: Singapore, 2010. [Google Scholar]
-
Thus,
is an eigenstate of
with an eigenvalue
.
-
.
- Bender, C.M.; Boettcher, S. Real spectra in non-hermitian hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex extension of quantum mechanics. Phys. Rev. Lett. 2002, 89, 270401–1. [Google Scholar]
- Bender, C.M.; Berry, M.V.; Mandilara, A. Generalized PT symmetry and real spectra. J. Phys. A 2002, 35, L467–L471. [Google Scholar]
- Znojil, M. SI potentials with PT symmetry. J. Phys. A 2000, 33, L61–L62. [Google Scholar]
- Levai, Z. Exact analytic study of the PT-symmetry-breaking mechanism. Czech. J. Phys. 2004, 54, 77–84. [Google Scholar]
- Znojil, M. Matching method and exact solvability of discrete Pt-symmetric square wells. J. Phys. A 2006, 39, 10247–10261. [Google Scholar]
- Quesne, C.; Bagchi, B.; Mallik, S.; Bila, H.; Jakubsky, V. PT supersymmetric partner of a short-range square well. Czech. J. Phys. 2005, 55, 1161–1166. [Google Scholar]
- Bagchi, B.; Quesne, C.; Roychoudhury, R. Isospectrality of conventional and new extended potentials, second-order supersymmetry and role of PT Symmetry. Pramana 2009, 73, 337–347. [Google Scholar]
- Miller, W., Jr. Lie Theory and Special Functions (Mathematics in Science and Engineering); Academic Press: New York,NY,USA, 1968. [Google Scholar]
- Gendenshtein, L.E. Derivation of exact spectra of the schrodinger equation by means of supersymmetry. JETP Lett. 1983, 38, 356–359. [Google Scholar]
- Gendenshtein, L.E.; Krive, I.V. Supersymmetry in quantum mechanics. Sov. Phys. Usp. 1985, 28, 645–666. [Google Scholar]
- Barclay, D.; Dutt, R.; Gangopadhyaya, A.; Khare, A.; Pagnamenta, A.; Sukhatme, U. New exactly solvable hamiltonians: Shape invariance and self-similarity. Phys. Rev. A 1993, 48, 2786–2797. [Google Scholar]
- Spiridonov, V.P. Exactly solvable potentials and quantum algebras. Phys. Rev. Lett. 1992, 69, 398–401. [Google Scholar]
- Sukhatme, U.P.; Rasinariu, C.; Khare, A. Cyclic shape invariant potentials. Phys. Lett. 1997, A234, 401–409. [Google Scholar]
- Gangopadhyaya, A.; Mallow, J.V.; Sukhatme, U.P. Supersymmetry and Integrable Models:. In Proceedings of Workshop on Supersymmetry and Integrable Models; Aratyn, H., Imbo, T.D., Keung, W.-Y., Sukhatme, U., Eds.; Springer-Verlag.
- Balantekin, A.B. Algebraic approach to shape invariance. Phys. Rev. A 1998, 57, 4188–4191. [Google Scholar]
- Gangopadhyaya, A.; Mallow, J.V.; Sukhatme, U.P. Translational shape invariance and the inherent potential algebra. Phys. Rev. A 1998, 58, 4287–4292. [Google Scholar]
- Chaturvedi, S.; Dutt, R.; Gangopadhyaya, A.; Panigrahi, P.; Rasinariu, C.; Sukhatme, U. Algebraic shape invariant models. Phys. Lett. 1998, A248, 109–113. [Google Scholar]
- Balantekin, A.; Candido Ribeiro, M.; Aleixo, A. Algebraic nature of shape-invariant and self-similar potentials. J. Phys. A 1999, 32, 2785–2790. [Google Scholar]
- We assume that as
, the supersymmetry remains unbroken.
- Dutt, R.; Khare, A.; Sukhatme, U. Supersymmetry, shape invariance and exactly solvable potentials. Am. J. Phys. 1998, 56, 163. [Google Scholar]
- Cooper, F.; Ginocchio, J.; Khare, A. Relationship between supersymmetry and solvable potentials. Phys. Rev. D 1987, 36, 2458. [Google Scholar]
- In the last line we have used the fact that
. This implies that for any analytical function
, we have
.
- Veselov, A.P.; Shabat, A.B. Dressing chains and spectral theory of the Schrödinger operator. Funct. Anal. Appl. 1993, 27, 81–96. [Google Scholar]
- These constraints are:
.
- We have used
.
- Dutt, R.; Gangopadhyaya, A.; Rasinariu, C.; Sukhatme, U. Coordinate realizations of deformed Lie algebras with three generators. Phys. Rev. A 1999, 60, 3482–3486. [Google Scholar] [CrossRef]
- Rocek, M. Representation theory of the nonlinear SU (2) algebra. Phys. Lett. B 1991, 255, 554–557. [Google Scholar]
- Adams, B.G.; Cizeka, J.; Paldus, J. Lie algebraic methods and their applications to simple quantum systems. Advances in Quantum Chemistry, 19th ed; Academic Press: New York,NY,USA, 1987. [Google Scholar]
- In some cases these are additive constants and subtracted away. If we provide a common floor to all potentials, demanding that their groundstate energies be zero, we will find that all known solvable potentials pick up a
dependent term.
- Shabat, A. The infinite-dimensional dressing dynamical system. Inverse Probl. 1992, 8, 303–308. [Google Scholar]
- Gangopadhyaya, A.; Mallow, J.V. Generating shape invariant potentials. Int. J. Mod. Phys. A 2008, 23, 4959–4978. [Google Scholar]
- Bougie, J.; Gangopadhyaya, A.; Mallow, J.V. Generation of a complete set of additive shape-invariant potentials from an euler equation. Phys. Rev. Lett. 2010, 210402–1. [Google Scholar]
- Bougie, J.; Gangopadhyaya, A.; Mallow, J.V. Method for generating additive shape invariant potentials from an euler equation. J. Phys. A 2012, 44, 275307–1. [Google Scholar]
- Normalizability of the groundstate
requires that
be greater than zero. Since an increase in
decreases
, there can only be a finite number of increases.
- By substituting
into Equation (50) we find that shape invariance requires that
.
- Quesne, C. Exceptional orthogonal polynomials, exactly solvable potentials and supersymmetry. J. Phys. A 2008, 41, 392001–1. [Google Scholar]
- Quesne, C. Solvable rational potentials and exceptional orthogonal polynomials in supersymmetric quantum mechanics. Sigma 2009, 5, 084–1. [Google Scholar]
- Odake, S.; Sasaki, R. Infinitely many shape invariant discrete quantum mechanical systems and new exceptional orthogonal polynomials related to the wilson and Askey-Wilson polynomials. Phys. Lett. B 2009, 682, 130–136. [Google Scholar]
- Odake, S.; Sasaki, R. Another set of infinitely many exceptional (Xl) laguerre polynomials. Phys. Lett. B 2010, 684, 173–176. [Google Scholar]
- Tanaka, T. N-fold supersymmetry and quasi-solvability associated with X-2-laguerre polynomials. J. Math. Phys. 2010, 51, 032101–1. [Google Scholar]
- Sree Ranjani, S.; Panigrahi, P.; Khare, A.; Kapoor, A.; Gangopadhyaya, A. Exceptional orthogonal polynomials, QHJ formalism and SWKB quantization condition. J. Phys. A 2012, 055210–1. [Google Scholar]
- Shiv Chaitanya, K.; Sree Ranjani, S.; Panigrahi, P.; Radhakrishnan, R.; Srinivasan, V. Exceptional polynomials and SUSY quantum mechanics. Available online: http://arxiv.org/pdf/1110.3738.pdf (accessed on 2 August 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bougie, J.; Gangopadhyaya, A.; Mallow, J.; Rasinariu, C. Supersymmetric Quantum Mechanics and Solvable Models. Symmetry 2012, 4, 452-473. https://doi.org/10.3390/sym4030452
Bougie J, Gangopadhyaya A, Mallow J, Rasinariu C. Supersymmetric Quantum Mechanics and Solvable Models. Symmetry. 2012; 4(3):452-473. https://doi.org/10.3390/sym4030452
Chicago/Turabian StyleBougie, Jonathan, Asim Gangopadhyaya, Jeffry Mallow, and Constantin Rasinariu. 2012. "Supersymmetric Quantum Mechanics and Solvable Models" Symmetry 4, no. 3: 452-473. https://doi.org/10.3390/sym4030452
APA StyleBougie, J., Gangopadhyaya, A., Mallow, J., & Rasinariu, C. (2012). Supersymmetric Quantum Mechanics and Solvable Models. Symmetry, 4(3), 452-473. https://doi.org/10.3390/sym4030452