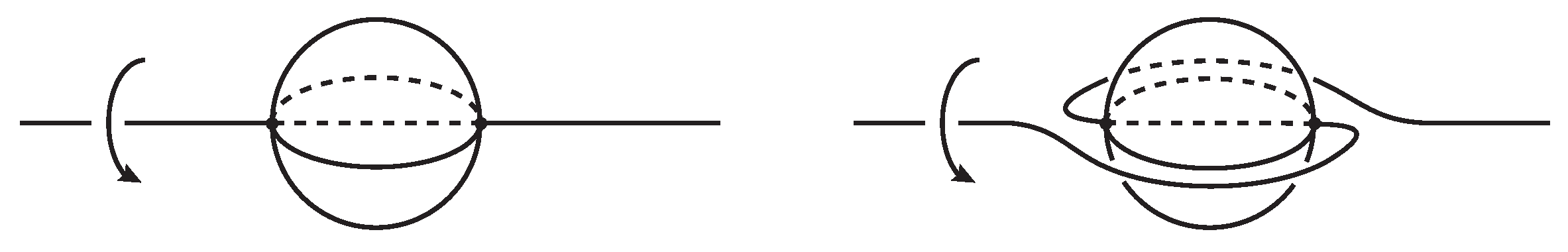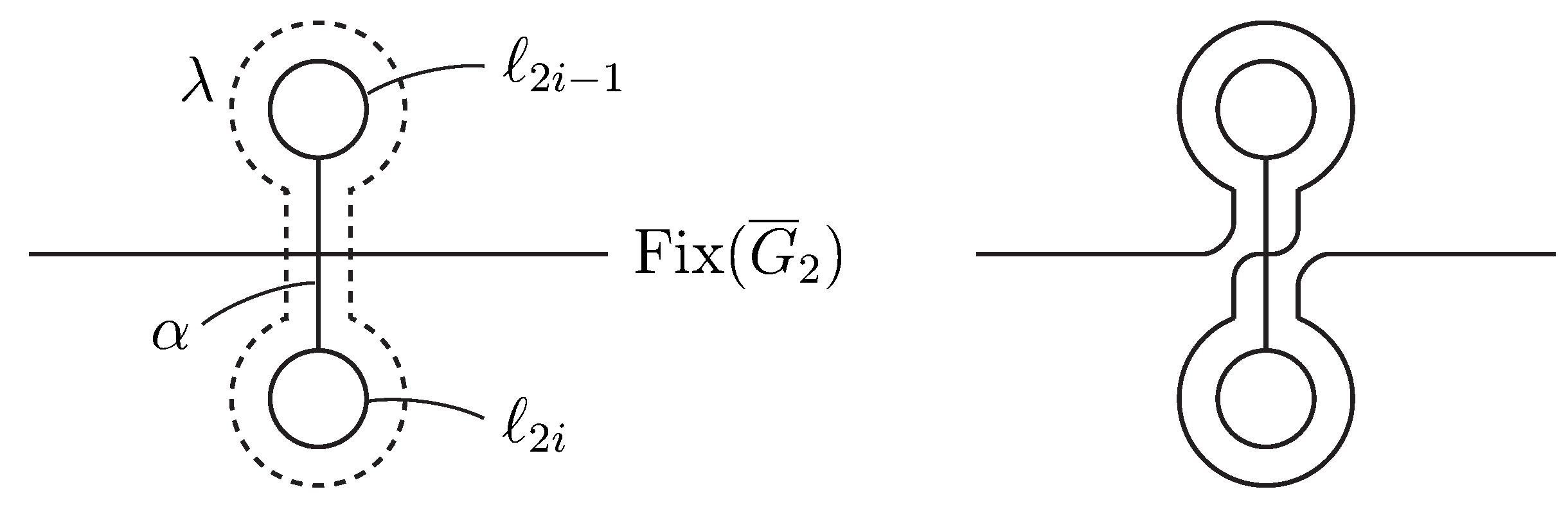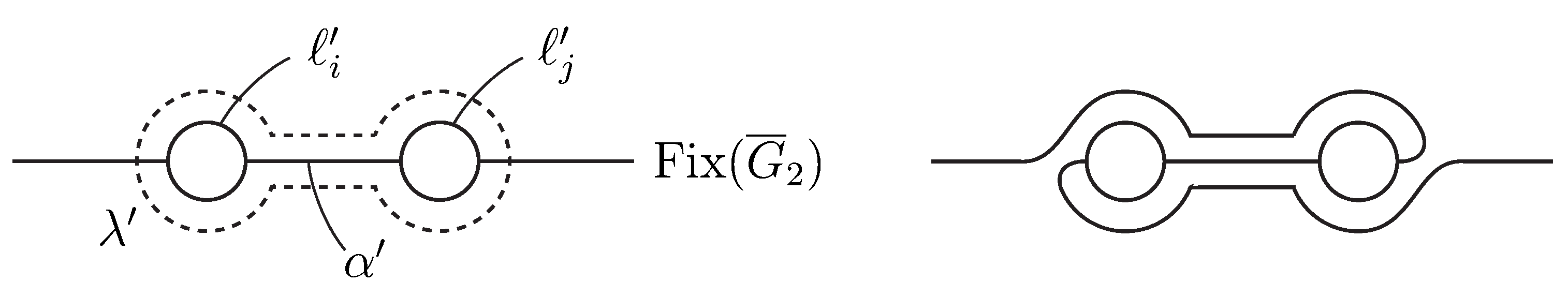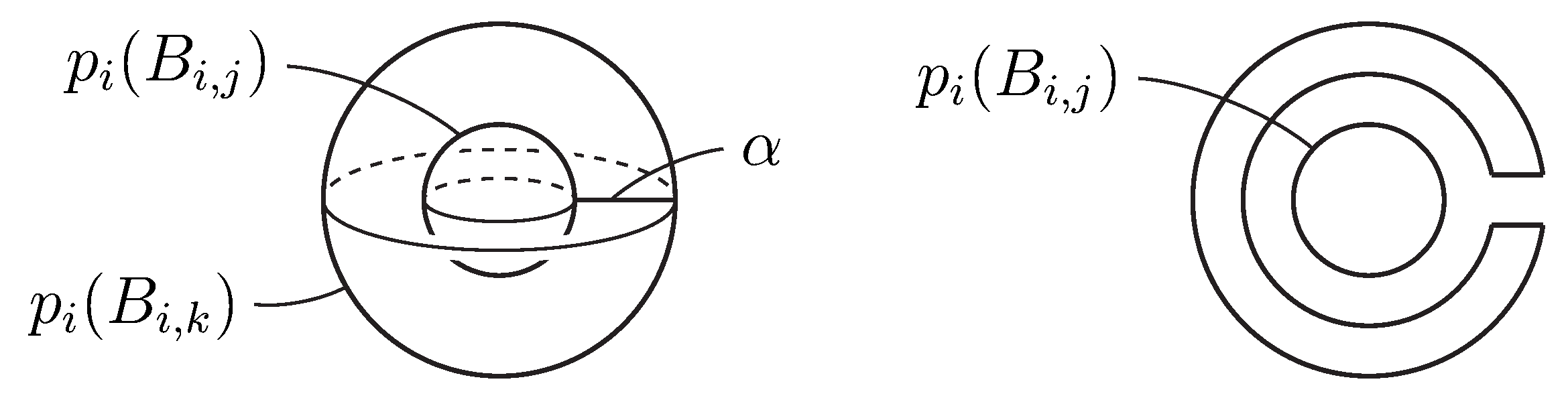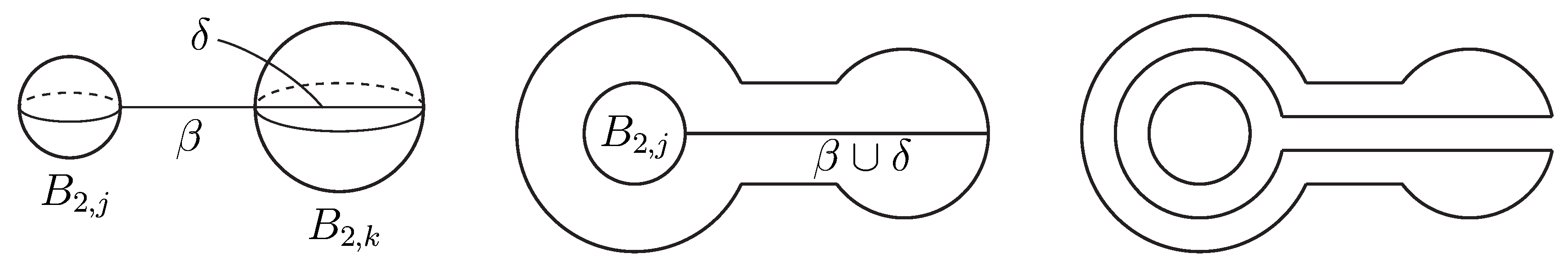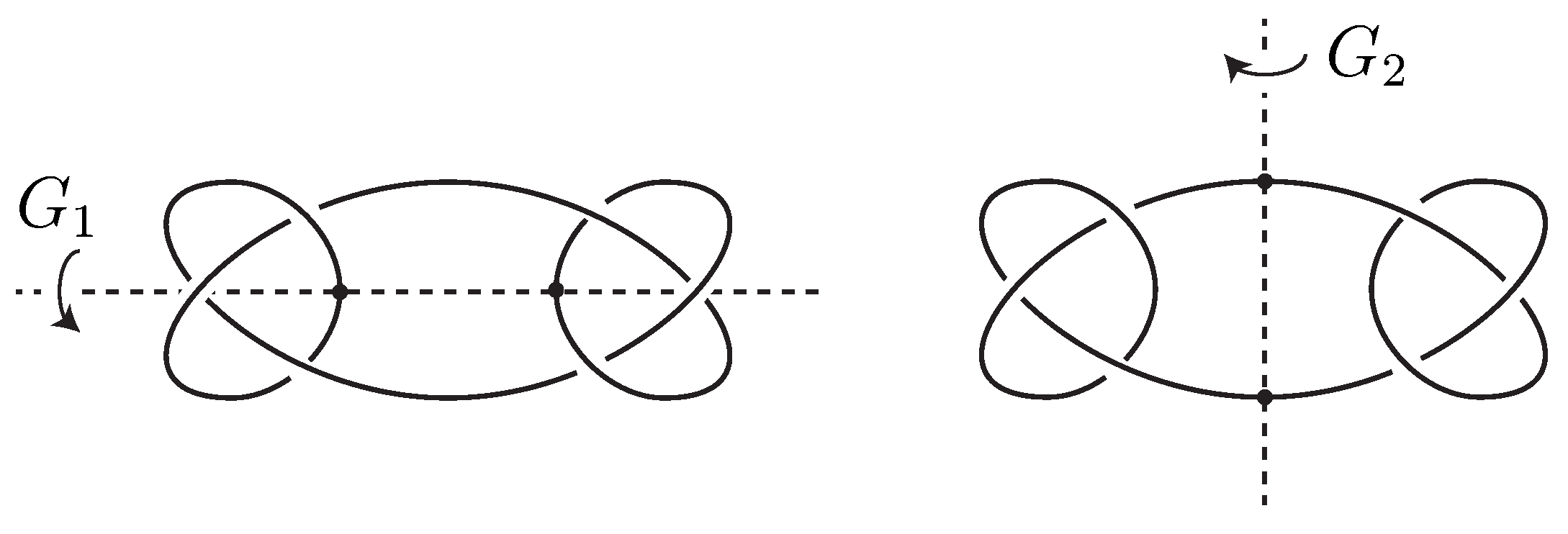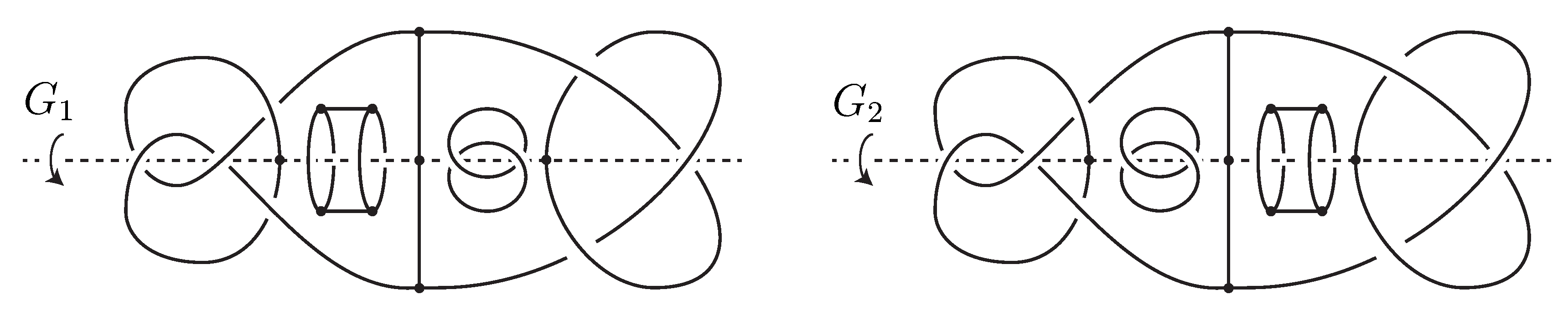Let
M be a Haken 3-manifold with incompressible boundary. The JSJ decomposition theorem and Thurston’s uniformization theorem [
15] assert that there is a canonical way of splitting the pair
along a disjoint, non-parallel, essential annuli and tori into pieces
each of which is one of the following four types:
Proof. It is enough by Lemma 2.4 of [
11] to consider the case where the actions of
and
on
are not free. For each
, Theorem 2.1 of [
16] implies that
admits a
-invariant product structure
, in which
consists of
I-fibers. Since each element of
takes a meridian of
T to a meridian of
T, the setwise stabilizer of each
I-fiber is a trivial group or a 2-fold cyclic group. Therefore, the quotient space
admits the induced
I-bundle structure over a 2-orbifold
B with underlying surface
F and
n cone points of index two. Since
T is a torus, the orbifold Euler characteristic
of
B is calculated as follows (see [
17]):
Since
,
F is a sphere and
holds.
Denote by the projection map onto the quotient space for each i, and by the T-fiber in . Connect the four cone points on cyclically by a collection of arcs , , , and with disjoint interiors. Each lifts to an essential loop on such that and with are disjoint if , and otherwise meets transversally in a point. Suppose that each is isotopic to a loop on along an annulus saturated by I-fibers in , and to a loop on along an annulus saturated by I-fibers in . Then the endpoints of each is connected by with or 2. Since the underlying surface of is a sphere, is isotopic to relative to the cone points. Therefore, is moved by an -equivariant isotopy relative to so as to agree with on .
The I-bundle structures in and respectively induce orbifold isomorphisms and such that setwise preserves the loop . The restriction of on is isotopic relative to the cone points to the identity map or an involution. Since splits into two disks with no cone point, is deformed by a -equivariant isotopy so that afterwards is the identity map or an involution.
Take an -invariant -bundle structure on with respect to which and are cross sectional, and an -invariant -bundle structure on with respect to which every fiber in splits into two cross sections. Then and induce a -invariant product structure on . Let be the lift of which takes each to . Then we have for some rational numbers m and n.
Assume . Take a rational number so that and are coprime integers. Then holds for some integers and . Let be the covering map given by . Denote by the linear transformation on represented by . Then the map conjugates h to . Thus, h extends to -twist along . Since h conjugates the action of on to itself, conjugates to a finite subgroup of . Therefore, it is enough to consider the case .
It is obvious that holds for any integers k and l. By verifying that, for some choice of k and l, the above argument applied to makes isotopic to relative to , we may assume that they agree.
By considering an isotopy of
relative to
which takes
to
on
, we may assume that
and
agree on
. Note that
splits
into disks, and that
splits
into balls. Then the identity map on
extends to an orbifold isomorphism
. Since the quotient space of any finite group action on
is isomorphic to one of the orbifolds listed on page 191 of [
15],
and the identity map on
extend to an orbifold isomorphism
. Thus,
and
are equivalent relative to
. Hence, the conclusion follows. □
Proof. The case
and
, the case
and
, and the case
and
respectively follow from Lemma 2.1 of [
11], Lemma 2.1 of this paper, and Theorem 8.1 of [
16]. We therefore exclude these cases.
Denote by
the system of the exceptional fibers
in
M. Let
be a fibered regular neighborhood of each
. It follows from Theorem 2.2 of [
16] that each
preserves some Seifert fibration
of
M. Then the uniqueness of a Seifert fibration of
M (see VI.18.Theorem of [
12]) implies that
is isotopic to a setwise
-invariant fibered regular neighborhood of the system of exceptional fibers in
. Since Lemma 3.1 of [
11] implies that the orders of the exceptional fibers are pairwise coprime, we may assume that
for each
k. Therefore, it is enough by Lemma 2.1 of [
11] to consider the case where
M is a product
-bundle.
It follows from Theorem 2.1 of [
16] that
M admits a
-invariant product structure
. If
,
M admits a
-invariant product structure
which agrees with
on
F (see Theorem 2.3 of [
16]). If
, we see
M as the quotient of the double
of
M along
by
generated by an orientation-reversing involution, and apply the same argument to the finite group action on
, which is the extension of
by
. Then we obtain a
-invariant product structure
of
M which agrees with
on
F.
By the uniqueness of the
-bundle structure of
M (see VI.18.Theorem of [
12]), there is a map
isotopic to the identity which takes the
-bundle structure induced by
to the
-bundle structure induced by
. Modify
in
by a fiber preserving isotopy in a fibered regular neighborhood of
F so as to restrict to the identity map on
F. By conjugating
by
, we may therefore assume that
and
induce the same
-bundle structure of
M.
Let
be the projection map onto the base surface
B. Each
induces a finite group action
on
B. We consider
B to be lying on
. Then each
extends to an action on
. Since
and
agree on
, the quotient spaces
and
are orbifold isomorphic to suborbifolds of the same spherical orbifold listed on page 188 of [
15]. We may assume that
and
are not orientation-preserving, otherwise the conclusion follows from Lemma 3.2 and Remark 3.3 of [
11]. Then the assumption
implies that each
is generated by the reflection of
in a loop. Since
and
permute the components of
similarly,
consists of loops
such that
- (1)
and interchange and for , and
- (2)
and setwise preserve for .
Without loss of generality, . Denote by the fixed point circle of the action of each on . Suppose that each is equipped with an orientation, and splits B into two pieces and so that and . We may assume without loss of generality that and for , and that we meets in order as we go along .
Suppose
and
for some
i. By taking a proper arc on
connecting
and
, we obtain a setwise
-invariant arc
on
B which meets
in a point and connects
and
. Then
is modified by the half twist along the loop
, denoted by
, so that afterwards
and
, as illustrated in
Figure 2. The argument presented for the proof of Lemma 2.1 implies that this modification is realized by a
-twist along the torus
which conjugates
to a subgroup of
. We may therefore assume
and
for
.
Suppose that
and
are connected by an arc
in
. Then
is modified by the half twists along the loop
so as to meet
and
in the reverse order, as illustrated in
Figure 3, which is realized by the conjugation of
by a
-twist along the torus
, as before. Since every permutation on the set
is a product of transpositions, we may assume that
meets
in order. Moreover, we can change the order in which
meets the two points in
by the half twists along
, which is also realized by a
-twist along the torus
. We may therefore assume that
is equivalent to
relative to
.
Now we may assume . Take a map which restricts to the identity map on F and takes to setwise preserving every -fiber. It is easy to verify that h is extendable to a map in . Hence, the conclusion follows by conjugating by h. □
Proof. It follows from Theorem 5.5 of [
18] that
admits two complete hyperbolic structures of finite volume, one is
-invariant and the other is
-invariant. Mostow’s rigidity theorem [
15] implies that complete hyperbolic structures of finite volume on
are unique up to isometry representing the identity map on
. We may therefore assume that
is endowed with the
-invariant hyperbolic structure, and that
is conjugate to an isometric action
by
which is isotopic to the identity map.
Next, we are going to modify
h in a regular neighborhood of
F so as to restrict to the identity map on
F. It follows from Propostition D.3.18 of [
19] that
F consists of tori. Let
be an isotopy from
h to the identity map. Denote by
the finite group action on
whose restriction on
is induced from the finite group action on
F given by the conjugate of
by
. In particular, the actions of
on
and
are respectively given by
and
. Note that
preserves the product structure
, and that we can embed
in
so that
extends to a finite group action on
.
We consider the partition of the set of the components of F into the orbits under the permutation induced by . Suppose that the orbits are represented by . Lemma 2.1 implies that a rational twist along conjugates the setwise stabilizer of in so that the action on is equivalent relative to to the action which preserves the product structure. Suppose that the rational twists along the tori in are equivariantly induced from those along . By conjugating by their composition, it is equivalent relative to to the action which preserves the product structure. This implies that h is modified equivariantly so as to restrict to the identity map on F.
Suppose that
and
agree on
F. Then
restricts to the identity map on
F. Since the isometry group of
is finite (see [
15]), Newman’s theorem [
20] implies
. Hence,
and
agree on
M. This completes the proof. □
Proof. We see M as the quotient of by generated by an orientation-reversing involution. Each induces a finite group action on which is an extension of by . As in the proof of Lemma 2.3, we consider endowed with a -invariant hyperbolic structure. Then some , which is isotopic to the identity map, conjugates to an isometric action . Clearly, meets in a totally geodesic surface, and therefore holds.
Suppose that
and
respectively induce
and
which agree on
F. Then
restricts to an isometry on each component
of
, which is a compact surface of negative Euler characteristic (see Propostition D.3.18 of [
19]). Since
is trivial in
,
and
agree on
. Therefore, [
20] implies
. Hence, some
, which setwise preserves
and is isotopic to the identity map, conjugates the action of
on
M to
.
It follows from Proposition D.3.18 of [
19] that
consists of tori. As in the proof of Lemma 2.3, modify
h in
by rational twists along tori in
so that afterwards
h restricts to the identity map on
and conjugates the action of
on
M to
. Moreover, we may assume by Lemma 2.3 of [
11] that
h restricts to the identity map on
. Since
h extends to an automorphism of
which is diffeomorphic outside
M, the conclusion follows. □
Proof. The equivariant loop theorem (see Chapter VII of [
15] and [
21]) implies that there is a
-invariant system
of disjoint disks properly embedded in
which splits
into pieces with incompressible boundary. The equivariant Dehn’s lemma [
21,
22] implies that the boundary loops of
bound a
-invariant system
of disjoint disks properly embedded in
. Since
is non-splittable,
is irreducible. Therefore, there is an isotopy of
relative to
which takes
to
. Since any finite group action on
is orthogonal [
15], we may assume that
and
agree on
. Moreover, the induced actions on the balls obtained by splitting
along
are equivalent relative to the boundary (see [
15]). Therefore, it is enough to consider the case where
is a Haken manifold with incompressible boundary.
We may assume by the equivariant JSJ decomposition theorem (see Theorem 8.6 of [
16]) and by the uniqueness of the JSJ decomposition [
13,
14] that there is a
-invariant and
-invariant system
of essential annuli and tori in
realizing the canonical JSJ decomposition of the pair
.
The argument presented for the proof of Proposition 3.10 of [
11] implies that some
, which is isotopic to the identity map relative to
, conjugates
to a finite group action which agree with
on the annuli in
. We may therefore assume that
contains no annuli.
The rest of the proof proceeds by induction on the number of tori in . Take a piece attaching . By Lemmas 2.2, 2.3 and 2.4, it is enough to consider the case where agrees with on . Moreover, we may assume by Lemma 2.1 that and agree on the components of each of which is a product I-bundle over a torus. Hence, the conclusion follows by the induction hypothesis. □