Symmetries of Spatial Graphs and Rational Twists along Spheres and Tori

Abstract

A symmetry group of a spatial graph $\Gamma$ in $S^3$ is a finite group consisting of orientation-preserving self-diffeomorphisms of $S^3$ which leave $\Gamma$ setwise invariant. In this paper, we show that in many cases symmetry groups of $\Gamma$ which agree on a regular neighborhood of $\Gamma$ are equivalent up to conjugate by rational twists along incompressible spheres and tori in the exterior of $\Gamma$.

1. Introduction

There are several approaches to the theory of graphs embedded in the 3-sphere, which are often motivated by molecular chemistry, since the chemical properties of a molecule depend on the symmetries of its molecular bond graph (see, for example, [1]). The symmetries of an abstract graph $\Gamma$ are described by automorphisms. If $\Gamma$ is embedded in $S^3$, some of these automorphisms are induced from self-diffeomorphisms of $S^3$. For example, [2,3,4,5,6] studied the extendabilities of the automorphisms of $\Gamma$, mainly in the case of Möbius ladders, complete graphs, and 3-connected graphs.

Even if the automorphisms of $\Gamma$ extend to self-diffeomorphisms of $S^3$, we face the problem of the uniqueness of the extensions. In this situation, it is enough to consider $\Gamma$ to be a topological space, since we need to study self-diffeomorphisms of $S^3$ which agree on $\Gamma$. In the case of a non-torus knot in $S^3$, there are only finitely many conjugacy classes of symmetries (see [7,8]). For a cyclic period or a free period of a knot in $S^3$, it is shown in [9,10] that the cyclic group generated by the periodic self-diffeomorphism of $S^3$ defining the symmetry is unique up to conjugate in some cases. Moreover, the author [11] generalized this result to the case of links in $S^3$. In this paper, we generalize these results to the case of symmetries of spatial graphs in $S^3$.

Suppose that any component of $\Gamma$ is a non-trivial graph with no leaf. We see $\Gamma$ as a geometric simplicial complex, and denote by $\left|\Gamma \right|$ the underlying topological space of $\Gamma$. A tame embedding of $\left|\Gamma \right|$ into $S^3$ is called a spatial embedding of $\Gamma$ into $S^3$, or simply a spatial graph $\Gamma$ in $S^3$. We say that $\Gamma$ is splittable if there exists a sphere in $S^3$ disjoint from $\Gamma$ that separates the components of $\Gamma$. We say that $\Gamma$ is non-splittable if it is not splittable. Suppose that an incompressible torus in $S^3-\Gamma$ bounds a solid torus V in $S^3$ containing $\Gamma$. The core of V is called a companion knot of $\Gamma$ if it is not ambient isotopic to $\Gamma$ in V. If there is no companion knot of $\Gamma$, every incompressible torus in $S^3-\Gamma$ separates the components of $\Gamma$.

Let M be a 3-manifold, and X a submanifold of M. Denote by $N\left(X\right)$ a regular neighborhood of X, and by $E\left(X\right)=M-\mathrm{int}N\left(X\right)$ the exterior of X. We refer to a finite subgroup G of the diffeomorphism group $\mathrm{Diff}\left(M\right)$ as a finite group action on M. Finite group actions $G_1$ and $G_2$ on M are equivalent (relative to X) if some $h\in \mathrm{Diff}\left(M\right)$ conjugates $G_1$ to $G_2$ (and restricts to the identity map on X). A symmetry group G of a spatial graph $\Gamma$ in $S^3$ is a finite group action on the pair $(S^3,\Gamma )$ which preserves the orientation of $S^3$.

Let $S^2$ be the unit sphere in ${\mathbb{R}}^3$, and $S^1$ the unit circle in the $xy$-plane in ${\mathbb{R}}^3$. Denote by ${\mathrm{Rot}}_{\theta }\in \mathrm{Diff}\left({\mathbb{R}}^3\right)$ the rotation about the z-axis through angle $\theta$. Suppose that ${\sigma }_n\in \mathrm{Diff}(S^2\times I)$ and ${\tau }_n\in \mathrm{Diff}(S^1\times S^1\times I)$, where $n\in \mathbb{R}$, is given by ${\sigma }_n(x,t)=({\mathrm{Rot}}_{2\pi nt}\left(x\right),t)$ and ${\tau }_n(x,y,t)=({\mathrm{Rot}}_{2\pi nt}\left(x\right),y,t)$. Let F be a 2-sided sphere or torus embedded in a 3-manifold M. Split M open along F into a (possibly disconnected) 3-manifold $M_F$. Denote by $F_{-}$ and $F_{+}$ the boundary components of $M_F$ originated from F. An n-twist along F is a discontinuous map on M induced from a diffeomorphism on $M_F-F_{-}$ which restricts to the identity map on $E\left(F_{+}\right)$ and the map on $N\left(F_{+}\right)$ conjugate to ${\sigma }_n$ or ${\tau }_n$ according as F is a sphere or not. We say that the n-twist is rational if $n\in \mathbb{Q}$. Figure 1 illustrates a rotational symmetry of $S^3$ with a setwise invariant sphere S, and its conjugate by a $1/2$-twist along S.

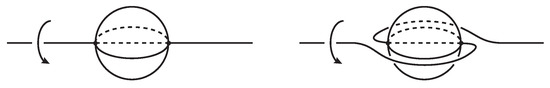
Figure 1. Conjugation by a $1/2$-twist along a sphere S.

Our main theorem is the following:

Theorem 1.1.

Let Γ be a spatial graph in $S^3$ with no companion knot. Suppose that $G_1$ and $G_2$ are symmetry groups of Γ such that

(1)

$G_1\left(\gamma \right)=G_2\left(\gamma \right)=\gamma$ for at least one component γ of Γ,

(2)

either Γ is non-splittable, or $G_1$ and $G_2$ are cyclic groups acting on Γ freely, and

(3)

$G_1$ and $G_2$ agree on $N\left(\Gamma \right)$.

Then there is a finite sequence of rational twists along incompressible spheres and tori in $E\left(\Gamma \right)$ whose composition conjugates $G_2$ to a symmetry group of Γ equivalent to $G_1$ relative to $N\left(\Gamma \right)$.

This paper is arranged as follows. In Section 2, we study symmetry groups of non-splittable spatial graph in terms of the equivariant JSJ decomposition of the exteriors. In Section 3, we establish a canonical version of the equivariant sphere theorem for the exteriors of spatial graphs with cyclic symmetry groups, and prove Theorem 1.1.

2. Non-splittable Case

For a non-splittable spatial graph $\Gamma$ in $S^3$ with a non-trivial symmetry group, there is a canonical method for splitting $E\left(\Gamma \right)$ equivariantly into geometric pieces by the loop theorem, the Dehn’s lemma, and the JSJ decomposition theorem (see [12,13,14]).

Let M be a Haken 3-manifold with incompressible boundary. The JSJ decomposition theorem and Thurston’s uniformization theorem [15] assert that there is a canonical way of splitting the pair $(M,\partial M)$ along a disjoint, non-parallel, essential annuli and tori into pieces $(M_i,F_i)$ each of which is one of the following four types:

(1)

$M_i$ is an I-bundle over a compact surface and $F_i$ is the $\partial I$-subbundle,

(2)

$M_i$ admits a Seifert fibration in which $F_i$ is fibered,

(3)

$\mathrm{int}{M}_i$ admits a complete hyperbolic structure of finite volume, and

(4)

the double of $(M_i,F_i-\mathrm{int}{\Phi }_i)$ along a non-empty compact submanifold ${\Phi }_i$ of $F_i$ is of type (3).

For a finite group action G on M, the fixed point set $\mathrm{Fix}\left(G\right)$ of G is the set of points in M each of which has the stabilizer G. The singular set $\mathrm{Sing}\left(G\right)$ of G is the set of points in M each of which has a non-trivial stabilizer.

Lemma 2.1.

Let T be a torus embedded in $S^3$. Suppose that $G_1$ and $G_2$ are orientation-preserving finite group actions on $S^3$ such that

(1)

$G_1\left(N\left(T\right)\right)=G_2\left(N\left(T\right)\right)=N\left(T\right)$,

(2)

$G_1$ and $G_2$ do not interchange the components of $\partial N\left(T\right)$, and

(3)

$G_1$ and $G_2$ agree on $\partial N\left(T\right)$.

Then a rational twist along a component of $\partial N\left(T\right)$ conjugates $G_2$ to a finite group action ${\widehat{G}}_2$ on $S^3$ such that the actions of $G_1$ and ${\widehat{G}}_2$ on $N\left(T\right)$ are equivalent relative to $\partial N\left(T\right)$.

Proof. 

It is enough by Lemma 2.4 of [11] to consider the case where the actions of $G_1$ and $G_2$ on $N\left(T\right)$ are not free. For each $G_i$, Theorem 2.1 of [16] implies that $N\left(T\right)\cong T\times I$ admits a $G_i$-invariant product structure ${\mathcal{P}}_i$, in which $\mathrm{Sing}\left(G_i\right)\cap N\left(T\right)$ consists of I-fibers. Since each element of $G_i$ takes a meridian of T to a meridian of T, the setwise stabilizer of each I-fiber is a trivial group or a 2-fold cyclic group. Therefore, the quotient space $N\left(T\right)/G_i$ admits the induced I-bundle structure over a 2-orbifold B with underlying surface F and n cone points of index two. Since T is a torus, the orbifold Euler characteristic ${\chi }_{\mathrm{orb}}\left(B\right)$ of B is calculated as follows (see [17]):

$${\chi }_{\mathrm{orb}}\left(B\right)=\chi \left(F\right)-n/2=0.$$

Since $n>0$, F is a sphere and $n=4$ holds.

Denote by $p_i:N\left(T\right)\to N\left(T\right)/G_i$ the projection map onto the quotient space for each i, and by $T_t$ the T-fiber $T\times \left\{t\right\}$ in ${\mathcal{P}}_1$. Connect the four cone points on $p_1\left(T_0\right)$ cyclically by a collection of arcs ${\overline{a}}_1$, ${\overline{a}}_2$, ${\overline{a}}_3$, and ${\overline{a}}_4$ with disjoint interiors. Each ${\overline{a}}_i$ lifts to an essential loop $a_i$ on $T_0$ such that $a_i$ and $a_j$ with $i\ne j$ are disjoint if $|j-i|=2$, and otherwise $a_i$ meets $a_j$ transversally in a point. Suppose that each $a_i$ is isotopic to a loop $b_i$ on $T_1$ along an annulus $B_i$ saturated by I-fibers in ${\mathcal{P}}_1$, and to a loop $c_i$ on $T_1$ along an annulus $C_i$ saturated by I-fibers in ${\mathcal{P}}_2$. Then the endpoints of each $p_2\left(c_i\right)$ is connected by $p_2\left(b_j\right)$ with $|i-j|=0$ or 2. Since the underlying surface of $p_2\left(T_1\right)$ is a sphere, ${\bigcup }_{i=1}^4{p}_2\left(c_i\right)$ is isotopic to ${\bigcup }_{i=1}^4{p}_2\left(b_i\right)$ relative to the cone points. Therefore, $G_2({\bigcup }_{i=1}^4{C}_i)$ is moved by an $G_2$-equivariant isotopy relative to $T_0$ so as to agree with $G_1({\bigcup }_{i=1}^4{B}_i)$ on $T_1$.

The I-bundle structures in ${\mathcal{P}}_2$ and ${\mathcal{P}}_1$ respectively induce orbifold isomorphisms ${\phi }_1:p_2\left(T_1\right)\to p_2\left(T_0\right)$ and ${\phi }_2:p_2\left(T_0\right)\to p_2\left(T_1\right)$ such that $\overline{h}={\phi }_2\circ {\phi }_1$ setwise preserves the loop ${\bigcup }_{i=1}^4{p}_2\left(b_i\right)$. The restriction of $\overline{h}$ on ${\bigcup }_{i=1}^4{p}_2\left(b_i\right)$ is isotopic relative to the cone points to the identity map or an involution. Since ${\bigcup }_{i=1}^4{p}_2\left(b_i\right)$ splits $p_2\left(T_1\right)$ into two disks with no cone point, ${\mathcal{P}}_2$ is deformed by a $G_2$-equivariant isotopy so that afterwards $\overline{h}$ is the identity map or an involution.

Take an $\overline{h}$-invariant $S^1$-bundle structure ${\mathcal{S}}_1$ on $p_2\left(T_1\right)-p_2(b_1\cup b_3)$ with respect to which $p_2\left(b_2\right)$ and $p_2\left(b_4\right)$ are cross sectional, and an $\overline{h}$-invariant $S^1$-bundle structure ${\mathcal{S}}_2$ on $p_2\left(T_1\right)-p_2(b_2\cup b_4)$ with respect to which every fiber in ${\mathcal{S}}_1$ splits into two cross sections. Then ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ induce a $G_2$-invariant product structure $S^1\times S^1$ on $T_1$. Let $h:T_1\to T_1$ be the lift of $\overline{h}$ which takes each $c_i$ to $b_i$. Then we have $h={\mathrm{Rot}}_{2\pi m}\times {\mathrm{Rot}}_{2\pi n}$ for some rational numbers m and n.

Assume $(m,n)\ne (0,0)$. Take a rational number $\gamma$ so that $\gamma m$ and $\gamma n$ are coprime integers. Then $\alpha \gamma m+\beta \gamma n=1$ holds for some integers $\alpha$ and $\beta$. Let $\rho :{\mathbb{R}}^2\to S^1\times S^1$ be the covering map given by $\rho (x,y)=({\mathrm{Rot}}_{2\pi x}(1,0),{\mathrm{Rot}}_{2\pi y}(1,0))$. Denote by $\phi$ the linear transformation on ${\mathbb{R}}^2$ represented by $\left(\begin{array}{cc}\alpha & \beta \\ -\gamma m& \gamma n\end{array}\right)$. Then the map $\rho \circ \phi \circ {\rho }^{-1}\in \mathrm{Diff}(S^1\times S^1)$ conjugates h to ${\mathrm{Rot}}_{2\pi /\gamma }\times {\mathrm{id}}_{S^1}$. Thus, h extends to $1/\gamma$-twist $\tau$ along $T_1$. Since h conjugates the action of $G_2$ on $T_1$ to itself, $\tau$ conjugates $G_2$ to a finite subgroup of $\mathrm{Diff}\left(S^3\right)$. Therefore, it is enough to consider the case $(m,n)=(0,0)$.

It is obvious that $h={\mathrm{Rot}}_{2\pi k}\times {\mathrm{Rot}}_{2\pi l}$ holds for any integers k and l. By verifying that, for some choice of k and l, the above argument applied to ${\mathrm{Rot}}_{2\pi k}\times {\mathrm{Rot}}_{2\pi l}$ makes $G_2({\bigcup }_{i=1}^4{C}_i)$ isotopic to $G_1({\bigcup }_{i=1}^4{B}_i)$ relative to $\partial N\left(T\right)$, we may assume that they agree.

By considering an isotopy of $N(T)$ relative to $\partial N(T)$ which takes ${\mathcal{P}}_2$ to ${\mathcal{P}}_1$ on $\mathrm{Sing}(G_1)\cap N(T)$, we may assume that $G_1$ and $G_2$ agree on $\mathrm{Sing}(G_1)\cap N(T)$. Note that $\mathrm{Sing}(G_1)\cap N(T)$ splits $G_1({\bigcup }_{i=1}^4{B}_i)$ into disks, and that $G_1({\bigcup }_{i=1}^4{B}_i)$ splits $N(T)$ into balls. Then the identity map on $p_2(\mathrm{Sing}(G_2)\cap N(T))$ extends to an orbifold isomorphism $\psi :p_2({\bigcup }_{i=1}^4{C}_i)\to p_1({\bigcup }_{i=1}^4{B}_i)$. Since the quotient space of any finite group action on $D^3$ is isomorphic to one of the orbifolds listed on page 191 of [15], $\psi$ and the identity map on $p_2(\partial N(T))$ extend to an orbifold isomorphism $p_2(N(T))\to p_1(N(T))$. Thus, $G_1$ and $G_2$ are equivalent relative to $\partial N(T)$. Hence, the conclusion follows. □

Lemma 2.2.

Let M be a Seifert manifold in $S^3$ with non-empty boundary, and F a non-empty closed submanifold of $\partial M$. Suppose that $G_1$ and $G_2$ are finite group actions on $S^3$ such that

(1)

$G_1\left(M\right)=G_2\left(M\right)=M$ and $G_1\left(F\right)=G_2\left(F\right)=F$,

(2)

$G_1\left(T\right)=G_2\left(T\right)=T$ for at least one component T of F,

(3)

$G_1$ and $G_2$ induce the same permutation on the set of the components of $\partial M$, and

(4)

$G_1$ and $G_2$ agree on F.

Then there is a finite sequence of rational twists along incompressible tori in M whose composition conjugates $G_2$ to a finite group action ${\widehat{G}}_2$ on $S^3$ such that the actions of $G_1$ and ${\widehat{G}}_2$ on M are equivalent relative to F.

Proof. 

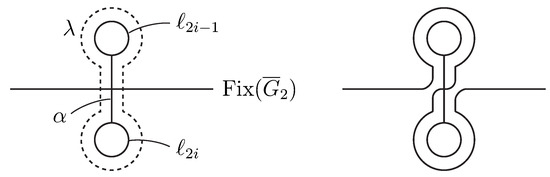
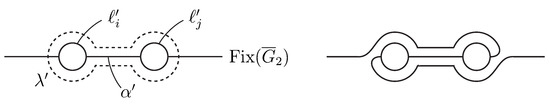
The case $M=D^2\times S^1$ and $F=\partial M$, the case $M=S^1\times S^1\times I$ and $F=\partial M$, and the case $M=S^1\times S^1\times I$ and $F\ne \partial M$ respectively follow from Lemma 2.1 of [11], Lemma 2.1 of this paper, and Theorem 8.1 of [16]. We therefore exclude these cases.

Denote by ${\bigcup }_k{\xi }_k$ the system of the exceptional fibers ${\xi }_k$ in M. Let $N\left({\xi }_k\right)$ be a fibered regular neighborhood of each ${\xi }_k$. It follows from Theorem 2.2 of [16] that each $G_i$ preserves some Seifert fibration ${\mathcal{S}}_i$ of M. Then the uniqueness of a Seifert fibration of M (see VI.18.Theorem of [12]) implies that ${\bigcup }_{k}N\left({\xi }_k\right)$ is isotopic to a setwise $G_i$-invariant fibered regular neighborhood of the system of exceptional fibers in ${\mathcal{S}}_i$. Since Lemma 3.1 of [11] implies that the orders of the exceptional fibers are pairwise coprime, we may assume that $G_1\left(N\left({\xi }_k\right)\right)=G_2\left(N\left({\xi }_k\right)\right)=N\left({\xi }_k\right)$ for each k. Therefore, it is enough by Lemma 2.1 of [11] to consider the case where M is a product $S^1$-bundle.

It follows from Theorem 2.1 of [16] that M admits a $G_1$-invariant product structure ${\mathcal{P}}_1$. If $F=\partial M$, M admits a $G_2$-invariant product structure ${\mathcal{P}}_2$ which agrees with ${\mathcal{P}}_1$ on F (see Theorem 2.3 of [16]). If $F\ne \partial M$, we see M as the quotient of the double $\overline{M}$ of M along $\partial M-F$ by ${\mathbb{Z}}_2$ generated by an orientation-reversing involution, and apply the same argument to the finite group action on $\overline{M}$, which is the extension of ${\mathbb{Z}}_2$ by $G_2$. Then we obtain a $G_2$-invariant product structure ${\mathcal{P}}_2$ of M which agrees with ${\mathcal{P}}_1$ on F.

By the uniqueness of the $S^1$-bundle structure of M (see VI.18.Theorem of [12]), there is a map $\phi \in \mathrm{Diff}\left(M\right)$ isotopic to the identity which takes the $S^1$-bundle structure induced by ${\mathcal{P}}_1$ to the $S^1$-bundle structure induced by ${\mathcal{P}}_2$. Modify $\phi$ in ${\mathcal{P}}_2$ by a fiber preserving isotopy in a fibered regular neighborhood of F so as to restrict to the identity map on F. By conjugating $G_2$ by $\phi$, we may therefore assume that ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ induce the same $S^1$-bundle structure of M.

Let $p:M\to B$ be the projection map onto the base surface B. Each $G_i$ induces a finite group action ${\overline{G}}_i$ on B. We consider B to be lying on $S^2$. Then each ${\overline{G}}_i$ extends to an action on $S^2$. Since ${\overline{G}}_1$ and ${\overline{G}}_2$ agree on $p\left(F\right)$, the quotient spaces $B/{\overline{G}}_1$ and $B/{\overline{G}}_2$ are orbifold isomorphic to suborbifolds of the same spherical orbifold listed on page 188 of [15]. We may assume that ${\overline{G}}_1$ and ${\overline{G}}_2$ are not orientation-preserving, otherwise the conclusion follows from Lemma 3.2 and Remark 3.3 of [11]. Then the assumption $G_1\left(T\right)=G_2\left(T\right)=T$ implies that each ${\overline{G}}_i$ is generated by the reflection of $S^2$ in a loop. Since $G_1$ and $G_2$ permute the components of $\partial M$ similarly, $\partial B$ consists of loops ${\ell }_1,\dots ,{\ell }_{2k},{\ell }_1^{\prime },\dots ,{\ell }_n^{\prime }$ such that

(1)

${\overline{G}}_1$ and ${\overline{G}}_2$ interchange ${\ell }_{2i-1}$ and ${\ell }_{2i}$ for $1\le i\le k$, and

(2)

${\overline{G}}_1$ and ${\overline{G}}_2$ setwise preserve ${\ell }_i^{\prime }$ for $1\le i\le n$.

Without loss of generality, ${\ell }_1^{\prime }=p\left(T\right)$. Denote by $\mathrm{Fix}\left({\overline{G}}_i\right)$ the fixed point circle of the action of each ${\overline{G}}_i$ on $S^2$. Suppose that each $\mathrm{Fix}\left({\overline{G}}_i\right)$ is equipped with an orientation, and splits B into two pieces $B_{i,1}$ and $B_{i,2}$ so that ${\ell }_1^{\prime }\cap B_{1,1}={\ell }_1^{\prime }\cap B_{2,1}$ and ${\ell }_1^{\prime }\cap B_{1,2}={\ell }_1^{\prime }\cap B_{2,2}$. We may assume without loss of generality that ${\ell }_{2i-1}\subset B_{1,1}$ and ${\ell }_{2i}\subset B_{1,2}$ for $1\le i\le k$, and that we meets ${\ell }_1^{\prime },\dots ,{\ell }_n^{\prime }$ in order as we go along $\mathrm{Fix}\left({\overline{G}}_1\right)$.

Suppose ${\ell }_{2i-1}\subset B_{2,2}$ and ${\ell }_{2i}\subset B_{2,1}$ for some i. By taking a proper arc on $B/{\overline{G}}_2$ connecting ${\ell }_{2i}/{\overline{G}}_2$ and $\mathrm{Fix}\left({\overline{G}}_2\right)/{\overline{G}}_2$, we obtain a setwise ${\overline{G}}_2$-invariant arc $\alpha$ on B which meets $\mathrm{Fix}\left({\overline{G}}_2\right)$ in a point and connects ${\ell }_{2i-1}$ and ${\ell }_{2i}$. Then $\mathrm{Fix}\left({\overline{G}}_2\right)$ is modified by the half twist along the loop $\partial N({\ell }_{2i-1}\cup {\ell }_{2i}\cup \alpha )\cap \mathrm{int}B$, denoted by $\lambda$, so that afterwards ${\ell }_{2i-1}\subset B_{2,1}$ and ${\ell }_{2i}\subset B_{2,2}$, as illustrated in Figure 2. The argument presented for the proof of Lemma 2.1 implies that this modification is realized by a $1/2$-twist along the torus $p^{-1}\left(\lambda \right)$ which conjugates $G_2$ to a subgroup of $\mathrm{Diff}\left(S^3\right)$. We may therefore assume ${\ell }_{2i-1}\subset B_{2,1}$ and ${\ell }_{2i}\subset B_{2,2}$ for $1\le i\le k$.

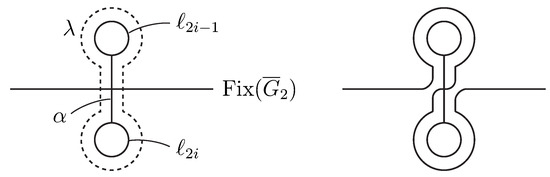
Figure 2. Half twist along $\lambda$.

Suppose that ${\ell }_i^{\prime }$ and ${\ell }_j^{\prime }$ are connected by an arc ${\alpha }^{\prime }$ in $\mathrm{Fix}\left({\overline{G}}_2\right)\cap B$. Then $\mathrm{Fix}\left({\overline{G}}_2\right)$ is modified by the half twists along the loop ${\lambda }^{\prime }=\partial N({\ell }_i^{\prime }\cup {\ell }_j^{\prime }\cup {\alpha }^{\prime })\cap \mathrm{int}B$ so as to meet ${\ell }_i^{\prime }$ and ${\ell }_j^{\prime }$ in the reverse order, as illustrated in Figure 3, which is realized by the conjugation of $G_2$ by a $1/2$-twist along the torus $p^{-1}\left({\lambda }^{\prime }\right)$, as before. Since every permutation on the set $\{{\ell }_2^{\prime },\dots ,{\ell }_n^{\prime }\}$ is a product of transpositions, we may assume that $\mathrm{Fix}\left({\overline{G}}_2\right)$ meets ${\ell }_1^{\prime },\dots ,{\ell }_n^{\prime }$ in order. Moreover, we can change the order in which $\mathrm{Fix}\left({\overline{G}}_2\right)$ meets the two points in ${\ell }_i^{\prime }\cap \mathrm{Fix}\left({\overline{G}}_2\right)$ by the half twists along ${\ell }_i^{\prime }$, which is also realized by a $1/2$-twist along the torus $p^{-1}\left({\ell }_i^{\prime }\right)$. We may therefore assume that ${\overline{G}}_2$ is equivalent to ${\overline{G}}_1$ relative to $\partial B$.

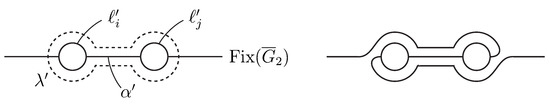
Figure 3. Half twist along ${\lambda }^{\prime }$.

Now we may assume ${\overline{G}}_1={\overline{G}}_2$. Take a map $h\in \mathrm{Diff}\left(M\right)$ which restricts to the identity map on F and takes ${\mathcal{P}}_2$ to ${\mathcal{P}}_1$ setwise preserving every $S^1$-fiber. It is easy to verify that h is extendable to a map in $\mathrm{Diff}\left(S^3\right)$. Hence, the conclusion follows by conjugating $G_2$ by h. □

Lemma 2.3.

Let M be a compact connected 3-manifold in $S^3$ with non-empty boundary whose interior admits a complete hyperbolic structure of finite volume, and F a non-empty closed submanifold of $\partial M$. Suppose that $G_1$ and $G_2$ are finite group actions on $S^3$ such that

(1)

$G_1\left(M\right)=G_2\left(M\right)=M$ and $G_1\left(F\right)=G_2\left(F\right)=F$,

(2)

$G_1$ and $G_2$ induce the same permutation on the set of the components of $\partial M$, and

(3)

$G_1$ and $G_2$ agree on F.

Then there is a sequence of rational twists along tori in F whose composition conjugates $G_2$ to a finite group action ${\widehat{G}}_2$ such that the actions of $G_1$ and ${\widehat{G}}_2$ on M is equivalent relative to F.

Proof. 

It follows from Theorem 5.5 of [18] that $\mathrm{int}M$ admits two complete hyperbolic structures of finite volume, one is $G_1$-invariant and the other is $G_2$-invariant. Mostow’s rigidity theorem [15] implies that complete hyperbolic structures of finite volume on $\mathrm{int}M$ are unique up to isometry representing the identity map on $\mathrm{Out}\left({\pi }_1\left(M\right)\right)$. We may therefore assume that $\mathrm{int}M$ is endowed with the $G_1$-invariant hyperbolic structure, and that $G_2$ is conjugate to an isometric action $G_2^{\prime }$ by $h\in \mathrm{Diff}\left(M\right)$ which is isotopic to the identity map.

Next, we are going to modify h in a regular neighborhood of F so as to restrict to the identity map on F. It follows from Propostition D.3.18 of [19] that F consists of tori. Let $h_t$ be an isotopy from h to the identity map. Denote by ${\overline{G}}_2$ the finite group action on $F\times I$ whose restriction on $F\times \left\{t\right\}$ is induced from the finite group action on F given by the conjugate of $G_2$ by $h_t$. In particular, the actions of ${\overline{G}}_2$ on $F\times \left\{0\right\}$ and $F\times \left\{1\right\}$ are respectively given by $G_2^{\prime }$ and $G_2$. Note that ${\overline{G}}_2$ preserves the product structure $F\times \partial I$, and that we can embed $F\times I$ in $S^3$ so that ${\overline{G}}_2$ extends to a finite group action on $S^3$.

We consider the partition of the set of the components of F into the orbits under the permutation induced by $G_2$. Suppose that the orbits are represented by $T_1,\dots ,T_n$. Lemma 2.1 implies that a rational twist along $T_i\times \left\{1\right\}$ conjugates the setwise stabilizer of $T_i\times I$ in ${\overline{G}}_2$ so that the action on $T_i\times I$ is equivalent relative to $T_i\times \partial I$ to the action which preserves the product structure. Suppose that the rational twists along the tori in $F\times \left\{1\right\}$ are equivariantly induced from those along $T_1\times \left\{1\right\},\dots ,T_n\times \left\{1\right\}$. By conjugating ${\overline{G}}_2$ by their composition, it is equivalent relative to $F\times \partial I$ to the action which preserves the product structure. This implies that h is modified equivariantly so as to restrict to the identity map on F.

Suppose that $g_1\in G_1$ and $g_2\in G_2$ agree on F. Then $g_1\circ g_2^{-1}$ restricts to the identity map on F. Since the isometry group of $\mathrm{int}M$ is finite (see [15]), Newman’s theorem [20] implies $g_1=g_2$. Hence, $G_1$ and $G_2^{\prime }$ agree on M. This completes the proof. □

Lemma 2.4.

Let M be a compact connected 3-manifold in $S^3$ with non-empty boundary such that the double $\overline{M}$ of M along a non-empty compact submanifold Φ of $\partial M$ admits a complete hyperbolic structure of finite volume in its interior. Let F be a closed submanifold of $\partial M$ containing Φ. Suppose that $G_1$ and $G_2$ are finite group actions on $S^3$ such that

(1)

$G_1\left(M\right)=G_2\left(M\right)=M$ and $G_1\left(F\right)=G_2\left(F\right)=F$,

(2)

$G_1$ and $G_2$ induce the same permutation on the set of the components of $\partial M$, and

(3)

$G_1$ and $G_2$ agree on F.

Then there is a finite sequence of rational twists along tori in F whose composition conjugates $G_2$ to a finite group action ${\widehat{G}}_2$ such that the actions of $G_1$ and ${\widehat{G}}_2$ on M are equivalent relative to F.

Proof. 

We see M as the quotient of $\overline{M}$ by ${\mathbb{Z}}_2$ generated by an orientation-reversing involution. Each $G_i$ induces a finite group action ${\overline{G}}_i$ on $\overline{M}$ which is an extension of ${\mathbb{Z}}_2$ by $G_i$. As in the proof of Lemma 2.3, we consider $\mathrm{int}\overline{M}$ endowed with a ${\overline{G}}_1$-invariant hyperbolic structure. Then some $\overline{h}\in \mathrm{Diff}\left(\overline{M}\right)$, which is isotopic to the identity map, conjugates ${\overline{G}}_2$ to an isometric action ${\overline{G}}_2^{\prime }$. Clearly, $\Phi$ meets $\mathrm{int}\overline{M}$ in a totally geodesic surface, and therefore $\overline{h}\left(\Phi \right)=\Phi$ holds.

Suppose that ${\overline{g}}_1\in {\overline{G}}_1$ and ${\overline{g}}_2\in {\overline{G}}_2^{\prime }$ respectively induce $g_1\in G_1$ and $g_2\in G_2$ which agree on F. Then ${\overline{g}}_1^{-1}\circ {\overline{g}}_2$ restricts to an isometry on each component ${\Phi }_i$ of $\Phi$, which is a compact surface of negative Euler characteristic (see Propostition D.3.18 of [19]). Since ${\overline{g}}_1^{-1}\circ {\overline{g}}_2$ is trivial in $\mathrm{Out}\left({\pi }_1\left({\Phi }_i\right)\right)$, ${\overline{g}}_1$ and ${\overline{g}}_2$ agree on ${\Phi }_i$. Therefore, [20] implies $g_1=g_2$. Hence, some $h\in \mathrm{Diff}\left(M\right)$, which setwise preserves $\Phi$ and is isotopic to the identity map, conjugates the action of $G_1$ on M to $G_2$.

It follows from Proposition D.3.18 of [19] that $F-\Phi$ consists of tori. As in the proof of Lemma 2.3, modify h in $N(F-\Phi )$ by rational twists along tori in $F-\Phi$ so that afterwards h restricts to the identity map on $F-\Phi$ and conjugates the action of $G_1$ on M to $G_2$. Moreover, we may assume by Lemma 2.3 of [11] that h restricts to the identity map on $\Phi$. Since h extends to an automorphism of $S^3$ which is diffeomorphic outside M, the conclusion follows. □

Proposition 2.5.

Theorem 1.1 is true, if Γ is non-splittable.

Proof. 

The equivariant loop theorem (see Chapter VII of [15] and [21]) implies that there is a $G_1$-invariant system ${\mathcal{D}}_1$ of disjoint disks properly embedded in $E\left(\Gamma \right)$ which splits $E\left(\Gamma \right)$ into pieces with incompressible boundary. The equivariant Dehn’s lemma [21,22] implies that the boundary loops of ${\mathcal{D}}_1$ bound a $G_2$-invariant system ${\mathcal{D}}_2$ of disjoint disks properly embedded in $E\left(\Gamma \right)$. Since $\Gamma$ is non-splittable, $E\left(\Gamma \right)$ is irreducible. Therefore, there is an isotopy of $E\left(\Gamma \right)$ relative to $\partial E\left(\Gamma \right)$ which takes ${\mathcal{D}}_2$ to ${\mathcal{D}}_1$. Since any finite group action on $D^2$ is orthogonal [15], we may assume that $G_1$ and $G_2$ agree on ${\mathcal{D}}_1$. Moreover, the induced actions on the balls obtained by splitting $E\left(\Gamma \right)$ along ${\mathcal{D}}_1$ are equivalent relative to the boundary (see [15]). Therefore, it is enough to consider the case where $E\left(\Gamma \right)$ is a Haken manifold with incompressible boundary.

We may assume by the equivariant JSJ decomposition theorem (see Theorem 8.6 of [16]) and by the uniqueness of the JSJ decomposition [13,14] that there is a $G_1$-invariant and $G_2$-invariant system $\mathcal{T}$ of essential annuli and tori in $E\left(\Gamma \right)$ realizing the canonical JSJ decomposition of the pair $\left(E\right(\Gamma ),\partial E(\Gamma \left)\right)$.

The argument presented for the proof of Proposition 3.10 of [11] implies that some $h\in \mathrm{Diff}\left(S^3\right)$, which is isotopic to the identity map relative to $N\left(\Gamma \right)$, conjugates $G_2$ to a finite group action which agree with $G_1$ on the annuli in $\mathcal{T}$. We may therefore assume that $\mathcal{T}$ contains no annuli.

The rest of the proof proceeds by induction on the number of tori in $\mathcal{T}$. Take a piece $M_k$ attaching $\partial E\left(\Gamma \right)$. By Lemmas 2.2, 2.3 and 2.4, it is enough to consider the case where $G_2$ agrees with $G_1$ on $G_1\left(M_k\right)$. Moreover, we may assume by Lemma 2.1 that $G_1$ and $G_2$ agree on the components of $\mathrm{cl}(E\left(\Gamma \right)-G_1\left(M_k\right))$ each of which is a product I-bundle over a torus. Hence, the conclusion follows by the induction hypothesis. □

3. Possibly Splittable Case

For a symmetry group G of a splittable spatial graph $\Gamma$ in $S^3$, there is a setwise G-invariant system $\mathcal{S}$ of spheres realizing the prime factorization of $E\left(\Gamma \right)$ (see [23]). However, $\mathcal{S}$ is not unique in contrast to the JSJ decomposition of a Haken 3-manifold. If some component of $\Gamma$ is setwise invariant and every essential sphere in $E\left(\Gamma \right)$ has a trivial stabilizer, there is a canonical choice of $\mathcal{S}$ (see [11]). We first prove that this is possible also in the setting of Theorem 1.1.

Lemma 3.1.

Let Γ be a splittable spatial graph in $S^3$. Suppose that $G_1$ and $G_2$ are symmetry groups of Γ such that

(1)

$G_1\left(\gamma \right)=G_2\left(\gamma \right)=\gamma$ for at least one component γ of Γ,

(2)

$G_1$ and $G_2$ are cyclic groups acting on Γ freely, and

(3)

$G_1$ and $G_2$ agree on $N\left(\Gamma \right)$.

Then each $G_i$ admits a setwise $G_i$-invariant system ${\mathcal{B}}_i$ of disjoint balls in $S^3$ not containing γ such that each $\partial {\mathcal{B}}_i$ realizes the prime factorization of $E\left(\Gamma \right)$. Moreover, for some choice of ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$, there is a finite sequence of rational twists along incompressible tori in $E\left(\Gamma \right)-\mathrm{int}{\mathcal{B}}_2$ and a map in $\mathrm{Diff}\left(S^3\right)$ which restricts to the identity map on $N\left(\Gamma \right)$ whose composition conjugates the action of $G_2$ on $S^3-\mathrm{int}{\mathcal{B}}_2$ to the action of $G_1$ on $S^3-\mathrm{int}{\mathcal{B}}_1$.

Proof. 

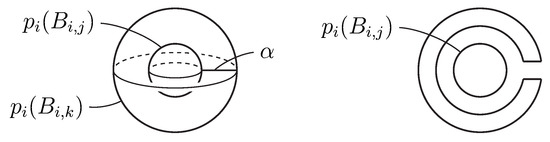
Denote by ${\Gamma }_{\gamma }$ the non-splittable spatial subgraph of $\Gamma$ containing $\gamma$ which is obtained by the prime factorization of $E\left(\Gamma \right)$. It follows from the equivariant sphere theorem [23] that each $G_i$ admits a setwise $G_i$-invariant system ${\mathcal{S}}_i=S_{i,1}\cup \cdots \cup S_{i,n}$ of disjoint, non-parallel, essential spheres in $E\left(\Gamma \right)$ realizing the prime factorization. Suppose that each $S_{i,j}$ bounds a ball $B_{i,j}$ disjoint from $\gamma$. Note that $\mathrm{Sing}\left(G_i\right)$ avoids $B_{i,j}$ or meets $B_{i,j}$ in a trivial 1-string tangle (see [15]).

Suppose $B_{i,j}\subset B_{i,k}$ for some distinct j and k. Denote by $p_i:S^3\to S^3/G_i=S^3$ the projection map onto the quotient space. Take an arc $\alpha$ properly embedded in $p_i(B_{i,k}-\mathrm{int}{B}_{i,j})$ which connects $p_i(\partial B_{i,k})$ and $p_i(\partial B_{i,j})$. Suppose that $\alpha$ lies on $p_i\left(\mathrm{Sing}\left(G_i\right)\right)$ if $\mathrm{Sing}\left(G_i\right)$ connects $\partial B_{i,j}$ and $\partial B_{i,k}$. By replacing $B_{i,j}$ with another ball in $\mathrm{int}{B}_{i,k}$ if necessary, $\alpha$ meets ${\mathcal{S}}_i$ in its endpoints. By drilling into $p_i\left(B_{i,k}\right)$ along $\alpha \cup p_i\left(B_{i,j}\right)$, $B_{i,k}$ is deformed to a ball disjoint from $B_{i,j}$, as illustrated in Figure 4 in which the result of the deformation is presented in a cross-sectional view. By a finite repetition of this operation, we obtain a system ${\mathcal{B}}_i=B_{i,1}\cup \cdots \cup B_{i,n}$ of disjoint balls. This proves the first half of the lemma. Without loss of generality, $\Gamma \cap B_{2,j}=\Gamma \cap B_{1,j}$ for $1\le j\le n$.

Figure 4. Modification of $p_i\left(B_{i,k}\right)$ which makes $p_i\left(B_{i,k}\right)$ disjoint from $p_i\left(B_{i,j}\right)$.

Proposition 2.5 implies that there is a finite sequence of rational twists along incompressible tori in $E\left({\Gamma }_{\gamma }\right)$ whose composition h conjugates $G_2$ to a symmetry group ${\widehat{G}}_2$ of ${\Gamma }_{\gamma }$ equivalent to $G_1$ relative to $N\left({\Gamma }_{\gamma }\right)$. By a $G_2$-equivariant isotopy, we may assume that these incompressible tori are disjoint from ${\mathcal{B}}_2$. Then h restricts to the identity map on ${\mathcal{B}}_2$. Suppose that $H\in \mathrm{Diff}(S^3,{\Gamma }_{\gamma })$ realizes the above equivalence of ${\widehat{G}}_2$ and $G_1$. Then H takes $\mathrm{Sing}({\widehat{G}}_2)$ to $\mathrm{Sing}(G_1)$. As a consequence of the affirmative answer to the Smith conjecture [15], $\mathrm{Sing}\left(G_1\right)$ is either an empty set, a trivial knot, or a Hopf link whose components have different indices. Suppose that the orientation of $\mathrm{Sing}\left(G_1\right)$ is induced from the orientation of $\mathrm{Sing}({\widehat{G}}_2)$ by H.

Suppose that $B_{2,j}$ and $B_{2,k}$ are connected by an arc $\beta$ in $\mathrm{Sing}({\widehat{G}}_2)-\mathrm{int}{\mathcal{B}}_2$, and that $\mathrm{Sing}({\widehat{G}}_2)$ meets $B_{2,k}$ in an arc $\delta$. Then $B_{2,k}$ can be modified by a ${\widehat{G}}_2$-equivariant deformation along $\beta \cup B_{2,j}$ similar to the inverse of that mentioned above so as to contain $B_{2,j}$. Moreover, it can be deformed along $\beta \cup \delta \cup B_{2,j}$ so as to avoid $B_{2,j}$ again, as illustrated in Figure 5. Note that this operation changes the order in which the circle in $\mathrm{Sing}({\widehat{G}}_2)$ containing $\beta$ meets the balls in $\{B_{2,1},\dots ,B_{2,n}\}$.

Figure 5. Modification of $B_{2,k}$ realizing the transposition of $B_{2,j}$ and $B_{2,k}$.

Let C be a component of $\mathrm{Sing}\left(G_1\right)$. Without loss of generality, C meets $B_{1,1},\dots ,B_{1,r}$ in order, and avoids $B_{1,r+1},\dots ,B_{1,n}$. Since $G_1$ and $G_2$ agree on $N\left(\Gamma \right)$, the component $H^{-1}\left(C\right)$ of $\mathrm{Sing}({\widehat{G}}_2)$ meets $B_{2,1},\dots ,B_{2,r}$ possibly not in order. Since every permutation on the set $\{B_{2,1},\dots ,B_{2,r}\}$ is a product of transpositions realized by the above operation, we may assume that $H^{-1}\left(C\right)$ meets $B_{2,1},\dots ,B_{2,r}$ in order. Apply this argument to each component of $\mathrm{Sing}\left(G_1\right)$. Since each $\partial {\mathcal{B}}_i$ realizes the prime factorization of $E\left(\Gamma \right)$, we can modify H by a $G_1$-equivariant isotopy relative to $N\left({\Gamma }_{\gamma }\right)$ so that we have $H(\mathrm{Sing}({\widehat{G}}_2))=\mathrm{Sing}(G_1)$ and $H\left(B_{2,j}\right)=B_{1,j}$ for each j. Thus, H is modified so as to conjugate the action of ${\widehat{G}}_2$ on $S^3-\mathrm{int}{\mathcal{B}}_2$ to the action of $G_1$ on $S^3-\mathrm{int}{\mathcal{B}}_1$.

After this modification, H restricts to an orientation-preserving homeomorphism on ${\mathcal{B}}_1$. Therefore, $H(\Gamma \cap {\mathcal{B}}_2)$ is ambient isotopic to $\Gamma \cap {\mathcal{B}}_1$ in ${\mathcal{B}}_1$. Hence, H can be modified in ${\mathcal{B}}_1$ so as to restrict to the identity map on $N\left(\Gamma \right)$. This completes the proof. □

Lemma 3.2.

Suppose that $G_1$ and $G_2$ are orientation-preserving finite cyclic group actions on $S^2\times I$ such that

(1)

$G_1$ and $G_2$ do not interchange the components of $S^2\times \partial I$, and

(2)

$G_1$ and $G_2$ agree on $S^2\times \partial I$.

Then a rational twist along $S^2\times \left\{1\right\}$ conjugates $G_2$ to a finite group action equivalent to $G_1$ relative to $S^2\times \partial I$.

Proof. 

It is enough to consider the case where $G_1$ is not trivial. It follows from the remark after Theorem 8.1 of [16] that $S^2\times I$ admits a $G_1$-invariant product structure ${\mathcal{P}}_1$ and a $G_2$-invariant product structure ${\mathcal{P}}_2$. Since the actions of $G_1$ and $G_2$ on $S^2\times \left\{0\right\}$ are conjugate to a rotation of $S^2$ (see [15]), each $\mathrm{Fix}\left(G_i\right)$ consists of two I-fibers in ${\mathcal{P}}_i$. Since $G_1$ and $G_2$ agree on $S^2\times \partial I$, we have $\partial \mathrm{Fix}\left(G_1\right)=\partial \mathrm{Fix}\left(G_2\right)$.

Denote by $p_i:S^2\times I\to S^2\times I/G_i$ the projection map onto the quotient space for each i, and by $S_t$ the $S^2$-fiber $S^2\times \left\{t\right\}$ in ${\mathcal{P}}_1$. Connect the two cone points of $p_1\left(S_0\right)$ by an arc $\overline{a}$ embedded in $p_1\left(S_0\right)$. Then $p_1^{-1}\left(\overline{a}\right)$ is a spatial ${\theta }_n$-curve consisting of two vertices on the fixed points and $n>1$ edges each connecting them. Denote by $A_i$ the branched surface consisting of I-fibers in ${\mathcal{P}}_i$ attaching $p_1^{-1}\left(\overline{a}\right)$ for each i. Then each $p_1(A_i\cap S_1)$ is an arc connecting the two cone points on $p_1\left(S_1\right)$. Since the underlying space of $p_1\left(S_1\right)$ is a sphere, $p_1(A_2\cap S_1)$ is isotopic to $p_1(A_1\cap S_1)$ relative to the cone points. Therefore, $A_2$ is deformed by a $G_2$-equivariant isotopy relative to $S_0$ so that $A_1\cap S_1=A_2\cap S_1$. There are two cases depending on whether $\mathrm{Fix}\left(G_1\right)$ and $\mathrm{Fix}\left(G_2\right)$ are isotopic relative to the endpoints or not.

Assume that $\mathrm{Fix}\left(G_1\right)$ and $\mathrm{Fix}\left(G_2\right)$ are isotopic relative to the endpoints. Then ${\mathcal{P}}_2$ is deformed by an isotopy relative to $S^2\times \partial I$ so as to agree with ${\mathcal{P}}_1$ on a setwise $G_1$-invariant tubular neighborhood $N\left(\mathrm{Fix}\left(G_1\right)\right)$ saturated in the I-bundle structure induced from ${\mathcal{P}}_1$. Since each $A_i$ meets the solid torus $(S^2\times I)-\mathrm{int}N\left(\mathrm{Fix}\left(G_1\right)\right)$ in the system of meridian disks, $A_2$ is moved to $A_1$ by an isotopy relative to $(S^2\times \partial I)\cup N\left(\mathrm{Fix}\left(G_1\right)\right)$. We may therefore assume $A_1=A_2$, and that $G_1$ and $G_2$ agree on $N\left(\mathrm{Fix}\left(G_1\right)\right)$. Then the I-bundle structures in ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ respectively induce the orbifold isomorphisms ${\phi }_1:p_2\left(S_1\right)\to p_2\left(S_0\right)$ and ${\phi }_2:p_2\left(S_0\right)\to p_1\left(S_1\right)$ such that ${\phi }_2\circ {\phi }_1$ is isotopic to the identity map by an isotopy relative to the cone points which setwise preserves $p_2(A_2\cap S_1)$. Then we can deform ${\mathcal{P}}_2$ by an isotopy on $p_2(S^2\times I)$ relative to $p_2\left(S_0\right)$ which setwise preserves $p_2(A_2\cap S_1)$ so that ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ induce the same $\partial I$-bundle structure on $S^1\times \partial I$. Hence, the diffeomorphism of $S^2\times I$ which takes ${\mathcal{P}}_2$ to ${\mathcal{P}}_1$ induces the equivalence of $G_1$ and $G_2$ relative to $S^2\times \partial I$, as required.

Assume that $\mathrm{Fix}\left(G_1\right)$ and $\mathrm{Fix}\left(G_2\right)$ are not isotopic relative to the endpoints. Let $h:S_1\to S_1$ be a lift of an orientation-preserving involution on $p_1\left(S_1\right)$ which interchanges the cone points. Then h is a diffeomorphism isotopic to the identity map which conjugates the action of $G_2$ on $S_1$ to itself and is realized by a $1/2$-twist along the sphere $S_1$. We may therefore assume that $\mathrm{Fix}\left(G_1\right)$ and $\mathrm{Fix}\left(G_2\right)$ are isotopic relative to the endpoints. Hence, the conclusion follows by the argument presented for the previous case. □

Proof of Theorem 1.1.

It is enough by Proposition 2.5 to prove the theorem in the case where $\Gamma$ is splittable. Then $G_1$ and $G_2$ are cyclic groups acting on $\Gamma$ freely. We may assume by Lemma 3.1 that there is a setwise $G_1$-invariant and setwise $G_2$-invariant system $\mathcal{B}$ of disjoint balls in $S^3$ not containing $\gamma$ such that $\partial \mathcal{B}$ realizes the prime factorization of $E\left(\Gamma \right)$, and that $G_1$ and $G_2$ agree on $E\left(\mathcal{B}\right)$.

Suppose that $\mathcal{B}$ consists of balls $B_1,\dots ,B_n$. Each $\Gamma \cap B_i$ is a non-empty, non-splittable, spatial subgraph of $\Gamma$. By applying Proposition 2.5 to the actions of the setwise stabilisers of $B_i$ in $G_1$ and $G_2$ on $B_i$, we may assume that $G_1$ and $G_2$ agree on $E(\partial \mathcal{B})$. Hence the conclusion follows by applying Lemma 3.2 to the actions of $G_1$ and $G_2$ on $N(\partial \mathcal{B})$ equivariantly. □

Remark 3.3.

Theorem 1.1 requires the spatial graph $\Gamma$ to have no companion knot, and the symmetry groups $G_1$ and $G_2$ of $\Gamma$ to act on $\Gamma$ freely if $\Gamma$ is splittable. These requirements are needed because of the following examples.

(1)

Suppose that $\Gamma$ is a granny knot. Then $\Gamma$ has two companion knots $K_1$ and $K_2$, both of which are trefoil knots. We obtain $E\left(K_1\right)$, $E\left(K_2\right)$, and a 2-fold composing space by the JSJ decomposition of $E\left(\Gamma \right)$. Figure 6 illustrates ${\mathbb{Z}}_2$-symmetries $G_1$ and $G_2$ of $\Gamma$ such that $G_2$ interchanges $E\left(K_1\right)$ and $E\left(K_2\right)$ but $G_1$ does not. By conjugating $G_1$ by a map in $\mathrm{Diff}\left(S^3\right)$ which moves $N\left(\Gamma \right)$ in the longitudinal direction, $G_1$ and $G_2$ are not equivalent but agree on $\partial N\left(\Gamma \right)$. Moreover, any rational twists along incompressible tori in $E\left(\Gamma \right)$ cannot change the induced symmetries of $E\left(K_1\right)$ and $E\left(K_2\right)$, since the trefoil knot exterior is atoroidal.

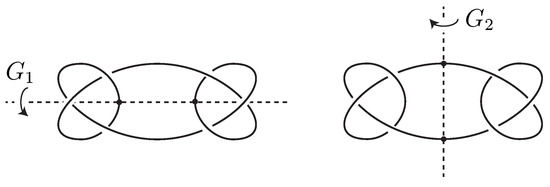Figure 6. ${\mathbb{Z}}_2$-symmetries of a spatial graph with companion knots.

(2)

Suppose that $\Gamma$ is a spatial graph which splits into non-splittable spatial graphs ${\gamma }_1$, ${\gamma }_2$ and ${\gamma }_3$, as illustrated in Figure 7, where ${\gamma }_1$ is a spatial $\theta$-curve. According to the choice of two edges of ${\gamma }_1$, we obtain a trefoil knot $K_1$, a figure-eight knot $K_2$, or their connected sum $K_1\#K_2$. Then any map in $\mathrm{Diff}(S^3,\Gamma )$ does not permute these edges. The ${\mathbb{Z}}_2$-symmetries $G_1$ and $G_2$ of $\Gamma$ illustrated in Figure 7 are not equivalent, since there is no map in $\mathrm{Diff}(S^3,\Gamma )$ which takes $\mathrm{Sing}\left(G_1\right)$ to $\mathrm{Sing}\left(G_2\right)$ and interchanges ${\gamma }_2$ and ${\gamma }_3$. Moreover, we cannot perform rational twists along incompressible spheres and tori in $E\left(\Gamma \right)$ to make $G_2$ equivalent to $G_1$, since any setwise $G_2$-invariant incompressible sphere in $E\left(\Gamma \right)$ separates ${\gamma }_2$ and ${\gamma }_3$.

Figure 7. ${\mathbb{Z}}_2$-symmetries which are not free on a splittable spatial graph.