Symmetry as an Intrinsically Dynamic Feature
Abstract
:1. Introduction
2. Symmetry Constancy



2.1. Dynamics Through Erosion



- When going from a regular pattern to a modified version of it, any perturbation gives a signature. Moreover, experiments about ratios of pattern size over defect size, or about the number of defects, allow precision assessment.
- Curve variations follow, at least in a qualitative manner, tendencies of symmetry variations with the angle: constancy, monotony, smoothness etc.
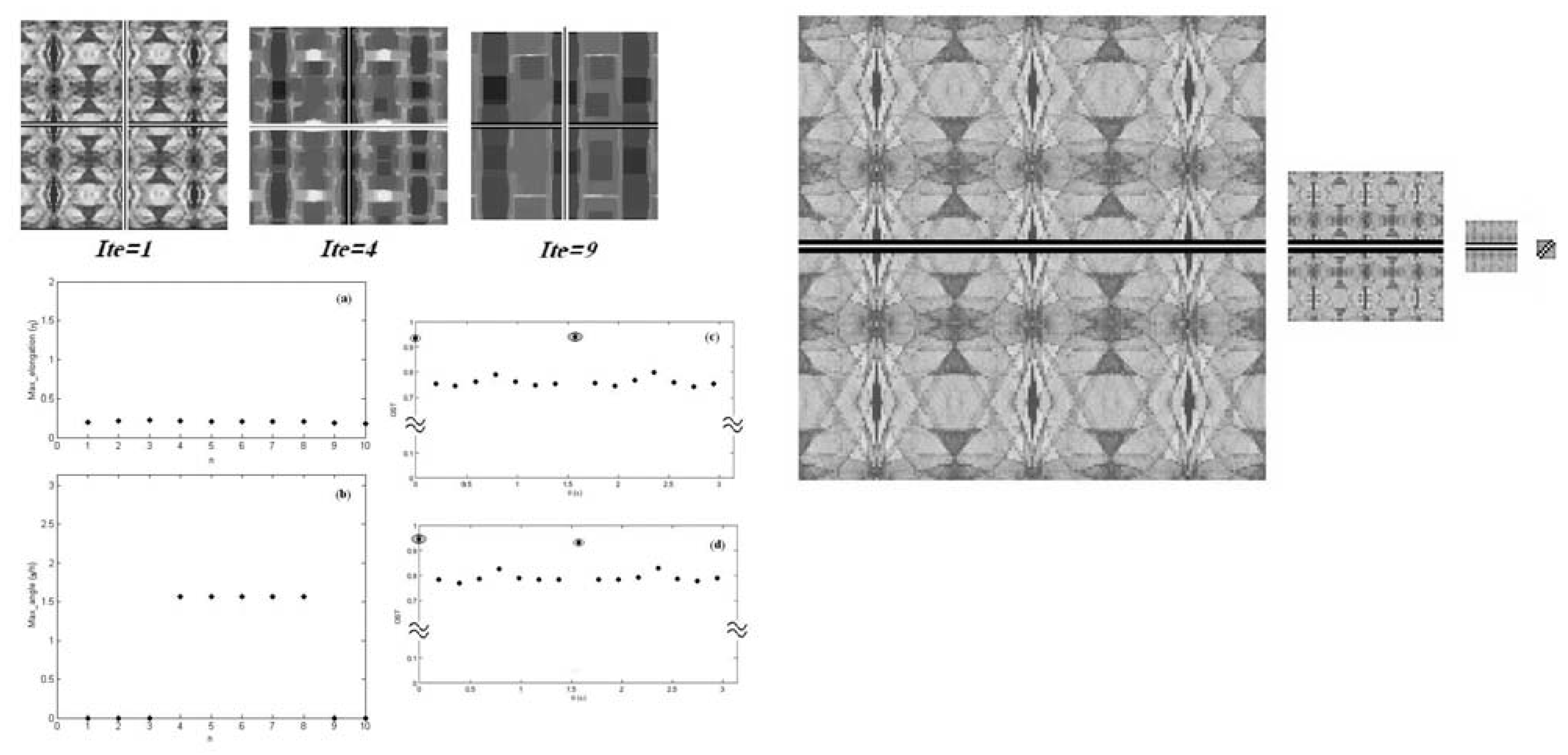
2.2. Dynamics Through Multi-Resolution
- direct: building the pyramid and running the symmetry operator S layer by layer;
- indirect: running S at the bottom (image) and then building the pyramid from these values;
- hierarchical: recursively running S to build the pyramid.



3. Capturing Symmetry
- a model is made explicit to support optimality claims;
- this model puts forward:
- the invariance to the transform again in relying on explicit comparison between the pattern and a transformed version of it;
- the distance that could evolve into approximate comparison for similarity;
- pattern inclusion introduces set operations (such as Minkowski’s), associating as a result logic and geometry.
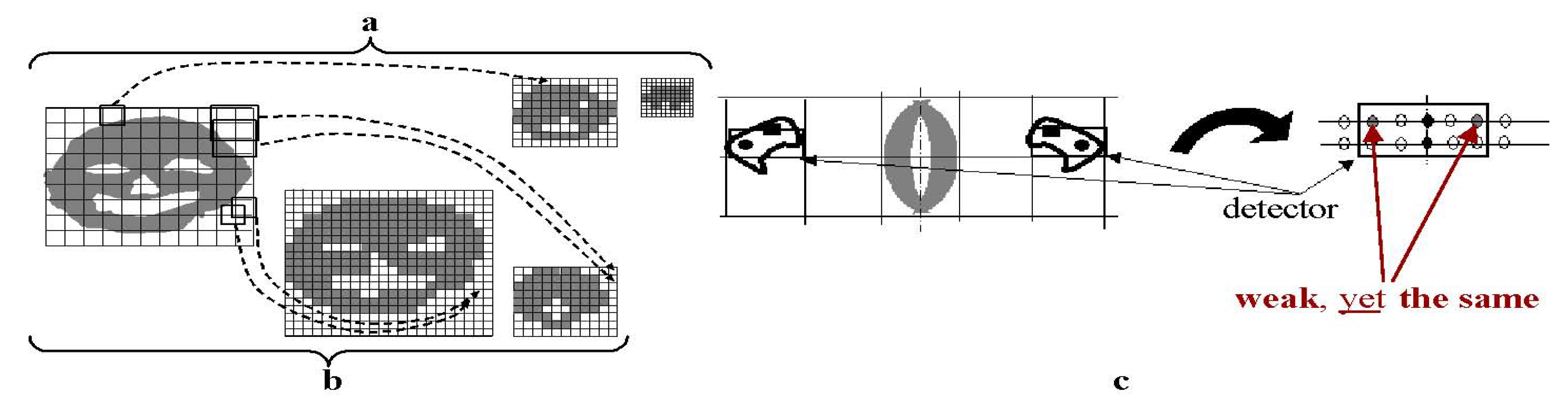
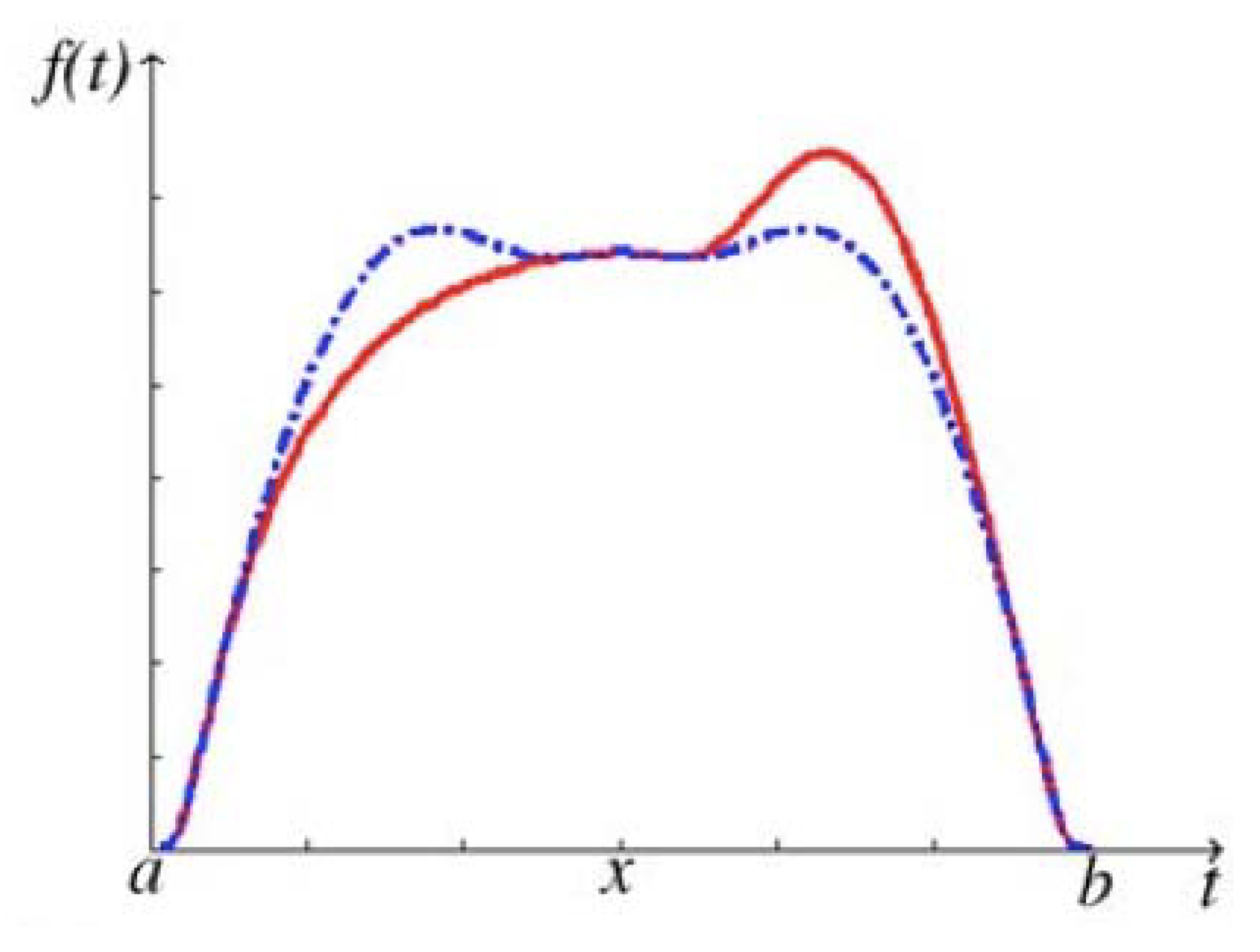
3.1. Optimal Symmetry Detection



 and that gives a computing process by the same token. It is based on convolution i.e., the map product of symmetry and correlation.
and that gives a computing process by the same token. It is based on convolution i.e., the map product of symmetry and correlation.

3.2. Symmetry Measures





 be a given symmetric version of P when the invariant (axis or centre) is in x. The inner and outer kernels are respectively:
be a given symmetric version of P when the invariant (axis or centre) is in x. The inner and outer kernels are respectively:






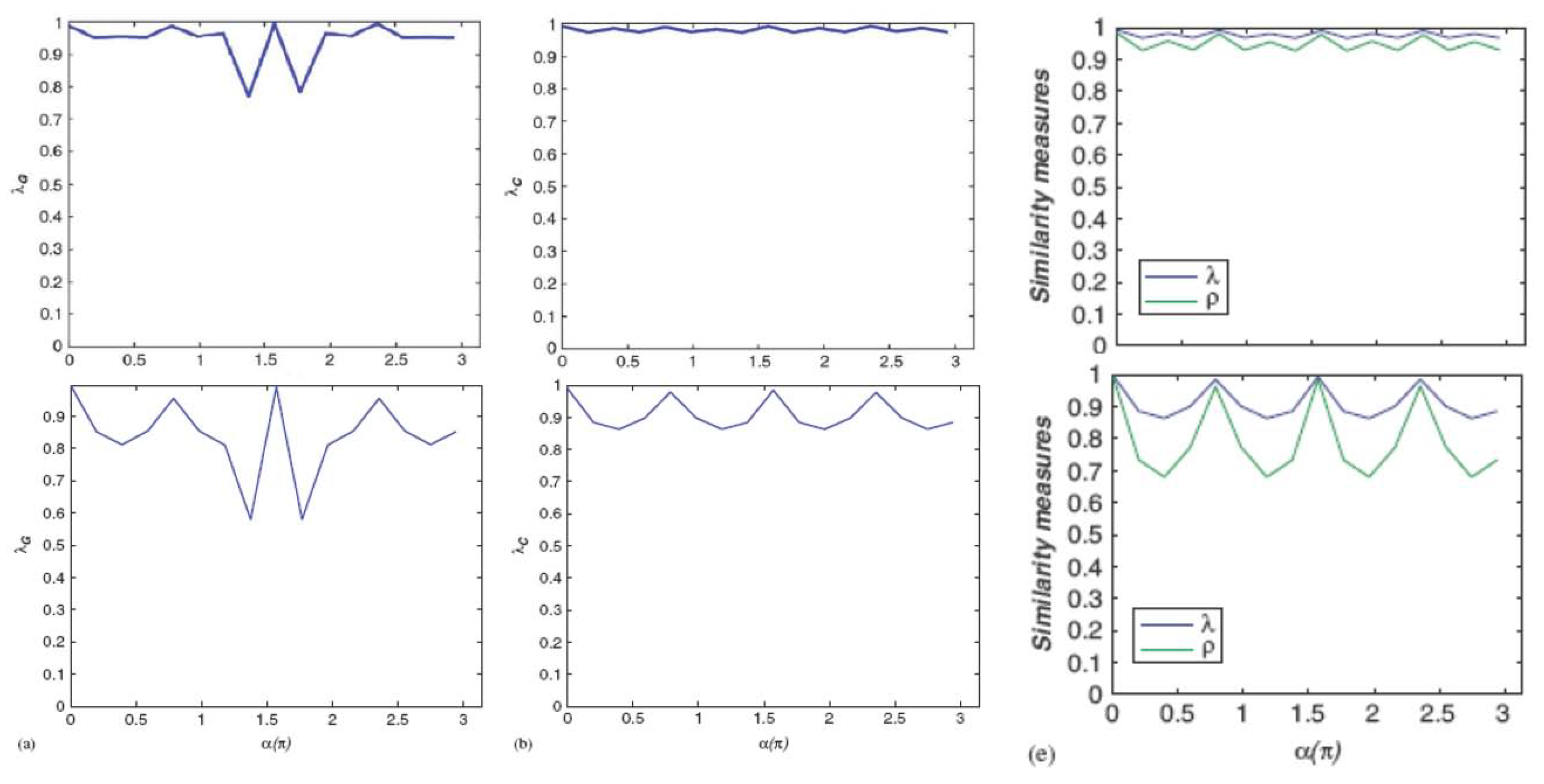
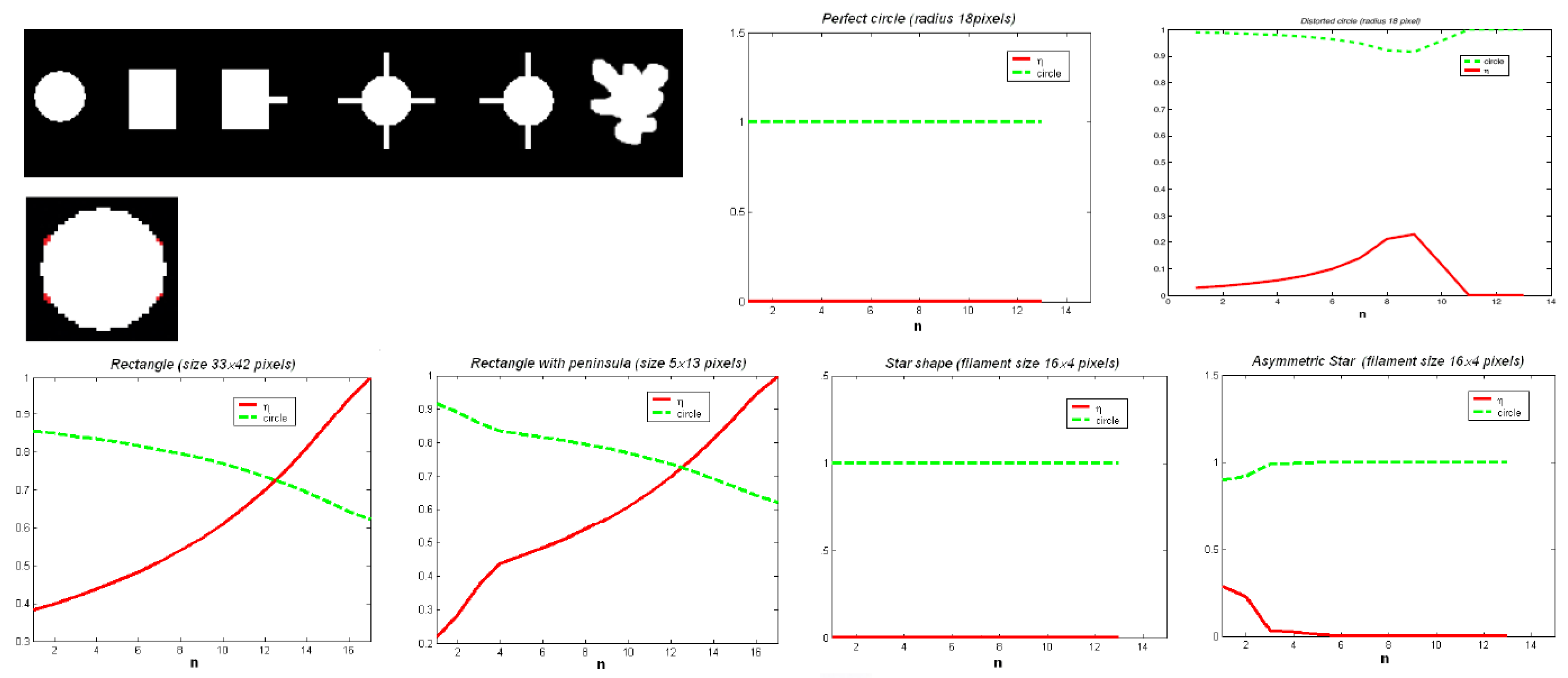
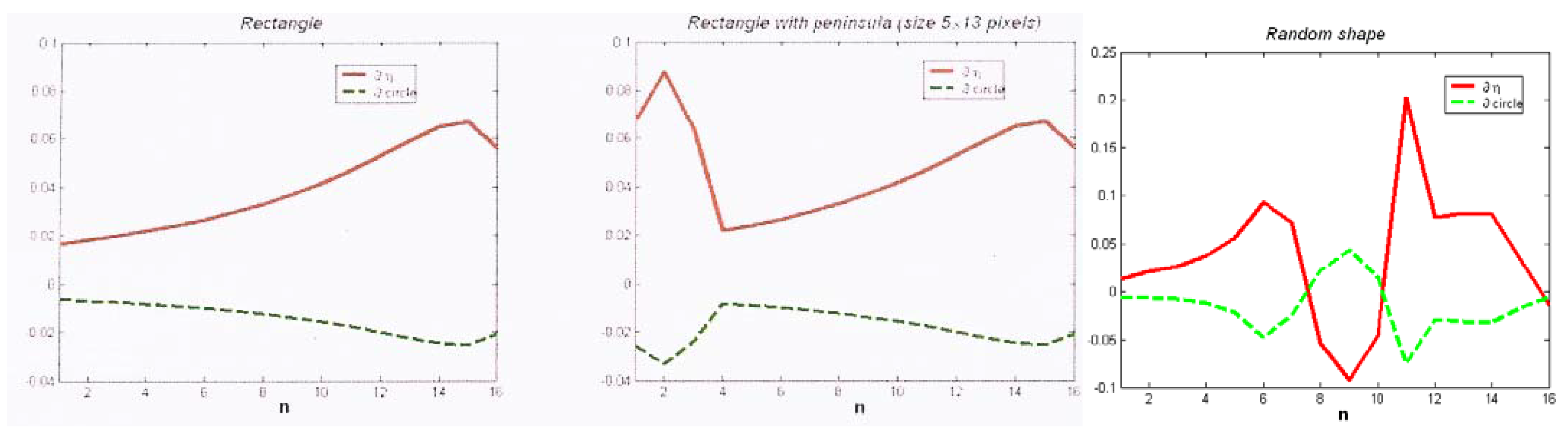
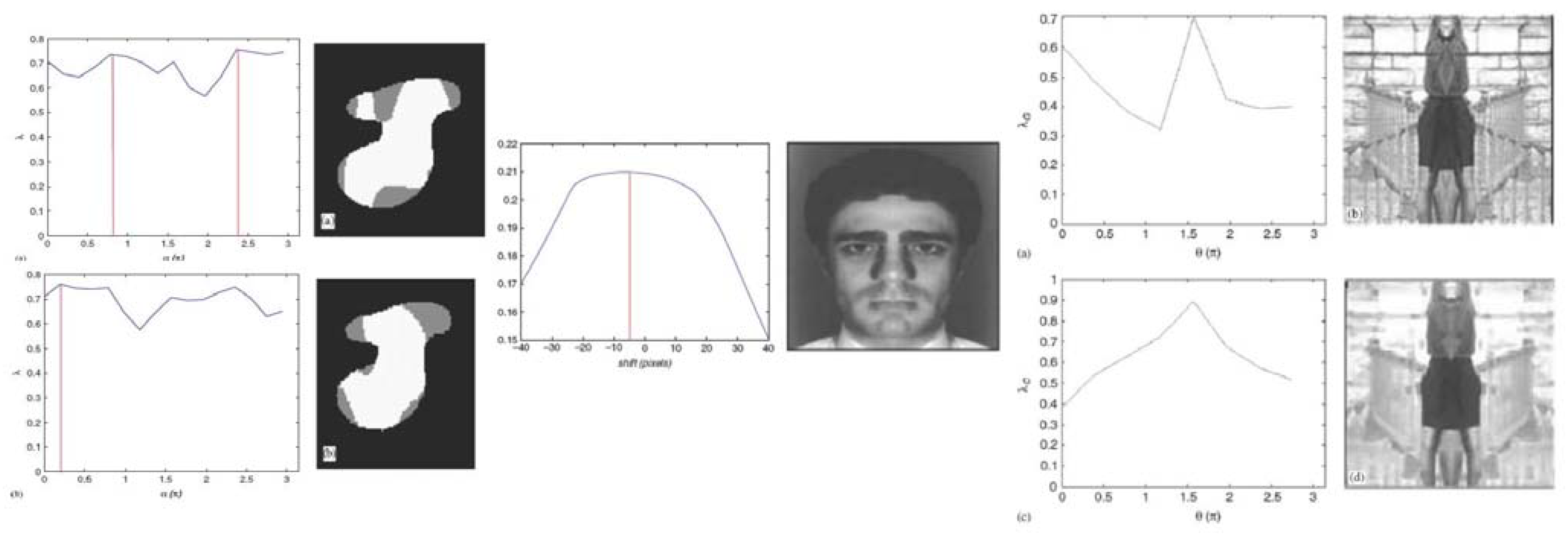
3.3. Results
- sensitivity of the symmetry detection to the centre position
- validity of λ the measure (degree) of symmetry in comparing patterns to their kernel through the elongation η and then the kernel evolutions with IOT
- quality of the correlation kernel wrt the kernel
- validity of the symmetry axis from correlation wrt the best axis over shifts
4. Symmetry Detection and Face Expressions
4.1. An Approach to Face Expression Recognition Based on Broken Symmetry Detection
- Human face is by nature mostly symmetrical. More so in the so-called Neutral expression (see FACS [19]).
- Any expression different from Neutral is obtained by stretching a different subset of face muscles (the so-called action units [20]).
- Such stretching is rarely completely symmetrical; as such, the more marked those changes in expression are, the more breakage of symmetry is introduced in different parts of the face.
- Collecting and measuring those differences in symmetry from different portions of the face allows us to compile a typical signature for each expression. These signatures are then vectorized and feed to a classifier.



4.2. Method
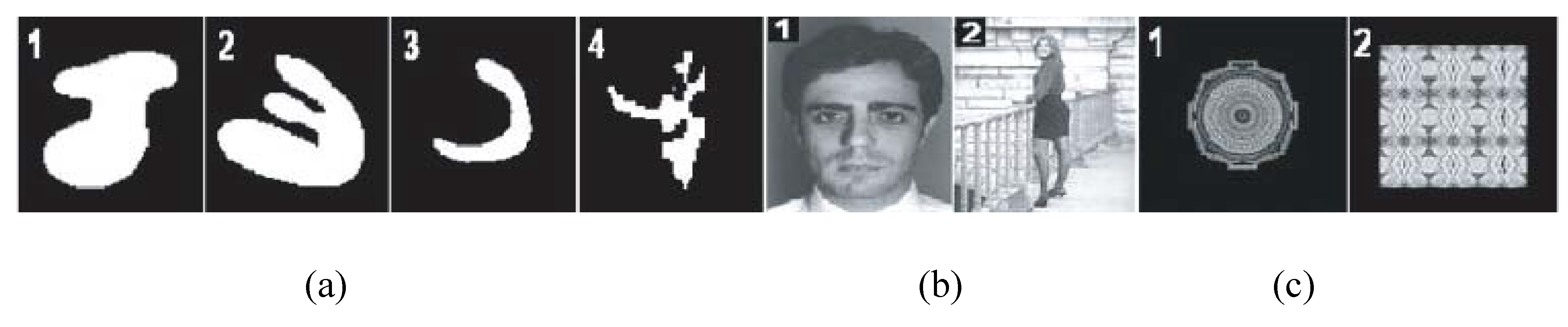
4.2.1. Dataset
4.2.2. Procedure


- 1)
- parameters (e.g., axis position and angle) for which max_included and min_including are obtained are the same, and
- 2)
- the measure given above is invariant for translation, rotation, and scaling.


4.3. Experimental Results and Discussion
5. Conclusions
References
- Kanizsa, G. The role of regularity in perceptual organization. In Studies in perception: Festschrift for Fabio Metelli; Martello-Giunti Editore: Firenze, Italia, 1975. [Google Scholar]
- Palmer, S.E. The Role of Symmetry in Shape Perception. Acta Psychol. 1985, 59, 67–90. [Google Scholar] [CrossRef]
- Zavidovique, B.; DiGesù, V. The S-kernel: A measure of symmetry of objects. Pattern Recogn. Lett. 2007, 40, 839–852. [Google Scholar] [CrossRef]
- DiGesú, V.; Zavidovique, B. Iterative symmetry detection: Shrinking vs. decimating patterns. Integr. Comput. Aided Eng. 2005, 12, 319–332. [Google Scholar] [CrossRef]
- Palmer, S. Vision Science: Photons to Phenomenology; Bradford Books/MIT Press: Cambridge, MA, USA, 1999; pp. 4–15. [Google Scholar]
- DiGesù, V.; Valenti, C. Symmetry operators in computer vision. Vistas Astron. 1996, 40, 461–468. [Google Scholar] [CrossRef]
- DiGesù, V.; Zavidovique, B. A note on the iterative object symmetry transform. Pattern Recogn. Lett. 2004, 25, 1533–1545. [Google Scholar] [CrossRef]
- DiGesú, V.; Lo Bosco, G.; Zavidovique, B. Classification Based on Iterative Object Symmetry Transform. In ICIAP ’03: Proceedings of the 12th International Conference on Image Analysis and Processing; IEEE Computer Society: Washington, DC, USA, 2003. [Google Scholar]
- Zavidovique, B.; Di Gesú, V. Pyramid symmetry transforms: From local to global symmetry. Image Vision Comput. 2007, 25, 220–229. [Google Scholar] [CrossRef]
- Oliva, D.; Samengo, I.; Leutgeb, S.; Mizumori, S. A Subjective Distance Between Stimuli: Quantifying the Metric Structure of Representations. Neural Comput. 2005, 17, 969–990. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327–352. [Google Scholar] [CrossRef]
- Di Gesu`, V.; Zavidovique, B. S-Kernel: A New Symmetry Measure. In Pattern Recognition and Machine Intelligence; Pal, S., Ed.; Springer Verlag: Berlin-Heidelberg, Germany, 2005. [Google Scholar]
- Moghaddam, B.; Pentland, A.P. Face recognition using view-based and modular eigenspaces. In Proc. SPIE; SPIE: San Diego, CA, USA, 1994; Volume 2277. [Google Scholar]
- Zhao, W.; Chellappa, R.; Phillips, P.J.; Rosenfeld, A. Face recognition: A literature survey. ACM Comput. Surv. 2003, 35, 399–458. [Google Scholar] [CrossRef]
- Shakhnarovich, G.; Moghaddam, B. Face Recognition in Subspaces. In Handbook of Face Recognition; Stan, Z.L., Anil, K.J., Eds.; Springer-Verlag: Secaucus, NJ, USA, 2004; Volume I, Chapter 7; pp. 141–168. [Google Scholar]
- Jain, A.K.; Ross, A.; Prabhakar, S. An introduction to biometric recognition. IEEE Trans. Circ. Syst. Video Technol. 2004, 14, 4–20. [Google Scholar] [CrossRef]
- Pelachaud, C.; Poggi, I. Multimodal communication between synthetic agents. In Proceedings of the Working Conference on Advanced Visual Interfaces; ACM: L’Aquila, Italy, 1998. [Google Scholar]
- Shan, C.; Gong, S.; McOwan, P.W. A Comprehensive Empirical Study on Linear Subspace Methods for Facial Expression Analysis. In CVPRW ’06: Proceedings of the 2006 Conference on Computer Vision and Pattern Recognition Workshop; IEEE Computer Society: Washington, DC, USA, 2006. [Google Scholar]
- Ekman, P.; Friesen, W. Facial Action Coding System: A Technique For The Measurement Of Facial Movement; Consulting Psychologists Press: Palo Alto, CA, USA, 1978. [Google Scholar]
- Essa, I.A.; Pentland, A.P. Coding, Analysis, Interpretation, and Recognition of Facial Expressions. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 757–763. [Google Scholar] [CrossRef]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding Facial Expressions with Gabor Wavelets. In IEEE International Conference on Automatic Face and Gesture Recognition; IEEE Computer Society: Los Alamitos, CA, USA, 1998. [Google Scholar]






















| Image | λg | αg | λc | αc | OST | αOST |
|---|---|---|---|---|---|---|
| 1a | 0.76 | 135.00° | 0.76 | 11.25° | 0.86 | 112.50° |
| 2a | 0.74 | 90.00° | 0.79 | 33.75° | 0.93 | 101.00° |
| 3a | 0.82 | 157.50° | 0.76 | 22.50° | 0.87 | 56.25° |
| 4a | 0.76 | 0.00° | 0.80 | 0.00° | 0.80 | 0.00° |
| 1b | 0.80 | 90.00° | 0.80 | 90.00° | 0.72 | 90.00° |
| 2b | 0.70 | 90.00° | 0.89 | 90.00° | 0.92 | 45.00° |
| 1c | 0.99 | 90.00° | 0.99 | 135.00° | 0.90 | 90.00° |
| 2c | 0.99 | 0.00° | 0.99 | 90.00° | 0.96 | 0.00° |
| Image | ρ | α |
|---|---|---|
| 1a | 0.67 | 101.25° |
| 2a | 0.67 | 112.50° |
| 3a | 0.58 | 112.50° |
| 4a | 0.55 | 157.50° |
| 1b | 0.80 | 90.00° |
| 2b | 0.94 | 90.00° |
| 1c | 0.99 | 90.00° |
| 2c | 0.98 | 0.00° |
| Neutral | Anger | Disgust | Fear | Happiness | |
|---|---|---|---|---|---|
| Neutral | 0,88 | 0,00 | 0,02 | 0,05 | 0,05 |
| Anger | 0,07 | 0,61 | 0,12 | 0,13 | 0,07 |
| Disgust | 0,02 | 0,00 | 0,93 | 0,00 | 0,05 |
| Fear | 0,07 | 0,07 | 0,05 | 0,76 | 0,05 |
| Happiness | 0,15 | 0,07 | 0,12 | 0,05 | 0,61 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Di Gesu, V.; Tabacchi, M.E.; Zavidovique, B. Symmetry as an Intrinsically Dynamic Feature. Symmetry 2010, 2, 554-581. https://doi.org/10.3390/sym2020554
Di Gesu V, Tabacchi ME, Zavidovique B. Symmetry as an Intrinsically Dynamic Feature. Symmetry. 2010; 2(2):554-581. https://doi.org/10.3390/sym2020554
Chicago/Turabian StyleDi Gesu, Vito, Marco E. Tabacchi, and Bertrand Zavidovique. 2010. "Symmetry as an Intrinsically Dynamic Feature" Symmetry 2, no. 2: 554-581. https://doi.org/10.3390/sym2020554
APA StyleDi Gesu, V., Tabacchi, M. E., & Zavidovique, B. (2010). Symmetry as an Intrinsically Dynamic Feature. Symmetry, 2(2), 554-581. https://doi.org/10.3390/sym2020554




