1. Introduction
It is usual, among researchers dealing with vibrational and rotational Spectroscopy, to classify the energy levels according to the irreducible representations of a group determined by the molecular geometry. Point groups, consisting of the operations related to all symmetry elements of a molecule, are in general adopted in the case of molecules undergoing only small amplitude vibrational deformations with respect to an unique reference geometry [
1,
2,
3]. Permutation-inversion groups, consisting of permutations of identical nuclei and permutations followed by inversion through the mass centre, are used in the presence of large amplitude deformations, which may involve changes in the molecular conformation [
4]. In any case, groups consisting only of geometrical operations are usually employed.
One should remember that what really matters, in order to choose the group suitable to the classification of energy states, is the symmetry of the Hamiltonian and not of the molecule. For instance, pure rotational states can be classified according to the irreducible representations of a group formed by the symmetry operations of the ellipsoid of inertia of the molecule, which has a higher symmetry than the molecule itself. However, when vibrational modes have to be considered too, the geometrical symmetry of the Hamiltonian matches the symmetry of the molecule.
In the absence of magnetic fields, the Hamiltonian is also invariant with respect to the inversion of the direction of motion, that is the inversion of all momenta and angular momenta, including spin. Such inversion implies the change of sign of the time derivatives of all coordinates, therefore the inversion of the direction of motion is usually referred to as “time reversal” [
5,
6]. Time reversal can be expressed as the product of a linear operator times the complex conjugation operator, therefore it transforms all constants, scalars and wavefunctions into their complex conjugates. In fact, the quantum mechanical operators corresponding to observables which imply a time derivative in their classical definition (e.g., the components of linear and angular momenta), contain the factor i which multiplies a coordinate derivative, and change sign under time reversal because of their imaginary nature. Thus, in principle, time reversal should be considered as well as the geometrical symmetry operations forming the groups usually applied in Spectroscopy, and this may require appropriate extensions of these groups. We shall see that other types of extensions might be required for symmetry groups applied to molecules with large amplitude periodical motions.
2. Double Degenerate Vibrational Modes
Double degenerate vibrational modes occur in molecules having one symmetry axis (z-axis) with order larger than two, or one four-fold or higher order rotation-reflection axis (alternating z-axis). Such modes consist of two orthogonal components oscillating at the same frequency, which we call Q
a and Q
b. The respective harmonic Hamiltonians, in terms of normal coordinates and associated momenta, are
where ω=2πν, ν is the vibrational frequency, and
Q and
P represent the operators corresponding to a normal vibrational coordinate and its conjugate momentum.
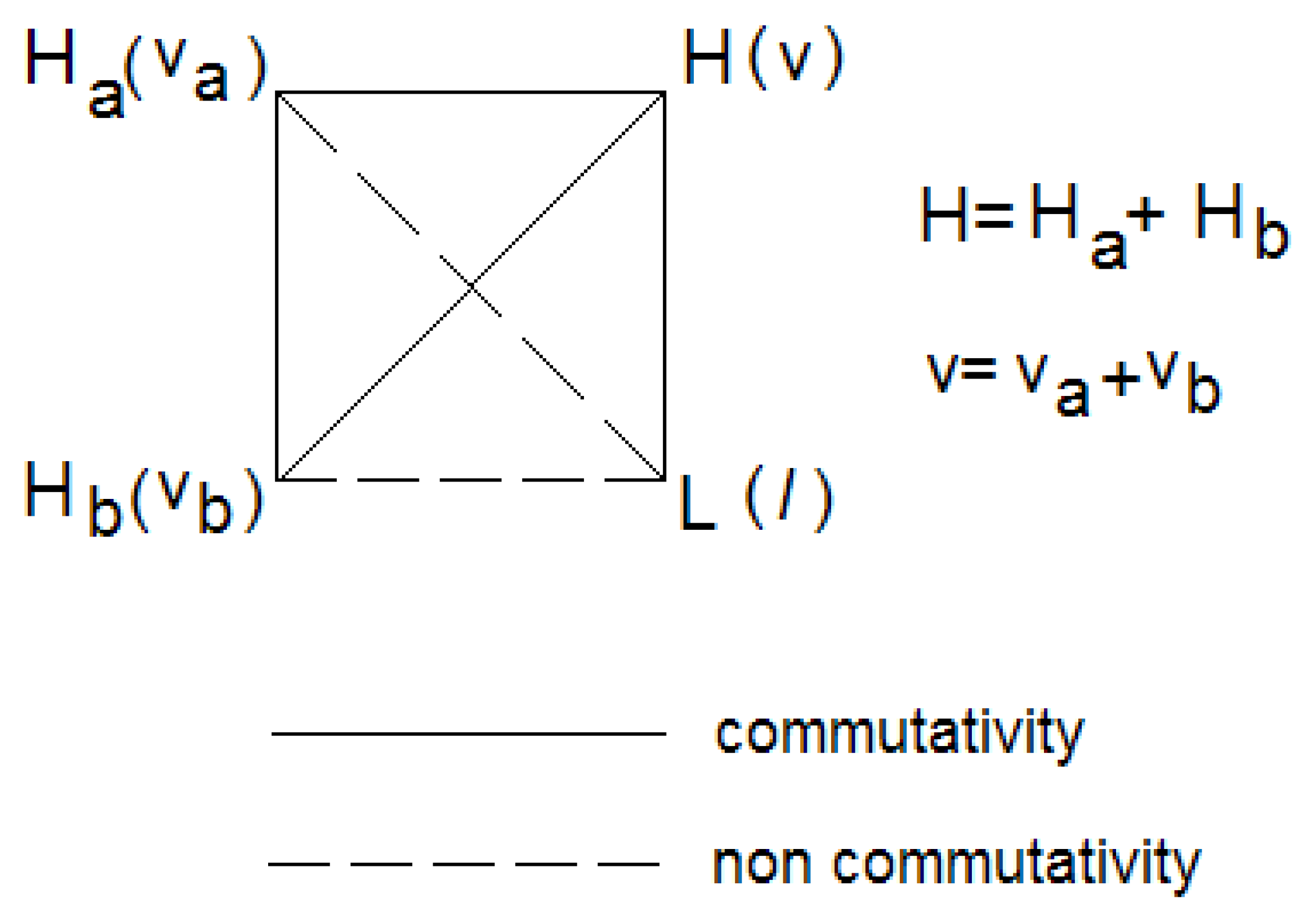
The two components can generate an angular momentum about the top axis z, whose operator is
Figure 1 shows that
H,
Ha and
Hb commute with each other, but
L commutes only with the total Hamiltonian
H. The figure also shows the quantum numbers associated with the eigenvalue of each operator. Thus, representing a general vibrational state as
, with v=v
a+v
b, the states of a degenerate fundamental pair can be taken either as
and
(for short
and
) or as
and
(for short
and
).
With the first choice, one knows the total energy and the excitation in each of the two components, but the angular momentum is not defined. With the second choice, one knows the total energy and the angular momentum generated by the vibrational pairs (ζ
l, that is ±ζ
in fundamentals, where ζ is the Coriolis coupling coefficient of the pair under consideration). The relation between the two sets of components is:
The states
and
are mixed under rotation about the z-axis (they would not be mixed only under a rotation by a multiple of π). On the contrary, the functions
are only multiplied by a unitary factor under the top axis rotation. They can be mixed only by a reflection through a plane containing the top axis or by a rotation about an axis normal to it, an operation called “second orientating operation” by Henry and Amat [
7]. We call this operation
, reserving the symbol
for the top axis operation (“first orientating operation”). Thus, in the absence of symmetry planes containing the top axis and of axes normal to it (that is, for molecular geometries corresponding to the point groups
Cn,
Cnh,
Sn), each of two
functions would constitute the basis of a one-dimensional irreducible representation. In spite of this group theoretical conclusion, the physical intuition and the equivalence of the directions normal to z in the case of high rotational symmetry about the z-axis still suggest that the a and b vibrational modes should occur in degenerate pairs. This is even more evident for the rotational states, because the moments of inertia about x and y would be equal anyway. It is for this reason that the one-dimensional symmetry species spanned by the components of a
pair in the mentioned class of molecules are called by Herzberg “separably degenerate irreducible representations” [
2]. This odd situation is clarified if the time reversal operation is applied, and this can be understood without entering any mathematical treatment. In fact, the components of a
pair differ from each other by the sign of the vibrationally generated angular momentum, then they are interchanged if the direction of motion is inverted, and must form the basis of a two-dimensional corepresentation, in a group which includes the time reversal operation.
We show as an example the extension of the point group C3 through direct multiplication by (E, Θ).
Table 1 shows the irreducible representations and their characters for the point group
C3, and the behavior of the components of typical polar vectors (linear displacement
T) and axial vectors (angular displacement
R). Polar and axial vectors describing motion (linear momentum
P and angular momentum
J) also behave as
T and
R, respectively, since the group contains only geometrical symmetry operations. Note that the “separably degenerate” species E
+ and E
- are two mono-dimensional species, and that circular vector components of the form x+iy and x-iy are basis of these two separate representations. On the contrary, their components along x and y are basis of a two-dimensional reducible representation, whose characters are the sum of those of E
+ and E
-, that is 2,-1,-1, and which can be completely reduced to E
++E
- by a transformation to circular components, such as that in equation (4).
If the symmetry operations of
C3 are multiplied by (
E, Θ ), one obtains the six operations shown on the top of
Table 2. They form a group if
Θ2 =
E, that is for systems with integral spin. Anyway, here we are dealing with vibration-rotation energy states and the resolution of spin structures is not considered. Also (
E, Θ ) is a group if
Θ2 =
E.
Table 2 shows the characters of the transformations of vector components. The components of vectors that imply motion, such as
P and
J, or do not imply motion, such as
T and
R, transform with opposite signs under the operations containing time reversal. However, their behavior under the antiunitary operations (those containing
Θ in
Table 2) is reversed if the vectors are multiplied by the imaginary unity
i. This can be seen in the upper part of
Table 2. It is evident in this table that only the unitary operations have definite characters in a given corepresentation of a group containing unitary and antiunitary operations, whereas the characters of the antiunitary operations depend on the basis and can be affected also by phase choices [
4,
5]. More complicated characters for antiunitary operations would be obtained for general phases, consistently with transformations as
Θ (e
iφq) = e
-2iφ(e
iφq) and
Θ (e
iφp) = - e
-2iφ(e
iφp), for coordinates and momenta.
The lower part of
Table 2 applies if the x and y-components of vectors are expressed in the circular form x±
iy. It can be easily understood that circular components of the form x±
iy are switched into each other under the antiunitary operations, therefore they are bases of a corepresentation in which the characters of the antiunitary operations vanish (E-corepresentation in the lower part of
Table 2). Comparison of the corepresentations E′, E″ and E clearly shows that a change of basis can affect only the characters for the antiunitary operations.
The components Q
a and Q
b of perpendicular vibrational modes of
C3-molecules can be chosen to transform as
Tx and
Ty, therefore their circular combinations, with defined angular momentum, span the non-degenerate species E
+ and E
- of this point group, see
Table 1. However, they transform according to the E-corepresentation of
C3×(
E, Θ ), therefore they are actually degenerate.
3. Spin Double Groups and Kramers Degeneracy
It is customary in several procedures of Spectroscopy to start with entities, such as operators and wavefunctions, classified under the full rotation group (the group of all rotations, by any angle and about any axis), and then to exploit the resolution of the species of this highly symmetric group into those of less symmetric groups, which apply to the specific cases. The sets of angular momentum wavefunctions are typical bases of the irreducible representations of the full rotation group, since the wavefunctions associated with the components of an angular momentum with principal quantum number
j span the 2
j+1-dimensional species Γ
(j). In particular, if the orientation of the components of a given Γ
(j) set is chosen in such a way that they are simultaneous eigenfunctions of
j2 and
jz, with good quantum numbers
j and
k, they transform under a rotation by φ about z as:
It is evident that is invariant under a rotation by 2π, that is replacing φ by φ+2π, if k (and j) has an integral value.
Applying this machinery to functions with half integral angular momentum, which actually occur in the presence of half integral spin, one finds from (5) that these functions change sign under a rotation by 2π. Thus, it is customary to add to the operations of the full rotation group, or of the symmetry group of the molecule, a somewhat fictitious element
R, and to extend the group by direct multiplication by (
E,
R) [
4,
8]. The species symmetric under
R occur in integral spin states and are called
single valued, those anti-symmetric under
R occur with half integral spin and are called
double valued. It can be shown that states corresponding to double valued representations of the extended group occur always at the least in degenerate pairs (Kramers degenerate doublets). In low-symmetry groups, some or all spin functions may span non-degenerate species, but in this case, for half integral spin, each non-degenerate species occurs at least twice, corresponding to Kramers doublets of the same energy. However, Kramers degeneracy can be lifted by the presence of a magnetic field.
In these considerations, one is faced with two difficult points. One point is that, in spite of the previous considerations,
R is a new operation, distinct from any operation
R(2π) of the extended full rotation group (see table 55 of Ref. [
8], where the operations
R(2π) are included under the symbol
, with φ=2π, and the new operation
R occurs as well). Another point is that we cannot explain why a magnetic field could lift the Kramers degeneracy. Both points are clarified if the fictitious operation
R is replaced by the square of time reversal operator,
Θ2 [
4]. This will also make the understanding of Kramers degeneracy in the absence of fields easier. One has to remember that all components of the spin operators, as for angular momenta, change sign under time reversal.
The spin functions with defined values of the z-component are written as
. In the absence of external magnetic fields, it is convenient to choice a quantization z-axis fixed to the molecule. We adopt the phase conventions that the functions with
Σ = 0 or +1/2 transform under time reversal as
We also adopt the widespread convention that the matrix elements of the ladder operators
S± are real and positive. With these conventions, building up the spin function
by applying
S- to
and operating with time reversal, we also find from (7):
Then, building up spin functions
by applying
to
or
to
, whatever applies, one finds:
Note that equations (6–8) are special cases of equation (9).
Operating by
Θ on both sides of equation (9), one finds eventually:
Equation (10) shows that function with integral spin are invariant under
Θ2, but those with half integral spin change sign, just as for the operation
R.
Moreover, using combinations of spin functions with
Σ and −
Σ, one finds:
Since
S-
Σ and
S+
Σ have the same parity for integral
S, but opposite parities for half integral
S, one finds that
and
Equations (12,13) show that for integral
S time reversal transforms the spin functions of above into themselves, with a change of sign at the most, whereas for half integral
S Θ transforms the above spin functions into different functions, orthogonal to them. Now if the Hamiltonian is invariant under time reversal, the eigenstates ψ and
Θψ (inclusive of spin) have the same energy (in fact, in this case the equation
ΘHψ =
ΘEψ becomes
HΘψ =
EΘψ), therefore they must be degenerate if they are different functions, that is if
S is half integral. On the other hand, in the presence of a magnetic field the Hamiltonian is not invariant under time reversal, and
Θψ and ψ are no longer bound to have the same energy. This explain why a magnetic field can lift the Kramers degeneracy.
Thus an extended spin double group is actually the unitary subgroup of the group obtained by direct product of the original symmetry group and the group (
E,
Θ,
Θ2,
Θ3), see Ref. [
4].
4. The Extended Symmetry Group (E,)×(E,Θ), With Θ2 = E
The point groups possessing an
symmetry element, consisting of either a binary rotation axis normal to the main axis (chosen as the angular momentum quantization axis z) or of a reflection plane containing z, always have a subgroup (
E,
). The ensemble of operations (
E,
)
×(E,
Θ ) is also a group, as
(E,
Θ ) does, if
Θ2 = E. This group can be effectively employed to classify vibration-rotation coordinates, operators and wavefunctions, including their real or imaginary nature [
9]. Spin structure is not considered and one can assume that
Θ2 = E. It is a subgroup of the extended group resulting by the multiplication of the point group or molecular group by
(E,
Θ ).
Table 3 shows the characters of the corepresentations of this group, which apply to bases of Cartesian components of vectors, with either real or imaginary coefficients, see also the upper part of
Table 2.
The upper index in the species symbols are associated with the invariance or change of sign with respect to time reversal, whereas the lower index refers to the behavior under . Hamiltonian operators with real coefficients containing even or odd powers of momenta are invariant or change sign under time reversal.
In order to determine the relative phases of the rotational basis functions
, we only need to define a phase angle δ
k relative to the shift of
k, since in the absence of external fields the Hamiltonian is diagonal in
J and
M. For non-degenerate oscillators, the values of the phase angles δ
v(s) and δ
v(a), relative to the shift in the vibrational quanta of modes symmetric or anti-symmetric under
, have to be defined. For two-dimensional oscillators, using circular components, the value of δ
vt±δ
lt, where δ
lt is the phase angle relative to the shift of l
t, the quantum number related to the angular momentum generated by the degenerate vibrational modes, has to be defined. For three-dimensional oscillators, using spherical components, one has to define the phase angles δ
vt(s) ±δ
lt(s), δ
mt(s), δ
vt(a) ±δ
lt(a) and δ
mt(a), where l and m apply to the angular momentum generated by the three-dimensional mode and its z-component, and (s) and (a) apply to three-dimensional modes with character 1 or -1 under
. Classifying the vibration-rotation operators according to the symmetry species of the group in
Table 3, and exploiting the property that the rotational and vibrational factors in the Hamiltonian must have the same symmetry, we have shown that it is possible to determine values of δ
k and of all the vibrational phase angles in such a way that all vibration-rotation matrix elements are real [
9,
10].
The calculation of vibration-rotation transition moments also requires to define two additional phase angles
and
δM, relative to the shifts of
J and
M [
9,
10,
11]. We have also shown that with the phase conventions leading to real vibration-rotation matrix elements, and with
either 0 or π (modulo 2π) the matrix elements of vibration-rotation transition moment operators are all real if
is a reflection and all imaginary if
is a rotation [
9,
10].
The problem of defining convenient phase conventions for vibration-rotation spectroscopy was of actual interest already in the early sixties. We believe that a general satisfactory definition took so long time to be found, because of the little attention paid to the convenience of extending the geometrical symmetry groups applied to molecules, to account for time reversal.
5. Symmetry Groups for Floppy Molecules
There are molecules undergoing one or more periodic deformations of large amplitude, with a potential surface with several minima. They can assume different inter-converting geometries or conformations, and are usually referred to as “floppy molecules”.
It is obvious that the energy levels of floppy molecules cannot be classified according to a point group. In fact, a suitable point group consists of the operations related to the symmetry elements of a molecule in a unique reference geometry.
The most general group for a molecule consists of all permutations of nuclei of the same species, followed or not by the inversion of all particles through the molecular mass centre, and of their combinations, and is called “complete nuclear permutation inversion group” (CNPI) [
4]. It can be easily understood that a given CNPI implies only the knowledge of the number of nuclei of each species present in a molecule, that is of its brute chemical formula, without any knowledge about the permitted molecular geometry (or geometries). In principle, this is the group that should be considered by a theoretician “ab-initioist”, searching to find how could all the nuclei assemble together in the formation of the molecule, without making use of any experimental evidence and then without any assumption about preferred geometries.
In practical cases, when not all permutations of identical nuclei can occur in the vibrational molecular motion, the use of a CNPI group would generate plenty of useless labels, that would allow one to distinguish components of energy levels whose splitting will never be observable. Thus it is convenient to select from a CNPI group those elements which bring the molecule into geometries that can actually be attained, and can be brought back to the initial geometry by allowed large amplitude deformations and overall rotations (feasible operations). The ensemble of these feasible operations forms the molecular symmetry group.
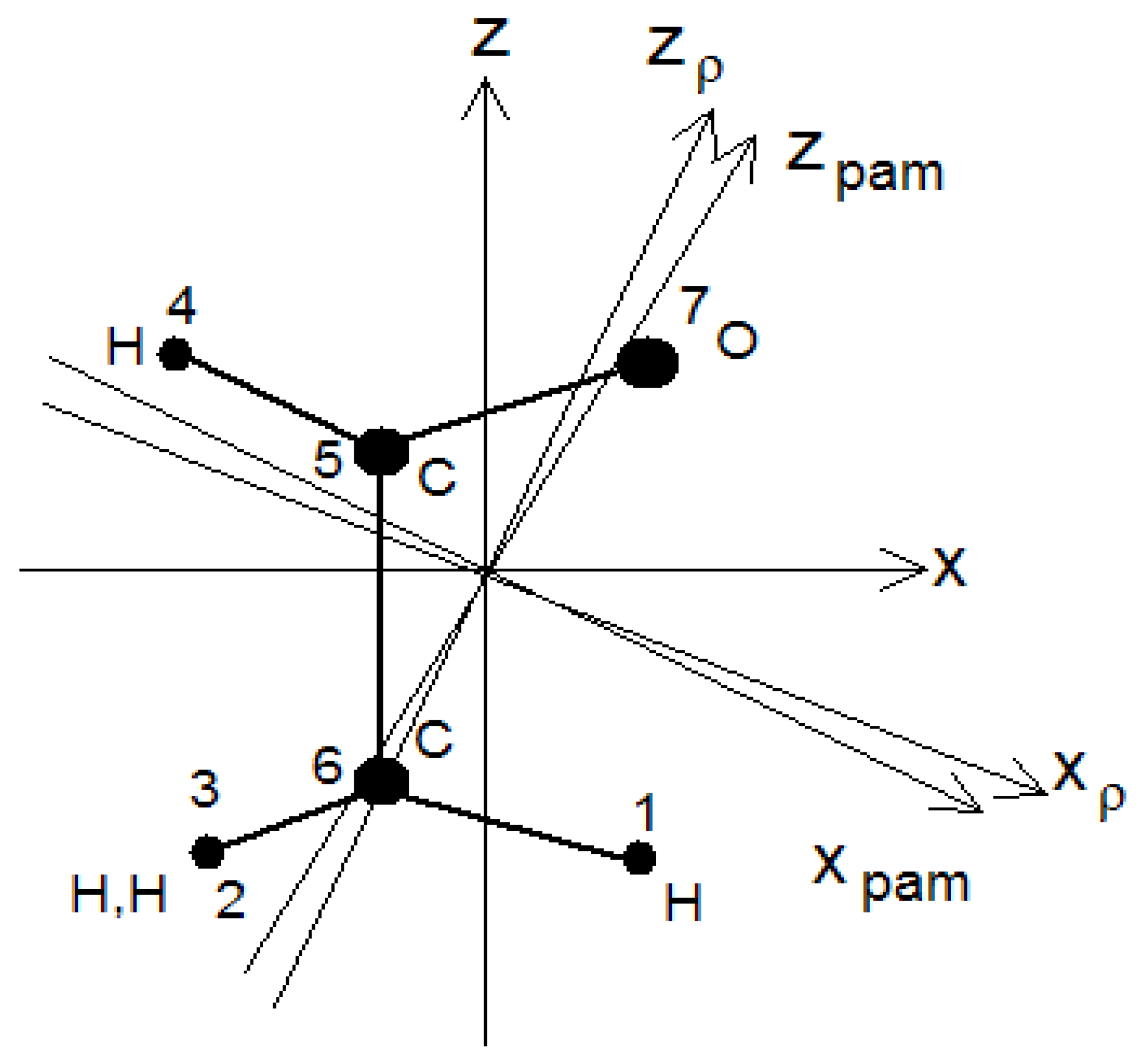
As an example, we examine the acetaldehyde molecule (
Figure 2). Three system of axes, all with the y-axis normal to the plane of the page, are shown in the figure. The axis z is parallel to the internal rotation axis z
a, x
pam and z
pam are principal inertia axes, z
ρ is the axis about which the whole molecule must rotate to compensate for the angular momentum caused by the internal rotation of the methyl group (top) with respect to the aldehyde group H-C-O. We also shall make use of a coordinate system x
a, y
a, z
a, fixed to the internally rotating top (methyl group), with x
a and y
a parallel to x and y in the reference conformation with the internal rotation angle τ equal to zero.
This molecule can assume three conformations with one hydrogen of the methyl group eclipsed with the hydrogen of the HCO group (we call them eclipsed), and three conformations with one methyl hydrogen eclipsed with the oxygen of the HCO group (we call them staggered). They can be inter-converted by the internal rotation of the methyl group with respect to the HCO group, about the C-C axis. The molecular symmetry group of acetaldehyde, G
6, consists of the identity, the two circular permutations (123) and (132), and the three permutation-inversion operations (12)*, (13)* and (23)*. The molecular geometries generated by the circular permutations can be brought back to the initial one again by an internal rotation, those generated by the permutation-inversion operations also require a rotation by π about an axis normal to the HCO plane (y
t in
Figure 2). The operations of the CNPI group containing permutations of a methyl hydrogen with the hydrogen of the HCO group, the permutation of the two carbon atoms, the permutations (12), (13) and (23), the permutation-inversion operations (123)* and (132)*, and the inversion through the mass center E* have been disregarded as “non feasible”, leading to geometries that the molecule cannot actually attain. The character table of the G
6 molecular symmetry group is reported in
Table 4.
If the internal rotation would become no longer feasible, one can verify that the molecular symmetry group would contain only E and (23)*, with reference to a “rigid" geometry as in
Figure 2. This group is isomorphic with the point group C
s, with (23)* corresponding to the reflection through the symmetry plane. In fact, the energy levels of molecules with only small amplitude vibrational modes can be classified under the appropriate point group.
Molecular symmetry groups are fully adequate for application to all floppy molecules, if the allowed inter-conversions of different geometries or conformations are completely free from hindrance. If these inter-conversions are somewhat hindered, additional information on the vibrational dynamics of the molecule can be obtained by the correlation of the vibrational energy levels (and their symmetries), with the levels (and their point group symmetries) of the molecule vibrating about given supposedly stable geometries. This may require an extension of the molecular symmetry group.
In the next section we examine the case of typical molecules with internal rotation, such as methanol or acetaldehyde, nitromethane, and ethane.
6. G6 and G12 Molecules with Internal Rotation
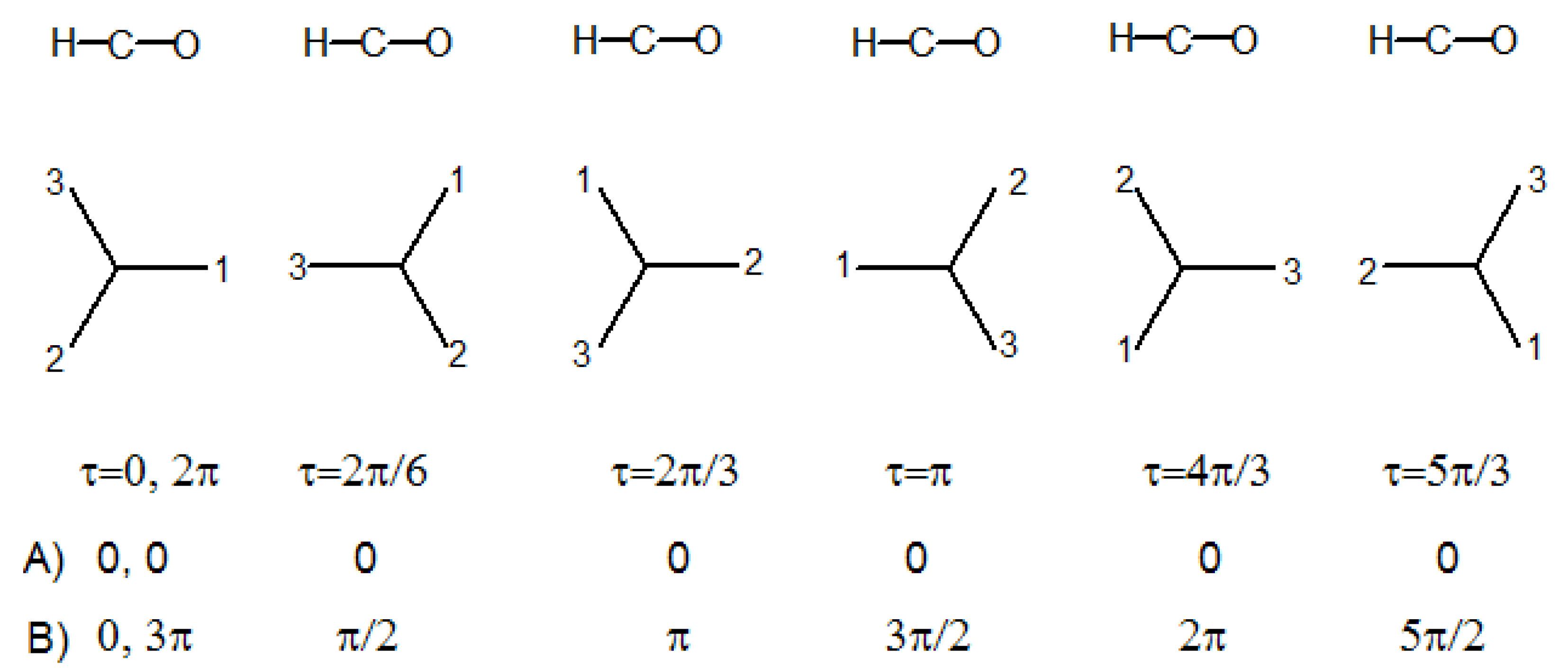
Let us consider the acetaldehyde molecule, and its G
6 molecular symmetry group in
Table 4. If the methyl group rotates from 0 to 2π radians about the C-C bond, with respect to the HCO plane, the molecule will assume six times a geometry of C
s symmetry, where HCO is a symmetry plane. The H atom of the aldehyde group is staggered with respect to the hydrogens of the methyl group in three of the C
s geometries, and eclipsed to one of them in the other three, see
Figure 3.
In the case of free internal rotation, the interaction between the methyl group (top) and the aldehyde group (frame) vanishes, therefore the mechanical behavior of the molecule is independent of the angle of internal rotation τ, being identical at any conformation. Thus the correlation of the vibrational modes of the floppy molecule with corresponding modes of the “semirigid" molecule, vibrating with small amplitudes about any C
s point group geometry, is meaningless. Therefore molecular symmetry groups are fully adequate to classify the energy levels of molecules with free internal rotation, even if they contain no elements that could make the above mentioned correlations feasible. When the internal rotation is not free, the vibrational deformations of head and tail interact with each other in a manner which depends on the torsional angle τ, and the molecular motion behaves as if it had somehow “memory" of how it would be in the limit semi-rigid geometries. In this case it is instructive, and in general helpful, to establish a correlation of the vibrational symmetry species in the molecular symmetry group with those of point groups corresponding to characteristic symmetries attained at particular values of τ (e.g., the staggered and eclipsed conformations of acetaldehyde in
Figure 3). Thus it may be convenient to extend the molecular symmetry group, if it contains no elements that could make the desired correlations feasible.
This problem actually occurs with the vibrational deformations normal to the internal rotation axis.
Particularly convenient coordinates for these vibrations are those that have fixed directions in what we call “molecular axis system", the system of molecular axes whose orientation in space defines the rotational variables or coordinates (direction cosines and/or Euler angles). A clear advantage of these rotational coordinates is due to the fact that their direction in the laboratory space does not depend on τ, but only on the Euler angles. Therefore the largest contributions to vibrational transitions moments allow for transitions without change of the torsional state.
For acetaldehyde, it is convenient to choose a molecular axis system fixed in the HCO aldehyde group (frame or b-unit), with z parallel to the internal rotation axis, see
Figure 2. Thus τ is the angle of rotation of the methyl group (top or a-unit) with respect to the frame.
Representing by
and
two equivalent orthogonal components of a deformation in the methyl group, we can build up the new coordinates oriented along x and y:
In the absence of interaction between top and frame, the coordinates in equations (14) and (15) form a degenerate E-pair, and can be expressed in the circular form
where the symbol E
2 will become clear later, with reference to the expanded molecular group G
6(EM). In the presence of interaction between top and frame, the coordinates
(A
1) and
(A
2), spanning A
1 and A
2 symmetry species under the molecular symmetry group G
6, respectively, are no longer degenerate and can mix with deformations of the frame of the same symmetries. As their orientation is fixed in an axis system fixed at the HCO plane, A
1 coordinates are always symmetric (A′ under C
s) and A
2 coordinates are always anti-symmetric (A″ under C
s) when the molecule passes through the conformations shown in
Figure 3, where the HCO plane becomes a symmetry plane. Other typical coordinates obtained by combining
and
with τ-dependent coefficients are the following:
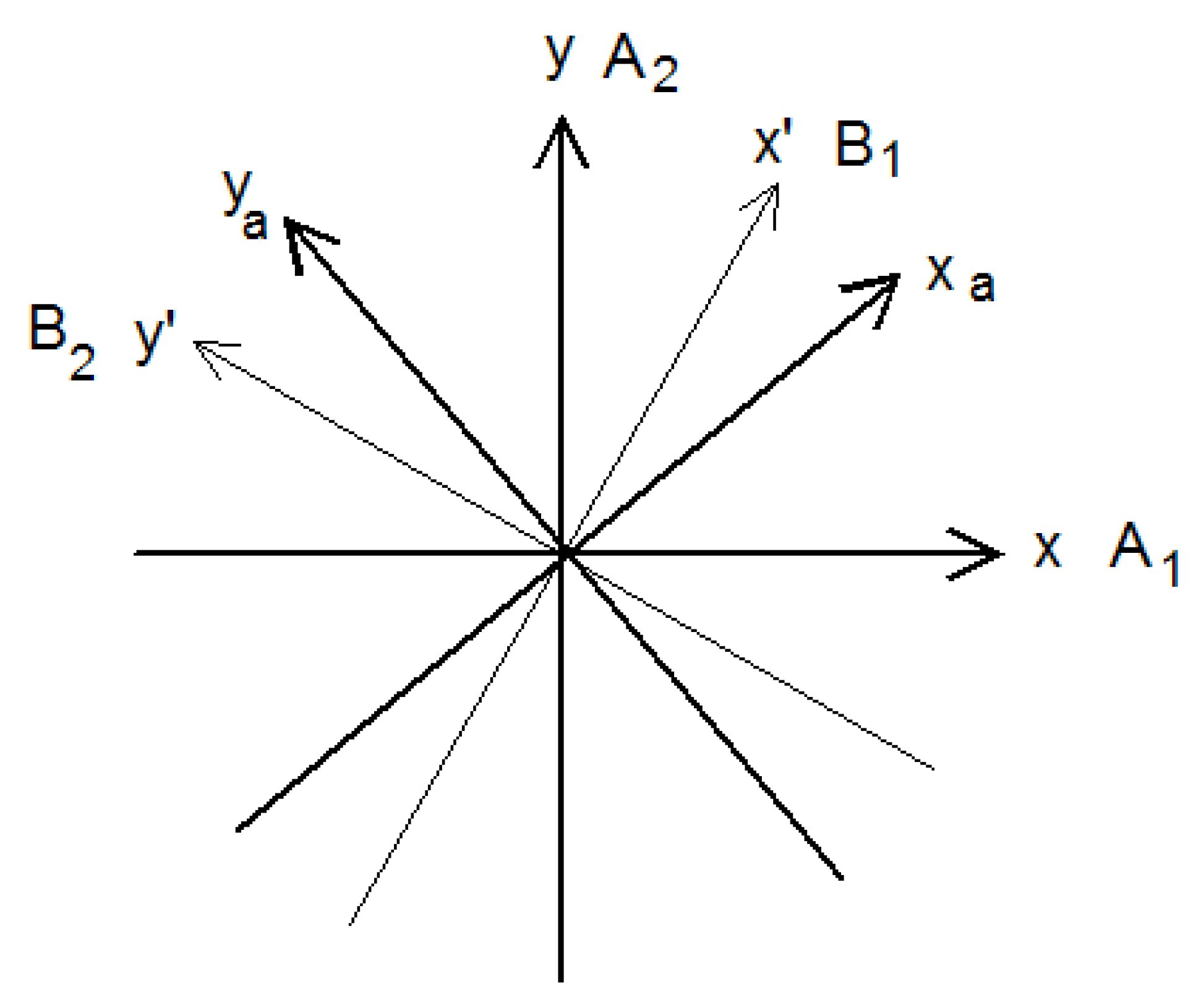
These coordinates are obtained by projecting
and
on the axes x′ and y′, which rotate about the internal rotation axis z at the angular velocity
, see
Figure 4. Thus these coordinates, oriented along x′ and y′, change direction by 90° when the torsional angle changes by 60°, therefore their representation changes from A′ to A″, or from A″ to A′, at each step illustrated in
Figure 3. B
1(B
2) coordinates are A′(A″) in the staggered conformations and A″(A′) in the eclipsed conformations.
In the absence of interaction between top and frame, these coordinates form a degenerate E-pair and can be expressed in the circular form
B
1 and B
2 coordinates rotate by 180°, that is they change sign, if the torsional angle changes by an odd multiple of 120°, therefore they change sign under the operation
E′, consisting of a complete internal rotation by 360° (double valued coordinates). Therefore if B
1 and B
2 coordinates occur in a given treatment,
E′ can no longer be considered equal to the identity E, and the G
6 molecular symmetry group has to be multiplied by (
E,
E′) yielding the extended molecular symmetry group G
6(EM), see
Table 5.
Apart from these geometrical and symmetry considerations about the form and properties of A and B deformations, it can be shown that the vibration-torsion interaction terms of the Hamiltonian which depend on deformations normal to the internal rotation axis contains two leading parts. One of them is diagonal with the adoption of single valued A coordinates, the other one with the adoption of double valued B coordinates. Thus A and B modes correspond to limit situations, the actual modes being in general a mixture of the two, depending on the magnitude of the different terms in the vibration-torsion interaction energy and on their resonance conditions [
12,
13,
14]. In particular, these resonance conditions are mainly determined by the Coriolis interaction of the angular momentum generated by a pair of orthogonal vibrational components and the angular momentum generated by the internal rotation (torsional Coriolis interaction) [
13], and the form of the actual modes for a given degenerate pair is mostly determined by this mechanism.
The choices of A or B vibrational basis functions in a practical problem obviously lead to the same results by numerical calculations, but with different values of certain parameters occurring in the vibration-rotation-torsion Hamiltonian.
The two choices also differ in the different way of separating the wavefunctions into a vibrational and a torsional factor. To show this point, we recall that a torsional basis function corresponding to free internal rotation is conveniently written as e
i(Ma-ρkρ)τ, where
Ma is the quantum number relative to the angular momentum of the top about the internal rotation axis,
kρ is the quantum number of the angular momentum of the whole molecule about the z
ρ (the axis about which the whole molecule must rotate in order to cancel the angular momentum generated by the rotation of the top about the internal rotation axis z, see
Figure 2), and
ρ is the ratio of the moment of inertia of the top about z and that of the whole molecule about z
ρ [
15,
16]. Thus from equations (16) and (19) one finds that, for given
kρ:
This means that the value of the torsional quantum number Ma changes with the adopted vibrational basis, because different amounts of the torsional angular momentum are incorporated in the vibrational function, for different vibrational basis sets.
The molecular symmetry group G
12, which applies to molecules like nitromethane or toluene, contains already four non-degenerate species: A
1′ and A
2′, symmetric under the permutation of the two oxygen atoms, and A
1″ and A
2″, anti-symmetric under the mentioned permutation. It can be shown that the A
1′ and A
2′ coordinates are single valued and are given by the equations (14) and (15), whereas the A
1″ and A
2″ coordinates are double valued and are given by the equations (17) and (18). However this molecular symmetry group does not need to be extended, because it can be shown that a torsion by 2π, applied to a nitromethane molecule distorted by a mode that would be double valued under G
6(EM), would transform the molecule into a geometry which could be brought back to the initial one by the permutation of the two oxygen atoms in the frame [
13]. Thus
Table 3 also applies to G
12 molecules if the operation
E′ is replaced by the permutation of the two oxygen atoms, and the species A
1, A
2, B
1, B
2, E
2 and E
1 are replaced by A
1′, A
2′, A
1′, A
2′, E′ and E′, respectively. Similar operations replacing
E′ can be identified in toluene (permutations of all carbons and hydrogens in the right half of the benzene ring with those in the left half), and other G
12 molecules.
The choice of a vibrational basis under G
6(EM), either single valued (A) or double valued (B), in an actual problem is a matter of convenience, and the preferred basis is not necessarily the one which is closer to the eigenstates. For instance, it has been found that the perpendicular vibrations of the methyl group of methanol are closer to the B-limit, see Ref. [
12,
13,
17] and references therein, but it may be easier to work with A-vibrational bases in the numerical treatment of an actual problem. One point for this choice may be the handling of selection rules, which are simpler with vibrational coordinates with fixed orientation in the x,y,z-system.
7. G36(EM) Molecules
In ethane-like molecules with free internal rotation, the double degenerate vibrations in the two molecular halves, a and b, are identical since the deformations of a do not interact with those of b. Thus they form modes with four degenerate components (single valued G-modes, called Gs after the group extension discussed hereafter). The two components in the a-unit, in circular coordinates, are called , and generate overall and torsional angular momenta with the same sign. The corresponding circular coordinates in the b-unit generate overall and torsional angular momenta with opposite signs.
Owing to the identity of the two molecular halves, it is customary not to fix the molecular axis system at one half of the molecule (frame), but to define an x,y,z-system with z along the internal rotation axis (as za and zb), and with x and y bisecting the angles between xa and xb and ya and yb, respectively. The torsional angle τ is set to zero when the three systems of axes are coincident, therefore a torsion by τ implies that the two moieties a and b rotate about z by τ/2 and –τ/2, respectively. Often the angle γ=τ/2 is used to define the torsion. The interaction of a and b causes the mixing of their deformations, and the components of a Gs-mode in a and b mix together generating double degenerate modes. As before, typical limit situations, with characteristic forms of degenerate modes, can be defined.
Projecting the components of a G
s-mode on the x and y axes, we obtain vibrational coordinates with fixed orientations in the x,y,z-system [
18,
19]. Their circular components are
These coordinates are multiplied by e
±iπ = -1 as τ changes by 2π, therefore they are double valued and require the extension of the molecular symmetry group to G
36(EM) = G
36×(E,E′), just as for G
6 molecules. Other typical coupled coordinates, single valued, are obtained by projecting the displacements in the a-unit of a G
s-mode on an axis system which rotates about z at the angular velocity
, and the displacements in the b-units on an axis system rotating at the angular velocity -
. Thus their directions in a and b rotate by 90° and -90° if τ changes by 60°, showing that the directions of the deformations in a and b of modes described by these coordinates change from cis(trans) to trans(cis) at any conversion between eclipsed and staggered conformations.
The circular components are [
13,
19,
20]:
All modes in equations (23–26) do not generate torsional angular momentum, because the contributions from the units a and b cancel out. However, the interaction of E1d and E2d modes or of E1s and E2s modes can generate torsional angular momentum.
Again there are terms in the Hamiltonian which favour the formation of double valued or single valued E-modes, and the mechanism of formation of the actual states is ruled by the torsional Coriolis coupling, which can tune more or less to resonance basis levels linked by specific head-tail interaction operators [
13,
20,
21,
22].
Combinations and overtones in G36(EM) molecules
In the numerical analysis of vibration-rotation-torsion spectra of ethane-like molecules it is convenient to adopt E
1d and E
2d basis vibrational functions for the degenerate fundamentals, owing to the properties of vibrational modes with fixed orientations in the chosen x,y,z molecular axis system. However, a complication arises in the presence of combinations or overtones with the excitation of an even number of degenerate vibrational quanta. In fact, from group theory it follows that the degenerate components of these combinations and overtones should be E
2s or E
1s [
23], see also Ref. [
24]. This is only a formal complication, because the total vibration-rotation-torsion functions are always single valued, and the problem only concerns the choice about their partition into the partial factors. We do not investigate this point in detail here, but we note that since the above partition is arbitrary, it is possible to refer to E
1d or E
2d basis functions also for overtones and combinations with an even number of quanta of double valued degenerate vibrational modes.
We have shown that an E
1s or E
2s function of circular type is a combination of E
1d terms multiplied by factors containing
or
and E
2d terms multiplied by factors containing
or
[
20], consistently with the symmetries of
(A
1d) and
(A
3d). The presence of τ-dependent coefficients in these transformations gives evidence to the fact that the torsional bases associated to the single valued and double valued vibrational bases are different.