1. Introduction
The unconventional class of liquid crystals discovered one decade ago, which is constituted with non-chiral bent-core molecules [
1], presents a rich polymorphism [
2] with extraordinary features and symmetry properties, the most prominent being the spontaneous onset of chirality in the ordered smectic phases [
3]. Despite many attempts to describe these phases with acrobatic combinations of classical order parameters [
3,
4,
5,
6], smectic density waves, polarization, and tilt vectors, a simpler and more elegant description involving a single vector-wave order parameter [
7,
8] seems to us necessary to account of the available experimental data [
7,
8,
9]. In particular, from the thermodynamical point of view the fact that a direct transition occurs commonly between the isotropic liquid and the ordered phases is much more likely when a single order parameter is involved. This permits us to predict the structure of the stable phases together with their thermodynamical behaviour [
7,
8], and more specifically the behaviour of several important physical tensors describing, for instance, the biaxiality, electro-optic response and chirality of the predicted structures. In addition, we have successfully extended our model to almost all observed bi-dimensionally and tri-dimensionally ordered bent-core phases [
9].
This single order parameter can be equivalently spanned by either a polarization wave or a tilt wave, since they transform according to the same irreducible representation of the non-chiral euclidean group when the wave vector is different from zero. It combines thus in a single object the degrees of freedom involved by distinct classical order parameters. We have shown in Refs. [
7,
8] that this model permits to foresee the stabilization of four ordered phases, denoted by C, R, and EL corresponding, respectively, to linear, circular and elliptic polarizations of the order-parameter wave. R describes the smectic C
P phase predicted in 1992 [
10] and then observed in bent-core systems [
10,
11], EL describes the commonly observed B2 phase [
12,
13], and we have proposed that C is an unmodulated approximation of the intriguing B7 phase found in 1999 [
2]. In these phases the polarization and tilt waves are "parallel", in a sense explained below. However, we shall show that when one permits the two waves to be "non parallel",
i.e., relatively shifted along the smectic normal or relatively rotated, four additional phases can be stabilized. The reason of this unusual extension of the polymorphism, which is characteristic of transitions with continuous-symmetry breakdowns, has been described within the context of superconductivity in Ref. [
14].
The bent-core theory exhibits a quite remarkable analogy [
7] with the theory of d-wave superconductors in 2D systems [
15], such as high-T
c lamellar superconductors or unconventional superfluid films. This analogy relies upon the fact that the two theories have the same "image group" [
16], that is, the same set of matrices associated with the symmetries of the parent, isotropic or normal, phases. The main consequence of this peculiarity is that both systems have the same list of phases with analog symmetry groups, the same theoretical phase diagrams, and the same thermodynamic variations of the primary and secondary order parameters. At first sight the analogy is rather formal since a common matrix can be associated with distinct actual symmetry elements in each system. For instance, a gauge symmetry in superconductors yields the same matrix as a translation in liquid crystals. Thus, we do not expect a common behavior of the same physical quantities. However, the analogy is more subtle for it relates in fact the behaviors of distinct, but analog, tensors. For instance, the macroscopic polarization normal to the smectic planes exhibits exactly the same thermodynamic behavior as the linear magneto-electric suceptibility in superconductors. More precisely, both cancel in analog sets of ordered phases, with the same critical exponents.
This universality property relating distinct systems is a well-known feature of the Landau theory of phase transitions [
16,
17,
18]. When the image group is small, the physical consequences of the analogy are poor, and the number of analog systems is large, and conversely when the image group is large. For instance, deGennes used such an analogy between s-pairing superconductors and smectic A liquid crystals [
19], on the one hand, and between neutral superfluids and smectic C [
20], on the other hand. These two analogies bear much information because the image groups are continuous. In the first analogy gauge symmetries correspond to translations in Smectic A, while in the second analogy they correspond to rotations in Smectic C. In both cases the order parameter is bidimensional, describing density waves, on the one hand, and the molecular tilt, on the other hand. deGennes extended further the former analogy by proposing a liquid crystal analog of the superconducting gauge-type coupling with the magnetic field [
21,
22,
23], which goes much beyond the coincidence between image groups.
In the case of bent-core mesophases the image group contains four connected bicontinuous parts [
7,
8]. This very large group yields thus a still more fruitful analogy, which permits to relate precisely the rich polymorphisms of the two systems, and an infinite set of tensors accounting for most of their physical properties. It mixes the two deGennes analogies since both rotations and translations are simultaneously broken in the bent-core ordered mesophases. We shall use this analogy to complete the d-wave theory, and to predict the behavior of its stable phases. In particular, we shall focus attention on the properties of the electronic excitation spectrum, which is a key physical feature of these systems crucially depending on symmetry considerations.
The analogy is complicated by the dual internal structure of the two theories. Indeed, the image groups are products of two isomorphic one-dimensional subgroups, which can be interchanged without modifying the formal structure of the theories. This duality relates rotations and translation in the liquid crystal system, and rotations and gauge symmetries in superconductors. In both cases it defines an inner automorphism of the bicontinuous group, which is realized by a dual operator permuting its subgroups. The fact that the free energies are invariant under this operator yields many interesting consequences. Firstly, it permits to classify all the objects involved in these theories, phases, symmetry groups, and physical tensors, into either self-dual objects or dual-conjugated pairs, revealing many non-trivial features of these systems. Secondly, it provides a deep insight into both mathematical and physical aspects of the theories. We shall show in particular how the classification of line defects in bent-core phases results from the dual character of the order parameter.
2. The Vector-Wave Model
The primary order parameter of the vector-wave model describing ordered bent-core mesophases [
7,
8] is spanned by a transverse polarization wave
(z):
where the axis Oz is parallel to the wave vector
, so that its two components remain parallel to Ox and Oy. p
x, p
y,
and
are the real amplitudes and phases of the wave. The characteristic features of
(z) may be more conveniently expressed in terms of the following complex amplitudes:
Although this order parameter contains only four components,
, the vector wave belongs in fact to an infinite-dimensional irreducible representation of the Euclidean group O(3)
T
3, where O(3) is the orthogonal group generated by rotations and inversion, and T
3 is the 3D continuous translation group. It is spanned by an infinite set of waves propagating along all the directions of space. However, since for stabilizing ordered smectic-type phase one needs to consider only the two parallel wave vectors
=k
and -
appearing in Eq. (1), one can restrict the symmetry analysis to the subgroup
of O(3)
T
3 leaving the set {
and -
} invariant.
is generated by the rotations
around z, the space inversion I, one mirror plane
parallel to
and the translations T
t parallel to Oz. The action of these symmetries on the complex amplitudes (
) is given by the matrices:
One can refine the description of the symmetry-breaking mechanism by considering a secondary wave
(z) representing the mean tilt vector of the molecules located at position z:
where
and
form a basis of unit orthogonal axial vectors. The complex amplitudes of
are defined as in Eq. (2):
The corresponding matrices of are deduced from those in Eq. (3) by changing the signs of the inversion I and of the mirror plane .
The presence of two continuous symmetries in (3) implies that the order parameters split into two “Goldstone angles”
and
:
and six “energetic components”: On the one hand, a
1, a
2 and
, which describe the shape of
and
separately, and, on the other hand,
which describe the relative orientation and z-position of the two waves.
is naturally associated with the subgroup generated by rotations and the space inversion I since it transforms as:
whereas
is associated with translations and the mirror plane
since:
In a single domain of any ordered phase and can be set to zero by suitably choosing the coordinate frame. In the sequel we shall often implicitly assume such a choice.
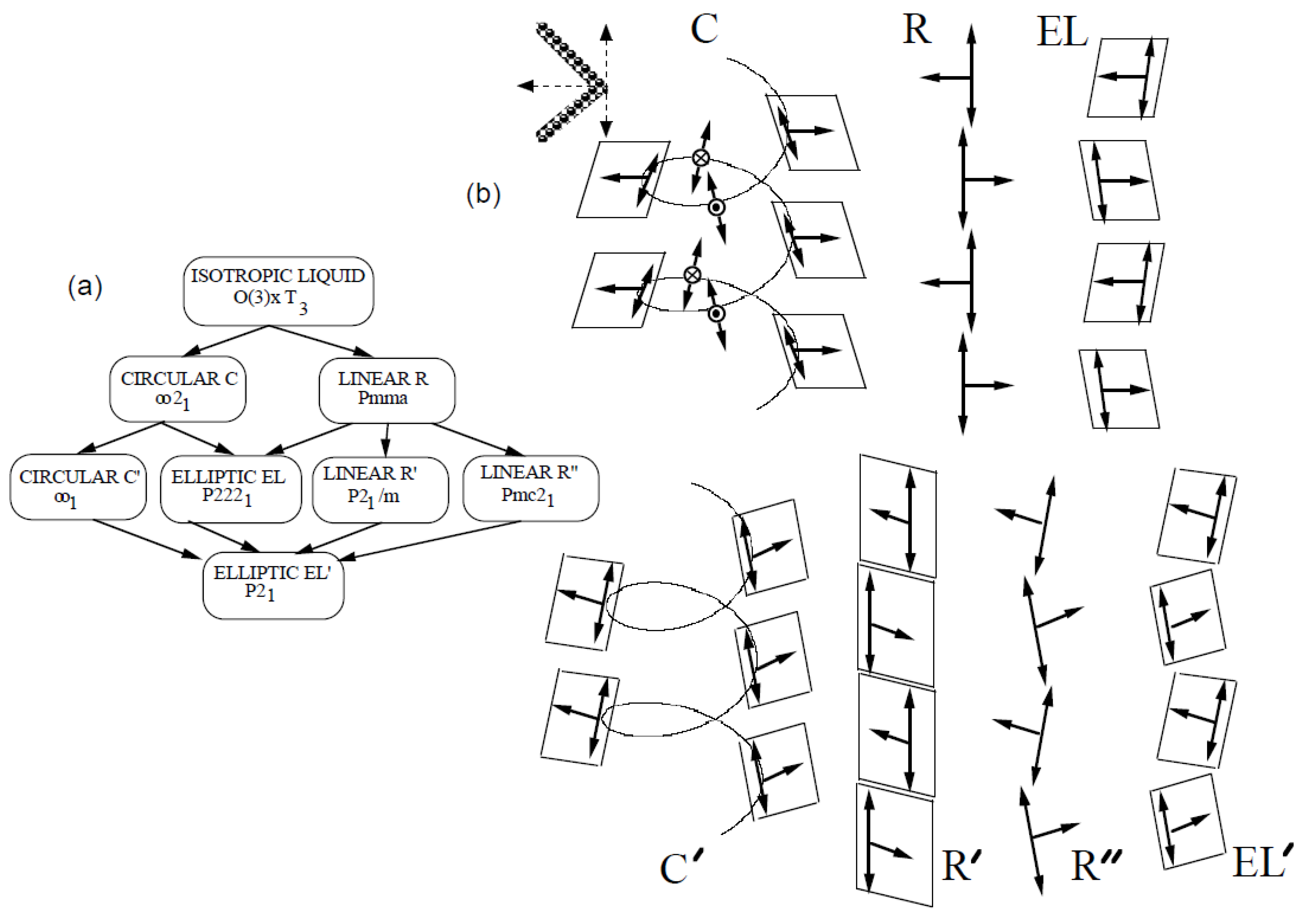
Eight phases are stabilized. In a first set of four phases already described in Refs. [
5] the two order parameters are “parallel” (in a broad sense indicating that the symmetry groups of
(z) and
(z) coincide). In this set all the phases, denoted by L, R, C and EL, satisfy the "parallelism" constraints:
L: Isotropic liquid.
R: Linear phase. and are both linearly polarized. The plane of polarization of is normal to that of and the maximums of the primary wave coincide with the nodes (zeroes) of the secondary wave, and reciprocally. Its symmetry is the non-chiral orthorhombic space group Pmma.
C: Circular phase. The two waves are circularly polarized, and is everywhere parallel to . Its chiral helical symmetry is (generated by and U2x).
EL: Elliptic phase: The two waves are elliptically polarized. The system of elliptic axes of and are parallel so that the two fields are parallel at positions where they are either maximum or minimum. The group is P2122.
In the second set of four phases, which were not considered in [
7,
8], the polar and axial waves are no longer “parallel”:
C’: The two waves are circularly polarized. (z) is shifted along z with respect to (z) so that they are turned everywhere to the same angle . The group is .
R’: The two waves are still linearly polarized but the two corresponding planes are no longer perpendicular. The plane of is rotated with respect to the plane of by an angle . The relationships between the maxima and the zeroes of the two waves in R persist in R’. The group is P21/m.
R”: The converse situation occurs in R”. The two polarization planes are again perpendicular, but the maximums of one wave are now shifted along z with respect to the zeroes of the other wave to a distance . The group is P21ma.
EL’: The two waves are elliptically polarized and oriented along independent directions. The group is P21.
We present in
Figure 1 schemes of the molecular structures associated with the various ordered phases and the group-subgroup relationships characterizing this polymorphism. We have discussed in our previous articles the assignment of the observed phases with our predictions for unprimed phases and 2D and 3D structures stabilized when one considers several waves with non-parallel wave vectors.
Let us notice that our thermodynamical analysis is based on the homogeneous part of the free energy which does not contain the gradient invariants of the Ginzburg-Landau approach. The model yields only homogeneous stable states. For the inhomogeneous states it gives the access only to their local structure, but not to the global one. We have shown in Ref. [
7,
8] that homogeneous single domains of the phases C and R can be stabilized, while EL, because of its spontaneous chirality, is automatically submitted to an incommensurate longitudinal deformation. We expect also that this phase presents transverse deformations, which could account for the complex inhomogeneous spatial structure reported experimentally in the bent-core phase B7.
Numerous phases and subphases have yet been observed in bent-core systems. They are usually identified by characteristic textures, while their molecular organization and space groups are often not known exactly. In particular variants associated with a single texture can be associated, or not, with distinct symmetries, i.e. distinct phases. We have identified sixteen among the main phases and subphases within the vector-wave model. On the one hand, most of them are two- or three- dimensional, so that waves with non-parallel wave vectors participate to the ordered structure. On the other hand, the one-dimensional phases are (provisionally) identified as follow: SmCP=R, B2=EL, C’ or EL’, B6=R’ or R", B7= C, C’ or EL’, Sm0=EL’, and B8 is a subphase of EL’ obtained with an additional homogeneous order parameter.
The physical behavior of each phase is characterized by a number of secondary tensors waves. Among the most important one may notice: (i) Density waves, which give the phases R, R’, R”, EL and EL’ the structure of layered smectic phases. (ii) Macroscopic polarization along Oz arising in R” and EL’. (iii) Anisotropic components of the optic tensor in the monoclinic and orthorhombic linear and elliptic phases.
In order to classify the infinite set of tensors waves let us introduce the following convenient notation, in which in most cases two integers, namely [n,p], are sufficient: One [n] indicates its tensor properties, and the other [p] its wave vector. These numbers refer to the irreducible representations of the Euclidean group O(3)T3. For non-zero wave vectors, the tensor waves are classified according to the 2D-rotation little group SO(2) of .
(a) First, let us denote a 2D-tensor of rank n>0 with the symbol and, for n=0 by its parity with respect to the mirror plane (scalar , and pseudo scalar ). For instance, a polar vector (Vx,Vy,Vz), splits into one 2D-vector (:Vx,Vy) plus one even 2D-scalar (:Vz).
(b) Since all the ordered phases are periodic the tensor waves have wave vectors =p (p integer). At p=0 there is a single homogeneous “wave”, which can be either even or odd under I. Hence, the classification of waves is similar to that of 2D-tensors in (a), and one may use the same symbols , and for representing the corresponding waves.
We shall denote now symbolically by a tensor wave of rank n and wave vector p. Its dimension is either 1 (), 2 ( or ) or 4 (). The index n indicates how the wave transforms under rotations, and p how it transforms under translations. For instance, there are two polar-vector waves with wave vector : One transverse wave () which coincides with the primary order parameter of our model, and one longitudinal wave ().
We classify these tensor waves with respect to the group G
L=
, which is isomorphic to the abstract group O(2)
O(2). The first copy of the 2D orthogonal group O(2) is
, generated by the rotations about Oz and the mirror plane
. The second copy contains the group T
1 of translations along Oz (mod. 2
/k since we consider only waves with wave vectors p
) and the space inversion I. Thus the image group can be rewritten as:
where
indicates the semi-direct product, and
the direct product. The indices R and T denote the rotation and translation O(2)-subgroups of G
L. C
S={e,
} and C
i={e,I} (rigorously speaking the actual image group is rather G
L/{e,
} since
is represented by the identity matrix in Eq. (3)).
The previous classification of tensor waves is directly related to the representations of GL. The irreducible representations of OT(2) and OR(2) are both labeled , and n (n positive integer). For OR(2), 0+ and 0– represent 2D-scalars, respectively even and odd with respect to , and n represents a 2D-tensor of rank n. In OT(2), 0+ and 0– represent homogeneous quantities respectively even and odd with respect to I, and p represents a wave with wave vector p. Then the full set of tensor waves can be classified according to the following irreducible representations of OR(2) OT(2):
: homogeneous scalar, invariant under and I (e.g., density).
: homogeneous scalar, invariant under and odd under I (P).
: homogeneous scalar, odd under and invariant under I (A).
: homogeneous scalar, odd under and I (chiral index ).
n: homogeneous tensor of rank n, symmetric under I (A, A for n=1).
n: homogeneous tensor of rank n, odd under I (P, P for n=1).
p: scalar wave with wave vector p (density wave or Pz(z) for p=1).
p: pseudo-scalar wave with wave vector p (e.g., Az(z) for p=1).
np: tensor wave with rank n and wave vector p (e.g., order parameters (z) and (z) for n=p=1).
The chiral index is a pseudo scalar, which vanishes in non-chiral phases and changes its sign in two domains of opposite handedness in chiral phases. (0) and (0) are homogeneous axial and polar vectors, whereas (z) and (z) are axial and polar transverse vector waves with wave vector . The transverse components of the axial vector (0) represent the tilt vector. Its longitudinal component A can be interpreted as the component txxz+tyyz of the second-order electroclinic tensor tijk defined by A=tijkEjEk, which describes the action of high electric fields on the homogeneous tilt vector. The dielectric and optic tensors {} are examples of 2, whereas the first-order electroclinic tensor {}, where , provides an example of 2.
These tensors permit also to visualize geometric (translational and rotational) aspects of the wave
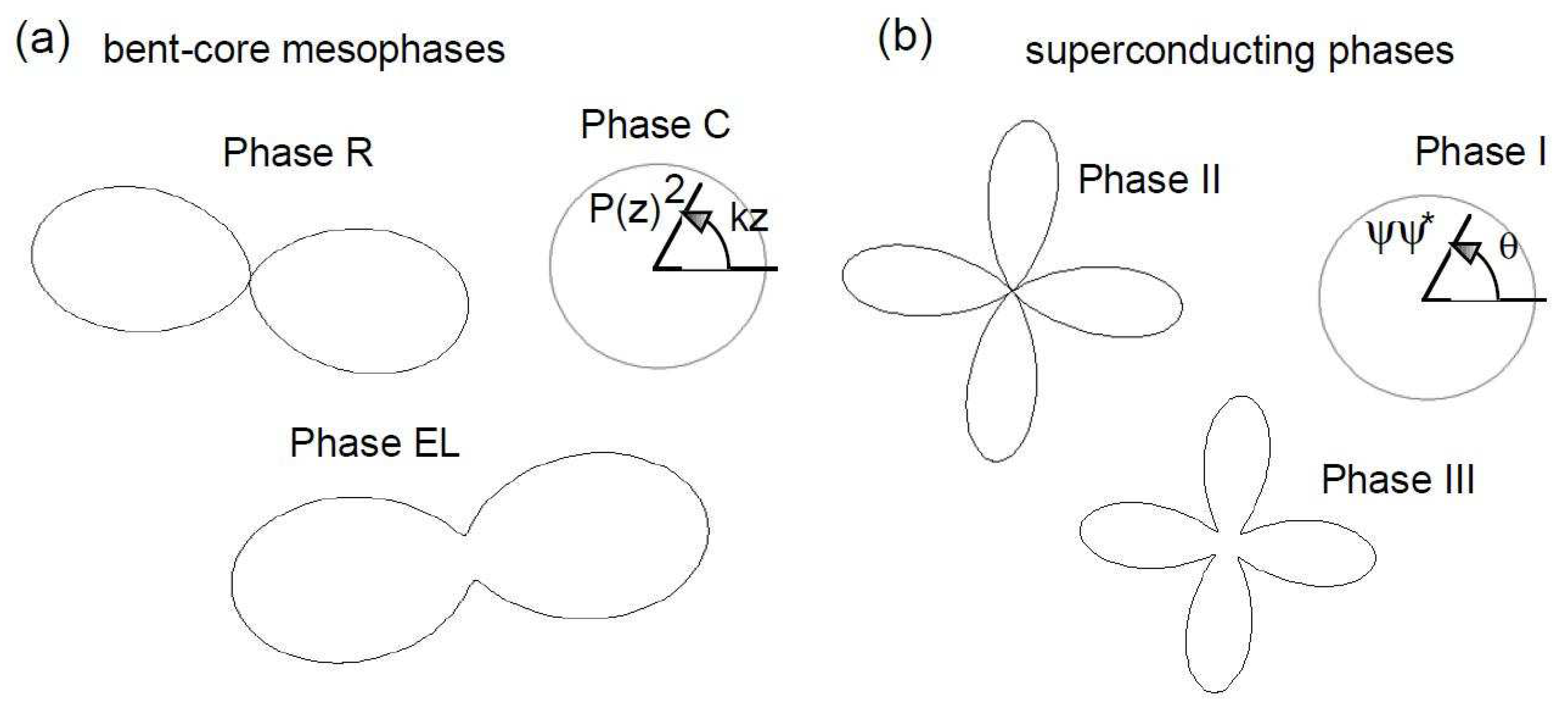
(z). To isolate its translational properties let us define the scalar function:
where n
L the scalar
, and
transforms as
. To visualize M(z) we consider M and kz as the radial and angular polar coordinates, respectively, in an abstract plane where the function M(z) defines then a closed orthorhombic curve (
Figure 2a). It is invariant under a rotation
, and it rotates under a translation T
t. In the EL-phase the curve has the shape of a double balloon which becomes circular in the C-phase, and which splits into two parts in the R-phase. The splitting results from the cancellation of
P(z) at periodic positions, denoted by “nodes” of the wave, along z in R. The presence of a node is associated with specific symmetry elements that we shall discuss below. Let us notice that a "dual" description of the angular properties of the wave is provided by the
–type tensor:
. Finally, these two tensors and corresponding figures can be similarly defined with the secondary wave
(z) in order to distinguish graphically primed and unprimed phases.
All tensors and tensor waves (except density) vanish in the isotropic liquid and can get finite values in one or several ordered phases. The list of the corresponding "permitted" tensors is given in
Table 1 for all the ordered phases.
One sees that if a phase is symmetric under the screw rotation , then the tensor waves with n+p odd vanish. This rule forbids, for instance, transverse ferrielectricity (because P=P=0) and ferriclinicity (A=A=0), on the one hand, and longitudinal antiferroelectricity (cancellation of the wave Pz(z) with period ), and anticlinicity (wave Az(z) with period ), on the other hand. Then, the ordered phases can only be transversely antiferro- and longitudinally ferro- electric or -clinic. Likewise, only even harmonics of the density wave can condense, so that the smectic character of the phases corresponds always to a bilayer ordering (smectic period = /2).
More generally,
Table 1 displays the main physical effects permitting one to distinguish experimentally the various ordered phases arising in the model:
(i) In C, all the tensor waves with n=p condense and are circularly polarized. The corresponding polarization has, of course, always the same handedness as the structure. Since phase C is chiral, takes opposite values in domains with different handedness. C remains non-smectic (zero density wave), non-polar, and optically uniaxial. In contrast, in C’ a homogeneous polarization (P) takes place along the helix axis. Moreover the presence of a homogeneous longitudinal tilt vector along Oz (A) leads to a macroscopic second-order electroclinic effect.
(ii) R is smectic (with period /2), non-chiral, and optically biaxial (). The RR’ transition is characterized by the onset of a second-order electroclinic effect (txxz+tyyz). But, in contrast to C’, no homogeneous polarization arises along the helix axis. Conversely, at the RR” transition the system becomes longitudinally ferroelectric, but without any second-order electroclinic effect.
(iii) At the CEL transition first-order electroclinic coefficients () arise, and the phase becomes optically biaxial () and smectic. At the REL transition, the system becomes chiral () and first-order electroclinic (). At the ELEL’ transition the system becomes homogeneously polarized along Oz, and begins to exhibit a second-order electroclinic effect (txxz+tyyz). Finally, at the R’EL’ transition the system becomes chiral, polar along Oz with first-order electroclinicity, whereas at the R”EL’ transition the chirality is accompanied by a longitudinal pseudo-scalar wave with period /2 and a second-order electroclinic tensor.
Table 1 exhibits spectacular regularities: In all the phases, except R’ and R”, if a tensor wave of the type
(R)(T) (R, T=n,
or
) is permitted, then the “dual” tensor
(T)(R) is also permitted. Furthermore, if
(R)(T) is permitted in R’ then
(T)(R) is permitted in R”. Finally, all tensors of the symmetric type (
(T)(T)) and only them, are permitted in C. The following section is devoted to explain and formalize these regularities that we shall denote by the
rotation/translation dual character of the vector-wave model.
3. The Dual Symmetry
The properties of the two Goldstone angles and shown in Eq. 6 together with the previous classification of tensor waves reveal the duality relating translations and rotations in the vector-wave model. This duality originates (i) in the structure of the image group GL (Eq. 7), in which the translation subgroup T1Ci is isomorphic to the rotation subgroup , (ii) in the fact that the tensor-wave representation associated with the order parameter (z) is , in which the indices have the same unit value (n=p=1) for its tensor (rotations) and wave (translations) aspects. This duality relates different symmetry operations (e.g., rotations to translations ), different tensor fields (e.g., to ) different components of the order parameter ( to ) and different phases (e.g. R’ to R”). It permits one to explain also various specific properties of “self-dual” objects such as , or the C-phase.
The duality idea can be rigorously formalized by means of a “dual operator” D, defined by the following matrix in the primary order-parameter space (
):
and by the same matrix in the secondary (
) space. The fact that D transforms translation-like objects into rotation-like ones is made clear by using the following notation for the basis functions in the order-parameter spaces:
, where the first index ± is associated with the wave part (
) of the basis function (appearing in Eqs. (1) and (4)) and the second index with its vector part (
). Then, D simply permutes the wave and vector indices:
(note that any combination of D with a symmetry of G
L might be used as well as the definition of a possible duality operator). Furthermore, D permutes also the elements of O
R(2) with those of O
T(2):
If one combines D with GL, then one finds an “extended” group which contains “dual-free” elements g (belonging to GL) together with dual combinations gD of D with dual-free operations. is not a symmetry group in the usual sense because D is a classificatory operation, which has a descriptive role, and not a dynamical symmetry constraining the physical properties of the system. However, the free energy of the vector-wave model is invariant under D, so that the list of low-symmetry phases and their thermodynamic properties have well-defined dual features (e.g., dual pairs of phases appear in symmetric parts of the theoretical phase diagram). This makes a classification of the phases based on the duality operator consistent. We denote by the extended symmetry group of the phase "ph" (=C, R, EL, R’…), defined as the subgroup of leaving (z) and (z) invariant.
In the domain obtained by canceling the angles and the extended groups of C, R, and EL contain D itself. This property is reminiscent of the “magnetic groups” in which the time-reversal operation (formally analogous to D in our approach) may be or not combined with spatial symmetries. When a group contains the time reversal, it characterizes the properties of a paramagnetic structure (denoted by G1’ in Shubnikov’s notation, where G is any space group). However, this classification is not directly relevant for duality because D can be present in the group of one domain of a phase and absent in another domain (where it is replaced by another possible duality operator gDg−1). Thus, it turns out to be more convenient to distinguish between “dual-free groups” (containing only dual-free operations) and “dual groups” (containing dual operations). The unprimed phases (R, C, EL) have dual groups while the primed phases (C’, R’, R”, EL’) have dual-free groups. In a phase with a dual group it is always possible to find one domain (by setting the two Goldstone phases to zero) in which D is present. Accordingly, we use the Shubnikov’s notation applied to this special domain for denoting the extended symmetry groups of the unprimed phase as whereas in the primed phase .
Unlike time reversal, D does not commute with all the elements of GL. It commutes only with the operations provided that (n integer) and with the twofold axes U2x and U2y (or with a different pair of perpendicular twofold axes if one chooses another definition for D). We denote such operations as “self-dual” (they form a group coinciding with that of a cholesteric). For the non self-dual operations g one can thus define their dual conjugate DgD (DgD=g when g is self-dual, because D2 is the identity operation). This permits one to make a more subtle classification of the low-symmetry groups that splits them into “self-dual groups” (which contain only self-dual operations), “globally self-dual groups” (such that DD=) and non-self-dual groups. In the latter case is associated with its “dual-conjugate” DD. Any dual group is automatically globally self-dual. C, C’, EL and EL’ are self-dual, R is globally self-dual, and R’ and R” are non-self-dual phases which are mutually dual conjugated. The analogy between duality and time reversal is correct only for the self-dual groups, since in this case D is present in all the domains of the dual phases. C and EL are then analogous to paramagnetic structures whereas C’ and EL’ are analogous to ferromagnetics.
In order to discuss the consequences of this classification let us first extend the duality idea to tensor waves. A set of measurable physical quantities transforming as (a,b=,,1,2,3…) is either “self-dual” if a=b or associated with its “dual-conjugate” transforming as . For instance, the order-parameter modulus (, which transforms as ) and the chiral index are self-dual scalars, whereas the order parameters (z) and (z) are self-dual vector waves. On the other hand, the homogeneous polarization P and the homogeneous “tilt vector” A are dual-conjugated scalars. The homogeneous tilt vector in the x-y plane (A, A) is dual-conjugated with the first harmonic (i.e., with wave vector ) of the density wave, whereas the homogeneous polarization (P,P) is dual-conjugated with the first harmonic of the chirality wave (z). The macroscopic optic tensor (xx–yy,xy) (second-rank homogeneous tensor) is dual-conjugated with the second harmonic of the density wave.
The main physical consequences of the duality result from the following fact: Whenever a dual-free symmetry g forbids the existence of a tensor wave (or some of its components) transforming as , its dual-conjugate DgD forbids (the same components of) . For instance, the inversion I cancels the three components P and (P,P) of the macroscopic polarization, then the mirror plane =DID cancels the homogeneous tilt A and the first harmonic of the chirality wave (z). Consequently, in a globally self-dual phase the forbidden tensor waves are either self-dual or appear as dual-conjugated pairs. The same property occurs for the allowed tensor waves. Furthermore, allowed dual-conjugated tensor waves have similar thermodynamic properties: They vanish at the same temperature with the same critical exponents. Analogously, in the dual conjugated phases R’ and R”, whenever a tensor wave is forbidden (or allowed) in one phase, then its dual conjugate is forbidden (or allowed) in the other phase (with the same thermodynamic behavior):
1- In the C-phase the homogeneous polarization (P,P) and tilt vector (A, A) are forbidden, then their dual-conjugates, namely the first harmonic of the density wave and of (z), are also forbidden. Moreover, GC forbids any homogeneous tensor (except scalars) and, according to the previous duality rule, any scalar wave. Thus, C is macroscopically 2D-isotropic and not smectic: It is optically uniaxial, on the one hand, and it does not give rise to Bragg peaks in normal (non-resonant) x-ray diffraction, on the other hand. Moreover, the order-parameter modulus nL () and the chirality index () are permitted while the macroscopic longitudinal polarization P () and tilt vector A () vanish. Indeed, the helical symmetry of C makes it “maximally self-dual” because it allows only self-dual tensor waves () and, furthermore, all the self-dual tensor waves. For instance, in the x–y plane a single harmonic (with wave vector ) of the polarization (z) and tilt (z) waves are allowed, hence making the C-phase perfectly helielectric. Similarly, a single harmonic (with wave vector 2) of the 2D-optic tensor (xx(z)–yy(z),xy(z)) is permitted, yielding the same rotatory-power effect than in a cholesteric phase, and the same optic gap features (within a much shorter wavelength range).
2- C’ differs from C only by the onset of P and A: It is ferroelectric along Oz because the molecular polarization, which is normal to in C, is uniformly tilted around an axis normal to and to the molecular symmetry axis. On the other hand, several tensor waves with the same transformation properties (as, for instance, (z) and (z)), which are locked in parallel directions in C, may have different orientations in C’. For instance, (z) and (z) are mutually shifted by a constant angle in C’.
3- In the group of the linear R-phase the mirror planes (and inversion) are not self-dual but they appear by pairs of dual-conjugated operations: and . R is smectic and permits all the even harmonics of the density wave () and all the homogeneous even-rank tensors () as for instance the 2D-optic tensor (xx–yy,xy), which makes the phase biaxial. R is also characterized by the onset of all the odd harmonics of (), each one giving one resonant Bragg peak at (2p+1). Simultaneously, the first harmonic of all the odd-rank tensor waves () are present in R.
The dual features of R’ and R” appear clearly as one considers the tensors appearing at the transitions RR’ and RR”. A homogeneous tilt vector A appears in R’ while a homogeneous polarization P appears in R”. A indicates that in R’ the direction of the transverse polarization (or equivalently of the molecular planes) is not locked, as in R, and can change with temperature. Along the same way, in R’ all the even harmonics of the chirality wave (z) appear, whereas their dual conjugates, the homogeneous pseudo tensors of even ranks, appear in R”. Moreover, on approaching the R’R transition temperature T’ the amplitude of the 2n’th harmonic vanishes as (T–T’)n, whereas the modulus of the tensor with rank 2n vanishes as (T–T”)n at the R”R transition temperature T”.
3- In EL all the tensor waves permitted in C and in R are also permitted. Moreover the odd harmonics of the density wave () together with the homogeneous tensors of odd rank () take non-zero values.
5. Analogy With d-Wave Superconductivity
Attracting fermions in two-dimensional systems condense at low temperature into bound states, the so called Cooper pairs [
24]. These states may be classified according to their angular and spin moments [
26,
27,
28]. For instance, in a conventional superconductor two electrons form a charged Cooper pair with zero orbital and spin moments. These « s-wave » pairs are responsible on the specific properties (zero resistivity, magnetic flux expulsion and Josephson effect) of the superconducting state. At the symmetry point of view superconductors are characterized by the breakdown of the electromagnetic gauge symmetry [
29]. Such gauge operations, denoted by g
, transform the Cooper pair wave-function
into equivalent wave functions exp(i
)
. In the superconducting state
is different from zero and the gauge symmetries are broken. However, since the s-wave function is isotropic it does not break the rotational symmetry. On the contrary, the wave function can break spatial symmetries when its orbital momentum is different from zero. Such a phenomenon occurs in various superfluid systems, such as the superfluid He
3 (p-wave pairing) [
26,
27,
28], the heavy fermions (p or d-wave pairing) [
30] and the high-T
c oxide superconductors (d-wave pairing) [
31,
32]. We shall show now that the theory of d-wave 2D superconductors is strongly analogous to the theory of bent-core liquid crystals.
Let S
1z and S
2z be the spins of two fermions at positions
1 and
2, and
(r,
,S
1z,S
2z) their wave function. r and
are the polar coordinates of the relative position
1-
2. In a d-wave the orbital momentum is L=2, and the spin is in the singlet state S(S
1z,S
2z) [
15]:
D
+=|D
+|exp(i
+), D
−=|D
−|exp(i
−), D
+* and D
−* are the four complex components of the order parameter. They transform according to an irreducible representation of the normal phase symmetry group, which contains the gauge transformations g
, the continuous 2D rotations C
, as well as the discrete time reversal T and mirror plane
x operations. The corresponding matrices are given by:
in the basis {D
+,D
+*,D
–,D
–*}. These matrices generate the “image group”:
where O
G(2) contains gauge and time reversal transformations whereas O
R(2) is the 2D rotation group C
v. As in the vector wave model O
G(2) and O
R(2) are isomorphic copies of the 2D orthogonal group O(2) (see Eq. (7)). One sees immediately that the order parameter (12) transforms as the irreducible representation
1(G)⊗
1(R) of O
G(2)⊗O
R(2). The analogy between the bent-core and d-wave models results from, (i) the group isomorphism of their high-symmetry phases (see Eqs. 7 and 13), (ii) the fact that in both cases the order parameter spans the irreducible representation
1⊗
1 of these groups. Consequently, the d-wave model [
15] exhibits a rotation/gauge duality completely analog to the translation/rotation duality of bent-core mesophases.
In order to realize concretely the analogy we may identify the image groups of the two systems along two ways. In the first way the rotation group of the liquid crystal is identified with the rotation group of the superfluid whereas the translation group is identified with the gauge group. In the second way the identifications are reversed. These cases are obviously dual-conjugated. More precisely:
First analogy: A rotation of the liquid crystal by an angle
is equivalent to a rotation of the superfluid by an angle
/2. A translation of
z along the helical axis is equivalent to a gauge transformation by an angle
=k
z (as in the deGennes’ analogy for Sm-A [
19,
21]). Space inversion I is equivalent to time reversal T, and the liquid crystal mirror plane
x is equivalent to the superfluid mirror
x. This yields the following identification between the order-parameters:
Second analogy: In the second identification the rotational properties of the superconductor are equivalent to the translational properties of the liquid crystal (as in the deGennes’ analogy for Sm-C [
20,
21]):
Accordingly, the physical (i.e., gauge-invariant) properties of d-wave Cooper pairs identify with either liquid crystal translational properties or with their dual rotational analogs.
This comparison allows us to expose the properties of superconducting phases by simply translating those studied in bent-core phases. However, the analogy is actually complete when one defines a secondary wave function, analog to
, with the same symmetry properties as
(r,
,S
1z,S
2z). This can be achieved in many different ways, one of them being described in Ref. [
14] within the context of s-wave superconductivity. Thus, the four unprimed phases, which have already been calculated with a single wave function in Ref. [
15], can then be complemented by four additional primed phases. Their properties are summarized in
Table 2a and
Table 2b, and compared with their bent-core analogs. The gauge part of the symmetry groups are not indicated in these tables. Moreover, in systems containing a mirror plane parallel to x,y (for instance in high-T
c superconductors), this plane is never broken by the order parameter, and it must be included in the ordered symmetry groups. For instance, the magnetic symmetry of phase II becomes 4mmm1’.
Phase III and EL help us to illustrate some aspects of the analogy physical meaning. Indeed, the phase-III wave function can be understood as a quantum superposition of Cooper pairs with orbital moments oriented toward +z and pairs oriented toward –z. Likewise, the elliptic phase results from the superimposition of two circularly polarized waves of opposite handedness. In II the up and down pairs arise with the same amplitude so that the total magnetic moment vanishes. In the analog linear R phase the right and left helices have the same amplitude, so that there is no winding of the polarization. On the other hand, in I all the pairs are up and the magnetization is maximum, whereas in its analog C an helix with a single handedness is present so that the chirality is maximum.
The dual classification of physical quantities has a different interpretation with the superconductors. Indeed, the representation
np can be associated with an observable only when n=0 since only gauge-invariant quantities are measurable. Thus, we have only to consider the quantities
,
,
p, which represent scalars, pseudo scalars and p-rank tensors invariant under time reversal, on the one hand, and their antisymmetric time-reversal counterparts
,
,
p, on the other hand. Their values in the ordered phases can be deduced from
Table 1 on using any one of the previous analogies (being careful that a tensor of rank p in liquid crystal is associated with a tensor of rank 2p in superconductors!).
Let us now consider the lowest-degree tensors:
a) Scalars: Pair density n
S, z projection of the orbital momentum L
z and z projection of an axial vector A
z. The scalar
antisymmetric under time-reversal is the response coefficient associated with a second-order magneto-electric effect:
=
. In structures where
is finite a polarization
perpendicular to the electric field
appears when a magnetic field
is applied. This effect happens for instance in unconventional s+s’ superconductors [
21].
b) Second-rank tensors: Dielectric tensor: [2xy, xx-yy], and a second-rank tensor antisymmetric under time-reversal [2xy, xx–yy]. The 3D tensor is the response function of the linear magneto-electric effect = where is the polarization and the magnetic field.
c) Forth-rank tensors: [A,B] on the one hand, and a fourth-rank tensor antisymmetric under time reversal [A’,B’]. The latter tensor may represent the elastic (uij) response (Mijkl) to a bilinear magneto-electric excitation: uij=MijklBkEl. Where A’=M1111–M2211–M1122+M2222, and B’=M1112–M2212–M1121+M2221.
The superconducting tensors and their liquid-crystal analogs are indicated in
Table 3. As an example, the bilinear magneto-electric coefficient
in the superconducting phase has two analogs, a homogeneous longitudinal polar vector P
z and a homogeneous longitudinal axial vector A
z. Note again that according to the first analogy liquid-crystal tensors of rank r are associated with superconducting tensors of rank 2r. For instance, the fourth-rank elastic coefficients in the superconducting system are associated with the second-rank optical tensor in the liquid crystal.
As with bent-core mesophases, four physical quantities quadratic in the order-parameter components are sufficient to characterize most of the physical properties in the unprimed phases:
nS =|D+|2+|D−|2 represents the Cooper pair density ().
Lz =|D+|2–|D−|2 represents the 2D orbital momentum ().
A = D
+*D
− + D
−*D
+, B = i (D
+*D
− + D
−*D
+ ) form a quadrivalent tensor (
2), which can be used to characterize the angular variation of the pair wave function. Indeed, let us write the gauge-invariant norm of
as:
This expression permits one to draw the wave function in each unprimed phase (
Figure 2b). It is circular in the isotropic phase I whereas it presents four branches in the other phases. In phase II the wave function vanishes along four directions. Along the corresponding directions in the reciprocal space nodes appear in the quasiparticle excitation spectrum. This means that when the wave vector
of a quasiparticle lies parallel to this direction, its energy vanishes continuously as
get closer to the Fermi surface, while a gap is present in general directions. The occurrence of such nodes results from specific symmetry operations in the phase-II group, and yields most of the unconventional dynamic and thermodynamic properties of this phase [
26,
27,
28].
A superconductor with four nodes in the excitation spectrum gap (phase II) is analog to a linearly-polarized vector wave (R-phase). The relation between nodes in the superconducting gap and zeroes of the polar wave is reinforced by comparing the four-leave curves (Eq.15) representing
* in phase II (
Figure 2b) and the bean-shaped curve M(z) (Eq.8) summarizing the translation properties of the polarization wave in the R-phase (
Figure 2a). In the latter, only two leaves are present instead of four in its superconducting analog. This inessential difference results from the second-rank tensor angular character of a d-wave Cooper pair
vs. first-rank of the polarization wave.
The analogy between nodes in the excitation spectrum and zeroes of the polar wave in phases II and R is a consequence of their common symmetry features. For instance, from analogy 2 the linear character of the vector-wave (due to the mirror plane x) is related to the paramagnetic feature of phase II (due to the time reversal T). Let us consider one domain of phase II defined by +=−=0. Its symmetry group is generated by gC, T and x. gC changes the sign of the wave function after a 90° rotation, therefore () must vanish along four directions. This is the symmetry origin of the four nodes occurring in the gap. In order to determine the vanishing directions let us consider the symmetry gCx=gxy, which changes the sign of the wave function together with a mirror plane directed along x+y, which transforms into /2-: gxy()=−(/2−). The invariance of under gxy provides immediately the four nodes directions: (/4)=(3/4)=(5/4)=(7/4)=0. The zeroes of the vector-waves result from the same arguments. According to the second analogy the generators of the R-phase are CT, x and I. CT means that the transverse vector-waves reverse their directions after a translation of /2. x indicates that (z) is polarized in the (y-z)-plane and (z) in the (x,z)-plane. Since the transverse axial and polar vector-waves are linearly polarized and reverse their directions after /2, they must vanish on a lattice of points separated by /2. To determine the positions of these zeroes, let us consider the mirror plane CTI normal to Oz and located at z=/4. This plane forces to vanish at z=/4 and 3/4. On the contrary, the zeroes of are determined by the location of the inversion centers I located at z=0 and (analogy 2 makes apparently and closer than and , because of the sign change D−−2* in the correspondences (13), a /2 phase shift appears between (z) and () as we introduce the additional correspondence kz).
In conclusion, let us note that in high-Tc superconductors (other superconductors or superfluid are either 3D or do not exhibit d-wave pairing) the exact symmetry is difficult to obtain experimentally (because it involves gauge transformations) and the phase can be identified by indirect gap measurements. In the experimental literature, only the most symmetric phases (I and II) are discussed. As usually in the theory of phase transitions, the least symmetric phases are much less likely, so that we do not really expect that all the predicted phases be actually stabilized."