Research on Buckling Failure Test and Prevention Strategy of Boom Structure of Elevating Jet Fire Truck

Abstract

The purpose of this study is to investigate the buckling behavior and failure mechanism of the boom of large-scale elevating jet fire trucks, so as to provide support for its safety design and service life improvement. In terms of research methods, a combination of double-version control tests and refined finite element simulations was adopted to carry out a systematic study. The research results show that the boom base plate exhibits typical sinusoidal wave buckling deformation when the load coefficient is between 0.45 and 0.5, and the wavelength is highly consistent with the theoretical prediction; under the critical load, the strain amplitude shows a significant nonlinear jump, which confirms the buckling mechanism of the coupling between geometric nonlinearity and material plasticity; under the ultimate load, the structure undergoes local buckling failure, the failure location is in good agreement with the simulation prediction, and the test results are highly consistent with the simulation results within the engineering allowable range, which verifies the reliability and applicability of the model. The research conclusion is the establishment of evaluation criteria for buckling failure of box-type knuckle arms: visible buckling waves appear, and the strain exceeds 40%. Based on this conclusion, optimizing the width-thickness ratio of the plate, strengthening the web constraint and improving the manufacturing process can effectively enhance the anti-buckling performance of the thin-walled box structure.

1. Introduction

Large-scale aerial fire-fighting vehicles, as core special equipment in modern fire rescue operations, integrate composite functions of emergency at heights and elevated fire suppression spraying. Leveraging technical advantages such as rapid response, operational mobility, and adaptability to complex scenarios, these vehicles serve as critical support for building a modern fire rescue system and enhancing capabilities in handling major disasters. Their role is indispensable in emergency scenarios such as fires in high-rise buildings and large-scale chemical plant rescues [1,2]. However, under prolonged high-intensity continuous operation, the structural reliability and durability of key load-bearing components face severe challenges [3,4]. Among these, the boom, as the primary load-bearing component, directly determines operational safety. Once buckling instability occurs [5,6,7], the equipment loses operational capability instantly, potentially triggering boom collapse, rescue disruption, and other cascading accidents, resulting in equipment damage, personnel, and irreparable consequences [8,9,10,11,12].

This study focuses on the buckling accident of the boom in a large-scale elevating jet fire truck (Figure 1a). As can be seen from the accident site image shown in Figure 1b, the failed boom section exhibits a typical structural local buckling failure mode, with the failure area characterized by prominent depressions [13]. The depressed parts are concentrated at the joint region between the web and the base plate in the middle section of the boom, and no overall structural fracture is accompanied, which further confirms its failure attribute of local buckling. In practical engineering applications, although the occurrence probability of boom buckling accidents in large-scale elevating jet fire trucks is relatively low, given that catastrophic consequences will occur once such accidents happen, the mechanism analysis [14,15,16] and prevention research [17,18] on such accidents hold significant engineering value [19,20]. From the perspective of mechanical loading characteristics, during the operation of the fire truck, the boom must continuously bear cyclic loads composed of self-weight, jet water load and wind load, while superimposing the vibration effect during equipment operation [21,22]. This leads to the continuous accumulation of stress damage [23,24] in the thin-plate areas of the boom (the welded area between the web and the base plate). When the accumulated damage exceeds the structural bearing limit, local buckling failure will be induced [25,26,27]. Finally, preventive strategies such as optimizing the width-thickness ratio of plates, strengthening web constraints and improving manufacturing processes are proposed [28,29,30].

This study addresses the key issue of boom buckling failure, innovatively proposes a test method, provides data support and practical guidance for analyzing its failure mechanism, and also refines buckling prevention methods for similar construction machinery. The conclusions not only facilitate the design optimization of the boom of elevated jet fire trucks, but also support the safety assessment and reliability improvement of large-scale special equipment, thus possessing both academic and engineering value.

2. Materials and Methods

2.1. Test Scheme and Purpose

This paper details the test method by taking the test of boom 2 (Figure 2 and Figure 3) as an example. A V402EX (MTS Systems (China) Co., Ltd., Minneapolis, MN, USA) wireless strain testing system was adopted, and a strain gauge array was accurately arranged in the buckling-sensitive areas of boom 2 (structural base plate and double-side webs). Quasi-static stepwise loading was applied via an actuator (from an initial load of 0 N to structural instability failure), and data on critical failure load and dynamic stress field were collected synchronously. This design aims to reconstruct the actual service load spectrum of the boom, and the real-time acquired strain-load response provides core experimental basis for the analysis of failure mechanisms [31]. The test focuses on obtaining three types of key data: (1) Critical buckling load and buckling mode shape, i.e., the classic instability threshold that induces buckling deformation of the compressed plate; (2) Ultimate failure load and macroscopic failure mode, which characterize the critical state where the structure finally loses its load-bearing capacity; (3) Strain evolution law, including the strain-load curve of measuring points (used for accurate identification of buckling initiation points) and the strain spatial distribution curve (used for analyzing the characteristics of buckling waveforms) [32]. The obtained data were systematically compared and verified with the nonlinear finite element model: on the one hand, the calculation accuracy of the model in stress field reconstruction and plastic development path prediction was checked, and the material constitutive relation and boundary condition settings were optimized; on the other hand, through mutual verification between test and simulation, the stress transfer mechanism and local stress concentration effect of the boom were revealed, and a method for identifying structural weak areas was established. To verify the universality of the conclusions, the boom specimen was replaced for repeatability verification after the first round of testing [33]. To verify the universality of the conclusions, two rounds of repeatability tests were conducted.

As shown in Figure 2, the actual gravitational load F and bending moment load M on the right side of boom 3 were converted into the axial loads of two actuators (F₁ = 239.2 kN and F₂ = −282.1 kN) based on the principle of mechanical equivalence (equivalence basis: load F = 4372.4 kg, bending moment M = 58,466,845.6 kg·mm under actual working conditions). In the test, this stress state was accurately reconstructed through synchronous proportional loading by the two actuators (Figure 3), and the loading regime was implemented in stages according to the preset percentage of the rated load (1× boom structure mass + 1.25× water mass) (

Table 1. Test load table.

Laod Coefficient	F1/kN	F2/kN	Specification
0.20	47.8	−56.4	Rated Load 20%
0.25	59.8	−70.5	Rated Load 25%
…	…	…	…
1.00	239.2	−282.1	Rated Load 100%
1.05	251.2	−296.2	Rated Load 105%
…	…	…	…
1.90	454.6	−536.0	Rated Load 190%

). To systematically study the failure mechanism, boom 2 was designed as two versions of control samples: the weakened version (thin-plate configuration) was used to capture the critical buckling behavior, while the reinforced version (thick-plate configuration) was used to explore the ultimate failure characteristics. When the load factor reaches 1.2, buckling occurs in the test structure; When the load factor reaches 1.9, the test structure fails. The test procedure strictly followed the steps below: ① Structural assembly and sensor calibration; ② Implementation of quasi-static proportional loading according to Table 1; ③ Synchronous collection of load–displacement response and strain field data. Through the innovative strategies of mechanical equivalent conversion and complementary verification with two versions, this scheme achieved three goals:

1.

Accurately simulating the actual multi-axial combined stress state

2.

Separating the evolution processes of buckling initiation (weakened version) and final failure (reinforced version)

3.

Establishing the mapping relationship between load percentage control and real failure modes

A high-resolution strain monitoring network was deployed in the buckling—sensitive area of boom 2 (Figure 4). This network was equipped with a total of 65 strain measurement points (Figure 5, Figure 6, Figure 7 and Figure 8, The measurement unit is mm in standard form), and their spatial distribution strictly followed the structural mechanical response characteristics: three columns (Columns A–C, 39 measurement points) were arranged on the base plate, and Columns D/E (26 measurement points in total) were, respectively, arranged on the webs on both sides. Each column contained 13 measurement points, forming an axial gradient distribution, and the gradient design of the spacing between measurement points covered the characteristic length of buckling wave propagation. The measurement point cluster was accurately positioned in the area with the maximum buckling factor, and its deployment scheme served three key functions:

Full-field strain characterization: The 5 measurement lines form an orthogonal strain monitoring matrix to simultaneously capture the coupling deformation mechanism between the base plate and the webs.

Data continuity guarantee: Strain gauges were not replaced during the entire test sequence, eliminating sensor reset errors.

Model verification benchmark: Providing a spatiotemporal comparison dataset for the stable stress area in finite element simulation.

A sample correlation control strategy was adopted in the test: when replacing a new boom specimen, strain gauges were reattached strictly according to the positioning dimensions to ensure the consistency of measurement points among different specimens. By balancing data continuity and data independence, this strategy simultaneously supported two research objectives:

(1)

Structural model accuracy verification (through systematic comparison between test results in the linear phase and simulation results)

(2)

Research on the evolution mechanism of boom failure (through high-density data to track the initiation and propagation path of local buckling)

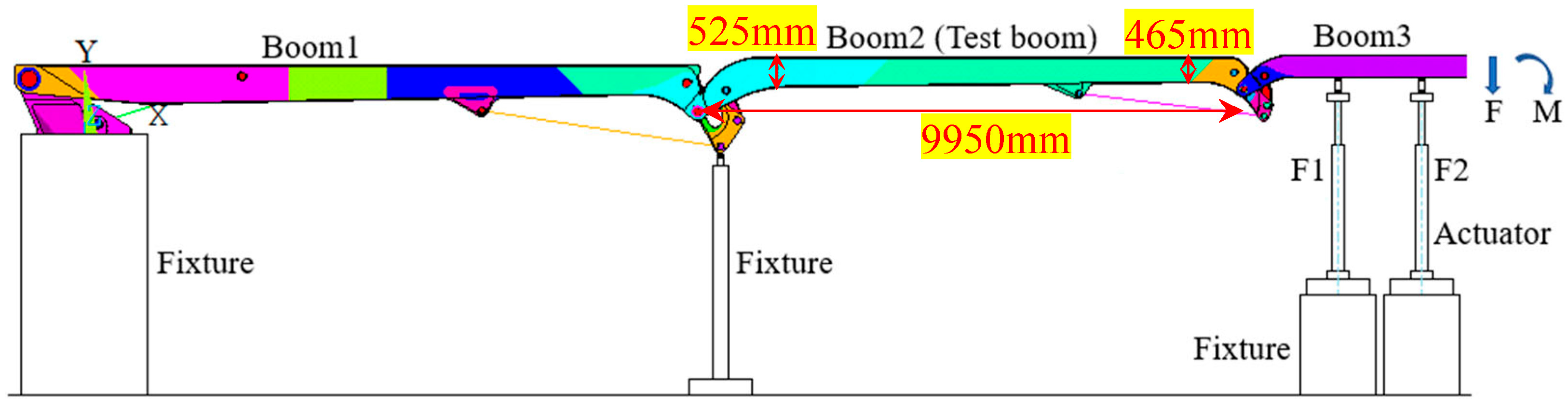
2.2. Test Equipment

As shown in Figure 5, the test equipment includes strain gauges, stress sensors, a signal transmission system, and a data processing system [34]. These devices together form a complete test platform, which is used to measure and analyze the stress changes in the boom under different working conditions. According to the structural characteristics of the boom and the direction of bending deformation, the strain gauges are placed on the surface of the lower base plate and side plates of the boom, and the pasting direction is arranged along the length of the boom to ensure the accuracy and validity of stress results during the real-time monitoring of the boom loading process [35]. To realize real-time monitoring and transmission of data, the strain gauges are connected to the stress sensors via wires. The stress sensors are responsible for converting the stress signals detected by the strain gauges into transmittable electrical signals, which are then transmitted to the data processing system through the wireless transmission system; the complete signal transmission process is shown in Figure 5. The data processing system is composed of a computer and dedicated software, which is specially used to receive, store, and analyze the signals transmitted from the stress sensors. It can display the stress changes in the boom in real time, process and analyze the acquired data, and select the maximum stress value as the test result.

2.3. Simulation Method

During the modeling process using ANSYS 2022R1 software (Figure 9), the boom structure was discretely simulated using Shell181 shell elements. This element is a quadratic superparametric shell element designed for thin-walled structures, and its mathematical model is based on the Mindlin-Reissner shell theory, which can accurately simulate plate and shell components where the thickness is much smaller than the size of the mid-surface. Numerical verification shows that when the thickness of the plate-shell structure meets the applicable conditions of the element, this model can accurately capture the stress distribution and deformation characteristics of welded box-shaped components under actual working conditions. Based on this, a high-fidelity mechanical simulation system containing 75,835 elements was constructed, which significantly improved the calculation accuracy and engineering applicability of the finite element analysis. The von Mises stress formula is given by:

$${\mathrm{\sigma }}_{\mathrm{v}\mathrm{m}}=\sqrt{{\displaystyle \frac{1}{2}}\left[{\left({\mathrm{\sigma }}_1-{\mathrm{\sigma }}_2\right)}^2+{\left({\mathrm{\sigma }}_2-{\mathrm{\sigma }}_3\right)}^2+{\left({\mathrm{\sigma }}_3-{\mathrm{\sigma }}_1\right)}^2\right]}$$

(1)

Herein, ${\mathrm{\sigma }}_1$, ${\mathrm{\sigma }}_2$ and ${\mathrm{\sigma }}_3$, respectively, represent the first, second, and third principal stresses in the spatial context.

2.4. Material Properties

The boom structure adopts Q890D high-strength steel to meet the load-bearing requirements. Key mechanical property indicators of this material, such as elastic modulus and yield strength, are presented in

Table 2. Properties of structural materials.

Material Property	Q890D
Density (kg/m3)	7850
Young’s Modulus (GPa)	210
Poisson’s Ratio	0.3
Tensile Yield Stress (MPa)	890
Ultimate Tensile Stress (MPa)	1000

, which provides data support for subsequent analyses. The test structure, fabricated by the equipment manufacturer in accordance with actual technical requirements and standard process specifications, was inspected to show no obvious initial defects and no abnormalities during the manufacturing process. In the finite element analysis, the bilinear isotropic plastic constitutive model was activated via the TB, BISO command, and the TBDATA command was used to assign the yield strength of 890 MPa and the tangent modulus of 1000 MPa for the plastic stage, respectively; this parameter setting is applicable to the nonlinear buckling numerical simulation of steel thin-walled structures.

2.5. Constraints and Loads

In this simulation model, the constraints and loads correspond one-to-one with those in the experiment. A full constraint is applied to the bottom of the turntable (Figure 10) to ensure the base remains stable and stationary during the loading process. The connections between the boom and the turntable, connecting rods, and loading tooling are all established via pin shafts (beam elements) to ensure the rotational degree of freedom between each structure.

To ensure the consistency and accuracy between the calculation results and the test conditions, vertical loads were applied at the corresponding positions of the connecting tooling (Figure 10), denoted as F1 and F2, respectively. The numerical values of these loads were strictly set with reference to the test-measured data, and their acting directions were completely consistent with the actual load directions in the test.

3. Results

To systematically reveal the failure mechanism of the box-shaped boom, a control sample system was constructed using two versions of boom 2: the weakened version (thin-plate configuration) focuses on capturing the critical buckling behavior, while the reinforced version (thick-plate configuration) emphasizes the investigation of ultimate failure characteristics. Hierarchical research on the failure mechanism was achieved through differentiated design. Aiming at the problem of original data redundancy caused by a large number of measuring points, the arithmetic mean method was used to statistically process the repeated test data under the same working conditions, so as to obtain characterization results with statistical significance. The test average values after data normalization (

Table 3. Test strain values of middle measuring points on the base plate of boom 2 with load variation (με).

Load Coefficient	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11	B12	B13
0	−865.3	−861.4	−847.2	−831.6	−818.3	−808.0	−799.3	−794.9	−787.9	−782.1	−776.0	−770.0	−763.5
0.2	−808.6	−848.8	−879.3	−872.5	−855.0	−830.3	−791.0	−766.5	−760.1	−761.3	−760.4	−769.1	−782.2
0.25	−806.9	−849.0	−904.9	−892.1	−875.7	−843.8	−787.8	−790.6	−763.2	−759.4	−758.0	−775.3	−796.3
0.3	−919.7	−999.1	−1053.2	−1093.2	−1139.6	−1066.8	−1025.9	−942.3	−933.1	−884.2	−943.0	−982.4	−987.6
0.35	−1145.6	−1216.0	−1302.4	−1344.4	−1358.7	−1305.4	−1228.1	−1109.5	−1073.8	−1043.0	−1105.8	−1146.1	−1274.6
0.4	−1296.0	−1392.2	−1460.7	−1547.9	−1516.8	−1498.7	−1374.8	−1297.8	−1220.7	−1139.7	−1253.2	−1293.1	−1404.5
0.45	−1421.9	−1506.8	−1585.4	−1638.9	−1670.7	−1673.1	−1555.1	−1410.7	−1372.2	−1281.4	−1442.4	−1540.6	−1601.4
0.5	−1510.6	−1619.8	−1840.9	−1910.9	−1943.6	−1850.3	−1752.6	−1512.9	−1401.1	−1309.7	−1471.0	−1601.6	−1782.1
0.55	−1248.6	−1567.5	−2017.4	−2281.0	−2294.4	−2206.5	−1925.8	−1453.3	−1238.4	−1198.8	−1296.8	−1503.6	−1813.1
0.6	−1158.7	−1596.2	−2109.2	−2393.8	−2457.0	−2375.2	−2085.6	−1296.4	−1103.7	−1038.3	−1150.2	−1450.7	−1903.2
0.65	−1068.8	−1624.9	−2171.1	−2580.8	−2654.6	−2518.7	−2132.6	−1215.9	−919.7	−869.1	−1103.1	−1523.2	−2033.2
0.7	−998.9	−1653.6	−2232.9	−2663.5	−2727.6	−2588.2	−2179.6	−1196.8	−853.7	−798.6	−1074.4	−1575.1	−2143.3
0.75	−949.0	−1682.3	−2294.7	−2746.2	−2800.7	−2657.7	−2226.6	−1177.8	−787.6	−728.1	−1045.6	−1626.9	−2253.3
0.8	−899.1	−1711.0	−2356.6	−2828.9	−2873.7	−2727.2	−2273.6	−1158.7	−721.6	−657.6	−1016.9	−1678.8	−2363.4
0.85	−849.2	−1739.7	−2418.4	−2911.6	−2946.8	−2796.7	−2320.6	−1139.7	−655.5	−587.1	−988.1	−1730.6	−2473.4
0.9	−799.3	−1768.4	−2480.2	−2994.3	−3019.8	−2866.2	−2367.6	−1120.6	−589.5	−516.6	−959.4	−1782.5	−2583.5
0.95	−749.4	−1797.1	−2542.0	−3077.0	−3092.9	−2935.7	−2414.6	−1101.6	−523.4	−446.1	−930.6	−1834.3	−2693.5
1	−699.5	−1825.8	−2603.9	−3159.7	−3165.9	−3005.2	−2461.6	−1082.5	−457.4	−375.6	−901.9	−1886.2	−2753.6
1.05	−649.6	−1854.5	−2665.7	−3242.4	−3239.0	−3074.7	−2508.6	−1063.5	−391.3	−305.1	−873.1	−1938.0	−2813.6
1.1	−599.7	−1883.2	−2727.5	−3325.1	−3312.0	−3144.2	−2555.6	−1044.4	−325.3	−234.6	−844.4	−1989.9	−2923.7
1.15	−549.8	−1911.9	−2789.4	−3407.8	−3385.1	−3213.7	−2602.6	−1025.4	−259.2	−164.1	−815.6	−2041.7	−3033.7
1.2	−499.9	−1940.6	−2851.2	−3490.5	−3458.1	−3283.2	−2649.6	−1006.3	−193.2	−93.6	−786.9	−2093.6	−3143.8

) and the simulation calculation results (

Table 4. Calculated strain values of middle measuring points on the base plate of boom 2 with load variation (με).

Load Coefficient	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11	B12	B13
0	−863.7	−861.4	−847.1	−831.4	−818.3	−808.0	−799.2	−794.7	−787.9	−782.0	−776.0	−770.0	−763.5
0.2	−824.6	−822.6	−809.8	−795.9	−784.5	−775.7	−768.2	−764.4	−758.7	−753.9	−748.9	−744.0	−738.6
0.25	−799.7	−797.9	−785.9	−772.9	−762.4	−754.4	−747.5	−744.1	−739.0	−734.7	−730.2	−725.9	−721.0
0.3	−885.9	−885.9	−873.2	−858.6	−846.5	−837.3	−829.8	−826.2	−821.1	−817.0	−812.5	−808.2	−803.2
0.35	−1010.3	−1014.6	−1001.6	−984.1	−968.6	−956.5	−947.2	−943.1	−938.1	−934.5	−930.4	−926.1	−920.7
0.4	−1102.4	−1112.6	−1101.4	−1081.9	−1062.3	−1046.2	−1034.3	−1029.6	−1025.1	−1023.0	−1020.3	−1017.0	−1011.6
0.45	−1196.5	−1220.0	−1217.5	−1198.1	−1170.5	−1142.9	−1121.8	−1114.4	−1110.2	−1113.4	−1117.8	−1119.9	−1116.4
0.5	−1468.0	−1345.8	−1125.9	−973.4	−997.2	−1187.7	−1421.5	−1527.0	−1593.7	−1467.3	−1199.8	−926.7	−775.6
0.55	−830.4	−995.2	−1473.8	−1918.1	−2055.1	−1773.4	−1157.4	−764.6	−285.0	−200.6	−496.9	−1069.7	−1638.8
0.6	−638.6	−734.0	−1390.5	−2051.7	−2335.4	−2115.9	−1371.1	−814.9	−79.6	145.2	−69.4	−699.1	−1510.8
0.65	−436.2	−472.4	−1329.7	−2185.4	−2546.6	−2355.6	−1521.5	−837.2	97.9	403.9	236.8	−421.5	−1416.6
0.7	−241.6	−99.5	−1136.2	−2245.1	−2714.2	−2604.5	−1784.8	−996.7	192.7	631.3	550.2	−41.6	−1178.7
0.75	−100.9	367.6	−976.2	−2265.3	−2865.6	−2792.6	−1887.4	−1122.6	275.0	782.7	750.5	344.2	−933.2
0.8	35.0	536.0	−722.5	−2282.3	−2931.7	−2911.4	−2189.3	−1302.3	285.5	959.1	978.7	536.3	−727.6
0.85	211.1	863.7	−525.3	−2324.8	−3050.6	−3042.5	−2356.0	−1418.7	370.5	1149.6	1191.8	806.4	−524.8
0.9	393.6	1106.9	−425.7	−2400.0	−3153.4	−3135.7	−2444.8	−1446.9	494.8	1319.5	1360.6	992.7	−428.1
0.95	554.5	1340.2	−304.6	−2449.4	−3240.7	−3220.0	−2545.8	−1500.3	596.2	1477.8	1517.8	1182.2	−304.0
1	694.1	1562.0	−181.4	−2485.0	−3315.5	−3292.2	−2644.6	−1559.8	686.5	1625.5	1662.1	1367.3	−170.8
1.05	814.2	1772.4	−44.9	−2499.0	−3375.9	−3352.4	−2749.6	−1641.8	749.9	1762.5	1794.6	1550.3	−12.6
1.1	1024.3	2042.0	71.0	−2570.8	−3473.0	−3436.4	−2836.0	−1650.1	933.0	1971.8	1973.1	1759.3	87.4
1.15	1180.2	2261.0	184.8	−2616.0	−3551.0	−3508.3	−2912.1	−1653.7	1105.6	2156.5	2120.8	1947.4	190.7
1.2	1265.1	2445.1	336.1	−2609.9	−3612.7	−3573.5	−3003.7	−1694.0	1225.4	2315.9	2253.3	2131.5	324.1

) together constitute the core basic data for the subsequent comparative analysis and verification of the failure mechanism.

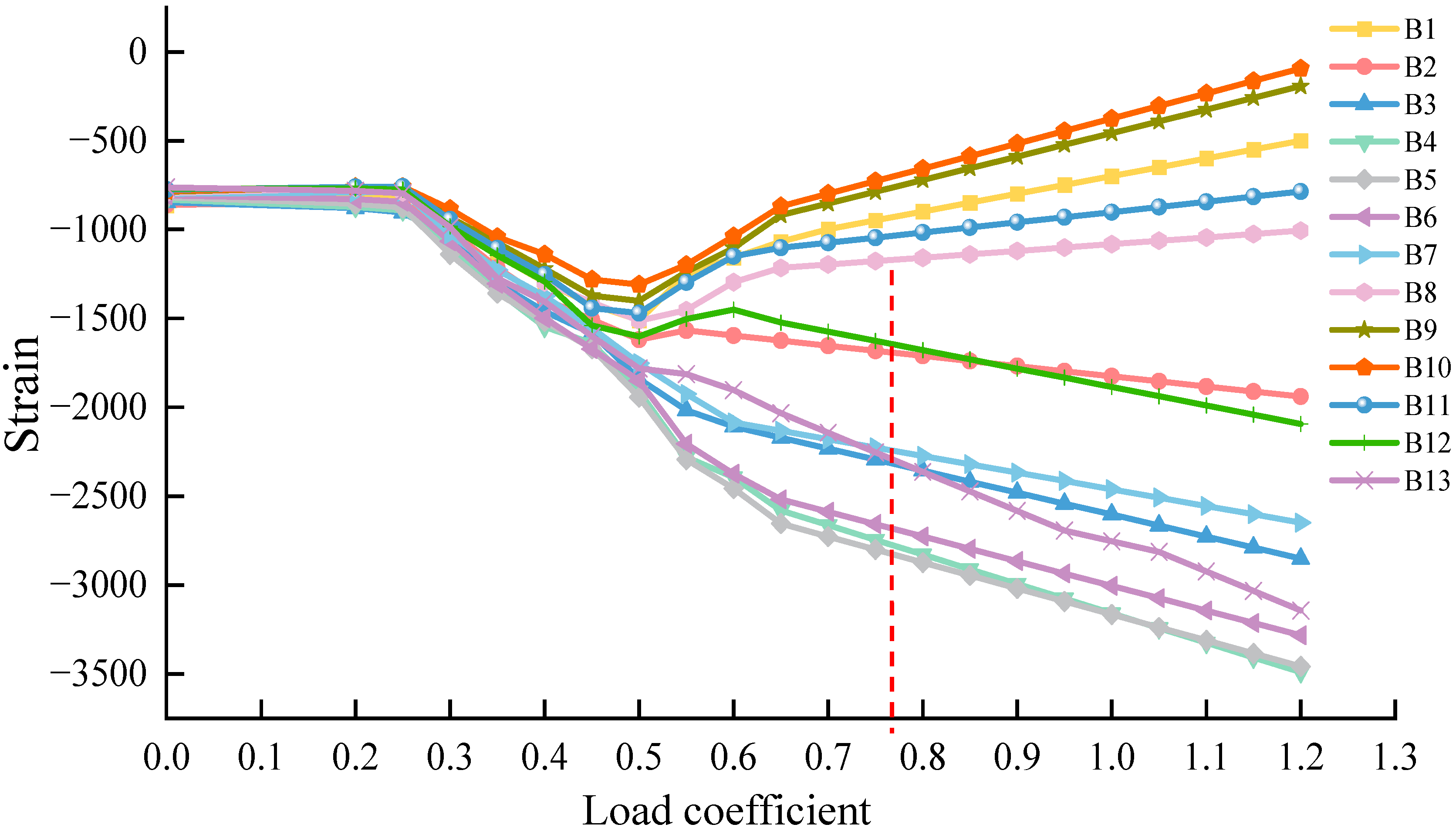
3.1. Boom Buckling Test Results

Based on the load coefficient (0–1.2), when the load factor reaches 1.2, the structure has already undergone obvious buckling, and for the B1-B13 test strain data (Table 3), it can be clearly determined that the overall data presents a “threshold-triggered” three-stage variation law as follows:

Initial stable stage (load coefficient: 0–0.25): In this stage, all strain data are concentrated in the range of −905 με (1 με = 10⁻⁶ ε) to −763.5 με. When the load coefficient is 0.25, the maximum difference between the data is only 10.6 με, and there is no monotonic variation trend. The low load does not exceed the “initial equilibrium threshold” of the system, and the numerical fluctuation only results from local minor disturbances, so the system as a whole remains in a state of dynamic equilibrium.

Sharp variation stage (load coefficient: 0.3–0.55): This stage takes a load coefficient of 0.3 as the trigger point, and all strain data show a cliff-like drop. The difference between B5 (with a drop of 263.9 με) and B13 (with a drop of 191.3 με) highlights the “sensitivity differentiation” characteristic of parameters for the first time: the high-sensitivity group (B3-B5) has a drop range of 143.6–180.3% and serves as the “dominant sensitive parameters”; the medium-sensitivity group (B1, B2, B6–B8) has a moderate drop range and shows a “follow-up response”; the low-sensitivity group (B9–B13) has a drop range of 137.5% and acts as the “stable support parameters”.

Sustained extension stage (load coefficient: 0.6–1.2): All strain data show a stable monotonic increasing trend, with an approximate increment of 100–150 με for every 0.05 increase in the load coefficient. After the load exceeds the “limit response threshold” of 0.55, the structural system enters a “stable load-bearing state”, where the strain exhibits a uniform recovery trend and the sensitivity difference becomes stabilized.

As shown in Figure 11 and Figure 12, when the load coefficient reaches 0.5, the structure of Boom 2 undergoes significant buckling deformation. Observations indicate that the buckling mode exhibits a typical sinusoidal waveform characteristic. Specifically, 4 complete wave crests and 4 wave troughs are formed in the web region. Within the key strain gauge monitoring area, the base plate presents 1 wave crest and 2 wave troughs, while the web corresponds to 1 wave crest and 2 wave troughs. These observation results clearly reveal the structural instability behavior and its deformation mode under a specific load level, providing important experimental evidence for understanding the mechanical response mechanism of the boom structure under dynamic loads.

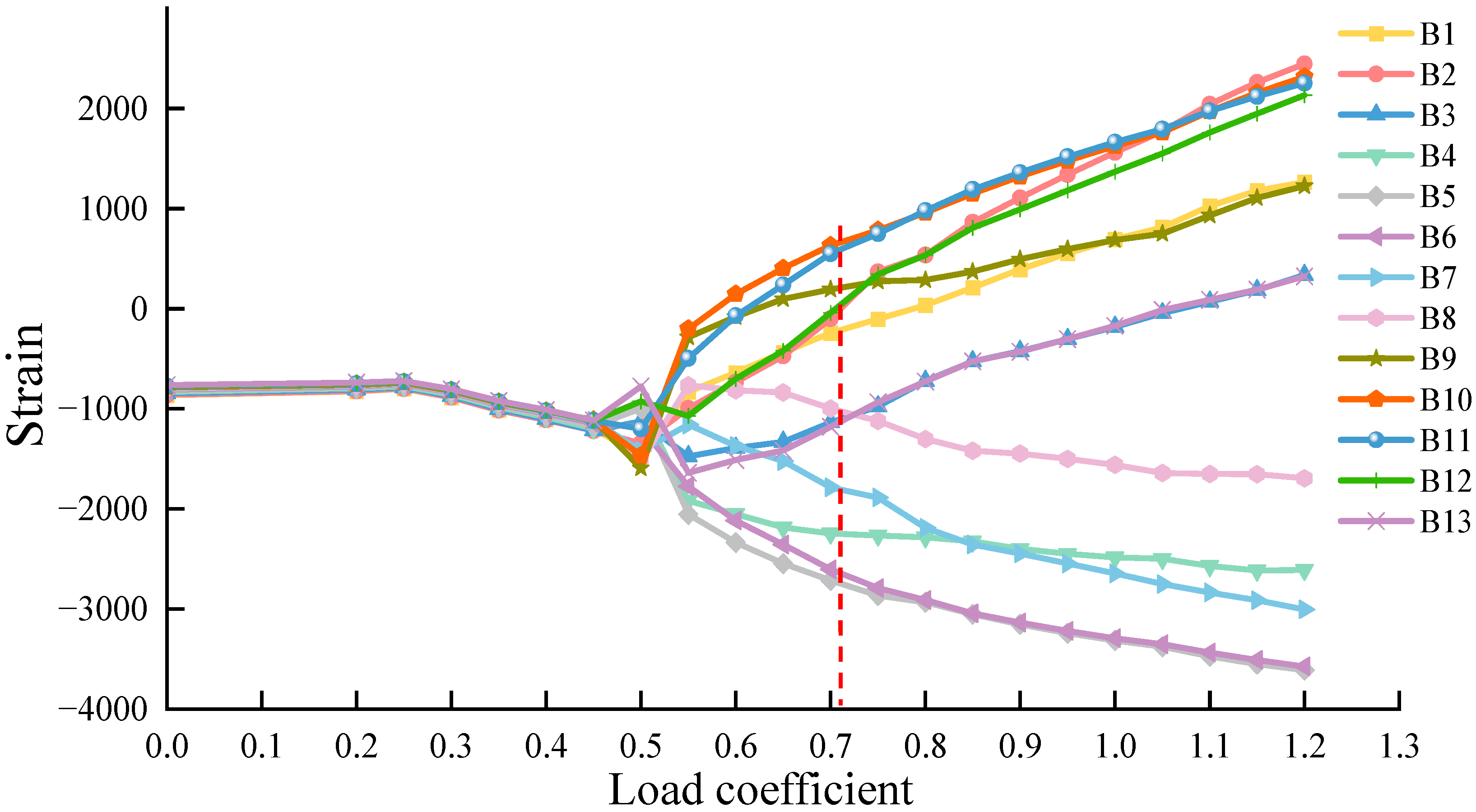
3.2. Boom Buckling Simulation Results

Based on the load coefficient (0–1.2) and the calculated strain data of measuring points B1–B13 (Table 4), the overall data presents a “segmented asymmetric response” law, including three core stages:

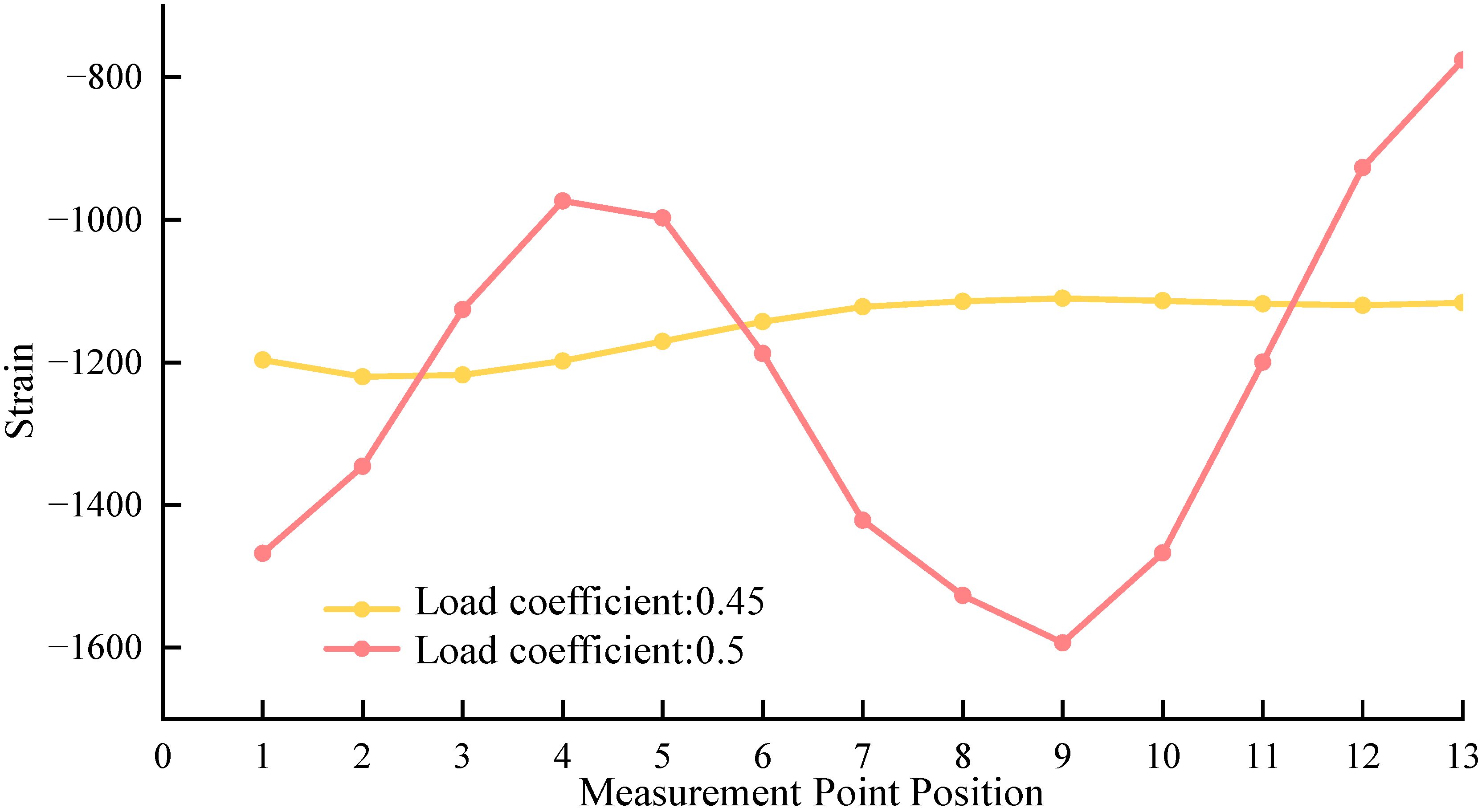
(1)

Initial stable stage (load coefficient: 0–0.45): Parameter convergence under low loadIn this stage, all strains are maintained in the range of −1468 με to −721 με, with gentle fluctuations and no significant differentiation. When the load coefficient increases from 0 to 0.45, the maximum absolute value of strain increases by 46.2–70.0%, and the difference between strains is always less than 100 με. Since the load does not exceed the “initial load-bearing threshold”, the structure only undergoes elastic deformation, and the responses of each monitoring point are convergent.

(2)

Critical mutation stage (load coefficient: 0.5–0.55): Extreme parameter differentiation after load exceeds the threshold. In this stage, parameters show extreme differentiation after the load exceeds the “critical buckling threshold”. At a load coefficient of 0.5, the values of the negative extreme group (B4–B8) drop sharply (B9 reaches −1593.7 με with a decrease of 43.5%), while the decrease range of the transition group (B1–B3, B10–B13) is less than 30%; at a load coefficient of 0.55, B5 reaches −2055.1 με (a decrease of 106.0% compared with that at 0.5), and the maximum strain difference expands to 1770.1 με. This is due to local buckling of the structure, which leads to a prominent difference in the mechanical states of different monitoring points.

(3)

Unidirectional extension stage (load coefficient: 0.6–1.2): Bidirectional stable extension of parameters under high load. In this stage, the parameters show “bidirectional monotonic extension”. The positive extension group (B1–B3, B9–B13) changes from negative compressive strain to positive tensile strain; for example, B1 increases from −638.6 με to 1265.1 με, with an increase of 100–200 με for every 0.05 increase in load coefficient. The negative extension group (B4–B8) maintains compressive strain and the absolute value increases; for example, B5 decreases from −2335.4 με to −3612.7 με, with a constant difference of 1000–1200 με. This is because the structure completes buckling reconstruction and enters a “plastic stable load-bearing state”.

As shown in Figure 13 and Figure 14, when the load factor reaches 0.45, the boom 2 structure exhibits significant buckling deformation, with its buckling mode showing a typical sinusoidal waveform, which is highly consistent with the buckling phenomenon measured on-site. Specifically, the entire web forms 4 complete wave crests and 4 wave troughs; within the monitoring area of key strain gauges, the base plate presents 1 wave crest and 2 wave troughs (Figure 14, 3× magnification), and the corresponding web shows 1 wave crest and 2 wave troughs. This observation result clearly reveals the instability behavior and deformation characteristics of the structure under specific loads, and explains the mechanical response mechanism of the boom structure under dynamic loads.

3.3. Boom Buckling Failure Results

To investigate the structural load-bearing limit and failure mechanism of the strengthened version of the telescopic boom 2, a structural failure test was conducted on it. During the test, axial loads were applied step-by-step based on the rated load, and structural stress and deformation data were collected in real time using monitoring equipment such as displacement gauges and strain gauges. When the load was applied to 1.9 times the rated load (Table 1), the structure lost its load-bearing capacity and failed (Figure 15). The failure location was identified at Measuring Point 4, where obvious buckling phenomena occurred in both the web and the base plate of this area. Macroscopically, it manifested as concave deformation in the local area, which conforms to the typical local buckling failure characteristics of box-type structures caused by local section stress exceeding the material yield strength under concentrated loads. This result provides key experimental basis for the optimal design and safety factor verification of this strengthened version of the structure.

To accurately reproduce the stress-induced failure process of the reinforced version of Knuckle boom 2, the geometric and material double-nonlinear analysis method was employed in finite element calculation for numerical simulation of the full experimental loading process. During the simulation, a refined finite element model was constructed to simultaneously account for the nonlinear characteristics of structural geometric deformation and the nonlinear stress–strain relationship of the material. When the applied load in the calculation reached 1.8 times the rated load, structural failure occurred (Figure 16). At this moment, the maximum stress was concentrated at Measurement Point 4; distinct sinusoidal buckling waveforms appeared in the bottom plate and web regions; and the stress in large areas of the structure (the red parts in the finite element contour plot) reached the material yield limit, indicating that the structure entered the buckling failure stage. The failure location and mode obtained from the simulation were highly consistent with the results of the physical experiment, which verified the accuracy of the finite element model and the reliability of the analysis method.

3.4. Deviation Results

To scientifically evaluate the consistency between the “test average value” and “finite element simulation value” in the mechanical performance test of the telescopic boom structure, this study selects the deviation index as the core evaluation parameter [36,37]. To avoid evaluation result deviations caused by differences in reference selection and ensure the uniqueness and comparability of evaluation standards, the measured average value—obtained through real-time collection by high-precision sensors during the test, followed by data validity verification and outlier elimination—is clearly defined as the reference value for deviation calculation. By comparing this reference value with the simulation value, the degree of difference between them in key mechanical parameters such as stress and displacement is quantified. The specific deviation calculation method is defined as follows:

$$\mathrm{Deviation}(\%)=\mid {\displaystyle \frac{\mathrm{Experimental} \mathrm{Value}-\mathrm{Simulated} \mathrm{Value}}{\mathrm{Experimental} \mathrm{Value}}}\mid \times 100\%$$

(2)

To further verify the calculation reliability of the geometric and material nonlinear numerical model, this study established strict standards in the data screening stage: only load conditions in the linear working stage before structural buckling failure (corresponding to load coefficients of 0.2 and 0.25) and with consistent variation laws between test strains and simulation strains were selected for deviation comparison. This was done to eliminate the interference of mechanical behavior complexity in the nonlinear stage and differences in data trends on error analysis, with specific comparison data shown in

Table 5. Deviation values between calculated and test strains of 13 measuring points in column B (%).

Load Coefficient	1	2	3	4	5	6	7	8	9	10	11	12	13
0.2	2.0	3.1	7.9	8.8	8.2	6.6	2.9	0.3	0.2	1.0	1.5	3.3	5.6
0.25	0.9	6.0	8.9	9.4	12.9	10.6	5.1	5.9	3.2	3.3	3.7	6.4	9.5

.

This comparison covers 13 key measuring points of the structure (including critical locations such as stress concentration areas and typical stress-bearing sections). For each measuring point, one set of strain error data was generated under each of the two load coefficients, ultimately forming 26 valid analysis samples, which ensures the representativeness and objectivity of the statistical results.

From the perspective of error distribution characteristics, statistical analysis shows that the deviation magnitude of 42.3% of the samples is less than 5%. This part of the data reflects a high degree of consistency between the test values and simulation values, indicating that the simulation accuracy of the model for mechanical responses in some key areas has reached a high level. More importantly, the deviation magnitude of 92.31% of the samples is controlled within 10%, which fully meets the engineering confidence requirements for numerical model accuracy in the field of mechanical analysis of mechanical structures.

This error distribution law not only verifies the reliability of the strain test system (including sensor selection, data collection and processing methods) but also confirms quantitatively that the established geometric and material nonlinear numerical model can accurately capture the stress–strain distribution characteristics of the structure in the linear stage. The model’s representation of material constitutive relations, restoration of geometric parameters, and application methods of boundary conditions and loads are all reasonable and effective. This conclusion provides key support for subsequent nonlinear response analysis of structural buckling failure stages using this model, and also offers a reference paradigm for error control and model verification in numerical simulation studies of similar box-type structures.

4. Discussion

This study focuses on the intrinsic mechanism of base plate buckling in cantilever box-section structures under bending, analyzing and summarizing from the perspectives of stress states, thin plate stability, and the coupling effects of boundary constraints. When the structure is subjected to bending, the normal stress across the cross-section exhibits a linear distribution, with the base plate below the neutral axis experiencing significant non-uniform compressive stress. As a high-width-to-thickness-ratio thin-walled member, once the longitudinal compressive stress in the base plate reaches the critical threshold, instability occurs, disrupting the planar equilibrium state. At the boundaries, the base plate is constrained laterally by the webs on both sides and longitudinally by transverse stiffeners, limiting the unsupported length. Due to the significantly lower out-of-plane bending stiffness compared to in-plane compressive stiffness, even minor disturbances can trigger dynamic instability, leading to multi-wave buckling modes longitudinally. The critical buckling stress is influenced by boundary types, aspect ratios, and other factors, while initial geometric imperfections and residual stresses reduce the critical value and accelerate instability. After buckling, the structure enters the post-buckling stage, where stress redistribution forms an “effective width” load-bearing mechanism. This is accompanied by stiffness degradation, stress concentration, and an increased risk of fatigue failure. Under sustained loading, further degradation of the overall load-bearing capacity may occur. This mechanistic understanding provides key insights for the design of thin-walled box girders, offering theoretical support for enhancing their buckling resistance.

4.1. Discussion on Boom Buckling Test Results

To delve into the buckling mechanism of the base plate of Boom 2, an analysis was conducted by integrating the experimental strain curves of the base plate under varying loads (Figure 17). The core mechanism of buckling in thin-walled components of box-section structures was revealed from three aspects: the evolution law of mechanical behavior, the nature of nonlinear transition, and theoretical verification.

From the perspective of mechanical behavior reflected by the strain curves, the evolution of the base plate exhibits three distinct stages, which provide direct experimental evidence for analyzing the occurrence and development of buckling:

(1) Initial linear elastic stage (load coefficient ≤ 0.25): The strain at all measuring points exhibits a strictly proportional relationship with the load, and the curves are flat with a constant slope, fully complying with Hooke’s Law. In this stage, the structure is in a linear elastic equilibrium state, where only elastic deformation occurs in the base plate. The in-plane compressive stress has not yet reached the critical value for instability, and the stress–strain transfer path remains stable.

(2) Subcritical compression stage (load factor of 0.25–0.5): strain increases linearly but at a decreasing rate, with the decreasing slope indicating the weakening of stiffness due to accumulated compressive stress. Elastic strain energy continues to accumulate within the base plate, and while the structure does not exhibit instability, it transitions from a stable equilibrium state to a metastable state, laying the foundation for subsequent buckling transformation. This confirms the “gradual stiffness degradation” pre-buckling characteristics of thin-walled members before reaching the critical load.

(3) Critical Buckling Stage (Load Factor > 0.5): The system undergoes a sudden buckling characteristic transition. The strain curves of the five upper measurement points change from negative to positive slope, indicating their position in the half-wave peak region, dominated by membrane tension effects. The originally compressed areas, due to out-of-plane buckling, transform into tension zones. Simultaneously, the six lower measurement points exhibit a steep increase in compressive strain gradient, corresponding to intensified compressive stress concentrations in the wave trough region. The neutral layer dynamically shifts during buckling, with significant spatial differentiation in strain polarity. These features collectively serve as key diagnostic indicators of the buckling mode, visually demonstrating the abrupt stress state transformation in the base plate.

From the perspective of mechanics, the nonlinear transition mechanism of the base plate in box-section structures with high width-to-thickness ratio has been revealed. Due to the significantly lower out-of-plane bending stiffness compared to the in-plane compressive stiffness of the base plate, once the in-plane compressive stress exceeds the stability limit, even minor disturbances will trigger an exponential increase in out-of-plane displacement, driving the structure from a planar equilibrium state into a buckled configuration through bifurcation. After bifurcation, the wave crest region undergoes biaxial tension to form a tension zone, while the wave trough region, constrained by the webs on both sides, develops a high-stress concentration core. The spatial variation in section strain polarity directly validates the propagation mechanism of the buckling half-wave and the “effective width” load-bearing theory.

The experimentally observed dual-mode strain response (tension in the wave crest and stress concentration in the wave trough) aligns closely with the post-buckling path in classical shell theory, empirically confirming that a load coefficient of 0.5 represents the critical instability threshold of the base plate. Concurrently, this phenomenon uncovers the coupling mechanism between load redistribution and the membrane effect, which synergistically regulates the post-buckling load-bearing capacity of the structure.

This mechanistic understanding not only provides experimental support for the accurate identification of buckling failure modes in box-section structures but also offers critical guidance for engineering design. By optimizing the width-to-thickness ratio and adding stiffeners, the out-of-plane stiffness of the base plate can be enhanced to delay the stiffening degradation process. Additionally, a comprehensive consideration of the critical instability threshold and post-buckling load-bearing characteristics can prevent sudden buckling failure during service, thereby improving the anti-instability performance and safety reliability of box-section structures.

4.2. Discussion on Boom Buckling Calculation Results

To delve into the buckling mechanism of the base plate of Boom 2, an analysis was conducted by integrating the finite element strain curves (Figure 18), focusing on the division of load response stages, the mutation characteristics of mechanical behavior, and the intrinsic mechanism. This analysis allows for a clear deconstruction of the occurrence and development laws of buckling in thin-walled plates:

(1)

Initial Stage (Load Factor ≤ 0.25): The strain-load relationship at all measurement points exhibits a strict linear proportionality, with the strain curve cluster forming parallel straight lines. The structure remains in a linear elastic equilibrium state, with internal force distribution conforming to classical beam theory. Elastic strain energy accumulates steadily without nonlinear disturbances, and the in-plane load-bearing capacity of the base plate is unaffected. This stage represents the “stable load-bearing period” prior to buckling.

(2)

When the load factor is in the range of 0.25–0.45, the strain increment maintains linear growth, but the curve slope exhibits a systematic negative deviation, revealing that accumulated compressive stress gradually weakens section stiffness. This phenomenon arises from the coupled interaction between microscopic lattice distortion hardening effects and the initial emergence of macroscopic geometric nonlinearity. At this stage, the structure exists in a metastable equilibrium state, with no significant buckling occurring yet, but the weakening of stiffness already harbors instability, constituting the “pre-buckling transition stage.”

(3)

Upon reaching a load factor of 0.45, the strain field undergoes an irreversible transformation, marking the onset of buckling feature transition. The eight upper measurement points exhibit strain sign reversal, abruptly transitioning from compressive to tensile strains with a maximum jump of 300% relative to the initial value. This originates from mid-surface tension deformation induced by buckling half-wave elevation, transforming the originally uniaxially compressed areas into biaxially tensioned states. Simultaneously, the five lower measurement points display a 200% increase in compressive strain gradient, forming triaxial stress confinement singularity zones and triggering localized plastic flow bands. The neutral strain layer shifts downward along the plate thickness, with its displacement magnitude serving as a quantifiable indicator of buckling mode deformation amplitude.

These three mutations (strain sign reversal, gradient nonlinear jump, and dynamic migration of the neutral layer) constitute the deterministic criteria for the buckling characteristic transition: the spatial differentiation of strain polarity confirms the mechanical state decoupling between the wave crest region (dominated by membrane tension) and the wave trough region (strengthened by compressive concentration) of the buckling half-wave, while the neutral layer offset characterizes the initiation of the cross-sectional internal force redistribution mechanism. Essentially, the strain field mutation at a load coefficient of 0.45 is a characteristic parameter for the coupling effect of geometric nonlinearity and material plasticity. Through the causal chain of “microscopic strain evolution → macroscopic mode reconstruction → failure path transformation”, a cross-scale diagnostic system is established. This not only clarifies the complete mechanism of thin-walled plate buckling from pre-buckling to characteristic transition but also provides a theoretical framework with both physical clarity and parameter sensitivity for the stability design of thin-walled structures.

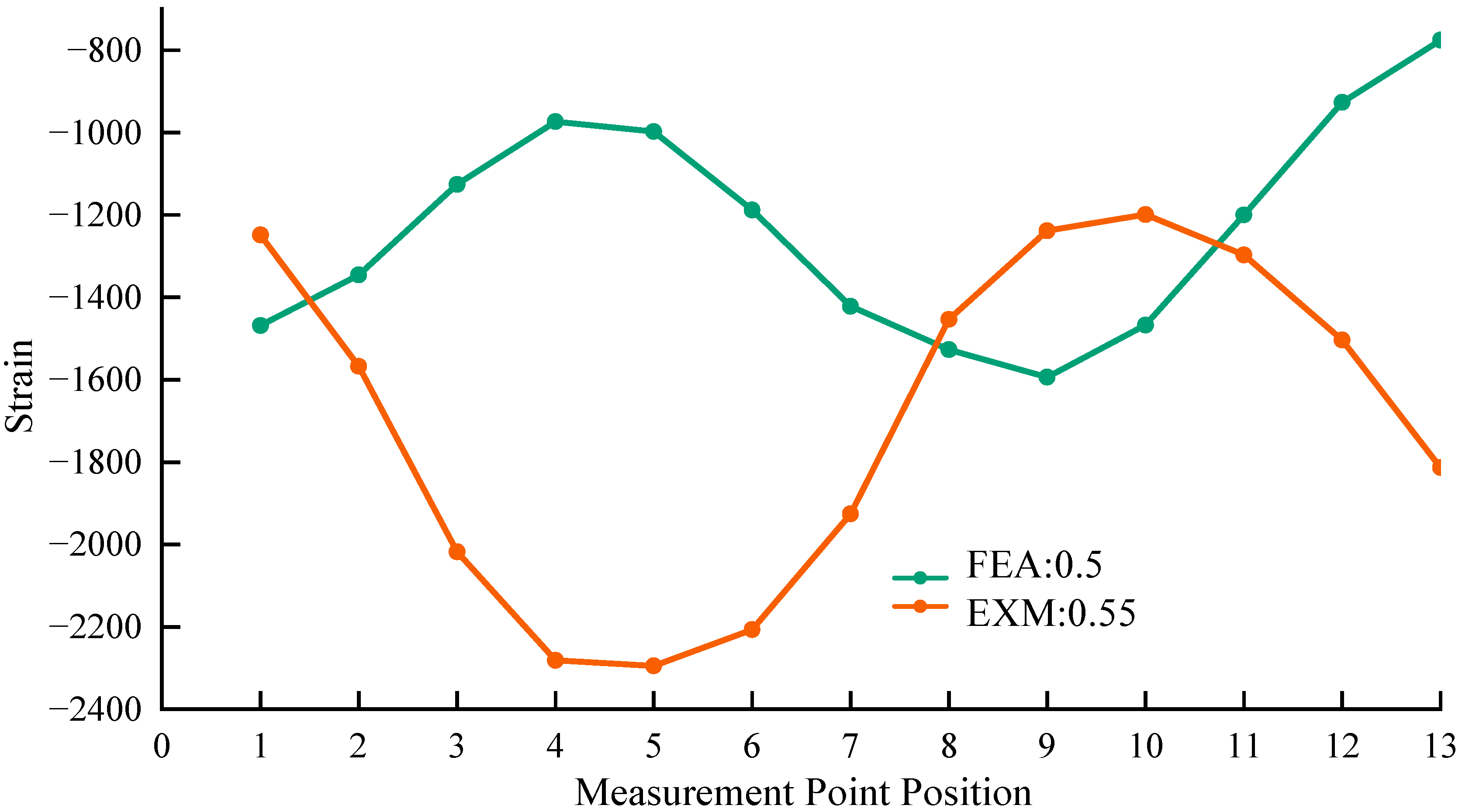
4.3. Discussion on the Comparison Results of Boom Buckling Test and Calculation

As shown in Figure 19, this is the measured strain curve of the middle measuring points on the base plate of Boom 2 varying with position. The spatial distribution rule of the measuring points is as follows: taking the hinge center of Boom 1–2 as the origin, Measuring Point 1 is positioned at 3421 mm, and the measuring points are arranged at equal intervals of 75 mm along the axial direction. The core mechanism of the occurrence and development of buckling is deconstructed from three aspects: strain waveform characteristics, critical evolution law, and criterion system:

(1)

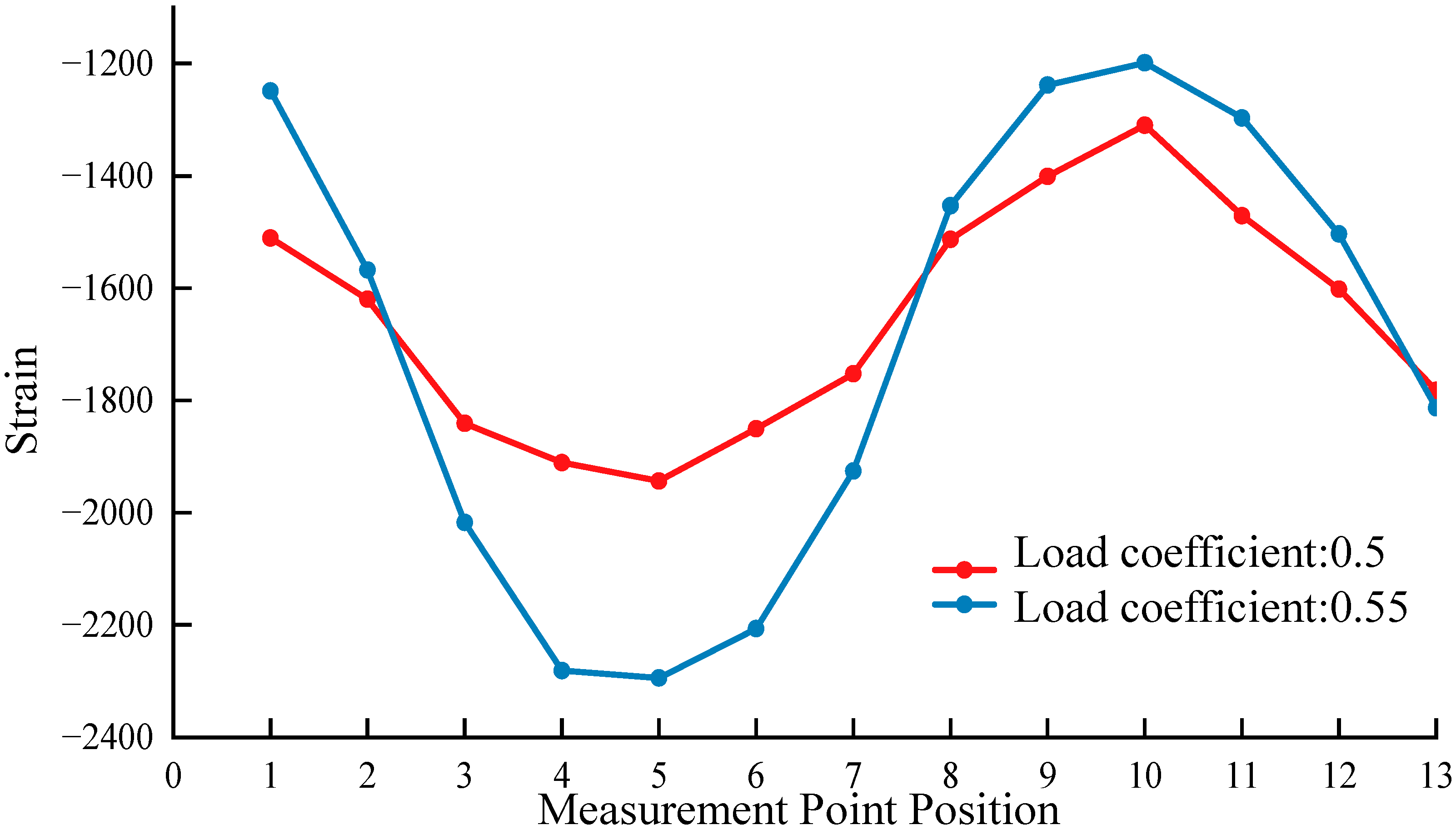
When the load factor increases to 0.5, the strain curves exhibit a typical sinusoidal buckling waveform with a peak-to-peak value of 650 με. The spatial phase characteristics of this waveform provide three critical instability diagnostic criteria: First, the zero-crossing points of the waveform precisely correspond to the projected position of the base plate’s theoretical neutral surface, confirming the geometric completeness of the buckling mode through the symmetry of the cosine function, indicating the formation of a regular half-wave buckling morphology. Second, upon reaching a load factor of 0.55, the peak-to-peak value of the waveform nonlinearly increases to 1100 με—a 69.2% rise—attributable to the nonlinear coupling between membrane compression effects in the wave trough region and bending curvature, reflecting the rapid development phase of buckling. Third, the peak spacing of the waveform stabilizes at 675 mm, fully consistent with finite element predictions, confirming that the buckling mode has entered an energy-stable state and validating its reliability.

(2)

Mechanistically, experimental data reveals two critical instability evolution mechanisms: At the material level, the 650 με waveform amplitude triggers microscopic plastic flow in steel, forming plastic strain concentration zones (local strains exceeding 1100 με), marking the transition from elastic to plastic behavior. Morphologically, the displacement of extrema in the cosine function’s derivative reveals the migration of buckling half-wave inflection points toward the boundaries.

(3)

This phenomenon establishes a predictive framework from experimental strain to engineering failure: The relative deflection of the base plate corresponding to the 650 με cosine amplitude at initial buckling approaches the elastic limit for thin plate deformation. Once the amplitude exceeds 1000 με, accumulated plasticity will accelerate structural stiffness degradation. The mutual validation of experimental and theoretical findings demonstrates that the sinusoidal waveform at a 0.5 load factor serves as morphological evidence of buckling initiation. Its phase symmetry, amplitude discontinuity, and constant wavelength constitute a triple verification system for instability criteria, forming a cross-scale diagnostic paradigm of “morphological identification → amplitude alerting → wavelength calibration.” This reveals the complete mechanism of buckling from initiation, development to approaching failure.

As shown in Figure 20, this is the calculated strain curve of the middle measuring points on the base plate of Boom 2 varying with position. The core mechanism is clarified through the evolution law of the buckling mode during the load increment process:

(1)

Upon reaching a load factor of 0.45 times the critical value, the axial strain distribution exhibits an initial buckling mode with fixed wavelength, forming a complete sinusoidal waveform characterized by a peak-to-peak strain of 140 με. The spatial positioning of its peaks and troughs demonstrates a high degree of alignment with the phase characteristics of the first-order instability mode predicted by classical plate-shell buckling theory. This marks the initiation of buckling in the base plate, signifying the departure from planar equilibrium and entry into the pre-instability phase.

(2)

When the load factor increases to 0.5, the buckling morphology enters an enhanced development stage, characterized by a sudden increase in strain peak-to-peak value from 140 με to 750 με—a remarkable 434% rise. This dramatic amplification stems from the coupled interaction of membrane tension and bending deformation under geometric nonlinearity: out-of-plane buckling of the base plate induces additional tensile stress in the mid-surface, which, superimposed on the original bending stresses, leads to disproportionate strain growth. During this phase, the distance between wave peaks stabilizes at 600 mm, yielding a span-to-buckling-wavelength ratio of 1:2.34, fully consistent with theoretical analytical results for rectangular plate buckling wavelengths.

(3)

This evolutionary sequence reveals two fundamental mechanical mechanisms: First, the magnitude jump in strain amplitude signifies the transition of the buckling equilibrium path from the pre-buckling to post-buckling branch, reflecting physically the release of mid-surface strain energy triggered by buckling half-wave elevation, propelling the structure from an elastic stable state toward a nonlinear instability state. Second, the sustained stability of the waveform’s spatial phase confirms the energy optimization characteristic of the buckling mode, indicating that the structure inherently selects the path of minimal potential energy to achieve energy dissipation minimization. The study confirms that the initial sinusoidal waveform and its spatial evolution characteristics at a 0.45 load factor clearly indicate that the base plate of Section 2 has entered the buckling state, providing critical experimental validation for thin-walled plate buckling mechanisms.

To analyze the 75 mm phase shift and direction inversion between the finite element (FE) calculated and experimental buckling waveforms in Figure 21, it is necessary to start from the coupled effects of multi-scale initial defects induced by the manufacturing process of the box-section boom, and explore their influence mechanism on the selection of the buckling path:

(1)

Based on an ideal geometric configuration, the finite element model derived a standard sinusoidal buckling wave, characterized by theoretical zero points strictly coinciding with the neutral surface and peak positions analytically determined by boundary constraints, representing an idealized defect-free buckling mode. Experimental observations revealed a buckling waveform shifted axially by 75 mm and exhibiting a cosine morphology inverted relative to the theoretical wave. This discrepancy originates from the cumulative effect of third-order defect fields introduced throughout the manufacturing process of Boom 2.

(2)

At the geometric level, laser cutting-induced thermal deformation creates edge gradients in individual panels, which are further amplified during welding assembly to form localized warping, causing an axial offset of the actual neutral surface. Mechanistically, residual tensile stresses from weld cooling interact asymmetrically with the compressive zone of the base material, generating an asymmetric membrane stress field that induces phase rotation in the buckling mode. This results in an axial shift of 75 mm between the experimental and theoretical waveforms along the patch direction. At the physical essence level, the thermal cycles during welding alter the microstructural texture of the wave node zone, creating localized yield strength disparities that force the buckling equilibrium path from symmetric bifurcation toward asymmetric instability, ultimately manifesting as a deterministic 180° directional inversion between experimental and finite element solutions.

(3)

This phenomenon validates the sequence-dependent regulatory role of initial defects in thin-walled box beam buckling behavior: manufacturing processes introduce coupled chains of geometric imperfections, residual stresses, and microstructural defects that modify the structural potential energy surface topology. This prompts the critical buckling mode to migrate along specific hypersurfaces in the phase space, ultimately manifesting as deterministic phase and directional shifts in the waveform. The discrepancy between finite element and experimental waveforms is not a contradiction of mechanical principles but an inevitable consequence of the interaction between the ideal model and actual manufacturing defects in the structure.

(4)

As core load-bearing components of heavy machinery, boom performance and reliability directly determine equipment operational safety. Common structural overweight issues in multi-section boom systems of large-scale heavy machinery not only increase the self-weight load of the boom system but also disrupt load distribution rationality through force transmission coupling effects, posing potential impacts on carrying stability and service safety. Therefore, lightweight optimization of boom sections represents a crucial research direction for enhancing the comprehensive performance of boom systems. Scientific lightweight design can effectively reduce boom self-weight while synergistically decreasing the load-bearing burden of undercarriage structures, improving overall anti-overturning performance, and optimizing equipment load distribution. This provides technical support for enhancing boom mechanical performance and extending service life, holding significant academic and engineering value in promoting the development of heavy machinery toward lightweighting, efficiency enhancement, and extended service life.

5. Conclusions

By combining experimental and simulation methods, this study thoroughly investigates the buckling behavior and failure mechanisms of cantilever box-section boom arms under bending. The results indicate that the base plate of Section 2 undergoes significant buckling deformation within a load coefficient range of 0.45 to 0.5. Failure analysis reveals that the structure experiences localized buckling failure under 1.9 times the rated load. Deviation analysis confirms good consistency between experimental and simulation results, validating the reliability of the model. Finally, relevant buckling evaluation criteria are provided, offering theoretical support for the design and safety assessment of this type of structure. The following conclusions are drawn:

• Clear buckling mechanism: The boom base plate undergoes buckling deformation when the load coefficient ranges from 0.45 to 0.5, with the strain curve presenting a typical sine waveform. The wavelength is consistent with the theoretical prediction, which confirms the instability mechanism of thin-walled plates when the in-plane compressive stress exceeds the critical value.
• Relationship between load and deformation: The buckling deformation has a nonlinear relationship with the load. After the load exceeds the critical threshold, the strain amplitude increases sharply, the waveform amplitude rises significantly, and the buckling mode enters the stage of intensified development. This is consistent with the theoretical expectation of the coupling effect between geometric nonlinearity and material plasticity.
• Consistency between simulation and experiment: The finite element simulation results are highly consistent with the experimental data, verifying the accuracy and applicability of the model and providing a reliable numerical tool for the buckling analysis of thin-walled structures.
• Failure mode: The structure suffers local buckling failure under the ultimate load, and the failure location is consistent with the simulation prediction. This indicates that the stress concentration in the connection area is the key factor leading to failure.
• Based on the research findings, a box girder buckling evaluation criterion with both scientific rigor and engineering applicability is established. This criterion must satisfy two core conditions: first, the surface of the box girder must exhibit typical buckling ripples, forming a visual buckling characterization; second, during the buckling critical mutation stage, the strain amplitude must reach and exceed 40%.
• The boom involved in the buckling accident discussed in this paper adopted the measure of optimizing plate thickness, with the original plate thickness increased by 1 mm. For similar or analogous thin-walled box-section structures, the buckling deformation can be suppressed by means of design approaches such as optimizing plate thickness and adding stiffening ribs, thereby significantly improving the anti-instability performance and service safety level of the structures.