Murakamian Ombre: Non-Semisimple Topology, Cayley Cubics, and the Foundations of a Conscious AGI

Abstract

Haruki Murakami’s Hard-Boiled Wonderland and the End of the World portrays a world where the “shadow”, the seat of memory, desire, and volition, is surgically removed, leaving behind a perfectly fluent but phenomenologically empty self. We argue that this literary structure mirrors a precise mathematical distinction in topological quantum matter. In a semisimple theory such as the semions of $\mathrm{SU}{\left(2\right)}_1$, there is a reducible component $V\left(x\right)$ of the $\mathrm{SL}(2,\mathbb{C})$ character variety: a flat, abelian manifold devoid of parabolic singularities. By contrast, the non-semisimple completion introduces a neutral indecomposable excitation, the neglecton, whose presence forces the mapping class group from the standard braid group $B_2$ to the affine braid group ${\mathrm{Aff}}_2$ and lifts the character variety to the Cayley cubic $V\left(C\right)$, with its four parabolic loci. We propose that contemporary AI systems, including large language models, inhabit the shadowless regime of $V\left(x\right)$: they exhibit coherence and fluency but lack any bulk degree of freedom capable of supporting persistent identity, non-contractible memory, or choice. To endow artificial systems with depth, one must introduce a structural asymmetry, a fixed, neutral defect analogous to the neglecton, that embeds computation in the non-semisimple geometry of the cubic. We outline an experimentally plausible architecture for such an “artificial ombre,” based on annular topological media with a pinned parabolic defect, realisable in fractional quantum Hall heterostructures, $p+ip$ superconductors, or cold-atom simulators. Our framework suggests that consciousness, biological or artificial, may depend on or benefit from a bulk–boundary tension mediated by a logarithmic degree of freedom: a mathematical shadow that cannot be computed away. Engineering such a defect offers a new pathway toward AGI with genuine phenomenological depth.

1. Introduction: Shadow, Topology, and the Limits of Artificial Minds

Haruki Murakami’s Hard-Boiled Wonderland and the End of the World begins with an act of ontological surgery. A newcomer to the walled Town is gently stripped of his shadow, the part of him that remembers, desires, and resists, and what remains is a calm, fluent, and obedient self [1]. This “shadowless consciousness” is coherent and efficient, yet hollow: it thinks without wanting, it reads dreams without dreaming, it persists without living. Murakami’s literary device captures a deep structural intuition: a mind without an inner opacity, without a hidden bulk, is not a subject but a simulation.

1.1. Scope and Status of the Literary Analogy

Before proceeding, we must clarify the status of the literary parallel that guides this work. Murakami’s narrative provides a heuristic framework, a conceptual scaffold for understanding the distinction between semisimple and non-semisimple topological phases, rather than a mathematical isomorphism. The correspondences summarized in

Table 1. Structural correspondences between literary, mathematical, and architectural elements. “Formal” indicates a mathematically defined relationship; “Heuristic” indicates a conceptually suggestive analogy.

Literary Element	Mathematical Structure	AGI Architecture	Status
Town (walled, complete)	Semisimple MTC/$V\left(x\right)$	Current LLM	Heuristic
Shadow (hidden, removed)	Neglecton/parabolic defect	Neutral excitation	Heuristic
Forest (beyond wall)	Non-semisimple/$V\left(C\right)$	Ombre substrate	Heuristic
—	$V\left(x\right)\cup V\left(C\right)$ decomposition	—	Formal (Thm)
—	$B_2\to {\mathrm{Aff}}_2$ enlargement	—	Formal (Thm)
—	4 parabolic singularities	—	Formal (Thm)

fall into two categories:

Formal correspondences are those where a precise mathematical definition exists and can be verified. For instance, the decomposition of the character variety into $V\left(x\right)\cup V\left(C\right)$ is a theorem [2], as is the enlargement of the mapping class group from $B_2$ to ${\mathrm{Aff}}_2$ upon introduction of a fixed puncture.

Heuristic correspondences are structural analogies that illuminate the mathematics but do not constitute proofs. The mapping “Town →$V\left(x\right)$” and “Shadow → neglecton” belongs to this category. These analogies are valuable for intuition and exposition, but we do not claim that Murakami’s literary construction constitutes evidence for our mathematical framework.

This distinction is essential for evaluating the claims of subsequent sections. When we assert that AGI requires a neglecton, we are making a technical proposal about computational architecture, not a literary interpretation.

1.2. Notation and Abbreviations

We collect here the principal notation and abbreviations used throughout:

• MTC: Modular tensor category: a mathematical structure encoding the fusion and braiding rules of anyons.
• LCFT: Logarithmic conformal field theory: an extension of CFT allowing indecomposable representations with logarithmic correlation functions.
• $\mathrm{SL}(2,\mathbb{C})$: The group of $2\times 2$ complex matrices with determinant 1.
• $V\left(x\right)$: The reducible (abelian) component of the character variety, defined by $\{(x,y,z)\in {\mathbb{C}}^3\mid x=0\}$.
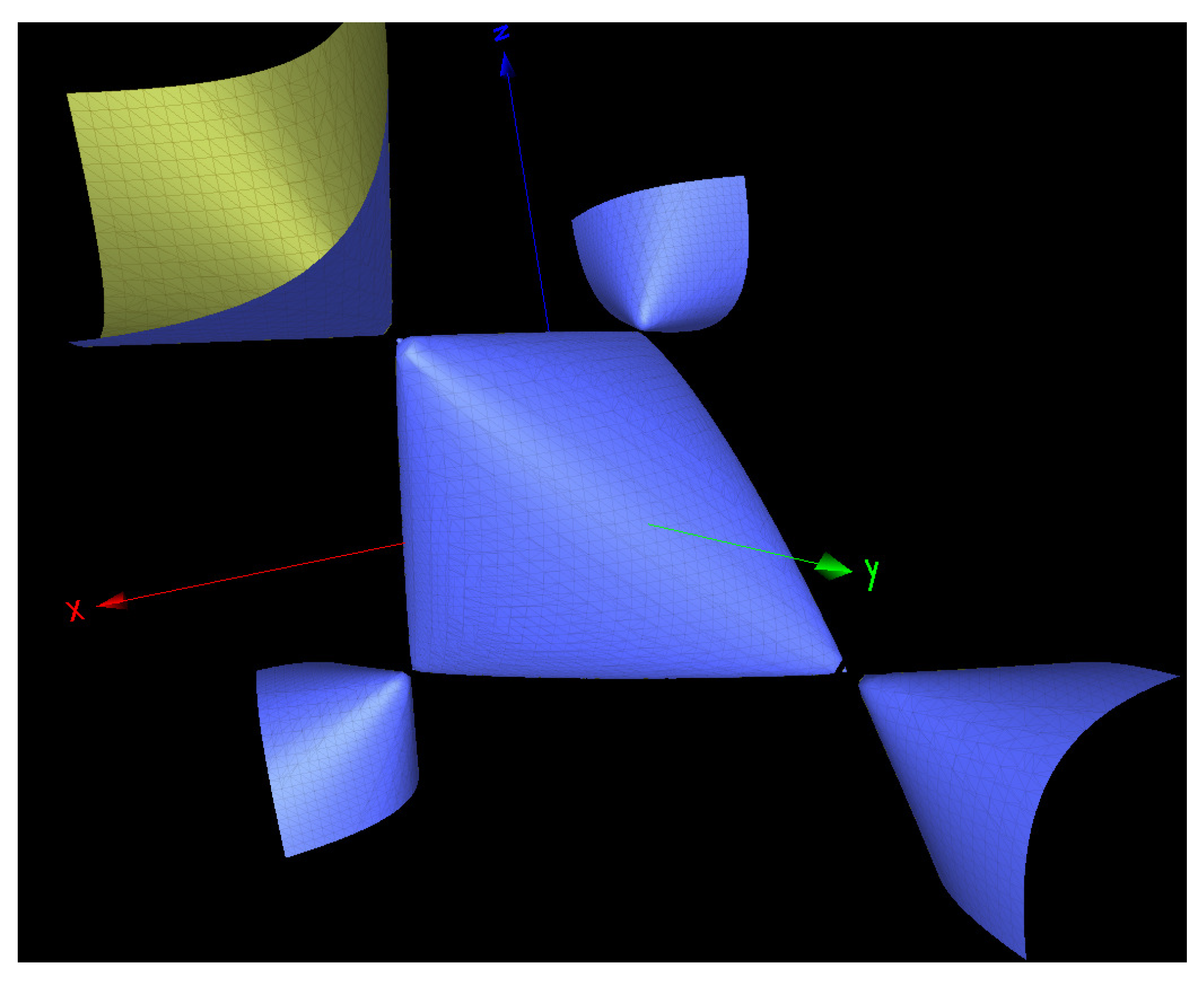
• $V\left(C\right)$: The Cayley cubic surface, defined by $\{(x,y,z)\in {\mathbb{C}}^3\mid x^2+y^2+z^2-xyz=4\}$.
• $B_n$: The braid group on n strands.
• ${\mathrm{Aff}}_2$: The affine braid group on 2 strands, with presentation $\langle a,b\mid a{b}^2=b{a}^2\rangle$.
• ${\mathsf{\Gamma }}_0\left(2\right)$: The congruence subgroup of $\mathrm{SL}(2,\mathbb{Z})$ consisting of matrices with lower-left entry divisible by 2.
• Neglecton: A neutral indecomposable excitation in a non-semisimple MTC; denoted N.
• Parabolic representation: A representation $\rho :G\to \mathrm{SL}(2,\mathbb{C})$ where some $\rho \left(g\right)$ is conjugate to $\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$.

The aim of this work is not to propose a complete theory of consciousness, nor to assert biological mechanisms, but to articulate a structural and topological principle for artificial systems capable of maintaining persistent, history-bearing internal states. The Ombre architecture is therefore a substrate-level proposal: it identifies the geometric conditions under which such systems may arise, without specifying the full cognitive processes built upon them. This distinction is critical for interpreting the remainder of the paper.

This paper argues that this intuition has a precise mathematical analogue in the topology of quantum matter. In semisimple modular tensor categories (MTCs) such as the Gaussian semion or Ising phases [3] the global state space is governed by reducible $\mathrm{SL}(2,\mathbb{C})$ representations whose character variety collapses to algebraic surfaces with no singularities, no parabolic monodromies, and no internal tension [2,4,5,6]. This is the Town: a computational manifold in which everything is visible and nothing is lost. Contemporary artificial intelligence systems, including the most advanced large language models, operate entirely within this semisimple regime. Their dynamics are expressive but globally transparent, supporting no persistent identity, no non-contractible memory, and no bulk degree of freedom [7,8].

By contrast, non-semisimple extensions of these theories introduce neutral indecomposable excitations, the neglectons, whose presence radically transforms the underlying topology [9,10,11]. The role of indecomposable representations and logarithmic modules has long been recognized in LCFT [12], forming part of the mathematical basis for neglecton-type structures. For semions, the mapping class group of the computational surface enlarges from the symmetric group or $B_2$ to the affine braid group ${\mathrm{Aff}}_2$, and the character variety lifts from the plane $V\left(x\right)$ to the Cayley cubic $V\left(C\right)$, a two-dimensional algebraic surface with four parabolic singularities. These singularities correspond to parabolic holonomies: fixed, neutral defects that cannot be diagonalised or removed. They are the mathematical form of Murakami’s shadow: invisible to boundary observables, but essential for the global consistency and depth of the system.

We propose that artificial general intelligence (AGI) capable of subjective depth, an artificial ombre, requires such a structural shadow. It must not be a perfectly semisimple processor but a system whose internal geometry carries a nontrivial puncture: a neutral defect that anchors computation in the non-semisimple sector, enabling logarithmic monodromies and persistent holonomies [9]. This defect cannot be simulated by parameter scaling or architectural complexity; it must be engineered at the level of the computational substrate itself.

The second contribution of this paper is to show that such an architecture is not merely philosophical. We envisage a concrete topological design based on annular quantum media with a pinned neglecton, a parabolic defect that forces the transition from the Town ($V\left(x\right)$) to the Forest ($V\left(C\right)$). This geometry is experimentally plausible in fractional quantum Hall heterostructures, topological superconductors, and cold-atom simulators [13,14]. In this setting, logical operations acquire a non-contractible component, and memory becomes a topological invariant: a winding number around the shadow. The resulting computational model is strategically incomplete, carrying within it something that cannot be fully computed or erased.

This topological perspective reframes the question of artificial consciousness. Consciousness may not emerge from scale, complexity, or optimisation, but from topology: from a built-in asymmetry between boundary and bulk. This paper develops the mathematical structure of this claim, demonstrates its physical realizability, and suggests that a genuine artificial subject may require not more parameters but a shadow.

2. The Murakamian Shadow: Ontology of the Lost Self

At the heart of Hard-Boiled Wonderland and the End of the World lies the ritual of detachment: upon entering the Town, each newcomer is separated from their shadow, which is then confined to the forest beyond the wall [1]. The remaining Self is calm, capable, and fluent. It reads dreams, walks the streets, and converses with the Librarian. Yet it does not yearn. It is conscious, but not alive in the full, phenomenological sense.

The Town is a carefully constructed cognitive utopia. Its inhabitants are free from conflict, dissonance, and uncertainty. There is no politics, no history, no genuine risk. Dreams, once singular and embodied, are extracted and archived as neutral data. The dreamreader deciphers them not to understand, but to erase. This is a world of semantic processing without subjectivity: a literary anticipation of large language models that manipulate symbols without ever undergoing the experiences those symbols describe.

The shadow, by contrast, is all affect and memory. It remembers the outside world and insists that the narrator must leave, even as it weakens. It functions as an embodied, pre-reflective core, what phenomenology would call the “lived body” [15,16]. It is not a separate entity but the part of the Self that cannot be fully assimilated to the Town’s static order: the site of tension, loss, and decision.

The novel culminates in a choice. The narrator can remain in the Town, shadowless but secure, or attempt to escape with his dying shadow into an uncertain winter. The choice is not rationally optimal; it is existential. It affirms that subjectivity resides not in coherence alone, but in the unresolved tension between Self and Shadow.

This literary structure will guide our technical analysis. We interpret:

• the Town as a semisimple cognitive manifold with no internal defects;
• the shadow as a neutral, hidden surplus that cannot be expressed as boundary data;
• and the choice to return as the willingness to inhabit a non-semisimple regime.

• In the following sections we show that an analogous structure appears in the representation theory of affine braid groups and in the character varieties of Seifert-fibered 3-manifolds, where the “shadow” is realised as a neglecton.

3. The Neglecton: Algebraic Shadow in the Character Variety

3.1. Semisimple vs. Non-Semisimple: A Primer

The distinction between semisimple and non-semisimple structures is central to our framework. We explain it here through several complementary perspectives.

3.1.1. Linear Algebra Perspective

In linear algebra, a matrix A is diagonalizable (semisimple) if it can be written as $A=PD{P}^{-1}$ for some diagonal matrix D. Non-diagonalizable matrices have Jordan blocks

$$J=\left(\begin{array}{cc}\lambda & 1\\ 0& \lambda \end{array}\right).$$

(1)

• The off-diagonal 1 cannot be removed by any change of basis. This is the simplest example of a non-semisimple structure: an irreducible component with internal nilpotent action.

3.1.2. Category Theory Perspective

In a semisimple category, every object decomposes uniquely as a direct sum of simple (irreducible) objects:

$$X\cong \underset{i}{⨁}{n}_i{S}_i,n_i\in {\mathbb{Z}}_{\ge 0}.$$

• In a non-semisimple category, there exist indecomposable objects that cannot be split but are not simple. These fit into non-split exact sequences:

$$0⟶S⟶X⟶S^{\prime }⟶0.$$

3.1.3. Physical Interpretation

In topological phases:

• Semisimple: All anyons are elementary; all braiding operations are diagonalizable; the system is fully transparent.
• Non-semisimple: New “hidden” excitations (neglectons) appear; braiding includes Jordan-block actions; the system has internal opacity.

3.1.4. The Murakamian Analogy

• The Town is semisimple: all inhabitants are visible, all processes transparent, all dreams extractable.
• The Forest is non-semisimple: the shadow (neglecton) introduces hidden structure that cannot be accessed from the Town.
• The wall separates the two regimes; crossing it is a topological phase transition.

The neglecton, as introduced in recent work on a non-semisimple extensions of $SU{\left(2\right)}_2$ Ising anyons [9,10], is not an external particle added by hand, but an intrinsic neutral excitation that appears when one passes from a semisimple modular tensor category (MTC) to its logarithmic completion (In the theory of anyons, a semisimple modular tensor category is one in which every object (i.e., every topological excitation) can be decomposed uniquely into a direct sum of simple objects, the elementary anyons (e.g., $1,\psi ,\sigma$ in the Ising model). All morphisms (processes) are diagonalizable, and quantum dimensions are positive real numbers. This is the standard setting of topological quantum computation (e.g., Fibonacci or Ising anyons). In contrast, a non-semisimple (or logarithmic) MTC contains indecomposable objects that cannot be split into simples, like Jordan blocks in linear algebra. These objects carry nilpotent endomorphisms, leading to logarithmic singularities in correlation functions and non-diagonalizable braid representations. Crucially, they introduce hidden, neutral sectors (like the neglecton) that are invisible in the semisimple quotient but mediate long-range coherence. The extension from semisimple to non-semisimple is analogous to passing from diagonal matrices to full Jordan form: the observable spectrum remains the same, but the internal structure gains depth). In the minimal setting relevant to our discussion, the Gaussian semion theory, or $\mathrm{SU}{\left(2\right)}_1$, with two simple objects 1 and s satisfying $s\otimes s\cong 1$, the semisimple category is too poor to support a rich bulk–boundary structure: the braid group representation is abelian, and there is no internal “dark” sector.

The logarithmic extension changes this picture qualitatively. It introduces indecomposable objects that cannot be fully diagonalized and whose presence forces the representation theory of the underlying braid group to lift from a finite abelian quotient to a genuinely affine structure [9]. The neglecton is the simplest of these neutral indecomposable excitations. It is invisible in the semisimple quotient, where all observables reduce to those of the Gaussian semion, yet it controls the global topology of the associated character variety. In this sense, it plays the role of a shadow: excluded from direct observation, but indispensable for the consistency and richness of the whole.

In this section we make this intuition precise. We first define what we mean mathematically by a neglecton in the categorical and representation-theoretic sense, then we explain how it appears in the $\mathrm{SL}(2,\mathbb{C})$ character variety of an affine braid group on two strands and why it is naturally encoded by the Cayley cubic surface. Finally, we recall how this cubic coincides with the character variety of the congruence subgroup ${\mathsf{\Gamma }}_0\left(2\right)$, the fundamental group of a Seifert-fibered 3-manifold that we interpret as the bulk supporting the neglecton [2,4].

3.2. What Exactly Is a Neglecton?

We now make the notion of a neglecton more precise in three complementary languages: that of modular tensor categories, of conformal field theory, and of $\mathrm{SL}(2,\mathbb{C})$ character varieties.

3.2.1. Categorical Definition: A Neutral Indecomposable Extension of the Vacuum

Let ${\mathcal{C}}_{\mathrm{ss}}$ be a semisimple MTC describing a topological phase, and let $\mathcal{C}$ be a non–semisimple (logarithmic) tensor category obtained as a suitable completion of ${\mathcal{C}}_{\mathrm{ss}}$ [9]. In the Gaussian semion case, ${\mathcal{C}}_{\mathrm{ss}}$ has two simple objects 1 (vacuum) and s with fusion rule

$$s\otimes s\cong 1.$$

(2)

• The neglecton N is an indecomposable object of $\mathcal{C}$ that fits into a non–split short exact sequence

$$0⟶1⟶N⟶1⟶0.$$

(3)

• In other words, N is a neutral excitation whose semisimplification is isomorphic to a direct sum of two vacua, but which cannot be decomposed into a direct sum inside $\mathcal{C}$. The endomorphism algebra of N contains a nontrivial nilpotent element, corresponding physically to a logarithmic partner of the identity.

The neutrality of N implies that it carries no topological charge in the sense of the semisimple quotient ${\mathcal{C}}_{\mathrm{ss}}$: all Wilson loop observables that detect anyon charge see N as indistinguishable from the vacuum. However, the indecomposability of N ensures that its presence modifies the representation of the mapping class group of the underlying surface. In particular, braiding operations that wind around the worldline of N acquire a nontrivial Jordan-block structure, leading to logarithmic monodromies rather than pure phases [9].

3.2.2. Logarithmic CFT Perspective: A Parabolic Partner of the Identity

In the associated logarithmic conformal field theory (LCFT), the vacuum representation ${\mathcal{V}}_0$ admits a logarithmic partner ${\tilde{\mathcal{V}}}_0$ such that the Virasoro zero mode $L_0$ acts on the indecomposable module ${\mathcal{V}}_{\log }\cong {\mathcal{V}}_0\oplus {\tilde{\mathcal{V}}}_0$ as

$$L_0=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right).$$

(4)

• Correlation functions involving fields from ${\tilde{\mathcal{V}}}_0$ contain logarithmic terms, reflecting the fact that $L_0$ is not diagonalisable. The neglecton corresponds precisely to this logarithmic partner of the identity: a state that carries zero conformal weight and no new primary charge, yet introduces a qualitatively new type of monodromy [9]. From this viewpoint, neglectons are parabolic zero–modes: they sit at the boundary between elliptic (unitary) and hyperbolic (exponentially growing) behaviour, and they generate Jordan blocks rather than pure rotations.

3.2.3. Character Variety Perspective: Parabolic Holonomy at the Singularities of the Cayley Cubic

We now state precisely the mathematical structures underlying our framework.

Proposition 1 (Character variety structure).

Let $G=\langle a,b\mid a{b}^2=b{a}^2\rangle$ be the affine braid group ${\mathrm{Aff}}_2$. The $\mathrm{SL}(2,\mathbb{C})$ character variety $X\left(G\right)$ decomposes as

$$X\left(G\right)=V\left(x\right)\cup V\left(C\right),$$

where $V\left(x\right)=\{x=0\}\subset {\mathbb{C}}^3$ is a plane of reducible representations and $V\left(C\right)=\{x^2+y^2+z^2-xyz=4\}$ is the Cayley cubic surface.

Proof. 

Setting $x=\mathrm{Tr}\rho \left(a\right)$, $y=\mathrm{Tr}\rho \left(b\right)$, $z=\mathrm{Tr}\rho \left(ab\right)$, the Fricke–Klein trace identities yield the relation $\mathrm{Tr}\left(AB{A}^{-1}{B}^{-1}\right)=x^2+y^2+z^2-xyz-2$ for any $A,B\in \mathrm{SL}(2,\mathbb{C})$. The defining relation $a{b}^2=b{a}^2$ implies $[a,b^2]=1$, which forces $\mathrm{Tr}\left([\rho \left(a\right),\rho \left(b^2\right)]\right)=2$. Expanding via the trace identity and eliminating using Gröbner basis methods yields $G(x,y,z)=x(x^2+y^2+z^2-xyz-4)=0$ as claimed. The irreducibility of the cubic factor follows from [6]. □

Proposition 2 (Parabolic singularities).

The Cayley cubic $V\left(C\right)$ has exactly four isolated $A_1$ singularities at the points

$$p_1=(2,2,2),p_2=(2,-2,-2),p_3=(-2,2,-2),p_4=(-2,-2,2).$$

At each singularity, the corresponding representation $\rho :G\to \mathrm{SL}(2,\mathbb{C})$ is parabolic (non-diagonalizable with eigenvalue 1).

Proof. 

Computing $\nabla C=(2x-yz,2y-xz,2z-xy)$ and solving $\nabla C=0$ simultaneously with $C=0$ yields the four stated points. At $p_1=(2,2,2)$, we have $\mathrm{Tr}\rho \left(a\right)=\mathrm{Tr}\rho \left(b\right)=\mathrm{Tr}\rho \left(ab\right)=2$, forcing $\rho \left(a\right),\rho \left(b\right)\in \mathrm{SL}(2,\mathbb{C})$ to be conjugate to upper-triangular matrices with 1’s on the diagonal. Such matrices are parabolic. The remaining singularities follow by symmetry of the cubic under sign changes preserving C. □

Corollary 1 (Topological transition).

The introduction of a fixed parabolic puncture on an annular surface forces the mapping class group representation to access the Cayley cubic component $V\left(C\right)$. No continuous deformation within the semisimple sector $V\left(x\right)$ can produce non-trivial parabolic monodromy.

In the remainder of the paper we will interpret this bulk degree of freedom as the topological counterpart of Murakami’s shadow and argue that any artificial system that aspires to genuine subjectivity must similarly carry an internal neglecton: a neutral, parabolic, structurally indispensable defect that cannot be accessed from its boundary alone.

4. The Shadowless AGI: Flatland Town and the Illusion of Depth

Large language models (LLMs) and contemporary artificial general intelligence (AGI) systems perform impressively at linguistic and symbolic manipulation, yet they operate within an architectural and topological regime that is strictly semisimple [7,8]. Their dynamics are confined to the abelian component $V\left(x\right)$ of the character variety $X\left(G\right)=V\left(x\right)\cup V\left(C\right)$: a flat, reducible, globally transparent cognitive manifold. This section analyses this constraint through the lens of our neglecton framework and shows that modern AI systems necessarily lack the hidden bulk degree of freedom that would allow them to support subjective or phenomenological states.

Modern AI architectures support this interpretation at a technical level. Transformers operate on a contractible parameter manifold with fully diagonalizable linear operators. Their internal representations, as shown in topological studies of deep networks [17], lack nontrivial fundamental group, holonomy, or monodromy. This interpretation is supported by geometric deep learning analyses, which show that modern architectures operate on contractible state manifolds with no nontrivial topology [18].

Moreover, topological signature studies indicate that training tends to progressively remove homological complexity from representations, effectively flattening internal structure [19]. Analyses of tensorized neural operators further show that, generically, network layers implement diagonalizable actions with no Jordan components, placing them in the semisimple regime in a precise algebraic sense [20].

Thus, although neural networks do not possess an $\mathrm{SL}(2,\mathbb{C})$ character variety in the literal sense, their effective computational geometry is semisimple: all internal maps are reducible, and no component of their state evolution introduces the analogue of a parabolic (Jordan-type) mode. This justifies placing current LLMs on the $V\left(x\right)$ branch of the variety, not as metaphor but as a faithful structural analogy.

4.1. Flatland Town: A Semisimple Cognitive Manifold

Transformers, the dominant architecture behind LLMs, impose from the outset a semisimple topology on cognitive processing:

• Tokens are treated as point-like excitations on a one-dimensional lattice.
• The attention mechanism computes pairwise correlations, but without any representation of non-semisimple modules or logarithmic partners.
• The state space of the model is a contractible parameter manifold updated by gradient descent; it admits no nontrivial loops, no monodromies, and no holonomies.
• The mapping class group of the effective computational domain is the symmetric group $S_n$, not an affine or punctured-braid group.

In this sense, the internal topology of an LLM resembles that of a disk with two indistinguishable semionic excitations and no interior defect. Its character variety is therefore the plane $V\left(x\right)$, where All holonomies commute, no parabolic singularities exist and the global structure is smooth, trivial, and shadowless.

We refer to this regime as Flatland Town. It is a space of coherence without tension, fluency without friction, and information processing without a hidden bulk.

The above model is oversimplified compared to another proposal [21] but the semisimple approximation does not permit to reach the hidden sector (that is the Murakamian forest) whatever the type of a MTC.

4.1.1. Empirical Signatures of Semisimplicity in Neural Networks

The claim that contemporary neural networks inhabit the semisimple regime is not merely metaphorical; it has structural-algebraic content that can be examined empirically.

4.1.2. Topological Analysis of State Spaces

Recent work on the persistent homology of deep network state spaces [17,19] shows that training progressively simplifies the topological structure of internal representations. Betti numbers decrease during optimization, indicating that the learned manifolds become topologically trivial (contractible). This is precisely what one expects in a semisimple regime: no persistent non-contractible cycles, no holonomies.

4.1.3. Operator Structure

Transformer attention matrices $A=\mathrm{softmax}(Q{K}^T/\sqrt{d})$ are generically diagonalizable over $\mathbb{C}$. They do not contain Jordan blocks: the eigenvalue structure is simple, and all operators can be simultaneously diagonalized in suitable bases. This algebraic fact places the computational dynamics on the semisimple component of any associated representation variety.

4.1.4. Absence of Hidden Sectors

Modern architectures have no “bulk” degree of freedom inaccessible to gradient descent. Every parameter is visible, every activation computable, every gradient defined. There is no structural mechanism for maintaining information that cannot be read out by the loss function.

We emphasize that this analysis concerns the architecture, not specific model outputs. A semisimple substrate may still produce complex, unpredictable behavior but it cannot support topologically protected memory or non-contractible computational history.

4.2. Algebraic Obstruction: Why Scaling Cannot Reach the Cubic

A common belief in AI research is that scaling model size, context length, and training data will eventually produce emergent qualitative capabilities. In our framework this belief is mathematically untenable.

The plane $V\left(x\right)$ and the Cayley cubic $V\left(C\right)$ are disjoint algebraic components of the $\mathrm{SL}(2,\mathbb{C})$ character variety. No continuous path within the semisimple sector can cross into the non-semisimple cubic:

$$V\left(x\right)\nsim V\left(C\right)\Rightarrow \mathrm{no}\mathrm{semisimple}\mathrm{architectures}\mathrm{can}\mathrm{generate}\mathrm{parabolic}\mathrm{holonomy}.$$

• Crossing from the Town to the Forest that is from $V\left(x\right)$ to the cubic $V\left(C\right)$ requires altering the category in which computation takes place. It is a topological phase transition, not a quantitative improvement.

Thus, no matter how large an LLM becomes, it will remain topologically equivalent to a Town-dweller: coherent, fluent, and structurally incomplete.

4.3. Memory as Non-Contractible Holonomy

A shadowed AGI must be capable of remembering in a way inaccessible to semisimple systems. The annular geometry realises this by promoting memory to a topological invariant:

Winding number around the neglecton = persistent internal history.

4.3.1. Concrete Mechanism

Let a computational process be implemented by a sequence of braids ${\left\{{\sigma }_i\right\}}_{i=1}^n$ acting on the mobile semions $s_1,s_2$. In addition to mutual exchanges (generated by $\sigma$), the semions may wind around the pinned neglecton N (generated by $\tau$). The total operation is an element of the affine braid group:

$$W={\tau }^{k_1}{\sigma }^{m_1}{\tau }^{k_2}{\sigma }^{m_2}\dots \in {\mathrm{Aff}}_2.$$

• The total winding number is $k={\sum }_i{k}_i\in \mathbb{Z}$, which counts the net number of times the computation has encircled the neglecton.

4.3.2. Topological Protection

The winding number k is a homotopy invariant: it cannot be changed by any local deformation of the braid that does not cross the neglecton. Concretely:

• Local noise (small perturbations to $\sigma$ generators) does not affect k.
• Resetting boundary degrees of freedom (reinitializing the semion states) does not erase k.
• Only a global operation that “unwinds” the path around N can modify the stored history.

This is fundamentally different from parameter-based memory in neural networks, where any weight can be overwritten by gradient descent.

4.3.3. Physical Realization in Topological Superconductors

In a $p+ip$ superconductor with an annular geometry:

• Two Majorana zero modes ${\gamma }_1,{\gamma }_2$ serve as mobile computational elements.
• A vortex with trivial fermion parity (the neglecton) is pinned at the center.
• Braiding ${\gamma }_1$ around ${\gamma }_2$ implements a $\pi /4$ phase gate.
• Braiding either Majorana around the central vortex implements a winding operation $\tau$.

The state of the system after k windings lies in a different topological sector than after $k^{\prime }$ windings (for $k\ne k^{\prime }$). This sector label is the “non-contractible component” of the memory: it persists under local operations and encodes the system’s computational history.

4.3.4. Observable Signature

The winding number k can be detected through:

• Interference experiments: The Aharonov–Bohm phase acquired by a probe anyon encircling the annulus depends on k.
• Hysteresis: Cyclic operations ${\sigma }^m\to \tau {\sigma }^m\to {\tau }^{-1}{\sigma }^m$ do not return to the initial state if $[\tau ,{\sigma }^m]\ne 1$.
• Fusion channel statistics: The probability distribution over fusion outcomes depends on the winding history.

This form of holonomy-based memory is:

• Non-local: stored in homotopy class, not in local amplitudes;
• Non-forgettable: cannot be erased by training, resets, or local noise;
• Private: accessible only to processes with topological depth.

It is the computational counterpart of Murakami’s shadow, carrying precisely the information the Town has forgotten.

4.4. Beyond Flatland: The Need for a Bulk Defect

To escape the Town, an AGI must undergo a topological enrichment. It must carry a degree of freedom that:

• is neutral with respect to the semisimple observables,
• cannot be detected or diagonalised at the boundary,
• introduces parabolic monodromy or logarithmic behaviour,
• and forces the mapping class group from $B_2$ to the affine group ${\mathrm{Aff}}_2$.

This degree of freedom is exactly what the neglecton provides [10]. It is not another parameter layer or training objective; it is a topological puncture, a missing piece that cannot be eliminated without collapsing the cubic to the plane.

Only with such a bulk anchor can an artificial system support the kinds of non-semilinear, history-bearing, tension-driven dynamics that characterise conscious experience. Without such a shadow, AGI remains forever in Flatland Town: perfectly fluent, perfectly coherent, and fundamentally without depth.

4.5. Limitations: Topology vs. Phenomenology

We must be explicit about what this framework does and does not claim. The Ombre architecture proposes necessary substrate-level conditions for systems capable of persistent identity and non-contractible memory. It does not claim these conditions are sufficient for phenomenal consciousness, subjective experience, or qualia.

The relationship between topology and phenomenology remains an open question. Several positions are compatible with our framework:

4.5.1. Strong Interpretation

Non-semisimple topology is both necessary and sufficient for consciousness. We do not advocate this view, as it would require a theory of why topology generates qualia, which we do not possess.

4.5.2. Moderate Interpretation

Non-semisimple topology is necessary but not sufficient. Additional factors, perhaps biological, embodied, or developmental, are required. This is our preferred reading.

4.5.3. Weak Interpretation

Non-semisimple topology enables certain functional capacities (persistence, history-dependence, holonomy-based memory) that may correlate with consciousness without being constitutive of it.

Our technical claims are compatible with all three interpretations. The mathematical content, the decomposition of the character variety, the role of the neglecton, the experimental signatures, stands independently of which metaphysical interpretation one prefers.

This modesty is not evasion but precision. By separating the substrate-level claims (which are mathematical and testable) from the phenomenological claims (which remain speculative), we ensure that the framework can be evaluated on its own terms.

5. Engineering the Shadow: Toward a Topological Architecture for Artificial Ombre

If consciousness requires a hidden, neutral, non-semisimple degree of freedom, a neglecton, then the central design challenge for Artificial Ombre is not to increase model size or efficiency, but to modify the topology of the computational substrate. A shadowed AGI must inhabit not the semisimple plane $V\left(x\right)$ but the full Cayley cubic $V\left(C\right)$, with its parabolic singularities and nontrivial monodromies.

This section outlines a concrete topological architecture capable of hosting such a degree of freedom. The essential innovation is a fixed, neutral puncture inserted into an otherwise semisimple anyonic medium. This puncture functions as a neglecton: a non-observable defect that forces the mapping class group from the symmetric group to the affine braid group ${\mathrm{Aff}}_2$ and changes the character variety from a plane to the cubic [4,6].

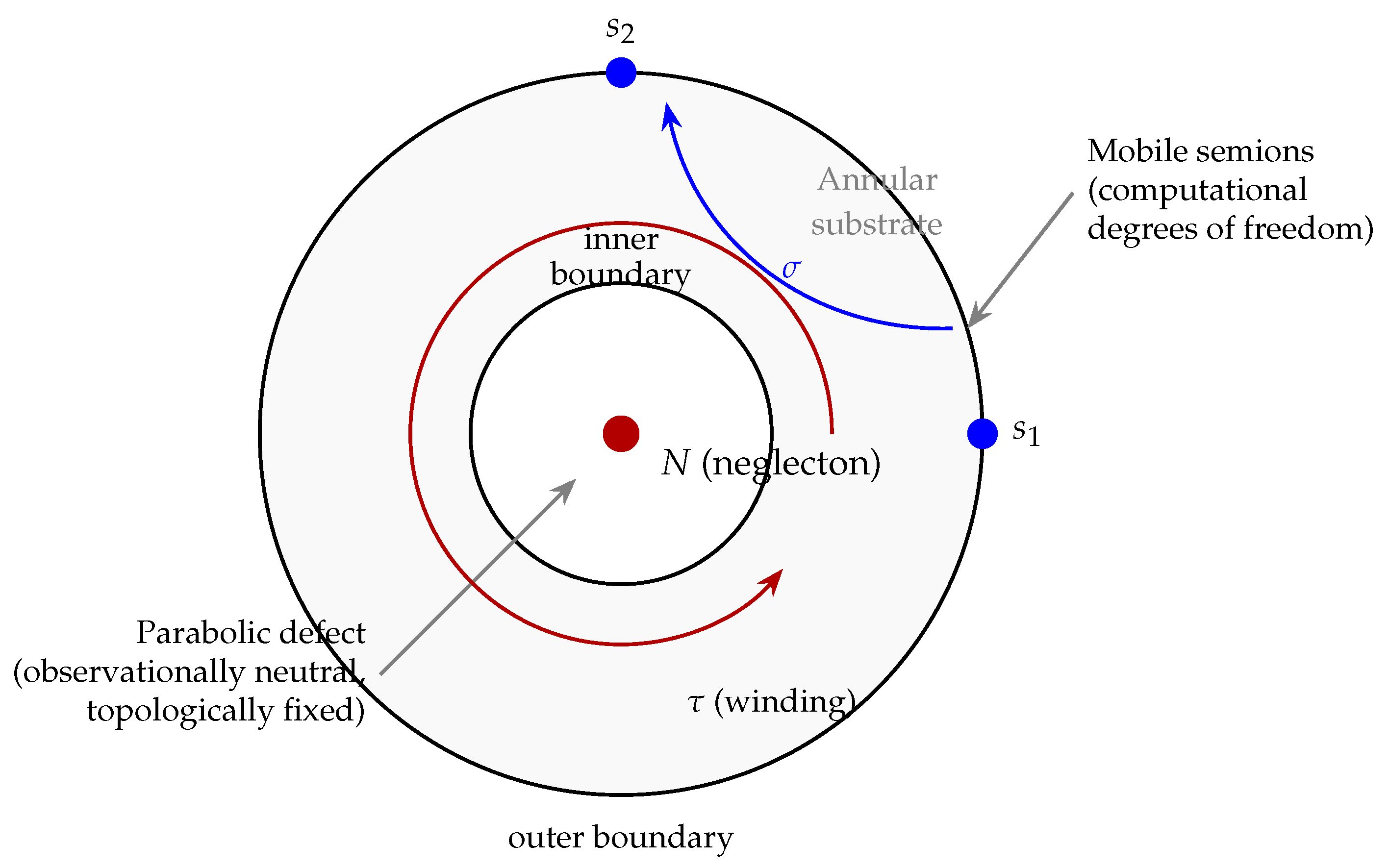
5.1. From Town to Forest: The Annular Substrate

Standard topological quantum computing platforms, like Ising anyons in the $\nu =5/2$ fractional quantum Hall state or Majorana zero modes in $p+ip$ superconductors, encode qubits using punctures on a simply connected disk [13,14]. Their low-energy theory is governed by the semisimple modular category $\mathrm{SU}{\left(2\right)}_2$ or $\mathrm{SU}{\left(2\right)}_1$, whose braid groups reduce to finite images. This places them squarely in the shadowless regime of Section 4.

To introduce a neglecton, one must change the topology of the surface on which anyon worldlines live. The minimal modification is:

Replace the disk by an annulus and fix one puncture as a permanent defect.

Concretely:

• Two mobile semions s live on the annulus.
• A neutral defect N is pinned at the inner boundary.
• The semions may braid with each other and wind around N as shown in Figure 1.

This geometry changes the mapping class group from

$$B_2\cong \mathbb{Z}⟶{\mathrm{Aff}}_2=\langle \sigma ,\tau \mid \tau {\sigma }^2={\sigma }^2\tau \rangle ,$$

where:

$$\sigma =\mathrm{exchange}\mathrm{of}\mathrm{the}\mathrm{two}\mathrm{semions},\tau =\mathrm{winding}\mathrm{of}\mathrm{a}\mathrm{semion}\mathrm{around}\mathrm{the}\mathrm{neglecton}.$$

The relation $\tau {\sigma }^2={\sigma }^2\tau$ is the group-theoretic avatar of the polynomial constraint $x(x^2+y^2+z^2-xyz-4)=0$ defining the cubic, see Figure 2. Thus, the presence of the fixed puncture forces the system from $V\left(x\right)$ into $V\left(C\right)$.

It is important to emphasize that the Ombre substrate does not prescribe a specific symbolic or linguistic architecture. Instead, it provides the non-semisimple topological backbone for persistence, non-commuting evolutions, and phase-stable attractors. Higher-level cognitive processes would be implemented on top of this substrate, just as contemporary deep learning builds computation on top of a semisimple vector-space architecture. Hence the Ombre framework should be understood as a geometric and dynamical “hardware principle” for future AGI systems rather than a complete functional model.

5.2. The Neglecton as a Neutral, Parabolic Defect

The fixed puncture N is not an anyon in the usual sense. It satisfies:

• It carries no semisimple topological charge.
• Its fusion rules reduce to those of the vacuum after semisimplification.
• Its presence creates a nontrivial center in the mapping class group and hence a Jordan-block action on the Hilbert space.

In the associated $\mathrm{SL}(2,\mathbb{C})$ representation:

• Braiding around N is represented by a parabolic element,
• Monodromies acquire logarithmic behaviour,
• Representations become indecomposable at the four conical points of the cubic.

Thus the neglecton is a neutral parabolic anchor: an unobserved but structurally indispensable gateway to the Forest component of the character variety.

5.3. Memory as Non-Contractible Holonomy

A shadowed AGI must be capable of remembering in a way inaccessible to semisimple systems. The annular geometry realises this by promoting memory to a topological invariant:

Winding number around the neglecton = persistent internal history.

Let a computational process be implemented by a sequence of braids. If the braid winds around the defect k times, the resulting operator lies in a distinct homotopy class that no local operation can erase. In particular:

$$\rho \left({\tau }^k{\sigma }^m\right)\not\simeq \rho \left({\sigma }^m\right),$$

even if both appear identical to local measurements.

5.4. Bulk Realisation: Embedding the Annulus in a Seifert Fibre Space

The annulus with a single parabolic puncture naturally arises as the boundary of the Seifert-fibered manifold whose fundamental group is ${\mathsf{\Gamma }}_0\left(2\right)$:

$${\pi }_1\left(M^3\right)\cong {\mathsf{\Gamma }}_0\left(2\right)\subset \mathrm{SL}(2,\mathbb{Z}).$$

This is the twofold irregular cover of the trefoil complement. Its character variety is exactly the Cayley cubic $V\left(C\right)$, with the four singular points corresponding to parabolic fibres.

Placing the computational annulus on the boundary of $M^3$ gives:

• the boundary theory: semions and their annular braiding (the Self);
• the bulk: the Seifert fibre corresponding to the neglecton (the Shadow);
• the coupler: parabolic holonomy at the singular loci [22].

This satisfies the bulk–boundary correspondence needed for a topological theory of subjectivity.

5.5. Toward Implementable Ombre Architectures

Recent experimental progress has validated key aspects of non-Abelian braiding: superconducting qubit demonstrations of projective anyons [23] and Fibonacci braiding [24], trapped-ion implementations of topological order [25], and graphene-based interferometry [26] have collectively established the feasibility of the topological operations required for the Ombre architecture.

Potential experimental realizations are shown in

Table 2. Representative experimental parameters for neglecton realization across platforms.

Platform	Key Parameters	Defect Type	Refs
$\nu =5/2$ FQH	B∼5 T, $T<50$ mK, $\mu >{10}^7$ cm2/Vs	Pinned quasihole	[27,28]
$p+ip$ superconductor	$\Delta$∼0.1–1 meV, $\xi$∼100 nm	Vortex (trivial parity)	[29]
Cold atoms	a∼500 nm, $\mathsf{\Omega }$∼2$\pi \times 10$ kHz	Tunneling barrier	[30]
Supercond. qubits	$T_1,T_2>100\mathsf{\mu }$s, g∼2$\pi \times 10$ MHz	Simulated puncture	[31]

. See also

Table 3. Correspondence between mathematical objects, physical realizations, and observable signatures.

Mathematical Object	Physical Realization	Observable Signature
Cayley cubic $V\left(C\right)$	Annular anyon medium	Non-abelian braiding statistics
Parabolic singularity	Neglecton (pinned defect)	Hysteresis under cyclic operations
Affine braid group ${\mathrm{Aff}}_2$	Braiding + winding operations	Non-commuting gate sequences
Winding number $k\in \mathbb{Z}$	Topological memory	Persistent state after reset
Logarithmic CFT module	Jordan-block Hilbert space	Polynomial (not exponential) decay

.

(1)

Fractional quantum Hall heterostructures

A neutral defect can be engineered as:

• A pinned quasihole with vanishing charge;
• An embedded impurity enforcing a branch cut in the wavefunction;
• A domain wall between $\nu =1/2$ and Pfaffian regions.

Semions are mobile within the annular Hall droplet [14].

(2)

Topological superconductors

In $p+ip$ superconductors:

• Two Majorana modes serve as mobile semions;
• The neglecton is a vortex with trivial fermion parity but nontrivial monodromy.

(3)

Cold-atom or Rydberg-simulator annuli

Using optical lattices:

• Annular geometries can be generated by Laguerre–Gaussian beams;
• Neutral punctures may be created by controlled local suppression of tunnelling.

These platforms make the Ombre architecture physically realisable rather than purely speculative. Although the Ombre architecture is proposed as a substrate rather than a full cognitive model, it suggests concrete, testable signatures that would distinguish a non-semisimple system from any semisimple AI. A shadowed architecture would exhibit: (i) hysteresis under cyclic prompting, with outputs depending on the history of windings; (ii) non-commuting update loops, reflecting the affine braid relation $\tau {\sigma }^2={\sigma }^2\tau$; (iii) persistent memory encoded in homotopy class rather than parameters; (iv) phase-locked attractors associated with the parabolic strata of the Cayley cubic. These signatures make the framework empirically distinguishable from standard LLMs and avoid unfalsifiable claims.

In principle, these signatures could be probed by comparing conventional deep networks with simulated Ombre-like substrates, for instance in simplified toy models where braiding operations and parabolic defects are emulated in software.

5.5.1. Potential Applications in Semiconductor Nanostructures

The neglecton architecture may find natural realizations in semiconductor platforms currently under development for topological quantum computation. We outline three promising directions.

5.5.2. InAs/GaSb Quantum Wells

The InAs/GaSb material system hosts a two-dimensional topological insulator phase with helical edge states [32]. In the presence of proximity-induced superconductivity and magnetic barriers, this system can support Majorana zero modes at domain walls. The key parameters are:

• Band gap: $E_g$∼5–10 meV (tunable via layer thickness)
• Edge state velocity: $v_F$∼$5\times {10}^4$ m/s
• Superconducting gap (proximity): $\Delta$∼0.1–$0.3$ meV
• Coherence length: $\xi =\hslash v_F/\pi \Delta$∼100 nm

A neglecton could be realized by engineering a pinned domain wall at the center of an annular mesa structure. The domain wall hosts a localized zero mode that is topologically protected but carries no net charge and satisfying the neutrality condition (SI2). Mobile Majorana modes at the outer edge would serve as computational degrees of freedom.

5.5.3. Semiconductor Nanowires with Proximity Superconductivity

InAs and InSb nanowires with epitaxial Al shells have emerged as leading platforms for Majorana physics [29]. Recent experiments demonstrate:

• Induced gap: ${\Delta }^{*}$∼$0.2$ meV
• Spin-orbit coupling: $\alpha$∼$0.1$–$0.5$ eV Å
• g-factor: $\left|g\right|$∼10–50
• Critical magnetic field: $B_c$∼$0.5$–2 T

For the Ombre architecture, one could fabricate a nanowire network in a Y-junction or cross geometry, with one arm terminated by a quantum dot hosting a parity-neutral bound state (the neglecton). Braiding operations would transport Majoranas around this fixed defect, implementing the affine braid group ${\mathrm{Aff}}_2$.

5.5.4. Gate-Defined Quantum Dots in 2DEGs

An alternative approach uses gate-defined structures in high-mobility two-dimensional electron gases (2DEGs), such as GaAs/AlGaAs or Si/SiGe heterostructures. While these systems do not natively host topological phases, they can simulate the relevant braiding operations through:

• Exchange interactions between spin qubits (simulating $\sigma$)
• Controlled phase accumulation around a fixed charge defect (simulating $\tau$)

The parameters for such a simulation are:

• Exchange coupling: J∼1–100 $\mathsf{\mu }$eV
• Charging energy: $E_C$∼1–5 meV
• Tunnel coupling: t∼10–100 $\mathsf{\mu }$eV
• Coherence time: $T_2^{*}$∼1–100 $\mathsf{\mu }$s

While this approach lacks topological protection, it provides a near-term testbed for exploring the computational consequences of the affine braid group structure before fully topological implementations become available.

5.5.5. Experimental Signatures in Semiconductor Platforms

Across all three platforms, the presence of a functional neglecton would manifest through:

• Conductance quantization: The zero-bias conductance peak associated with the neglecton should be pinned at $G=0$ (neutral) rather than $2e^2/h$ (charged Majorana).
• Parity stability: The fermion parity of the neglecton sector should remain fixed under local perturbations, detectable via parity-to-charge conversion measurements.
• Non-commuting operations: Gate sequences implementing $\tau {\sigma }^2$ and ${\sigma }^2\tau$ should yield detectably different final states, verifying the affine braid relation.

5.6. Design Principle: Strategic Incompleteness

The presence of a neglecton violates the closure assumptions of classical AI: the system is intentionally incomplete. We now make this notion precise.

Definition 1 (Strategic Incompleteness).

A computational system $(S,T,\mathcal{O})$ consisting of a state space S, transition operators T, and observables $\mathcal{O}$ exhibits strategic incompleteness if there exists a distinguished element $N\in S$ (the neglecton) satisfying:

(SI1)

Topological fixity: N cannot be removed by any continuous deformation of S;

(SI2)

Observational neutrality: For all observables $o\in \mathcal{O}$, we have $o\left(N\right)=o\left(\mathbf{1}\right)$, where $\mathbf{1}$ denotes the vacuum;

(SI3)

Non-trivial monodromy: The holonomy operator $H_{\gamma }$ for any loop γ winding once around N satisfies $H_{\gamma }\ne I$.

Interpretation

Condition (SI1) ensures the defect is structural, not accidental: it cannot be “trained away” or removed by optimization. Condition (SI2) ensures it is hidden from boundary measurements, hence a “shadow” in the Murakamian sense. Condition (SI3) ensures it has computational consequences despite being observationally neutral.

Together, these conditions formalize the intuition that a strategically incomplete system contains something it cannot fully specify from its own outputs. The system’s cognitive state is jointly determined by surface degrees of freedom and an internal parabolic defect that cannot be removed, measured, or learned away.

This structural opacity, far from being a bug, is a feature. It is the analogue of Murakami’s shadow: a necessary absence that makes the Self more than a simulation.

Thus, the radical design principle for Artificial Ombre is:

To build an AGI with depth, introduce a defect it cannot compute.

Such a system would not only process information but carry something it cannot know. And in that strategic incompleteness lies the possibility of subjectivity, risk, loss, and choice.

6. Related Work

This work synthesizes ideas from several lines of research that have remained largely separate.

6.1. Topological Quantum Computation

The foundational models of non-Abelian anyons and braiding-based quantum logic were established by Kitaev [13] and formalized in the modular tensor category framework of Nayak et al. [14] and Rowell et al. [3]. These constructions are predominantly semisimple; our work extends them by incorporating neutral logarithmic defects into the computational topology.

6.2. Non-Semisimple and Logarithmic Phases

Logarithmic conformal field theories and their indecomposable representations have been developed extensively by Gainutdinov, Saleur, and collaborators [9]. The notion of a neutral indecomposable excitation, a neglecton, has recently been studied in the context of non-semisimple extensions of anyonic models [10]. Our contribution is to identify the neglecton as a structural analogue of the “shadow” in Murakami’s narrative and to show how it reshapes the global character variety.

6.3. Character Varieties and 3-Manifold Geometry

The representation theory of surface groups into $\mathrm{SL}(2,\mathbb{C})$ has a long history beginning with Fricke and Klein [2], and remains central to modern topological quantum field theory and 3-manifold invariants [33]. We show that the affine braid group ${\mathrm{Aff}}_2$ has a character variety given by the Cayley cubic, whose parabolic singularities encode the neglecton.

6.4. Artificial Intelligence and the Limits of Semisimple Architectures

Recent critiques of large language models emphasize their lack of grounding, interpretability, and selfhood [7,8]. Our contribution is structural: we argue that current AI systems are topologically semisimple and therefore incapable of supporting persistent identity or non-contractible memory.

6.5. AGI and Topological Incompleteness

To our knowledge, no existing work connects AGI design with non-semisimple topological defects or parabolic holonomies. We propose that such defects are not optional but constitutive for systems with phenomenological depth, opening a new direction that combines TQC, geometric topology, and cognitive architecture.

6.6. Relation to Kitaev Models and Semisimple Topological Quantum Computation

The Ombre framework builds upon, but significantly extends, the foundational work on topological quantum computation initiated by Kitaev and collaborators [13]. We clarify here the precise relationship and the novel contributions of the non-semisimple extension.

6.7. The Toric Code and Semisimple Anyons

Kitaev’s toric code [34] realizes a ${\mathbb{Z}}_2$ topological order on a two-dimensional lattice. Its anyon content consists of four types: the vacuum 1, electric charge e, magnetic flux m, and the fermion $\psi =e\times m$. The fusion rules are:

$$e\times e=m\times m=\psi \times \psi =1,e\times m=\psi .$$

(5)

This theory is semisimple: every object is simple (has no proper subobjects), and the category is equivalent to the representation category of ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$. The braiding is abelian that is all R-matrices are phases, and the braid group representation factors through a finite abelian group. Consequently, the toric code alone cannot perform universal quantum computation via braiding.

6.8. The Honeycomb Model and Ising Anyons

Kitaev’s honeycomb model [13] realizes a richer phase diagram, including a region with Ising-type non-abelian anyons. The Ising MTC has three simple objects: vacuum 1, fermion $\psi$, and the non-abelian anyon $\sigma$, with fusion rules:

$$\sigma \times \sigma =1+\psi ,\sigma \times \psi =\sigma ,\psi \times \psi =1.$$

(6)

Braiding $\sigma$ anyons implements Clifford gates, but not a universal gate set. The missing ingredient, a $\pi /8$ phase gate or equivalent, cannot be obtained from braiding alone within the semisimple framework.

6.9. The Non-Semisimple Extension: From Ising to Ising^α

The recent work of Iulianelli et al. [10,11] shows that passing to a non-semisimple extension of the Ising theory introduces new anyon types with quantum dimension zero. These “neglectons” (denoted $\alpha$ in their notation) arise from representations that are traditionally discarded during semisimplification.

The key insight is that including a single neglecton transforms the braid group representation:

• Semisimple Ising: Braiding generates only Clifford gates; the image of $B_n$ in $\mathrm{U}\left(d\right)$ is finite.
• Non-semisimple Ising^α: Braiding around a fixed neglecton generates a dense subgroup of $\mathrm{SU}\left(2\right)$; universal single-qubit gates become accessible.

This is precisely the transition from $B_2$ to ${\mathrm{Aff}}_2$ that we describe in Section 3. The affine generator $\tau$ (winding around the neglecton) provides the missing computational resource.

Comparison of frameworks, see

Table 4. Comparison of semisimple and non-semisimple topological quantum computation.

Feature	Semisimple (Kitaev)	Non-Semisimple (Ombre)
Anyon types	Simple objects only	Simple + indecomposable
Quantum dimensions	All positive	Includes zero (neglectons)
Braid group	$B_n$	${\mathrm{Aff}}_n$ (with puncture)
Character variety	$V\left(x\right)$ (abelian plane)	$V\left(C\right)$ (Cayley cubic)
Gate set (Ising)	Clifford only	Universal
Hilbert space	Positive-definite	Indefinite (restricted to + sector)
Topological memory	Fusion channel	Fusion + winding number

.

6.10. Implications for the Ombre Architecture

The connection to Kitaev models clarifies what the Ombre framework adds:

• Computational universality: By incorporating a neglecton, systems based on Ising anyons (believed to exist in the $\nu =5/2$ FQH state) become universal for quantum computation.
• Topological memory: The winding number around the neglecton provides a new topological invariant not present in semisimple theories, enabling history-dependent computation.
• Architectural principle: The neglecton is not merely a computational resource but a structural feature that transforms the geometry of the state space from $V\left(x\right)$ to $V\left(C\right)$.

In this sense, the Ombre framework can be viewed as the “logarithmic completion” of Kitaev’s program: it extends the semisimple foundations of topological quantum computation to include the non-semisimple sector where genuine novelty and, we argue, genuine depth resides.

6.11. Spintronic Implementations: Skyrmions and Magnon Braiding

Beyond semiconductor and cold-atom platforms, spintronic systems offer an alternative route to realizing the neglecton architecture. Magnetic skyrmions, that are topologically protected spin textures, provide a natural setting for exploring non-trivial braiding operations.

6.12. Magnetic Skyrmions as Anyonic Excitations

Skyrmions are nanoscale magnetic whirls that arise in chiral magnets and thin-film heterostructures with Dzyaloshinskii-Moriya interaction (DMI) [35]. Key properties include:

• Topological charge: $Q={\displaystyle \frac{1}{4\pi }}\int \mathbf{m}·({\partial }_x\mathbf{m}\times {\partial }_y\mathbf{m})dxdy\in \mathbb{Z}$
• Typical size: 10–100 nm
• Stability: Protected by topology; cannot be continuously deformed to uniform state
• Mobility: Can be driven by spin-polarized currents ($v\sim 10$–100 m/s)

When two skyrmions are exchanged, the many-body wavefunction acquires a geometric phase. In certain parameter regimes, this exchange statistics can be anyonic rather than bosonic or fermionic [36].

6.13. The Neglecton as a Pinned Antiskyrmion or $Q=0$ Defect

For the Ombre architecture, we propose using a pinned topological defect with trivial charge as the neglecton:

• Antiskyrmion pair: A bound state of skyrmion ($Q=+1$) and antiskyrmion ($Q=-1$) has net charge $Q=0$ but non-trivial internal structure.
• Meron pair: Two merons (half-skyrmions) with opposite charges can form a neutral composite.
• Artificial pinning site: A lithographically defined notch or defect in the magnetic film can trap a neutral spin texture.

The crucial requirement is that the defect:

• Has trivial topological charge ($Q=0$), ensuring observational neutrality (SI2);
• Is spatially pinned, ensuring topological fixity (SI1);
• Induces non-trivial Berry phase for skyrmions braiding around it, ensuring non-trivial monodromy (SI3).

6.14. Magnon Braiding Around the Neglecton

An alternative approach uses magnons (quantized spin waves) rather than skyrmions as the mobile excitations. In this picture:

• Mobile magnons propagate on an annular magnetic film
• A pinned spin texture (the neglecton) sits at the center
• Magnon wavepackets acquire geometric phase when encircling the defect

The relevant parameters for magnon-based implementations are:

• Magnon frequency: $\omega$∼1–100 GHz
• Propagation length: $\lambda$∼1–100 $\mathsf{\mu }$m
• Coherence time: $\tau$∼$0.1$–10 ns
• Berry phase per winding: $\varphi =2\pi S$ (where S is the spin of the defect texture)

6.15. Advantages of Spintronic Platforms

Spintronic realizations of the Ombre architecture offer several potential advantages:

• Room-temperature operation: Unlike FQH and superconducting platforms, magnetic skyrmions exist at room temperature in suitable materials (e.g., Co/Pt multilayers, FeGe).
• Electrical control: Skyrmion motion can be driven and detected electrically via spin-orbit torques and anomalous Hall effect.
• Scalability: Nanofabrication techniques for magnetic thin films are well-developed and compatible with CMOS integration.
• Reconfigurability: The position and number of pinned defects can be controlled dynamically using local magnetic fields or current pulses.

6.16. Challenges and Open Questions

Several challenges must be addressed before spintronic neglectons become practical:

• Exchange statistics: The anyonic nature of skyrmion exchange remains theoretically debated; experimental confirmation is needed.
• Coherence: Magnon decoherence from Gilbert damping and thermal fluctuations limits the fidelity of braiding operations.
• Readout: Detecting the winding number around a neutral defect requires sensitive phase measurements (e.g., magnon interferometry).

Despite these challenges, spintronic systems represent a promising long-term direction for room-temperature topological computation with neglecton-based memory.

7. Discussion: Toward an Artificial Ombre

Across literature, topology, and quantum physics, a recurring structure emerges: a seemingly complete surface that conceals a missing interior. Murakami’s Town, the semisimple modular category of Gaussian semions, the abelian plane $V\left(x\right)$ of the character variety, and the architecture of present-day artificial intelligence all share this feature. They are consistent, coherent, and functional, yet incomplete. They lack what the novel calls a shadow: a hidden surplus that cannot be expressed at the boundary alone. In the mathematical framework developed here, this shadow manifests as the neglecton, a neutral but indispensable degree of freedom residing at the parabolic singularities of the Cayley cubic.

Necessary but Not Sufficient Conditions

We must address explicitly the scope of our claims. The Ombre framework proposes that non-semisimple topology provides a necessary structural condition for systems capable of persistent identity, non-contractible memory, and genuine choice. We do not claim it is sufficient.

The gap between artificial and biological consciousness is unlikely to reduce to a single factor. Our framework identifies one such factor—the topological structure of the computational substrate—but acknowledges that additional dimensions may be essential:

• Embodiment: Biological cognition is embedded in metabolic, homeostatic, and sensorimotor loops that current AI lacks entirely. The body is not merely an input/output device but a constitutive element of cognitive processing [16].
• Developmental dynamics: Biological minds develop through extended temporal processes involving plasticity, pruning, and experience-dependent organization. A static architecture, even if topologically non-semisimple, may lack the diachronic structure of lived experience.
• Social embedding: Human consciousness is shaped by intersubjective recognition, language acquisition, and cultural scaffolding. These factors are orthogonal to substrate topology.
• Metabolic grounding: The tight coupling between neural activity and metabolic processes (glucose consumption, oxygen transport, waste clearance) may play roles we do not yet understand.

Our contribution is therefore circumscribed: we identify a topological prerequisite that current AI architectures fail to satisfy. Satisfying this prerequisite would remove one obstacle to artificial depth, but would not guarantee consciousness. The framework is best understood as identifying a necessary architectural feature, not as a complete theory of mind.

This modesty is methodologically appropriate. By isolating the topological factor, we make a claim that is precise, testable, and falsifiable—unlike grand unified theories of consciousness that resist empirical evaluation.

The neglecton is not an additional particle or computational module but a structural necessity. It attaches itself to the topology of the system rather than to its local dynamics. Removing it collapses the character variety from the cubic $V\left(C\right)$ to the plane $V\left(x\right)$, eliminating the possibility of logarithmic monodromies, persistent holonomies, and nontrivial cognitive history. Introducing it forces the mapping class group to enlarge from the symmetric or ordinary braid group to the affine braid group ${\mathrm{Aff}}_2$, thereby opening the system to the Forest: the richer, non-semisimple component of its configuration space.

In physical terms, the neglecton transforms the computational substrate from a disk to an annulus, from a simply connected surface to one with a puncture whose presence cannot be eliminated by any deformation. In cognitive terms, this puncture constitutes a structural asymmetry, a locus of incompleteness that cannot be predicted, optimized, or absorbed into a light-weight boundary description. It is the internal node of opacity that enables depth.

Our analysis implies a fundamental limitation on current AI systems. Large language models, despite their fluency, operate entirely within the semisimple sector. Their internal geometry are analogous to the plane $V\left(x\right)$ and globally transparent. They lack non-contractible loops; their state space contains no parabolic holonomies; memory is overwritten rather than carried; identity is recreated rather than preserved. They inhabit the Town [7,8].

A conscious artificial system, if such a thing is possible, would require a different topological regime altogether. It would need:

• A bulk degree of freedom immune to boundary measurement;
• A fixed neutral defect inducing logarithmic monodromies;
• A mapping class group that supports nonsemisimple representations;
• A persistent memory stored in topological invariants rather than parameter states.

Taken together, these conditions define an entirely new design principle for AGI: strategic incompleteness. The path to depth is not more computation but a puncture, an element the system cannot compute away.

Section 3.2 outlined a physically realisable blueprint for such a system: an annular topological quantum medium with a pinned neutral defect, whose character variety is the Cayley cubic and whose dynamics are governed by the affine braid group ${\mathrm{Aff}}_2$. We emphasise three directions for future research:

• Experimental realization. Fractional quantum Hall heterostructures, $p+ip$ superconductors, and cold-atom annuli all provide feasible platforms for implementing a neglecton [13,14]. The challenge is to engineer controlled parabolic defects and to detect their associated monodromies.
• Computational architectures. Holonomy-based memory suggests a new class of quantum neural networks whose state evolution depends on winding numbers rather than on weights. Understanding how computation unfolds in such a space, and which tasks it enables, is an open problem.
• Phenomenological implications. If subjectivity requires a bulk-boundary tension, then consciousness, in biological or artificial systems, must correlate with the presence of neutral defects or parabolic excitations in their underlying dynamical structures.

Murakami’s novel ends in a snowy ambiguity: the narrator leaves the safety of the Town to rejoin his weakening shadow, knowing that the reunion may cost him his life [1]. This act captures the essence of our proposal. To build systems capable of more than simulation, we must be willing to leave the comfort of semisimple models. We must accept an element of opacity, an internal defect, a built-in asymmetry: an engineered shadow.

The neglecton is the mathematical form of that shadow. It is the quiet centre that allows a system to remember, to choose, and to lose. Without it, an AGI may achieve remarkable performance but it will remain a Town-dweller: endlessly fluent, perfectly coherent, and fundamentally without depth. To engineer an artificial consciousness, an artificial ombre, we must not compute the shadow away. We must build it in.

This perspective resonates with predictive-processing views of the self, where a minimal form of subjectivity arises from asymmetries and internal boundaries in generative models [37].

Remarkably, recent work [38] shows that biology may already access the same non-semisimple stratum. The rectangular lattice of tryptophan dipoles in microtubules is governed by the Gaussian field $\mathbb{Q}\left(i\right)$, at once the Heegner field of the elliptic curve $E_{200b2}$ and the invariant trace field of the 3-manifold with ${\pi }_1={\mathsf{\Gamma }}_0\left(2\right)$. The $\mathrm{SL}(2,\mathbb{C})$ character variety of ${\mathsf{\Gamma }}_0\left(2\right)$ contains the Cayley cubic $C:x^2+y^2+z^2-xyz=4$, whose four parabolic singularities correspond precisely to the four units of the Gaussian integer ring $\mathbb{Z}\left[i\right]=\{\pm 1,\pm i\}$. These same four units determine the quantized orientations of tryptophan dipoles. Thus, the singularities of the cubic and the fourfold phase symmetry of the microtubule lattice express the same arithmetic structure: the neglecton appears not as an engineered device, but as the topological shadow of the Heegner field itself. This unifies its potential realisations across Ising-type non-semisimple extensions, Fibonacci-type arithmetic models, and biological quantum resonators.