Computational Methods and Simulation of UAVs’ Micro-Motion Echo Characteristics Using Distributed Radar Detection

Abstract

The large number of UAVs under supervision at low altitudes have brought serious security risks to the field of air defense. Accurately analyzing the characteristics of UAVs’ echo signals is of great research significance for the detection and recognition of UAVs. Based on the principle of radar detection, the echo spatial correlation in the distributed radar detection mode is studied. According to the influence of different movement speeds on the micro-motion characteristics of UAVs, the echo signal models of UAVs in two flight states are established. Combined with the instantaneous micro-Doppler frequency model of the ideal motion state of UAVs, micro-Doppler frequency calculation functions of UAVs at different attitude angles are constructed. Through simulation calculation, the variation curves between the observation angle and the echo spatial correlation using different detection distances are given. Based on time–frequency images of UAVs in their ideal motion state, changes in the time–frequency images at different motion speeds and attitude angles are analyzed. These research results will help radar detection systems to accurately recognize UAVs in an uncertain motion state and can also provide a basis for predicting the next motion action of UAVs in subsequent target tracking.

1. Introduction

With the development of unmanned aerial vehicle (UAV) technology, various types of UAVs have emerged, bringing unprecedented technological advancement and innovation to the development of various industrial and defense fields as well as convenience to people’s lives. In particular, UAVs have advantages such as low risk, high cost-effectiveness, strong concealment and flexibility in national defense applications, as well as multi-tasking and collaborative combat abilities. They are an indispensable and important component of future wars. For instance, operators of UAVs can remotely control them from locations far from the battlefield, which avoids the direct exposure of operators to dangerous environments; this significantly reduces the risk of pilot casualties [1]. The design of UAVs does not need to take into account complex factors such as human–machine interaction and environmental control, and their manufacturing cost is much lower than that of manned aircraft. UAVs are small in size and have small radar cross-sectional areas, making them difficult to detect for the enemy. They can enter areas that are hard for manned aircraft to reach and can also launch at any time to perform short-term reconnaissance or long-endurance surveillance missions; their purpose is to adapt to diverse combat requirements [2]. UAVs are equipped with various sensors to perform tasks such as reconnaissance, surveillance, attack, electronic warfare, and communication relay. Combat efficiency can be enhanced through UAVs’ swarm formation or manned aircraft collaboration, etc. While UAVs have demonstrated irreplaceable advantages in national defense applications, they have also brought serious security challenges to national airspace. For instance, using UAVs to carry ammunition can enable rapid strikes against military targets. UAVs’ vision systems can be used to spy on military bases. Space targets can be intercepted by leveraging the multi-mission and collaborative capabilities of UAVs in conjunction with guided ammunition carried on board [3], etc. Therefore, how we might detect and recognize small targets of UAVs is a challenging task in the field of defense operations.

For the detection of low-altitude UAVs, existing detection and recognition technologies mainly focus on radio detection technology, photoelectric detection technology, acoustic detection technology, and radar detection technology, etc. Radio detection technology is a technique that uses the propagation and reception of radio waves to detect the target in the external environment, and it is classed as a passive detection method [4]. The core of this detection technology lies in the propagation characteristics of electromagnetic waves of different frequencies. As radio waves have the widest frequency range, this detection technology has the capacity for long-distance transmission [5]. In a complex electromagnetic environment, radio signals are prone to interference, leading to unstable or interrupted data transmission. The transmission distance of radio signals is limited by the performance of base stations. If the signal exceeds the range of the base stations, it may be weakened or lose, resulting in a short detection distance. Photoelectric detection technology is a sensing, transmission and detection technology that uses light waves as the carrier for detecting target information and energy [6]. The target information entering the detection area is detected through the core components of the photoelectric detector, and the target is detected and tracked by using signal processing technology. The acquisition of target information by photoelectric detection technology is easily affected by environmental illumination. Acoustic detection technologies are divided into active detection technology and passive detection technology. Active detection technology mainly utilizes detectors to emit specific forms of sound waves and receives the echoes reflected by the target to detect the target and locate it. Passive detection technology mainly involves directly receiving the sounds emitted by the target and then recognizes the target and obtains the target position.

For low-altitude UAVs, the acoustic information generated by UAVs is relatively weak, especially in long-distance scenarios. The acquisition sensors are restricted by detection sensitivity, and it is easy to lose effective discrimination data when detecting long-distance UAVs, thus making it impossible to obtain the position of UAVs. Radar detection technology mainly utilizes a transmitter to generate high-frequency electrical signals, amplifies them, and sends them to the antenna. When the electromagnetic waves reflected back by the target reach the antenna, the antenna receives them. Through the signal-processing module, the received signals are filtered and analyzed. Based on the time delay, frequency variation and other characteristics of the signals, the position, speed, and other characteristics of the detection target are determined. The detection range of the radar depends on the power, frequency, and working conditions of electromagnetic waves. Radar can detect targets within a range of several kilometers to several hundred kilometers, so it is an important means of detection for low-altitude UAVs at present. The structural materials of a UAV’s fuselage determine its radar cross-sectional area (RCS), and the echo intensity weakens as the RCS decreases. When the UAV’s echo signal is obtained at the receiving end, the features of the UAV are extracted through processes such as frequency mixing and pulse compression [7,8]. Peng Chen et al. conducted research on the micro-Doppler characteristics of the rotor of moving helicopters, considering the uncertain motion state of UAVs in actual situations. They established the micro-Doppler model of the helicopter echo using the PO method and simulated and analyzed the micro-Doppler effects with linear motion and different attitude angles. Their research results can provide a reference for subsequent target recognition [9]. Weijie Zhan et al. established an analytical model for the time–frequency distribution characteristics of near and far-field micro-motion echoes based on local scattering centers, comprehensively analyzed the time–frequency distribution characteristics of micro-motion echoes caused by the rotation of target blades under near and far-field detection conditions. The research results are helpful for the refined modeling and classification recognition of targets [10]. Jiao Ma et al. studied the micro-Doppler characteristic analysis and feature extraction method of multi-rotor UAVs, established the echo model of multi-rotor UAVs, and analyzed the influence of parameters such as the number of blades, rotor speed and initial phase on the micro-Doppler features through simulation [11]. Yongbin Chen et al. carried out the modeling of rotor blade echoes and mechanism analysis of scintillation phenomena. Based on the scattering coefficient and distribution of scattering points, they constructed a scattering point model of rotor blade echoes and analyzed the influence of scattering point distribution on echoes. They also studied the physical scattering mechanism of the echo time-domain scintillation phenomenon and analyzed micro-Doppler characteristics and the time–frequency domain scintillation phenomenon in combination with time–frequency analysis and lateral resolution [12]. Xiaolong Chen et al. studied the radar micro-Doppler measurement method of bird and rotor UAVs and modeled and parameterized the flapping motion of bird wings, the main body motion of UAVs, and the rotation of rotors. They extracted Doppler frequency shift information from the radar echo and analyzed the influence of radar observation angle, modulation period, and length of time–frequency analysis on micro-motion characteristics [13]. Yongbin Chen et al. conducted research on the modeling and characteristic analysis of helicopter rotor blade echoes; constructed a scattering point integral mathematical model of rotor blade echoes; analyzed the flickering phenomena of echoes in the time domain and frequency domain, as well as their causes; and verified that the scattering point integral model is more conducive to extracting micro-Doppler features, providing a theoretical basis for further target recognition [14]. Chen Song et al. proposed a method for estimating the micro-motion characteristic parameters of multi-rotor UAVs based on the time–frequency concentration index and derived the mapping relationship between the micro-motion characteristic parameters and the micro-Doppler component signal parameters. This method improves the parameter estimation accuracy of multi-component micro-Doppler signals and also has good robustness in low-signal-to-noise-ratio environments [15]. Lutao Liu et al. studied a method for analyzing the echo characteristics and parameter estimation of rotor UAVs. Based on the time-domain integral echo model of rotor UAVs and the principle of the cepstral algorithm, they derived the frequency-domain expression and cepstral expression of the echo signal and analyzed the corresponding relationship between the echo signal parameters, the frequency domain, and the cepstral characteristics. This method can more accurately estimate the bandwidth and rotation frequency of the UAVs’ echo signal, thereby providing an important reference for the detection and recognition of UAVs [16]. Pengfei Zhang et al. studied the classification and recognition of UAVs based on the fusion of micro-motion features of dual radars.

To enhance the robustness of UAV classification based on micro-Doppler, multiple radars were used to simultaneously observe UAVs from different angles, and a UAV recognition method based on the fusion of micro-motion features observed by multi-angle radars was proposed. The experimental results verified that the classification accuracy obtained by the fusion of observations from two radar sensors is superior to that of a single radar sensor [17]. For low-altitude UAV targets, based on the radar detection mechanism, most researchers use a single radar to conduct research on target detection and recognition methods, while some researchers use a dual-radar detection target classification and recognition method. Particular attention is paid to data fusion using multi-band radar detection from different angles, providing a basis for subsequent classification and recognition [18]. Detailed research has not been conducted on the modeling of echo signals of a dual-radar detection target in the same band under uncertain motion conditions (in particular, the correlation between radar echo signals). Based on the micro-motion characteristics of rotorcraft UAVs, the next step of work also needs to consider advanced imaging methods and combine the two aspects. This not only improves the performance of target imaging at long distances but also helps the system to accurately recognize targets under low-signal-to-noise-ratio conditions [19,20].

At present, in the field of low-altitude air defense security, there are numerous uncertainties regarding invading UAVs, such as the motion state of incoming UAVs, the number and distribution of incoming UAVs, and environmental interference. This means there are still many scientific problems to be solved in the detection and recognition of UAVs based on radar detection. In particular, given the uncertain motion state of suddenly appearing UAVs and the differing distribution of the number of UAVs based on a single radar detection system, it is impossible to directly characterize the echo characteristics of individual targets of UAVs and to correlate the echo characteristics of multiple UAVs. Establishing an echo characteristic model suitable for detecting a random number of UAVs remains a difficult problem. The main contributions of this paper are as follows:

(1) Based on the principle of dual-radar intersection detection and in combination with the influence of different movement speeds on the micro-motion characteristics of UAVs, echo signal models of UAVs in two flight states are established. This can provide a basis for the accurate recognition of UAVs in uncertain movement states using a radar detection system.

(2) According to the instantaneous micro-Doppler frequency calculation function of the ideal motion state of UAVs, the calculation methods of the micro-Doppler frequency of UAVs at different attitude angles are studied. The influence of different attitude angles on the peak value of the micro-Doppler frequency is analyzed, which can predict the next motion state of UAVs and is helpful for subsequent target tracking.

(3) Echo spatial correlation is studied using the dual-radar detection; the correlation of the observation angle, the echo spatial correlation, and the vertical distance between the UAV and radar are established. The ranges of the observation angle and the echo spatial correlation coefficient at different vertical distances are determined; these results can provide a means for the subsequent elimination of false targets in the radar detection process.

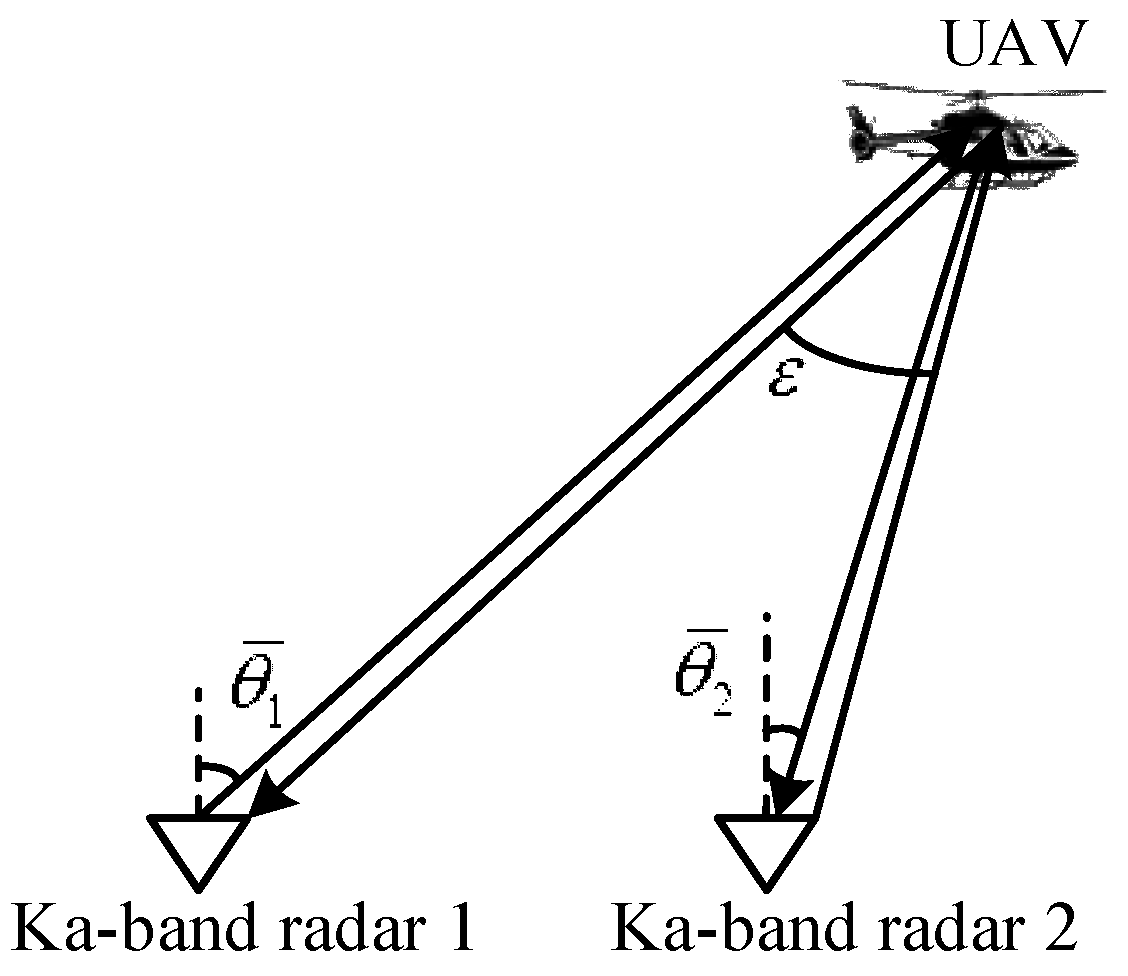
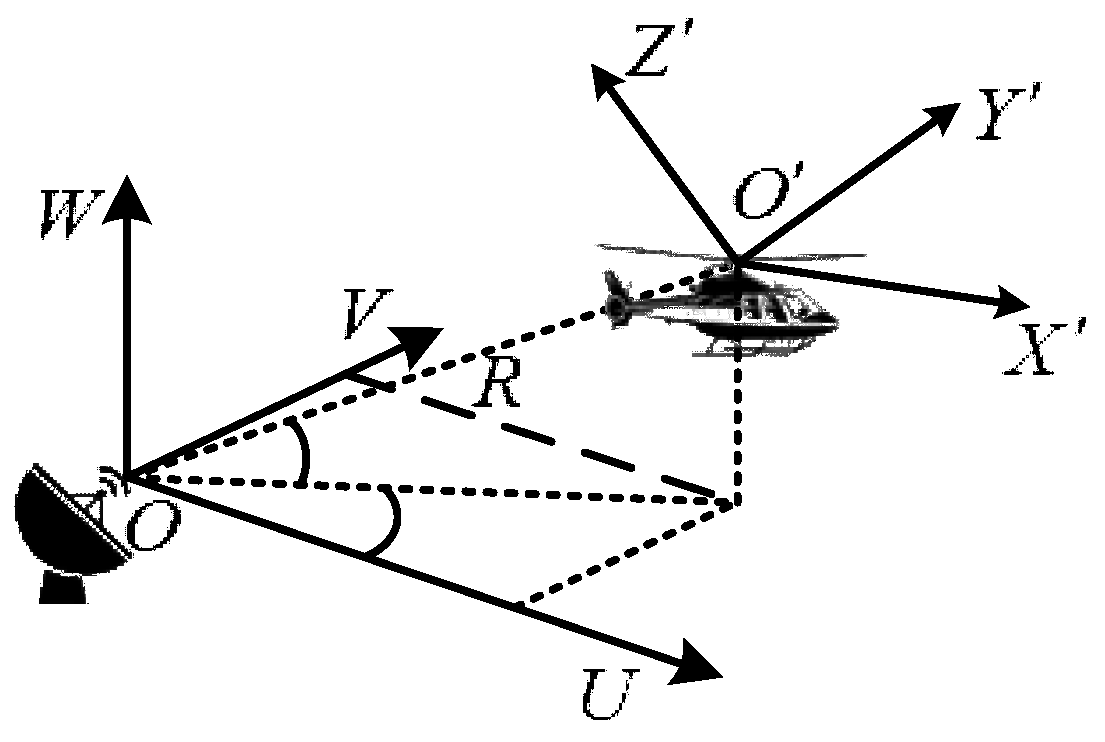
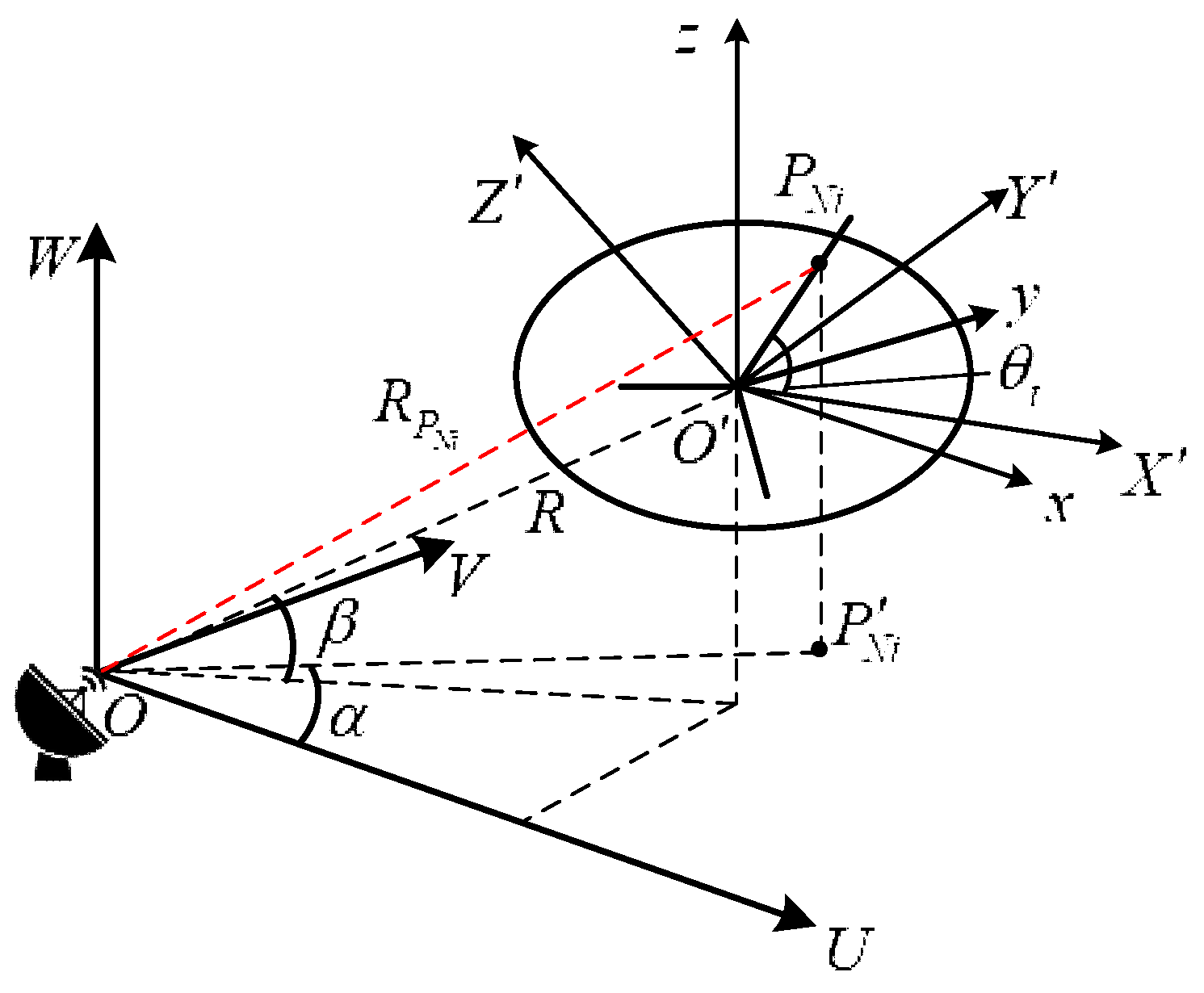
2. UAVs Echo Model Using Distributed Radar Detection

In order for the radar detection system to accurately recognize low-altitude UAVs, two Ka-band radars are used to detect UAVs. The state angles of two radars are ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$, respectively; the distance between them is $d^{\prime }$; and the observation angle formed between two radars and UAVs is $\epsilon$. An illustration of the dual-radar detection UAVs is shown in Figure 1.

For the detection of low-altitude UAVs targets, a distributed radar detection system is adopted. Based on the differences in the field of view angles of radar observations at each sub-station and the established UAV echo signal model, the echo spatial correlation from different radar sub-stations is analyzed, providing a prerequisite for the efficient recognition of UAVs. For rotor UAVs, when using the scattering point model for modeling, the rotor blades can be equivalent to a set of scattering points with a certain scattering coefficient distributed at equal intervals [21]. The echo model of rotor UAVs includes the echo of the UAV’s fuselage and the echo of the rotor blades. Since the UAV’s fuselage does not rotate, the rotational motion of the rotor blades is mainly considered. The geometric relationship between single-station radar and rotor UAVs is shown in Figure 2, and a three-dimensional model of the rotor blades is shown in Figure 3.

In Figure 2 and Figure 3, the radar coordinate system is $OUVW$, the reference coordinate system $O^{\prime }xyz$ is parallel to the radar coordinate system, and the UAV coordinate system is $O^{\prime }{X}^{\prime }{Y}^{\prime }{Z}^{\prime }$. The distance between the rotor center $O^{\prime }$ and the radar center $O$ is $R$, and its azimuth and elevation angles are $\alpha$ and $\beta$, respectively. Taking single-rotor UAVs as an example, the length of the rotor blades is $l$, and the echo signal is modeled using the scattering point model. Assuming that the interval between the scattering points on each blade is $d$, the blade can be equivalent to $k$ uniformly distributed scattering points; then, the interval between the scattering points is $d=l/(k-1)$. $P_{Ni}(i=1,2,\cdots ,k)$ represents the i-th scattering point of the N-th blade of single-rotor UAVs, and the distance $R_{P_{Ni}}$ between the scattering point $P_{Ni}$ and the radar can be calculated based on the coordinates of the scattering points in the UAV coordinate system and the coordinates of the rotation center of single-rotor UAVs in the radar coordinate system. At this time, the baseband echo of the scattering points $P_{Ni}$ is

$$s_{P_{Ni}}(t)=\sigma \exp \left({\displaystyle \frac{-\mathrm{j}4\pi R_{P_{Ni}}(t)}{\lambda }}\right)$$

(1)

where $\sigma$ is the scattering coefficient, $\lambda$ is the carrier wavelength of the radar, and ${\Phi }_{P_{Ni}}(t)=4\pi R_{P_{Ni}}(t)/\lambda$, ${\Phi }_{P_{Ni}}(t)$ is the phase function, which is related to the state of the rotor blade in three-dimensional space.

Based on the fact that all scattering points on the rotor blade generate echoes, according to the mechanism of electromagnetic scattering, the blade echo is essentially the vector sum of the echoes from all scattering points on the blade in the radar line-of-sight direction [22]. The echo model on the first blade can be obtained by integrating Formula (1).

$$s(t)={\displaystyle {\int }_0^l{s}_{P_{Ni}}}(t)\mathrm{d}{x}_i=\sigma l\exp \left({\displaystyle \frac{-\mathrm{j}4\pi R_{P_{Ni}}(t)}{\lambda }}\right)\exp \left[{\displaystyle \frac{-\mathrm{j}2\pi l{f}_1(t)}{\lambda }}\right]\sin \mathrm{c}\left[{\displaystyle \frac{2l{f}_1(t)}{\lambda }}\right]$$

(2)

where $f_1(t)$ is the angle of the first blade.

Due to the different initial rotation angles of the $N$ blades on the single-rotor UAVs, assuming the initial rotation angle of the n-th blade is ${\theta }_n$, $(n=1,2,\cdots ,N)$, then ${\theta }_n={\theta }_1+(n-1)2\pi /N$. After time $t$, the rotation angle becomes ${\theta }_t$, and ${\theta }_t={\theta }_n+2\pi f_{\mathrm{rot}}t$; the angle information of the blade is $f_n(t)$. Compared with $f_n(t)$ and $f_1(t)$, the initial rotation angle ${\theta }_n$ contained in ${\theta }_t$ is increased by $2\pi (n-1)/N$. Considering the initial rotation angle and the number of blades, the echo of the radar detection of single-rotor UAVs is

$$s_{\Sigma }(t)={\displaystyle \sum _{n=1}^N{s}_n}(t)={\displaystyle \sum _{n=1}^N\sigma }l\exp \left({\displaystyle \frac{-\mathrm{j}4\pi R_{P_{Ni}}(t)}{\lambda }}\right)\exp \left[{\displaystyle \frac{-\mathrm{j}2\pi l{f}_1(t)}{\lambda }}\right]\sin \mathrm{c}\left[{\displaystyle \frac{2l{f}_1(t)}{\lambda }}\right]$$

(3)

If the target is a multi-rotor UAV with $M$ rotors, the distance from each rotor to the center of the fuselage needs to be considered. At this time, the distance between the scattering points on the blades of each rotor and the radar is $R_{P_{Ni}}^m$, $m=1,2,\cdots ,M$. Then, the echo of the radar detecting multi-rotor UAVs is

$$s_{total}(t)={\displaystyle \sum _{m=1}^M{s}_{\Sigma }(t)}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{s}_n}(t)}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N\sigma }l}\exp \left({\displaystyle \frac{-\mathrm{j}4\pi R_{P_{Ni}}^m(t)}{\lambda }}\right)\exp \left[{\displaystyle \frac{-\mathrm{j}2\pi l{f}_1(t)}{\lambda }}\right]\sin \mathrm{c}\left[{\displaystyle \frac{2l{f}_1(t)}{\lambda }}\right]$$

(4)

Due to the fact that the width of the rotor blades of UAVs is much smaller than their length, the UAV echo model is established according to the one-dimensional discrete point distribution, and the echo spatial correlation in the dual-radar distributed detection mode is established Formula (5).

$$\rho =\sin \mathrm{c}\left(2{\displaystyle \frac{\sin {\overline{\theta }}_2-\sin {\overline{\theta }}_1}{\lambda }}l\right)$$

(5)

As can be seen in Figure 1, ${\overline{\theta }}_1=\epsilon +{\overline{\theta }}_2$, the relationship of these angles is

$$\sin {\overline{\theta }}_2-\sin {\overline{\theta }}_1=\sin \epsilon \cos {\overline{\theta }}_1$$

(6)

Then, the echo spatial correlation is

$${\rho }^{\prime }=\sin \mathrm{c}\left(2{\displaystyle \frac{\sin \epsilon \cos {\overline{\theta }}_1}{\lambda }}l\right)$$

(7)

It can be seen that once the operating frequency of the radar used by the system is determined, its wavelength is also determined. In the system, two radars are placed on the ground in an intersection state, forming a detection area in space for detecting low-altitude flying UAVs targets. The size of the detection area is related to the detection ability of the radar. The stronger the detection ability of the radar itself, the wider the detection area. The higher the vertical distance between radar and UAVs, the shorter the horizontal distance between the radar and UAVs. This is mainly due to the detection ability of the radar, which also results in a smaller maximum observation angle formed between the two radars and the low-altitude UAVs and a smaller change in the observation angle range. As a result, the echo spatial correlation coefficient is relatively large. When the radar detection system and UAVs are determined, the echo spatial correlation using dual-radar detection is related to the observation angle [23].

3. The Influence of UAVs’ Motion on Micro-Motion Characteristics Under Uncertain Conditions

3.1. Analysis of Micro-Motion Characteristics with Different UAV Motion Speeds

Considering the rotation of the rotor blades, the spherical coordinate system can better describe the motion state of the scattering points on the rotor blades. Taking the rotation center $O^{\prime }$ of the UAV’s blade as the origin, the spherical coordinate system is established. In the spherical coordinate system, the rotation of the rotor blades is summarized as rotating around the $x^{\prime }$ axis, the $y^{\prime }$ axis, and the $z^{\prime }$ axis. The schematic diagram of the motion state of the rotor blades is shown in Figure 4.

Suppose the elevation angle and azimuth angle of the scattering point $P_i$ on the rotor blades in the spherical coordinate system of UAVs are ${\theta }_i$ and ${\eta }_i$, respectively; ${\theta }_{\mathrm{ref}}$ is the initial elevation angle of the blade; and ${\eta }_{\mathrm{ref}}$ is the initial azimuth angle of the blade. The rotation vectors are ${\gamma }_{x^{\prime }}$, ${\gamma }_{y^{\prime }}$ and ${\gamma }_{z^{\prime }}$, respectively, and ${\gamma }_{x^{\prime }}={\left[1 0 0\right]}^{\mathrm{T}}$, ${\gamma }_{y^{\prime }}={\left[0 1 0\right]}^{\mathrm{T}}$, ${\gamma }_{z^{\prime }}={\left[0 0 1\right]}^{\mathrm{T}}$. Under different rotation conditions, the rotation axes of the UAVs blades are different. By introducing the rotation axis judgment vector $b={\left[0 0 1\right]}^{\mathrm{T}}$ and comparing the judgment vector with the rotation vector, ${\theta }_i(t_m)$ and ${\varphi }_i(t_m)$ for different rotation axes can be obtained using Formula (8).

$$\left\{\begin{array}{l}{\theta }_i(t)={\theta }_0+2\pi f_{\mathrm{rot}}t{\gamma }^{\mathrm{T}}b\hfill \\ {\varphi }_i(t)={\varphi }_0+2\pi f_{\mathrm{rot}}t\left(1-{\gamma }^{\mathrm{T}}b\right)\hfill \end{array}\right.$$

(8)

where $f_{\mathrm{rot}}$ is the rotational frequency of UAVs blades. When the rotation axes of the blade are the $x^{\prime }$ axis and the $y^{\prime }$ axis, the rotation vector ${\varphi }_i(t)$ changes. When it rotates around the $z^{\prime }$ axis, ${\theta }_i(t)$ changes.

When the UAV accelerates during flight, that is, when the acceleration is greater than zero, within a relatively short period of time, the UAV will tilt forward and maintain the forward tilt angle to continue flying. When the UAV decelerates during flight, that is, the acceleration is less than zero, and within a relatively short period of time, the UAV will tilt backward and maintain the backward tilt angle to continue flying. Suppose the forward/backward tilt velocity is $2\pi f_{tilt}$ and the duration time is $t_{tilt}$, ${\theta }_{\mathrm{ref}}$ will change within the $[0,t_{tilt}]$, meaning that

$${\theta }_{\mathrm{ref}}={\theta }_{{\mathrm{ref}}_0}\pm 2\pi f_{tilt}tt\in [0,t_{tilt}]$$

(9)

where ${\theta }_{{\mathrm{ref}}_0}$ is the initial elevation angle.

Therefore, the echo model of radar detection for multi-rotor UAVs is

$$\begin{array}{l}{s}_{total}(t)={\displaystyle \sum _{m=1}^M{s}_{\Sigma }(t)}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{s}_n}(t)}\\ ={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N\sigma }l\exp \left(\frac{-\mathrm{j}4\pi R_{P_{Ni}}^m(t)}{\lambda }\right)\exp \left[\frac{-\mathrm{j}2\pi l{f}_n(t)}{\lambda }\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \beta \right]\sin \mathrm{c}\left[\frac{2l{f}_n(t)}{\lambda }\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \beta \right]}\end{array}$$

(10)

When the UAV accelerates during flight, if the radial acceleration of the UAV is $a$, the forward tilt velocity is $2\pi f_{tilt}$, the duration time is $t_{tilt}$, and the initial elevation angle of the UAV is $\pi /2$. The analysis is conducted based on the relationship between $2\pi f_{tilt}{t}_{tilt}$ and $\beta$.

(1) When the UAV is flying towards the station, and $2\pi f_{tilt}{t}_{tilt}\le \beta$, the Doppler frequency of the UAV’s fuselage is $2(v+at)/\lambda$, located on the positive half-axis of the frequency domain, with a positive slope. The Doppler frequency of the fuselage increases over time, and the micro-Doppler frequencies of the blades are symmetrically distributed on both sides of the fuselage. At this moment, the echo model of radar detection for multi-rotor UAVs is

$$\begin{array}{l}{s}_{total}(t)={\displaystyle \sum _{m=1}^M{s}_{\Sigma }(t)}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{s}_n}(t)}\\ ={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N\sigma }l\exp \left(\frac{-\mathrm{j}4\pi R_{P_{Ni}}^m(t)}{\lambda }\right)\exp \left[\frac{-\mathrm{j}2\pi l{f}_n(t)}{\lambda }\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \left(\beta -2\pi f_{\mathrm{tilt}}t\right)\right]}\sin \mathrm{c}\left[{\displaystyle \frac{2l{f}_n(t)}{\lambda }}\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \left(\beta -2\pi f_{\mathrm{tilt}}t\right)\right]\end{array}$$

(11)

The micro-motion characteristics of the blade are modulated by $\cos \left(\beta -2\pi f_{tilt}t\right)$. The larger the $\cos \left(\beta -2\pi f_{tilt}t\right)$, the larger the micro-Doppler frequency range in the frequency domain. This is manifested in the frequency domain as the micro-Doppler frequency range of the blade increasing over time until the forward tilt time ends.

(2) When the UAV is flying towards the station, and $2\pi f_{tilt}{t}_{tilt}>\beta$, the Doppler frequency of the UAV’s fuselage is $2(v+at)/\lambda$, located on the positive half-axis of the frequency domain, with a positive slope. The Doppler frequency of the fuselage increases with time. At this time, the change in the elevation angle of the blade is large, and the function $\cos \left(\beta -2\pi f_{tilt}t\right)$ will experience reaching the maximum value and then decrease from the maximum value. In the frequency domain, it is manifested as the blade micro-Doppler frequency range broadening to the maximum with the increase in time and then starting to decrease with the increase in time until the forward tilt time ends.

(3) When UAV is flying away from the station, the Doppler frequency of the UAV’s fuselage is $-2(v+at)/\lambda$, located on the negative half-axis of the frequency domain, with a negative slope. The Doppler frequency of the fuselage decreases over time, and the micro-Doppler frequencies of the blades are symmetrically distributed on both sides of the fuselage. Then, the echo model of radar detection for multi-rotor UAVs is

$$\begin{array}{l}{s}_{total}(t)={\displaystyle \sum _{m=1}^M{s}_{\Sigma }(t)}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{s}_n}(t)}\\ ={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N\sigma }l\exp \left(\frac{-\mathrm{j}4\pi R_{P_{Ni}}^m(t)}{\lambda }\right)\exp \left[\frac{-\mathrm{j}2\pi l{f}_n(t)}{\lambda }\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \left(\beta +2\pi f_{\mathrm{tilt}}t\right)\right]}\sin \mathrm{c}\left[{\displaystyle \frac{2l{f}_n(t)}{\lambda }}\cos \left({\theta }_1+2\pi f_{\mathrm{rot}}t\right)\cos \left(\beta +2\pi f_{\mathrm{tilt}}t\right)\right]\end{array}$$

(12)

The micro-motion characteristics of the blade are modulated by $\cos \left(\beta +2\pi f_{tilt}t\right)$, and $\cos \left(\beta +2\pi f_{tilt}t\right)$ decreases over time. In the frequency domain, it is manifested as the micro-Doppler frequency range of the blade beginning to decrease with the increase in time until the forward tilt time ends.

Similarly, when the UAV decelerates during flight, if the radial acceleration of the UAV is $-a$, the forward tilt velocity is $2\pi f_{tilt}$, the duration time is $t_{tilt}$, and the initial elevation angle of the UAV is $\pi /2$. The analysis is conducted based on the relationship between $2\pi f_{tilt}{t}_{tilt}$ and $\beta$.

(1) When the UAV is flying away from the station, and $2\pi f_{tilt}{t}_{tilt}\le \beta$, the Doppler frequency of the UAV fuselage is $-2(v-at)/\lambda$, located on the negative half-axis of the frequency domain, with a negative slope. The Doppler frequency of the fuselage decreases over time, and the micro-Doppler frequencies of the blades are symmetrically distributed on both sides of the fuselage. At this time, the echo model is the same as Formula (11), and its performance in the frequency domain also follows the same variation rule.

(2) When the UAV is flying away from the station, and $2\pi f_{tilt}{t}_{tilt}>\beta$, the Doppler frequency of the UAV fuselage is $-2(v-at)/\lambda$, located on the negative half-axis of the frequency domain, with a negative slope. The Doppler frequency of the fuselage decreases over time. The micro-Doppler frequencies of the blades are symmetrically distributed on both sides of the fuselage. At this time, the elevation angle of the blade changes and increases. The function $\cos \left(\beta -2\pi f_{tilt}t\right)$ will reach a peak and then decrease from the peak. It is the same as the situation in which the UAV is flying towards the station, and $2\pi f_{tilt}{t}_{tilt}>\beta$.

(3) When the UAV is flying towards the station, the Doppler frequency of the UAV fuselage is $2(v-at)/\lambda$, located on the positive half-axis of the frequency domain, with a negative slope. The Doppler frequency of the fuselage decreases over time, and the micro-Doppler frequencies of the blades are symmetrically distributed on both sides of the fuselage. At this time, the echo model is the same as Formula (12), and its performance in the frequency domain also follows the same variation rule.

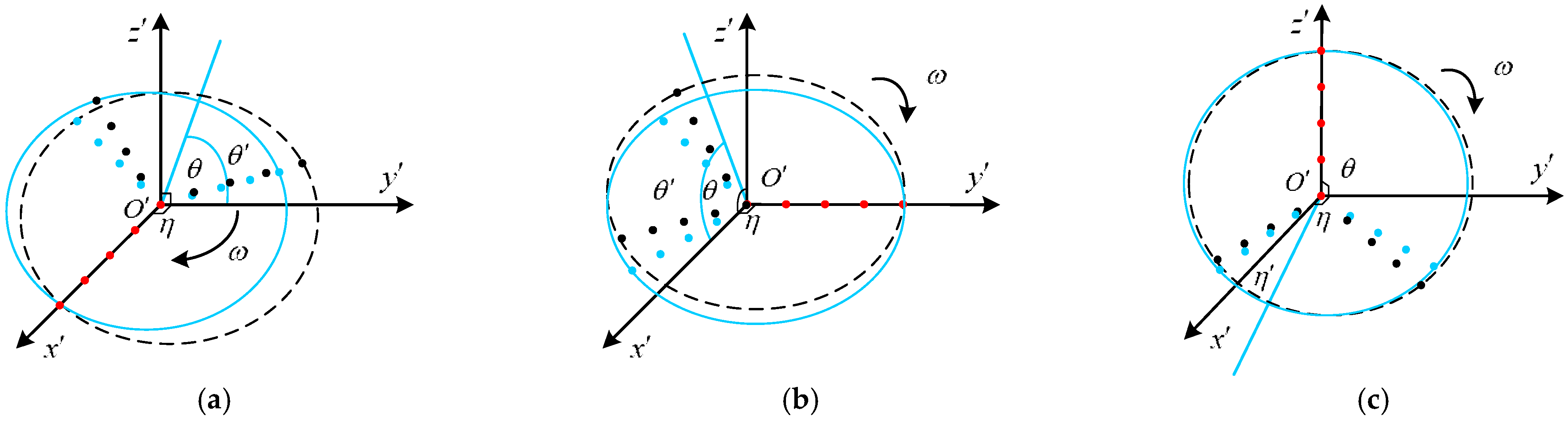
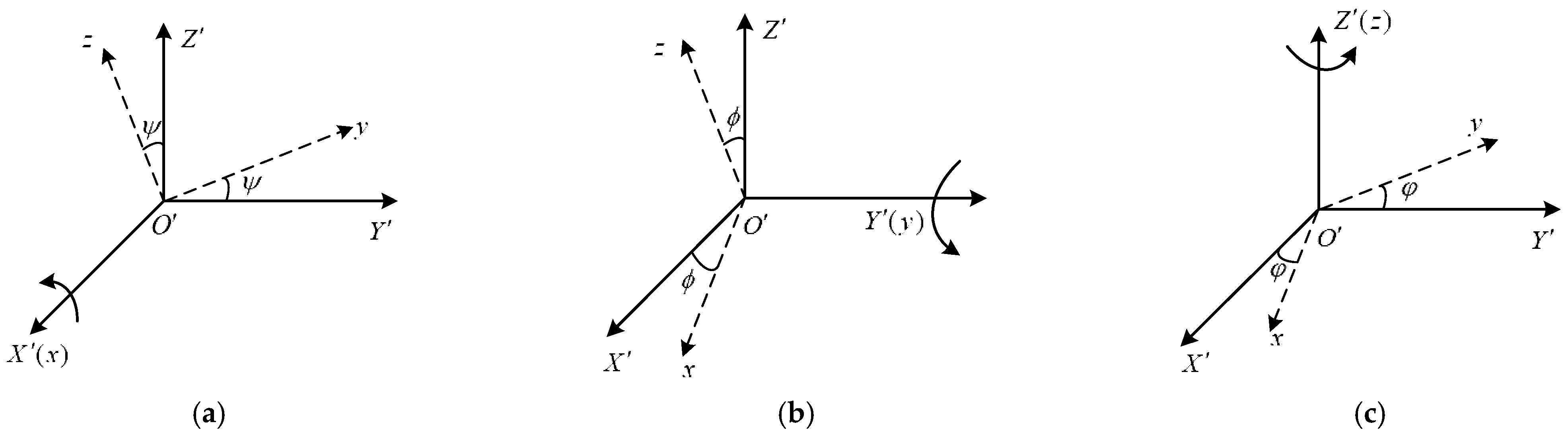
3.2. Analysis of the Micro-Motion Characteristics Under Different UAVs Attitude Angles

When studying the flight status of rotor UAVs, Euler angles $(\psi ,\varphi ,\phi )$ are used to describe the attitude changes in UAVs rotor blades. The rotational changes at different attitude angles are shown in Figure 5, where $\psi$ is the angle between the $X^{\prime }$ axis and $x$ axis, which is defined as the roll angle. $\varphi$ is the angle between the $Y^{\prime }$ axis and $y$ axis, which is defined as the pitch angle. $\phi$ is the angle between the $Z^{\prime }$ axis and $z$ axis, which is defined as the yaw angle, $0°\le \psi ,\varphi ,\phi \le 90°$.

After the spatial attitude change, the coordinates of any point on the rotor blade in the UAV coordinate system are transformed into the reference coordinate system through the rotation matrix [24,25]. The rotation matrix is

$$\Re =\left(\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \psi & \sin \psi \\ 0& -\sin \psi & \cos \psi \end{array}\right)\cdot \left(\begin{array}{ccc}\cos \varphi & 0& -\sin \varphi \\ 0& 1& 0\\ \sin \varphi & 0& \cos \varphi \end{array}\right)\cdot \left(\begin{array}{ccc}\cos \phi & \sin \phi & 0\\ -\sin \phi & \cos \phi & 0\\ 0& 0& 1\end{array}\right)$$

(13)

where $\left\{\begin{array}{l}{r}_{11}=\cos \varphi \cos \phi \hfill \\ r_{12}=\cos \varphi \sin \phi \hfill \\ r_{13}=-\sin \varphi \hfill \end{array}\right.$, $\left\{\begin{array}{l}{r}_{21}=\sin \psi \sin \varphi \cos \phi -\cos \psi \sin \phi \hfill \\ r_{22}=\sin \psi \sin \varphi \sin \phi +\cos \psi \cos \phi \hfill \\ r_{23}=\sin \psi \cos \varphi \hfill \end{array}\right.$, $\left\{\begin{array}{l}{r}_{31}=\cos \psi \sin \varphi \cos \phi +\sin \psi \sin \phi \hfill \\ r_{32}=\cos \psi \sin \varphi \sin \phi -\sin \psi \cos \phi \hfill \\ r_{33}=\cos \psi \cos \varphi \hfill \end{array}\right.$.

The instantaneous micro-Doppler frequency caused by the scattering point $p_i$ is obtained by Formula (14).

$$f_{d{P}_{Ni}}(t)=-{\displaystyle \frac{1}{2\pi }}{\displaystyle \frac{d}{dt}}{\Phi }_{P_{Ni}}(t)=(4\pi f_{\mathrm{rot}}{x}_i/\lambda )\left[\cos \beta (r_{11}\sin {\theta }_t-r_{12}\cos {\theta }_t)+\sin \beta (r_{31}\sin {\theta }_t-r_{32}\cos {\theta }_t)\right]$$

(14)

The motion of rotor UAVs in space can be equivalent to the changes in three attitude angles: roll angle, pitch angle, and yaw angle. If $\psi =0^{°}$, $\varphi =0^{°}$, $\phi =0^{°}$, the micro-Doppler frequency caused by the i-th scattering point on the n-th blade of a single rotor is

$$f_{d{P}_{i,n}}(t)={\displaystyle \frac{4\pi f_{rot}{x}_i}{\lambda }}\sin {\theta }_t\cos \beta$$

(15)

where ${\theta }_t={\theta }_1+2\pi (n-1)/N+2\pi f_{rot}t$. If $x_i=l$ and $\sin {\theta }_t=1$. The peak micro-Doppler frequency caused by the scattering points on the blade is $f_{\mathrm{dmax}}=4\pi l{f}_{\mathrm{rot}}\cos \beta /\lambda$ [26,27,28].

If the UAV motion is the roll state, that is, $\psi \ne 0^{°}$, $\varphi =0^{°}$, $\phi =0^{°}$, Formula (15) is transformed into Formula (16).

$$f_{d{P}_{i,n1}}(t)={\displaystyle \frac{4\pi f_{rot}{x}_i}{\lambda }}(\cos \beta \sin {\theta }_t+\sin \beta \sin \psi \cos {\theta }_t)$$

(16)

It can be seen that $\psi$ and $\beta$ will have an impact on the micro-Doppler frequency peak and rotation angle.

If the UAV motion is the pitch state, that is, $\psi =0^{°}$, $\varphi \ne 0^{°}$, $\phi =0^{°}$, Formula (15) is transformed into Formula (17).

$$f_{\mathrm{d}{P}_{i,n2}}(t)={\displaystyle \frac{4\pi f_{\mathrm{rot}}{x}_i}{\lambda }}\sin \left({\theta }_t\right)\cos \left(\beta -\varphi \right)$$

(17)

It can be seen from Formula (17) that the variation in the pitch angle will change the absolute value of the micro-Doppler frequency of the scattering points on different blades of rotor UAVs.

If the UAV motion is the yaw state, that is, $\psi =0^{°}$, $\varphi =0^{°}$, $\phi \ne 0^{°}$, Formula (15) is transformed into Formula (18).

$$f_{\mathrm{d}{P}_{i,n3}}(t)={\displaystyle \frac{4\pi f_{\mathrm{rot}}{x}_i}{\lambda }}\cos \beta \sin \left({\theta }_t-\phi \right)$$

(18)

It can be seen from Formula (18) that when $x_i=l$ and $\sin \left(\phi -{\theta }_t\right)=1$, the micro-Doppler frequency caused by the rotor is the largest, so the yaw motion has no effect on the peak value of the micro-Doppler frequency of the rotor [29,30,31].

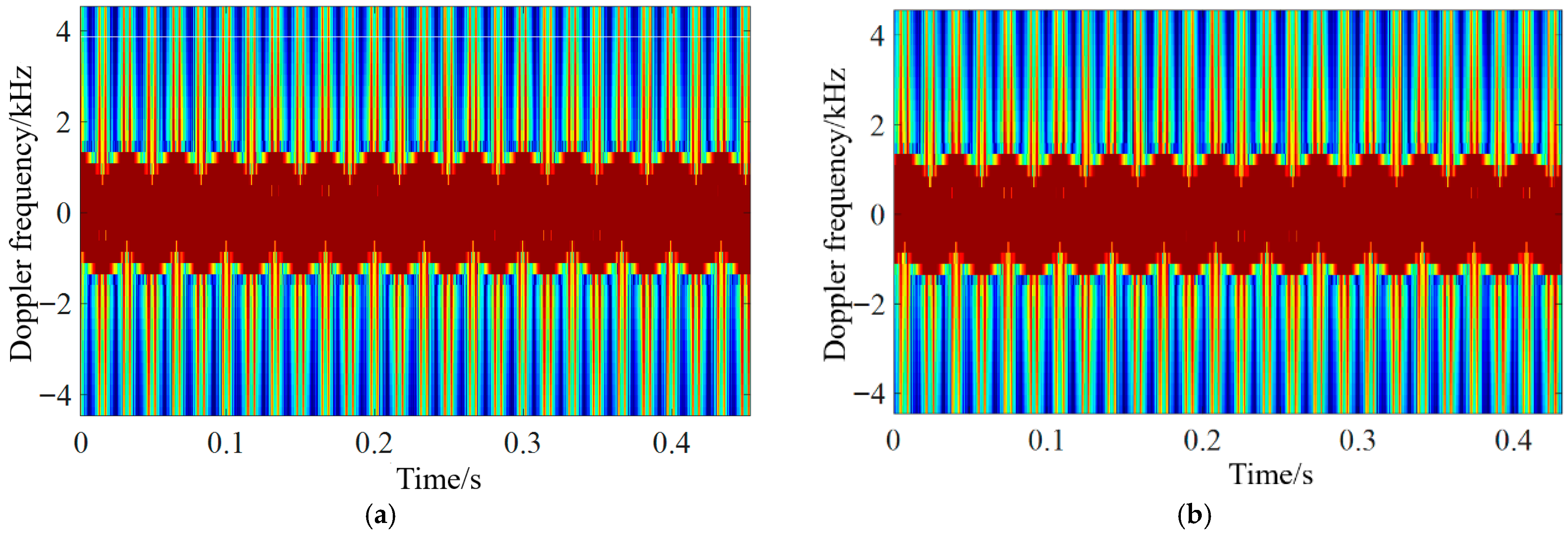
4. Simulation and Analysis

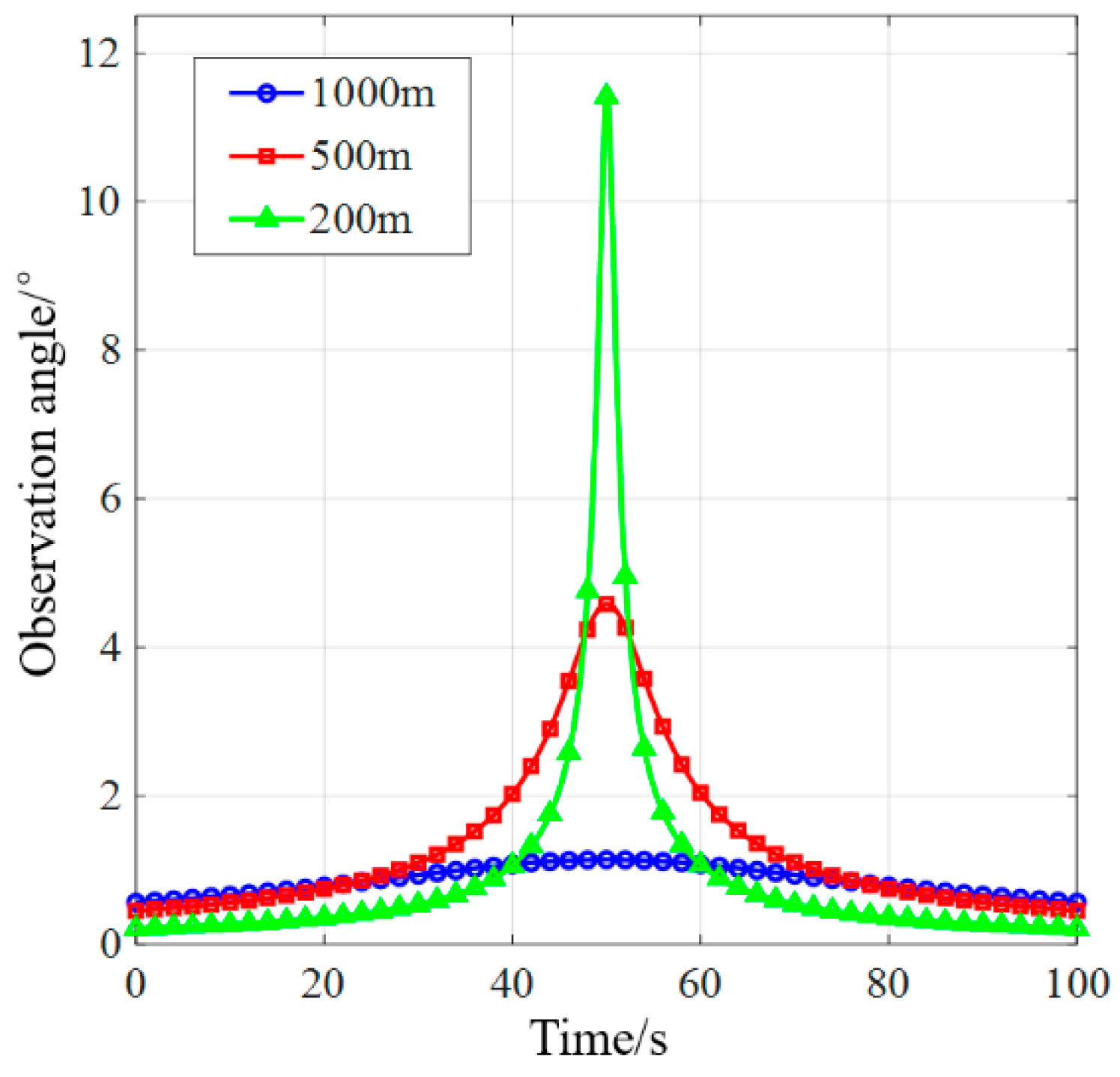
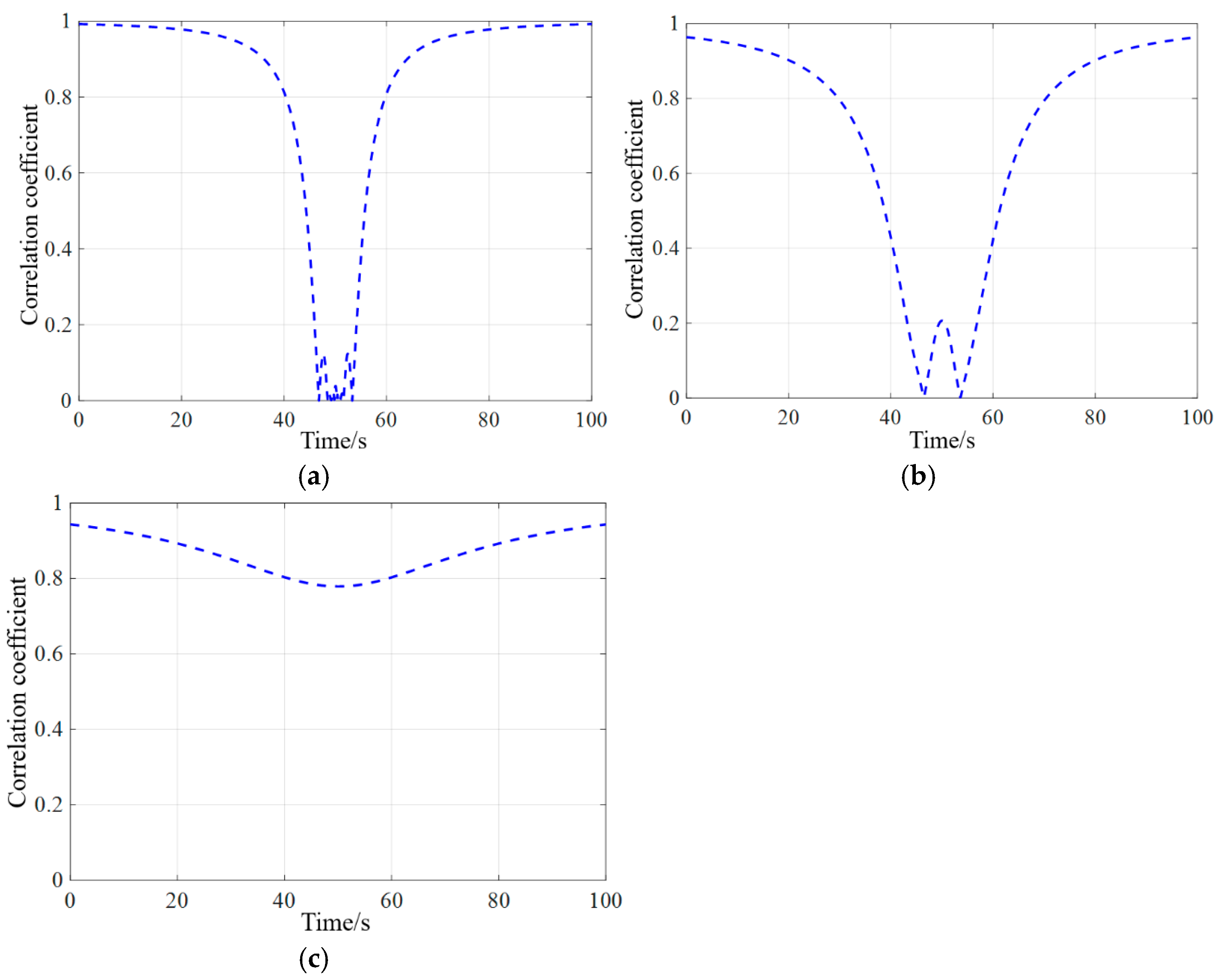
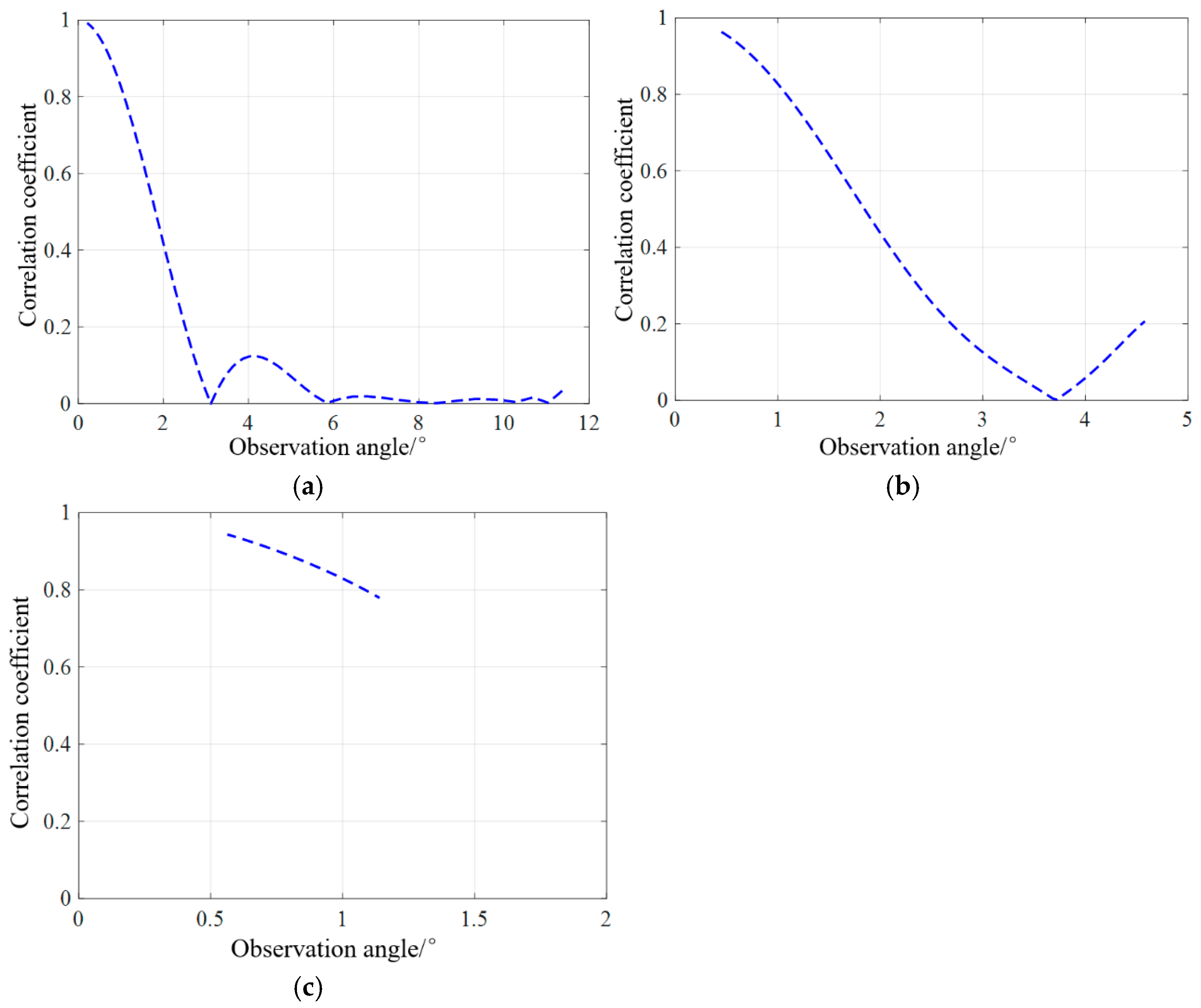
4.1. Spatial Correlation Analysis of UAV Echoes in Different Test Scenarios

Assuming the distance between the two radars is 40 m, the vertical distance between the UAV and radar ranges from 200 m to 1000 m, and the maximum horizontal distance between the UAV and radar exceeds 1000 m, the variation in the observation angles between two radars and the UAV over time is calculated and is shown in Figure 6. As can be seen from Figure 6, when the vertical distance between the UAV and radar is approximately 200 m, this distance is in single-digit multiples of the magnitudes of the distances between two radars. Starting from the moment the UAV enters the detection area, the observation angle gradually increases over time. When it is at the center of the detection area of two radars, the observation angle reaches its maximum. As the UAV leaves the detection area, the observation angle gradually decreases until it becomes the minimum. The maximum observation angle is approximately 11.4°, and the variation range of the observation angle is 0.21° to 11.4°, with a relatively large variation. When the vertical distance between the UAV and radar is 500 m, the maximum observation angle is 4.6°,which is less than 5°, and the variation range of the observation angle is 0.45° to 4.6°, with a relatively small change. The vertical distance between the UAV and radar is 1000 m, and the maximum observation angle is 1.14°, which is slightly greater than 1°; the variation range of the observation angle is very small. Although the variation distances are different, they follow the same variation rule. The observation angle first increases and then decreases over time, and the observation angle is the largest when the UAV is between two radars.

Based on Formula (7), the variation curve of the echo spatial correlation of two radars with time at different vertical distances is obtained as shown in Figure 7.

It can be seen from Figure 7 that when the vertical distance between the UAV and radar is 200 m, the correlation coefficient ranges from 0 to 0.988. When the vertical distance between the UAV and radar is 500 m, the correlation coefficient ranges from 0 to 0.962. When the vertical distance between the UAV and radar is 1000 m, the correlation coefficient ranges from 0.779 to 0.943. The echo spatial correlation trend at different vertical distances over time is not completely the same. The vertical distance is 200–500 m, and the correlation coefficient variation curve is steep; the results show that when the UAV first enters the detection area, the echo signals of the UAV detected by two radars are quite different, and the obtained correlation coefficient is large. As the UAV approaches the center of the detection area, the echo signals are similar, resulting in a decrease in the correlation coefficient. When the vertical distance reaches 1000 m, the correlation coefficient variation curve follows the rule of first changing and then increasing. However, the curve changes relatively slowly, and the range of the correlation coefficient decreases. This is because the observation angle formed by the two radars detecting the same target at a longer detection distance is small.

It can be seen from Formula (7) that there is a certain relationship between the echo spatial correlation and the observation angle. The variation curve at different vertical distances is obtained as shown in Figure 8.

It can be seen from Figure 8 that as the observation angle increases, the echo spatial correlation gradually decreases. For different vertical distances between the UAV and radar, the observation angles with correlation coefficients approaching the minimum value also vary. When the vertical distance between the UAV and radar is 200 m and the observation angle is approximately 3.1°, the correlation coefficient is the smallest, approaching 0. When the vertical distance between the UAV and radar is 500 m and the observation angle is approximately 3.7°, the correlation coefficient is the smallest and is close to 0. When the vertical distance between the UAV and radar is 1000 m and the observation angle is approximately 1.1°, the correlation coefficient is the smallest, at approximately 0.77. This is because the value of the echo spatial correlation coefficient is relatively large and the variation range is small when the detection distance is long.

4.2. Analysis of UAV Micro-Motion Echo Characteristics in Different Motion States and at Attitude Angles

(1) Analysis of UAV micro-motion echo characteristics in different motion states

Suppose the carrier frequency of radar is 34.6 GHz, the bandwidth is 1.2 GHz, the pulse repetition rate is 125 KHz, and the distance between the radar and the center of the quadcopter UAVs rotor is 500 m. The blade length on each rotor is 0.12 m, and the distance between each rotor and the center of the quadcopter UAVs is 0.15 m; each rotor has three blades, and its rotational speed is 10 r/s. To better observe the changes in the time–frequency images in different motion states of quadcopter UAVs, the sampling time is set to 0.5 s. UAV micro-motion echo characteristics in both acceleration and deceleration states are studied. In both acceleration and deceleration states, the UAV has three states. According to the elevation angle as well as the forward/backward tilt time, the forward/backward tilt angles are set. The motion parameters of quadcopter UAVs are shown in

Table 1. The motion parameters of quadcopter UAVs.

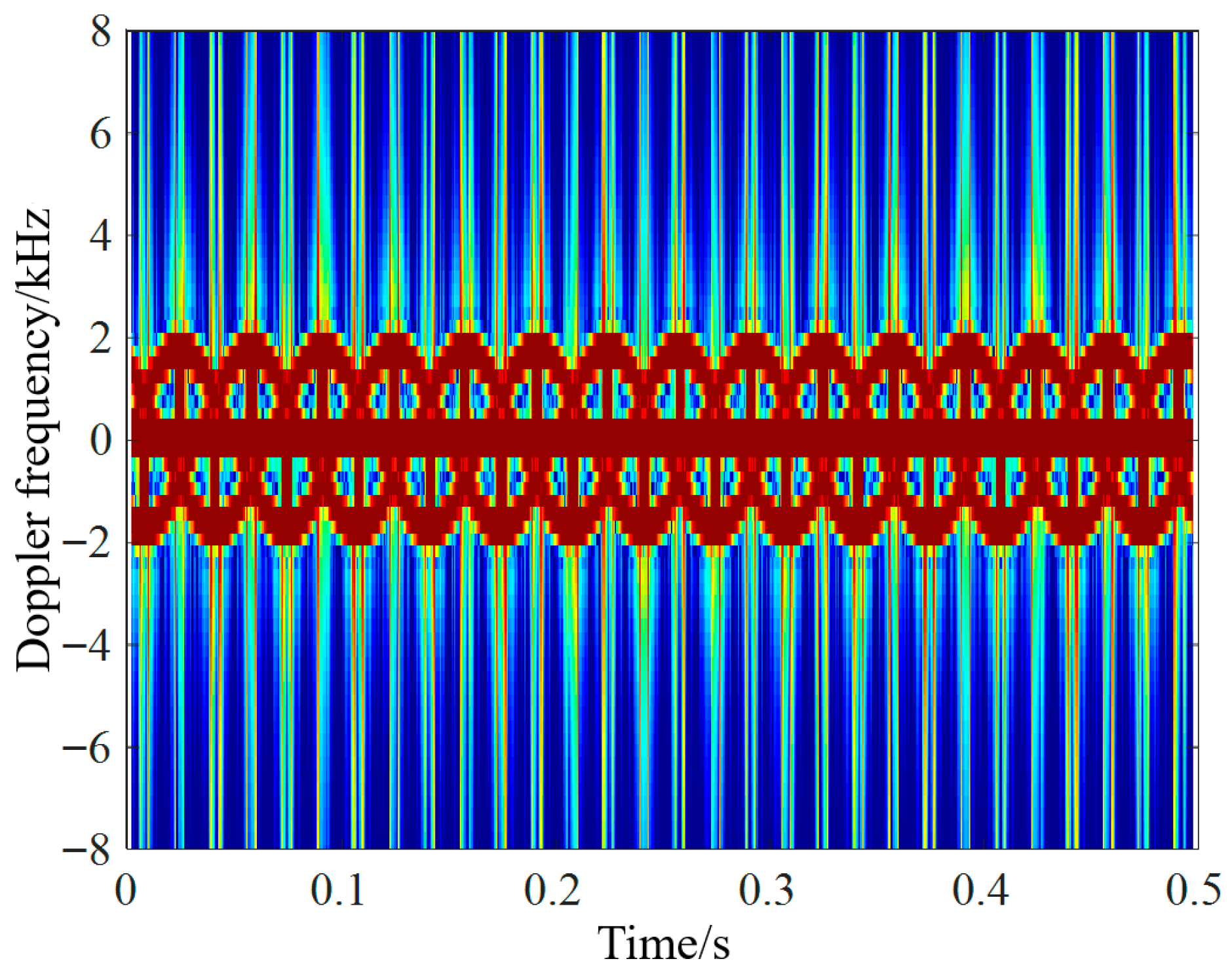
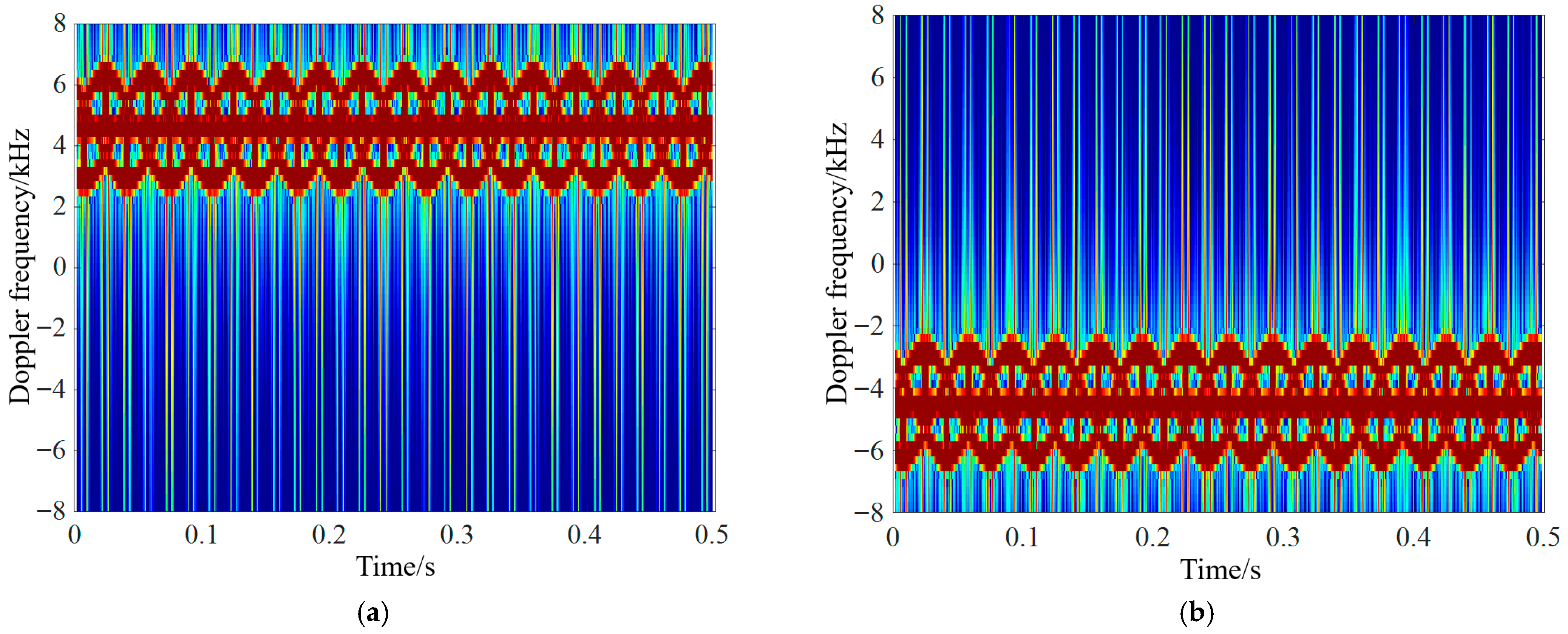
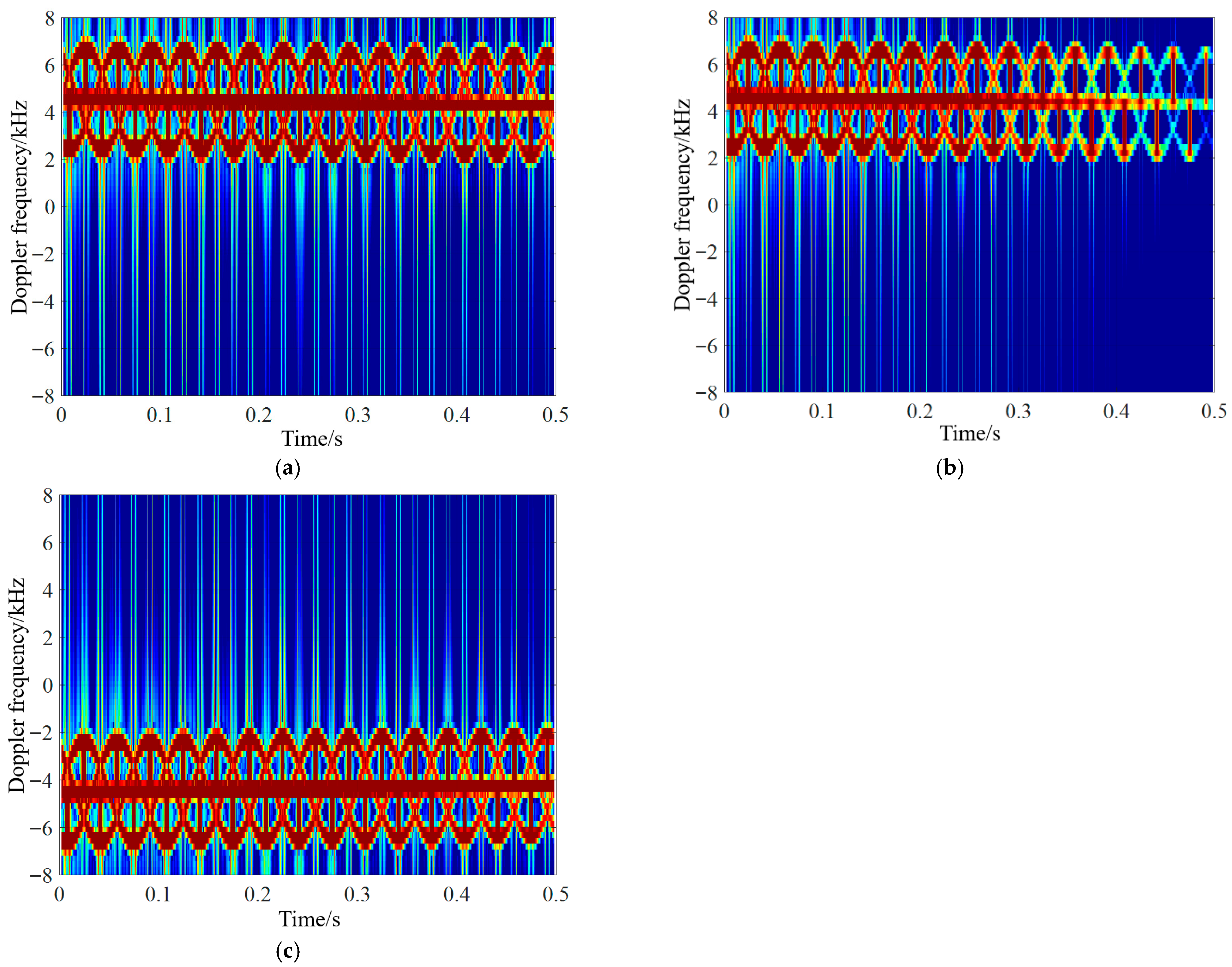
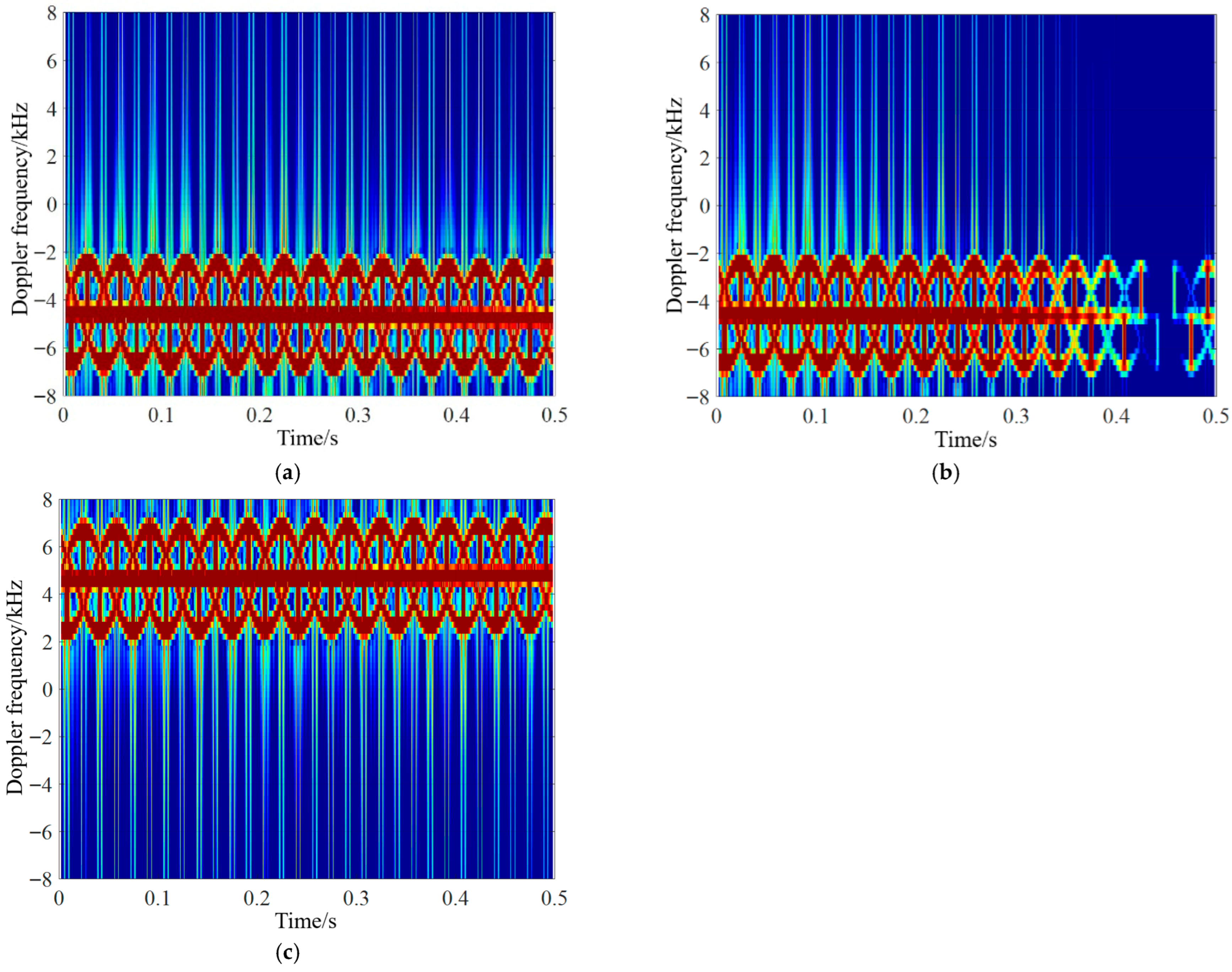
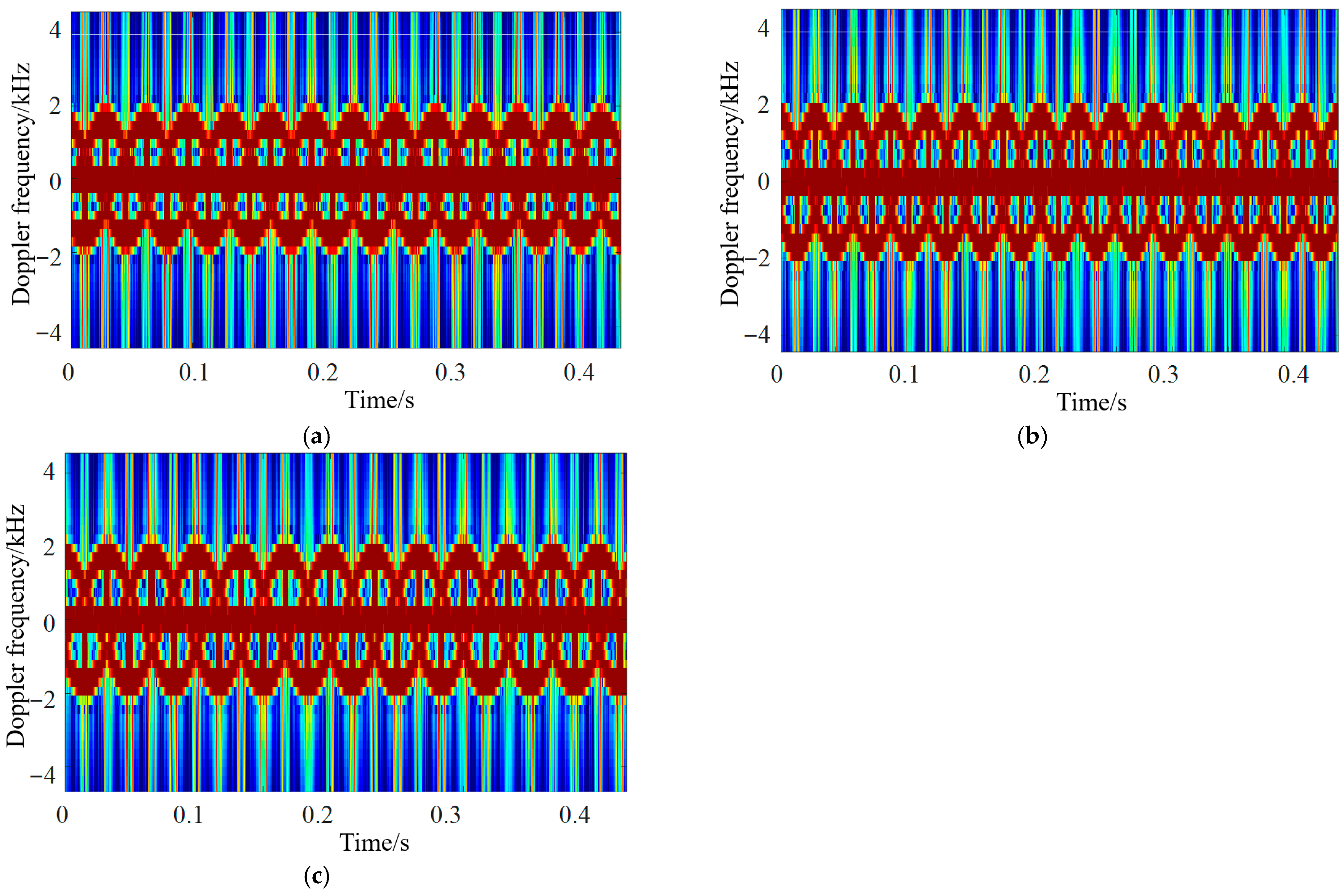
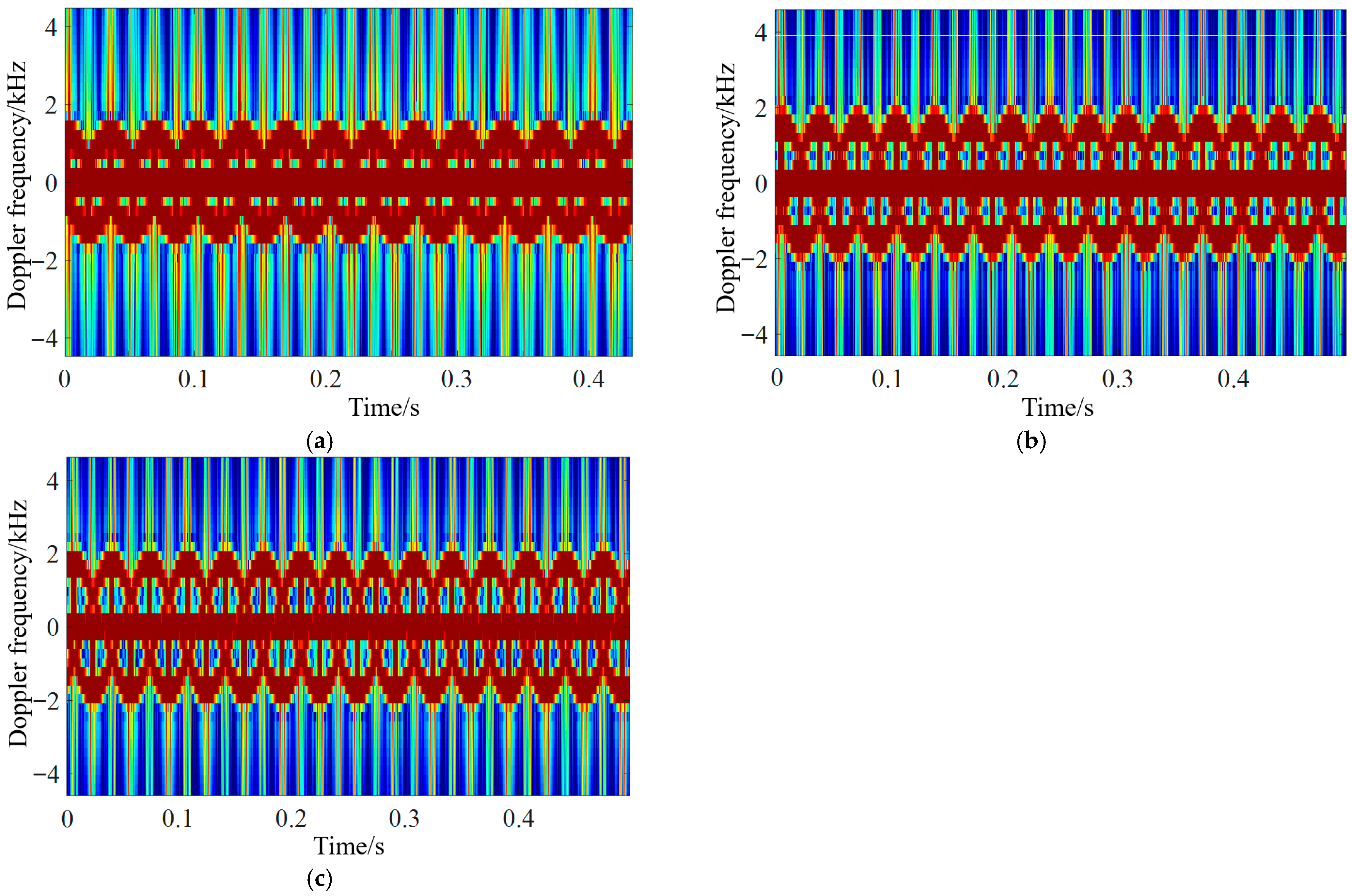
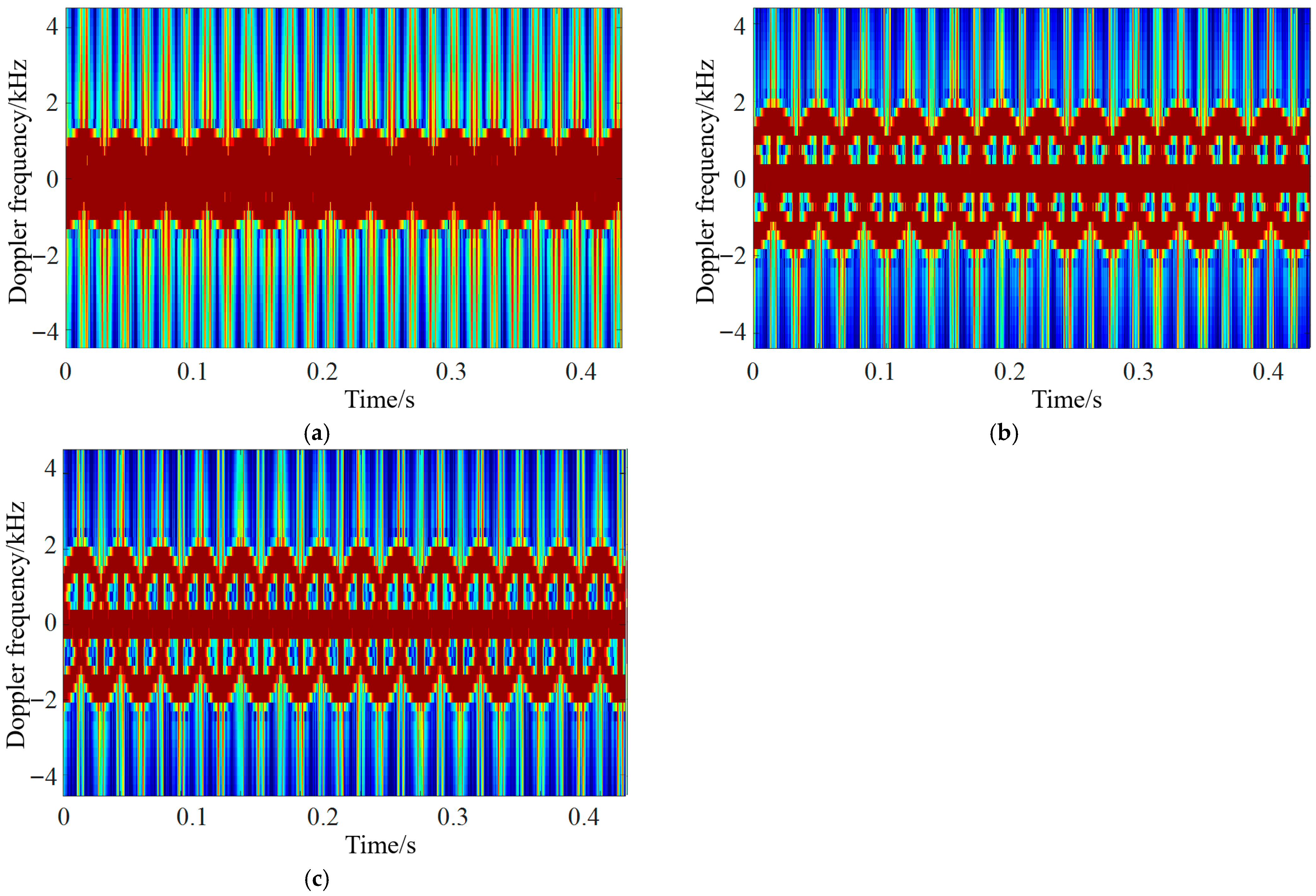
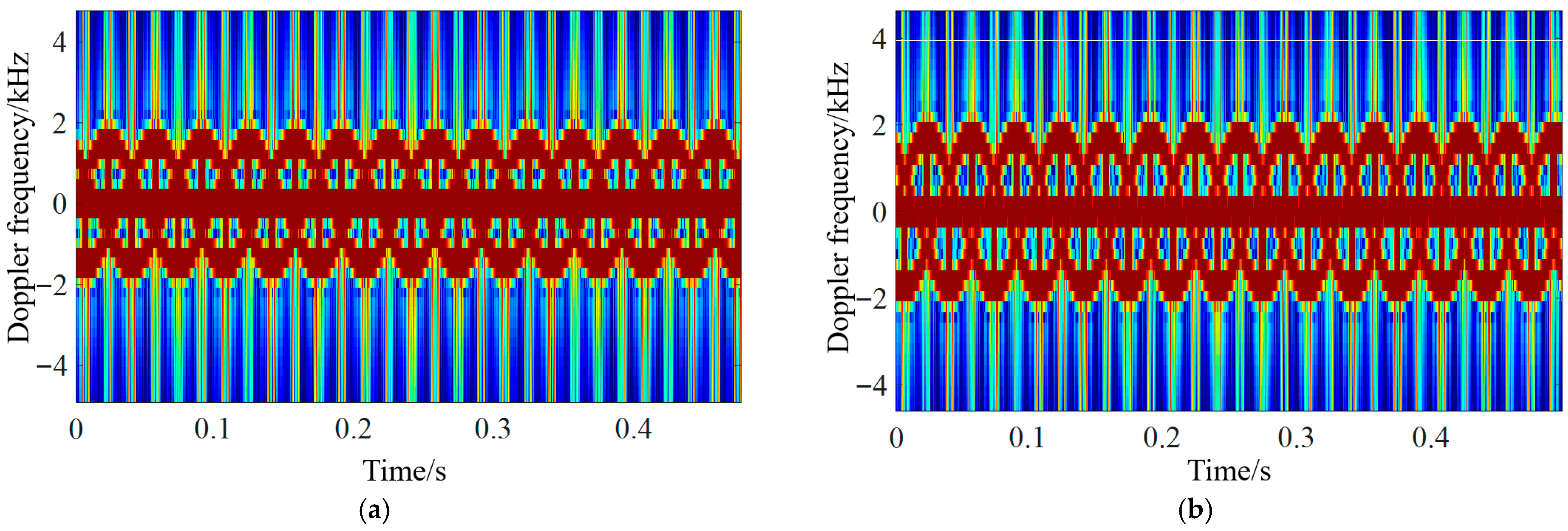
Motion State	State 1	State 2	State 3
Acceleration motion	The UAV is flying towards the station, Speed is 20 m/s, Acceleration is 3 m/s, Forward tilt speed is 5°/s.	The UAV is flying towards the station, Speed is 20 m/s, Acceleration is 3 m/s, Forward tilt speed is 10°/s.	The UAV is flying away from the station, Speed is −20 m/s, Acceleration is −3 m/s, Forward tilt speed is 5°/s.
Deceleration motion	The UAV is flying away from the station, Speed is −20 m/s, Acceleration is 3 m/s, Backward tilt speed is 5°/s.	The UAV is flying away from the station, Speed is −20 m/s, Acceleration is 3 m/s, Backward tilt speed is 10°/s.	The UAV is flying towards the station, Speed is 20 m/s, Acceleration is −3 m/s, Backward tilt speed is 5°/s.

.

Assuming the quadcopter UAV is in a hovering state with an attitude angle of 0, the time–frequency images of the quadcopter UAV under these ideal conditions are shown in Figure 9. Meanwhile, to illustrate the influence of the acceleration or deceleration state of the quadcopter UAV on the echo signal, when the quadcopter UAV moves at a constant speed and flies towards or away from the station, the obtained time–frequency image is shown in Figure 10.

As can be seen from Figure 9, the micro-Doppler frequency of quadcopter UAVs detected by radar is symmetrically distributed with regard to the main Doppler frequency shift under ideal conditions. In the time–frequency domain, the peak micro-Doppler frequency is 2325 Hz, and the first positive flicker moment of the rotor blade is 0.0256 s. In Figure 10, Figure 10a shows the time–frequency image when the quadcopter UAV is flying towards the station at a constant speed of 20 m/s with a forward tilt speed of 0. Figure 10b shows the time–frequency image when the quadcopter UAV is flying away from the station at a constant speed of 20 m/s with a forward tilt speed of 0. As can be seen from the comparison of Figure 9 and Figure 10, when the quadcopter UAV is in uniform motion, the micro-Doppler sideband is approximately offset by more than 4000 Hz. During the entire observation period, the micro-Doppler frequency of the quadcopter UAV did not show significant fluctuations, indicating that the UAV’s micro-motion echo characteristics are relatively stable when in uniform motion.

When the quadcopter UAV accelerates during flight, time–frequency images in different motion states are shown in Figure 11. When the quadcopter UAV decelerates during flight, time–frequency images in different motion states are shown in Figure 12.

In Figure 11, Figure 11a shows the time–frequency image when the quadcopter UAV is flying towards the station; its speed is 20 m/s, its acceleration is 3 m/s, and its forward tilt speed is 5°/s. Compared with state 1, Figure 11b shows the time–frequency image when the forward tilt speed increases to 10°/s. Compared with state 1, Figure 11c shows the time–frequency image when the quadcopter UAV is flying with its back to the station. In Figure 12, Figure 12a shows the time–frequency image when the quadcopter UAV is flying away from the station; its speed is −20 m/s, its acceleration is 3 m/s, and its backward tilt speed is 5°/s. Compared with state 1, Figure 12b shows the time–frequency image when the backward tilt speed increases to 10°/s. Compared with state 1, Figure 12c shows the time–frequency image when the quadcopter UAV is flying towards the station. By comparing Figure 11 and Figure 12 with Figure 10, we can see that when the UAV changes its motion state, whether it accelerates or decelerates, the radar detection echo of the UAV will change at this time.

Under the condition of state 1, both the forward tilt angle and the backward tilt angle of the quadcopter UAV meet the requirements of $2\pi f_{tilt}{t}_{tilt}\le \beta$, and at this time, the elevation angle gradually decreases during the forward or backward tilt process. As can be seen from Figure 11a, when the quadcopter UAV accelerates and is flying towards the station, the time–frequency image shows that the Doppler frequency of the fuselage gradually increases, and the micro-Doppler frequency range generated by the blades on both sides gradually expands. It can be seen from Figure 12a that when the quadcopter UAV decelerates and is flying away from the station, the change in the time–frequency image is consistent with those in Figure 11a when the quadcopter UAV accelerates and is flying towards the station. This is because during the acceleration towards the station or deceleration away from the station, the instantaneous radial velocity differences between different rotor blades are amplified, which is manifested as the micro-Doppler sideband expanding to higher and lower frequencies and the micro-Doppler frequency range becoming wider. Under the conditions of state 2, both the forward tilt angle and the backward tilt angle of the quadcopter UAV meet the requirements of $2\pi f_{tilt}{t}_{tilt}>\beta$. At this time, the elevation angle will undergo a process of decreasing to 0° and then gradually increasing during the forward or backward tilt. As can be seen from Figure 11b, when the quadcopter UAV accelerates and is flying towards the station, in the time–frequency image, the Doppler frequency of the fuselage gradually increases, and the micro-Doppler frequency range generated by the blades on both sides gradually expands to the maximum value and then begins to decrease. It can be seen from Figure 12b that when the quadcopter UAV decelerates and is flying away from the station, the change in the time–frequency image is consistent with those in Figure 11b when the quadcopter UAV accelerates and is flying towards the station. This is because during the acceleration towards the station or deceleration away from the station, if the forward tilt angle increases and the projection of the rotational linear velocity of the rotor blade tip on the radar radial gradually increases, there is an expansion of the micro-Doppler frequency shift range. When the forward tilt angle exceeds the critical value, the projected component of the linear velocity at the rotor blade tip on the radar radial significantly decreases. At this time, the contribution of the rotor’s rotational motion to the radar radial velocity decreases, and the micro-Doppler frequency shift range narrates accordingly. In state 3, as can be seen from Figure 11c, when the quadcopter UAV accelerates and is flying away from the station, the time–frequency image shows that the Doppler frequency of the fuselage gradually increases, while the micro-Doppler frequency range generated by the blades on both sides gradually decreases. It can be seen from Figure 12c that when the quadcopter UAV decelerates and is flying towards the station, the change in the time–frequency image is consistent with that in Figure 11c when the quadcopter UAV accelerates and is flying away from the station. When the quadcopter UAV accelerates and is flying away from the station, the quadcopter UAV moves away from the radar, and the radial velocity increases; this causes the Doppler frequency shift to increase in the negative frequency direction. In the frequency domain, this is manifested as a reduction in the range of the micro-Doppler sideband generated by the rotation of the blade. When the quadcopter UAV decelerates and is flying toward the station, the radial velocity of the quadcopter UAV gradually decreases, the Doppler frequency shift synchronously reduces, and the micro-Doppler sideband becomes smaller.

(2) Analysis of UAVs micro-motion echo characteristics under different attitude angles

To verify the influence of three attitude angles variations on the UAV’s micro-motion echo characteristics, the time–frequency images of quadcopter UAV under different attitude angles are given. When the pitch angles are 30°, 60° and 90°, respectively, the time–frequency images of the quadcopter UAV with roll angles of 30°, 60° and 90° are given as shown in Figure 13, Figure 14 and Figure 15.

As can be seen from Figure 13 and Figure 15, for the same pitch angle and an equivalent increase value, the peak micro-Doppler frequency of the rotor blade increases with the increase in the roll angle. When the pitch angle is small, the change in the roll angle has a relatively small impact on the equivalent increase in the peak micro-Doppler frequency of the rotor. When the pitch angle is large, the change in the roll angle has a significant impact on the equivalent increase in the peak micro-Doppler frequency of the rotor. For the same roll angle, as the pitch angle increases, the peak value of the micro-Doppler frequency of the rotor becomes smaller and smaller. When the roll angle is relatively small, the change in the pitch angle has a significant impact on the peak micro-Doppler frequency of the rotor. When the roll angle is large, the change in the pitch angle has a relatively small impact on the peak micro-Doppler frequency of the rotor. With the same roll angle and different pitch angles, the time–frequency image shows that the first positive flashing moment of the rotor blades is also different. With the same pitch angle and different roll angles, the time–frequency image shows that the first positive flashing moment of the rotor blades is almost the same, and the results show that the pitch angle has a significant influence on the initial rotation angle.

When the pitch angles are 30° and 60°, respectively, the time–frequency image of the quadcopter UAV is shown in Figure 16. When the yaw angles are 30° and 60°, respectively, the time–frequency image of the quadcopter UAV is shown in Figure 17.

As can be seen from Figure 16, when the pitch angles are 30° and 60°, respectively, the peak micro-Doppler frequencies of the quadcopter UAV are 2072 Hz and 2305 Hz, respectively. Although the increase in the roll angle leads to an increasing trend in the peak value of the micro-Doppler frequency, the difference from the peak value of the micro-Doppler frequency in the ideal state becomes smaller, indicating that a smaller roll angle has a greater impact on the change in the peak value of the micro-Doppler frequency. It can be seen from Figure 17 that when the yaw angles are 30° and 60°, the first positive flashing moments of the blade are 0.03471 s and 0.04571 s, respectively. According to the relationship between the rotation angle difference and the time difference, $\Delta \theta =2\pi f_{\mathrm{rot}}\Delta t$, the initial rotation angle differences of the rotor blades in the two cases can be determined to be 30.4615° and 59.1549°, respectively. The error values are 0.4615° and 0.8451°, respectively. Therefore, the yaw motion state is equivalent to reducing the initial rotation angle of the rotor blades, and the reduction value is the size of the yaw angle. At the same time, it causes the curve of time–frequency image to shift to the right along the time axis but has no effect on the peak micro-Doppler frequency of the rotor.

5. Conclusions

To make up for the deficiencies of a single radar in detecting low-altitude UAVs, this paper conducts research on the dual-radar detection mode. Based on the mechanism of electromagnetic scattering, a UAV echo signal calculation model using distributed radar detection is established. Based on the observation angles between two radars and the detected UAV, the correlation between the echo spatial correlation and the observation angles is studied. The influence of different motion speeds and attitude angles on UAV micro-motion echo characteristics is analyzed; calculation models of UAV echo signals in two flight states and at different motion speeds are established; and calculation methods of micro-Doppler frequencies at different attitude angle states are studied. Through simulation and analysis, the variation laws of the vertical distance between the radar and UAV, the observation angle, and the echo spatial correlation are given, providing a means for the subsequent elimination of false targets in the echo signal. The research results herein regarding the micro-motion characteristics of a UAV target at different movement speeds and attitude angles not only enhance the precise recognition of targets in random motion states but also contribute to the accurate prediction of the further actions of targets in subsequent target tracking.