Generalized Ishikawa Iterative Algorithm with Errors and Variable Generalized Ishikawa Iterative Algorithm for Nonexpansive Mappings in Symmetric Banach Spaces

Abstract

We present a generalized Ishikawa iterative algorithm with an error term and a variable generalized Ishikawa iterative algorithm. Leveraging the geometric symmetry inherent in uniformly convex Banach spaces, we establish their respective weak convergence theorems for nonexpansive mappings. As applications, we extend several recent results in the literature related to the proximal point algorithm and the split feasibility problem. Consequently, we propose a hyper-generalized proximal point algorithm and a hyper-generalized perturbation CQ algorithm. Our work not only broadens the application scope of these methods but also highlights the foundational role of symmetric space properties in ensuring algorithmic convergence.

1. Introduction

This paper adopts the following conventional notations: H for a Hilbert space, E for a real Banach space with its dual $E^{*}$. $Fix\left(T\right)$ for the set of fixed points of an operator T. Furthermore, the symbols ⇀ and → denote weak and strong convergence, respectively, while $\omega \left(x_n\right):=\left\{x:\left\{x_{n_k}\right\}\subset \left\{x_n\right\}\right.,s.t.\left.x_{n_k}\rightharpoonup x\right\}$ represents the set of all weak convergence points of the sequence $\left\{x_n\right\}$.

Fixed point theory for nonexpansive mappings plays a pivotal role in modern nonlinear analysis and optimization. The seminal contributions by Browder [1] and Kirk [2] paved the way for its rapid development. A particularly fruitful line of inquiry has been the extensive study of iterative methods for locating fixed points of these mappings. Among many algorithms, the KM iterative algorithm is the most commonly used and has a remarkable effect.

The famous KM iteration algorithm was proposed by Krasnosel’skii [3] and Mann [4]. Given some $x_0\in H$, the iteration format is

$$x_{n+1}=(1-\alpha )x_n+\alpha T{x}_n,\forall n=0,1,2,\cdots ,$$

(1)

Subsequently, Reich [5] changed the coefficient $\alpha$ for each iteration to ${\alpha }_n\in [0,1]$, and proposed a more general iteration format

$$x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n,\forall n=0,1,2,\cdots ,$$

(2)

when ${\alpha }_n$ is satisfied

$$\sum _{n=0}^{\infty }{\alpha }_n(1-{\alpha }_n)=\infty .$$

(3)

A key result regarding the weak convergence of (3) in Banach spaces was provided by Reich.

In 2017, the generalized KM iterative algorithm was introduced by Kanzow and Shehu [6] for nonexpansive mappings T in Hilbert spaces H. ${\alpha }_n,{\beta }_n\in [0,1]$ satisfy ${\alpha }_n+{\beta }_n\le 1$, $\left\{r_n\right\}$ is error sequence. Given some $x_0\in H$, the iteration format is

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}T{x}_n+r_n,\forall n=0,1,2,\cdots .$$

(4)

If the following conditions hold: (i) ${\sum }_{n=0}^{\infty }{\alpha }_n{\beta }_n=\infty$; (ii) ${\sum }_{n=0}^{\infty }(1-{\alpha }_n-{\beta }_n)<\infty$; (iii) ${\sum }_{n=0}^{\infty }\parallel r_n\parallel <\infty$, then the sequence $\left\{x_n\right\}$ converges weakly to the fixed point of T. The proposed generalized KM iteration algorithm relaxes the convex combination condition satisfied by the original coefficient ${\alpha }_n$ to allow for the sum of coefficients to be less than or equal to 1, which broadens and enhances the flexibility of coefficient selection.

In 2019, Zhang et al. [7] presented the weak convergence result of the generalized KM iterative algorithm in Banach spaces. Zhang et al. [7] extended this result to Banach spaces by proving the weak convergence of the generalized KM iterative algorithm, building on the findings of the document. They subsequently applied this conclusion to the zero point problem. Furthermore, he also proposed a variable generalized KM iterative algorithm [8] in Banach spaces, the iteration format is

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_n{T}_n{x}_n,\forall n=0,1,2,\cdots .$$

(5)

By leveraging the previous research methods, he proved the weak convergence and applied it to the split feasibility problem.

Over time, the KM iteration algorithm has seen continued advancement, the Ishikawa iteration [9], which is more general in form and more applicable in application, is proposed based on the KM iteration. Its iteration format is

$$x_{n+1}=t_{n}T(s_{n}T{x}_n+(1-s_n)x_n)+(1-t_n)x_n,n=0,1,2,\cdots ,$$

(6)

where $\left\{t_n\right\},\left\{s_n\right\}$ are within $[0,1]$ two sequences of satisfying certain conditions. Obviously, when $s_n\equiv 0$, the Ishikawa iteration format degenerates into the KM iteration format. In 1993, the weak convergence of Ishikawa iterations on bounded sets was established by Tan and Xu [10].

In recent years, the primary trajectory of research on the generalized Ishikawa iterative algorithm has evolved from the convergence analysis of its classical form. It has progressively shifted toward constructing more general and applicable algorithmic frameworks by means of relaxed conditions, error terms, extended operators, and expanded spaces, ultimately achieving deep integration with specific applied problems [11,12,13,14,15].

In 2018, Wang [11] proposed the generalized Ishikawa iteration:

$$x_{n+1}:={\alpha }_n{x}_n+{\beta }_{n}T(s_n{x}_n+t_{n}T{x}_n),\forall n=0,1,2,\cdots .$$

(7)

When the coefficients ${\alpha }_n, {\beta }_n, s_n, t_n$ satisfy certain conditions, he established the weak convergence of the iterative algorithm in Hilbert spaces, along with its application to variational inequalities.

The objective of this work is the enhancement of algorithm (7) and the investigation into the weak convergence of the modified algorithm in Banach spaces, building on the research of Zhang [7] and Wang [11]. The format of the improved generalized Ishikawa algorithm is

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{x}_n+r_n,\forall n=0,1,2,\cdots ,$$

(8)

which is called the generalized Ishikawa iterative algorithm with errors term. More precisely, the weak convergence of algorithm (8) will be established for a uniformly convex Banach space E, provided that E satisfies either the Opial property or the KK-property (both of which will be defined later).

The remainder of this paper is structured into the following sections: Section 2 provides a review of fundamental concepts and results that require further analysis. Section 3 is dedicated to analyzing the weak convergence of the generalized Ishikawa iterative algorithm with errors and explores its application to the hyper-generalized proximal point algorithm. Section 4 addresses the weak convergence of the variable generalized Ishikawa iterative algorithm and discusses its application to the hyper-generalized perturbation CQ algorithm. Finally, Section 5 presents the concluding remarks.

2. Preliminaries

For every $\epsilon \in (0,2]$, there is a number $\delta \left(\epsilon \right)$ such that if $x,y\in E$, $\parallel x\parallel =\parallel y\parallel =1$ and $\parallel x-y\parallel \ge \epsilon$, it holds that

$$∥{\displaystyle \frac{1}{2}}(x+y)∥\le 1-\delta \left(\epsilon \right),$$

then E is termed a uniformly convex space.

We say that E exhibits the KK-property in the case that for any sequence $\left\{x_n\right\}$ in E, conditions $x_n\rightharpoonup x$ and $\parallel x_n\parallel \to \parallel x\parallel$ imply that $x_n\to x$. On the other hand, Opial’s property is defined by the requirement that for any sequence $\left\{x_n\right\}$ in E with the condition $\parallel x_n\parallel \to \parallel x\parallel$ implies

$$\underset{n\to \infty }{lim}sup\parallel x_n-x\parallel <\underset{n\to \infty }{lim}sup\parallel x_n-y\parallel ,y\in E,y\ne x.$$

To conclude, this section presents several necessary lemmas and propositions. This will be beneficial for our subsequent convergence analysis.

Lemma 1

([10]). Let $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ be sequences of nonnegative real numbers. $\forall n\ge 0$, the following formula holds

$$a_{n+1}\le a_n+b_n,\sum _{n=0}^{\infty }{b}_n<\infty ,$$

then ${lim}_{n\to \infty }{a}_n$ exists.

Lemma 2

([11]). If $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ are nonnegative real number columns, and satisfy the following conditions

$$\sum _{n=0}^{\infty }{\alpha }_n{\beta }_n<\infty ,\sum _{n=0}^{\infty }{\alpha }_n=\infty ,$$

then ${lim}_{n\to \infty }inf{\beta }_n=0.$

Lemma 3

(Demiclosedness principle [16]). D is a nonempty closed convex subset of E, $T:D\to D$ is a nonexpansive mapping, $I-T$ is called demiclosed if and only if

$$(\left(x_n\right)\subset D,x_n\rightharpoonup x,x_n-T{x}_n\to y)\Rightarrow x-Tx=y.$$

Remark 1

([16]). Demiclosedness principle naturally holds in uniformly convex Banach spaces.

Analogous to the proof of proposition 3.2 in the reference by Kim [17], the following proposition can be simply proved to be true.

Proposition 1.

Let E be a uniformly convex Banach space, and the sequence $\left\{x_n\right\}$ is generated by the following iterations:

$$x_{n+1}={\alpha }_{n}T(s_{n}T{x}_n+t_n{x}_n+e_n)+{\beta }_n{x}_n+r_n,n=0,1,2,\cdots ,$$

then

(i) 

For $\forall p,q\in Fix\left(T\right)$ and $0\le t\le 1$, ${lim}_{n\to \infty }\parallel t{x}_n+(1-t)p-q\parallel$ exists;

(ii) 

If, in addition, the dual space $E^{*}$ of E has the KK-property, then the weak limit set of $\left\{x_n\right\}$, denoted by $\omega \left(x_n\right):=\{x:\left\{x_{n_k}\right\}\subset \left\{x_n\right\},s.t.x_{n_k}\rightharpoonup x\}$ is a singleton.

3. On the Convergence of the Generalized Ishikawa Iterative Algorithm with Errors Term and Its Applications

3.1. Weak Convergence of Generalized Ishikawa Iterative Algorithm with Errors

This section will establish the weak convergence of the generalized Ishikawa iterative algorithm with errors. The findings not only expand the scope of the generalized Ishikawa iterative algorithm, but also further enhance the applicability and performance of the generalized KM iterative algorithm, resulting in an Ishikawa iterative algorithm with broader application and improved performance.

Theorem 1.

Let E be a uniformly convex Banach space whose dual $E^{*}$ has the KK property or E itself satisfies the Opial property. Let D be a nonempty closed convex subset of E, and $T:D\to D$ a nonexpansive mapping satisfying condition $Fix\left(T\right)\ne ⌀$. The sequence $\left\{y_n\right\}$ is generated by the following iterative scheme:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n,n=0,1,2,\cdots ,$$

(9)

where $a_n,b_n,u_n,v_n\in [0,1]$, $\left\{a_n\right\}$ consistently greater than 0 and $a_n+b_n\le 1,u_n+v_n\le 1$, $\left\{e_n\right\}$ and $\left\{r_n\right\}$ are error sequences. The following conditions are assumed to hold:

(i) 

${\sum }_{n=0}^{\infty }{u}_n{v}_n=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }(1-u_n-v_n)<\infty$, ${\sum }_{n=0}^{\infty }(1-a_n-b_n)<\infty$;

(iii) 

${\sum }_{n=0}^{\infty }\parallel e_n\parallel <\infty$, ${\sum }_{n=0}^{\infty }\parallel r_n\parallel <\infty$;

(iv) 

${\sum }_{n=0}^{\infty }{a}_n{u}_n<\infty$.

Then the sequence $\left\{y_n\right\}$ generated by the iteration (9) converges weakly to the fixed point of T.

Proof. 

We divide the proof into four steps.

Step 1 For $\forall y^{*}\in Fix\left(T\right)$, we will show ${lim}_{n\to \infty }\parallel y_n-y^{*}\parallel$ exists.

By setting

$$E_n:=e_n-y^{*},R_n:=r_n-y^{*},$$

we know from the definition of $e_n$ and $r_n$ that,

$$0<\parallel E_n\parallel <+\infty ,0<\parallel R_n\parallel <+\infty .$$

Moreover,

$$\begin{array}{cc}\hfill & \parallel y_{n+1}-y^{*}\parallel \hfill \\ \hfill & =\parallel a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n-y^{*}\parallel \hfill \\ \hfill & \le a_n\parallel u_{n}T{y}_n+v_n{y}_n+e_n-y^{*}\parallel +b_n\parallel y_n-y^{*}\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel R_n\parallel +(a_n+b_n)\parallel r_n\parallel \hfill \\ \hfill & \le a_n\parallel u_n(T{y}_n-y^{*})+v_n(y_n-y^{*})+(1-u_n-v_n)E_n+(u_n+v_n)e_n\parallel \hfill \\ \hfill & +b_n\parallel y_n-y^{*}\parallel +(1-a_n-b_n)\parallel R_n\parallel +\parallel r_n\parallel \hfill \\ \hfill & =a_n(u_n\parallel T{y}_n-y^{*}\parallel +v_n\parallel y_n-y^{*}\parallel )+a_n\parallel (1-u_n-v_n)E_n+(u_n+v_n)e_n\parallel \hfill \\ \hfill & +b_n\parallel y_n-y^{*}\parallel +(1-a_n-b_n)\parallel R_n\parallel +\parallel r_n\parallel \hfill \\ \hfill & \le a_n(u_n+v_n)\parallel y_n-y^{*}\parallel +a_n\parallel (1-u_n-v_n)E_n+(u_n+v_n)e_n\parallel \hfill \\ \hfill & +b_n\parallel y_n-y^{*}\parallel +(1-a_n-b_n)\parallel R_n\parallel +\parallel r_n\parallel \hfill \\ \hfill & \le \parallel y_n-y^{*}\parallel +a_n(1-u_n-v_n)\parallel E_n\parallel +a_n\parallel e_n\parallel +(1-a_n-b_n)\parallel R_n\parallel +\parallel r_n\parallel .\hfill \end{array}$$

(10)

It follows from conditions (ii) and (iii) and Lemma 1applied to (10) with ${\alpha }_n:=\parallel y_n-y^{*}\parallel$ and ${\beta }_n:=a_n(1-u_n-v_n)\parallel E_n\parallel +a_n\parallel e_n\parallel +(1-a_n-b_n)\parallel R_n\parallel +\parallel r_n\parallel$ that ${lim}_{n\to \infty }\parallel y_n-y^{*}\parallel$ exists, whence the sequence $\left\{y_n\right\}$ is bounded.

Step 2 We now demonstrate that ${lim}_{n\to \infty }inf\parallel {Ty}_n-y^{*}\parallel =0$ is satisfied.

Set

$$d_n:=u_{n}T{y}_n+v_n{y}_n+e_n,$$

and

$$\begin{array}{cc}\hfill M_n& :={(1-u_n-v_n)}^2\parallel E_n{\parallel }^2+\parallel e_n{\parallel }^2+{(1-a_n-b_n)}^2\parallel R_n{\parallel }^2+{\parallel r_n\parallel }^2\hfill \\ \hfill & +2(1-u_n-v_n)\parallel E_n\parallel (\parallel e_n\parallel +\parallel y_n-y^{*}\parallel +a_n{b}_n\parallel y_n-y^{*}\parallel +a_n\parallel r_n\parallel )\hfill \\ \hfill & +2\parallel r_n\parallel (\parallel y_n-y^{*}\parallel +a_n\parallel e_n\parallel )+2(1+a_n{b}_n)\parallel e_n\parallel ·\parallel y_n-y^{*}\parallel \hfill \\ \hfill & +2(1-a_n-b_n)\parallel R_n\parallel (\parallel r_n\parallel +\parallel y_n-y^{*}\parallel +a_n\parallel e_n\parallel )\hfill \\ \hfill & +2a_n(1-u_n-v_n)(1-a_n-b_n)\parallel E_n\parallel ·\parallel R_n\parallel .\hfill \end{array}$$

For $\forall y^{*}\in Fix\left(T\right)$, we obtain

$$\begin{array}{cc}\hfill & \parallel y_{n+1}-y^{*}{\parallel }^2\hfill \\ \hfill & =\parallel a_{n}T{d}_n+b_n{y}_n+r_n-y^{*}{\parallel }^2\hfill \\ \hfill & =\parallel a_n(T{d}_n-y^{*})+b_n(y_n-y^{*})+(1-a_n-b_n)R_n+(a_n+b_n)r_n{\parallel }^2\hfill \\ \hfill & \le a_n^2\parallel d_n-y^{*}{\parallel }^2+{\parallel b_n(y_n-y^{*})+(1-a_n-b_n)R_n+(a_n+b_n)r_n\parallel }^2\hfill \\ \hfill & +2a_n\parallel d_n-y^{*}\parallel ·\parallel b_n(y_n-y^{*})+(1-a_n-b_n)R_n+(a_n+b_n)r_n\parallel \hfill \\ \hfill & \le a_n^2\parallel u_n(T{y}_n-y^{*})+v_n(y_n-y^{*}){\parallel }^2+a_n^2{\parallel (1-u_n-v_n)E_n+(u_n+v_n)e_n\parallel }^2\hfill \\ \hfill & +2a_n^2\parallel u_n(T{y}_n-y^{*})+v_n(y_n-y^{*})\parallel ·\parallel (1-u_n-v_n)E_n+(u_n+v_n)e_n\parallel \hfill \\ \hfill & +b_n^2\parallel y_n-y^{*}{\parallel }^2+{\parallel (1-a_n-b_n)R_n+(a_n+b_n)r_n\parallel }^2\hfill \\ \hfill & +2b_n\parallel y_n-y^{*}\parallel ·\parallel (1-a_n-b_n)R_n+(a_n+b_n)r_n\parallel \hfill \\ \hfill & +2a_n\parallel u_{n}T{y}_n+v_n{y}_n+e_n-y^{*}\parallel ·\parallel b_n(y_n-y^{*})+(1-a_n-b_n)R_n+(a_n+b_n)r_n\parallel \hfill \\ \hfill & \le a_n^2(u_n(u_n+v_n)\parallel T{y}_n-y^{*}{\parallel }^2+v_n(u_n+v_n)\parallel y_n-y^{*}{\parallel }^2-u_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel \left)\right)\hfill \\ \hfill & +b_n^2\parallel y_n-y^{*}{\parallel }^2+2a_n{b}_n{\parallel y_n-y^{*}\parallel }^2+M_n\hfill \\ \hfill & \le (a_n^2+b_n^2+2a_n{b}_n)\parallel y_n-y^{*}{\parallel }^2-a_n^2{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )+M_n\hfill \\ \hfill & \le \parallel y_n-y^{*}{\parallel }^2-a_n^2{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )+M_n,\hfill \end{array}$$

(11)

we know from (11) that

$$u_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )\le {\displaystyle \frac{1}{a_n^2}}(\parallel y_n-y^{*}{\parallel }^2-\parallel y_{n+1}-y^{*}{\parallel }^2+M_n).$$

(12)

It follows from conditions (ii) and (iii) that ${\sum }_{n=0}^{\infty }{M}_n<\infty .$ This inequality, together with (12), implies that

$$\sum _{n=0}^{\infty }{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )<\infty .$$

More precisely, ${lim}_{n\to \infty }{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )=0$. By an application of Lemma 2 under condition (i), we necessarily obtain

$$\underset{n\to \infty }{lim}inf\widehat{h}(\parallel T{y}_n-y_n\parallel )=0,$$

and hence

$$\underset{n\to \infty }{lim}inf\parallel T{y}_n-y_n\parallel =0.$$

Step 3 We now prove that ${lim}_{n\to \infty }\parallel T{y}_n-y_n\parallel =0$. To this end, first observe that

$$\begin{array}{cc}\hfill \parallel y_{n+1}-y_n\parallel & =\parallel a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{x}_n+r_n-y_n\parallel \hfill \\ \hfill & \le a_n\parallel u_{n}T{y}_n+v_n{y}_n+e_n-y_n\parallel +a_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel y_n\parallel +\parallel r_n\parallel \hfill \\ \hfill & \le a_n{u}_n\parallel T{y}_n-y_n\parallel +a_n(1-u_n-v_n)\parallel y_n\parallel +a_n\parallel e_n\parallel \hfill \\ \hfill & +a_n\parallel T{y}_n-y_n\parallel +(1-a_n-b_n)\parallel y_n\parallel +\parallel r_n\parallel .\hfill \end{array}$$

(13)

Then we have

$$\begin{array}{cc}\hfill \parallel T{y}_{n+1}-y_{n+1}\parallel & =\parallel T{y}_{n+1}-a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)-b_n{x}_n-r_n\parallel \hfill \\ \hfill & \le \parallel T{y}_{n+1}-T{y}_n\parallel +a_n\parallel T{y}_n-T(u_{n}T{y}_n+v_n{y}_n+e_n)\parallel \hfill \\ \hfill & +(1-a_n)\parallel T{y}_n-y_n\parallel +\parallel (1-a_n-b_n)y_n-r_n\parallel \hfill \\ \hfill & \le \parallel y_{n-1}-y_n\parallel +a_n\parallel y_n-u_{n}T{y}_n-v_n{y}_n-e_n\parallel \hfill \\ \hfill & +(1-a_n)\parallel T{y}_n-y_n\parallel +\parallel (1-a_n-b_n)y_n-r_n\parallel \hfill \\ \hfill & \le a_n(1+u_n)\parallel T{y}_n-y_n\parallel +a_n\parallel e_n\parallel +\parallel r_n\parallel \hfill \\ \hfill & +a_n(1-u_n-v_n)\parallel y_n\parallel +(1-a_n-b_n)\parallel y_n\parallel \hfill \\ \hfill & +a_n{u}_n\parallel T{y}_n-y_n\parallel +\parallel (1-u_n-v_n)y_n-a_n{e}_n\parallel \hfill \\ \hfill & +(1-a_n)\parallel T{y}_n-y_n\parallel +\parallel r_n\parallel +(1-a_n-b_n)\parallel y_n\parallel \hfill \\ \hfill & \le \parallel T{y}_n-y_n\parallel +(1+a_n)(1-u_n-v_n)\parallel y_n\parallel \hfill \\ \hfill & +2(a_n{u}_n\parallel T{y}_n-y_n\parallel +a_n\parallel e_n\parallel +\parallel r_n\parallel +(1-a_n-b_n)\parallel y_n\parallel ).\hfill \end{array}$$

(14)

We set

$$N_n:=(1+a_n)(1-u_n-v_n)\parallel y_n\parallel +2(a_n{u}_n\parallel T{y}_n-y_n\parallel +a_n\parallel e_n\parallel +\parallel r_n\parallel +(1-a_n-b_n)\parallel y_n\parallel ).$$

It follows from conditions (ii), (iii) and (iv) that ${\sum }_{n=0}^{\infty }{N}_n<\infty$.

Setting $g_n:=\parallel T{y}_n-y_n\parallel$ and $k_n:=N_n$, then Formula (14) can be written $g_{n+1}\le g_n+k_n.$ By applying Lemma 1, we have that ${lim}_{n\to \infty }\parallel y_n-{Ty}_n\parallel$ exists. Since ${lim}_{n\to \infty }inf\parallel y_n-T{y}_n\parallel =0$, this yields ${lim}_{n\to \infty }\parallel y_n-{Ty}_n\parallel =0$.

Step 4 An application of the demiclosedness principle for the operator $I-T$ yields the inequality $\omega \left(y_n\right)\subset Fix\left(T\right)$, where $\omega \left(y_n\right):=\{y:\left\{y_{n_k}\right\}\subset {\{y}_n\},s.t.y_{n_k}\rightharpoonup y\}$. Therefore, to establish the weak convergence of ${\{y}_n\}$ to a fixed point of T, it suffices to prove that the set of its weak cluster points $\omega \left(y_n\right)$ is a singleton. We proceed by considering two cases.

In the first case, where $E^{*}$ possesses the KK-property, we conclude that $\omega \left(y_n\right)$ is a singleton by appealing to Proposition 1.

In the second case, E satisfies Opial’s property.

Take $y^{*},y^{**}\in \omega \left(y_n\right)$, and let $\left\{y_{n_i}\right\}$ and $\left\{y_{m_j}\right\}$ be subsequences of ${\{y}_n\}$ such that $y_{n_i}\to y^{*}$ and $y_{m_j}\to y^{**}$, respectively. If $y^{*}\ne y^{**}$, then

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}∥y_n-y^{*}∥& =\underset{i\to \infty }{lim}∥y_{n_i}-y^{*}∥\hfill \\ & =\underset{j\to \infty }{lim}∥y_{m_j}-y^{**}∥\hfill \\ & <\underset{j\to \infty }{lim}∥y_{m_j}-y^{*}∥=\underset{n\to \infty }{lim}∥y_n-y^{*}∥,\hfill \end{array}$$

a contradiction. Hence, in both cases, we have shown that $\omega \left(y_n\right)$ is a singleton, which completes the proof. □

Setting $e_n=r_n=0$ in Theorem 1 yields the following corollary.

Corollary 1.

Let E be a uniformly convex Banach space that also possesses either the KK property (in its dual $E^{*}$) or the Opial property. Let D be a nonempty closed convex subset of E, and $T:D\to D$ a nonexpansive mapping satisfying $Fix\left(T\right)\ne ⌀$. The sequence ${\{y}_n\}$ is generated by the following iteration:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n,n=0,1,2,\cdots ,$$

(15)

where $a_n,b_n,u_n,v_n\in [0,1]$, $\left\{a_n\right\}$ consistently greater than 0 and $a_n+b_n\le 1,u_n+v_n\le 1$. Assume the following conditions hold:

(i) 

${\sum }_{n=0}^{\infty }{u}_n{v}_n=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }(1-u_n-v_n)<\infty$, ${\sum }_{n=0}^{\infty }(1-a_n-b_n)<\infty$;

(iii) 

${\sum }_{n=0}^{\infty }{a}_n{u}_n<\infty$.

Then the sequence $\left\{y_n\right\}$ generated by the iteration (15) converges weakly to the fixed point of T.

If we set $a_n:=v_n$, $b_n:=1-v_n$, $v_n:=1-u_n$ and $e_n=r_n=0$, then the following conclusion holds.

Corollary 2.

Let E be a uniformly convex Banach space. Assume, in addition, that either $E^{*}$ has the KK-property or E satisfies the Opial’s property. D is a nonempty closed convex subset of E. Let $T:D\to D$ be a nonexpansive mapping such that $Fix\left(T\right)\ne ⌀$. The sequence ${\{y}_n\}$ is generated by the following iteration:

$$y_{n+1}=v_{n}T(u_n{Ty}_n+(1-u_n)y_n)+(1-v_n)y_n,\forall n=0,1,2,\cdots ,$$

(16)

where $u_n,v_n\in [0,1]$, ${\{t}_n\}$ consistently greater than 0. Assume the following conditions hold:

(i) 

${\sum }_{n=0}^{\infty }{u}_n{(1-u}_n)=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }{v}_n{u}_n<\infty$.

Then the sequence $\left\{y_n\right\}$ generated by the iteration (16) converges weakly to the fixed point of T.

We next provide a concrete example to demonstrate that the sequence generated by recursion (9) of Theorem 1 converges weakly to a fixed point of T, when $a_n+b_n<1,u_n+v_n<1$, and compare the iterative results with the generalized KM iteration.

Example 1.

Define the mapping $T:R\to R$ by $Ty=max\{0,-y\}$. Then T is nonexpansive and possesses a unique fixed point at $y=0$.

Proof. 

We consider the following iterative scheme:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n,n=0,1,2,\cdots ,$$

where $a_n=u_n={\displaystyle \frac{1}{1+n}}, b_n=v_n=1-{\displaystyle \frac{1}{n}}, e_n={\displaystyle \frac{1}{n^2}}, r_n=0$. Then we have

$$y_{n+1}={\displaystyle \frac{1}{1+n}}max\left\{0,-\left({\displaystyle \frac{1}{1+n}}max\{0,-y_n\}+\left(1-{\displaystyle \frac{1}{n}}\right)y_n+{\displaystyle \frac{1}{n^2}}\right)\right\}+\left(1-{\displaystyle \frac{1}{n}}\right)y_n.$$

Observe that the selections of $a_n, b_n, u_n, v_n, e_n$ and $r_n$ adhere to conditions (i)–(iv) in Theorem 1, and $a_n+b_n<1,u_n+v_n<1$. Taking $y_1=-1$, by the iteration, we get that $y_2=0.$

We now turn to the generalized KM iterative scheme:

$$y_{n+1}=a_n{y}_n+b_{n}T{y}_n+r_n,\forall n=0,1,2,\cdots .$$

where $a_n=1-{\displaystyle \frac{1}{n}},b_n={\displaystyle \frac{1}{1+n}},r_n=0$. Then we have

$$y_{n+1}=\left(1-{\displaystyle \frac{1}{n}}\right)y_n+{\displaystyle \frac{1}{1+n}}max\{0,-y_n\}.$$

Taking $y_1=-1$, by the iteration, we get that $y_2={\displaystyle \frac{1}{2}}, y_3={\displaystyle \frac{1}{4}}, y_4={\displaystyle \frac{1}{6}}, y_5={\displaystyle \frac{1}{8}},\cdots$, when $n\ge 2$, $y_n={\displaystyle \frac{1}{2n}}$. □

Figure 1 compares the convergence behavior of the generalized Ishikawa iteration with errors and the generalized KM iteration. As shown, the generalized Ishikawa algorithm with errors exhibits faster convergence and higher computational accuracy.

A subsequent example is provided to compare the convergence rates of the generalized Ishikawa iteration with the generalized Ishikawa iteration with errors.

Example 2.

Define the mapping $T:R\to R$ by $Ty=-y+2$, which is readily verified to be nonexpansive.

First, consider the generalized Ishikawa iteration:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n,n=0,1,2,\cdots ,$$

where $a_n=u_n={\displaystyle \frac{1}{1+n}},b_n=v_n=1-{\displaystyle \frac{1}{n}}$, then we obtain

$$y_{n+1}={\displaystyle \frac{1}{1+n}}\left(-\left({\displaystyle \frac{1}{1+n}}(-y_n+2)+\left(1-{\displaystyle \frac{1}{n}}\right)y_n\right)+2\right)+\left(1-{\displaystyle \frac{1}{n}}\right)y_n.$$

Setting $y_1=0$ in the iteration yields $y_2={\displaystyle \frac{1}{2}}, y_3={\displaystyle \frac{2}{3}}, y_4={\displaystyle \frac{3}{4}}, y_5={\displaystyle \frac{4}{5}},\cdots .$ Furthermore, a straightforward induction demonstrates that when $n\ge 2$, it follows that $y_n={\displaystyle \frac{n-1}{n}}$.

Next, consider the generalized Ishikawa iteration with errors:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n,n=0,1,2,\cdots ,$$

where $a_n=u_n={\displaystyle \frac{1}{1+n}}, b_n=v_n=1-{\displaystyle \frac{1}{n}}, e_n=0, r_n={\displaystyle \frac{1}{n^2+1}}$, then we obtain

$$y_{n+1}={\displaystyle \frac{1}{1+n}}\left(-\left({\displaystyle \frac{1}{1+n}}(-y_n+2)+\left(1-{\displaystyle \frac{1}{n}}\right)y_n\right)+2\right)+\left(1-{\displaystyle \frac{1}{n}}\right)y_n+{\displaystyle \frac{1}{n^2+1}}.$$

Setting $y_1=0$ in the iteration yields $y_2=1$.

A comparison of the convergence rates between the generalized Ishikawa iteration, with and without errors, is shown in Figure 2.

The comparison of the two figures indicates that the generalized Ishikawa iteration with errors, as proposed in this study, exhibits not only improved convergence speed but also higher accuracy and performance compared to the generalized KM iteration and generalized Ishikawa iteration. The error term serves as a regulatory factor and enhances the efficiency of convergence.

Now, we present a new example addressing the convergence issue under “Rotation Mapping Problem”. For certain special mappings, such as small-angle rotations, standard iterative methods exhibit extremely slow convergence or even fail to converge. To tackle this problem, this paper employs a generalized Ishikawa iteration algorithm with an error term. By introducing a contraction error term, convergence is significantly accelerated. Taking a rotation mapping with an angle of $\pi /100$ as an example, we demonstrate the superior performance of the algorithm. The experiment is conducted in ${\mathbb{R}}^2$, with the mapping T defined as a rotation matrix about the origin by $\pi /100$ radians, and the initial point set as $(1,0)$.

Example 3.

The mapping $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ is defined as a rotation about the origin by θ radians: $T\left(\mathbf{x}\right)=R\left(\theta \right)\mathbf{x}$. Here, the rotation matrix R is given by: $R\left(\theta \right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)$, with the rotation angle $\theta =\pi /100$ (approximately $1.8°$). T is a nonexpansive mapping with the origin $\mathbf{0}=(0,0)$ as its unique fixed point.

For this problem, the generalized KM iteration algorithm cannot be directly applied because it is a single-step iteration (using T only once), whereas the generalized Ishikawa iteration is a two-step iteration (using T twice, i.e., a nested T). For rotation mappings, which exhibit strong directional behavior, algorithms with a two-layer structure can better adjust the direction through the construction of intermediate points, potentially leading to faster convergence. Therefore, in addressing this issue, we directly compare the performance of the generalized Ishikawa iteration algorithm and its variant incorporating an error term.

First, consider the generalized Ishikawa iteration:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n,n=0,1,2,\cdots ,$$

where

$$a_n={\displaystyle \frac{{ϵ}_a}{{(n+1)}^{{\alpha }_a}}},b_n=1-a_n,$$

$$u_n=u_{\mathrm{const}}-{\displaystyle \frac{{ϵ}_u}{{(n+1)}^{{\alpha }_u}}},v_n=1-u_n,$$

$${ϵ}_a=0.50,{\alpha }_a=1.05,u_{\mathrm{const}}=0.50,{ϵ}_u=0.10,{\alpha }_u=0.5.$$

Next, consider the generalized Ishikawa iteration with errors:

$$y_{n+1}=a_{n}T(u_{n}T{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n,n=0,1,2,\cdots ,$$

where the parameters $a_n, b_n, u_n, v_n$ are the same as those in the generalized Ishikawa iteration.

$$r_n=-c·{\displaystyle \frac{1}{{(n+1)}^p}}·y_n,c=2.0,p=1.1,e_n=0.$$

Observe that the selections of $a_n,b_n,u_n,v_n,e_n$, and $r_n$ adhere to conditions (i)–(iv) in Theorem 1.

For the rotation mapping problem, the comparison of convergence for the generalized Ishikawa iteration with and without errors is shown in Figure 3.

From Figure 3, it can be observed that the trajectory plot of the error-free generalized Ishikawa iteration shows the iteration points slowly circling on a circle, hardly converging to the fixed point. In contrast, the trajectory plot of the generalized Ishikawa iteration with errors shows the iteration points rapidly contracting toward the fixed point. The norm convergence plot displays the distance from the origin over time, while the norm convergence plot (log scale) more clearly illustrates the difference in convergence rates. A zoomed-in view of the last 50 iterations highlights the differences in convergence accuracy. The performance comparison table quantitatively presents various performance metrics, indicating that the generalized Ishikawa iteration with errors can approach the fixed point in as few as five steps, demonstrating excellent performance.

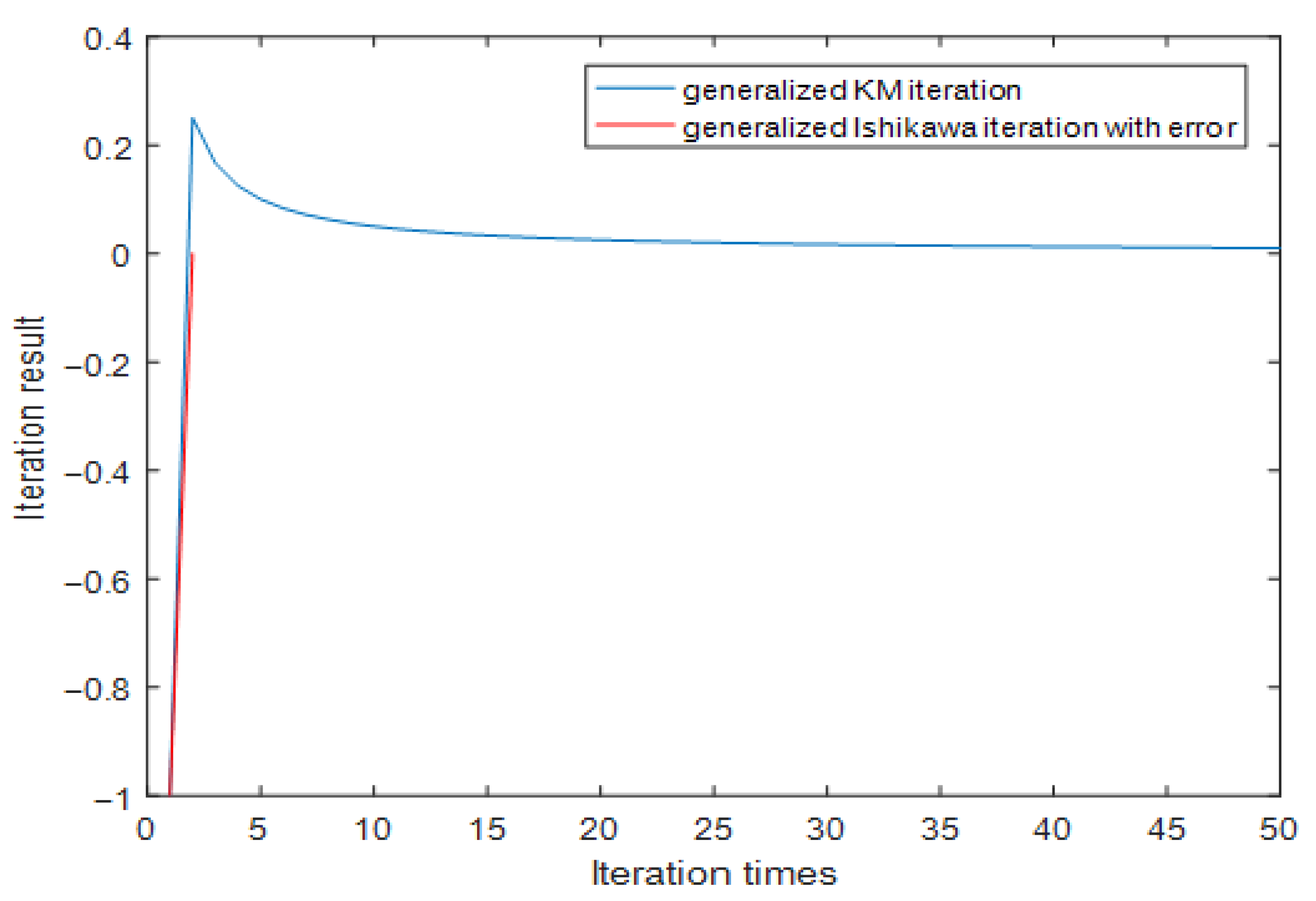
3.2. Application of Generalized Ishikawa Iterative Algorithm with Errors

This section demonstrates the applicability of Theorem 1 to the Hyper-Generalized Proximal Point Algorithm (HGPPA) for locating zeros of an m-accretive operator, that is,

$$0\in A\left(x\right),$$

(17)

where $A:E\rightrightarrows E$ is an m-accretive operator on a uniformly convex Banach space E. The solution set of problem (17), denoted by $zer\left(A\right)$, is taken to be nonempty. The proximal point algorithm (PPA) for solving (17), originating from the seminal work of Browder [16] and Martinet [18], iteratively generates a sequence ${\{y}_n\}$ by the scheme

$$0\in \gamma A\left(y_{n+1}\right)+y_{n+1}-y_n,$$

(18)

where the proximal parameter $\gamma$ is positive in a real Hilbert space, the resolvent operator $J_{\gamma A}$ is defined as $J_{\gamma A}:={(I+\gamma A)}^{-1}$. Consequently, the PPA iteration (18) admits the compact form

$$y_{n+1}:=J_{\gamma A}\left(y_n\right).$$

(19)

The convergence of the PPA (18) was first established in Hilbert spaces by Browder [16]. Kim et al. [17] later generalized this convergence result to the setting of uniformly convex Banach spaces and m-accretive operators. Specifically, they studied an algorithm of the form:

$$y_{n+1}:=(1-a_n)y_n+a_n(J_{\gamma A}\left(y_n\right)+e_n),$$

(20)

where $a_n\subset (0,1)$, $\left\{e_n\right\}$ being an error sequence in E. Zhang et al. [7] introduced the following Generalized Proximal Point Algorithm (GPPA):

$$y_{n+1}:=a_n{y}_n+b_n(J_{\gamma A}\left(y_n\right)+e_n),n=0,1,2,\cdots ,$$

(21)

where $a_n$ and $b_n$ are real sequences in $[0,1]$ satisfying $a_n+b_n\le 1$. The GPPA affords greater flexibility in parameter selection and admits a wider application scope than Algorithm (20). Zhang et al. also provided a proof of its weak convergence in uniformly convex Banach spaces.

This paper will further extend the algorithm (21), considering the hyper generalized proximal point algorithm (HGPPA):

$$y_{n+1}=a_n{J}_{\gamma A}(u_n{J}_{\gamma A}{y}_n+v_n{y}_n+e_n)+b_n{y}_n+r_n,n=0,1,2,\cdots ,$$

(22)

where $a_n,b_n,u_n,v_n\in [0,1]$, $\left\{a_n\right\}$ consistently greater than 0 and $a_n+b_n\le 1, u_n+v_n\le 1$, $\left\{e_n\right\}$ and $\left\{r_n\right\}$ are error sequences, (22) can be viewed as a generalization of several earlier proximal point algorithms.

Next, we proceed to establish the weak convergence of the HGPPA in uniformly convex Banach spaces.

Theorem 2.

Let E be a uniformly convex Banach space whose dual $E^{*}$ satisfies the KK property or which itself satisfies the Opial property. Let A be an m-accretive operator in E with $zer\left(A\right)\ne ⌀$. Suppose the sequence $\left\{y_n\right\}$ is generated by (22), where the parameters $a_n,b_n,u_n,v_n\in [0,1]$ satisfy $a_n+b_n\le 1,u_n+v_n\le 1$, with $\left\{a_n\right\}$ consistently greater than 0, and $\left\{e_n\right\}$, $\left\{r_n\right\}$ are error sequences. The following conditions are assumed to hold:

(i) 

${\sum }_{n=0}^{\infty }{u}_n{v}_n=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }(1-u_n-v_n)<\infty$, ${\sum }_{n=0}^{\infty }(1-a_n-b_n)<\infty$;

(iii) 

${\sum }_{n=0}^{\infty }\parallel e_n\parallel <\infty$, ${\sum }_{n=0}^{\infty }\parallel r_n\parallel <\infty$;

(iv) 

${\sum }_{n=0}^{\infty }{a}_n{u}_n<\infty$.

Then the sequence $\left\{y_n\right\}$ generated by the iteration (22) converges weakly to the fixed point of $zer\left(A\right)$.

Proof. 

Define the operator $T:=J_{\gamma A}$ for notational convenience. Note that, $Fix\left(T\right)=zer\left(T\right)\ne ⌀$, then HGPPA (22) can be rewritten as (9).

Since A is m-accretive, it follows from Lopez et al. [19] that T is nonexpansive. The application of Theorem 1 to (9) now yields the weak convergence of $\left\{y_n\right\}$ to a point in $zer\left(A\right)$. This concludes the proof. □

4. Convergence of Variable Generalized Ishikawa Iterative Algorithm and Its Application

4.1. Weak Convergence of Variable Generalized Ishikawa Iterative Algorithm

This section focuses on refining the iterative process of the variable generalized KM algorithm and introduces a new variable generalized Ishikawa iterative algorithm, defined as follows:

$$y_{n+1}=a_n{T}_n(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n,n=0,1,2,\cdots ,$$

(23)

We proceed to prove that the variable generalized Ishikawa iteration converges weakly.

Theorem 3.

Let E be a uniformly convex Banach space that satisfies the Opial property. Let D be a nonempty closed convex subset of E, and $T:D\to D$ a nonexpansive mapping satisfying condition $Fix\left(T\right)\ne ⌀$. Let $\left\{T_n\right\}$ be a sequence of nonexpansive operators on D. The sequence $\left\{y_n\right\}$ is generated by (23), where $a_n,b_n,u_n,v_n\in [0,1]$, $\left\{a_n\right\}$ consistently greater than 0 and $a_n+b_n\le 1,u_n+v_n\le 1$. The following conditions are assumed to hold:

(i) 

${\sum }_{n=0}^{\infty }{u}_n{v}_n=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }{a}_n{u}_n<\infty$;

(iii) 

${\sum }_{n=0}^{\infty }(1-u_n-v_n)<\infty$, ${\sum }_{n=0}^{\infty }(1-a_n-b_n)<\infty$;

(iv) 

$\forall \rho \ge 0$, ${\sum }_{n=0}^{\infty }{a}_n{D}_{\rho }^{\prime }(T_n,T)<\infty$, where

$$D_{\rho }^{\prime }(T_n,T):=sup\{\parallel T_{n}y-Ty\parallel :\parallel y\parallel \le \rho ,y\in E\},$$

then the sequence $\left\{y_n\right\}$ generated by the iteration (23) converges weakly to the fixed point of T.

Proof. 

We structure the proof into four steps for clarity.

Step 1 For $\forall z\in Fix\left(T\right)$, we will show ${lim}_{n\to \infty }\parallel y_n-z\parallel$ exists.

$$\begin{array}{cc}\hfill & \parallel y_{n+1}-z\parallel \hfill \\ \hfill & =\parallel a_n{T}_n(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n-z\parallel \hfill \\ \hfill & =\parallel a_n(T_n(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z)-(1-a_n-b_n)z\parallel \hfill \\ \hfill & \le a_n\parallel T_n(u_{n}T{y}_n+v_n{y}_n)-z\parallel +b_n\parallel y_n-z\parallel +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & \le a_n\parallel T_n(u_{n}T{y}_n+v_n{y}_n)-T_{n}z\parallel +a_n\parallel T_{n}z-z\parallel +b_n\parallel y_n-z\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & \le a_n\parallel u_{n}T{y}_n+v_n{y}_n-z\parallel +a_n\parallel T_{n}z-z\parallel +b_n\parallel y_n-z\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & =a_n\parallel u_n(T{y}_n-z)+v_n(y_n-z)-(1-u_n-v_n)z\parallel +a_n\parallel T_{n}z-z\parallel \hfill \\ \hfill & +b_n\parallel y_n-z\parallel +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & \le a_n(u_n\parallel T{y}_n-z\parallel +v_n\parallel y_n-z\parallel -(1-u_n-v_n)\parallel z\parallel )+a_n\parallel T_{n}z-z\parallel \hfill \\ \hfill & +b_n\parallel y_n-z\parallel +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & \le a_n\parallel y_n-z\parallel +(1-u_n-v_n)a_n\parallel z\parallel +a_n\parallel T_{n}z-z\parallel +b_n\parallel y_n-z\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel z\parallel \hfill \\ \hfill & \le \parallel y_n-z\parallel +a_n{D}_{\parallel z\parallel }(T_n,T)+(1-u_n-v_n)a_n\parallel z\parallel +(1-a_n-b_n)\parallel z\parallel .\hfill \end{array}$$

(24)

It follows from conditions (iii) and (iv) and Lemma 1 applied to (24) with ${\alpha }_n:=\parallel y_n-z\parallel$ and ${\beta }_n:=a_n{D}_{\parallel z\parallel }(T_n,T)+(1-u_n-v_n)a_n\parallel z\parallel +(1-a_n-b_n)\parallel z\parallel$ that ${lim}_{n\to \infty }\parallel y_n-z\parallel$ exists, whence the sequence $\left\{y_n\right\}$ is bounded.

Step 2 We now demonstrate that ${lim}_{n\to \infty }inf\parallel {Ty}_n-y_n\parallel =0$ is satisfied.

Set

$$p_n:=T_n(u_{n}T{y}_n+v_n{y}_n)-T(u_{n}T{y}_n+v_n{y}_n),$$

and

$$\begin{array}{cc}\hfill M_n& :=({(1-u_n-v_n)}^2{a}_n^2+{(1-a_n-b_n)}^2+2(1-u_n-v_n)(1-a_n-b_n)){\parallel z\parallel }^2\hfill \\ \hfill & +2((1-u_n-v_n)a_n^2+(1-u_n-v_n)a_n^2+(1-a_n-b_n))\parallel y_n-z\parallel ·\parallel z\parallel \hfill \\ \hfill & +2((1-a_n-b_n)+(1-u_n-v_n))a_n\parallel p_n\parallel ·\parallel z\parallel \hfill \\ \hfill & +a_n^2\parallel p_n{\parallel }^2+2a_n\parallel y_n-z\parallel ·\parallel p_n\parallel .\hfill \end{array}$$

For $\forall z\in Fix\left(T\right)$, we have

$$\begin{array}{cc}\hfill & \parallel y_{n+1}{-z\parallel }^2\hfill \\ \hfill & =\parallel a_n{T}_n(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n{-z\parallel }^2\hfill \\ \hfill & =\parallel a_n(T_n(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z)-(1-a_n-b_n){z\parallel }^2\hfill \\ \hfill & =\parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z)+a_n{p}_n+b_n(y_n-z)-(1-a_n-b_n){z\parallel }^2\hfill \\ \hfill & \le \parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z){\parallel }^2+{\parallel a_n{p}_n-(1-a_n-b_n)z\parallel }^2\hfill \\ \hfill & +2\parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z)\parallel ·\parallel a_n{p}_n-(1-a_n-b_n)z\parallel \hfill \\ \hfill & \le \parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z){\parallel }^2+{\parallel b_n(y_n-z)\parallel }^2\hfill \\ \hfill & +2a_n\parallel T(u_{n}T{y}_n+v_n{y}_n)-z\parallel ·b_n\parallel y_n-z\parallel \hfill \\ \hfill & +\parallel a_n{p}_n-(1-a_n-b_n){z\parallel }^2\hfill \\ \hfill & +2\parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z)\parallel ·\parallel a_n{p}_n-(1-a_n-b_n)z\parallel \hfill \\ \hfill & \le a_n^2(\parallel u_n(T{y}_n-z)+v_n(y_n-z){\parallel }^2+{(1-u_n-v_n)}^2{\parallel z\parallel }^2)\hfill \\ \hfill & +2a_n^2\parallel y_n-z\parallel ·(1-u_n-v_n)\parallel z\parallel \hfill \\ \hfill & +b_n^2\parallel y_n{-z\parallel }^2+2a_n\parallel T(u_{n}T{y}_n+v_n{y}_n)-z\parallel ·b_n\parallel y_n-z\parallel \hfill \\ \hfill & +\parallel a_n{p}_n-(1-a_n-b_n){z\parallel }^2\hfill \\ \hfill & +2\parallel a_n(T(u_{n}T{y}_n+v_n{y}_n)-z)+b_n(y_n-z)\parallel ·\parallel a_n{p}_n-(1-a_n-b_n)z\parallel \hfill \\ \hfill & \le a_n^2(u_n(u_n+v_n)\parallel T{y}_n{-z\parallel }^2+v_n(u_n+v_n)\parallel y_n{-z\parallel }^2-u_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel \left)\right)\hfill \\ \hfill & +b_n^2\parallel y_n{-z\parallel }^2+2a_n{b}_n{\parallel y_n-z\parallel }^2+M_n\hfill \\ \hfill & \le \parallel y_n{-z\parallel }^2-a_n^2{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )+M_n,\hfill \end{array}$$

(25)

we know from (25) that

$$u_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )\le {\displaystyle \frac{1}{a_n^2}}(\parallel y_n{-z\parallel }^2-\parallel y_{n+1}-z{\parallel }^2+M_n).$$

(26)

It follows from conditions (iii) and (iv) that ${\sum }_{n=0}^{\infty }{M}_n<\infty .$ This inequality, together with (26), implies that

$$\sum _{n=0}^{\infty }{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )<\infty .$$

More precisely, ${lim}_{n\to \infty }{u}_n{v}_n\widehat{h}(\parallel T{y}_n-y_n\parallel )=0$. By an application of Lemma 2 under condition (i), we necessarily obtain

$$\underset{n\to \infty }{lim}inf\widehat{h}(\parallel T{y}_n-y_n\parallel )=0,$$

and hence

$$\underset{n\to \infty }{lim}inf\parallel T{y}_n-y_n\parallel =0.$$

Step 3 We now prove that ${lim}_{n\to \infty }\parallel T{y}_n-y_n\parallel =0$. To this end, first observe that

$$\begin{array}{cc}\hfill & \parallel y_{n+1}-y_n\parallel \hfill \\ \hfill & =\parallel a_n{T}_n(u_{n}T{y}_n+v_n{y}_n)+b_n{y}_n-y_n\parallel \hfill \\ \hfill & =\parallel a_n(T_n(u_{n}T{y}_n+v_n{y}_n)-y_n)-(1-a_n-b_n)y_n\parallel \hfill \\ \hfill & \le a_n(\parallel T_n(u_{n}T{y}_n+v_n{y}_n)-T_n{y}_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel +\parallel T{y}_n-y_n\parallel )\hfill \\ \hfill & +(1-a_n-b_n)\parallel y_n\parallel \hfill \\ \hfill & \le a_n(\parallel u_{n}T{y}_n+v_n{y}_n-y_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel +\parallel T{y}_n-y_n\parallel )+(1-a_n-b_n)\parallel y_n\parallel \hfill \\ \hfill & =a_n(\parallel u_n(T{y}_n-y_n)-(1-u_n-v_n)y_n\parallel )+a_n\parallel T_n{y}_n-T{y}_n\parallel +a_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel y_n\parallel \hfill \\ \hfill & \le a_n{u}_n\parallel T{y}_n-y_n\parallel +(1-u_n-v_n)a_n\parallel y_n\parallel +a_n\parallel T_n{y}_n-T{y}_n\parallel +a_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel y_n\parallel ,\hfill \end{array}$$

(27)

Then we have

$$\begin{array}{cc}\hfill & \parallel T{y}_{n+1}-y_{n+1}\parallel \hfill \\ \hfill & =\parallel T{y}_{n+1}-a_n{T}_n(u_{n}T{y}_n+v_n{y}_n)-b_n{y}_n\parallel \hfill \\ \hfill & \le \parallel T{y}_{n+1}-T{y}_n\parallel +a_n\parallel T_n(u_{n}T{y}_n+v_n{y}_n)-T{y}_n\parallel +b_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)\parallel T{y}_n\parallel \hfill \\ \hfill & \le \parallel y_{n-1}-y_n\parallel +a_n(\parallel T_n(u_{n}T{y}_n+v_n{y}_n)-T_n{y}_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel )\hfill \\ \hfill & +b_n\parallel T{y}_n-y_n\parallel +(1-a_n-b_n)\parallel T{y}_n\parallel \hfill \\ \hfill & \le \parallel y_{n-1}-y_n\parallel +a_n(\parallel u_n(T{y}_n-y_n)-(1-u_n-v_n)y_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel )\hfill \\ \hfill & +b_n\parallel T{y}_n-y_n\parallel +(1-a_n-b_n)\parallel T{y}_n\parallel \hfill \\ \hfill & \le \parallel y_{n-1}-y_n\parallel +a_n(u_n\parallel T{y}_n-y_n\parallel +(1-u_n-v_n)\parallel y_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel )\hfill \\ \hfill & +b_n\parallel T{y}_n-y_n\parallel +(1-a_n-b_n)\parallel T{y}_n\parallel \hfill \\ \hfill & \le \parallel T{y}_n-y_n\parallel +2a_n(1-u_n-v_n)\parallel y_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel )+2a_n{u}_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)(\parallel y_n\parallel +\parallel T{y}_n\parallel ).\hfill \end{array}$$

(28)

We set

$$\begin{array}{cc}\hfill N_n& :=2a_n(1-u_n-v_n)\parallel y_n\parallel +\parallel T_n{y}_n-T{y}_n\parallel )+2a_n{u}_n\parallel T{y}_n-y_n\parallel \hfill \\ \hfill & +(1-a_n-b_n)(\parallel y_n\parallel +\parallel T{y}_n\parallel ).\hfill \end{array}$$

It follows from conditions (ii), (iii) and (iv) that ${\sum }_{n=0}^{\infty }{N}_n<\infty$.

Setting $g_n:=\parallel T{y}_n-y_n\parallel$ and $k_n:=N_n$, then formula (28) can be written $g_{n+1}\le g_n+k_n.$ By applying Lemma 1, we have that ${lim}_{n\to \infty }\parallel y_n-{Ty}_n\parallel$ exists. Since ${lim}_{n\to \infty }inf\parallel y_n-T{y}_n\parallel =0$, this yields ${lim}_{n\to \infty }\parallel y_n-{Ty}_n\parallel =0$.

Step 4 An application of the demiclosedness principle for the operator $I-T$ yields the inequality $\omega \left(y_n\right)\subset Fix\left(T\right)$, where $\omega \left(y_n\right):=\{y:\left\{y_{n_k}\right\}\subset {\{y}_n\},s.t.y_{n_k}\rightharpoonup y\}$. Therefore, to establish the weak convergence of ${\{y}_n\}$ to a fixed point of T, it suffices to prove that the set of its weak cluster points $\omega \left(y_n\right)$ is a singleton.

E satisfies the Opial’s property. Take $y^{*},y^{**}\in \omega \left(y_n\right)$, and let $\left\{y_{n_i}\right\}$ and $\left\{y_{m_j}\right\}$ be subsequences of ${\{y}_n\}$ such that $y_{n_i}\to y^{*}$ and $y_{m_j}\to y^{**}$, respectively. If $y^{*}\ne y^{**}$, then

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}∥y_n-y^{*}∥& =\underset{i\to \infty }{lim}∥y_{n_i}-y^{*}∥\hfill \\ & =\underset{j\to \infty }{lim}∥y_{m_j}-y^{**}∥\hfill \\ & <\underset{j\to \infty }{lim}∥y_{m_j}-y^{*}∥=\underset{n\to \infty }{lim}∥y_n-y^{*}∥,\hfill \end{array}$$

a contradiction. Thus, we have shown that $\omega \left(y_n\right)$ is a singleton, which completes the proof. □

By specializing Theorem 3 to a Hilbert space setting, we immediately obtain the following corollary.

Corollary 3.

Let H be a real Hilbert space and C a nonempty closed convex subset of H. Let $\left\{T_n\right\}$ be a sequence of nonexpansive operators on C, and $T:C\to C$ a nonexpansive mapping. The sequence $\left\{y_n\right\}$ is generated by (23) with $a_n,b_n,u_n,v_n\in [0,1]$ satisfying $a_n+b_n\le 1,u_n+v_n\le 1,$ and $\left\{a_n\right\}$ consistently greater than 0. The following conditions are assumed to hold

(i) 

${\sum }_{n=0}^{\infty }{u}_n{v}_n=\infty$;

(ii) 

${\sum }_{n=0}^{\infty }{a}_n{u}_n<\infty$;

(iii) 

${\sum }_{n=0}^{\infty }(1-u_n-v_n)<\infty$, ${\sum }_{n=0}^{\infty }(1-a_n-b_n)<\infty$;

(iv) 

$\forall \rho \ge 0$, ${\sum }_{n=0}^{\infty }{a}_n{D}_{\rho }^{\prime }(T_n,T)<\infty$, where

$$D_{\rho }^{\prime }(T_n,T):=sup\{\parallel T_{n}y-Ty\parallel :\parallel y\parallel \le \rho ,y\in E\},$$

then the sequence $\left\{y_n\right\}$ generated by the iteration (23) converges weakly to the fixed point of T.

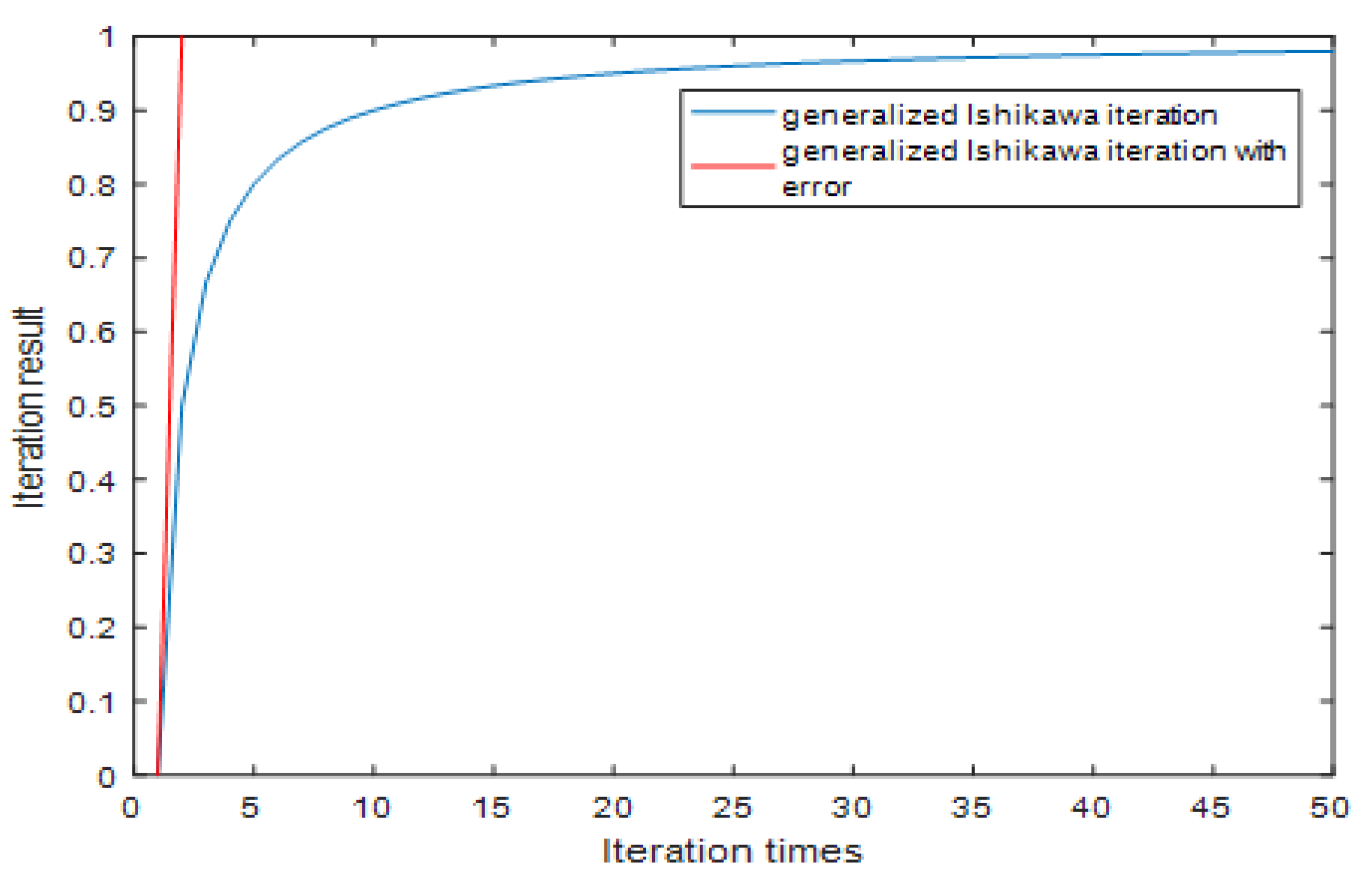
4.2. Application of Variable Generalized Ishikawa Iterative Algorithm

We apply the variable generalized Ishikawa iterative algorithm to the split feasibility problem (SFP) in this section, thereby establishing a more generalized convergence result.

First, let us review what a split feasible problem is [20]. A split feasible problem refers to the process of finding

$$x\in C\mathrm{satisfying}Ax\in Q$$

(29)

where C and Q are closed convex subset of the Hilbert space $H_1$ and $H_2$, respectively, and $A:H_1\to H_2$ is a bounded linear operator.

To solve the SFP (29), Byrne [21,22] proposed the CQ algorithm, generating the sequence $\left\{x_n\right\}$ through the following format:

$$x_{n+1}:=P_C(x_n-\gamma A^{*}(I-P_Q)A{x}_n),n\ge 0$$

(30)

where $P_C$ and $P_Q$ denote the metric projections onto the sets C and Q, $\gamma \in (0,{\displaystyle \frac{2}{\lambda }})$, $\lambda$ is the largest eigenvalue of $A^{*}A$, and $A^{*}$ is the adjoint of A.

Assuming that the SFP (29) is solvable, it is straightforward to observe that $x\in C$ is a solution to SFP (29) if and only if it satisfies the following equation:

$$x:=P_C(I-\gamma A^{*}(I-P_Q)A)x,x\in C$$

(31)

where $\gamma >0$ is an arbitrary positive constant. Furthermore, in reference [23], it is shown that the operator $P_C(I-\gamma A^{*}(I-P_Q)A)$ defined in (31) is nonexpansive for all sufficiently small $\gamma >0$. The CQ algorithm (30) can be viewed as a special case of the KM iterative. Applying the KM algorithm to the fixed-point operator $P_C(I-\gamma A^{*}(I-P_Q)A)$ from (31) yields the following iterative scheme for the sequence $\left\{x_n\right\}$:

$$x_{n+1}:=(1-{\alpha }_n)x_n+{\alpha }_n{P}_C(x_n-\gamma A^{*}(I-P_Q)A{x}_n).$$

(32)

If ${\alpha }_n$ satisfies condition (3), then the resulting sequence $\left\{x_n\right\}$ from iteration (32) is weakly convergent.

Zhao and Yang [24] incorporated perturbations into the closed convex sets C and Q, and investigated the following perturbed CQ algorithm:

$$x_{n+1}:=(1-{\alpha }_n)x_n+{\alpha }_n{P}_{C_n}(x_n-\gamma A^{*}(I-P_{Q_n})A{x}_n),n\ge 0,$$

(33)

where $\left\{C_n\right\}$ and $\left\{Q_n\right\}$ represent the sequence of sets to which Mosco converges for sets C and Q, and $\left\{{\alpha }_n\right\}\subset (0,1)$, with $\gamma$ being the spectral radius of the matrix $A^{T}A$.

Zhang [8] studied the following generalized perturbation CQ algorithm in the Hilbert space:

$$x_{n+1}:={\alpha }_n{x}_n+{\beta }_n{P}_{C_n}(x_n-\gamma A^{*}(I-P_{Q_n})A{x}_n),n\ge 0,$$

(34)

where $\left\{{\alpha }_n\right\}\subset [0,1],\left\{{\beta }_n\right\}\subset [0,1]$, and ${\alpha }_n+{\beta }_n\le 1$. Here, the $\rho$-distance function between two closed convex subsets $E_1$ and $E_2$ in the Hilbert space is introduced as follows:

$$d_{\rho }(E_1,E_2)=sup\{\parallel P_{E_1}x-P_{E_2}x\parallel ,\parallel x\parallel \le \rho \}.$$

The following conditions are assumed to hold:

($a_1$) ${\sum }_{n=0}^{\infty }{\alpha }_n{\beta }_n=\infty$;

($a_2$) ${\sum }_{n=0}^{\infty }(1-{\alpha }_n-{\beta }_n)<\infty$;

($a_3$) $\forall \rho \ge 0,{\sum }_{n=0}^{\infty }{\beta }_n{d}_{\rho }(C_n,C)<\infty \mathrm{and}{\sum }_{n=0}^{\infty }{\beta }_n{d}_{\rho }(Q_n,Q)<\infty$.

Then the sequence $\left\{x_n\right\}$ generated by the generalized perturbation CQ algorithm (34) converges weakly to a solution of the SFP (29).

Based on Zhang’s research, we further extend it and consider the following hyper generalized perturbation CQ algorithm in the Hilbert space:

$$\begin{array}{cc}\hfill x_{n+1}& :={\alpha }_n{P}_{C_n}(I-\gamma A^{*}(I-P_{Q_n})A)(s_n{P}_C(I-\gamma A^{*}(I-P_Q)A)x_n+t_n{x}_n)\hfill \\ \hfill & +{\beta }_n{x}_n,n\ge 0,\hfill \end{array}$$

(35)

Next, we will prove the convergence of the hyper generalized perturbation projection algorithm.

Theorem 4.

Let H be a real Hilbert space and C a nonempty closed convex subset of H. Let $\left\{T_n\right\}$ be a sequence of nonexpansive operators on C, and $T:C\to C$ a nonexpansive mapping. The sequence $\left\{x_n\right\}$ is generated by iterative scheme (23), where ${\alpha }_n,{\beta }_n,s_n,t_n\in [0,1]$, $\left\{{\alpha }_n\right\}$ consistently greater than 0 and ${\alpha }_n+{\beta }_n\le 1,s_n+t_n\le 1$. If the assumed conditions ($a_1$)–($a_3$) are assumed to hold, then the sequence $\left\{x_n\right\}$ generated by the iteration (35) converges weakly to the fixed point of SFP (29).

Proof. 

Set $T_n:=P_{C_n}(I-\gamma A^{*}(I-P_{Q_n})A)$, $T:=P_C(I-\gamma A^{*}(I-P_Q)A)$, then both $T_n$ and T are nonexpansive. Since the solution set of SFP (29) is nonempty, $Fix\left(T\right)\ne ⌀$. Noting that $Fix\left(T\right)$ is the solution of SFP (29), the generalized perturbation projection algorithm (35) can be written as

$$x_{n+1}={\alpha }_n{T}_n(s_{n}T{x}_n+t_n{x}_n)+{\beta }_n{x}_n,n=0,1,2,\cdots ,$$

For $\forall \rho >0,$ set

$$\overline{\rho }=sup\{max\{\parallel Ax\parallel ,\parallel x-\gamma A^{*}(I-P_Q)Ax\parallel \}:\parallel x\parallel \le \rho \}<\infty ,$$

then for $\forall x\in H$, $\parallel x\parallel \le \rho$. Next, calculate $\parallel T_{n}x-Tx\parallel$:

$$\begin{array}{cc}\hfill & \parallel T_{n}x-Tx\parallel \hfill \\ & \le \parallel P_{C_n}(I-\gamma A^{*}(I-P_{Q_n})A)x-P_{C_n}(I-\gamma A^{*}(I-P_Q)A)x\parallel \hfill \\ \hfill & +\parallel P_{C_n}(I-\gamma A^{*}(I-P_Q)A)x-P_C(I-\gamma A^{*}(I-P_Q)A)x\parallel \hfill \\ \hfill & \le \parallel P_{C_n}(I-\gamma A^{*}(I-P_Q)A)x-P_C(I-\gamma A^{*}(I-P_Q)A)x\parallel +\gamma \parallel A^{*}(P_{Q_n}Ax-P_{Q}Ax)\parallel \hfill \\ \hfill & \le d_{\overline{\rho }}(C_n,C)+\gamma \parallel A\parallel d_{\overline{\rho }}(Q_n,Q),\hfill \end{array}$$

that is $D_{\rho }(T_n,T)\le d_{\overline{\rho }}(C_n,C)+\gamma \parallel A\parallel d_{\overline{\rho }}(Q_n,Q)$. From assumption ($a_3$), we can conclude that

$$\sum _{n=0}^{\infty }{\beta }_n{D}_{\rho }(T_n,T)\le \sum _{n=0}^{\infty }{\beta }_n{d}_{\overline{\rho }}(C_n,C)+\gamma \parallel A\parallel \sum _{n=0}^{\infty }{\beta }_n{d}_{\overline{\rho }}(Q_n,Q)<\infty .$$

By Corollary 3, the sequence $\left\{x_n\right\}$ converges weakly to a solution of SFP (29). The proof is therefore complete. □

5. Conclusions

This work has established weak convergence theorems for generalized Ishikawa iteration with errors and variable generalized Ishikawa iterative in uniformly convex Banach spaces, generalizing prior work by Zhang [8] and Wang [11]. Furthermore, the applicability of these findings has been demonstrated through convergence analysis of the HGPPA and a perturbed CQ algorithm. Under specific regularity conditions, these weak convergence results can be strengthened to strong convergence in Hilbert spaces. A natural open question is whether such strong convergence remains valid in uniformly convex Banach spaces, which we leave as a direction for future research.