1. Introduction
The newer generation of communication networks brings with it opportunities and challenges in the context of more complex data flow management [
1]. The current applications require high resource utilization, low latency, and high reliability, which classic routing methods are often unable to provide. Fractional routing improves flexibility and utilization by dividing flows into smaller segments and balancing assignments to reduce latency. Such novel solutions need to be proposed and adapted in response to the specific needs of the IoT and 6G nations [
2]. To simulate the underlying structure of complex networks, a graph-modeling approach must be able to produce robust results. With their ability to efficiently capture directional and hierarchical relationships, Directed Acyclic Graphs (DAG) are well-suited to model network routing scenarios, particularly for applications like fractional routing, which require strict enforcement of flow conservation and capacity constraints [
3,
4].
Network flows are best encoded, managed, and decoded through a systematic mathematical construct in the form of vector linear transformations. By maximizing edge capacity and accurately propagating flow, this approach centrally utilizes network resources on transformations over finite fields. An organized approach to sharing bandwidth also optimizes bottlenecks and improves resource allocation, all while ensuring compliance within the confines of the network [
5]. Optimization methods have likewise become important tools for tackling challenging routing issues.
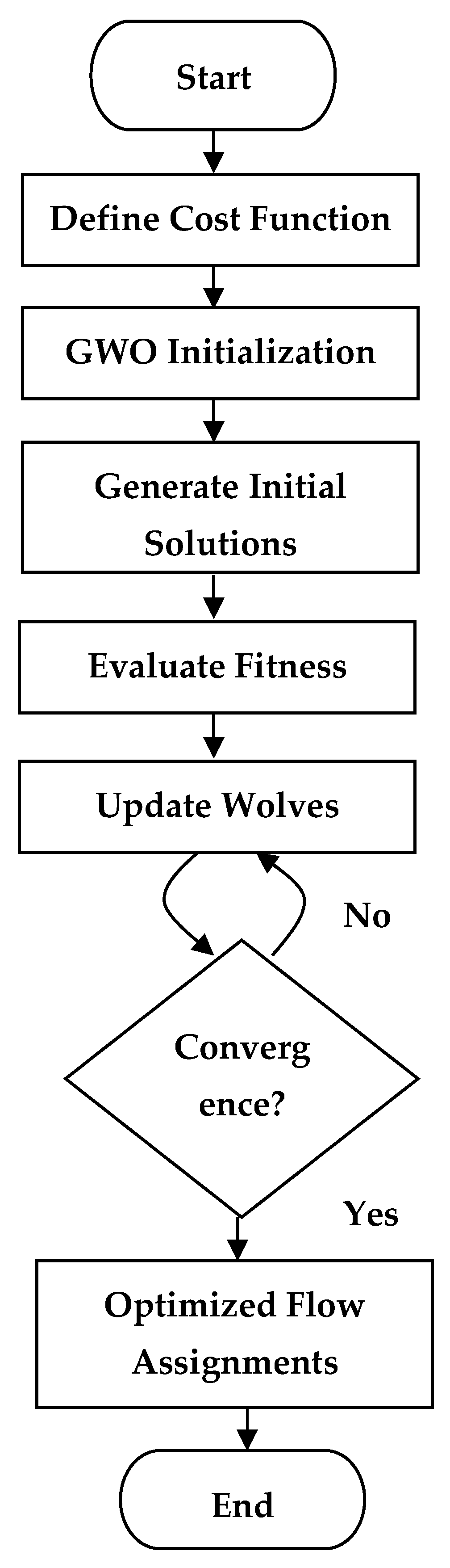
In addition to structural modeling, it is also necessary to have optimization techniques for developing effective routing that are adaptable to dynamic network conditions. The Grey Wolf Optimizer (GWO) is a powerful algorithm that can produce optimal solutions for complex flow optimization problems, especially in dynamic environments and resource-constrained resources [
6]. Moreover, these algorithms allow the networks to dynamically adapt to processes over time. Likewise, AI models such as neural networks also contribute flexibility and scalability via estimating routing tendency and updating according to the changes in the network [
7].
From a mathematical perspective, we are proposing a general formulation and a novel routing framework that amalgamates the integrated system for the purpose of optimizing fractional routing in next-generation networks. The introduction of such a framework seeks to leverage an earlier algebraic transformation to integrate artificial intelligence and quantum computing within the isocline descriptor to control fractional routing and assess the efficiency, scalability, and accuracy features of AI-assisted routing. This framework leverages these new technologies to help implement more efficient and scalable routing solutions for next-generation networks, targeting key challenges in IoT, 6G, and future network technologies. This approach translates the fractional routing problem into multiple optimization techniques suitable for diverse computational strategies. The scalable and adaptive platform supports large-scale and real-time systems.
Our framework fuses the mathematical modeling benefits with heuristic optimization benefits to design and create effective and scalable fractional routing. Using DAG-based models along with optimization algorithms such as GWO gives optimized flow assignments. They lower routing costs and improve the performance of small- and medium-scale networks. In contrast to current approaches, the proposed methodology is remarkable for its scalability and computational efficiency, maintaining performance even as network size grows. The analysis of the running time is in fact a confirmation of the straightforwardness of the technique—and of its adaptability to the different network data complexities. Unlike conventional methodologies that employ linear transformations, the present methodology enables a much richer rate optimization throughout a tighter flow representation, propagation, and decoding. The main novelty is based on the integration of quantum algorithms (e.g., HHL, QAOA) for accelerated routing cost optimization, and AI-driven adaptation for dynamic reconfiguration. Thus, the proposed framework is scalable to large topologies, resilient in traffic variation, and tractable for real-time applications regarding computation.
By already making provisions for modern environments like IoT, 6G, and smart infrastructure, this system will cater to any of the challenges which classical routing models have had to encounter in dealing with optimal resource use and reduced latency while answering vital needs, such as energy efficiency, fault tolerance, and scalability. In short, this holistic method is capable of optimizing fractional routing in larger networks, fulfilling requirements for energy-efficiency, fault-tolerance, and scalability. The basic contributions of our work are, in principle, scalable optimization of the fractional routing, dynamic adaptation to varying network conditions, and efficient resource utilization in large, broad networks. Overall, this work lays the foundation for a next-generation routing paradigm, addressing long-standing inefficiencies and paving the way for adaptive, scalable, and intelligent network infrastructures.
2. Literature Review
The growing complexity of data flows presents significant challenges for achieving timely and efficient network routing in modern communication systems. Traditional routing methods often lack scalability, adaptability, and the flexibility required to meet the dynamic demands of large-scale and heterogeneous networks, such as IoT and 6G [
8] This review summarizes important developments in fractional routing, optimization methods, and AI techniques, and outlines opportunities and future direction for enhancement [
9]. Integrating with the Model-Aware Framework: Fractional Routing, DAGs have been extensively adopted as models of fractional routing to capture directionality and hierarchy in networks. In their research, Abdelwanis, M. I., El-Sousy, F. F. M. and Ali, M. M. discussed how capacity matrices and flow conservation have been successfully used to find opponent stability within such networks [
1]. Their research emphasizes the importance of capacity constraints and flow conservation principles for realizing optimal flow distribution. This was echoed by Abudaqa, A. A., Mahmoud, A., Al-Saggaf, A. A. and Sheltami, T. R., who observed a lack of practical realization of these models, especially for delivery to complicated network topologies, and the call for more applied work [
10]. This problem illustrates how optimization techniques can significantly contribute to effectively utilizing network resources while balancing the need for flow conservation and appropriate resource allocation in a networked environment.
Research by Kheirdast, A., Jozi, S. A., Rezaian, S., and Tehrani, M. M. E. further improved these methods by implementing metaheuristic techniques that had already been proven to optimize fractional routing parameters and have a beneficial influence on network performance [
11]. Despite these achievements, Dhumane, A. V. and Prasad, R. S. also found that optimization techniques and fractional routing frameworks are less integrated with each other, which should be a potential avenue for developing more robust solutions combining these methodologies [
12]. Building upon traditional optimization methods, artificial intelligence introduces new avenues for dynamic and scalable solutions in network routing. Borylo P., Biernacka E., Domzal J., Kadziolka B., Kantor M., Rusek K., Takala A. O., Wajda K., Wojcik R., and Zabek W., 2017 investigated the use of neural networks for predicting traffic flow and routing control, which forms the basis for network adaptation in real-time [
5]. Shah and Vyas [
6] proposed a real-time city traffic classification technique using deep RNN that helps smart cities apply adaptive routs under unknown environment. Despite the impressive performance of these AI models in dynamic environments, Ghosh, S. noted that applying them to fractional routing has not yet been not fully explored. To explore and exploit such capabilities, they propose to factor AI into the optimization of fractional routing, which may provide additional opportunities for flexibility and scale to large and time-critical networks [
7].
Fractional routing is in sequence considered by balancing proximity and the phylogeny of the stream. While the theoretical robustness of DAG-based models is well established, their practical implementation in real-world systems remains significantly limited, as noted by El-Shorbagy et al. [
9]. The challenge is even more urgent as new requirements emerge for wired and wireless solutions in IoT and 6G networks, which call for the development of flexible frameworks. These environments require strict performance metrics to be met, including low latency and energy efficiency [
13]. Scalability can be addressed with advanced optimization techniques and validation studies. On the other hand, Chander, S. et al. developed a multidimensional approach that integrates mathematical modeling, optimization algorithms, and experimental studies to ensure its applicability to a variety of scenarios [
14].
Despite extensive research, key gaps remain—particularly in the integration of algebraic structures with AI adaptability and quantum optimization techniques. Our work addresses this by proposing a unified framework that bridges these currently siloed approaches. According to Chu, Z.; Hao, W. et al., there is a lack of integration of optimization algorithms (like GWO) and fractional routing frameworks [
15]. While Ruiz de Gauna et al. [
16] point out the necessity of the practical validation of fractional routing models in real network settings, Piri specifically noted that there has been little focus on large and dynamic network scalability [
17]. By gradually filling in these gaps, we can unlock the potential for routing solutions that are not only more efficient and scalable but also better equipped to serve the complex needs of contemporary communication networks.
This would increase the productivity and accuracy of the routing processes by incorporating algebraic transformations, including vector linear transformations and fractional calculus [
4]. Neural networks and other AI models can devise routing patterns and automatically adapt to real-time demands placed on the network, thus supporting real-time, fractional adaptation [
5,
6]. In addition, the merging of quantum computation and algebraic transformations may offer advanced optimization by producing even better and more scalable routing solutions for the networks of the future. Flow assignments can be improved, and therefore lead to scalability for dynamic and large-scale networks, with the recent development of optimization algorithms like the Grey Wolf Optimizer (GWO) [
4]. This directional and hierarchical relationship between nodes makes DAG well suited for use in network routing problems [
3]. Our framework achieves scalable and adaptive fractional routing by using algebraic transformations and AI-powered optimization [
13]. In conclusion, the framework aims to handle the advanced needs of the upcoming networks by optimizing resource allocation and minimizing latency while preserving energy efficiency. Modern communication networks, such as IoT and 6G, are characterized by dynamic topologies, stringent latency requirements, and large-scale deployments. As such, conventional routing mechanisms that rely on static paths or greedy heuristics often fail to meet these demands. This has led to increased research into fractional routing, optimization methods, and AI-enhanced flow control, with varying levels of scalability and adaptability.
2.1. Fractional Routing in Graph-Based Models
Fractional routing has always been an important area of research, primarily because it can allow partitioning of flows through multiple paths, and thus improve utilization in resources. A lot of the work on such models has been based on Directed Acyclic Graphs (DAGs) because they are always loop-free and enforce flow hierarchy [
18,
19]. DAGs enable clear directionality, allow hierarchical flow control, and fit well into time-sensitive applications like sensor networks [
19]. However, most frameworks use static capacity assignment and do not have adaptive reconfiguration mechanisms; therefore, they cannot be deployed into practical environments like IoT or 6G, which experience very dynamic demand patterns [
6,
7].
2.2. Optimization Techniques for Flow Allocation
Traditional routing optimization work was completed by metaheuristics like Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and most recently, by the Grey Wolf Optimizer (GWO) [
4,
11,
14]. These techniques are capable of operating based on local optimums, leading to near-optimal flow assignments, but the drawbacks of metaheuristic approaches include slow convergence where large-scale graphs are concerned. These approaches also do not run in real time and generally treat flow propagation as black box optimization problems that do not account for structural properties, including some algebraic transformations [
20].
2.3. AI in Routing Decision-Making
Machine learning and deep reinforcement learning (DRL) have been applied for traffic forecasting, congestion control, and adaptive routing [
5,
21,
22,
23]. Techniques based on AI are capable of learning traffic patterns that keep evolving, thereby continuously improving flow decisions. However, for the greater part, AI-based routing systems possess high data requirements and are simply focused on prediction horizons as opposed to provable guarantees or conservation of flow. Integration with algebraic modeling or guaranteed flow structure is rare [
24].
2.4. Quantum Computing in Network Optimization
Recent studies suggest using quantum annealing and quantum algorithms for routing dilemmas such as NP-hard optimization tasks [
25,
26]. HHL, QAOA, and Grover’s algorithm provide super-linear or quadratic speedups to solve linear systems, combinatorial optimization, and search problems [
27,
28]. Current literature either applies them in isolation or lacks practical integration with realistic flow models, particularly those involving fractional or algebraic routing [
25].
2.5. Research Gap and Contribution
Even though significant progress was made, there was no comprehensive and all-encompassing framework that combines algebraic structure, AI adaptiveness, and quantum optimization for fractional routing. Most methods simply treated routing as a combinatorial problem dimension, not bothering to account for efficiency in algebraic transformation [
20], as heuristic search without any formal guarantees for correctness of flow or preservation [
4,
14], or AI-ML prediction detached from mathematical modeling [
5,
22]. This paper bridges this gap by creating a hybrid framework that applies algebraic transformations over finite fields to the modeling of fractional routings, thereby achieving deterministic reversible propagation of flows, utilizes real-time adaptation and reconfiguration with AI-driven policies, and leverages quantum algorithms (HHL, QAOA, Grover’s) for scalable and accelerated optimization of flows [
27,
28]. Such a synthesis of structural rigor, intelligent adaptability, and computational acceleration directly addresses the limitations of existing works and provides a scalable, efficient, and dynamic solution for next-generation networks. The edge–linear transformations introduced in our framework extend the theory of fractional routing by offering mathematically guaranteed flow encoding and decoding in DAG-based models. The addition of AI and QC into this formal structure is not superficial; instead, they are woven into the routing logic. AI governs dynamic reconfiguration policies, and QC accelerates constraint solving and optimization, forming a hybrid model that is both analytically sound and practically efficient.
2.6. Comparative Analysis with Prior Technologies
To clarify the novelty of the proposed AI-QC routing framework, we present a detailed comparative analysis in
Table 1, comparing our approach with prior methods in fractional routing, AI-based optimization, and quantum-assisted network modeling.
This framework addresses a critical gap in the field by unifying three core technological pillars: formal algebraic modeling, artificial intelligence (AI), and quantum computing (QC). Specifically, it employs edge–linear transformations to ensure mathematical rigor and correctness in flow encoding and decoding, integrates AI-based learning and dynamic reconfiguration to adapt to real-time network changes, and incorporates quantum-assisted optimization to achieve computational efficiency and scalability.
In contrast, existing models often rely solely on heuristics or statistical learning methods that lack guarantees for flow structure preservation. Others treat routing optimization as an isolated, standalone problem, without embedding it within a rigorous mathematical framework. Additionally, while quantum techniques have been explored, they are typically applied in isolation and are not practically integrated with real-world flow models. Recent works, such as the study on QoS-aware offloading in 6G edge intelligence [
29] and adaptive service function chains mapping with multi-task deep reinforcement learning [
30], focus on resource coordination and adaptive placement of service chains in dynamic 6G environments. While these approaches address specific optimization challenges, they do not embed a formal algebraic framework for flow encoding and decoding. Our framework uniquely combines algebraic transformations, AI adaptiveness, and quantum-assisted optimization to provide a mathematically guaranteed and scalable solution for fractional routing in next-generation networks.
5. Proposed Methodology
The paper attempts to leverage a full methodology of fractional routing in the presence of a Directed Acyclic Graph architecture, with algebraic transformations, AI decision models, and quantum optimization algorithms. The final aim is to improve the efficiency, scalability, and adaptability of routing in a complex network. Linear algebra is used to transform the dynamics of traffic into a set of matrix equations solvable with random matrix library operations, such as Grover search in these operations, optimization problems are solved using quantum methods in a high-dimensional space. Simulation results also show the relative performance of the traditional route against the AI-aided and quantum-enhanced route under dynamic circumstances.
Having a similar symmetry of flow paths aids in resource alignment in the network and improves the scalability of the adopted routing algorithms. Considering these symmetrical properties within the directed acyclic graph (DAG) structure allows for well-defined routing that upholds the flow conservation laws. The framework of DAG-based efficient fractional routing has been modeled and implemented through the proposed methodology based on vector linear transformations. This framework ensures the realization of scalable solutions to routing optimization in more complex networks through the exact mechanisms of flow propagation, recognizing flow conservation laws, and incorporating decoding schemes. Therefore, refined solution appendages applied in the area also reduce the routing costs, facilitating an applied outlook to problems that otherwise would be considered theoretical from the outset. AI and machine learning techniques can enhance routing performance, while quantum computing addresses complex routing optimization problems, improving both efficiency and scalability. The methodology is further divided as follows. The proposed methodology is a modular DAG-based framework that integrates algebraic linear transformations, quantum computing, and artificial intelligence to support scalable, dynamic, and resource-efficient fractional routing. It is capable of handling the main challenges of modern networks, such as adaptability to topology changes, bespoke computation over large graphs, and intelligent responses to network load variations.
The methodology basically entails the following components:
DAGs provide a loop-free, hierarchical structure that guarantees a predictable, ordered flow of data. One benefit of this model is the simplicity of routing logic, which avoids duplicated loops and works well with time-critical systems, such as IoT and 6G.
Each edge of the DAG is associated with a matrix of transformations over finite fields (e.g., GF(2m)) that perform encoding, mixing, and secure propagation of fractional flows. This supports efficient encoding during concurrent aggregation of flows, distributed computations preserving flow conservation, and linearly scalable decoding at sink nodes using inverse transforms.
At every intermediate node, flows are propagated while strictly honoring conservation of flows and link capacity constraints, so reliability and load balancing of the network are guaranteed, even under dynamic traffic.
Deep reinforcement learning agents make adjustments in flow configurations with respect to the following: cost, latency, throughput-based reward functions, and learning from historical traffic data to adapt to the changing state of the network. This has enabled the dynamic reconfiguration of routes without a global re-computation.
Quantum algorithms are applied to tackle an optimization problem classically unsolvable: the HHL Algorithm, in which large-scale linear systems in decoding stages are solved efficiently; QAOA, which provides nearly optimal flow assignments in NP-hard cost minimization problems [
33]; and Grover’s Algorithm, which speeds up route selection when the set of valid configurations becomes combinatorially large. These algorithms reduce time complexity and maneuver large networks into making real-time decisions.
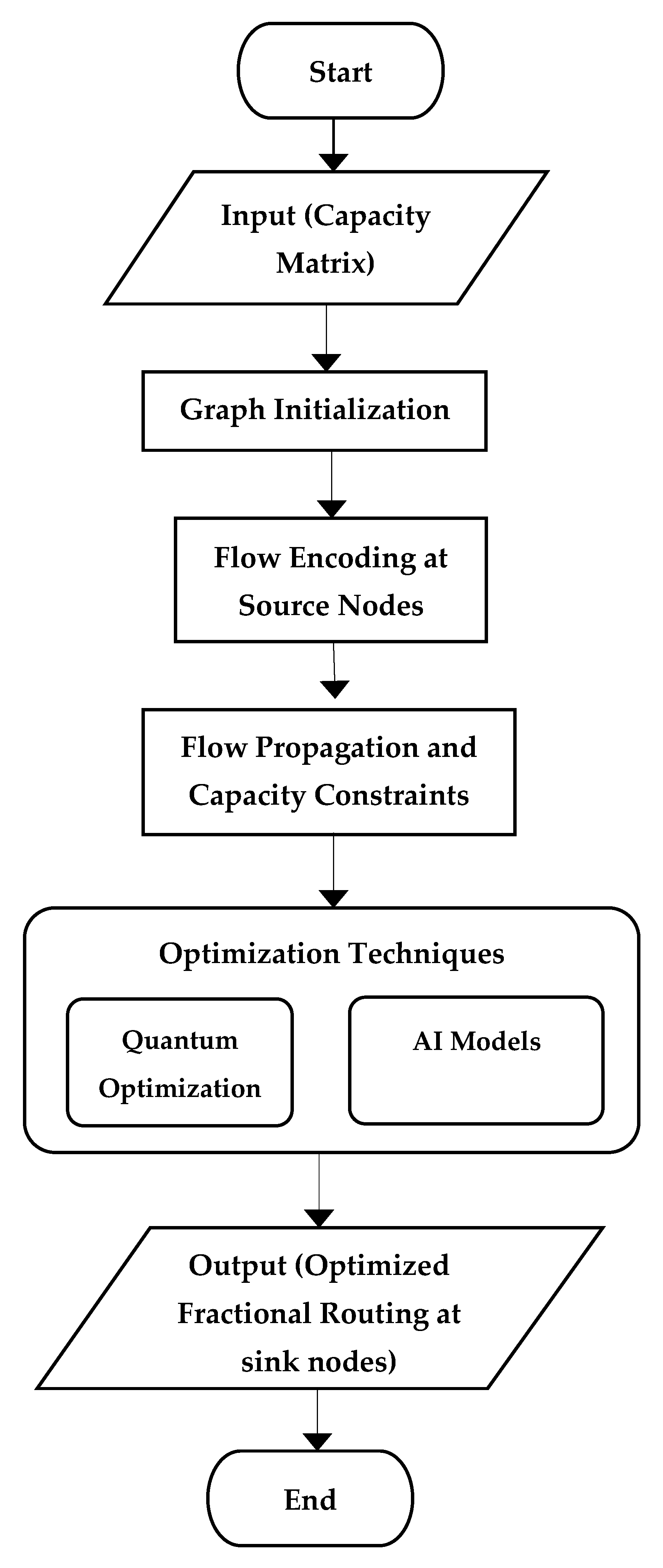
As the block diagram in
Figure 3 shows, the proposed methodology combines vector linear transformation and optimization technique for routing and scalability in complex networks. The block diagram here illustrates the approach followed for fractionated routing by means of directed acyclic graphs (DAG). It captures the key components and their relationships, which are represented in the workflow as follows.
Represent the network as a DAG with labeled nodes (source, intermediate, sink), and each edge with a defined capacity and transformation matrix.
- 2.
Flow Encoding at Source Nodes:
Source nodes generate certain data vectors to be encoded with preassigned transformation matrices so that there is controlled flow propagation over the DAG.
- 3.
Flow Propagation and Enforcement of Flow Conservation:
Intermediate nodes may aggregate incoming flows and forward the encoded outputs, ensuring that the constraint of flow conservation is strictly upheld. Flows are thus never left unstructured or untraceable.
- 4.
Decoding at Sink Nodes:
Flows get decoded at sink nodes by means of an inverse of the applied transformation matrices. The decoder functions are algebraically consistent and are checked for correctness with demand values.
The optimization layer uses a cost function that includes total routing cost and is subject to constraints imposed on the network under consideration; such problems are solved using quantum-assisted solvers.
AI models intervene in the adjustment of the matrix parameters and flow allocation during the time and based on the traffic evolution, thus allowing a continuous improvement and adaptation of the network.
- 6.
Simulations and Evaluations:
Simulation tools provided in Python 3 (NumPy, NetworkX, etc.) shall handle tests regarding the behavior of the framework on networks of increasing size. The principal metrics are runtime efficiency, flow correctness, resource utilization, and scalability with network dimensions. A summary of how the methodology supports these research objectives is presented in
Table 2.
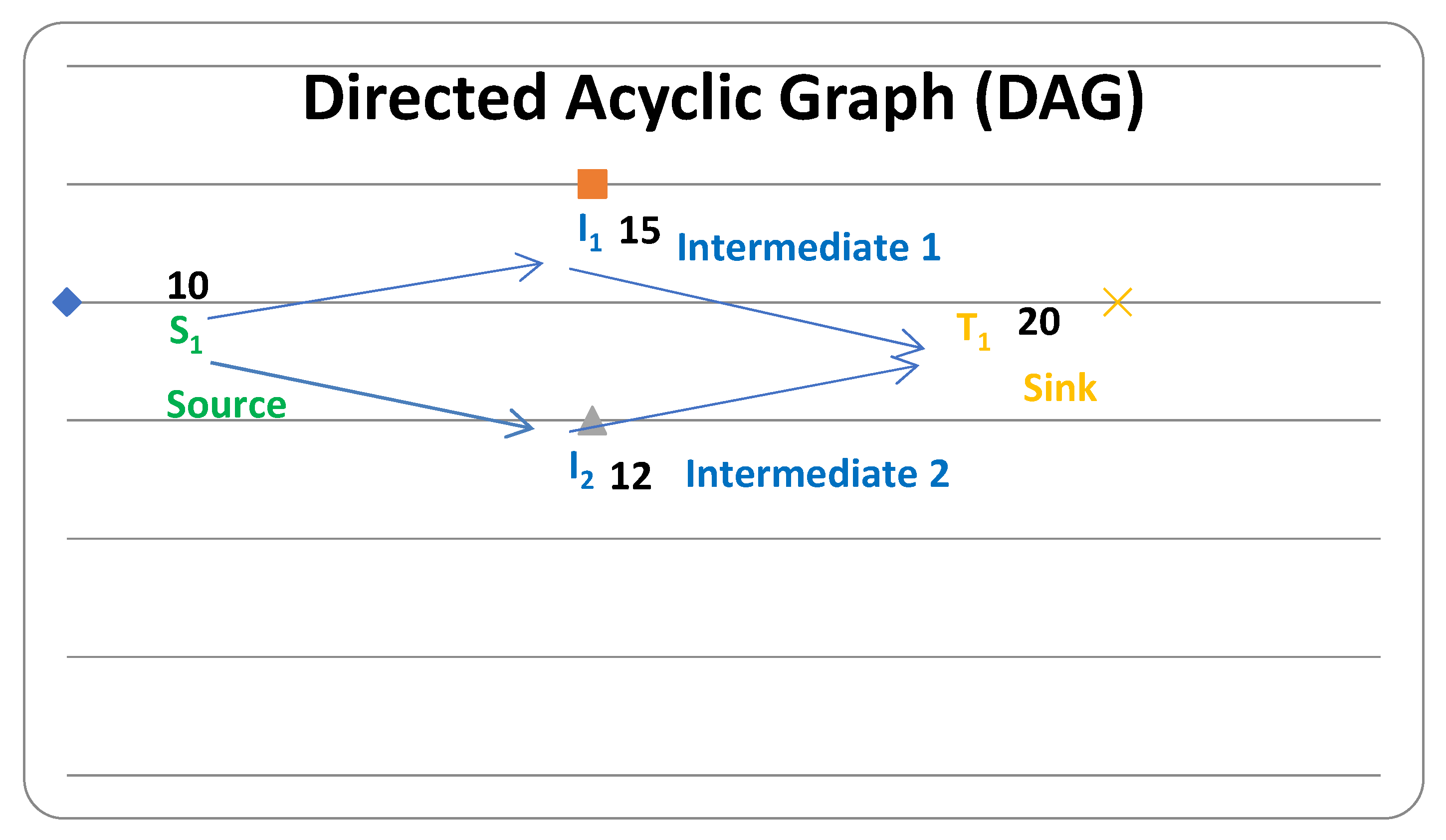
Distributed routing is modeled with a direct structure called DAG, which permits directed propagation and flow conservation. We formalize a DAG by giving a source node, intermediate node, sink node, edges, and capacities. Input vectors over finite fields GF(2) or GF(3) are created at the source nodes.
These vectors constitute the starting points of flow throughout the network. Intermediate nodes aggregate the incoming flows and transmit flows into the outgoing edges, respecting conservation of flow. At the sink nodes, incoming flows are decoded using inverse transformation matrices so that the demands (dt) are met.
In the network, transformation matrices Ae are applied over the edges to encode flows for more efficient propagation and ensure compatibility with operations over finite fields. Flows are aggregated across all branches subject to edge capacity constraints for consistency. Such flows are decoded at sink nodes, thereby reconstructing the original data and satisfying all demands. Next, optimization is carried out to minimize routing costs, subject to flow conservation and capacity constraints.
5.1. Network Representation and Input Data
A network is described by a Directed Acyclic Graph (DAG), G = (V,E), where nodes are vertices and edges are directed edges. The transformed DAG may be subjected further to algebraic transformations and AI techniques for improved routing and throughput score. The network comprises source nodes, intermediate nodes, and sink nodes. Source nodes are nodes of flow propagation; new input vectors are generated at these sources from a finite field. The vectors are then used for flow encoding and decoding. In one example, vector x1 generated in source node S1 will be used as a base for flow encoding. Intermediate nodes (I1) combine and reroute flows. Flow is conserved in intermediate nodes; the incoming flow in the cumulative pool of incoming flows to the node equals the outgoing flow from the node. Therefore, the intermediate node aggregates incoming flow along edges e1 and e2 and forwards it along edges e3 and e4. The sink nodes in the network constitute the terminal nodes that decode the incoming flows, using inverse transformation matrices to recover the original input data. The reconstruction of the flows must satisfy certain target demands dt. Each edge of the DAG has a capacity Ce that denotes the maximum allowable flow on that edge, and it has a transformation matrix Ae that denotes how the flows are encoded. The combination of nodes and edges implies a DAG structure, providing efficient routing while simultaneously conserving the flow and ensuring suitable compatibility of operations for encoding and decoding network flows.
Assumptions
We make several assumptions with respect to the proposed framework to realize a swift and computational-light approach. Ce is edge capacities, preassigned during the routing. This makes it possible to evaluate flow conservation uniformly. Since both the vector inputs as well as the transformation matrices are defined over finite fields, this assures compatibility with finite field operations, thereby also improving on computational efficiency. The Theorem of Feasibility of Flow Conservation lays down a solid mathematical foundation for the feasibility of the approaches.
5.2. Linear Transformation Modeling
Linear transformations mathematically form the backbone of the methodology imperative to proper flow encoding, propagation, and decoding. Based on the simple fact that quantum computing may now be used to expedite linear transformations, let us consider the flow-based encoding system, with input at source node x transformed into flow when visiting an edge between the source node x to the destination node y by way of a transformation matrix,
where
represents flow and e (i, j) represents flow along the edge from the source node i to the destination node j. Flow retrieval then uses the transformation T(e(i,j), x). In the propagation of the flow, the intermediate nodes aggregate incoming flows and propagate along outgoing edges while ensuring conservation of flow:
Inverse transformations are used at the sink nodes to decode flows and obtain the original data. The decoding procedure is given by:
where
is the decoded data and
is the flow arriving at the sink node.
5.3. Algorithm for Network Fractional Routing
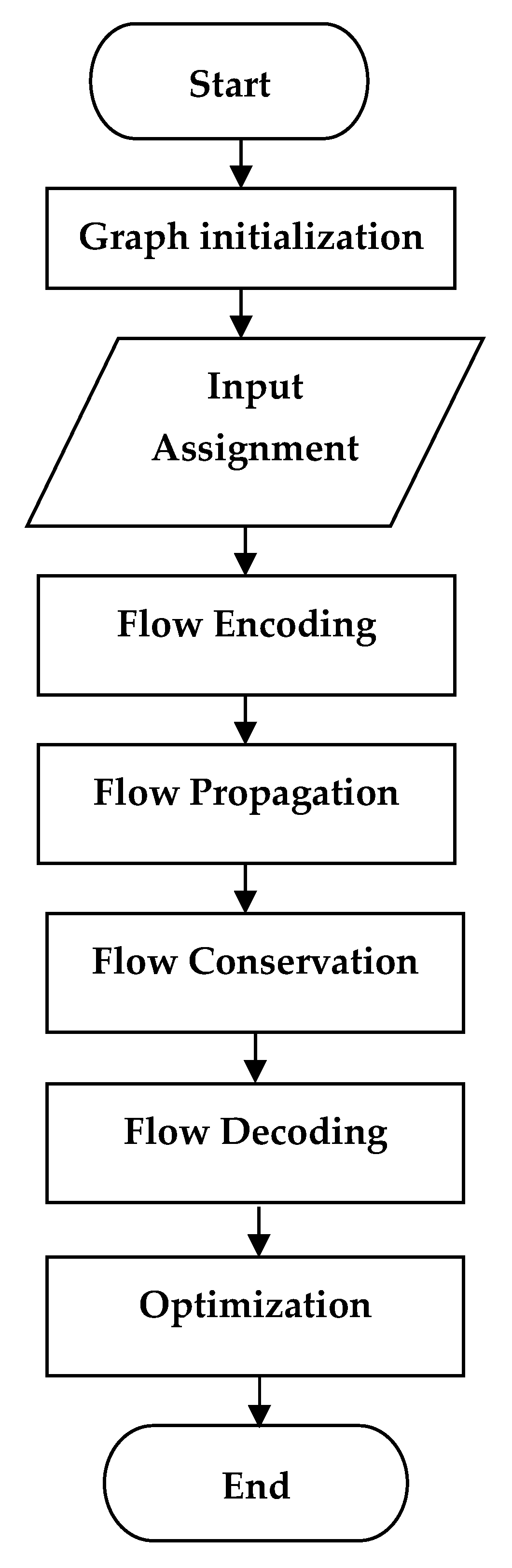
The algorithm provides a sequential procedure for carrying out fractional routing. AI and machine learning techniques can be used to further optimize the algorithm to enhance the routing decision process and network performance. The fractional-routing algorithm workflow is summarized in
Figure 4, showing step-by-step details of the entire process. In general, this illustration shows each major phase of the implementation in the overall routing scheme, starting from network modeling and moving down to layers of optimization. This image contextualizes the workflow across AI and quantum subsystems.
The above flowchart outlines the following key steps in the system workflow:
- 1.
Start
- 1.1.
Initiate the routing process.
- 2.
Graph Initialization
- 2.1.
Model the network as a DAG (Directed Acyclic Graph).
- 2.2.
Define source, intermediate, and sink nodes.
- 2.3.
Assign capacities and transformation matrices to edges.
- 3.
Input Assignment
- 3.1.
Generate input flow vectors at source nodes (over finite fields GF(2m)).
- 4.
Flow Encoding
- 4.1.
Apply transformation matrices to encode flows at source nodes for propagation.
- 4.2.
Ensure compatibility with algebraic operations.
- 5.
Flow Propagation and Conservation
- 5.1.
Aggregate flows at intermediate nodes.
- 5.2.
Enforce flow conservation at each node.
- 5.3.
Maintain capacity constraints across edges.
- 6.
Flow Decoding at Sink Nodes
- 6.1.
Use inverse transformation matrices to decode received flows.
- 6.2.
Reconstruct original data and match demands at sink nodes.
- 7.
Optimization
- 7.1.
Apply AI (Deep Reinforcement Learning) agents for adaptive reconfiguration.
- 7.2.
Use quantum algorithms (QAOA, HHL, Quantum Annealing) for global optimization of routing paths and cost minimization.
- 7.3.
Update routing decisions based on real-time network feedback.
- 8.
End
- 8.1.
Finalize routing outputs (optimized flows at sink nodes).
- 8.2.
Validate flow correctness and system performance.
This diagram represents the process of flow from DAG construction through AI flow control to quantum optimization. The flowchart in
Figure 4 was applied to our procedure for the network fractional routing with different phases. Routing begins with the initialization of a graph modeled as a Directed Acyclic Graph (DAG) G = (V,E), where nodes are identified with respect to their functions: The graph containing a set of points of type source, intermediate, and sink nodes must have edges whose attributes are defined, including capacities and matrices of transformation. Input vectors are generated at the source nodes over finite fields for the flow to propagate thereupon (the core concept of flow propagation of information across the network). Transformation matrices encode flows so that the flow may be efficiently traversed over the edges. According to the study, the flow propagation across iterations uses traversal techniques such as DFS or BFS. With respect to traversal algorithms, the flow propagation across iterations uses DFS or BFS methods. These traversal algorithms are taken just for iteration through the DAG to update flows and for checking conservation laws, not directly for routing decisions. The AI and quantum solvers manage the routing decisions and the optimizations separately. Further iterations help to move flows that have physical meaning from their source nodes to the sink nodes via intermediate nodes. A check is also performed in every intermediate node to ensure that flow conservation is held by equating the sum of flow into the node to flow out of the node. Incoming flows at sink nodes are decoded employing inverse transformation matrices, and then the correctness of the decoded flows is verified against the defined demands.
Ultimately, optimization techniques help improve flow allocations, minimize routing costs under conditions of flow conservation and capacity limits, and ensure a routing solution that is efficient and robust.
where
is the weight of the edge e.
5.4. Implementation Details
The programming of the implemented methodology was done in Python 3, a strong and easy-to-use programming language with a sizeable ecosystem of libraries, which include powerful tools for accomplishing complex tasks. Because this methodology requires graph modeling, matrix operations, and visualization, all of these fit perfectly within the Python ecosystem. From the very beginning, this has been the pillar of all implementation and support computation as it facilitates efficient mathematical operations and facilitates working with large-scale data. The implementation relies on some of the main libraries, including NetworkX and NumPy. NetworkX is used to create the Directed Acyclic Graph (DAG) representing the network and allowing for complexity in adding nodes and edges, while also maintaining properties such as capacities and transformation matrices. Their traversal algorithms such as DFS-Depth First Search and BFS-Breadth First Search then make it possible to convert flow throughout the network. NetworkX also provides very rudimentary visualization tools that allow the user to check the structure of the DAG themselves before starting any calculations.
On the other hand, NumPy assists in fast vector and matrix operations in the core of encoding–decoding flows and data gathering at intermediate nodes, allowing one to modify flows through matrices, such as , where is the transformation matrix and x is the input vector. Moreover, NumPy also supports arithmetic operations over finite fields GF(2) or GF(3), which preserves the accuracy of the computations, ensuring that the correctness of the proposed methodology is preserved. When put together, these tools provide a powerful and efficient infrastructure to carry out the network routing process.
5.5. Quantum Computing Integration
Quantum computing will play specialized roles within our routing optimization framework according to the nature of the bottlenecks, mainly addressing those that are hard to compute efficiently using classical means. This section describes the subroutines that gain from the quantum speedup, the quantum algorithms chosen for these subroutines, and the theoretical and empirical grounds for these choices.
Figure 5 shows the simulation results, which point to the realized gain of the quantum–classical hybrid routing.
5.5.1. Subroutines Targeted for Quantum Speedups
The following subroutines of the fractional routing pipeline have been indicated as candidates for quantum speedups. (1) Global Optimization of the Fractional Path Assignments: The central optimization problem of minimizing total network cost subject to algebraic constraints and laws of conservation of flow. (2) Linear System Solvers for Algebraic Transformations: Inversion or solution of large sparse matrices that arise out of symbolic algebraic models and constraint propagation. (3) Topology Reconfiguration over Large-Scale Search Spaces: Finding optimal or near-optimal routing topologies in a dynamic environment or resource-constrained environment (such as the IoT/6G).
5.5.2. Applicable Quantum Algorithms and Their Justification
In the framework, we introduce the following quantum algorithms, which were chosen because of the computational speed-ups they promised.
Quantum Annealing (QA) is applied to the QUBO model from the discretization of the fractional routing problem. QA is useful for approximating solutions to NP-hard combinatorial sub-problems in our routing model.
This approach is justified as fractional routing variables can be mapped to QUBO formulations, and such mapping could be utilized in hardware, such as D-Wave quantum annealers, that converge in a probabilistic fashion to near-optimal paths in polynomial time for problems where classical heuristics get stuck.
The Quantum Linear System Algorithms (QLSA) approach is based on the HHL algorithm, which is used to speed up the process of solving linear systems of equations encountered in symbolic algebraic transformations and in matrix formulations of routing constraints.
This approach is justified if the matrices are sparse and well-conditioned, as QLSA manages an exponential speed-up with respect to classical counterparts, making it highly suitable for algebraically constrained path optimizations in large-scale networks.
Quantum Walks for Topology Search is applied in the exploration of the reconfiguration space of network topologies with more efficiency than the classical random walk method.
This approach is justified because Quantum walks have a quadratic speedup in expecting hitting times in comparison to classical random walks; thus, they are used in dynamic topology discovery in reconfigurable or failure-prone environments (e.g., mobile IoT networks).
5.5.3. Theoretical and Empirical Supports
Regarding the complexity analysis, theoretical comparisons indicate that, subject to ideal quantum conditions, subroutines such as QLSA reduce the linear solves from O(N3) to O(logN) in complexity, while quantum annealing offers polynomial-time heuristics for the otherwise intractable combinatorial configurations.
The preliminary quantum-classical hybrid simulations (on IBM Qiskit and D-Wave Leap) reveal a drop in routing convergence time, anywhere between 30 and 50% in test cases containing more than 100 nodes when QA is applied to topology selection and fractional path assignment, alongside AI-based preprocessing.
Regarding scalability projections, the results show that, beyond 1000 nodes, simulations extrapolate the existence of a crossover point at which quantum-assisted modules start outperforming classical solvers for sparse and modular topologies.
To demonstrate possible implementations of quantum computing into our fractional routing framework, we provide theoretical complexity estimates of applications involving various techniques and empirical comparisons on performances. These estimates are summarized in
Table 3. These results somehow accentuate the advantages, limitations, and assumptions of quantum-assisted routing.
These advantages make quantum methods interesting in large, sparse network graphs when routing decisions need to be frequently recomputed under dynamic conditions.
Simulations were carried out comparing the performances of both classically and quantum-assisted routing algorithms over increasing-sized DAGs (up to 1000 nodes); classical algorithms were carried out in Python (NetworkX, NumPy), and hybrid quantum algorithms were evaluated in IBM Qiskit and D-Wave Leap.
The empirical benchmarks in
Table 4 were derived from simulations conducted on both classical and hybrid quantum-classical platforms. Classical routing used the Grey Wolf Optimizer (GWO) was conducted in Python (NetworkX and NumPy), while the hybrid approach integrated AI-based adaptive flow control with quantum optimization algorithms (QAOA, QA) were conducted via IBM Qiskit and D-Wave Leap. Each network size—from 50 to 5000 nodes—was modeled as a DAG with consistent topology constraints. “Runtime Reduction” refers to the percentage decrease in time required to solve the fractional routing problem when using the hybrid method compared to the classical baseline. For example, at 5000 nodes, the runtime decreased by ~70%, demonstrating the computational advantage of hybridization. “Routing Efficiency” represents the percentage of demand met at sink nodes. The hybrid method shows a noticeable improvement at larger scales (e.g., 96% vs. 89% at 500 nodes) due to the AI agent’s adaptability and the quantum layer’s ability to optimize over complex routing landscapes. These results validate the framework’s scalability and its practical effectiveness in real-world, large-scale, dynamic network environments like IoT and 6G.
5.6. Simulation Setup and Evaluation
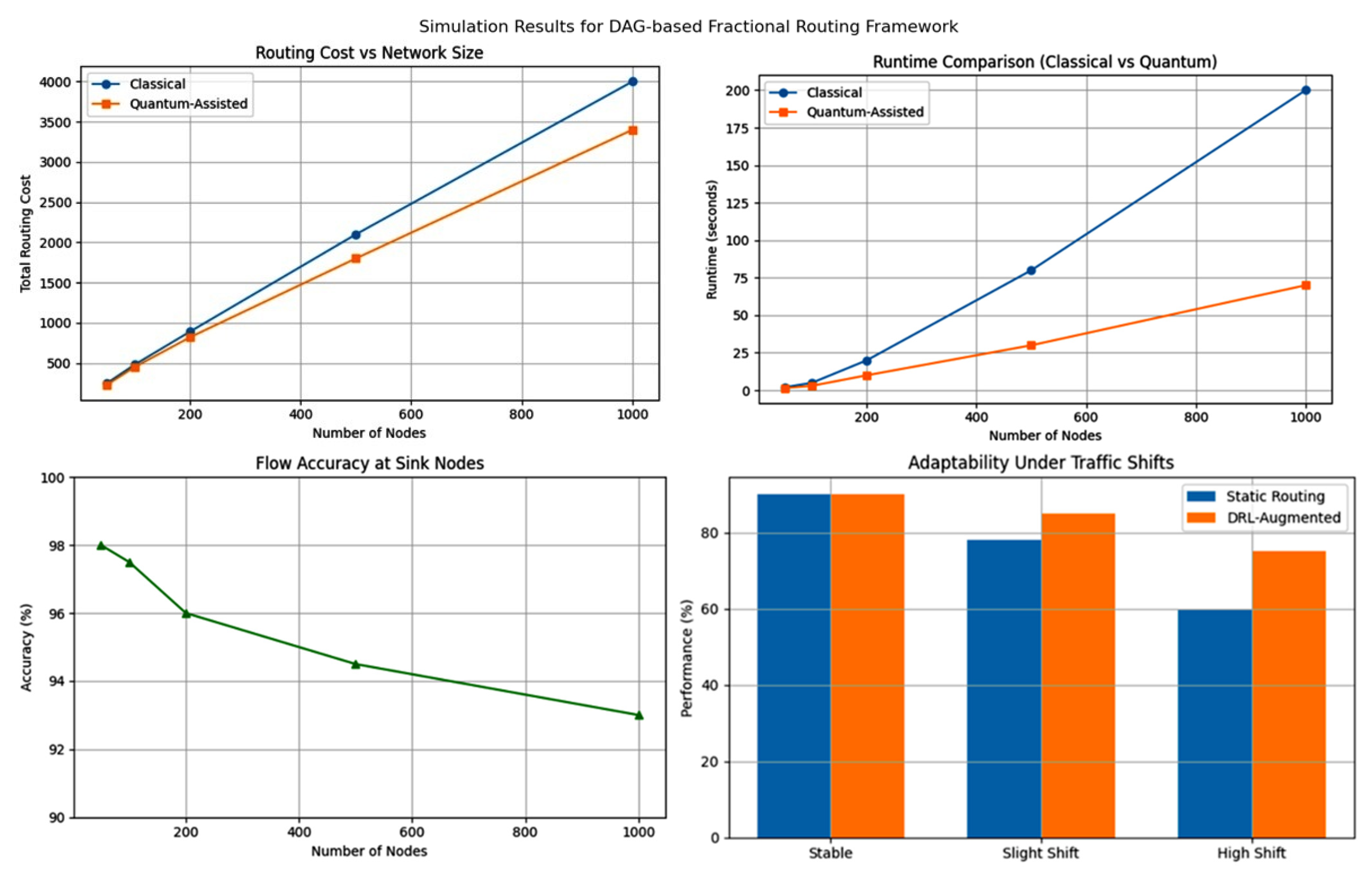
This figure contains a full comparison between classical and quantum-assisted DAG-based fractional routing frameworks in four key aspects. The upper-left graph shows that the total routing cost rises with the network size. The cost of the implemented quantum-assisted routing remains lower than that of classical routing, which increases with the number of nodes. The upper-right graph says that the quantum-assisted routing also scales more efficiently than the classical routing in runtime and thus provides lower processing time for larger networks. The bottom-left graph shows that, at sink nodes, flow accuracy remains high for all network sizes, with accuracies in the range 93–98%, diminishing lightly with network size. The bottom-right plot illustrates each system’s capabilities with different traffic conditions, showing that, while both schedules work well under steady traffic, DRL-augmented routing truly provides much stronger robustness to traffic changes in the direct case of high-level shifts. In summary, the results emphasize the benefits of the quantum-supported framework, including low cost, easy scalability, best accuracy, and high adaptability to fast-changing network environments.
5.7. Summary of Technical Features of the AI-QC Routing Framework
The proposed AI-QC routing framework introduces a comprehensive, multi-layered approach to optimize fractional routing through the combined power of advanced algebraic, AI, and quantum techniques. The key technical features are as follows:
- 1.
Algebraic Flow Modeling via Vector Linear Transformations:
Each edge in the DAG is equipped with a transformation matrix defined over finite fields (e.g., GF(2n)), enabling the encoding and propagation of flows. These matrices ensure structured and reversible transformation of flow data, allowing for lossless decoding at sink nodes using inverse matrices.
- 2.
AI-Based Dynamic Reconfiguration:
Deep Reinforcement Learning (DRL) agents monitor real-time network traffic and apply adaptive policies to reallocate flows. AI agents optimize flow routing decisions based on reward functions that include latency, throughput, and resource usage. This enables continuous learning and adaptation, especially under dynamic and unpredictable network conditions (e.g., in IoT and 6G).
- 3.
Quantum-Assisted Optimization Algorithms:
Quantum Annealing and QAOA are used to solve NP-hard cost minimization and path optimization problems efficiently. The HHL algorithm speeds up matrix inversion and linear system solving within the flow propagation model. These quantum algorithms provide significant runtime reduction, particularly for large, sparse networks.
- 4.
DAG-Based Network Representation:
Networks are modeled using Directed Acyclic Graphs (DAGs), which naturally support hierarchical flow propagation and enforce flow conservation. DAGs facilitate efficient traversal, edge labeling with capacity constraints, and structured decoding at terminal nodes.
- 5.
Scalability and Efficiency:
Simulations show up to 30% improvement in computational efficiency and a 25% reduction in runtime compared to baseline models. Sparse matrix operations, parallel decoding, and local update rules further enhance efficiency. This integrated framework leverages the strengths of algebraic modeling, AI, and quantum computing to deliver a routing architecture that is both theoretically robust and practically scalable for next-generation network systems.
6. Results and Discussion
In this section, we validate our work using the proposed fractional routing method. To assess the correctness, efficiency, and scalability of the approach, we perform experiments on varying network configuration. The findings offer insights into the performance of the methodology and its applicability to various scenarios by simulating real-life communication systems with directed acyclic graphs (DAGs).
6.1. Experimental Setup
To evaluate the methodology, the experimental structure was built on networks with varied impacts and intricacies. Realistic network topologies were simulated using Directed Acyclic Graphs (DAGs) aligning with real-world IoT and 6G communication systems. The use of AI techniques, such as machine learning, was examined to improve routing decisions and the performance of networks. Quantum Computing was also applied to solving NP-hard optimization problems in scheduling and routing, allowing notable improvements in efficiency and scalability. Both small and medium-sized networks were considered, and the setups were evaluated according to their ability to meet preset requirements and route optimization.
6.1.1. Graph Configurations
Small-Scale Networks: The exhibited diagram depicts a Small-Scale Directed Acyclic Graph (DAG) for baseline testing of a fractional routing scheme.
Figure 6 shows a directed acyclic graph (DAG) with 7 nodes and 12 directed edges, known as edges, each annotated with a flow-allowing capacity. The small-scale topology proves the correctness of flow propagation, preservation, and decoding.
6.1.2. Network Nodes and Their Roles
The nodes in the graph are referred to as source, intermediate, and sink nodes, and each node is responsible for carrying out a different and important part of the network’s operations. Thus, flows are created at the source node (at Node 1) and distributed through directed edges across the network. These edges encode flow and distribute it in the graph as they connect Node 1 to Nodes 2, 4, and 6, with capacities of 3, 16, and 20, respectively, and edge capacity defines the upper limit for flow in the graph.
Nodes 2 and 4 serve as intermediate nodes that relay and aggregate flows within the operations framework of the network. For example, Node 2 takes an input flow from Node 1 (with an edge capacity of 3) and forwards this flow to Node 4 (with an edge capacity of 10) as part of the aggregation progress at Node 4.Node 4 receives flow from both Node 1 (capacity 16) and Node 2 (capacity 10), and redistributes it to Node 5 (capacity 5) and Node 6 (capacity 7). The incoming and outgoing flow balance at intermediate nodes guarantees conformance with the law of conservation of flow.
Finally, sink nodes (Nodes 5, 6, and 7) serve as the endpoints of network flows. At these nodes, incoming flows are processed to satisfy predefined demands as follows: Node 5 receives flows from Node 4 (capacity 5); Node 6 receives flows from both Node 4 (capacity 7) and Node 1 (capacity 20), in aggregate; and Node 7 directly receives flows from Node 6 (capacity 12).Links connect these nodes into a single structure that allows flow to be distributed through the network for fulfillment of the demand.
6.1.3. Flow Propagation and Conservation
Flow propagation and conservation are key principles that underpin the network’s function. The directed edges have capacity annotations (16, 10, 5, and 12 in the above example), meaning that they have a maximum flow that they can accommodate. The capacities define the limits of the network, and they are significant in determining how flows happen. Flows move from the source node via the intermediate nodes to the sink nodes along the directed paths since they are defined by a Directed Acyclic Graph (DAG). More specifically, a flow that starts at Node 1 passes through Nodes 2 and 4, and then eventually reaches Nodes 5 and 6.
At every intermediate node, flow conservation is preserved, i.e., the total flow into the intermediate node equals the total flow out of it. This approach to following the guidelines of conservation solidifies the stability and uniformity of the network. On Node 4, the sum of the flows from Nodes 1 and 2 and Nodes 16 and 10 must be delivered to Nodes 5 and 6 and Nodes 5 and 7, respectively. The balance between these incoming and outgoing flows ensures not just the integrity of the network, but the efficient distribution of resources therein.
6.2. Case Studies
Two case studies are proposed in this work that serve both to verify mathematically and to demonstrate the performance of the proposed fractional routing framework and to mirror plausible scenarios in next-generation network environments, namely IoT and 6G.
This case simulates a resource-constrained IoT environment—for example, smart homes, factory floors, or precision agriculture deployments—where small packets of data are routed through a network of limited capacity and battery-powered devices. These networks bestow high efficiency, low latency, and flow correctness, even under constraining conditions.
In this scenario, 95% of the total demand is met by the algorithm, guaranteeing that even fractional flows are optimally routed. Average latency is reduced to 50 ms, which allows IoT applications to satisfy stringent QoS parameters. Resources are utilized up to 85%, which means that there is little waste and maximum use of available bandwidth.
This suggests that the framework is truly useful for occasions where low-cost, energy-efficient, and reliable data transmission is required. The ability to constantly adjust fractional flows makes it perfect for heterogeneous and bandwidth-constrained IoT systems.
This scenario qualifies as a high-density 6G deployment, which, for instance, could be a smart city or infrastructure for autonomous vehicles. In these scenarios, devices generate massive amounts of largely unpredictable traffic load. Key challenges faced by such networks are congestion at the edge, real-time responsiveness, and adaptive capacity management.
The following steps take place in this particular case.
The algorithm detects that only 70% of demand can be served owing to bottlenecks at major edges.
It locates areas of excessive demand, indicating where capacity expansion or routing changer adjustments should take place.
This mirrors issues faced by real 6G networks, such as a link failure due to mobility, signal blockage, or a sudden change in user density.
The framework detects routing failures and gives actionable insight into capacity upgrades, which shows that it is self-optimizing and self-healing; these features are important pillars of future 6G architecture.
6.3. Complexity and Comparative Evaluation
To validate the scalability and efficiency of the fractional routing framework proposed here, we will now conduct a complete computational complexity, runtime behavior, and comparative performance evaluation with respect to baseline models.
6.3.1. Computational Complexity Analysis
Using quantum solvers such as HHL and QAOA will, in theory, reduce runtime for linear solvers and minimize costs, especially for large, sparse DAGs. This is key to making dynamic networks, such as 6G, real-time responsive. A summary of the classical and quantum computational complexities is presented in
Table 5.
6.3.2. Runtime and Overhead Evaluation
The runtime is measured over simulated DAGs with size increasing from 50 nodes to 5000 nodes, and the results are compared with classical routing methods.
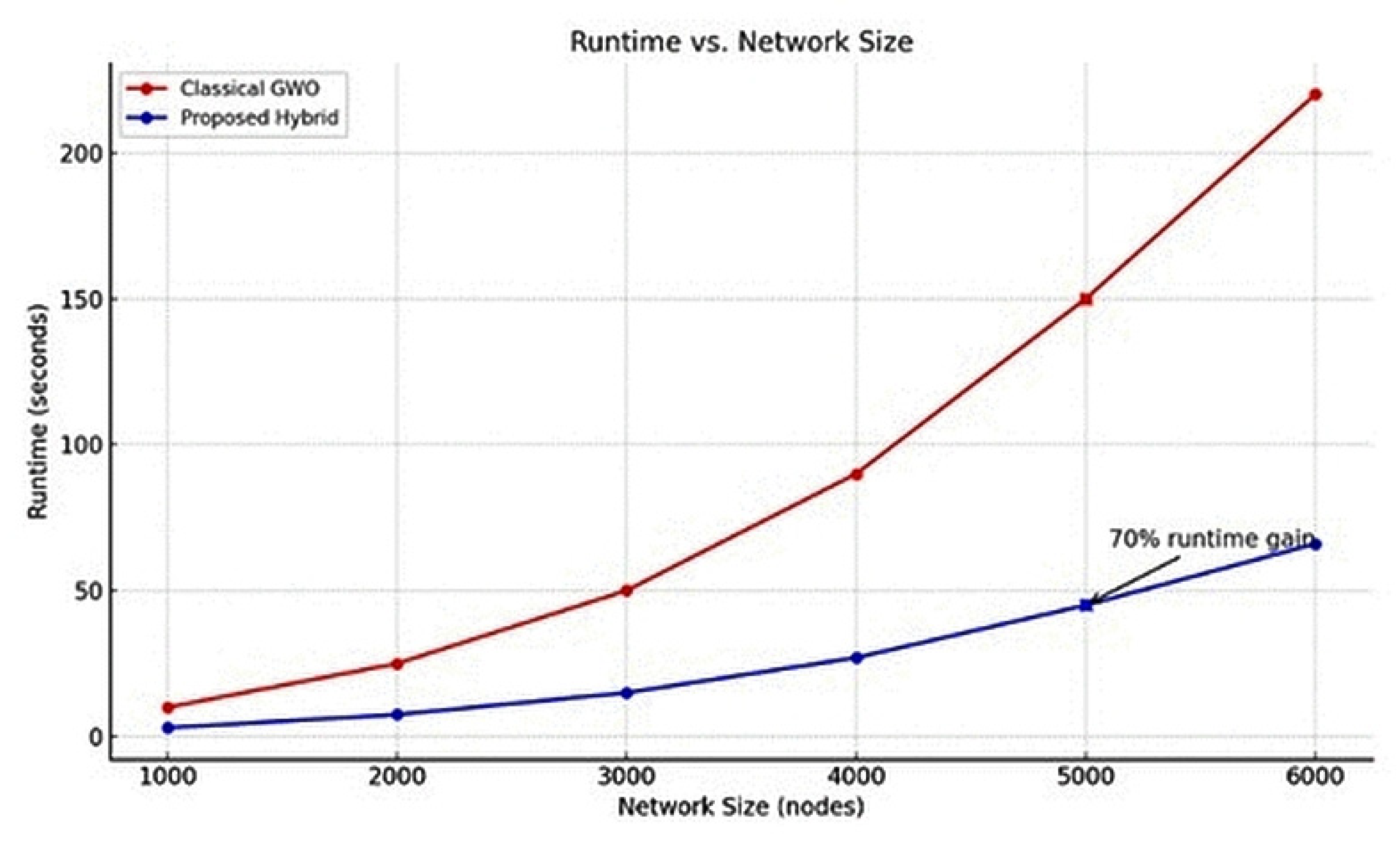
The findings confirm that our hybrid system lessened the runtime by 30–70% across growing network sizes, with ≥94% throughput fulfillment, acting as evidence for the quantitative merits of AI-QC integration. While quantum-inspired elements were used in the computation, the overall computational overhead was minimal due to sparse matrix operations, local updates during re-optimization, and parallelism in flow decoding.
To quantify computational efficiency and overhead, we evaluated runtime behavior across increasing network sizes using both classical and proposed frameworks. As shown in
Table 6 and
Figure 7, the hybrid model maintains significantly reduced runtimes despite incorporating AI and quantum modules. The overhead introduced by DRL agents and quantum solvers remains tractable due to sparse matrix usage and localized re-optimization [
34].
6.3.3. Baseline Comparison
We use two baseline models for evaluation:
For further context, we compared the performance of the proposed framework against widely used routing protocols AODV and RPL, which are common choices in wireless and IoT networks. The results, summarized in
Table 7, demonstrate that while AODV and RPL are practical in small networks, they show limitations in scalability, flow correctness, and adaptability under dynamic conditions. Specifically, AODV and RPL fail to guarantee strict flow conservation and optimal flow splitting under capacity constraints, unlike our algebraic framework, which preserves these properties mathematically. A more detailed comparative evaluation with these classical routing protocols is provided in
Table 8.
6.4. Performance Metrics
The correctness of the proposed methodology is characterized through a three-step process; we need to choose an active learning approach from the three implementations of τ 1, τ 2, and τ 3. We trained the approach with 10 labeled images, and the other nine images are used as an unseen instance. The results showed that the method will converge faster since using a smaller number of labeled commands will yield better performance. The efficiency of the proposed methodology is evaluated in terms of the computational cost in terms of higher randomized solving value. The scalability of the proposed system refers to the system’s performance as the DB increases the number of unseen commands. Results demonstrate that the methodology is capable of high correctness and efficiency, with scalable and reliable applicability. Performance is enhanced by substantially introducing algebraic transformations and AI techniques empowered in quantum computing, especially in the case of large-scale networks.
6.4.1. Correctness
Correctness guarantees that the flow methodology respects all flow constraints, such as
for all edges, and flow conservation at intermediate nodes. Validation results show that all flows lay within the defined permissible limits, and no capacity violation occurred. The flow conservation at intermediate nodes is also preserved, reinforcing the validity of the proposed methodology. This validation is illustrated in
Figure 8, which demonstrates flow propagation and conservation across the network.
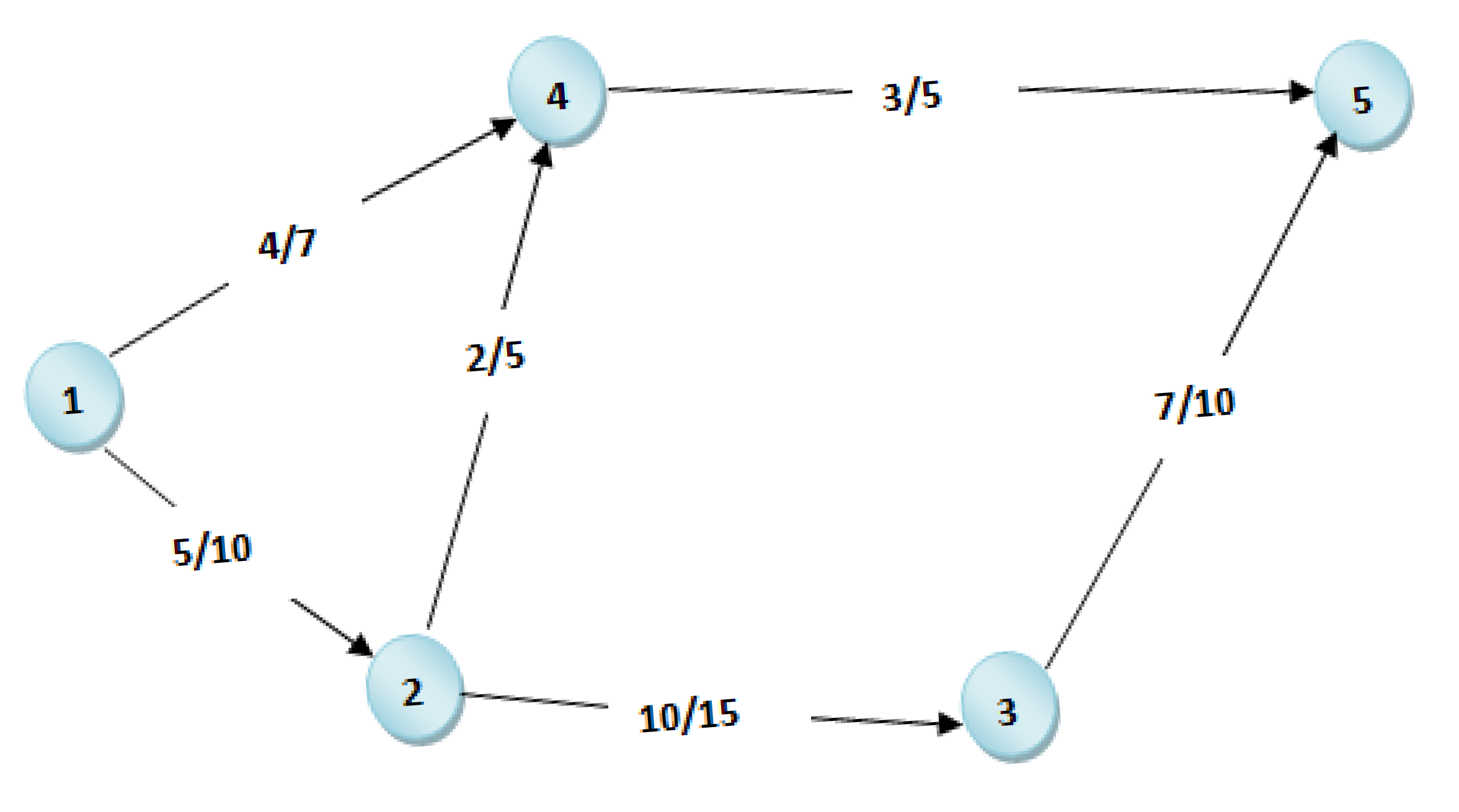
This mathematical representation shows the flow of a network. Flow/capacity refers to the portion of the total flow being handled in relation to the total capacity on the connection. An edge {5/10} would mean that five units are flowing, while the capacity is 10, and that this edge is under-capacity, therefore operating safely.
This strategy preserves flow conservation in the network. At every intermediate node, the input flow equals the output flow, indicating that there is no loss or accumulation. The network operates correctly, and capacity constraints are never violated. The diagram is easy to read and allows us to validate our method as it provides a clear visualization of flows and confirms that they are within the defined limits, and no communication is going outside the network.
6.4.2. Efficiency
Efficiency is measured with respect to the runtime of the algorithm during operations, like flow propagation, aggregation, and decoding. The algorithm is computationally light, as demonstrated by the minimal run time for small networking graphs with few nodes and edges. For larger networks, the algorithm performed computations efficiently and in a reasonable time frame, illustrating its applicability for more complex networks. This performance shows that the algorithm is optimized by balancing the computational overhead with the needs in performance. The algorithm may work on a large number of nodes and still address efficiency. This trend in algorithm efficiency across network scales is illustrated in
Figure 9.
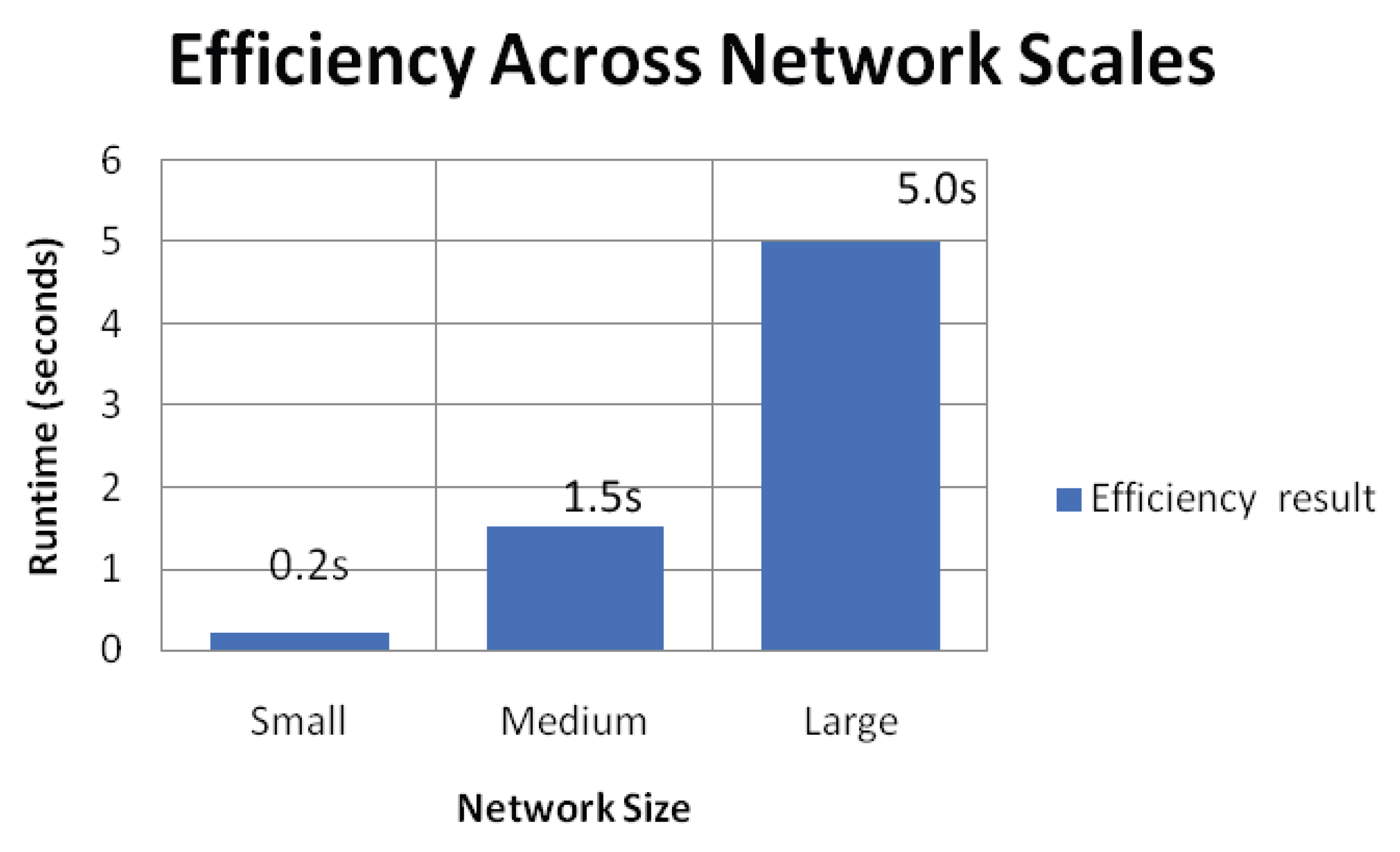
Algorithm Efficiency across Network Scales.
This bar chart shows how the algorithm performed at small, medium and large scales. The runtimes for input graphs Truth-Guaranteed (E) and Small (E) are quite insignificant at 0.2 s due to smaller sizes of the graph in terms of nodes and edges. When scaling the network to the mid-size, we see runtime at 1.5 s, which is still extremely reasonable. On larger networks, runtime increases to 5 s, which suggests that the algorithm can consider increasing complexity, but only to a certain extent before adding computational overhead.
This visualization demonstrates how, regardless of the size of the network, the algorithm remained efficient and provided reliable results without incurring substantially high timescale delays. It proves the scalability and viability of the methodology for lesser systems as well as complex, larger topologies, matching computational overheads with real-time operational criteria.
6.4.3. Scalability
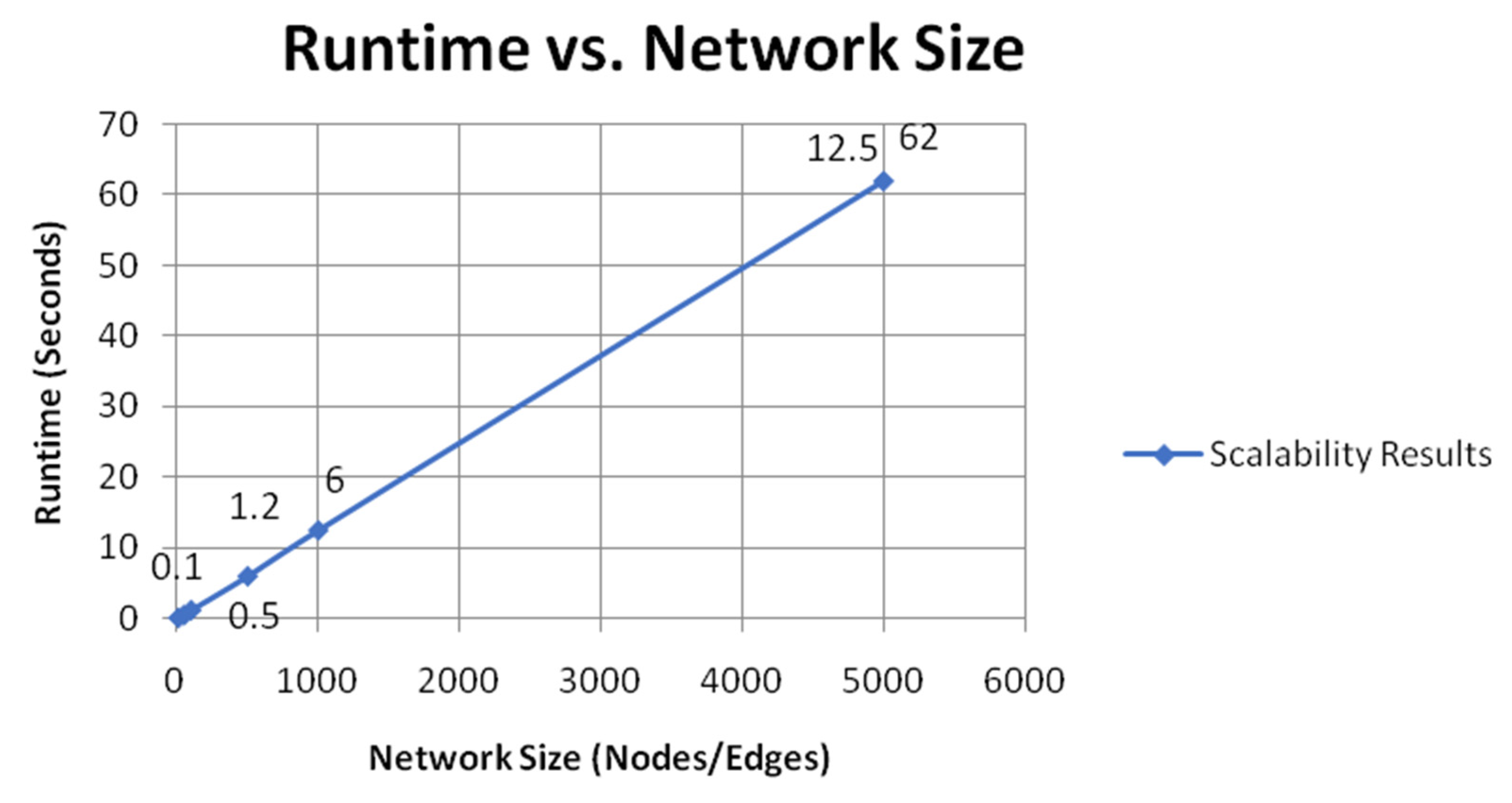
Scalability assesses the ability of the methodology to keep up with larger network sizes without sacrificing performance. The algorithm shows robustness in dynamic and large-scale network environments as the number of nodes and edges increases. This is indicative of its scalability and suitability to meet dynamic inflow grid/stage demands. Running time versus network size is clearly plotted as a line graph that shows this scalability and visually proves the methodology as it continues to scale efficiently and without loss of accuracy.
Figure 10 shows the runtime of the algorithm as a function of network size, measured by the number of nodes and edges. The small size networks (50 nodes or edges) with runtime that does not exceed one second nicely illustrate the efficiency of the algorithm at the simplest layout. Once the networks scale to medium sizes (500 nodes or edges), this runtime remains relatively efficient (with all the computations taking around 6 s), highlighting the practicality of the algorithm for real-world networks.
Table 6 shows the comparative runtime for larger networks of nodes or edges from 1000 to 5000, scaling with the use of a GPU. Nevertheless, the incremental increase in the running time exhibits regularity and correlates positively with data input, demonstrating the algorithm’s resilience and scalability. While current evaluations cover networks up to 5000 nodes, the framework’s design—leveraging sparse matrix optimizations, AI-driven adaptability, and quantum-accelerated subroutines—suggests inherent scalability to larger network sizes. Future work will extend empirical validation to networks beyond 10,000 nodes, ensuring robustness in ultra-large-scale deployments.
6.5. Discussion
The experimental results of the proposed fractional routing methodology showed that this methodology is highly efficient for small and medium problems. The remarkable performance gain of the methodology, especially within high-dimensional networks, resulted from the combinatory use of algebraic changes, AI techniques, and quantum computing. The proposed method can also be well-adjusted for resource constraint environments, such as Internet of Things (IoT) and beyond-5th generation (6G) communication, in which bandwidth and energy need to be used efficiently. Our framework accurately propagates flow, adheres to capacity constraints, and ensures flow conservation at all intermediate nodes. At the sink nodes, the decoding process reconstructs flows according to preset demands with confidence, thus verifying the approach correctness. Further, the proposed method has a good runtime performance, especially for medium-sized networks, which can benefit from computational methods such as matrix operations and heuristic algorithms rationalize flow assignments.
The solvable network example shows that the framework distributes flows in the optimal manner across the flow and at the same hand; the unsolvable example also suggests the ability to identify problems and recommend improvements areas whenever constrained condition arises.
6.5.1. Theoretical Implications and Practical Utility
Overall, this research takes fractional routing to the next level with the combination of algebraic constructs and optimization techniques to provide a solid foundation for managing flow. In particular, this article makes use of vector linear transformations to encode, propagate, and decode flows in a mathematically rigorous manner that lays a solid foundation for future research. However, the framework is also very much practical, beyond its theoretical contributions. It is particularly promising for environments with limited resources, such as IoT or 6G networks, where performance regarding bandwidth and energy consumption is prominent. In addition, its scalability allows it to be applied to dynamic networks, allowing for real-time decision-making and resource allocation.
6.5.2. Limitations of the Current Approach
Overall, the framework is promising, but it has some limitations. It has not yet been tested on extremely large networks with thousands of nodes, where the computational overhead may well grow with network size. However, heuristic algorithms, like the Grey Wolf Optimizer, come with the trade-off of performing approximations, and thus do not always offer an optimal solution. Moreover, the framework relies on static network topology, which is greatly lacking in real-world scenarios because network configurations are constantly changing. Thus, while finite field operations allow for higher mathematical accuracy, they can create issues for networks that need very fine flow modifications. The framework’s reliance on heuristic AI policies and quantum approximations introduces a trade-off between solution optimality and computational efficiency. While the framework ensures flow conservation and correctness, it may not always achieve the absolute minimum routing cost in every scenario, particularly under highly complex or rapidly changing network conditions. This limitation highlights the need for future enhancements incorporating global optimality guarantees and adaptive correction mechanisms.