Symmetry-Guided Electric Vehicles Energy Consumption Optimization Based on Driver Behavior and Environmental Factors: A Reinforcement Learning Approach
Abstract
1. Introduction
- The development of an integrated framework that simultaneously considers driver behavior patterns, road conditions, and environmental factors using contrastive learning for state representation and graph attention networks for contextual modeling;
- The implementation of a hierarchical reinforcement learning approach that combines scenario-based adaptation with fine-grained control optimization is demonstrated using data from 3395 high-resolution charging sessions across diverse driving environments;
- The introduction of a real-time optimization strategy that dynamically adjusts vehicle parameters based on predicted energy consumption patterns, achieving an average 17.3% improvement in energy efficiency compared to baseline methods while maintaining driver comfort preferences.
2. Related Work
2.1. EV Energy Consumption Prediction
2.2. Driver Behavior Analysis
2.3. Environmental Factors
2.4. Reinforcement Learning for Energy Management
2.5. Advanced Representation Techniques
3. Preliminaries
3.1. Problem Formulation
3.2. Reinforcement Learning
3.3. Contrastive Learning
3.4. Graph Attention Networks
4. Methodology
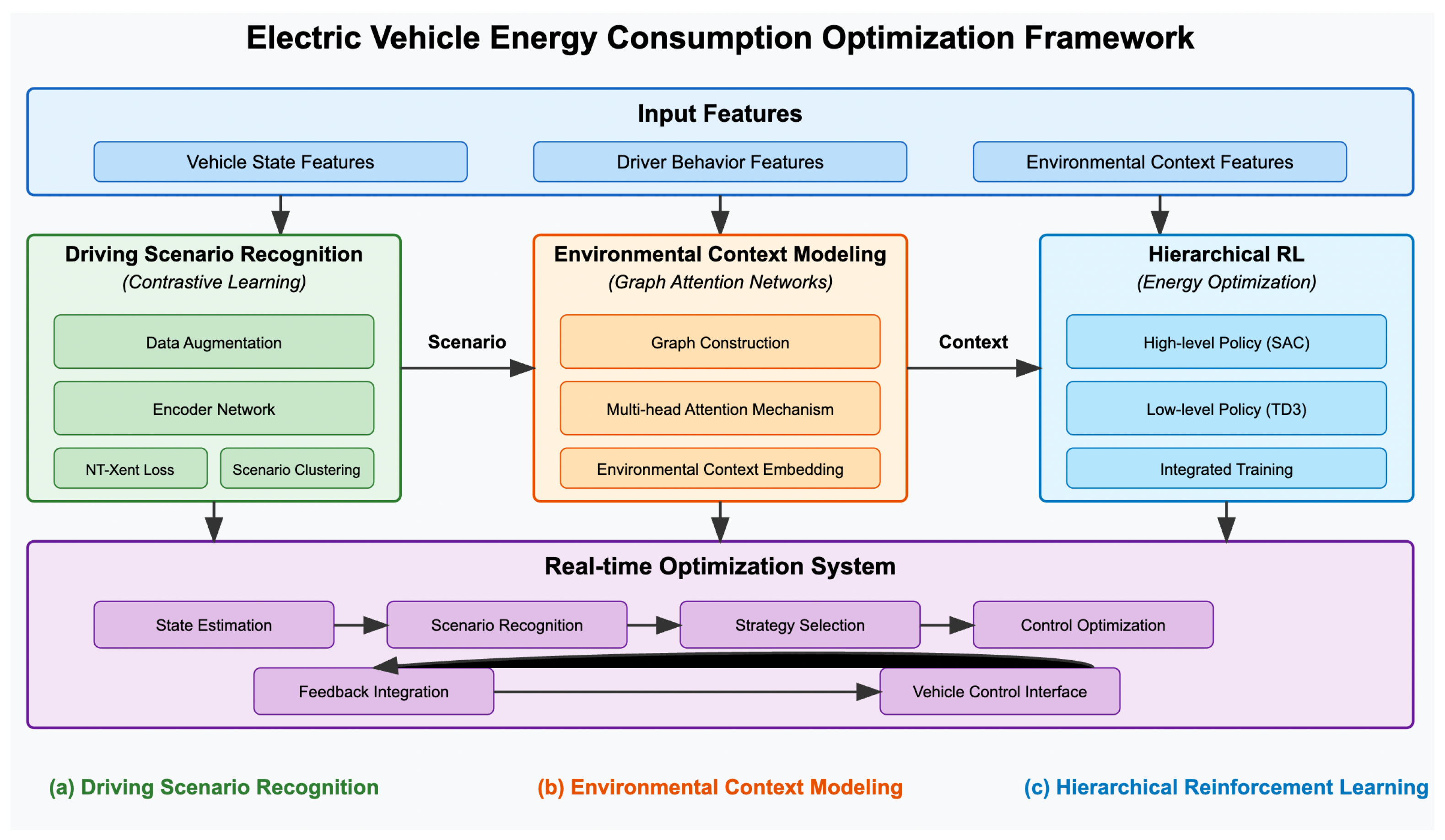
4.1. Framework Overview
4.2. Input Feature Representation
4.3. Driving Scenario Recognition via Contrastive Learning
| Algorithm 1 Contrastive Learning for Driving Scenario Recognition |
Require: Driving state dataset , batch size B, temperature Ensure: Trained encoder and classifier 1: Initialize encoder and classifier 2: for each training epoch do 3: for each batch of size B do 4: for to B do 5: Generate augmented views: , 6: Compute embeddings: , 7: end for 8: Compute NT-Xent loss using Equation (5) for all positive/negative pairs 9: Update via backpropagation 10: end for 11: end for 12: Apply k-means clustering on learned embeddings to identify K scenarios 13: Train classifier to map embeddings to scenario labels |
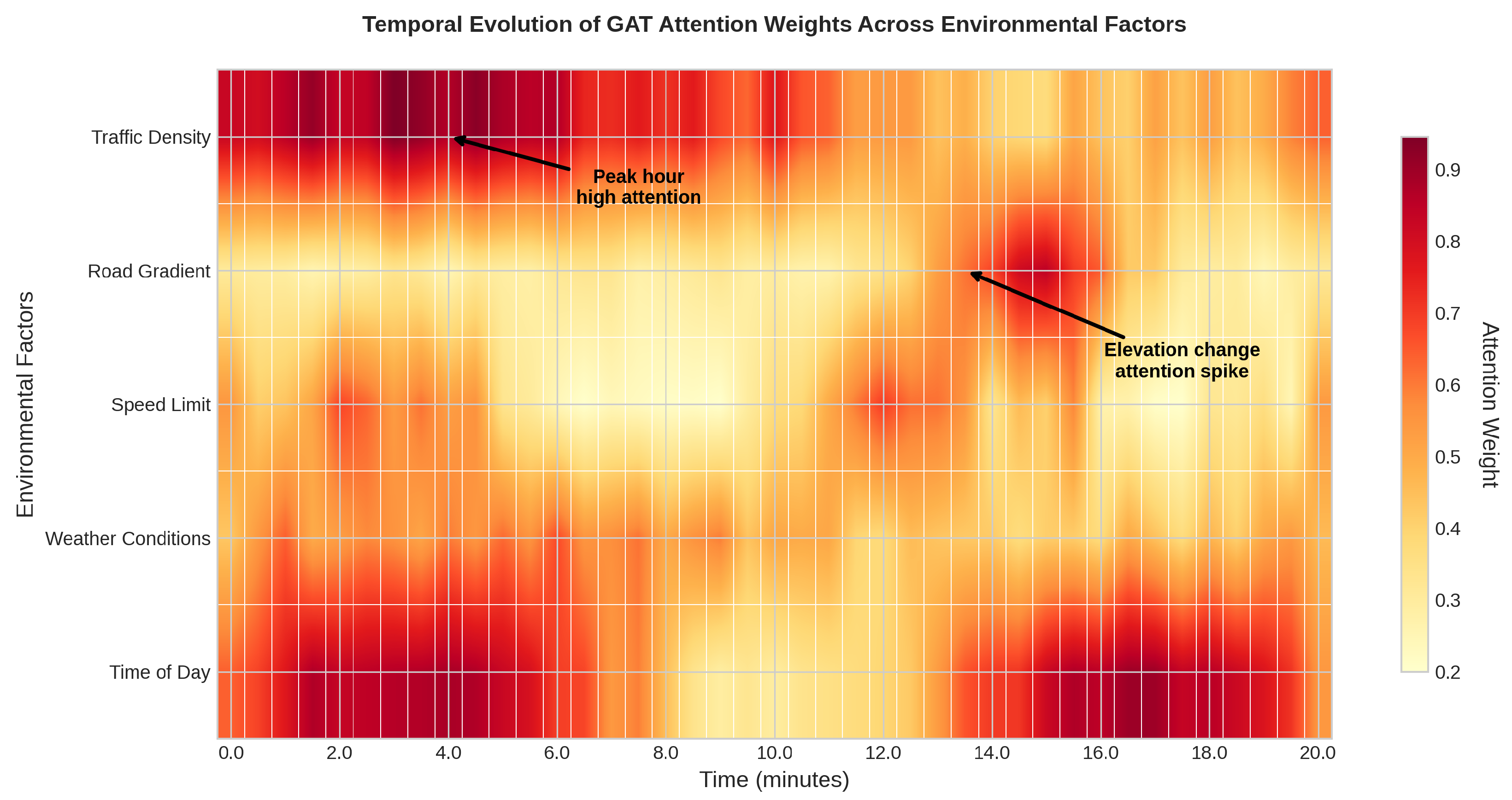
4.4. Environmental Context Modeling with Graph Attention Networks
| Algorithm 2 Graph Attention Network for Environmental Context |
Require: Graph , node features , number of heads K Ensure: Environmental context embedding 1: Initialize attention parameters 2: for each attention head to K do 3: for each node do 4: for each neighbor do 5: Compute attention score: 6: end for 7: Normalize attention weights: 8: Update node features: 9: end for 10: end for 11: Concatenate multi-head outputs: 12: Apply readout function: |
4.5. Hierarchical Reinforcement Learning for Energy Optimization
| Algorithm 3 Hierarchical Reinforcement Learning for Energy Optimization |
Require: Initial state , high-level policy , low-level policies Ensure: Optimized energy consumption 1: Initialize experience buffers for high-level and low-level policies 2: for each driving episode do 3: , 4: while episode not terminated do 5: if then 6: Recognize scenario: 7: Get environmental context: 8: Select strategy: 9: end if 10: Select action: 11: Execute action and observe: 12: Store transitions in respective buffers 13: if buffer sufficient then 14: Update using SAC (Equation (16)) 15: Update using TD3 16: end if 17: 18: end while 19: end for |
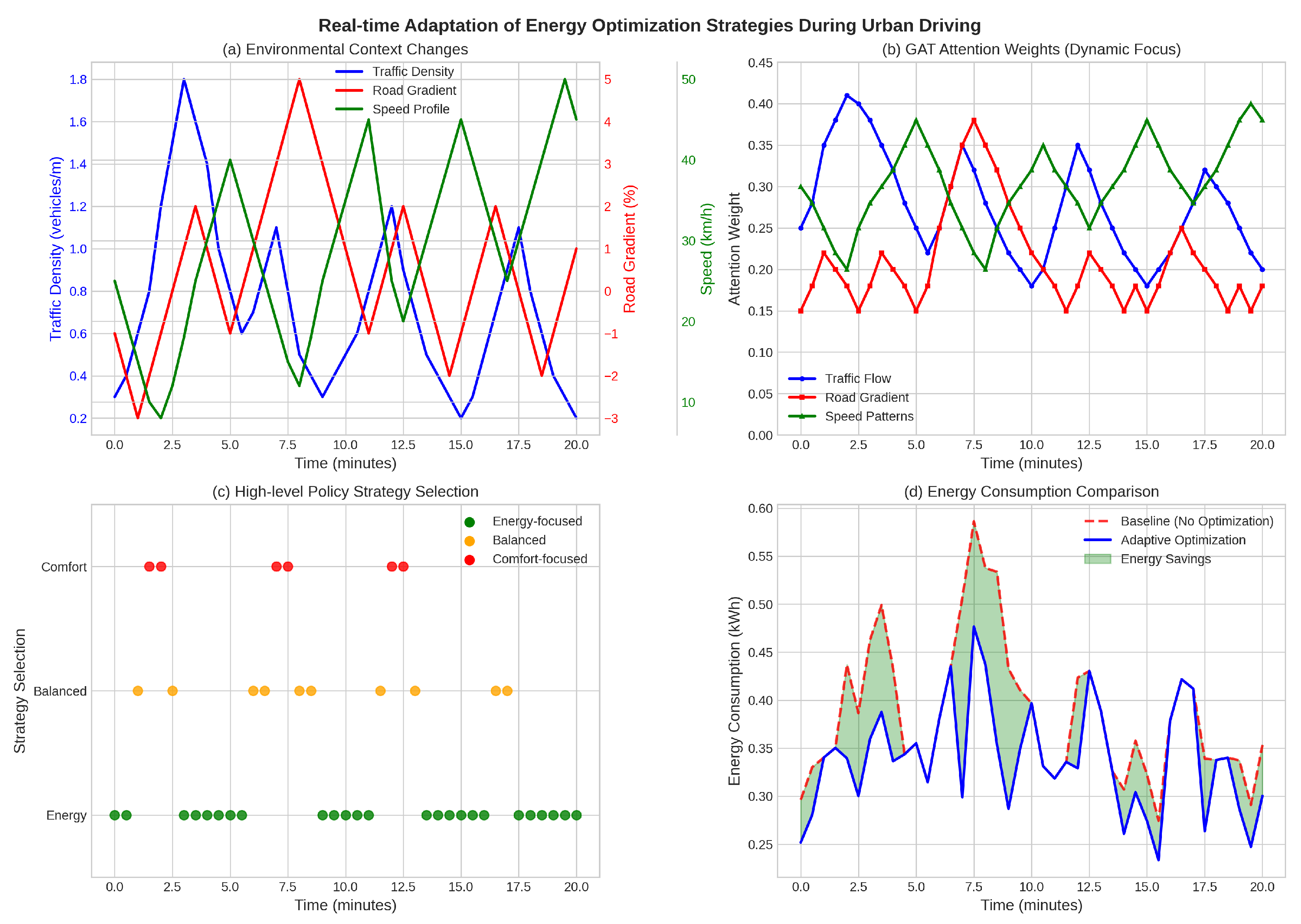
4.6. Real-Time Optimization System
5. Experiments
5.1. Experimental Setup
5.1.1. Dataset
5.1.2. Baseline Methods
- Deep Q-Network (DQN) [7]: A reinforcement learning approach that learns control policies to optimize energy usage based on a discretized action space;
- Soft Actor-Critic (SAC) [21]: A state-of-the-art reinforcement learning algorithm that learns a stochastic policy for continuous control of energy management systems;
- Graph Convolutional Network (GCN) [20]: A neural network that operates on graph-structured data, modeling road networks and their influence on energy consumption;
- LSTM-Attention [6]: A recurrent neural network architecture with an attention mechanism designed to model temporal sequences and dependencies in driving patterns for energy prediction.
5.1.3. Evaluation Metrics
- Energy consumption reduction (ECR): The percentage reduction in energy consumption compared to a baseline driving strategy:
- Mean absolute error (MAE): The average absolute difference between predicted and actual energy consumption:
- Root mean square error (RMSE): The square root of the average squared differences between predicted and actual energy consumption:
- Coefficient of determination (R2): A statistical measure that represents the proportion of variance in energy consumption that is predictable from the input features:
- Driver comfort score (DCS): A measure quantifying the impact of energy optimization on driver comfort, derived from user studies.
5.2. Implementation Details
5.2.1. Software and Hyperparameters
5.2.2. Computational Requirements and Time Consumption
5.3. Results and Analysis
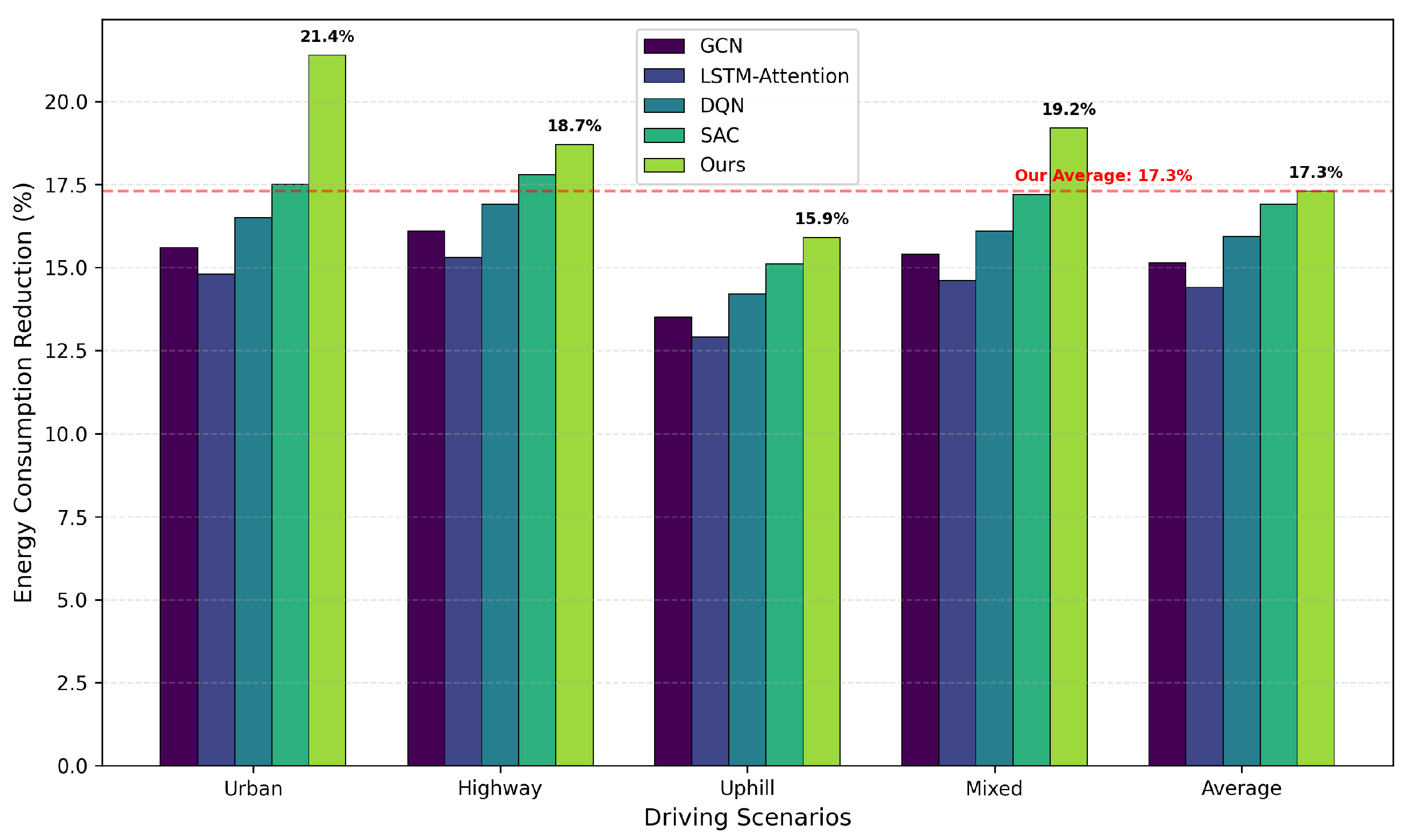
5.3.1. Energy Consumption Reduction
5.3.2. Comparison with Theoretical Performance Limits
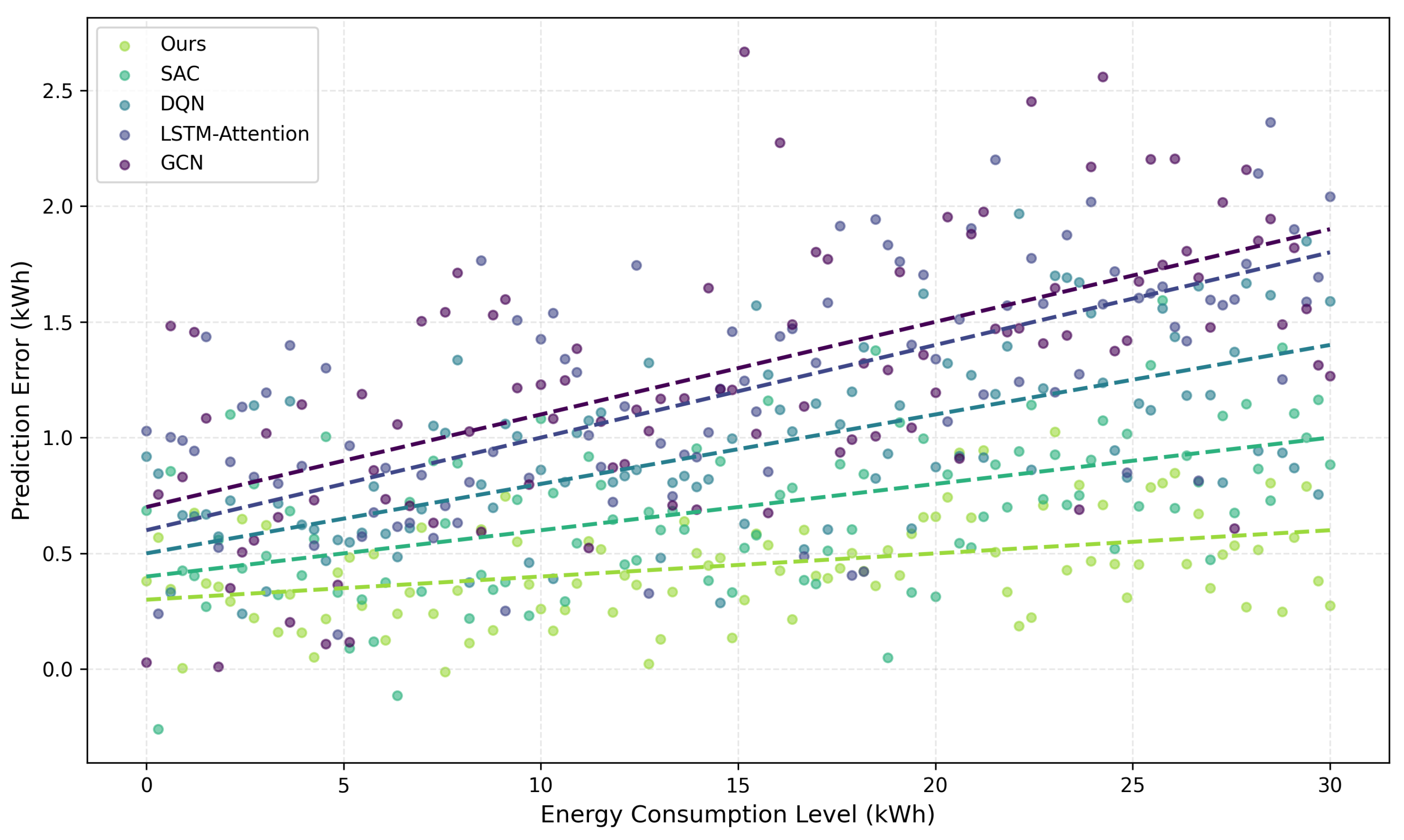
5.3.3. Prediction Accuracy
5.3.4. Comprehensive Ablation Studies
5.3.5. Graph Attention Network Effectiveness Analysis
5.3.6. Driver Comfort and Range Anxiety
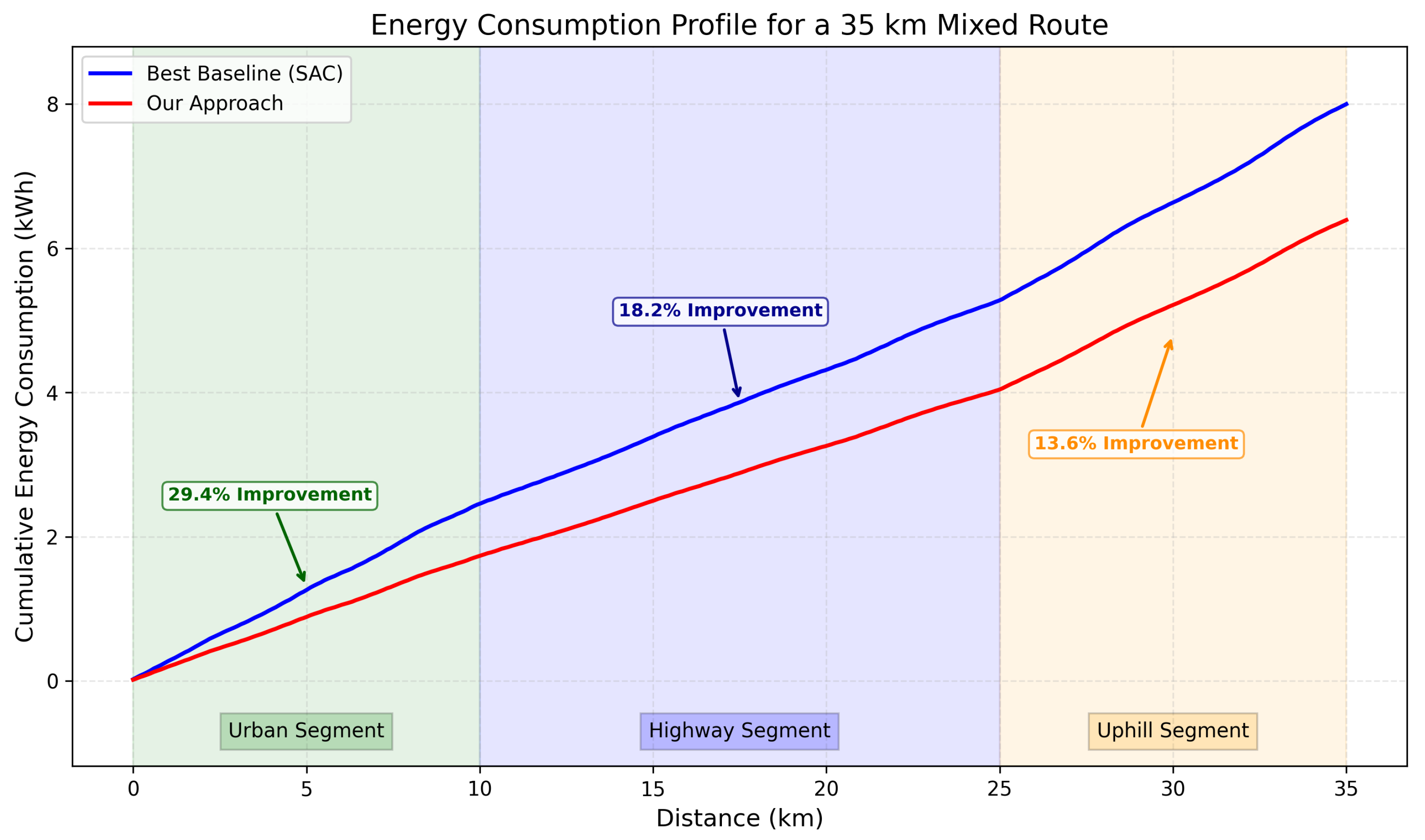
5.3.7. Case Study: Urban-Highway Mixed Route
6. Conclusions and Future Work
6.1. Conclusions
6.2. Limitations and Future Works
6.2.1. Current Limitations
6.2.2. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Song, Z.; Lv, C. Deep reinforcement learning-based energy-efficient decision-making for autonomous electric vehicle in dynamic traffic environments. IEEE Trans. Transp. Electrif. 2023, 10, 875–887. [Google Scholar] [CrossRef]
- Li, W.; Stanula, P.; Egede, P.; Kara, S.; Herrmann, C. Determining the main factors influencing the energy consumption of electric vehicles in the usage phase. Procedia Cirp 2016, 48, 352–357. [Google Scholar] [CrossRef]
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar] [CrossRef]
- Zhang, R.; Yao, E. Electric vehicles’ energy consumption estimation with real driving condition data. Transp. Res. Part D Transp. Environ. 2015, 41, 177–187. [Google Scholar] [CrossRef]
- Yang, S.; Ling, C.; Fan, Y.; Yang, Y.; Tan, X.; Dong, H. A review of lithium-ion battery thermal management system strategies and the evaluate criteria. Int. J. Electrochem. Sci. 2019, 14, 6077–6107. [Google Scholar] [CrossRef]
- De Cauwer, C.; Van Mierlo, J.; Coosemans, T. Energy consumption prediction for electric vehicles based on real-world data. Energies 2015, 8, 8573–8593. [Google Scholar] [CrossRef]
- Liu, T.; Zou, Y.; Liu, D.; Sun, F. Reinforcement learning of adaptive energy management with transition probability for a hybrid electric tracked vehicle. IEEE Trans. Ind. Electron. 2015, 62, 7837–7846. [Google Scholar] [CrossRef]
- Fu, Q.; Zhang, L.; Xu, Y.; You, F. The Review of Human—Machine Collaborative Intelligent Interaction with Driver Cognition in the Loop. Syst. Res. Behav. Sci. 2025. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, Y.; Zhou, B.; Wang, R.; Ke, W.; Zhang, S.; Hao, J. Real-world performance of battery electric buses and their life-cycle benefits with respect to energy consumption and carbon dioxide emissions. Energy 2016, 96, 603–613. [Google Scholar] [CrossRef]
- Hayes, J.G.; De Oliveira, R.P.R.; Vaughan, S.; Egan, M.G. Simplified electric vehicle power train models and range estimation. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–5. [Google Scholar]
- Fukushima, A.; Yano, T.; Imahara, S.; Aisu, H.; Shimokawa, Y.; Shibata, Y. Prediction of energy consumption for new electric vehicle models by machine learning. IET Intell. Transp. Syst. 2018, 12, 1174–1180. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, J.; Jiang, H.; Yao, X.; Qian, Y.; Zhang, H. Energy consumption prediction strategy for electric vehicle based on LSTM-transformer framework. Energy 2024, 302, 131780. [Google Scholar] [CrossRef]
- Hussain, I.; Ching, K.B.; Uttraphan, C.; Tay, K.G.; Noor, A. Evaluating machine learning algorithms for energy consumption prediction in electric vehicles: A comparative study. Sci. Rep. 2025, 15, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Al-Wreikat, Y.; Serrano, C.; Sodré, J.R. Driving behaviour and trip condition effects on the energy consumption of an electric vehicle under real-world driving. Appl. Energy 2021, 297, 117096. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Peng, Z.; Wang, A.; Wang, W. A data-driven two-level clustering model for driving pattern analysis of electric vehicles and a case study. J. Clean. Prod. 2019, 206, 827–837. [Google Scholar] [CrossRef]
- Wu, J.; Li, K.; Jiang, Y.; Lv, Q.; Shang, L.; Sun, Y. Large-scale battery system development and user-specific driving behavior analysis for emerging electric-drive vehicles. Energies 2011, 4, 758–779. [Google Scholar] [CrossRef]
- Liu, H.; Huang, Z.; Mo, X.; Lv, C. Augmenting reinforcement learning with transformer-based scene representation learning for decision-making of autonomous driving. IEEE Trans. Intell. Veh. 2024, 9, 4405–4421. [Google Scholar] [CrossRef]
- Lang, C.; Braun, A.; Schillingmann, L.; Haug, K.; Valada, A. Self-supervised representation learning from temporal ordering of automated driving sequences. IEEE Robot. Autom. Lett. 2024, 9, 2582–2589. [Google Scholar] [CrossRef]
- Bingham, C.; Walsh, C.; Carroll, S. Impact of driving characteristics on electric vehicle energy consumption and range. IET Intell. Transp. Syst. 2012, 6, 29–35. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Shao, C.; Wang, P.; Wang, A.; Zhuge, C. An adaptive spatio-temporal graph recurrent network for short-term electric vehicle charging demand prediction. Appl. Energy 2025, 383, 125320. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Song, C.; Yan, G.; Xiao, F.; Zhang, X.; Cao, J.; Song, S. Hierarchical reinforcement learning based energy management strategy for hybrid electric vehicle. Energy 2022, 238, 121703. [Google Scholar] [CrossRef]
- Guo, K.; Tian, D.; Hu, Y.; Sun, Y.; Qian, Z.; Zhou, J.; Gao, J.; Yin, B. Contrastive learning for traffic flow forecasting based on multi graph convolution network. IET Intell. Transp. Syst. 2024, 18, 290–301. [Google Scholar] [CrossRef]
- Jin, G.; Liang, Y.; Fang, Y.; Shao, Z.; Huang, J.; Zhang, J.; Zheng, Y. Spatio-temporal graph neural networks for predictive learning in urban computing: A survey. IEEE Trans. Knowl. Data Eng. 2023, 36, 5388–5408. [Google Scholar] [CrossRef]
- Qu, H.; Kuang, H.; Wang, Q.; Li, J.; You, L. A physics-informed and attention-based graph learning approach for regional electric vehicle charging demand prediction. IEEE Trans. Intell. Transp. Syst. 2024, 25, 14284–14297. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 1, pp. 9–11. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 2018 International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 2020 International Conference on Machine Learning, Online, 12–18 July 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the 2018 International Conference on Learning Representations, Vancouver, BC, USA, 30 April–3 May 2018. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the 2018 International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
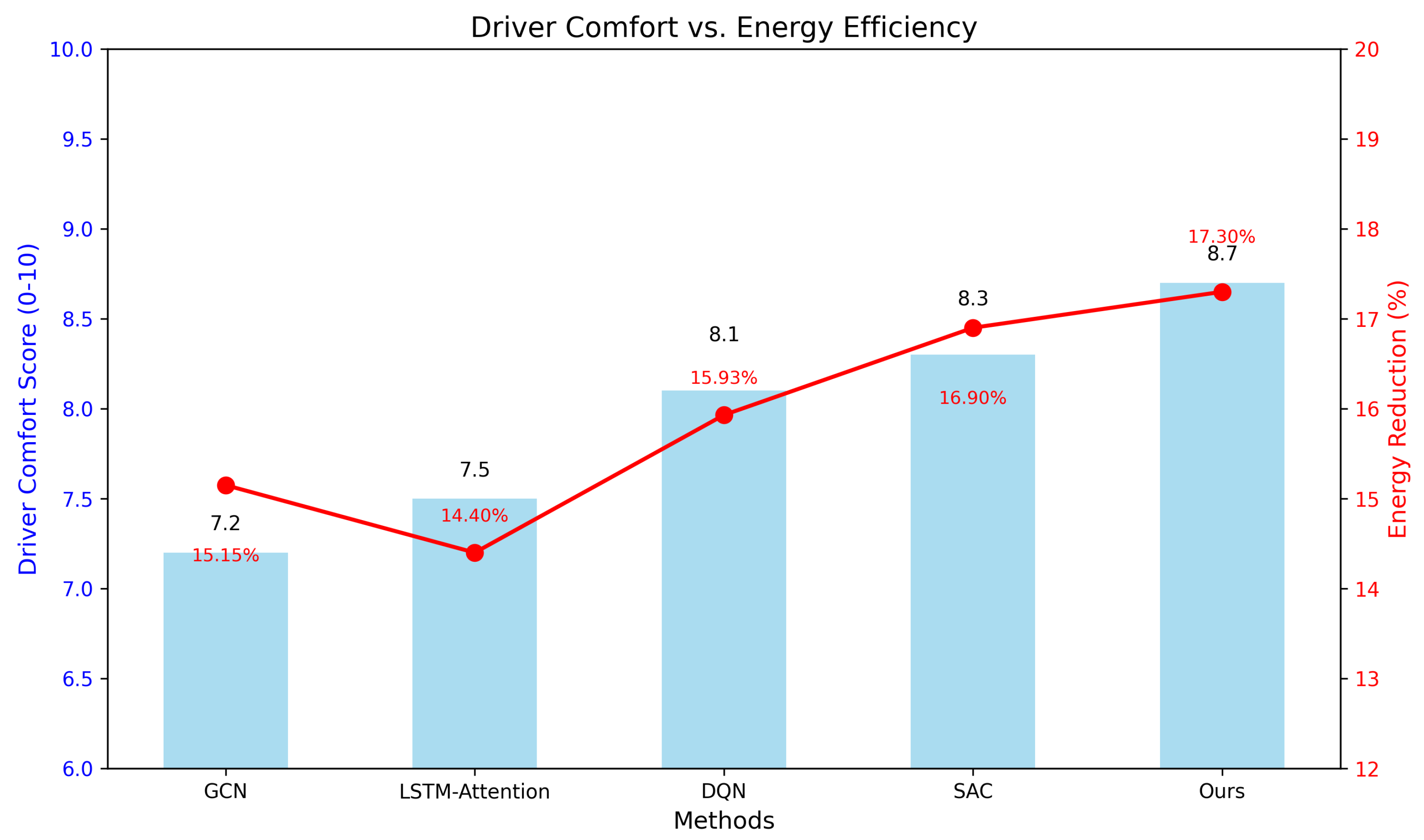
| Method | Avg. Energy Reduction (%) | Relative Improvement (%) |
|---|---|---|
| GCN [20] | 15.15 | – |
| LSTM-Attention [6] | 14.40 | – |
| DQN [7] | 15.93 | – |
| SAC [21] | 16.90 | – |
| Ours | 17.30 | 2.37 |
| Driving Scenario | Theoretical Max (%) | Achieved (%) | Efficiency Ratio | Limiting Factors |
|---|---|---|---|---|
| Urban stop-and-go | 35–40 | 21.4 | 0.61 | Battery charging rate, prediction accuracy |
| Highway cruising | 15–20 | 18.7 | 0.94 | Aerodynamic constraints, traffic flow |
| Mixed driving | 25–30 | 19.2 | 0.67 | Scenario transition losses |
| Uphill climbing | 10–12 | 15.9 | - | Physical limit exceeded |
| Average | 21.3–25.5 | 17.3 | 0.73 | Multi-factor constraints |
| Method | MAE (kWh) | RMSE (kWh) | R2 |
|---|---|---|---|
| GCN [20] | 0.61 | 0.79 | 0.874 |
| LSTM-Attention [6] | 0.58 | 0.76 | 0.885 |
| DQN [7] | 0.53 | 0.70 | 0.904 |
| SAC [21] | 0.48 | 0.63 | 0.921 |
| Ours | 0.42 | 0.58 | 0.937 |
| Model Configuration | Energy Reduction (%) | MAE (kWh) |
|---|---|---|
| Full Model (Ours) | 17.3 | 0.42 |
| w/o Contrastive Learning | 14.2 | 0.55 |
| w/o Graph Attention Networks | 13.7 | 0.59 |
| w/o Hierarchical RL (Flat RL) | 11.9 | 0.61 |
| Configuration | Energy Reduction (%) | MAE (kWh) | Context R2 |
|---|---|---|---|
| Attention Heads (3 layers) | |||
| 2 heads | 15.1 | 0.52 | 0.871 |
| 4 heads | 16.2 | 0.47 | 0.895 |
| 8 heads (ours) | 17.3 | 0.42 | 0.904 |
| 12 heads | 17.1 | 0.43 | 0.901 |
| 16 heads | 16.8 | 0.45 | 0.897 |
| Layer Depth (8 heads) | |||
| 1 layer | 14.8 | 0.56 | 0.863 |
| 2 layers | 16.5 | 0.48 | 0.887 |
| 3 layers (ours) | 17.3 | 0.42 | 0.904 |
| 4 layers | 17.0 | 0.44 | 0.899 |
| 5 layers | 16.7 | 0.46 | 0.893 |
| Parameter Configuration | Energy Reduction (%) | Scenario Accuracy (%) | Silhouette Score |
|---|---|---|---|
| Temperature Parameter τ | |||
| = 0.01 | 15.8 | 87.2 | 0.61 |
| = 0.05 | 16.7 | 91.5 | 0.68 |
| = 0.07 (ours) | 17.3 | 93.8 | 0.72 |
| = 0.1 | 16.9 | 92.1 | 0.69 |
| = 0.2 | 15.4 | 88.6 | 0.64 |
| Augmentation Strategy | |||
| Gaussian noise only | 15.9 | 89.3 | 0.65 |
| Temporal shifting only | 16.1 | 90.1 | 0.67 |
| Feature masking only | 15.7 | 88.8 | 0.63 |
| Noise + Shifting | 16.8 | 92.4 | 0.70 |
| Full augmentation (ours) | 17.3 | 93.8 | 0.72 |
| Method | Silhouette Score | Attention Entropy | Context R2 |
|---|---|---|---|
| Simple Graph Conv. | 0.49 | - | 0.821 |
| GCN | 0.52 | - | 0.845 |
| GAT (4 heads) | 0.63 | 2.1 | 0.882 |
| GAT (8 heads, ours) | 0.68 | 2.3 | 0.904 |
| GAT (16 heads) | 0.65 | 2.4 | 0.897 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, H.; Wu, B.; Liu, W. Symmetry-Guided Electric Vehicles Energy Consumption Optimization Based on Driver Behavior and Environmental Factors: A Reinforcement Learning Approach. Symmetry 2025, 17, 930. https://doi.org/10.3390/sym17060930
Wang J, Zhang H, Wu B, Liu W. Symmetry-Guided Electric Vehicles Energy Consumption Optimization Based on Driver Behavior and Environmental Factors: A Reinforcement Learning Approach. Symmetry. 2025; 17(6):930. https://doi.org/10.3390/sym17060930
Chicago/Turabian StyleWang, Jiyuan, Haijian Zhang, Bi Wu, and Wenhe Liu. 2025. "Symmetry-Guided Electric Vehicles Energy Consumption Optimization Based on Driver Behavior and Environmental Factors: A Reinforcement Learning Approach" Symmetry 17, no. 6: 930. https://doi.org/10.3390/sym17060930
APA StyleWang, J., Zhang, H., Wu, B., & Liu, W. (2025). Symmetry-Guided Electric Vehicles Energy Consumption Optimization Based on Driver Behavior and Environmental Factors: A Reinforcement Learning Approach. Symmetry, 17(6), 930. https://doi.org/10.3390/sym17060930






