Kinematic Skeleton Extraction from 3D Model Based on Hierarchical Segmentation
Abstract
1. Introduction
2. Related Work
2.1. Skeleton Extraction Methods for 3D Models
2.1.1. Thinning and Boundary Propagation Methods
2.1.2. Distance-Field-Based Methods
2.1.3. Geometric-Based Methods
2.1.4. Deep Learning-Based Methods
2.2. Preprocessing of Point Cloud Data for 3D Models
2.3. Deep Learning Models for Part Segmentation
2.4. Ensemble Methods for Deep Learning
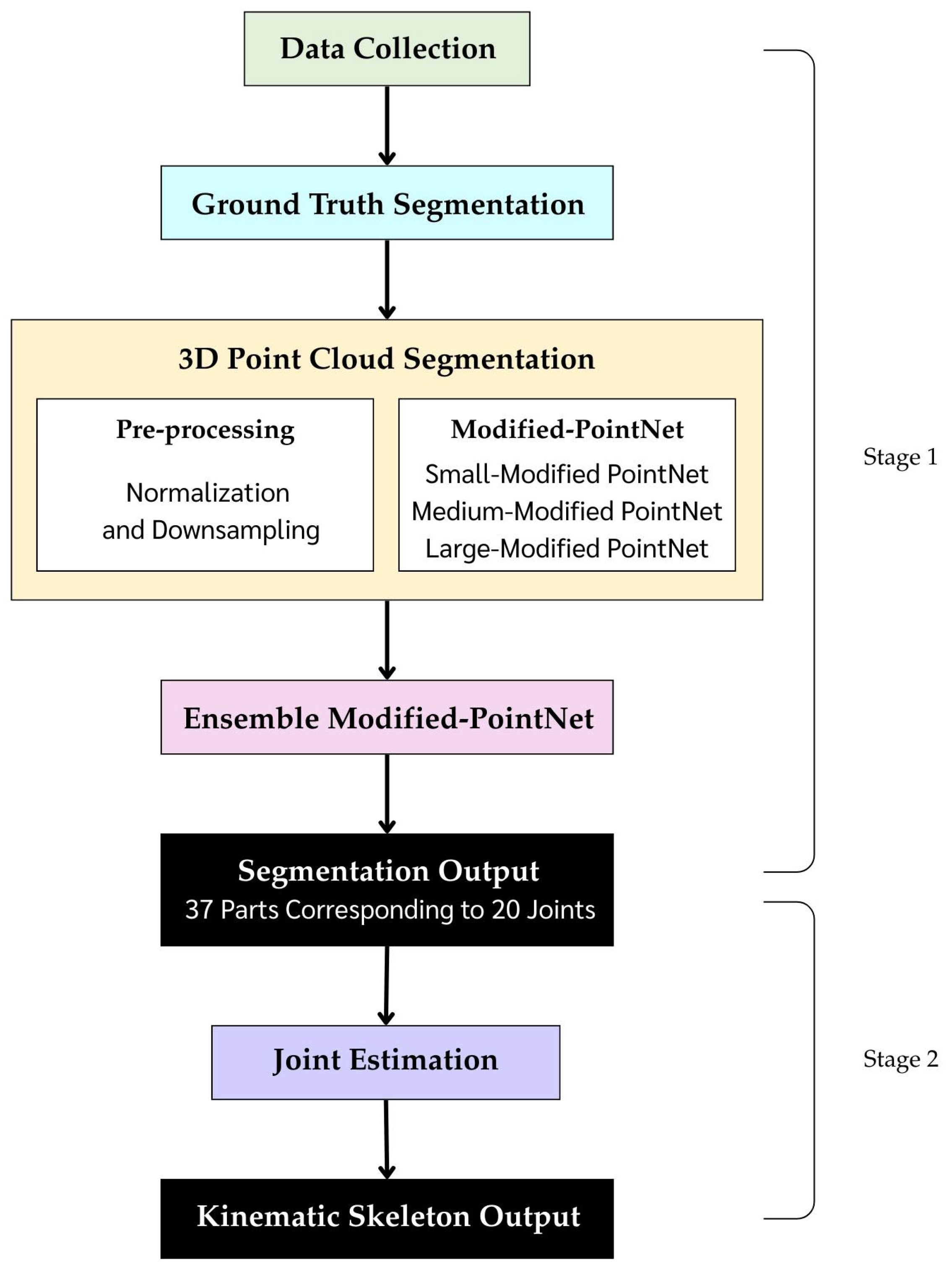
3. Proposed Framework
3.1. Data Collection
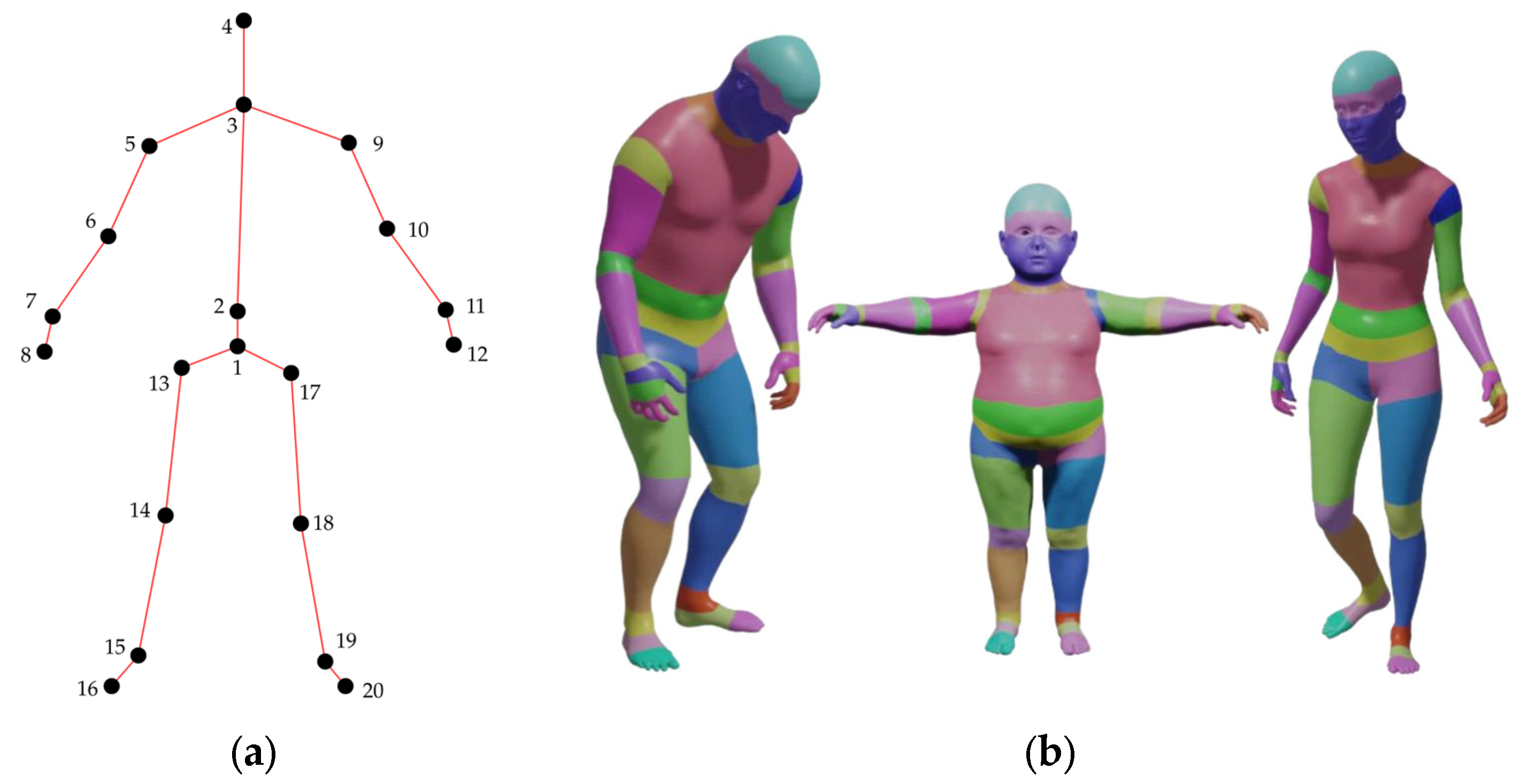
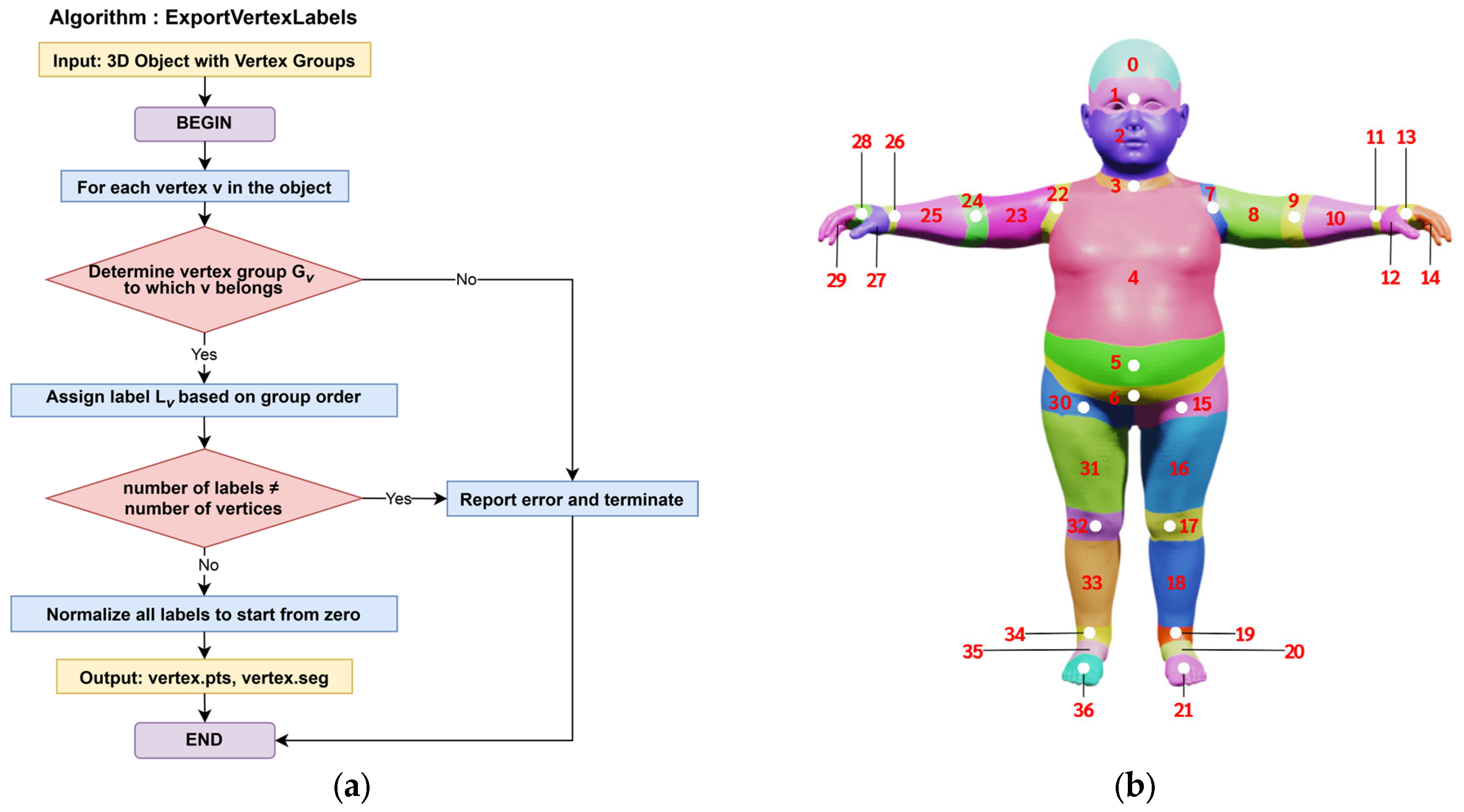
3.2. 3D Model Analysis and Ground Truth Generation for Part Segmentation
3.3. Point Cloud Preprocessing for 3D Model Segmentation
- Random Sampling (RS) selects points uniformly at random without regard to spatial arrangement. While computationally simple [50], RS often discards important local features and fails to maintain structural continuity.
- Farthest Point Sampling (FPS) iteratively selects the point farthest from all previously chosen ones, ensuring an even distribution across the model [51]. FPS is widely adopted in point cloud segmentation for its superior balance between global coverage and local feature retention.
- Cluster-KNN Sampling clusters spatially adjacent points and samples within each cluster [52]. This method preserves local geometry and boundary integrity better than RS or FPS in low-density conditions, though at higher computational cost.
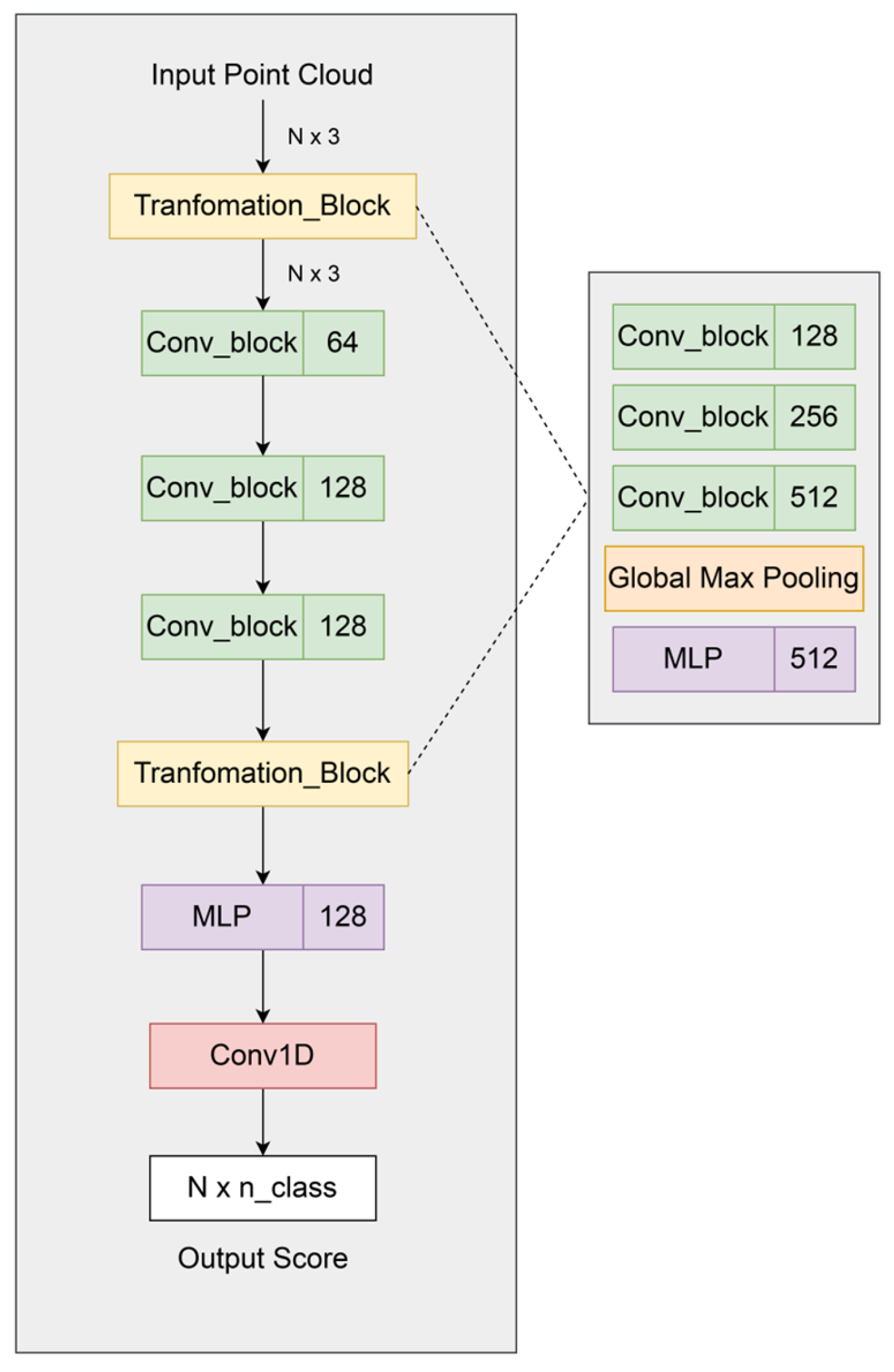
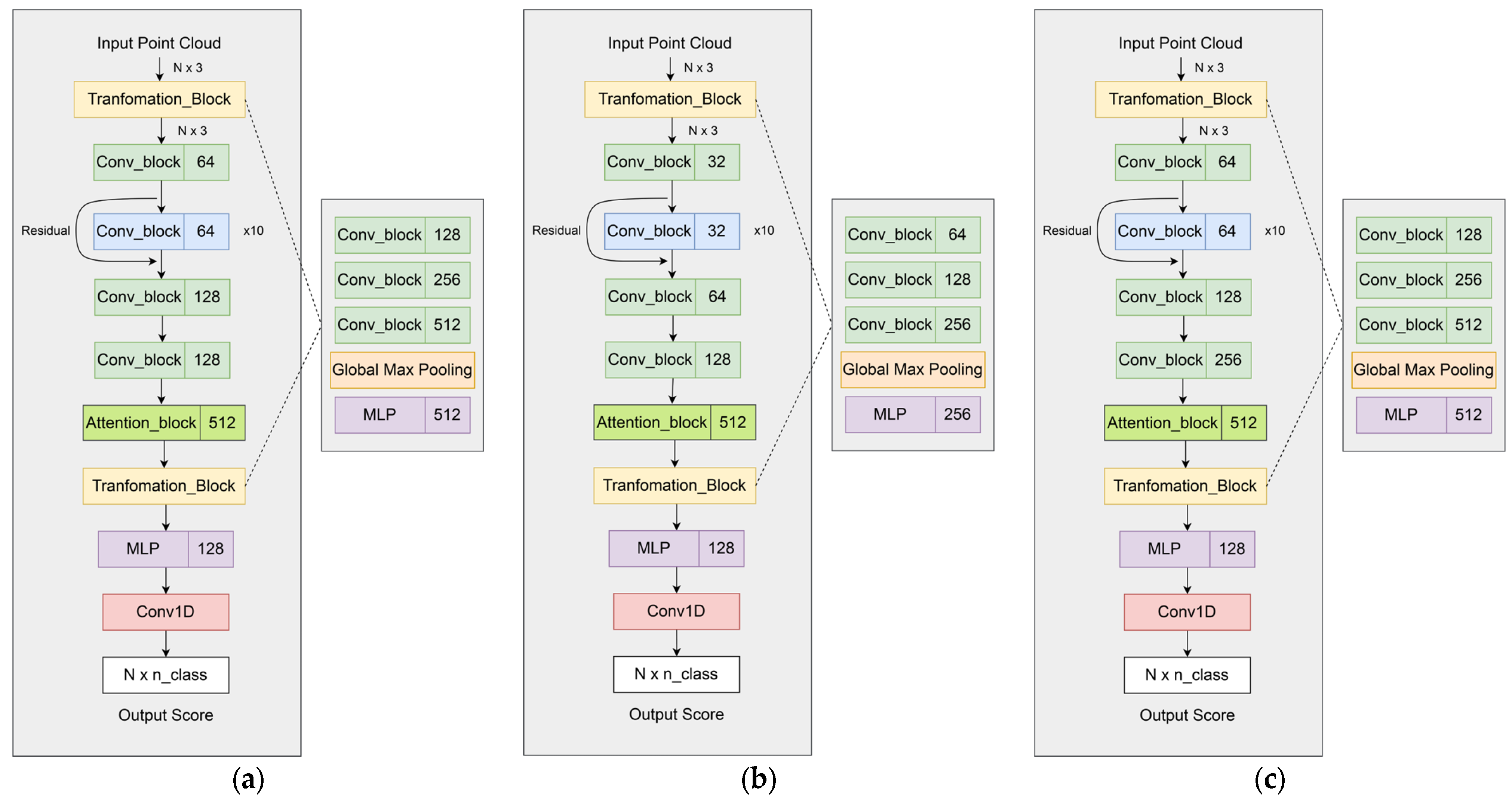
3.4. PointNet-Based Deep Learning Architecture for 3D Model Segmentation
3.4.1. Baseline Model: Standard PointNet Architecture for 3D Model Segmentation
3.4.2. Architectural Enhancements to PointNet
3.4.3. Medium-Modified PointNet Architecture
3.4.4. Small-Modified PointNet Architecture
3.4.5. Large-Modified PointNet Architecture
3.4.6. Data Augmentation for Improved Generalization
3.4.7. Optimization Algorithm Selection for Deep Learning
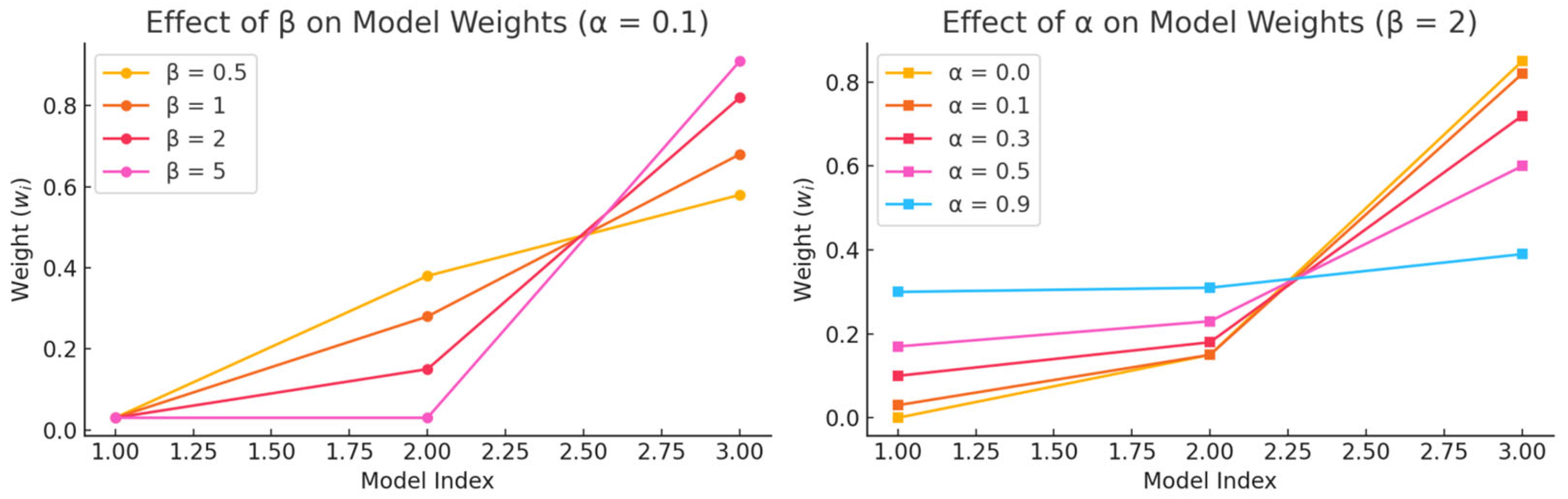
3.5. Ensemble Learning Strategies for Modified PointNet in 3D Segmentation
3.6. Kinematic Skeleton Extraction from 3D Models Based on Hierarchical Segmentation
3.6.1. Model Testing on DanceDB Dataset
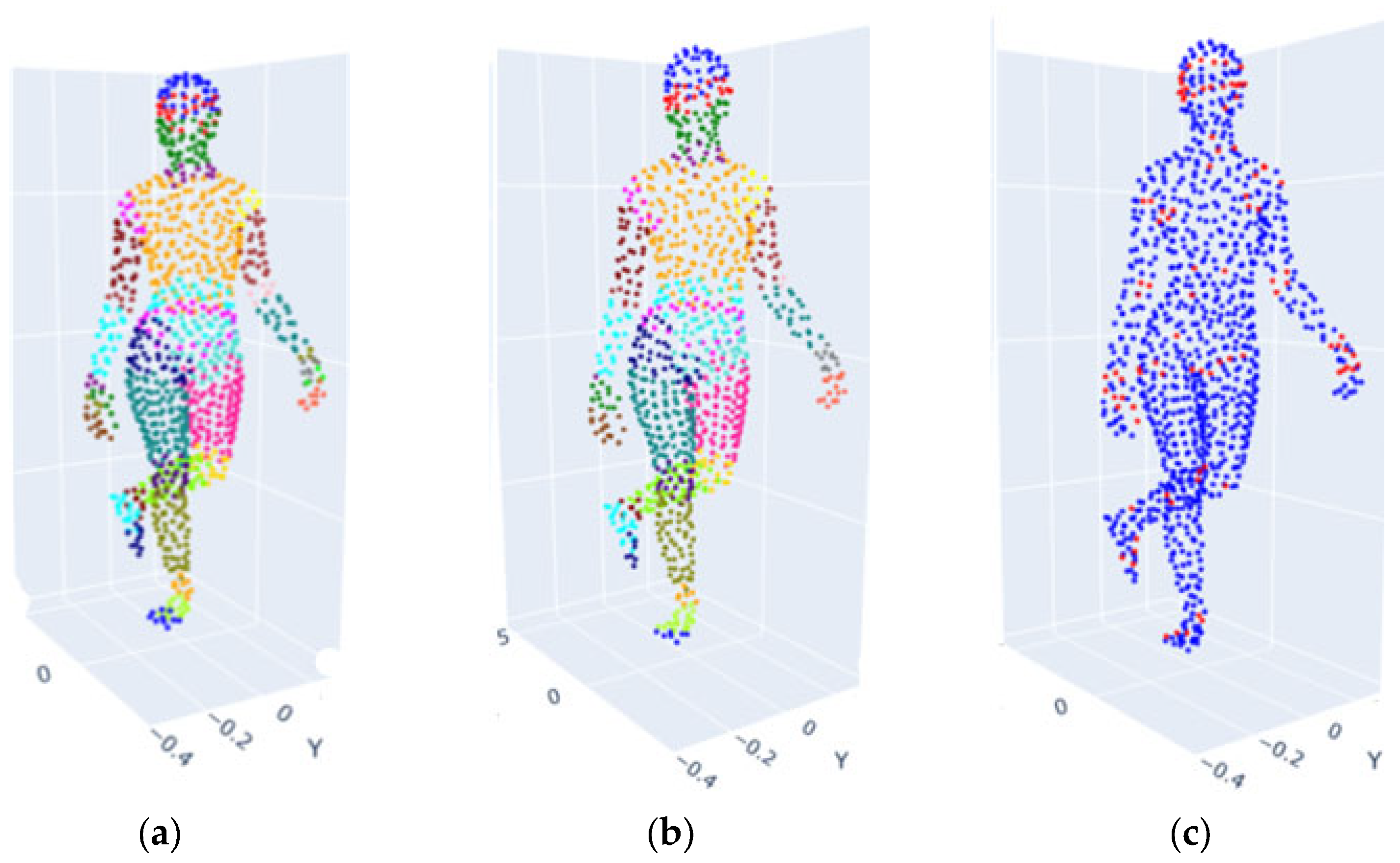
3.6.2. Centroid Calculation for Joint-Specific Point Clouds
3.6.3. Centroid Refinement with Radius Limitation
3.6.4. Evaluation of Extracted Joint Accuracy Using MPJPE
4. Results
4.1. Evaluation of Structure-Preserving Preprocessing Techniques for 3D Model Part Segmentation
4.2. Comparison of Deep Learning Model Performance and Ensemble Learning for 3D Model Part Segmentation
4.2.1. Experimental Setup
4.2.2. Performance Evaluation of Deep Learning Models for 3D Model Part Segmentation
4.2.3. Performance Evaluation with Different Preprocessing Techniques
4.2.4. Ensemble Learning for Enhanced 3D Model Segmentation
4.3. Development and Performance Evaluation of Kinematic Skeleton Extraction by Joint Position Estimation from 3D Model Part Segmentation
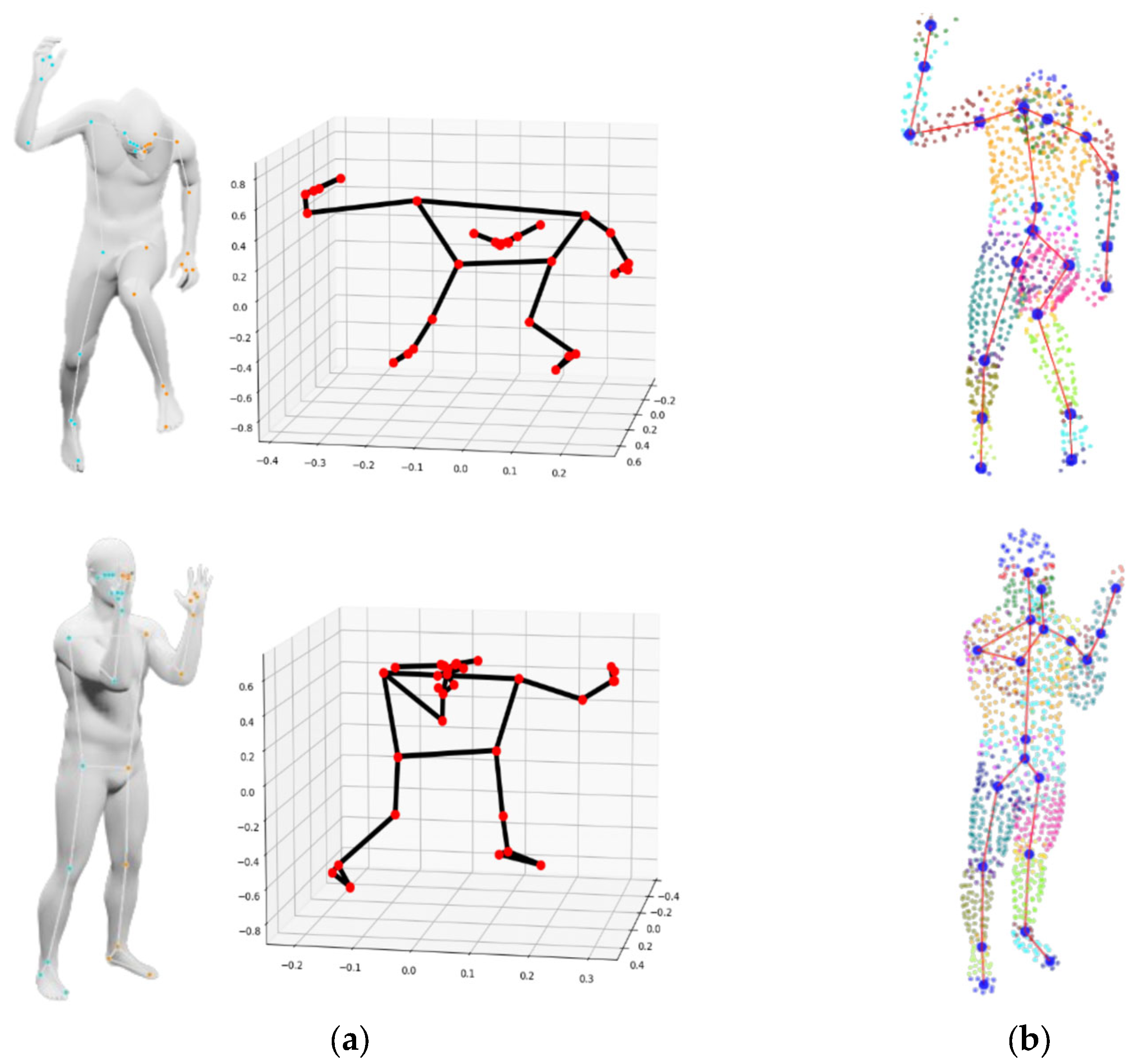
4.3.1. Joint Estimation Using Centroid-Based Refinement
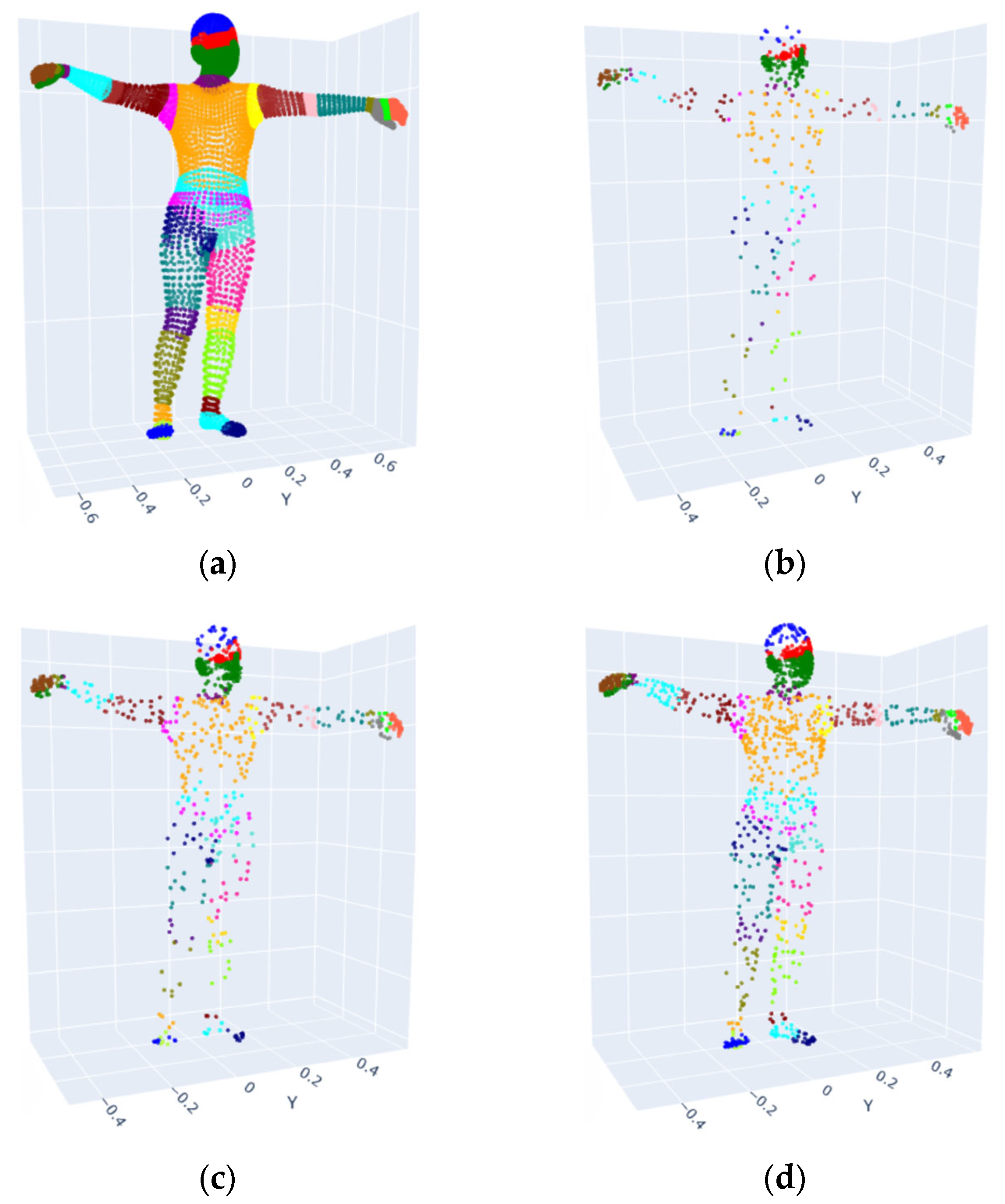
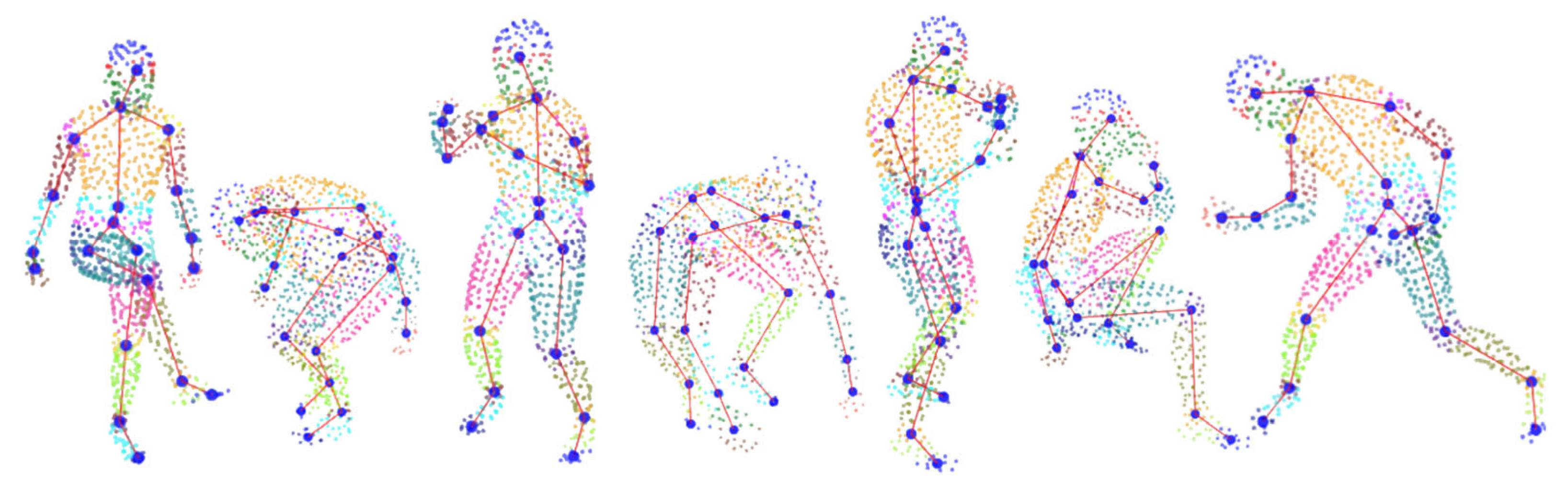
4.3.2. Qualitative Skeleton Structure Assessment
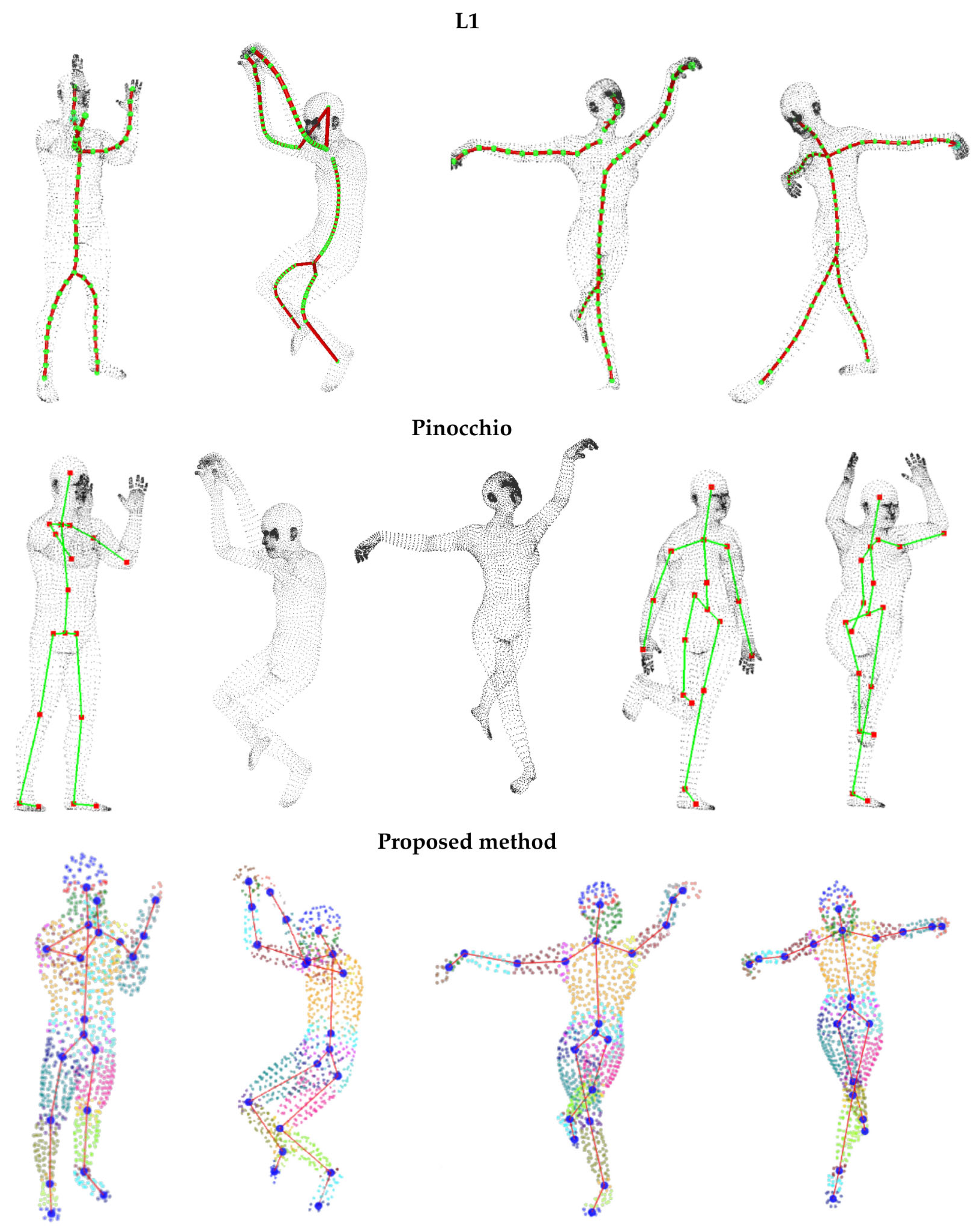
4.3.3. Comparative Analysis Against Benchmark Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhou, M.; Geng, G.; Xie, Y.; Zhang, Y.; Liu, Y. EPCS: Endpoint-based part-aware curve skeleton extraction for low-quality point clouds. Comput. Graph. 2023, 117, 209–221. [Google Scholar] [CrossRef]
- Wen, C.; Yu, B.; Tao, D. Learnable skeleton-aware 3d point cloud sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Xu, Z.; Zhou, Y.; Kalogerakis, E.; Landreth, C.; Singh, K. Rignet: Neural rigging for articulated characters. arXiv 2020, arXiv:2005.00559. [Google Scholar] [CrossRef]
- Fang, Y.; Tang, J.; Shen, W.; Shen, W.; Gu, X.; Song, L.; Zhai, G. Dual attention guided gaze target detection in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Hu, H.; Li, Z.; Jin, X.; Deng, Z.; Chen, M.; Shen, Y. Curve skeleton extraction from 3D Point clouds through hybrid feature point shifting and clustering. Comput. Graph. Forum 2020, 39, 111–132. [Google Scholar] [CrossRef]
- Liu, L.; Chen, N.; Ceylan, D.; Theobalt, C.; Wang, W.; Mitra, N.J. CurveFusion: Reconstructing thin structures from RGBD sequences. arXiv 2021, arXiv:2107.05284. [Google Scholar]
- Bærentzen, A.; Rotenberg, E. Skeletonization via Local Separators. ACM Trans. Graph. (TOG) 2021, 40, 1–18. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.; Bai, J.; Peng, C.; Li, Y.; Du, S. A Novel Skeleton-based Model with Spine for 3D Human Pose Estimation. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 26–29 January 2022. [Google Scholar]
- Bian, S.; Zheng, A.; Chaudhry, E.; You, L.; Zhang, J.J. Automatic generation of dynamic skin deformation for animated characters. Symmetry 2018, 10, 89. [Google Scholar] [CrossRef]
- Cai, Y.; Ge, L.; Liu, J.; Cai, J.; Cham, T.-J.; Yuan, J.; Thalmann, N.M. Exploiting spatial-temporal relationships for 3d pose estimation via graph convolutional networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Li, R.; Si, W.; Weinmann, M.; Klein, R. Constraint-based optimized human skeleton extraction from single-depth camera. Sensors 2019, 19, 2604. [Google Scholar] [CrossRef]
- Mahmood, N.; Ghorbani, N.; Troje, N.F.; Pons-Moll, G.; Black, M.J. AMASS: Archive of motion capture as surface shapes. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Black, M.; Daniilidis, K. Learning to reconstruct 3D human pose and shape via model-fitting in the loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.S.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Cai, Z.; Pan, L.; Wei, C.; Yin, W.; Hong, F.; Zhang, M.; Loy, C.C.; Yang, L.; Liu, Z. Pointhps: Cascaded 3d human pose and shape estimation from point clouds. arXiv 2023, arXiv:2308.14492. [Google Scholar]
- Zhang, F.; Chen, X.; Zhang, X. Parallel thinning and skeletonization algorithm based on cellular automaton. Multimedia Tools Appl. 2020, 79, 33215–33232. [Google Scholar] [CrossRef]
- Huang, H.; Wu, S.H.; Cohen-Or, D.; Gong, M.L.; Zhang, H.; Li, G.Q.; Chen, B.Q. L1-medial skeleton of point cloud. ACM Trans. Graph. (TOG) 2013, 32, 65:1–65:8. [Google Scholar] [CrossRef]
- Manolas, I.; Lalos, A.S.; Moustakas, K. Parallel 3D Skeleton Extraction Using Mesh Segmentation. In Proceedings of the 2018 International Conference on Cyberworlds (CW), Singapore, 3–5 October 2018. [Google Scholar]
- Baran, I.; Popović, J. Automatic rigging and animation of 3d characters. ACM Trans. Graph. (TOG) 2007, 26, 72-es. [Google Scholar] [CrossRef]
- Wang, J.-D.; Chao, J.; Chen, Z.-G. Feature-preserving skeleton extraction algorithm for point clouds. J. Graph. 2023, 44, 146. [Google Scholar]
- Qi, C.; Su, H.; Mo, K.; Guibas, L. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31, 828–838. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Tian, W.; Gao, Z.; Tan, D. Single-view multi-human pose estimation by attentive cross-dimension matching. Front. Neurosci. 2023, 17, 1201088. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, S.; Liu, Q.; Chen, L.; Chen, B. PointSkelCNN: Deep learning-based 3D human skeleton extraction from point clouds. Comput. Graph. Forum 2020, 39, 363–374. [Google Scholar] [CrossRef]
- Lin, C.; Li, C.; Liu, Y.; Chen, N.; Choi, Y.K.; Wang, W. Point2skeleton: Learning skeletal representations from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3d point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Lugaresi, C.; Tang, J.; Nash, H.; McClanahan, C.; Uboweja, E.; Hays, M.; Zhang, F.; Chang, C.L.; Yong, M.G.; Lee, J.; et al. Mediapipe: A framework for building perception pipelines. arXiv 2019, arXiv:1906.08172. [Google Scholar]
- Ma, X.; Qin, C.; You, H.; Ran, H.; Fu, Y. Rethinking network design and local geometry in point cloud: A simple residual MLP framework. arXiv 2022, arXiv:2202.07123. [Google Scholar]
- Sakae, Y.; Noda, Y.; Li, L.; Hasegawa, K.; Nakada, S.; Tanaka, S. Realizing Uniformity of 3D Point Clouds Based on Improved Poisson-Disk Sampling. In Methods and Applications for Modeling and Simulation of Complex Systems: 19th Asia Simulation Conference, AsiaSim 2019, Singapore, 30 October–1 November 2019, Proceedings 19; Springer: Singapore, 2019. [Google Scholar]
- Chen, X.; Chen, M. Skeleton partition models for 3D printing. In Proceedings of the Second International Conference on Medical Imaging and Additive Manufacturing (ICMIAM 2022), Xiamen, China, 25–27 February 2022. [Google Scholar]
- Han, X.F.; Cheng, H.; Jiang, H.; He, D.; Xiao, G. Pcb-randnet: Rethinking random sampling for lidar semantic segmentation in autonomous driving scene. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 13–17 May 2024. [Google Scholar]
- Battikh, M.S.; Lensky, A.; Hammill, D.; Cook, M. knn-res: Residual neural network with knn-graph coherence for point cloud registration. In Principle and Practice of Data and Knowledge Acquisition Workshop; Springer: Singapore, 2024. [Google Scholar]
- Han, M.; Wang, L.; Xiao, L.; Zhang, H.; Zhang, C.; Xu, X.; Zhu, J. QuickFPS: Architecture and algorithm co-design for farthest point sampling in large-scale point clouds. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 4011–4024. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5099–5108. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Atik, M.E.; Duran, Z. An Efficient Ensemble Deep Learning Approach for Semantic Point Cloud Segmentation Based on 3D Geometric Features and Range Images. Sensors 2022, 22, 6210. [Google Scholar] [CrossRef] [PubMed]
- Koguciuk, D.; Chechliński, Ł.; El-Gaaly, T. 3D object recognition with ensemble learning—A study of point cloud-based deep learning models. In International Symposium on Visual Computing; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Ruan, Y.; Singh, S.; Morningstar, W.; Alemi, A.A.; Ioffe, S.; Fischer, I.; Dillon, J.V. Weighted ensemble self-supervised learning. arXiv 2022, arXiv:2211.09981. [Google Scholar]
- Bogo, F.; Romero, J.; Pons-Moll, G.; Black, M.J. Dynamic FAUST: Registering human bodies in motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Carnegie Mellon University. Carnegie Mellon Motion Capture Database. Available online: http://mocap.cs.cmu.edu (accessed on 21 May 2024).
- Lähner, Z.; Rodola, E.; Bronstein, M.M.; Cremers, D.; Burghard, O.; Cosmo, L.; Dieckmann, A.; Klein, R.; Sahillioǧlu, Y. SHREC’16: Matching of deformable shapes with topological noise. In Eurographics Workshop on 3D Object Retrieval, EG 3DOR; Eurographics Association: Goslar, Germany, 2016. [Google Scholar]
- Wang, Z.; Ma, M.; Feng, X.; Li, X.; Liu, F.; Guo, Y.; Chen, D. Skeleton-based human pose recognition using channel state information: A survey. Sensors 2022, 22, 8738. [Google Scholar] [CrossRef]
- Tölgyessy, M.; Dekan, M.; Chovanec, Ľ. Skeleton tracking accuracy and precision evaluation of kinect v1, kinect v2, and the azure kinect. Appl. Sci. 2021, 11, 5756. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Learning semantic segmentation of large-scale point clouds with random sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8338–8354. [Google Scholar] [CrossRef]
- Li, J.; Zhou, J.; Xiong, Y.; Chen, X.; Chakrabarti, C. An adjustable farthest point sampling method for approximately-sorted point cloud data. In Proceedings of the 2022 IEEE Workshop on Signal Processing Systems (SiPS), Rennes, France, 2–4 November 2022. [Google Scholar]
- Mahdaoui, A.; Sbai, E.H. 3D Point Cloud Simplification Based on k-Nearest Neighbor and Clustering. Adv. Multimed. 2020, 2020, 8825205. [Google Scholar] [CrossRef]
- Desai, A.; Parikh, S.; Kumari, S.; Raman, S. PointResNet: Residual network for 3D point cloud segmentation and classification. arXiv 2022, arXiv:2211.11040. [Google Scholar]
- Gezawa, A.S.; Liu, C.; Jia, H.; Nanehkaran, Y.A.; Almutairi, M.S.; Chiroma, H. An improved fused feature residual network for 3D point cloud data. Front. Comput. Neurosci. 2023, 17, 1204445. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, B.; Guan, Q.; Zhang, J.; Wu, Q.; Xia, Y. Attention mechanisms in medical image segmentation: A survey. arXiv 2023, arXiv:2305.17937. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Feng, M.; Zhang, L.; Lin, X.; Gilani, S.Z.; Mian, A. Point attention network for semantic segmentation of 3D point clouds. Pattern Recognit. 2020, 107, 107446. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.; Hwang, D.; Lee, J.; Hwang, S.J.; Kim, H.J. Point cloud augmentation with weighted local transformations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Zhang, Z.; Hua, B.-S.; Yeung, S.-K. Shellnet: Efficient point cloud convolutional neural networks using concentric shells statistics. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Hermans, A.; Leibe, B. Exploring spatial context for 3D semantic segmentation of point clouds. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ju, C.; Bibaut, A.; van der Laan, M. The relative performance of ensemble methods with deep convolutional neural networks for image classification. J. Appl. Stat. 2018, 45, 2800–2818. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, S.; Huang, T.; Qian, L.; Liu, K. Method for measuring the center of mass and moment of inertia of a model using 3D point clouds. Appl. Opt. 2022, 61, 10329–10336. [Google Scholar] [CrossRef]
- Pavllo, D.; Feichtenhofer, C.; Grangier, D.; Auli, M. 3d human pose estimation in video with temporal convolutions and semi-supervised training. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
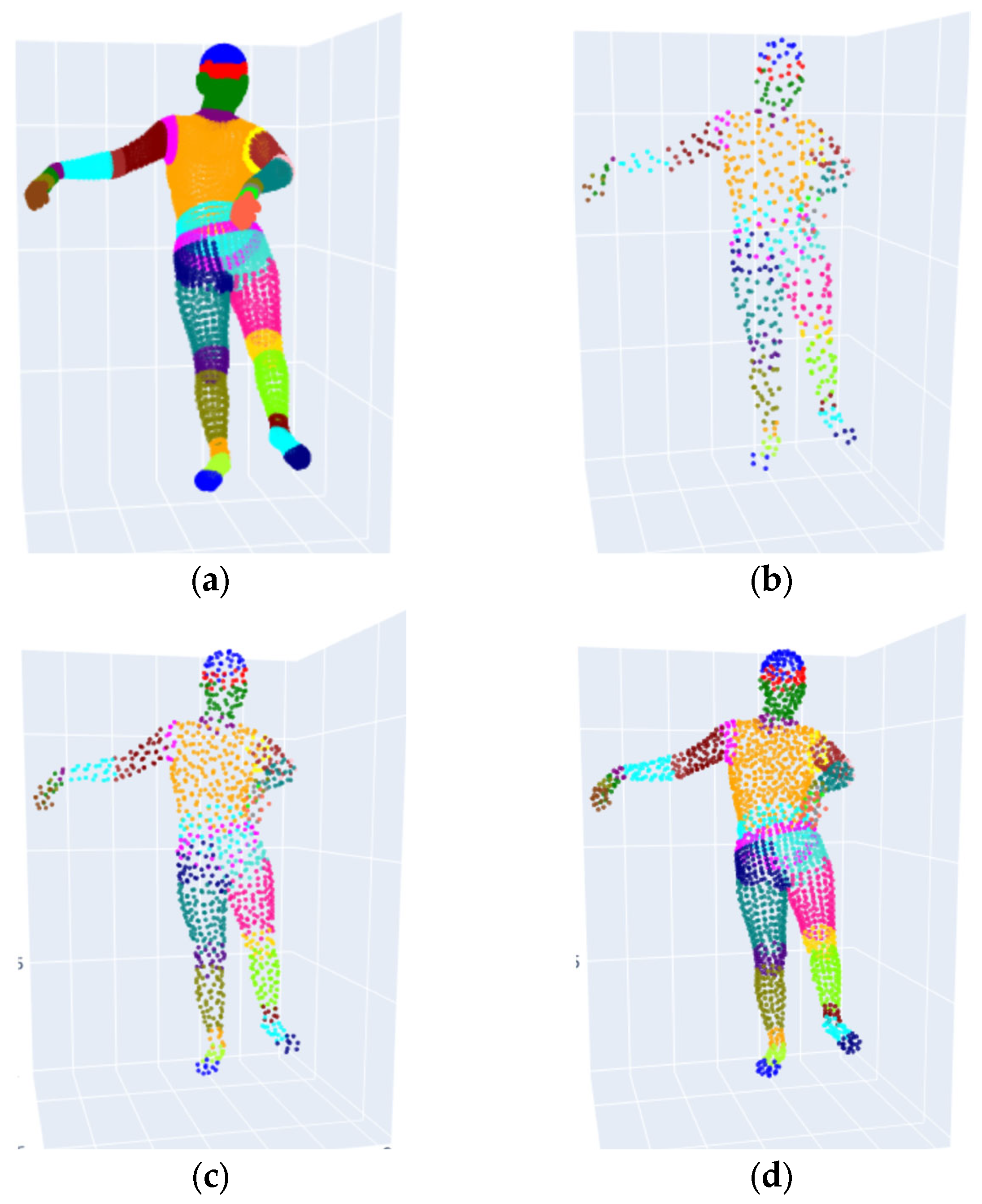
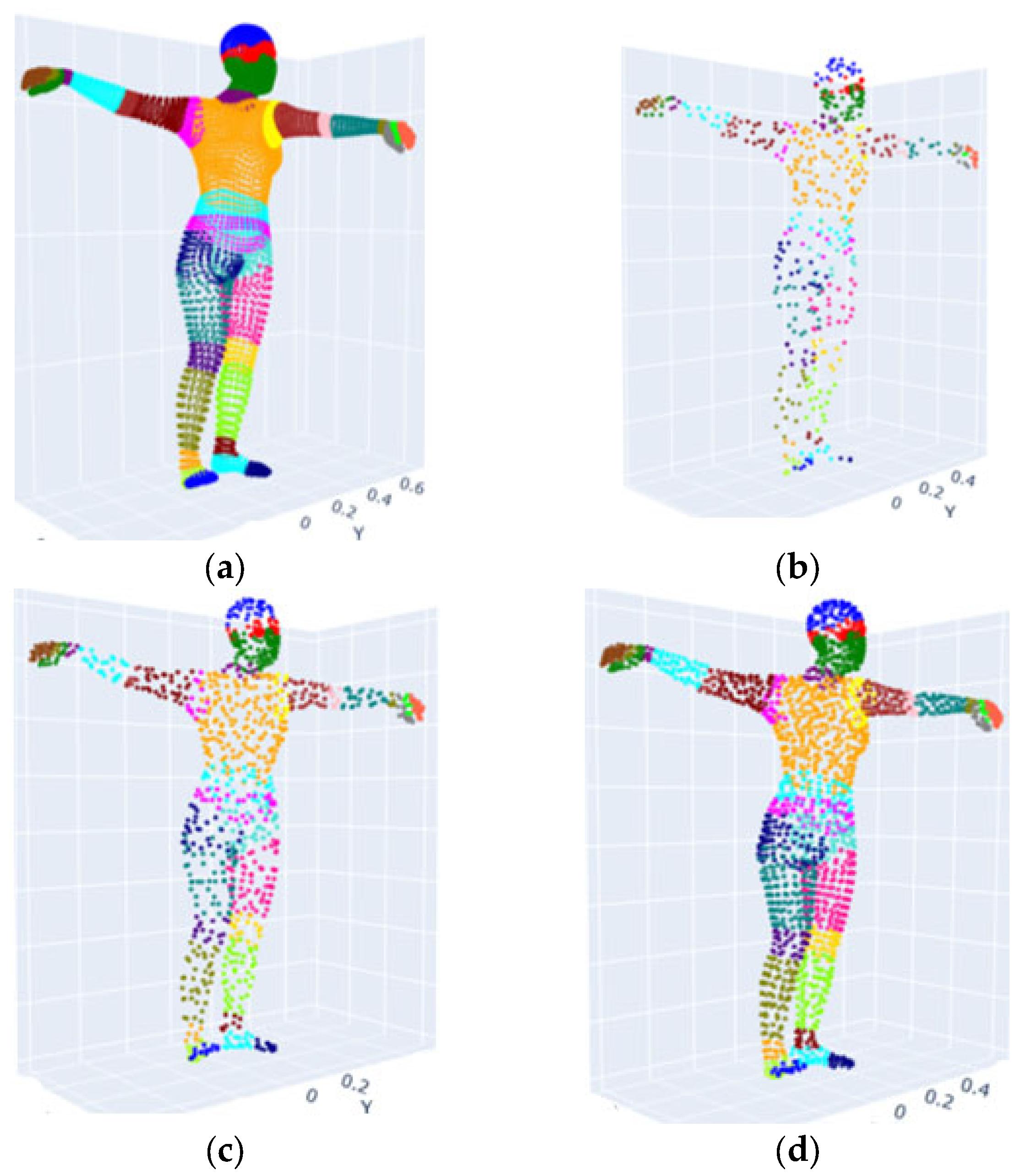

| Dataset Name | Number of Points | Gender | Model Characteristics | Total Poses |
|---|---|---|---|---|
| DFaust [44] DFaust [44] | 6890 | Male, Female | Multi-Person | 100 |
| 10,475 | Male, Female | Multi-Person | 673 | |
| EHF [45] | 10,475 | Male | Single Person | 100 |
| CMU [46] | 10,475 | Male, Female | Multi-Person | 1199 |
| Kids [47] | 59,727 | Male | Multi-Person | 32 |
| Total | 2104 | |||
| Aspect | Small-Modified | Medium-Modified | Large-Modified |
|---|---|---|---|
| Target Use Case | Real-time or low-resource systems | Balanced performance and efficiency | High-precision segmentation tasks |
| Convolutional + Residual Layers | 32 × 10 (residual), 64, 128 | 64 × 10 (residual), 128, 128 | 64 × 10 (residual), 128, 256 |
| Attention Block | 512 filters | 512 filters | 512 filters |
| MLP Size | 256 units | 128 units | 512 units |
| Transformation Blocks | Shallower | Standard | Standard |
| Global Max Pooling | Yes | Yes | Yes |
| Advantages | Lightweight, efficient, low latency | Good accuracy, stable training | Rich features, high spatial resolution |
| Disadvantages | Less accurate in complex geometry | Higher load than small, less detail than large | High computational cost, longer training time |
| Optimization Algorithm | Learning Algorithm | No Data Augmentation | ||
|---|---|---|---|---|
| Training Time | Accuracy Rate | mIoU | ||
| Adam | PointNet | 8:53 | 56.88 | 0.2862 |
| Small-Modified PointNet | 7:13 | 68.84 | 0.3968 | |
| Medium-Modified PointNet | 9:32 | 72.17 | 0.4221 | |
| Large-Modified PointNet | 30:32 | 71.57 | 0.4115 | |
| Adam + Learning Rate Schedule | PointNet | 9:48 | 58.98 | 0.3156 |
| Small-Modified PointNet | 7:34 | 70.51 | 0.3998 | |
| Medium-Modified PointNet | 9:53 | 72.98 | 0.4338 | |
| Large-Modified PointNet | 30:53 | 73.13 | 0.4322 | |
| Adam + Cyclical Learning Rate Schedule | PointNet | 8:30 | 59.45 | 0.3156 |
| Small-Modified PointNet | 7:55 | 70.69 | 0.4015 | |
| Medium-Modified PointNet | 10:14 | 73.21 | 0.4319 | |
| Large-Modified PointNet | 31:14 | 73.71 | 0.4357 | |
| Optimization Algorithm | Learning Algorithm | Data Augmentation and Number of Multiple Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X5 | X10 | ||||||||
| Training Time | Accuracy Rate | mIoU | Training Time | Accuracy Rate | mIoU | Training Time | Accuracy Rate | mIoU | ||
| Adam | PointNet | 9:32 | 60.33 | 0.3218 | 35:45 | 67.89 | 0.3872 | 1:10:23 | 70.21 | 0.4221 |
| Small-Modified PointNet | 7:43 | 71.30 | 0.3950 | 32:15 | 75.67 | 0.4544 | 1:03:45 | 77.32 | 0.4823 | |
| Medium-Modified PointNet | 10:02 | 75.21 | 0.4552 | 42:36 | 77.56 | 0.4798 | 1:24:27 | 78.21 | 0.4952 | |
| Large-Modified PointNet | 31:02 | 73.43 | 0.4407 | 2:17:06 | 76.21 | 0.4627 | 4:33:27 | 77.02 | 0.4809 | |
| Adam + Learning Rate Schedule | PointNet | 9:56 | 61.25 | 0.3405 | 37:50 | 68.45 | 0.395 | 1:12:30 | 71.34 | 0.4278 |
| Small-Modified PointNet | 8:04 | 73.77 | 0.4300 | 32:27 | 76.97 | 0.4709 | 1:03:48 | 77.25 | 0.4823 | |
| Medium-Modified PointNet | 10:23 | 76.17 | 0.4601 | 42:57 | 77.01 | 0.4677 | 1:24:48 | 77.52 | 0.4881 | |
| Large-Modified PointNet | 31:23 | 75.33 | 0.4590 | 2:17:27 | 77.78 | 0.4834 | 4:33:48 | 78.85 | 0.5016 | |
| Adam + Cyclical Learning Rate Schedule | PointNet | 9:57 | 64.78 | 0.3554 | 38:45 | 69.52 | 0.3996 | 1:13:07 | 72.89 | 0.4367 |
| Small-Modified PointNet | 8:25 | 71.21 | 0.3976 | 32:48 | 75.12 | 0.4518 | 1:04:09 | 77.34 | 0.4889 | |
| Medium-Modified PointNet | 10:44 | 75.62 | 0.4547 | 43:18 | 76.95 | 0.4678 | 1:25:09 | 77.78 | 0.4872 | |
| Large-Modified PointNet | 31:44 | 73.65 | 0.4420 | 2:17:48 | 76.32 | 0.4644 | 4:34:09 | 78.23 | 0.4921 | |
| Modified PointNet Architecture | Sample Point Method | Number Input of Points | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 512 | 1024 | 2048 | ||||||||
| Training Time (hh:mm:ss) | Accuracy Rate (%) | mIoU | Training Time (hh:mm:ss) | Accuracy Rate (%) | mIoU | Training Time (hh:mm:ss) | Accuracy Rate (%) | mIoU | ||
| Small- Modified PointNet (parameters size 17.81 M) | RS | 29:17 | 63.60 | 0.3160 | 55:57 | 64.52 | 0.3157 | 1:19:58 | 65.03 | 0.3398 |
| Farhest | 29:41 | 76.54 | 0.4523 | 57:27 | 77.18 | 0.4830 | 1:24:37 | 77.05 | 0.4822 | |
| Cluster-KNN | 31:01 | 72.18 | 0.4746 | 1:10:27 | 75.12 | 0.5028 | 2:12:28 | 75.03 | 0.4978 | |
| Medium-Modified PointNet (parameters size 37.91 M) | RS | 52:15 | 65.48 | 0.3474 | 1:39:14 | 68.42 | 0.3838 | 2:33:06 | 68.74 | 0.3857 |
| Farhest | 52:39 | 78.78 | 0.5120 | 1:40:44 | 79.25 | 0.5159 | 2:37:45 | 77.71 | 0.4955 | |
| Cluster-KNN | 53:59 | 73.97 | 0.4957 | 1:53:44 | 75.69 | 0.5151 | 3:25:36 | 74.25 | 0.4624 | |
| Large- Modified PointNet (parameters size 263.63 M) | RS | 2:04:16 | 72.28 | 0.4812 | 2:29:14 | 74.49 | 0.4965 | 5:23:08 | 73.29 | 0.4857 |
| Farhest | 2:04:40 | 78.92 | 0.5125 | 2:30:44 | 80.27 | 0.5178 | 5:27:47 | 80.07 | 0.5164 | |
| Cluster-KNN | 2:06:00 | 74.81 | 0.4862 | 2:43:44 | 75.63 | 0.4929 | 6:15:38 | 75.14 | 0.4923 | |
| Ensemble Modified PointNet | Parameter Size (M) | Training Time (hh:mm:ss) | Majority Vote | Unweight Average | Miou Weighted | Accuracy Weighted | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy Rate | mIoU | Accuracy Rate | mIoU | Accuracy Rate | mIoU | Accuracy Rate | mIoU | |||
| Ensemble 3 Large | 790.89 | 7:27:48 | 80.69 | 0.5304 | 80.93 | 0.5332 | 80.97 | 0.5343 | 80.96 | 0.5342 |
| Ensemble 3 Medium | 113.73 | 4:57:48 | 80.61 | 0.5281 | 80.79 | 0.5302 | 80.79 | 0.5305 | 80.80 | 0.5308 |
| Ensemble 5 Medium | 189.55 | 8:14:52 | 80.94 | 0.5336 | 81.05 | 0.5355 | 81.06 | 0.5359 | 81.09 | 0.5361 |
| Ensemble 7 Medium | 265.37 | 11:31:56 | 81.15 | 0.5374 | 81.22 | 0.5374 | 81.23 | 0.5379 | 81.25 | 0.5380 |
| Ensemble 5 Small | 89.05 | 4:38:27 | 77.58 | 0.4783 | 77.80 | 0.4806 | 77.87 | 0.4816 | 77.81 | 0.4809 |
| Ensemble 9 Small | 160.29 | 8:19:27 | 77.74 | 0.4809 | 77.85 | 0.4814 | 77.87 | 0.4817 | 77.88 | 0.4816 |
| Ensemble 13 Small | 231.53 | 12:00:27 | 77.97 | 0.4840 | 78.10 | 0.4847 | 78.13 | 0.4853 | 78.12 | 0.4848 |
| Modified PointNet Architecture | MPJPE (mm) | |
|---|---|---|
| Centroid Without Limit-Radius | Centroid with Limit-Radius | |
| PointNet | 51.81 | 38.87 |
| Small-Modified PointNet | 45.07 | 34.51 |
| Medium-Modified PointNet | 40.38 | 29.57 |
| Large-Modified PointNet | 39.57 | 28.85 |
| AW Ensemble 3 Large-Modified PointNet | 36.21 | 25.40 |
| AW Ensemble 7 Medium-Modified PointNet | 33.39 | 22.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mata, N.; Tangwannawit, S. Kinematic Skeleton Extraction from 3D Model Based on Hierarchical Segmentation. Symmetry 2025, 17, 879. https://doi.org/10.3390/sym17060879
Mata N, Tangwannawit S. Kinematic Skeleton Extraction from 3D Model Based on Hierarchical Segmentation. Symmetry. 2025; 17(6):879. https://doi.org/10.3390/sym17060879
Chicago/Turabian StyleMata, Nitinan, and Sakchai Tangwannawit. 2025. "Kinematic Skeleton Extraction from 3D Model Based on Hierarchical Segmentation" Symmetry 17, no. 6: 879. https://doi.org/10.3390/sym17060879
APA StyleMata, N., & Tangwannawit, S. (2025). Kinematic Skeleton Extraction from 3D Model Based on Hierarchical Segmentation. Symmetry, 17(6), 879. https://doi.org/10.3390/sym17060879








