1. Introduction
With the development of computer graphics (CG), computer-aided design (CAD), computer aided geometric design (CAGD), and scientific data visualization in engineering, constructing visually pleasing shape-preserving interpolation spline curves for positive, monotone, and/or convex sets of data being interpolated is an essential problem and has attracted widespread interest. In the past, various shape-preserving interpolation spline methods have been proposed; among the multitude of references on this subject, the reader is referred to the comprehensive reviews by Kvasov [
1] and Goodman [
2], where systematic comparisons and analyses of existing algorithms for shape-preserving spline interpolation are provided.
Piecewise rational quadratic and cubic spline methodologies have been extensively researched for developing shape-preserving interpolation splines. Multiple specialized rational cubic interpolation splines have been formulated for the graphical representation of strictly positive data sets by Hussain and Sarfraz [
3], Sarfaze [
4], and Qin et al. [
5]. Some specific rational cubic monotonicity-preserving interpolants have been proposed by Gregory [
6], Sarfraz [
7,
8], Hussain and Hussain [
9], Sarfraz et al. [
10], and Abbas et al. [
11]. Various rational cubic splines have been constructed by Delbourgo [
12], Sarfraz and Hussain [
13], Sarfraz et al. [
14], and Abbas et al. [
15] to produce convexity-preserving interpolation curves for convex data sets. These shape-preserving rational cubic interpolants typically achieve
continuity, whereas
continuity requires solving linear/nonlinear systems of compatibility equations for derivative specifications at knots; see the corresponding methods described in Delbourgo [
12] and Abbas et al. [
15]. Recently, by using weighted
quadratic and cubic splines, Kvasov developed weighted
quadratic/cubic spline algorithms with automated weight selection mechanisms for generating shape-preserving interpolants specific to monotonic or convex data sets; see Kvasov [
16,
17,
18]. Some
rational quartic shape-preserving interpolation splines were designed by Han [
19,
20], Zhu and Han [
21], and Zhu [
22,
23], avoiding solving global linear/nonlinear compatibility equation systems. However, the shape-preserving conditions of these methods are just sufficient but not necessary.
When constructing shape-preserving interpolation splines, a necessary and sufficient condition can always bring much convenience. For example, it can precisely judge whether the splines preserve the shape or not and estimate practicability. Therefore, the key aim of this paper is to find the necessary and sufficient conditions. There are a few papers concerning the construction of
shape-preserving interpolation splines with sufficient and necessary conditions. In [
24], Schmidt developed a kind of
rational quadratic interpolation splines with a parameter, with a necessary and sufficient criterion to ensure the property of positivity carries over from the data set. The criterion can always be satisfied if the parameters are properly chosen. Later, in [
25], Schmidt constructed a class of
quadratic and related exponential interpolation splines and discussed and deduced sufficient and necessary conditions for the interpolant preserving monotonicity and/or convexity.
In this work, we construct a kind of
rational quadratic interpolation spline possessing two symmetric parameters, which include the positivity-preserving rational quadratic interpolation splines with a parameter given in [
24] as a special case. Furthermore, the necessary and sufficient conditions for the new rational quadratic interpolation splines preserving convexity, monotonicity, and positivity are also developed. The rest of this paper is organized as follows.
Section 2 gives the construction of the new
rational quadratic interpolation spline with two symmetric parameters. Furthermore, the necessary and sufficient conditions of the proposed interpolation spline to preserve the shape of convex, monotonic, and positive sets of data are derived. In
Section 3, a particular approximated curvature is applied to select visually appealing shape-preserving interpolation spline curves. In
Section 4, several numerical examples and comparisons are given. Furthermore, a conclusion is given in
Section 5.
2. Shape-Preserving Interpolation Rational Quadratic/Linear Interpolation Spline
Let
be the given real data and
be the chosen first derivative values at knots
,
, where
is a partition of interval
. Furthermore, let parameters
,
be given. For
, we put
. For
,
,
, a new rational quadratic/linear interpolation spline
with two symmetric parameters
and
is constructed as follows
where
is a real parameter to be determined.
Remark 1. From (
1)
, it is easy to check that for , the rational quadratic/linear interpolation spline will return to the rational quadratic/linear interpolation spline with a parameter given in [24]. Thus, the rational quadratic/linear interpolation spline with two parameters given in (
1)
includes the rational quadratic/linear interpolation spline with a parameter given in [24] as a special case. From (
1), by direct computation, we have
. We want
to satisfy
for all
, from which we can determine the parameter
as follows
where
and the slopes
are defined as follows
We further require that
for all
, and these conditions lead to
with
and
as follows
Thus, conditions (
2) together with conditions (
4) concerning the first derivatives
of
in the nodes, can assure that for all
,
,
,
,
, which implies that
,
, and thus,
. Furthermore, if
is known, the spline
can be computed successively on the subintervals
,
. From (
2), as
,
, we have
; thus, for
, we have
In addition, for
,
, since
, we have
These imply that a small or large value of will make the interpolant locally approximate to a linear interpolant in the subinterval . Thus, the parameter serves as a tension parameter.
In the next three sections, we shall derive the necessary and sufficient conditions for the interpolant possessing convexity-preserving, monotonicity-preserving, and positivity-preserving properties.
2.1. Convexity Preserving Conditions
We say that
is a convex data set if and only if the slopes
,
satisfy
Assume that the slopes
satisfy (
6). For
, from (
1), by direct computation, we have
where
. From (
7), we can see that
if and only if
. Furthermore, from (
2), we can immediately obtain the following theorem.
Theorem 1. For the points , in convex position, the interpolant with and is convex on if and only if From Theorem 1 and with regard to the conditions (
4), the following problem arises: are there derivatives
,
such that
hold for all
.
For solving problem (
9), we set
. Then, from (
4), we have
and with
and
, we obtain
It follows immediately by induction that the following equation
holds. Therefore, since
, the requirement
holds for all
and is equivalent to
Then, from (
12), we can see that if
is satisfied, there belongs a convexity-preserving interpolation spline to every
. Summarizing this, the following theorem results.
Theorem 2. For the points , in a convex position, there exists a convexity-preserving interpolation spline if and only if the following condition holdswhere the numbers , are defined by (
10)
and (
13)
. For a strict convex data set, that is , we further show that there always exist parameters such that is always valid.
In fact, take
i is an even number, for example. We can always choose the parameters
,
in such a manner that
In fact, in view of (
10) and of
for
, the desired inequality
is always met for a sufficiently large
.
We can thus conclude the following theorem.
Theorem 3. Let be fixed, and assume (
6)
holds. Then, one always obtainsand in at least one case, Proof. Indeed, from (
10), we have
and
. This implies (
15). Furthermore, since
is valid, there are slopes
and
such that
. In these cases, inequality (
16) is obtained for all
. □
2.2. Monotonicity Preserving Conditions
We say that
is a monotone increasing data set if and only if
Now, let the given slopes
satisfy (
17). For
,
, direct computation gives that
From this, together with the conditions given in (
4), we can obtain the following theorem.
Theorem 4. With all and , holds for any if and only if the following conditions hold Proof. In fact, it suffices to verify that for any
,
,
holds if
and
. Indeed, from (
2) and (
4),
and
implies that
And thus, for
, we have
These imply the theorem. □
In view of Theorem 4 and the conditions given in (
4), one is now led to the following problem: are there derivatives
,
such that
hold for all
.
For treating (
20), we define
,
, and
By induction, we can easily obtain the following relation
Therefore,
,
are equivalent to
And with the following notations
we can obtain the following existence theorem.
Theorem 5. Under the assumption (
17)
, there exists a monotone increasing interpolation spline if and only ifwith and given by (
21)
and (
24)
. For strictly monotone increasing data points, that is , we further show that there always exist parameters such that is always valid.
In fact, take
i is an odd number, for example. We can always choose the parameters
,
in such a manner that
In fact, in view of (
21) and of
for
, the desired inequality
is always met for a sufficiently large
. We can thus conclude the follow theorem.
Theorem 6. Let be fixed, and suppose (
17)
. Then, one always hasand in at least one case, Proof. In fact, from (
21), we have
,
. This implies (
26). Furthermore, since
,
, in these cases, inequality (
16) is obtained for all
. □
If the data set is increasing and convex, that is
then there exists interpolation spline
, which is also increasing and convex, if and only if
Moreover, condition (
29) can be satisfied with sufficiently large parameters
,
if strong inequalities hold in (
28).
2.3. Positivity-Preserving Conditions
We say that
is a non-negative data set if and only if
,
satisfy
For
with
, from (
1), we have
where
Since
and
, from [
24], we can see that the non-negative of
on
is equivalent to
. Thus, we can obtain the following theorem.
Theorem 7. The rational quadratic spline interpolant is non-negative on if and only ifwhere From (
7) and with regard to the conditions given in (
4), the following problem arises: are there derivatives
,
such that
hold for all
.
For treating (
33), we define
and
where
.
From (
4), we can easily verify that
Hence, condition (
31) reads as
Thus, by setting
we can easily obtain the following theorem.
Theorem 8. For the non-negative data set , the interpolant with and is non-negative on if and only if For all , we further show that there always exist parameters such that is always valid.
In fact, since
for
, for a sufficiently large
,
, it follows that
and therefore, the condition (
37) is satisfied. Thus, we have the following theorem.
Theorem 9. For , . Then, for sufficiently large parameters , , the interpolant is non-negative on .
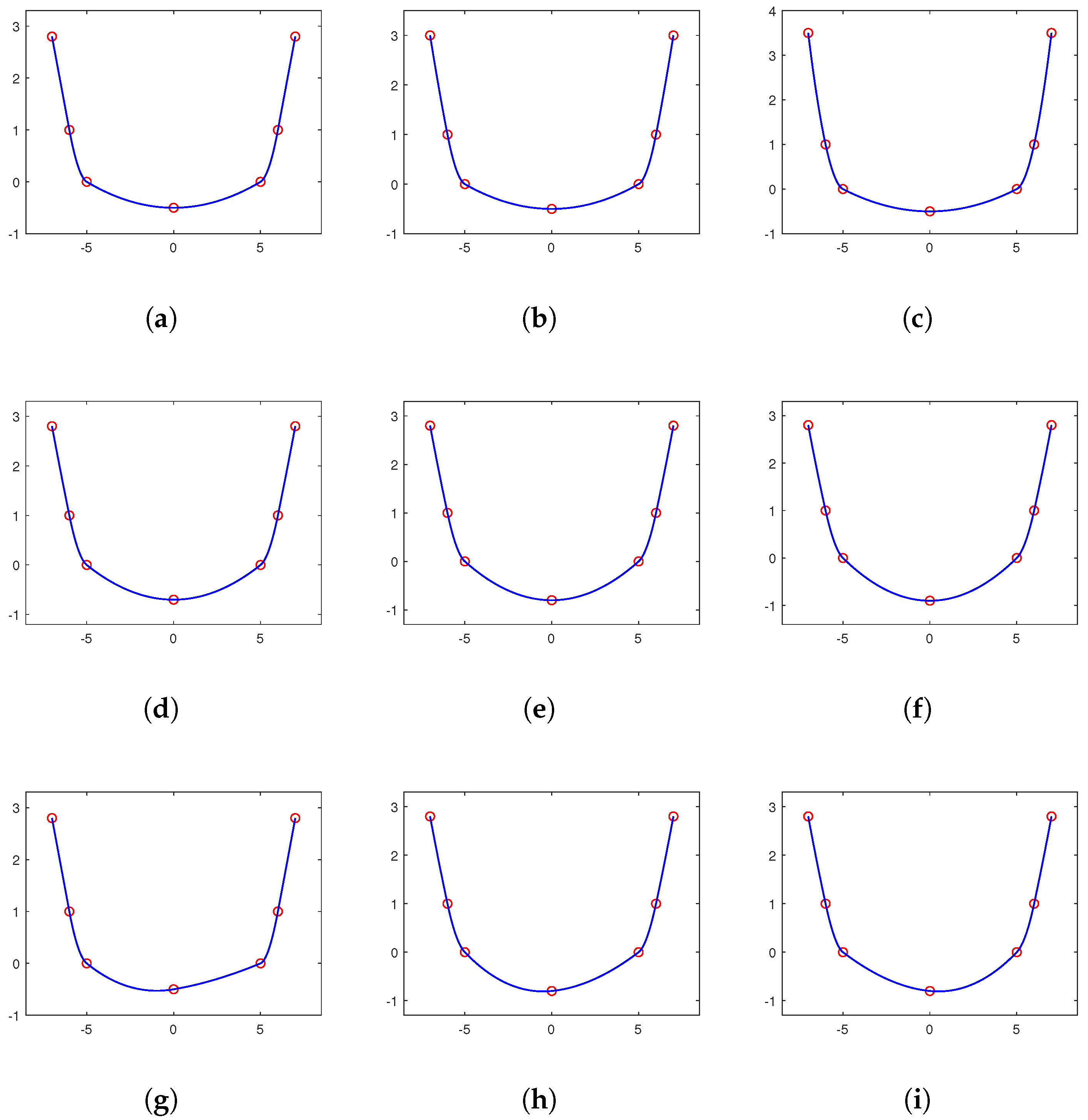
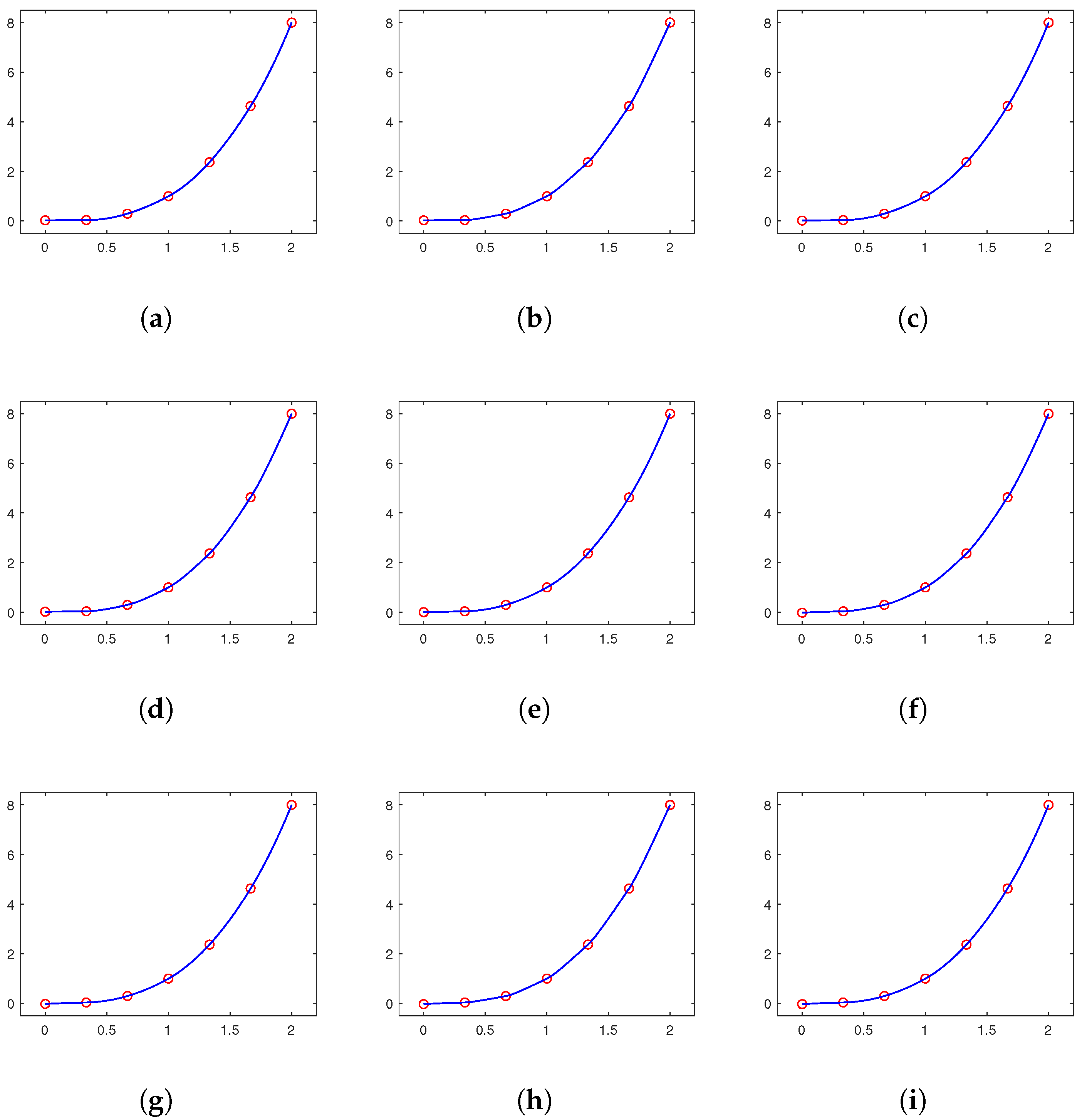
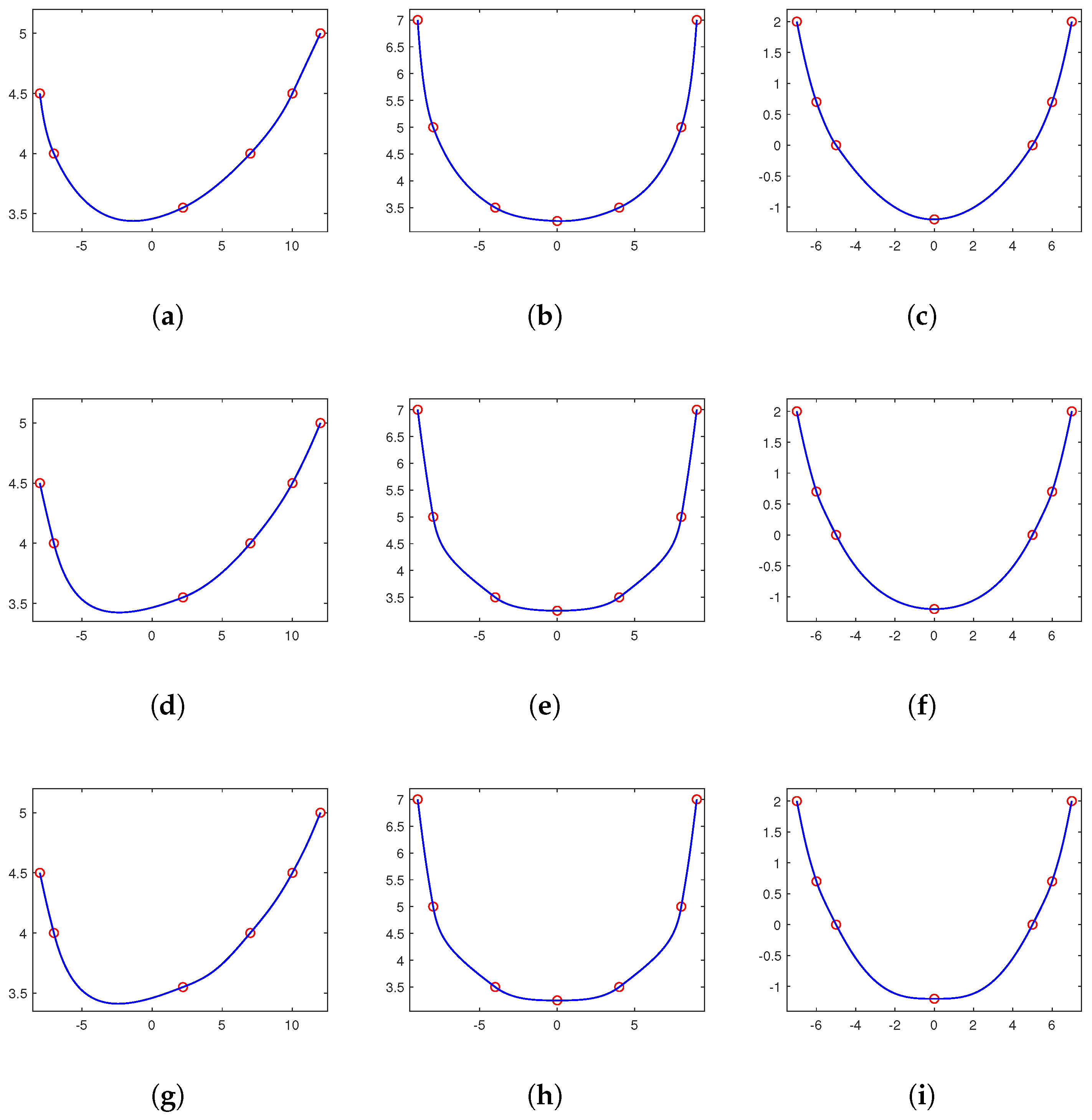
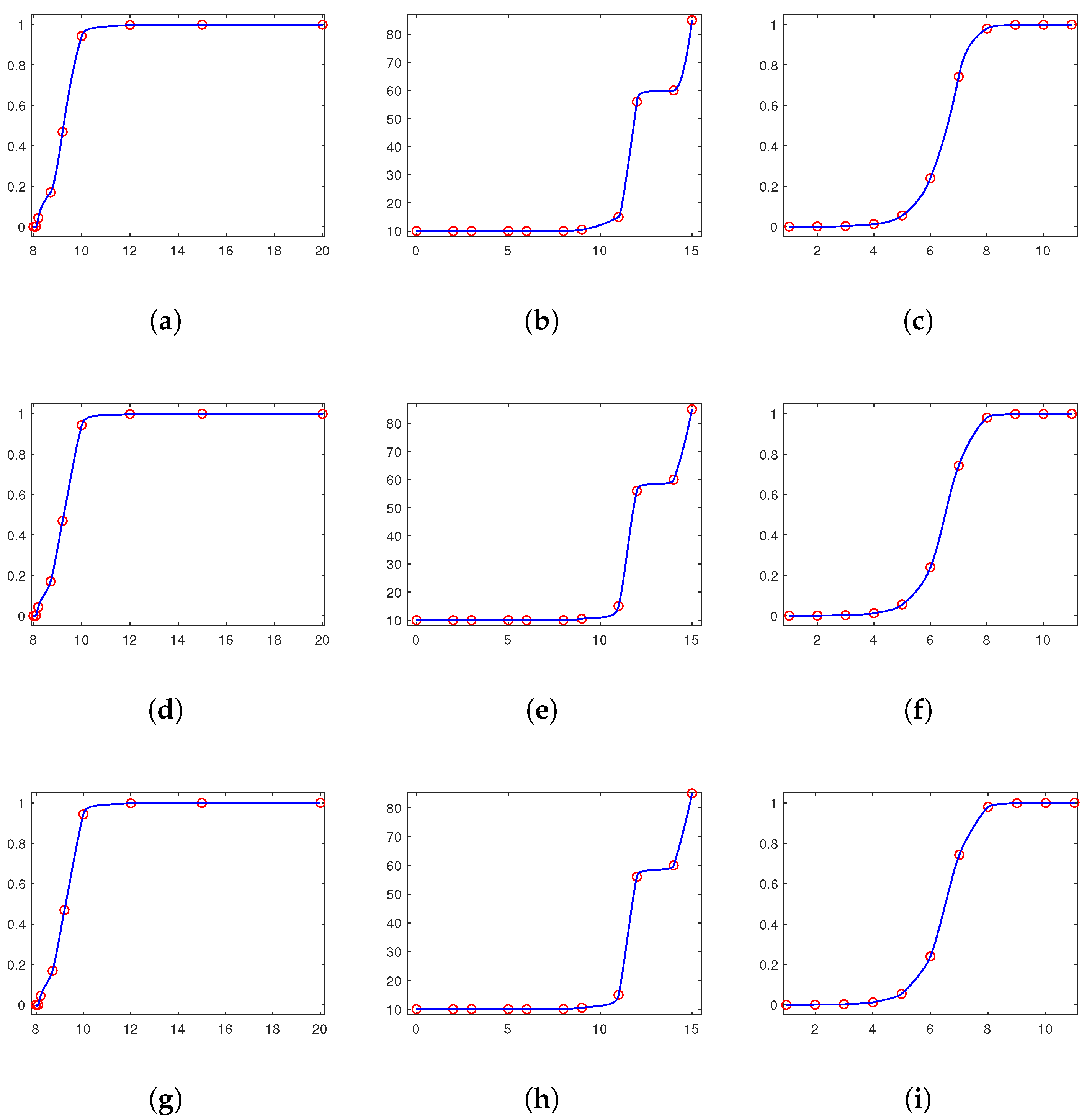
3. Adaptive Choice of Shape-Preserving Interpolation Splines
From the above Theorems 2, 5 and 8, we can see that convexity-, monotonicity- or non-negativity-preserving interpolants are uniquely solvable only for , or , respectively. Furthermore, for , or , there exists an infinite number of convexity-, monotonicity- or non-negativity-preserving interpolants . In this section, we shall minimize a particular approximated curvature to select a visually appealing shape-preserving interpolation spline.
The classical geometric curvature is defined as follows
which is usually used as an objective function, while in real applications, the denominator makes the integration a big difficulty. In order to obtain a more convenient objective function, we follow the method given in [
24] to approximate
by the slope
given in (
3) for
. Therefore, the following particular approximated curvature is taken as the objective function for selecting a shape-preserving interpolation spline
with
where
; see [
24].
Thus, when dealing with a convex set of data, we use the following quadratic program to select a convexity-preserving interpolant
Furthermore, when dealing with monotone increasing sets of data, we use the following quadratic program to select a monotonicity-preserving interpolant
Furthermore, when dealing with a non-negative set of data, we use the following quadratic program to select a non-negativity-preserving interpolant
The quadratic programs given in (
41)–(
43) are easily solved since the objective function and the constraints are actually functions of
alone. To be more concrete, by using the relations given in (
11), the quadratic program (
41) reduces to
and by using the relations given in (
22), the quadratic program (
42) reduces to
and by using the relations given in (
35), the quadratic program (
43) reduces to
Let the unconstrained minimizers of (
44)–(
46) be denoted as
,
and
, respectively, i.e.,
Summarizing the above discuss, we can conclude the following theorem.
Theorem 10. The optimal minimizers , , and of the programs (
44)
, (
45)
, and (
46)
, respectively, are given bywhere , , and are given in (
47)
, (
48)
, and (
49)
, respectively.