Improved Estimator Using Auxiliary Information in Adaptive Cluster Sampling with Networks Selected Without Replacement
Abstract
1. Introduction
2. Concept of ACS Without Replacement of Units
3. Concept of ACS with Networks Selected Without Replacement
4. Proposed Estimator in ACS Without Replacement of Networks
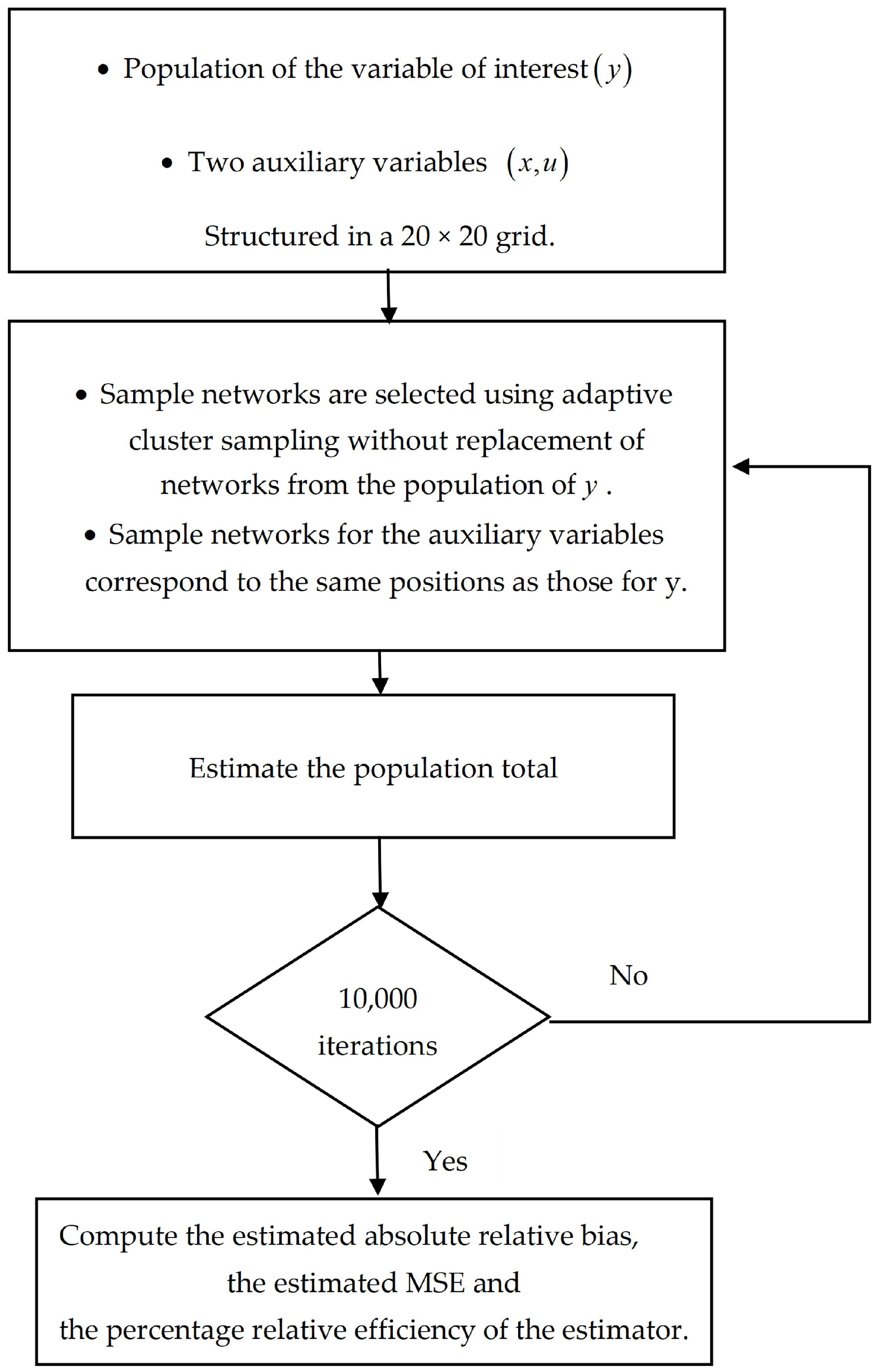
5. Results and Discussion
5.1. Simulation Study
5.2. Discussion
- The results in Table 1 demonstrate that, for all estimators, the estimated absolute relative bias decreased as the network sample size increased. Among the estimators, the product-type estimator consistently exhibited higher estimated absolute relative bias than the other estimators.
- Table 2 presents the estimated mean square error (MSE) of the estimators. Here, represents the estimated mean square error of the modified Des Raj estimator, which did not rely on auxiliary variable information, while refers to the proposed estimator that incorporates two auxiliary variables. For all network sample sizes, the estimated mean square error of the proposed estimator was lower than that of the modified Des Raj estimator, , when , (ratio-cum-product-type estimator), and , (the proposed estimator with optimal values). The proposed estimator with the optimal values as , achieved the lowest estimated MSE compared to the settings , and , corresponding to ratio-type, product-type, ratio-cum-product type, and product-cum-ratio-type estimators, respectively. The estimated MSE of the product-type estimator was particularly high, as this estimator was applied in scenarios where the variable of interest and the auxiliary variables were related in opposing directions.
- Table 3 presents the percentage relative efficiency (PRE) of the proposed estimator compared to the modified Des Raj estimator , where is set to 100. A PRE value greater than 100 indicates that the estimator is more efficient than . The results show that the product-type and product-cum-ratio-type estimators exhibited lower efficiency than across all network sample sizes. The ratio-type estimator demonstrated higher efficiency than when the network sample size was small. Meanwhile, the ratio-cum-product-type estimator and the proposed estimator with optimal values of and as had higher efficiency than for all network sample sizes. Among all the estimators, the proposed estimator with optimal values of and was the most efficient.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
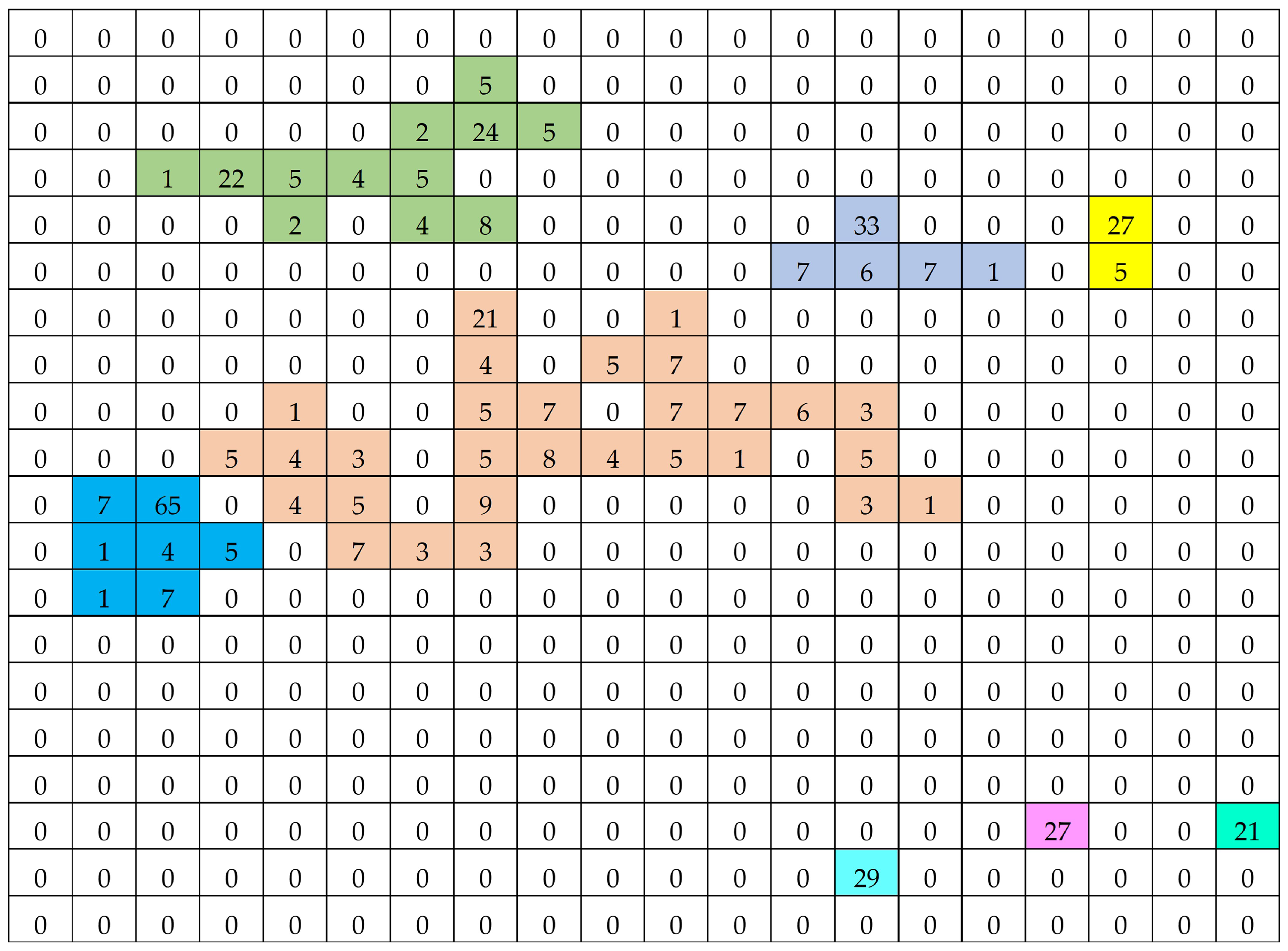
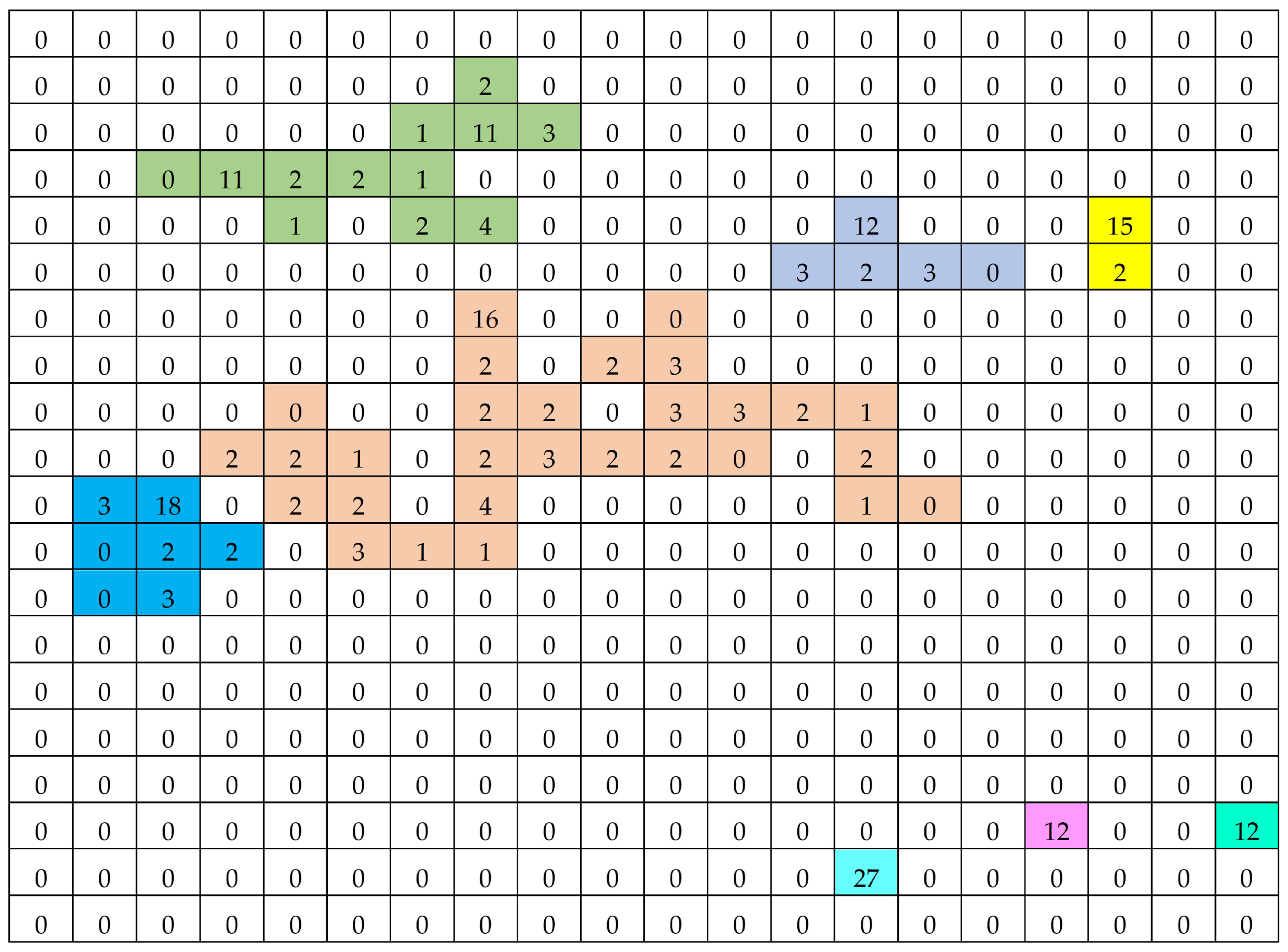
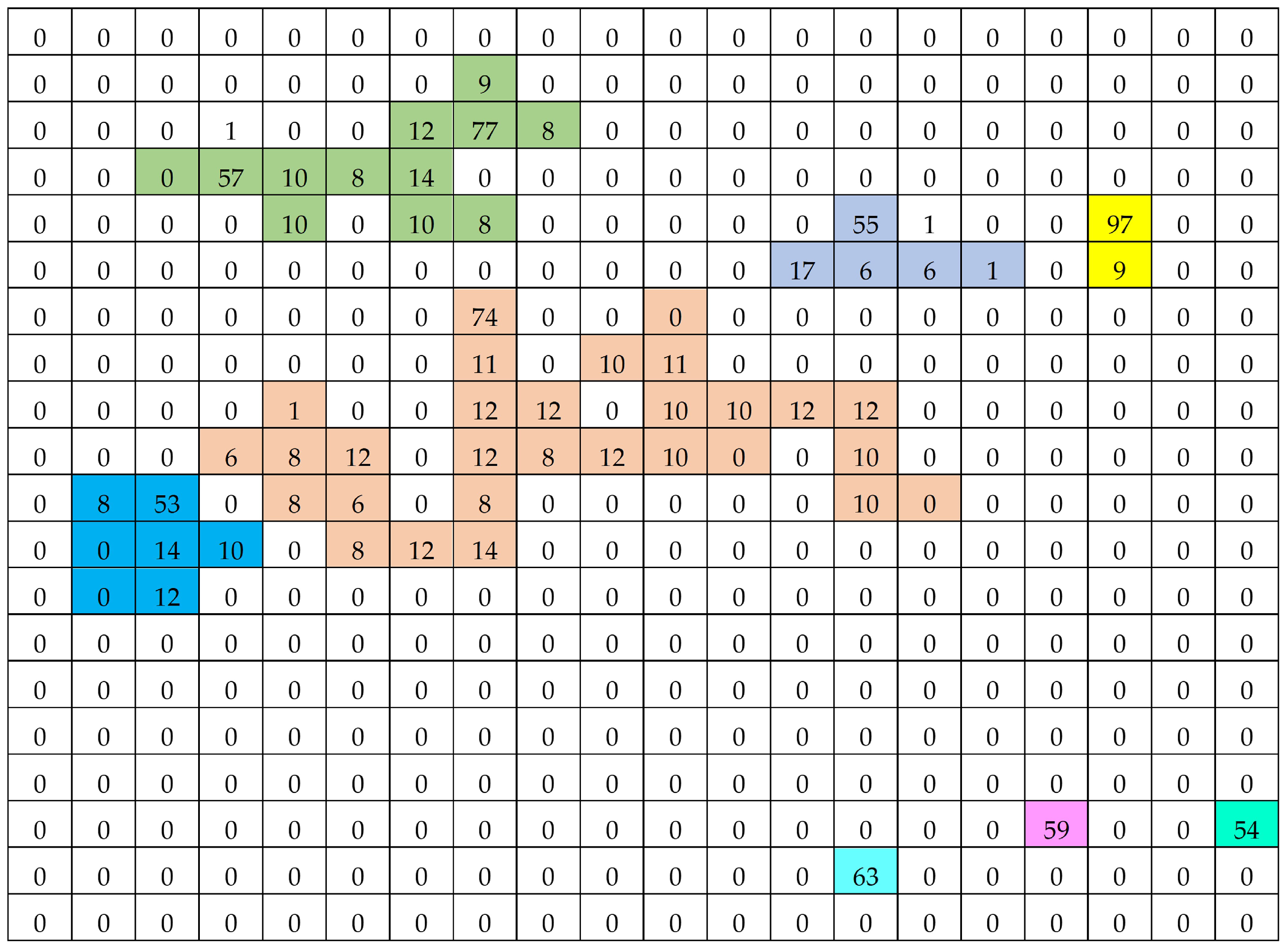
References
- Thompson, S.K. Adaptive cluster sampling. J. Am. Statist. Assoc. 1990, 85, 1050–1059. [Google Scholar] [CrossRef]
- Magnussen, S.; Kurz, W.; Leckie, D.G.; Paradine, D. Adaptive cluster sampling for estimation of deforestation rates. Eur. J. For. Res. 2005, 124, 207–220. [Google Scholar] [CrossRef]
- Noon, B.R.; Ishwar, N.M.; Vasudevan, K. Efficiency of adaptive cluster and random sampling in detecting terrestrial herpetofauna in a tropical rainforest. Wildl. Soc. Bull. 2006, 34, 59–68. [Google Scholar] [CrossRef]
- Sullivan, W.P.; Morrison, B.J.; Beamish, F.W.H. Adaptive cluster sampling: Estimating density of spatially autocorrelated larvae of the sea lamprey with improved precision. J. Great Lakes Res. 2008, 34, 86–97. [Google Scholar] [CrossRef]
- Smith, D.R.; Villella, R.F.; Lemarié, D.P. Application of adaptive cluster sampling to low-density populations of freshwater mussels. Environ. Ecol. Stat. 2003, 10, 7–15. [Google Scholar] [CrossRef]
- Conners, M.E.; Schwager, S.J. The use of adaptive cluster sampling for hydroacoustic surveys. ICES J. Mar. Sci. 2002, 59, 1314–1325. [Google Scholar] [CrossRef]
- Olayiwola, O.M.; Ajayi, A.O.; Onifade, O.C.; Wale-Orojo, O.; Ajibade, B. Adaptive cluster sampling with model based approach for estimating total number of Hidden COVID-19 carriers in Nigeria. Stat. J. IAOS 2020, 36, 103–109. [Google Scholar] [CrossRef]
- Chandra, G.; Tiwari, N.; Nautiyal, R. Adaptive cluster sampling-based design for estimating COVID-19 cases with random samples. Curr. Sci. 2021, 120, 1204–1210. [Google Scholar] [CrossRef]
- Stehlík, M.; Kiseľák, J.; Dinamarca, A.; Alvarado, E.; Plaza, F.; Medina, F.A.; Stehlíková, S.; Marek, J.; Venegas, B.; Gajdoš, A.; et al. REDACS: Regional emergency-driven adaptive cluster sampling for effective COVID-19 management. Stoch. Anal. Appl. 2022, 41, 474–508. [Google Scholar] [CrossRef]
- Hwang, J.; Bose, N.; Fan, S. AUV adaptive sampling methods: A Review. Appl. Sci. 2019, 9, 3145. [Google Scholar] [CrossRef]
- Giouroukis, D.; Dadiani, A.; Traub, J.; Zeuch, S.; Markl, V. A survey of adaptive sampling and filtering algorithms for the internet of things. In Proceedings of the 14th ACM International Conference on Distributed and Event Based Systems, Montreal, QC, Canada, 13–17 July 2020; pp. 27–38. [Google Scholar] [CrossRef]
- Salehi, M.M.; Seber, G.A.F. Adaptive cluster sampling with networks selected without replacement. Biometrika 1977, 84, 209–219. [Google Scholar] [CrossRef]
- Chao, C.T. Ratio estimation on adaptive cluster sampling. J. Chin. Stat. Assoc. 2004, 42, 307–327. [Google Scholar] [CrossRef]
- Dryver, A.L.; Chao, C.T. Ratio estimators in adaptive cluster sampling. Environmetric 2007, 18, 607–620. [Google Scholar] [CrossRef]
- Chutiman, N.; Kumphon, B. Ratio estimator using two auxiliary variables for adaptive cluster sampling. Thail. Stat. 2008, 6, 241–256. [Google Scholar]
- Chutiman, N. Adaptive cluster sampling using auxiliary variable. J. Math. Stat. 2013, 9, 249–255. [Google Scholar] [CrossRef]
- Yadav, S.K.; Misra, S.; Mishra, S. Efficient estimator for population variance using auxiliary variable. Am. J. Oper. Res. 2016, 6, 9–15. [Google Scholar] [CrossRef]
- Chaudhry, M.S.; Hanif, M. Generalized exponential-cum-exponential estimator in adaptive cluster sampling. Pak. J. Stat. Oper. Res. 2015, 11, 553–574. [Google Scholar] [CrossRef]
- Singh, R.; Mishra, R. Transformed ratio type estimators under adaptive cluster sampling an application to covid-19. J. Stat. Appl. Probab. Lett. 2022, 9, 63–70. [Google Scholar] [CrossRef]
- Bhat, A.A.; Sharma, M.; Shah, M.; Bhat, M. Generalized ratio type estimator under adaptive cluster sampling. J. Sci. Res. 2022, 67, 46–51. [Google Scholar] [CrossRef]
- Mishra, R.; Singh, R.; Raghav, Y.S. On combining ratio and product type estimators for estimation of finite population mean in adaptive cluster sampling design. Braz. J. Biom. 2024, 42, 412–420. [Google Scholar] [CrossRef]
- Chutiman, N.; Chiangpradit, M. Ratio estimator in adaptive cluster sampling without replacement of networks. J. Probab. Stat. 2014, 2014, 726398. [Google Scholar] [CrossRef]
- Raj, D. Some Estimators in sampling with varying probabilities without replacement. J. Am. Stat. Assoc. 1956, 51, 269–284. [Google Scholar] [CrossRef]
- Gupta, S.; Shabbir, J. On the use of transformed auxiliary variables in estimating population mean by using two auxiliary variables. J. Stat. Plan. Inference 2007, 137, 1606–1611. [Google Scholar] [CrossRef]
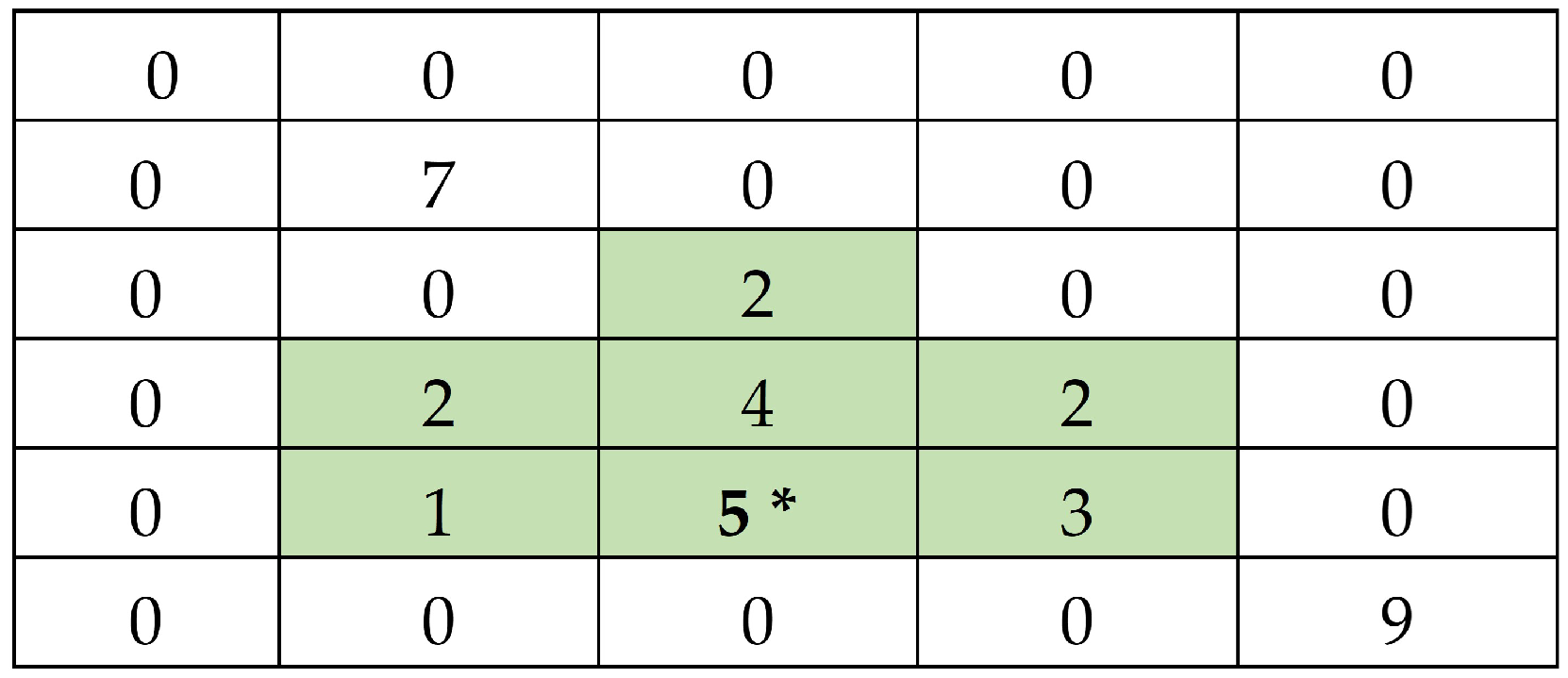
| n | ||||
|---|---|---|---|---|
| 2 | 0.9091 | 43.7092 | 0.0409 | 0.7103 |
| 5 | 0.5723 | 9.6476 | 0.0272 | 0.4120 |
| 10 | 0.4252 | 3.9173 | 0.0215 | 0.1237 |
| 15 | 0.3712 | 2.0932 | 0.0141 | 0.1210 |
| 20 | 0.3167 | 1.2775 | 0.0088 | 0.0960 |
| 25 | 0.3134 | 1.1377 | 0.0082 | 0.0765 |
| 50 | 0.1912 | 0.4281 | 0.0025 | 0.0143 |
| n | |||||||
|---|---|---|---|---|---|---|---|
| , | , | ||||||
| 2 | 6.8466 | 968,885.0341 | 204,764.3145 | 26,322,915,632.8267 | 926,194.3208 | 1,445,829.5306 | 188,667.2977 |
| 5 | 16.1432 | 375,678.8942 | 132,903.3653 | 556,216,006.2863 | 375,147.0977 | 535,979.9843 | 121,855.7443 |
| 10 | 29.3040 | 185,513.8035 | 146,738.8306 | 68,892,932.1431 | 172,073.9448 | 291,531.9326 | 68,099.7147 |
| 15 | 39.5225 | 117,455.5717 | 245,276.4686 | 16,271,424.1794 | 111,666.6914 | 176,639.4646 | 45,295.0030 |
| 20 | 53.0735 | 80,580.0398 | 309,571.7174 | 4,919,034.4968 | 76,522.4944 | 116,484.1294 | 27,811.8563 |
| 25 | 59.9526 | 64,537.0999 | 272,468.2427 | 3,344,904.9521 | 59,331.5526 | 100,902.1119 | 23,029.4124 |
| 50 | 93.7806 | 25,465.4180 | 84,934.4510 | 630,026.2443 | 22,545.9512 | 41,470.0784 | 5722.4797 |
| n | ||||||
|---|---|---|---|---|---|---|
| , | , | |||||
| 2 | 100 | 473.1708 | 0.0037 | 104.6093 | 67.0124 | 513.5416 |
| 5 | 100 | 282.6707 | 0.0675 | 100.1418 | 70.0920 | 308.2981 |
| 10 | 100 | 126.4245 | 0.2693 | 107.8105 | 63.6341 | 272.4149 |
| 15 | 100 | 47.8870 | 0.7219 | 105.1841 | 66.4945 | 259.3124 |
| 20 | 100 | 26.0295 | 1.6381 | 105.3024 | 69.1768 | 289.7327 |
| 25 | 100 | 23.6861 | 1.9294 | 108.7737 | 63.9601 | 280.2377 |
| 50 | 100 | 29.9824 | 4.0420 | 112.9490 | 61.4067 | 445.0067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chutiman, N.; Nathomthong, A.; Wichitchan, S.; Guayjarernpanishk, P. Improved Estimator Using Auxiliary Information in Adaptive Cluster Sampling with Networks Selected Without Replacement. Symmetry 2025, 17, 375. https://doi.org/10.3390/sym17030375
Chutiman N, Nathomthong A, Wichitchan S, Guayjarernpanishk P. Improved Estimator Using Auxiliary Information in Adaptive Cluster Sampling with Networks Selected Without Replacement. Symmetry. 2025; 17(3):375. https://doi.org/10.3390/sym17030375
Chicago/Turabian StyleChutiman, Nipaporn, Athipakon Nathomthong, Supawadee Wichitchan, and Pannarat Guayjarernpanishk. 2025. "Improved Estimator Using Auxiliary Information in Adaptive Cluster Sampling with Networks Selected Without Replacement" Symmetry 17, no. 3: 375. https://doi.org/10.3390/sym17030375
APA StyleChutiman, N., Nathomthong, A., Wichitchan, S., & Guayjarernpanishk, P. (2025). Improved Estimator Using Auxiliary Information in Adaptive Cluster Sampling with Networks Selected Without Replacement. Symmetry, 17(3), 375. https://doi.org/10.3390/sym17030375








