Lie Group Classification, Symmetry Reductions, and Conservation Laws of a Monge–Ampère Equation

Abstract

The nonhomogeneous Monge–Ampère equation, read as $w_{xx}{w}_{yy}-w_{xy}^2+h\left(w\right)=0$, is a nonlinear equation involving mixed second derivatives with respect to the spatial variables x and y, along with an additional source function $h\left(w\right)$. This equation is observed in several fields, including differential geometry, fluid dynamics, and magnetohydrodynamics. In this study, the Lie symmetry method is used to obtain a detailed classification of this equation. Symmetry analysis leads to a comprehensive classification of the equation, resulting in specific forms of the smooth source function $h\left(w\right)$. Furthermore, the one-dimensional optimal system of the associated Lie algebras is derived, allowing for symmetry reductions that yield several exact invariant solutions of the Monge–Ampère equation. In addition, conservation laws are constructed using the Noether approach, a highly effective and widely used method for deriving conserved quantities. These conservation laws can help evaluate the accuracy and reliability of numerical methods.

1. Introduction

The study of partial differential equations (Pdes), linear or nonlinear, occupies a pivotal role in simulating complex physical systems found in the real world. In addition, the understanding of nonlinear partial differential equations facilitates the formation of mathematical frameworks that illustrate diverse physical phenomena across various scientific disciplines. Among such equations, the nonlinear Monge–Ampère equation is of significant importance due to its wide applications in domains such as fluid dynamics, geometrical and surface theory, wave propagation, and optical transport theory [1,2]. This equation has a wide significance in affine differential geometry, especially in the study of affine spheres and maximal surfaces, where symmetry-based analysis helps discover important geometric properties. Numerous studies have discovered the classification and applications of Monge–Ampère equations using Lie symmetry methods, offering valuable contributions to both theoretical and applied mathematics [3,4].

The Monge–Ampère equation, in its classical form, is read as follows:

$$w_{xx}{w}_{yy}-w_{xy}^2=0,$$

(1)

characterized by quadratic nonlinearity in mixed and pure second derivatives, this equation presents distinct and complex challenges, requiring a thorough analysis by advanced mathematical techniques, such as Lie symmetry methods or numerical approaches. Symmetry analysis, which originated from the pioneered work of Sophus Lie, is an efficient, reliable, and systematic approach that facilitates transforming more complex nonlinear Pde into simpler versions by reducing the number of independent variables, often into ordinary differential equations (Odes) that are easier to tackle. For example, Ovsiannikov’s seminal work offered a systematic foundation for the applications of symmetry methods to Pdes, establishing a framework to find exact solutions [5]. Following this work, subsequent studies have been carried out to solve nonlinear differential equations [6]. Various books detail the applications of this method [7,8].

Studying the symmetry properties of nonlinear differential equations, such as the Monge–Ampère equation, involves finding the particular forms of the arbitrary functions and the Lie point symmetries by solving the determining system of equations which are often nonlinear and quite challenging to handle. These symmetries help researchers in classifying differential equations into various forms and conducting symmetry reductions, which aid in the construction of exact and invariant solutions. These solutions contribute to a complete understanding of the physical properties of the system described by the equations. Given the efficacy of Lie symmetry methods, numerous studies have applied this technique to solve nonlinear Pdes, including the Monge–Ampère equation [9]. In the domain of differential geometry, the Monge–Ampère equation, which is a highly nonlinear partial differential equation, models problems such as convex surfaces, optimal transport and Kähler metrics. One of the defining features of these types of equation lies in applied sciences, where they are used to model physical phenomena such as nonlinear elasticity, plasma flows, and electron magnetohydrodynamics. Despite the complexity of obtaining solutions for the Monge–Ampère type equation, Lie symmetry methods have proven to be effective in reducing this equation to a more manageable form and finding the closed-form and exact solutions of this equation, providing valuable insight into the associated physical dynamics and acting as standard benchmarks for validating numerical methods. For example, Polyanin et al. obtained the symmetry reductions and closed-form solutions of the homogeneous unsteady Monge–Ampère equation [10]. The asymptotic behavior of this equation was discussed by Ning An et al. [11]. Further, the symmetry properties of the homogeneous steady Monge–Ampère Equation (1) were studied by Ibragimov [9]. Moreover, using symmetry methods, various versions of Monge–Ampère equation have been studied by researchers. For instance, Fang Gao obtained the optimal system, symmetry reductions, and invariant solutions of the hyperbolic Monge–Ampère equation [12]. Yanzhi et al. derived the power series and periodic solutions of the logarithmic version of the Monge–Ampère equation [13]. Furthermore, recent studies have primarily focused on invariant Monge–Ampère equations on homogeneous contact manifolds of semisimple Lie groups, broadening the geometric understanding of these equations [14]. These studies highlight the crucial role of Lie symmetry methods in uncovering the new structural and solution properties of the Monge–Ampère equation across various fields.

In the present research, the focus is given to the nonhomogeneous Monge–Ampère equation, which is characterized by its quadratic nonlinearity in second mixed derivatives and can be written as follows:

$$w_{xx}{w}_{yy}-w_{xy}^2+h\left(w\right)=0,$$

(2)

where the generalization (2) of Equation (1), incorporated by the source function $h\left(w\right)$, governs more complex nonlinear dynamics, such as shockwaves, solitons, and pattern formations, based on the nature of the function $h\left(w\right)$. For example, in fluid dynamics, the presence of $h\left(w\right)$ in a system may signify external forces or applied magnetic fields, influence the evolution of magnetic fields, and highlight complex flow patterns. The source function can take various forms, such as polynomial, exponential, or a constant function, introducing nonlinearity into a system; depending on these forms, the system may exhibit a vast range of qualitative solution behaviors, including shockwave, soliton, or oscillatory behaviors. The special forms of $h\left(w\right)$ allow the identification of several exact solutions [9,15,16]. Unlike linear Pdes, Monge–Ampère equations generally lack straightforward exact and closed-form solutions, making Lie symmetry methods, reductions, and conservation laws useful for their analysis.

Conservation laws, in the context of nonlinear partial differential equations, are integral for their analysis and understanding the intrinsic behavior of their solutions. In general, these conservation laws can be expressed as divergence expressions, representing the invariance of physical quantities under the evolution of the system over time. Identifying conservation laws offers information on the stability and nature of solutions [8,17,18]. In addition, conservation laws help validate the stability, uniqueness, and precision of numerical methods. In recent years, associated with the Monge–Ampère equation, conservation laws have been derived using different approaches, including geometric and variational methods [19,20,21]. The present research also focuses on deriving the conservation laws of Equation (2) using the Noether’s approach [22], which first established the connection between symmetries and conservation laws. This approach is only applicable to problems that possess a variational structure, for example, Equation (2). However, to derive conservation laws for nonvariational problems, alternative techniques can be applied, including the partial Lagrangian approach, direct method, multiplier methods, and Ibragimov’s generalization of Noether’s theorem [17,23,24].

The present research addresses the analysis of the Lie group, the optimal system, the reductions in symmetry, and the conservation laws of the Monge–Ampère Equation (2) [25]. Lie symmetry analysis facilitates the derivation of Lie symmetries and the group classification of Equation (2), which in turn leads to the discovery of invariant solutions. For example, applying the Lie symmetry to a $(1+1)-$dimensional Pde, such as Equation (2), reduces its independent variables, thereby transforming it into equivalent Odes, known as symmetry reductions. These reductions often help in identifying the closed-form solutions, exact solutions, and traveling wave solutions. However, to obtain unique symmetry reductions, it is essential to derive the optimal system of Lie algebras, which comprises the minimal set of non-equivalent subalgebras, each corresponding to distinct reductions [8]. The technique described in the established works [5,7,9] is utilized to derive the optimal system and invariant solutions of Equation (2). To enhance the structural understanding of complex dynamics defined by Monge–Ampère equations, its classification has been widely studied. A foundational classification of the Monge–Ampère equation was proposed by Lychagin et al., which was later refined by Kruglikov for equations with two variables [26].

The structure of this paper is organized as follows. Section 2 covers the complete determination of the Lie symmetries of Equation (2), including identifying the specific forms of the unknown smooth function $h\left(w\right)$. Section 3 lists the optimal system for all the cases mentioned in Section 2. Subsequently, Section 4 focuses on performing reductions of Equation (2) based on the optimal system of Lie algebras derived in Section 3, and it also includes some invariant solutions. Finally, Section 5 outlines the conservation laws constructed using the Noether approach.

2. Symmetry Group Classification

This section examines the complete Lie group analysis for Equation (2) and provides the summary of the cases associated with the arbitrary source function $h\left(w\right)$. For this analysis, we utilize a one-parameter Lie group of point transformations that ensure the invariance of Equation (2) and those transformation formulas are widely used and are available in references such as [5]. The symmetry operator is defined as follows:

$$\mathcal{Y}={\tau }^1(w,y,x){\displaystyle \frac{\partial }{\partial x}}+{\tau }^2(w,y,x){\displaystyle \frac{\partial }{\partial y}}+\varphi (w,y,x){\displaystyle \frac{\partial }{\partial w}}.$$

(3)

According to the well-known concept as outlined in sources [5,7,8], we require a second-order prolongation compatible with the order of Equation (2), which is a second-order equation, and the required formula is provided by

$${\mathcal{Y}}^{\left[2\right]}=\mathcal{Y}+{\eta }^i{\displaystyle \frac{\partial }{\partial w_i}}+{\eta }^{ij}{\displaystyle \frac{\partial }{\partial w_{ij}}},$$

where ${\eta }^i$ and ${\eta }^{ij}$ are defined by

$$\begin{array}{cc}\hfill {\eta }^i& ={\mathcal{D}}_i\left(\varphi \right)-w_j{\mathcal{D}}_i{\tau }^j,\hfill \\ \hfill {\eta }^{ij}& ={\mathcal{D}}_j\left({\eta }^i\right)-w_{ji}{\mathcal{D}}_i{\tau }^j,i,j=1,2.,\hfill \end{array}$$

and ${\mathcal{D}}_i$ refers to the total derivative operator, defined by

$${\mathcal{D}}_i={\displaystyle \frac{\partial }{\partial z^i}}+w_i{\displaystyle \frac{\partial }{\partial w}}+\dots ,(z^1,z^2)=(x,y).$$

The expanded form of the above formula is given by

$${\mathcal{Y}}^{\left[2\right]}=\mathcal{Y}+{\varphi }^x{\displaystyle \frac{\partial }{\partial w_x}}+{\varphi }^y{\displaystyle \frac{\partial }{\partial w_y}}+{\varphi }^{xy}{\displaystyle \frac{\partial }{\partial w_{xy}}}+{\varphi }^{xx}{\displaystyle \frac{\partial }{\partial w_{xx}}}+{\varphi }^{yy}{\displaystyle \frac{\partial }{\partial w_{yy}}}.$$

(4)

In the context of the Lie symmetry approach, the operator defined in Equation (3) serves as a Lie point symmetry generator for Equation (2), provided that the following invariance condition holds:

$${\mathcal{Y}}^{\left[2\right]}\left(w_{xx}{w}_{yy}-w_{xy}^2+h\left(w\right)\right){|}_{(w_{xx}={\displaystyle \frac{1}{w_{yy}}}(w_{xy}^2-h\left(w\right)))}=0.$$

(5)

Consequently, the subsequent determining system of Pdes arises by the expansion of Equation (5) and comparison of the coefficients associated with the independent derivatives of w:

$$\begin{array}{cc}\hfill {\varphi }_{ww}& =0,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\varphi }_{xx}& =0,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\varphi }_{yy}& =0,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\varphi }_{xy}& =0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\tau }_{xx}^2& =0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\tau }_{yy}^1& =0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill 2{\varphi }_{wy}-{\tau }_{yy}^2& =0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill 2{\varphi }_{wx}-{\tau }_{xx}^1& =0,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\tau }_{xy}^1-{\varphi }_{wy}& =0,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\tau }_{xy}^2-{\varphi }_{wx}& =0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \varphi h_w+2({\tau }_x^1+{\tau }_y^2-{\varphi }_w)h\left(w\right)& =0.\hfill \end{array}$$

(16)

It follows from Equations (6) and (7) that

$$\varphi =\left(x\alpha \left(y\right)+\beta \left(y\right)\right)w+\left(x\gamma \left(y\right)+\psi \left(y\right)\right).$$

(17)

Next, Equation (9) yields

$${\alpha }_y=0={\gamma }_y.$$

Integrating with respect to y, and substituting the results in Equation (17), the following revised expression for Equation (17) emerges

$$\varphi =\left(x{a}_1+\beta \left(y\right)\right)w+\left(x{a}_2+\psi \left(y\right)\right).$$

(18)

Now, by using Equation (8), we obtain

$$\varphi =\left(x{a}_1+(a_{3}y+a_4)\right)w+\left(x{a}_2+(a_{5}y+a_6)\right).$$

(19)

From Equations (10) and (11)

$$\begin{array}{cc}\hfill {\tau }^2& =\mathcal{E}\left(y\right)x+\mathcal{F}\left(y\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\tau }^1& ={\mathcal{E}}^1\left(x\right)y+{\mathcal{F}}^1\left(x\right).\hfill \end{array}$$

(21)

Substituting Equation (20) in Equation (12) and Equation (21) in Equation (13), we obtain

$$\begin{array}{cc}\hfill {\mathcal{E}}_{yy}& =0={\mathcal{F}}_{yy},\hfill \\ \hfill {\mathcal{E}}_{xx}^1& =0={\mathcal{F}}_{xx}^1.\hfill \end{array}$$

Further, twice integration ${\mathcal{E}}_{yy}$, ${\mathcal{F}}_{yy}$ with respect to y and ${{\mathcal{E}}^1}_{xx}$, ${{\mathcal{F}}^1}_{xx}$ with respect to x, and substituting back into system, we obtain the following expressions for ${\tau }^1$ and ${\tau }^2$

$$\begin{array}{cc}\hfill {\tau }^1& =(c_1+c_{2}x)y+a_1{x}^2+c_{3}x+c_4,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\tau }^2& =(b_1+a_{1}y)x+a_3{y}^2-c_{3}y+b_4.\hfill \end{array}$$

(23)

If $h\left(w\right)$ is an arbitrary function in w, then the following conditions emerge from Equation (16):

$$\begin{array}{c}\hfill a_i=0,\mathrm{where}i=1,2,3,\dots ,6.\end{array}$$

Hence, for $h\left(w\right)$ being an arbitrary function, the five-dimensional Lie algebra is obtained, which represents the principal Lie algebra of Equation (2), and it is defined by

$$\begin{array}{cc}\hfill {\mathcal{Y}}_1& ={\displaystyle \frac{\partial }{\partial x}},{\mathcal{Y}}_2={\displaystyle \frac{\partial }{\partial y}},{\mathcal{Y}}_3=y{\displaystyle \frac{\partial }{\partial x}},{\mathcal{Y}}_4=x{\displaystyle \frac{\partial }{\partial y}},{\mathcal{Y}}_5=x{\displaystyle \frac{\partial }{\partial x}}-y{\displaystyle \frac{\partial }{\partial y}}.\hfill \end{array}$$

Equation (16) implies that

$$\varphi =-2({\tau }_x^1+{\tau }_y^2-{\varphi }_w){\displaystyle \frac{h}{h_w}}.$$

(24)

Differentiating Equation (24) with respect to w, we obtain

$${\varphi }_w=-2({\tau }_x^1+{\tau }_y^2-{\varphi }_w)({\displaystyle \frac{h}{h_w}}{)}_w.$$

(25)

Again differentiating the above equation with respect to w, we obtain

$$({\tau }_x^1+{\tau }_y^2-{\varphi }_w)({\displaystyle \frac{h}{h_w}}{)}_{ww}=0.$$

Now from this point, to extend the principal Lie algebra, we turn our focus to various cases.

• Case 1: ${\tau }_x^1+{\tau }_y^2-{\varphi }_w=0$

For this case, it follows from Equation (16) that

$$\varphi h_w=0,$$

implying that $h_w=0$, as $\varphi \ne 0.$ Thus, the resulting function is constant, i.e.,

$$h\left(w\right)=C,\left(constant\right).$$

(26)

Therefore, the principal Lie algebra is now extended to nine dimensions with the following additional symmetry generators:

$$\begin{array}{cc}\hfill {\mathcal{Y}}_6& =y{\displaystyle \frac{\partial }{\partial y}}+w{\displaystyle \frac{\partial }{\partial w}},\hfill \\ \hfill {\mathcal{Y}}_7& =x{\displaystyle \frac{\partial }{\partial w}},{\mathcal{Y}}_8=y{\displaystyle \frac{\partial }{\partial w}},{\mathcal{Y}}_9={\displaystyle \frac{\partial }{\partial w}}.\hfill \end{array}$$

• Case 2: $({\displaystyle \frac{h}{h_w}}{)}_{ww}=0$

In this case, we have

$$({\displaystyle \frac{h}{h_w}}{)}_{ww}=0,$$

integrating the above expression with respect to w, we obtain

$$({\displaystyle \frac{h}{h_w}}{)}_w=k.$$

(27)

In order to perform complete classifications of $h\left(w\right)$, we explore two more subcases:

• Subcase 2.1: $k\ne 0$

In this case, from Equation (29), we have

$${\displaystyle \frac{h}{h_w}}=kw+k_1.$$

After certain steps of calculations, we obtain the following form of the function $h\left(w\right)$:

$$h\left(w\right)=r{(w+n)}^m,\mathrm{where}m={\displaystyle \frac{1}{k}}.$$

For this form of $h\left(w\right)$, the following result is deduced from Equations (24) and (25):

$$\varphi =-{\displaystyle \frac{2}{m-2}}\left(3a_{3}y+3a_{1}x+c_3+b_3\right)(w+n).$$

(28)

By inserting Equation (28) into Equations (12) and (13), we obtain the following two additional subcases to deal with:

• Subcase 2.1.1: $m=-4$ and $a_1\ne a_3\ne 0$

This case leads to the following form of function $h\left(w\right)$:

$$h\left(w\right)=r{(w+n)}^{-4}.$$

As a result, the principal Lie algebra extends to nine dimensions, in addition to the subsequent symmetry generators:

$$\begin{array}{cc}\hfill {\mathcal{Y}}_6& =3y{\displaystyle \frac{\partial }{\partial y}}+(w+n){\displaystyle \frac{\partial }{\partial w}},{\mathcal{Y}}_7=xy{\displaystyle \frac{\partial }{\partial x}}+y^2{\displaystyle \frac{\partial }{\partial y}}+(w+n)y{\displaystyle \frac{\partial }{\partial w}},\hfill \\ \hfill {\mathcal{Y}}_8& =x^2{\displaystyle \frac{\partial }{\partial x}}+yx{\displaystyle \frac{\partial }{\partial y}}+(w+n)x{\displaystyle \frac{\partial }{\partial w}},{\mathcal{Y}}_9=3x{\displaystyle \frac{\partial }{\partial x}}+(w+n){\displaystyle \frac{\partial }{\partial w}}.\hfill \end{array}$$

• Subcase 2.1.2: $m\ne -4$ and $a_1=a_3=0$

In this case, the principal Lie algebra is expanded to six dimensions, accompanied by the following symmetry, defined as

$${\mathcal{Y}}_6={\displaystyle \frac{2-m}{2}}y{\displaystyle \frac{\partial }{\partial y}}+(w+n){\displaystyle \frac{\partial }{\partial w}}.$$

• Subcase 2.2: $k=0$

In this case, from Equation (29), we have

$$({\displaystyle \frac{h}{h_w}}{)}_w=0.$$

(29)

Upon integration with respect to w, this leads to the following expression of $h\left(w\right)$:

$$h\left(w\right)=\sigma e^{\delta w}.$$

Accordingly, the principal algebra expands to six dimensions, along with the associated symmetry generator:

$${\mathcal{Y}}_6=-{\displaystyle \frac{\delta }{2}}y{\displaystyle \frac{\partial }{\partial y}}+{\displaystyle \frac{\partial }{\partial w}}.$$

3. Optimal System of One-Dimensional Subalgebras

This section lists the commutation relations, adjoint tables, and the corresponding optimal system of one-dimensional subalgebras, addressing both the arbitrary case and the cases appearing from the group classification. Our purpose in identifying the optimal system, which mainly divides the symmetry generators into distinct classes, aids in minimizing the effort needed to obtain invariant solutions and unique symmetry reductions. The following subsections cover further details.

3.1. Commutator Table and Adjoint Representation

The following

Table 1. Commutation relations for arbitrary case.

$[{\mathcal{Y}}_{\mathit{i}}$, ${\mathcal{Y}}_{\mathit{j}}]$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$
${\mathcal{Y}}_1$	0	0	0	${\mathcal{Y}}_2$	${\mathcal{Y}}_1$
${\mathcal{Y}}_2$	0	0	${\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_2$
${\mathcal{Y}}_3$	0	$-{\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_5$	$2{\mathcal{Y}}_3$
${\mathcal{Y}}_4$	$-{\mathcal{Y}}_2$	0	${\mathcal{Y}}_5$	0	$-2{\mathcal{Y}}_4$
${\mathcal{Y}}_5$	$-{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-2{\mathcal{Y}}_3$	$2{\mathcal{Y}}_4$	0

,

Table 2. Commutation relations for Case 1.

$[{\mathcal{Y}}_{\mathit{i}}$, ${\mathcal{Y}}_{\mathit{j}}]$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_1$	0	0	0	${\mathcal{Y}}_2$	${\mathcal{Y}}_1$	0	0	0	0
${\mathcal{Y}}_2$	0	0	${\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_2$	${\mathcal{Y}}_2$	0	0	0
${\mathcal{Y}}_3$	0	$-{\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_5$	$2{\mathcal{Y}}_3$	$-{\mathcal{Y}}_3$	0	0	0
${\mathcal{Y}}_4$	$-{\mathcal{Y}}_2$	0	${\mathcal{Y}}_5$	0	$-2{\mathcal{Y}}_4$	${\mathcal{Y}}_4$	0	0	0
${\mathcal{Y}}_5$	$-{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-2{\mathcal{Y}}_3$	$2{\mathcal{Y}}_4$	0	0	0	0	0
${\mathcal{Y}}_6$	0	$-{\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-{\mathcal{Y}}_4$	0	0	0	0	0
${\mathcal{Y}}_7$	0	0	0	0	0	0	0	0	0
${\mathcal{Y}}_8$	0	0	0	0	0	0	0	0	0
${\mathcal{Y}}_9$	0	0	0	0	0	0	0	0	0

and

Table 3. Commutation relations for Cases 2.1.2 and 2.2.

$[{\mathcal{Y}}_{\mathit{i}}$, ${\mathcal{Y}}_{\mathit{j}}]$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$
${\mathcal{Y}}_1$	0	0	0	${\mathcal{Y}}_2$	${\mathcal{Y}}_1$	0
${\mathcal{Y}}_2$	0	0	${\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_2$	${\displaystyle \frac{2-m}{2}}{\mathcal{Y}}_2$
${\mathcal{Y}}_3$	0	$-{\mathcal{Y}}_1$	0	$-{\mathcal{Y}}_5$	$2{\mathcal{Y}}_3$	${\displaystyle \frac{m-2}{2}}{\mathcal{Y}}_3$
${\mathcal{Y}}_4$	$-{\mathcal{Y}}_2$	0	${\mathcal{Y}}_5$	0	$-2{\mathcal{Y}}_4$	${\displaystyle \frac{2-m}{2}}{\mathcal{Y}}_4$
${\mathcal{Y}}_5$	$-{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-2{\mathcal{Y}}_3$	$2{\mathcal{Y}}_4$	0	0
${\mathcal{Y}}_6$	0	${\displaystyle \frac{m-2}{2}}{\mathcal{Y}}_2$	${\displaystyle \frac{2-m}{2}}{\mathcal{Y}}_3$	${\displaystyle \frac{m-2}{2}}{\mathcal{Y}}_4$	0	0

present the commutation relations associated with the arbitrary cases and the cases 1, 2.1.2, and 2.2, which are later applied to determine the adjoint representations of the derived symmetry generators for all the cases.

Moreover, for each case, the following

Table 4. Adjoint table for arbitrary case.

$\mathit{Ad}\left({\mathit{e}}^{{\mathcal{Y}}_{\mathit{i}}}\right){\mathcal{Y}}_{\mathit{j}}$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$
${\mathcal{Y}}_1$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_4$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_5$
${\mathcal{Y}}_2$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_5$
${\mathcal{Y}}_3$	${\mathcal{Y}}_1$	$ϵ$${\mathcal{Y}}_1+{\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-{ϵ}^2{\mathcal{Y}}_3+ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_4$	$-2ϵ{\mathcal{Y}}_3+{\mathcal{Y}}_5$
${\mathcal{Y}}_4$	$ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-{ϵ}^2{\mathcal{Y}}_4-ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$2ϵ{\mathcal{Y}}_4+{\mathcal{Y}}_5$
${\mathcal{Y}}_5$	$e^{ϵ}$${\mathcal{Y}}_1$	$e^{-ϵ}$${\mathcal{Y}}_2$	$e^{2ϵ}$${\mathcal{Y}}_3$	$e^{-2ϵ}$${\mathcal{Y}}_4$	${\mathcal{Y}}_5$

,

Table 5. Adjoint table for Case 1.

$\mathit{Ad}\left({\mathit{e}}^{{\mathcal{Y}}_{\mathit{i}}}\right)$${\mathcal{Y}}_{\mathit{j}}$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_1$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_4$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_2$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_5$	$-ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_3$	${\mathcal{Y}}_1$	$ϵ$${\mathcal{Y}}_1+{\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-{ϵ}^2{\mathcal{Y}}_3+ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_4$	$-2ϵ{\mathcal{Y}}_3+{\mathcal{Y}}_5$	$ϵ{\mathcal{Y}}_3+{\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_4$	$ϵ$${\mathcal{Y}}_2+{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-{ϵ}^2{\mathcal{Y}}_4-ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$2ϵ{\mathcal{Y}}_4+{\mathcal{Y}}_5$	$-ϵ{\mathcal{Y}}_4+{\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_5$	$e^{ϵ}$${\mathcal{Y}}_1$	$e^{-ϵ}$${\mathcal{Y}}_2$	$e^{2ϵ}$${\mathcal{Y}}_3$	$e^{-2ϵ}$${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_6$	${\mathcal{Y}}_1$	$e^{ϵ}$${\mathcal{Y}}_2$	$e^{-ϵ}$${\mathcal{Y}}_3$	$e^{ϵ}$${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_7$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_8$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$
${\mathcal{Y}}_9$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$	${\mathcal{Y}}_7$	${\mathcal{Y}}_8$	${\mathcal{Y}}_9$

and

Table 6. Adjoint table for Cases 2.1.2 and 2.2.

$\mathit{Ad}\left({\mathit{e}}^{{\mathcal{Y}}_{\mathit{i}}}\right){\mathcal{Y}}_{\mathit{j}}$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$
${\mathcal{Y}}_1$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_4$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_5$	${\mathcal{Y}}_6$
${\mathcal{Y}}_2$	${\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_5$	${\displaystyle \frac{m-2}{2}}ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_6$
${\mathcal{Y}}_3$	${\mathcal{Y}}_1$	$ϵ{\mathcal{Y}}_1+{\mathcal{Y}}_2$	${\mathcal{Y}}_3$	$-{ϵ}^2{\mathcal{Y}}_3+ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_4$	$-2ϵ{\mathcal{Y}}_3+{\mathcal{Y}}_5$	${\displaystyle \frac{2-m}{2}}ϵ{\mathcal{Y}}_3+{\mathcal{Y}}_6$
${\mathcal{Y}}_4$	$ϵ{\mathcal{Y}}_2+{\mathcal{Y}}_1$	${\mathcal{Y}}_2$	$-{ϵ}^2{\mathcal{Y}}_4-ϵ{\mathcal{Y}}_5+{\mathcal{Y}}_3$	${\mathcal{Y}}_4$	$2ϵ{\mathcal{Y}}_4+{\mathcal{Y}}_5$	${\displaystyle \frac{m-2}{2}}ϵ{\mathcal{Y}}_4+{\mathcal{Y}}_6$
${\mathcal{Y}}_5$	$e^{ϵ}{\mathcal{Y}}_1$	$e^{-ϵ}$${\mathcal{Y}}_2$	$e^{2ϵ}{\mathcal{Y}}_3$	$e^{-2ϵ}$${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$
${\mathcal{Y}}_6$	${\mathcal{Y}}_1$	$e^{{\displaystyle \frac{2-m}{2}}ϵ}$${\mathcal{Y}}_2$	$e^{{\displaystyle \frac{m-2}{2}}ϵ}$${\mathcal{Y}}_3$	$e^{{\displaystyle \frac{2-m}{2}}ϵ}$${\mathcal{Y}}_4$	${\mathcal{Y}}_5$	${\mathcal{Y}}_6$

provide the adjoint action representation tables corresponding to the principal Lie algebra, as well as extended symmetry algebras.

The adjoint tables presented above are determined using the adjoint map, which is stated as follows:

$$Ad\left(e^{{\mathcal{Y}}_i}\right){\mathcal{Y}}_j={\mathcal{Y}}_j-ϵ[{\mathcal{Y}}_i,{\mathcal{Y}}_j]+{\displaystyle \frac{{ϵ}^2}{2!}}[{\mathcal{Y}}_i,[{\mathcal{Y}}_i,{\mathcal{Y}}_j]]+\dots .$$

(30)

For Cases 2.1.2 and 2.2, the commutator and adjoint tables are identical, so they are labeled as Table 3 and Table 6, respectively. However, in these tables, ${\displaystyle \frac{m-2}{2}}$ may be substituted with ${\displaystyle \frac{\delta }{2}}$ and ${\displaystyle \frac{2-m}{2}}$ to be replaced by $-{\displaystyle \frac{\delta }{2}}$. Moreover, the symmetry generator ${\mathcal{Y}}_6$ distinguishes the two commutation and adjoint tables.

3.2. Optimal System of One-Dimensional Subalgebras

Determining the optimal system of one-dimensional subalgebras involves assuming a generic element $\mathcal{X}\in {\zeta }_k$, which is expressed as

$$\mathcal{X}={\mu }_1{\mathcal{Y}}_1+{\mu }_2{\mathcal{Y}}_2+{\mu }_3{\mathcal{Y}}_3+\dots +{\mu }_k{\mathcal{Y}}_k.$$

(31)

Conversely, for each case, the parameter k may take a different value. For instance, in the arbitrary case, the principal algebra is five-dimensional, and thus $k=5.$ The generic element for arbitrary case is defined by

$$\mathcal{X}={\mu }_1{\mathcal{Y}}_1+{\mu }_2{\mathcal{Y}}_2+{\mu }_3{\mathcal{Y}}_3+{\mu }_4{\mathcal{Y}}_4+{\mu }_5{\mathcal{Y}}_5.$$

(32)

Consequently, applying the adjoint action representation given in Equation (30) on Equation (32), and referring to Table 4, we proceed to obtain the following optimal system for the arbitrary case:

$$\begin{array}{cc}\hfill {\mathcal{X}}^1& ={\mathcal{Y}}_1+{\mu }_3{\mathcal{Y}}_3+{\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^2& ={\mathcal{Y}}_3+{\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^3& ={\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^4& ={\mathcal{Y}}_2+{\mu }_3{\mathcal{Y}}_3+{\mathcal{Y}}_5,\hfill \\ \hfill {\mathcal{X}}^5& ={\mathcal{Y}}_3+{\mathcal{Y}}_5,\hfill \\ \hfill {\mathcal{X}}^6& ={\mathcal{Y}}_5,\hfill \\ \hfill {\mathcal{X}}^7& ={\mathcal{Y}}_2+{\mu }_3{\mathcal{Y}}_3,\hfill \\ \hfill {\mathcal{X}}^8& ={\mathcal{Y}}_3,\hfill \\ \hfill {\mathcal{X}}^9& ={\mathcal{Y}}_2,\hfill \\ \hfill {\mathcal{X}}^{10}& ={\mathcal{Y}}_1+{\mu }_2{\mathcal{Y}}_2.\hfill \end{array}$$

In the same manner, we obtain the following optimal systems for all the above-mentioned cases.

• Case 1:

For Case 1, the optimal system of subalgebras is represented as follows:

$$\begin{array}{cc}\hfill {\mathcal{X}}^1& ={\mathcal{Y}}_2+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_3+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^2& ={\mathcal{Y}}_3+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_4+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^3& ={\mathcal{Y}}_3+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^4& ={\mathcal{Y}}_4+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_5+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^5& ={\mathcal{Y}}_5+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^6& ={\mathcal{Y}}_2+{\mathcal{Y}}_5+{\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^7& ={\mathcal{Y}}_2+{\mathcal{Y}}_4+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{X}}^8& ={\mathcal{Y}}_4+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^9& ={\mathcal{Y}}_1+{\mu }_4{\mathcal{Y}}_4+{\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{10}& ={\mathcal{Y}}_4+{\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{11}& ={\mathcal{Y}}_6+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{12}& ={\mathcal{Y}}_1+{\mu }_4{\mathcal{Y}}_4+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{13}& ={\mathcal{Y}}_2+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{14}& ={\mathcal{Y}}_1+{\mu }_2{\mathcal{Y}}_2+{\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9,\hfill \\ \hfill {\mathcal{X}}^{15}& ={\mathcal{Y}}_7+{\mathcal{Y}}_8+{\mathcal{Y}}_9.\hfill \end{array}$$

• Case 2:

For Case 2.1.2, the optimal system of subalgebras is represented as follows:

$$\begin{array}{cc}\hfill {\mathcal{X}}^1& ={\mathcal{Y}}_2+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_3,\hfill \\ \hfill {\mathcal{X}}^2& ={\mathcal{Y}}_3+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^3& ={\mathcal{Y}}_3+{\mu }_6{\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^4& ={\mathcal{Y}}_4+{\mu }_6{\mathcal{Y}}_6+{\mathcal{Y}}_5,\hfill \\ \hfill {\mathcal{X}}^5& ={\mathcal{Y}}_5+{\mu }_6{\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^6& ={\mathcal{Y}}_2+{\displaystyle \frac{2-m}{2}}{\mathcal{Y}}_5+{\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^7& ={\mathcal{Y}}_2+{\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^8& ={\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^9& ={\mathcal{Y}}_1+{\mu }_4{\mathcal{Y}}_4+{\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^{10}& ={\mathcal{Y}}_4+{\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^{11}& ={\mathcal{Y}}_6,\hfill \\ \hfill {\mathcal{X}}^{12}& ={\mathcal{Y}}_1+{\mu }_4{\mathcal{Y}}_4,\hfill \\ \hfill {\mathcal{X}}^{13}& ={\mathcal{Y}}_2,\hfill \\ \hfill {\mathcal{X}}^{14}& ={\mathcal{Y}}_1+{\mu }_2{\mathcal{Y}}_2.\hfill \end{array}$$

The optimal systems for cases 2.1.2 and 2.2 overlap. However, for case 2.2, the term ${\displaystyle \frac{2-m}{2}}$ may be replaced by $-{\displaystyle \frac{\delta }{2}}$.

4. Reductions to Ordinary Differential Equations and Invariant Solutions

This section discusses the process of reducing the nonhomogeneous Monge–Ampère Equation (2) into Odes, employing the above derived optimal systems. Following the derivation of the optimal system, the next task is to reduce the partial differential equation into the ordinary differential equations, employing the corresponding symmetry generators. Usually, this process is performed by deriving the similarity variables associated with the symmetry generators, resulting in simplified forms of Pdes. Typically, these similarity transformations are derived through the characteristics method.

4.1. Reductions for Arbitrary Function $h\left(w\right)$

In this case, we opt to start the reduction with the symmetry generator

$${\mathcal{X}}^1={\displaystyle \frac{\partial }{\partial x}}+\upsilon y{\displaystyle \frac{\partial }{\partial x}}+x{\displaystyle \frac{\partial }{\partial y}},$$

and the associated characteristic equation can be written as

$${\displaystyle \frac{dx}{1+\upsilon y}}={\displaystyle \frac{dy}{x}}={\displaystyle \frac{dw}{0}},$$

and after certain manipulations, we derive the following similarity transformations:

$$s={\displaystyle \frac{1}{2}}(\upsilon y^2-x^2)+y,w=\theta \left(s\right).$$

Applying these similarity transformations, Equation (2) is simplified to the following Ode:

$$\upsilon {\theta }^{\prime 2}\left(s\right)+(2\upsilon s+1){\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)+h\left(\theta \right)=0.$$

Next, associated with the similarity variables

$$s={\displaystyle \frac{1}{2}}(x^2-y^2),w=\theta \left(s\right),$$

the following symmetry generator

$${\mathcal{X}}^2=y{\displaystyle \frac{\partial }{\partial x}}+x{\displaystyle \frac{\partial }{\partial y}},$$

reduces Equation (2) into the following form:

$${\theta }^{\prime 2}\left(s\right)+2s{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)-h\left(\theta \right)=0.$$

(33)

The symmetry generator

$${\mathcal{X}}^3=x{\displaystyle \frac{\partial }{\partial y}},$$

results in the following similarity variables

$$s=x,w=\theta \left(s\right),$$

and subsequently, using these transformations, we obtain

$$h\left(\theta \right)=0.$$

Now, using the symmetry generator ${\mathcal{X}}^4$, we obtain Equation (33), subject to the transformations given below

$$s=x(1-y)-\upsilon y,w=\theta \left(s\right).$$

Similarly, by applying ${\mathcal{X}}^5$, we derive Equation (33), with the following similarity variables

$$s=xy+{\displaystyle \frac{1}{2}}{y}^2,w=\theta \left(s\right).$$

Moreover, the following similarity variables are obtained through the use of ${\mathcal{X}}^6$

$$s=xy,w=\theta \left(s\right).$$

Following the same manner, we have

$$s{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)+h\left(\theta \right)=0,$$

corresponding to ${\mathcal{X}}^7$, whereas the associated similarity transformation is outlined as

$$s={\displaystyle \frac{1}{2}}\upsilon y^2-x,w=\theta \left(s\right).$$

The following similarity invariants

$$s=y,w=\theta \left(s\right),$$

which are obtained through ${\mathcal{X}}^8$, result in the ensuing reduction

$$\theta \left(s\right)=0.$$

The same reduced form is obtained for the symmetry generators ${\mathcal{X}}^9$ and ${\mathcal{X}}^{10}$, except the transformations differ, which are given by

$$s=x,w=\theta \left(s\right),$$

$$s=\upsilon x-y,w=\theta \left(s\right),$$

respectively.

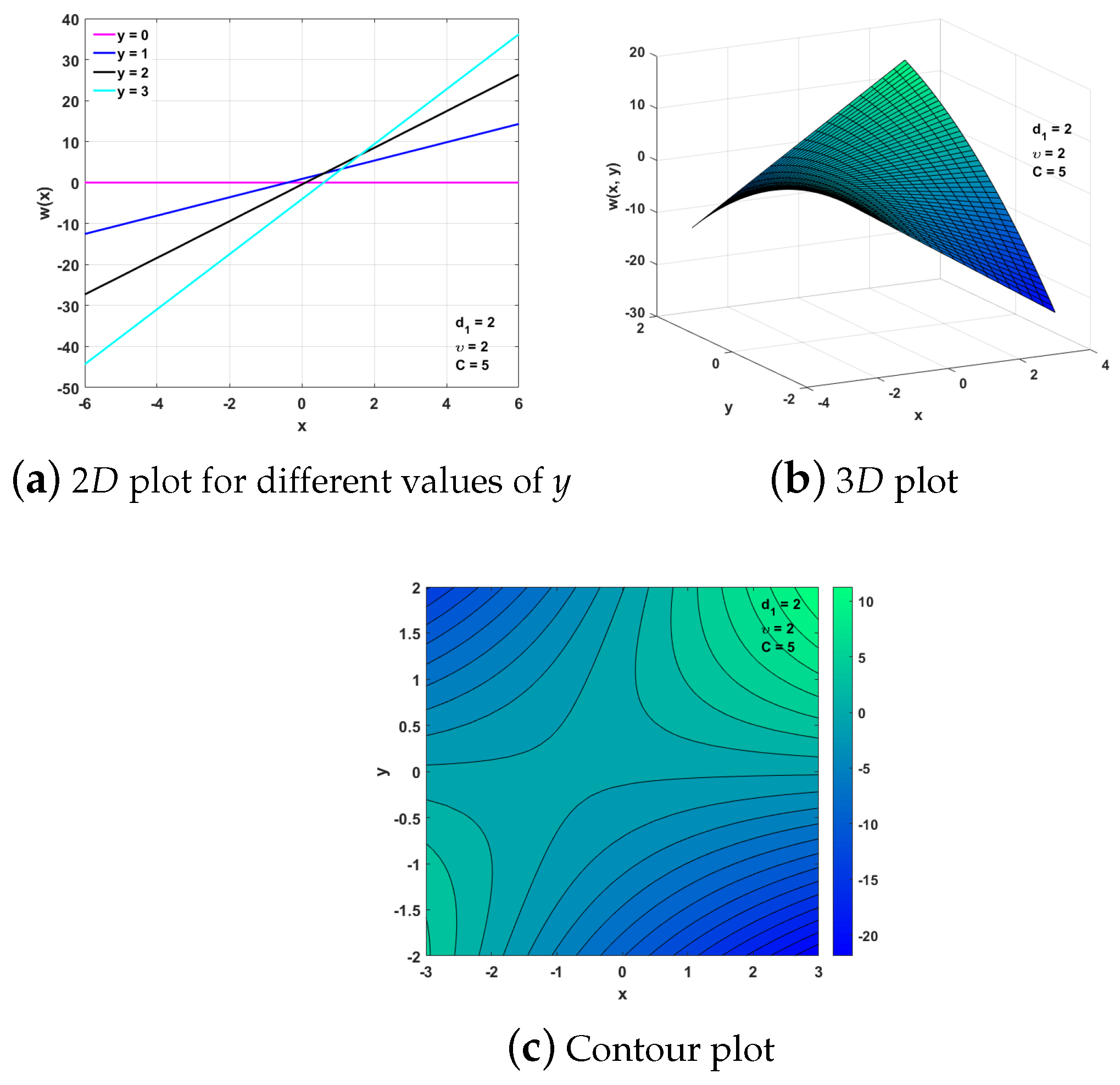
4.2. Reductions for Case 1

In this case, for the symmetry generator ${\mathcal{X}}^1$, Equation (2) is transformed into the subsequent Ode

$$-{\upsilon }^2{\theta }^{\prime 2}\left(s\right)+{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)+C=0,$$

associated with

$$s={\displaystyle \frac{1}{\upsilon }}y-{\displaystyle \frac{1}{{\upsilon }^2}}\ln (\upsilon y+1)-x,w=(\upsilon y+1)\theta \left(s\right).$$

The corresponding solution can be written as

$$\theta \left(s\right)=d_2\pm {\displaystyle \frac{1}{{\upsilon }^3}}(\sqrt{e^{2{\upsilon }^2(d_1+s)}+C}-\sqrt{C}{\tanh }^{-1}({\displaystyle \frac{\sqrt{e^{2{\upsilon }^2(d_1+s)}+C}}{\sqrt{C}}}\left)\right),$$

in terms of the original variables, we obtain

$$\begin{array}{c}{\displaystyle \frac{w(x,y)}{(\upsilon y+1)}}=d_2\pm {\displaystyle \frac{1}{{\upsilon }^3}}(\sqrt{e^{2{\upsilon }^2(d_1+({\displaystyle \frac{1}{\upsilon }}y-{\displaystyle \frac{1}{{\upsilon }^2}}\ln (\upsilon y+1)-x))}+C}-\hfill \\ \hfill \sqrt{C}{\tanh }^{-1}\left({\displaystyle \frac{\sqrt{e^{2{\upsilon }^2(d_1+(\frac{1}{\upsilon }y-\frac{1}{{\upsilon }^2}\ln (\upsilon y+1)-x))}+C}}{\sqrt{C}}}\right)).\end{array}$$

Another reduction of Equation (2) through ${\mathcal{X}}^2$ is given by

$$s{\theta }^{\prime 2}\left(s\right)+{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)-C=0,$$

(34)

with the similarity variables, expressed as follows:

$$s=(\upsilon y+x){(1-x)}^{{\upsilon }^2},w=(\upsilon y+x)\theta \left(s\right).$$

Its solution is given as

$$\theta \left(s\right)=\pm \int \sqrt{{\displaystyle \frac{C+2s^2+2d_{1}s}{s}}}ds+d_2,$$

and substituting back into the original variables, we obtain the following expression:

$${\displaystyle \frac{w(x,y)}{(\upsilon y+x)}}=\pm \int \sqrt{{\displaystyle \frac{C+2{\left((\upsilon y+x){(1-x)}^{{\upsilon }^2}\right)}^2+2d_1\left((\upsilon y+x){(1-x)}^{{\upsilon }^2}\right)}{(\upsilon y+x){(1-x)}^{{\upsilon }^2}}}}d\left((\upsilon y+x){(1-x)}^{{\upsilon }^2}\right)+d_2.$$

The subsequent transformations

$$s=\upsilon x-y,w=y\theta \left(s\right),$$

resulted from ${\mathcal{X}}^3$ reduce Equation (2) into

$${\upsilon }^2{\theta }^{\prime 2}\left(s\right)-C=0,$$

$$w(x,y)=y(d_1+{\displaystyle \frac{\sqrt{C}}{\upsilon }}(\upsilon x-y)),$$

where $d_1$ represents the constant. The graphical illustration of this solution is given by the following.

The symmetry generator ${\mathcal{X}}^4$, yields

$$s=x-y,w=y\theta \left(s\right),$$

which implies the following simplification of Equation (2):

$$-{\theta }^{\prime 2}\left(s\right)+C=0.$$

(35)

The solution associated with this equation is

$$\theta \left(s\right)=d_1+\sqrt{C}s,$$

which, in original variables, takes the following form

$$w(x,y)=y(d_1+\sqrt{C}(x-y)).$$

Graphically, for different values of parameters, it is represented in Figure 1 and Figure 2.

By using ${\mathcal{X}}^5$, we obtain following similarity variables

$$s=x^{\upsilon -1}{y}^{-1},w=x^{\upsilon }\theta \left(s\right),$$

providing the following reduction

$$s^3\upsilon (\upsilon -1)\left(s\theta {\theta }^{″}+2\theta {\theta }^{\prime }\right)+s^5{\theta }^{″}{\theta }^{\prime }(\upsilon (\upsilon -3)+2)+s^4(2{\upsilon }^2+6\upsilon +3){\theta }^{\prime 2}+C=0.$$

Next, we take ${\mathcal{X}}^6$, and this implies the following transformations

$$s=y-\ln x,w=x\theta \left(s\right),$$

resulting in a reduction of Equation (2) into the Ode, expressed as

$$-{\theta }^{\prime 2}\left(s\right)+{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)+C=0,$$

(36)

having a solution of the form

$$\theta \left(s\right)=\sqrt{e^{2(d_1+s)}+C}\pm \sqrt{C}{\tanh }^{-1}\left({\displaystyle \frac{\sqrt{e^{2(d_1+s)}+C}}{\sqrt{C}}}\right),$$

which in the original variables become

$$w(x,y)=x(\sqrt{e^{2(d_1+y-\ln x)}+C}\pm \sqrt{C}{\tanh }^{-1}({\displaystyle \frac{\sqrt{e^{2(d_1+y-\ln x)}+C}}{\sqrt{C}}}\left)\right),$$

where $d_1$ and $d_2$ signify the constants.

Additionally, for ${\mathcal{X}}^9$, we obtain the same reduction as defined in Equation (34), with the following similarity variables

$$s=(y+\upsilon (x+1))e^{-x},w=(\upsilon x+y)\theta \left(s\right).$$

In a similar way, ${\mathcal{X}}^{10}$ yields the same reduction as described in Equation (35), in correspondence with the similarity transformations, defined as follows:

$$s=x,w=(\upsilon x+y)\theta \left(s\right).$$

A similar reduction of Equation (2) is identified for the symmetry generator ${\mathcal{X}}^{11}$, given the transformations

$$s=x,w=y\theta \left(s\right).$$

Further, using the symmetry generator ${\mathcal{X}}^{12}$ leads to the following transformed form of Equation (2):

$$\upsilon {\theta }^{\prime }{\theta }^{″}+C=0,$$

associated with

$$s={\displaystyle \frac{1}{2}}\upsilon x^2-y,w=\theta \left(s\right).$$

The corresponding solution can be expressed as follows:

$$w(x,y)={\displaystyle \frac{(d_1\upsilon -2C(\frac{1}{2}\upsilon x^2-y){)}^{\frac{3}{2}}}{3C\sqrt{\upsilon }}}+d_2,$$

where $d_1$ and $d_2$ are constants. Graphically, for some specific values of parameters, it is represented in Figure 3.

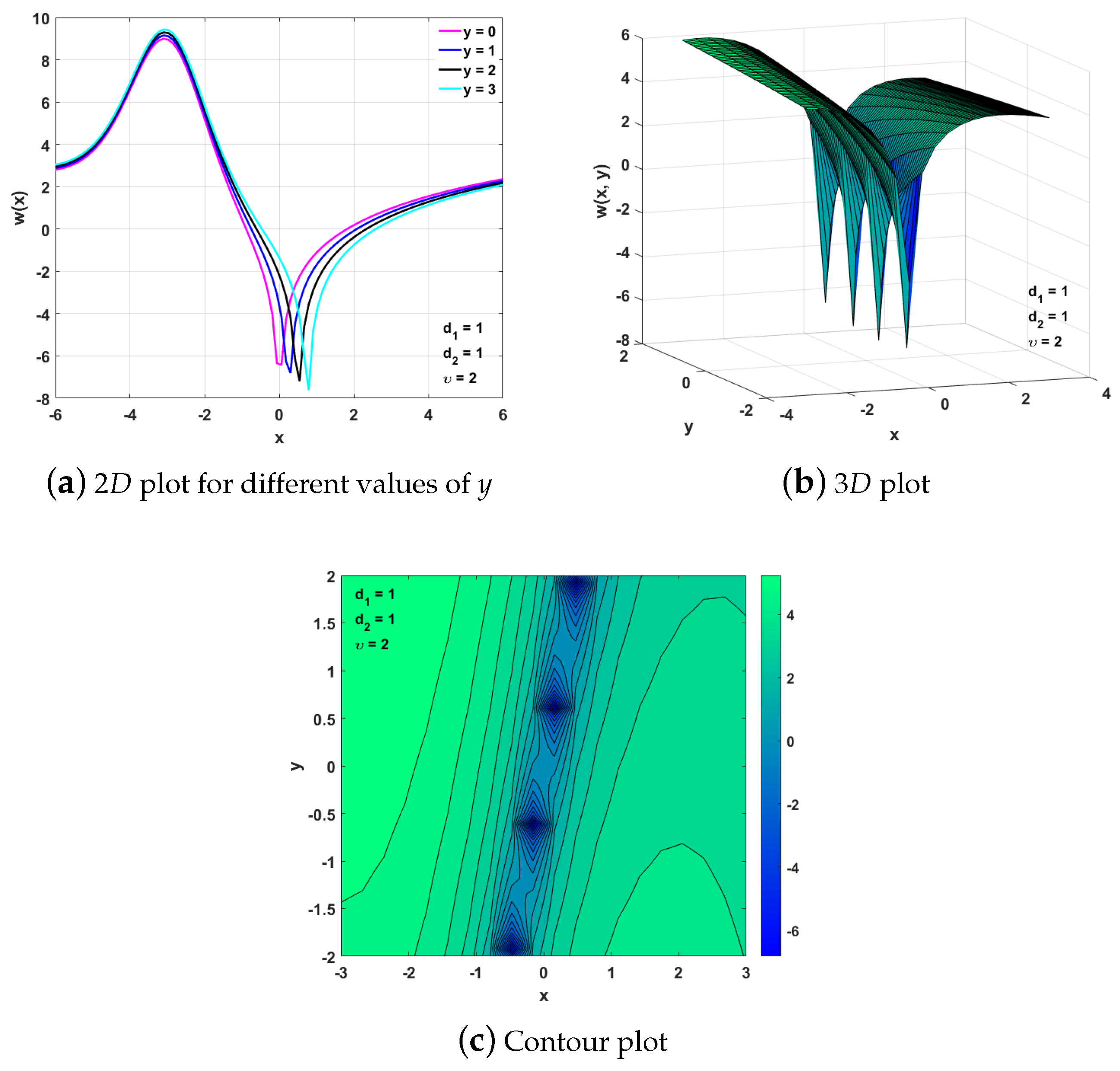
4.3. Reductions for Case 2.1.1

Associated with the symmetry generator

$$\mathcal{X}={\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{\partial }{\partial y}}+x{\displaystyle \frac{\partial }{\partial y}}+y{\displaystyle \frac{\partial }{\partial x}},$$

the similarity variables can be expressed as

$$s=x(1+{\displaystyle \frac{1}{2}}x)-y(1+{\displaystyle \frac{1}{2}}y),w=\theta \left(s\right),$$

which reduces Equation (2) into the subsequent Ode

$${\theta }^{\prime 2}\left(s\right)+2s{\theta }^{\prime }\left(s\right){\theta }^{″}\left(s\right)+r{(\theta +n)}^{-4}=0.$$

(37)

A similar reduced form is obtained for ${\mathcal{Y}}_5$, subject to

$$s=xy,w=\theta \left(s\right).$$

For ${\mathcal{Y}}_6$, we have

$$s=x,w=y^{{\displaystyle \frac{1}{3}}}\theta \left(s\right)-n,$$

and this transforms Equation (2) into the following form:

$${\theta }^{\prime 2}\left(s\right)+2\theta \left(s\right){\theta }^{″}\left(s\right)-9r\theta {\left(s\right)}^{-4}=0.$$

(38)

Similarly, the symmetry generator ${\mathcal{Y}}_9$ yields the same reduction, with the following transformations:

$$s=y,w=x^{{\displaystyle \frac{1}{3}}}\theta \left(s\right)-n.$$

Furthermore, the symmetry ${\mathcal{Y}}_7$ results in

$$s={\displaystyle \frac{x}{y}},w=y\theta \left(s\right)-n,$$

which gives the following reduction:

$$r\theta {\left(s\right)}^{-4}=0.$$

For, the symmetry generator ${\mathcal{Y}}_8$, we obtain

$$s={\displaystyle \frac{x}{y}},w=x\theta \left(s\right)-n,$$

which also leads to the above reduced form of Equation (2).

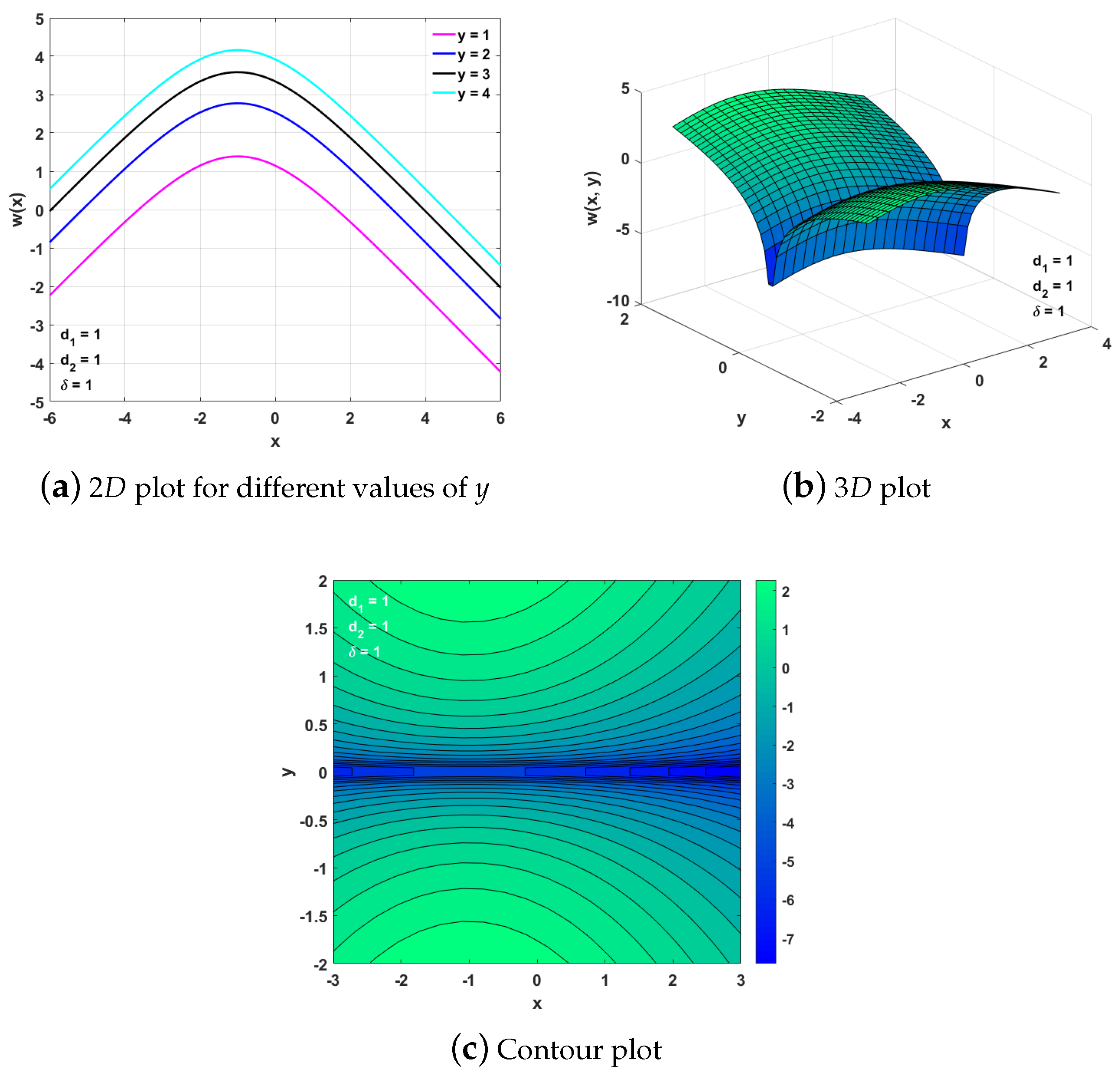
4.4. Reductions for Case 2.1.2

For this case, by applying ${\mathcal{X}}^1$, we arrive at the transformations

$$s={\displaystyle \frac{2}{(2-m)\upsilon }}\left(y-{\displaystyle \frac{\ln \left(\upsilon \right((2-m)/2)y+1)}{\upsilon \left(\right(2-m)/2)}}\right)-x,w={(y\upsilon +{\displaystyle \frac{2}{2-m}})}^{{\displaystyle \frac{2}{2-m}}}\theta \left(s\right)-n,$$

leading to the subsequent reduction of Equation (2)

$$2{\upsilon }^2(m-1)\theta {\theta }^{″}+{\theta }^{\prime }{\theta }^{″}-4{\upsilon }^2{\theta }^{\prime 2}+r{\theta }^m=0.$$

Associated with ${\mathcal{X}}^3$, we obtain

$${\displaystyle \frac{1}{2}}m{\upsilon }^2\theta {\theta }^{″}-{\upsilon }^2{\theta }^{\prime 2}+r{\theta }^m=0,$$

subject to

$$s={\displaystyle \frac{2-m}{2}}\upsilon x-y,w=y^{{\displaystyle \frac{2}{2-m}}}\theta -n.$$

The symmetry generator ${\mathcal{X}}^4$ results in the following similarity variables:

$$s=x^2+\left((2-m)\upsilon -2\right)xy,w=x^{\upsilon }\theta -n,$$

which yields the following transformed form of Equation (2):

$$\begin{array}{c}2s^4\upsilon (2+m\upsilon )\theta {\theta }^{″}+2s^5((m-2)\upsilon +4){\theta }^{\prime }{\theta }^{″}+4s^3\upsilon (2+m\upsilon ){\theta }^{\prime }\theta -\hfill \\ \hfill 4s^4({\upsilon }^2-\upsilon m-3){\theta }^{\prime 2}+r{(\upsilon (m-2)+2)}^{-2}{\theta }^m=0.\end{array}$$

(39)

Moreover, for ${\mathcal{X}}^5$, we obtain an identical reduction to that expressed in Equation (39), governed by the following similarity variables:

$$s=y^p{x}^{-1},u=y^{\upsilon p}\theta -n,$$

where $p={\displaystyle \frac{2}{(2-m)\upsilon -2}}.$ Subsequently, subject to ${\mathcal{X}}^6$, we obtain

$$(2+m)s^{3-m}{\theta }^{\prime }{\theta }^{″}+2(2+m)s^{2-m}{\theta }^{\prime 2}-{\displaystyle \frac{1}{2}}{m}^{2}r{\theta }^m=0,$$

where

$$s=x(y-{\displaystyle \frac{2}{m}}{)}^{{\displaystyle \frac{2}{m}}},w=x\theta -n.$$

Under the following similarity variables, resulted from ${\mathcal{X}}^{10}$

$$s=x,w=({\displaystyle \frac{2}{2-m}}x+y{)}^{{\displaystyle \frac{2}{2-m}}}\theta -n,$$

we obtain the following reduced form

$${\displaystyle \frac{2m}{{(2-m)}^2}}\theta {\theta }^{″}-{\displaystyle \frac{4}{{(2-m)}^2}}{\theta }^{\prime 2}+r{\theta }^m=0.$$

In addition, using ${\mathcal{X}}^{11}$, we derive the same reduction as outlined above, through the similarity transformations, expressed below

$$s=x,w=y^{{\displaystyle \frac{2}{2-m}}}\theta -n.$$

Corresponding to ${\mathcal{X}}^{12}$, the ensuing similarity variables

$$s={\displaystyle \frac{1}{2}}\upsilon x^2-y,w=\theta \left(s\right),$$

reduce Equation (2) into the subsequent form:

$$\upsilon {\theta }^{\prime }{\theta }^{″}+r{(\theta +n)}^m=0.$$

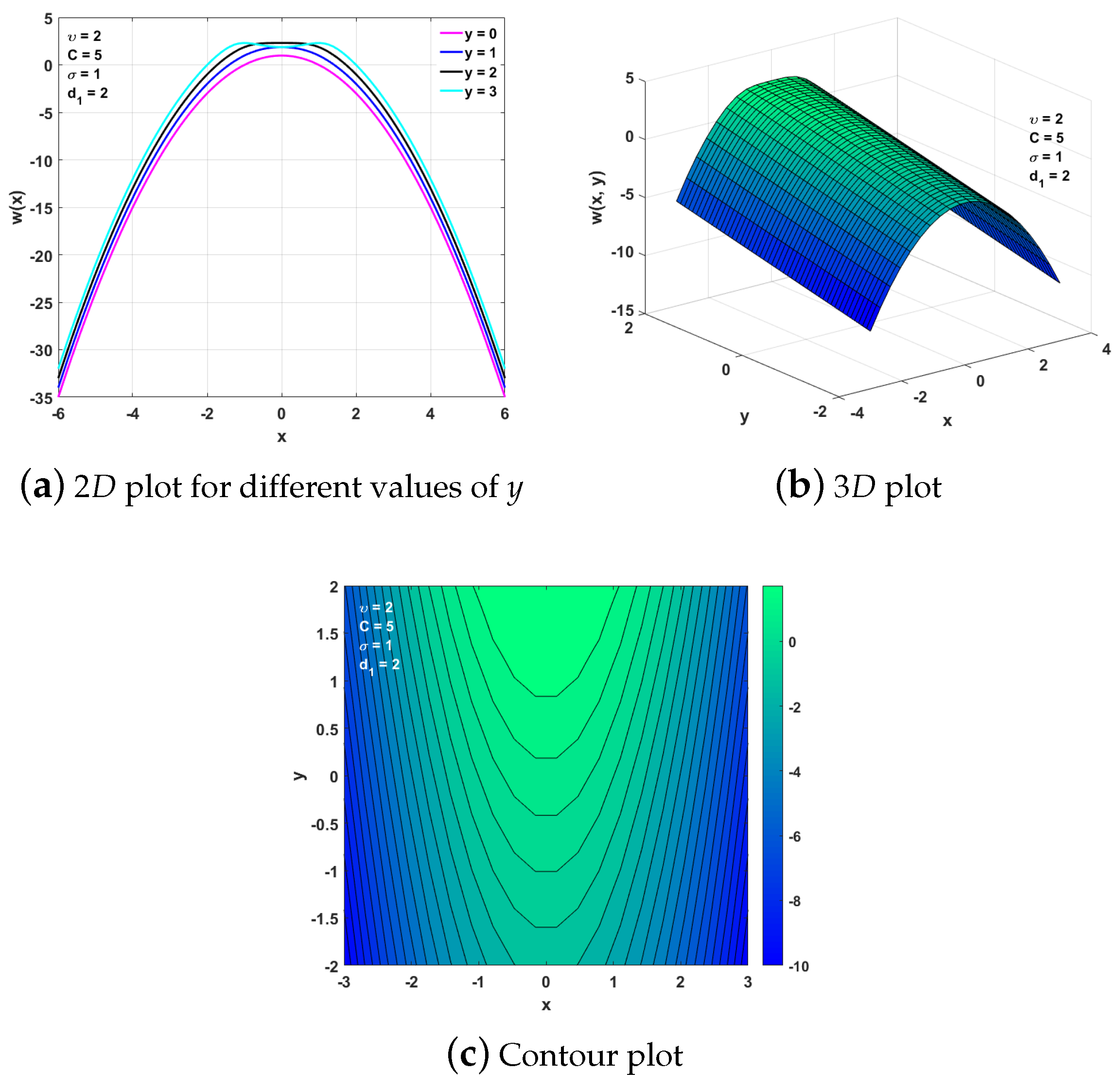
4.5. Reductions for Case 2.2

The symmetry generator ${\mathcal{X}}^1$ yields

$$s=x+{\displaystyle \frac{2}{\delta \upsilon }}y+{\displaystyle \frac{4}{{\delta }^2{\upsilon }^2}}\ln (\upsilon \delta y-2),w=\ln {(\upsilon y-{\displaystyle \frac{2}{\delta }})}^{-{\displaystyle \frac{2}{\delta }}}+\theta ,$$

which results in the following reduction of Equation (2)

$$(1+\delta ){\upsilon }^2{\theta }^{″}-{\theta }^{\prime }{\theta }^{″}+4\sigma e^{\delta \theta }=0.$$

(40)

Associated with ${\mathcal{X}}^2$, we obtain

$$-(4+\delta )s^2{\theta }^{\prime 2}+(1+\upsilon \delta )\upsilon {\theta }^{″}-{\theta }^{\prime }{\theta }^{″}+4{\upsilon }^2{\delta }^2\sigma e^{\delta \theta }=0,$$

through the transformations

$$s=(y-{\displaystyle \frac{2}{\upsilon \delta }}(x-1))e^{{\displaystyle \frac{\upsilon \delta }{2}}x},w=\ln {(\upsilon y-{\displaystyle \frac{2}{\delta }})}^{-{\displaystyle \frac{2}{\delta }}}+\theta .$$

Subject to the following similarity variables

$$s={\displaystyle \frac{2}{\upsilon \delta }}y+x,w=\upsilon x+\theta ,$$

obtained from ${\mathcal{X}}^3$, we arrive at

$$\sigma e^{\delta \theta }=0.$$

Similarly, ${\mathcal{X}}^6$ leads to the transformations

$$s=(y+{\displaystyle \frac{2}{2+\delta }}{)}^{{\displaystyle \frac{2}{2+\delta }}}{x}^{-1},w=\ln \left(x\right)+\theta ,$$

resulting in the following reduced form of Equation (2)

$$-{\displaystyle \frac{\delta }{2}}{s}^{\delta +3}\left({\theta }^{\prime }{\theta }^{″}+s^2{\theta }^{\prime }\right)-s^{\delta +4}\left({\displaystyle \frac{\delta +2}{2}}{\theta }^{\prime 2}+{\theta }^{″}\right)+\sigma e^{\delta \theta }=0.$$

(41)

The symmetry generators, ${\mathcal{X}}^4$ and ${\mathcal{X}}^5$, imply the following identical transformed form of Equation (2),

$${\delta }^2{\upsilon }^2\theta {\theta }^{″}-{\displaystyle \frac{\delta \upsilon }{2}}{s}^3\left({\theta }^{\prime }{\theta }^{″}+s{\theta }^{\prime }\right)-s^4\left({\displaystyle \frac{\delta \upsilon +2}{2}}{\theta }^{\prime 2}+{\theta }^{″}\right)+\upsilon \sigma e^{\delta \theta }=0,$$

except the similarity transformations differ, given respectively as shown below:

$$\begin{array}{cc}\hfill s& =x^{{\displaystyle \frac{4+\upsilon \delta }{2}}}(1-{\displaystyle \frac{4+\upsilon \delta }{2}}{\displaystyle \frac{y}{x}}),w=\ln {\left(x\right)}^{\upsilon }+\theta ,\hfill \\ \hfill s& =x{y}^{{\displaystyle \frac{2+\upsilon \delta }{2}}},w=\ln {\left(x\right)}^{\upsilon }+\theta .\hfill \end{array}$$

Now, we take ${\mathcal{X}}^9$, resulting in the transformations

$$s=(y-{\displaystyle \frac{2}{\delta }}\upsilon (x-{\displaystyle \frac{2}{\delta }}))e^{{\displaystyle \frac{\delta }{2}}x},w=\theta +x,$$

and these similarity transformations reduce Equation (2) to an ordinary differential equation given as

$$s{\theta }^{\prime }{\theta }^{″}+{\theta }^{\prime 2}-{\displaystyle \frac{4}{{\delta }^2}}\sigma e^{\delta \theta }=0.$$

Similarly, for ${\mathcal{X}}^{10}$, we have

$$4(1+\delta ){\theta }^{″}+{\delta }^2\sigma e^{\delta \theta }=0,$$

associated with

$$s=x,w=\theta +\ln (y-{\displaystyle \frac{2}{\delta }}\upsilon x{)}^{-{\displaystyle \frac{2}{\delta }}}.$$

The solution of this equation can be expressed as follows:

$$w(x,y)={\displaystyle \frac{1}{\delta }}\log (-{\displaystyle \frac{2(\delta +1)d_1\left({\tanh }^2\left(\frac{1}{2}\sqrt{{\delta }^2{d}_1{(d_2+x)}^2}\right)-1\right)}{\sigma \delta }})-\ln (y-{\displaystyle \frac{2}{\delta }}\upsilon x{)}^{-{\displaystyle \frac{2}{\delta }}},$$

for $\delta =1,$ and $\sigma =1$, we have

$$w(x,y)=\log (-4(d_1{\tanh }^2\left({\displaystyle \frac{1}{2}}\sqrt{d_1{(d_2+x)}^2}\right)-1))-\ln (y-2\upsilon x{)}^{-2}.$$

This solution for different values of parameters can be visualized as shown in Figure 4 and Figure 5.

An identical reduction is obtained for ${\mathcal{X}}^{11}$, subject to

$$s=x,w=\ln y^{-{\displaystyle \frac{2}{\delta }}}+\theta .$$

Graphically, it can be seen as follows:

Moreover, ${\mathcal{X}}^{12}$ yields

$$s={\displaystyle \frac{1}{2}}\upsilon x^2-y,w=\theta ,$$

leading to the following Ode

$$\upsilon {\theta }^{\prime }{\theta }^{″}+\sigma e^{\delta \theta }=0,$$

having the solution

$$s+d_1=\int {\displaystyle \frac{1}{\sqrt{2C-\frac{2\sigma }{\upsilon }}{e}^{\theta }}}d\theta ,$$

and solving explicitly for $\theta$ yields

$$\theta \left(s\right)=\ln \left({\displaystyle \frac{\frac{\upsilon C}{\sigma }}{\cosh (\sqrt{\frac{2\sigma }{\upsilon }}s+d_1)}}\right),$$

where C and $d_1$ represent the integration constants. Substituting back to the original variables, we obtain

$$w(x,y)=\ln \left({\displaystyle \frac{\frac{\upsilon C}{\sigma }}{\cosh (\sqrt{\frac{2\sigma }{\upsilon }}\frac{1}{2}\upsilon x^2-y+d_1)}}\right).$$

This solution for some specific values of parameters can be visualized as shown in Figure 6.

5. Conservation Laws

This section covers the conservation laws of Equation (2) using the Noether approach, based on Noether’s theorem, that establishes a link between the conserved quantities and symmetries of a system having a variational formulation. This method allows for the construction of conservation laws when the Lagrangian for the system is explicitly defined [22]. Nevertheless, this method provides an elegant and systematic way of deriving the conservation laws of partial differential equations, offering insights into the symmetries and physical dynamics possessed by the system. The application of the Noether approach generally begins with the consideration of several key steps:

• Determining the Lagrangian of the system;
• Implementing the Noether’s theorem.

Associated with Equation (2), the Lagrangian that satisfies the Euler–Lagrange equation ${\displaystyle \frac{\delta \mathcal{L}}{\delta w}}=0$ is given by

$$\mathcal{L}={\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-\int h\left(w\right)dw,$$

(42)

The operator in Equation (4) is called the Noether operator of Equation (2) in correspondence with the Lagrangian (42), provided it satisfies the following condition:

$${\mathcal{Y}}^{\left[2\right]}\mathcal{L}+({\mathcal{D}}_x{\tau }^1+{\mathcal{D}}_y{\tau }^2)\mathcal{L}={\mathcal{D}}_x{\mathcal{C}}^1+{\mathcal{D}}_y{\mathcal{C}}^2,$$

(43)

where ${\mathcal{C}}^1$ and ${\mathcal{C}}^2$ are the gauge terms dependent on the variables $(y,x,w)$. Equation (43) leads to the derivation of the following system of determining equations:

$$\begin{array}{cc}\hfill {\tau }_w^1=0,{\tau }_w^2& =0,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\tau }_y^1=0,{\tau }_x^2& =0,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\varphi }_{ww}=0,{\varphi }_x=0,{\varphi }_y& =0,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\tau }_{xx}^1=0,{\tau }_{yy}^2& =0,\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\mathcal{C}}_w^1=0,{\mathcal{C}}_w^2& =0,\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill 3{\varphi }_w-({\tau }_x^1+{\tau }_y^2)& =0,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill -\varphi h\left(w\right)-({\tau }_x^1+{\tau }_y^2)\int h\left(w\right)dw& ={\mathcal{C}}_x^1+{\mathcal{C}}_y^2.\hfill \end{array}$$

(50)

We use the following identity in order to obtain the conserved quantities of Equation (2):

$${\mathit{Q}}^i={\mathcal{C}}^i-{\tau }^i\mathcal{L}-(\varphi -{\tau }^1{u}_x-{\tau }^2{u}_y){\displaystyle \frac{\partial \mathcal{L}}{\partial w_i}},$$

(51)

where $i=(1,2)=(x,y).$ Consequently, for $i=(1,2)$, we derive the following two identities:

$$\begin{array}{cc}\hfill {\mathit{Q}}^x& ={\mathcal{C}}^1-{\tau }^1\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-\int h\left(w\right)dw\right)-{\displaystyle \frac{1}{2}}(\varphi -{\tau }^1{w}_x-{\tau }^2{w}_y)w_x{w}_{yy},\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill {\mathit{Q}}^y& ={\mathcal{C}}^2-{\tau }^2\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-\int h\left(w\right)dw\right)-{\displaystyle \frac{1}{2}}(\varphi -{\tau }^1{w}_x-{\tau }^2{w}_y)w_y{w}_{xx}.\hfill \end{array}$$

(53)

From Equations (46)–(49), we obtain

$$\begin{array}{cc}\hfill \varphi & ={\displaystyle \frac{1}{3}}({\tau }_x^1+{\tau }_y^2)w+c_1,\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill {\mathcal{C}}^1& ={\mathcal{C}}^1(x,y),{\mathcal{C}}^2={\mathcal{C}}^2(x,y),\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill {\tau }^1& =b_1+b_{2}x,{\tau }^2=a_1+a_{2}y.\hfill \end{array}$$

(56)

We derive the following updated expression of Equation (50) after substituting Equation (54) into Equation (50):

$$-\left({\displaystyle \frac{1}{3}}({\tau }_x^1+{\tau }_y^2)w+c_1\right)h\left(w\right)-({\tau }_x^1+{\tau }_y^2)\int h\left(w\right)dw={\mathcal{C}}_x^1+{\mathcal{C}}_y^2.$$

(57)

In the next step, we proceed by considering the following cases for smooth function $h\left(w\right)$:

• Case 1: $h\left(w\right)$ is an arbitrary function of w

For this case, we obtain the following results from Equation (57)

$$\begin{array}{cc}\hfill \varphi =0,a_2& =-b_2,\hfill \\ \hfill {\mathcal{C}}_x^1+{\mathcal{C}}_y^2& =0.\hfill \end{array}$$

As a result, Equations (52) and (53) yield the following conserved quantities

$$\begin{array}{cc}\hfill {\mathit{Q}}^x& ={\mathcal{C}}^1-(b_1+b_{2}x)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-\int h\left(w\right)dw\right)+{\displaystyle \frac{1}{2}}((b_1+b_{2}x)w_x+(a_1-b_{2}y)w_y)w_x{w}_{yy},\hfill \\ \hfill {\mathit{Q}}^y& ={\mathcal{C}}^2-(a_1-b_{2}y)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-\int h\left(w\right)dw\right)+{\displaystyle \frac{1}{2}}((b_1+b_{2}x)w_x+(a_1-b_{2}y)w_y)w_y{w}_{xx}.\hfill \end{array}$$

In this context, $b_j$, $a_j,$ and $c_1$ signify constants, where $j=1,2.$; hence, there are three independent conserved quantities associated with $(a_1=1,b_1=0=b_2)$, $(b_1=1,a_1=0=b_2)$, and $(b_2=1,b_1=0=a_1)$.

• Case 2: $h\left(w\right)$ is not an arbitrary function of w

In this case, differentiating Equation (57) twice with respect to w, we obtain

$${\varphi }_w=-{\displaystyle \frac{4}{3}}({\tau }_x^1+{\tau }_y^2)({\displaystyle \frac{h}{h_w}}{)}_w.$$

(58)

Again differentiating with respect to w, we obtain

$$0=({\tau }_x^1+{\tau }_y^2)({\displaystyle \frac{h}{h_w}}{)}_{ww}.$$

(59)

Further, two cases arise from here:

• Subcase 2.1: $({\tau }_x^1+{\tau }_y^2)=0$ and $h\left(w\right)=h$

Equation (57), in this case, yields the following:

$$\begin{array}{cc}\hfill \varphi & =c_1,a_2=-b_2,\hfill \\ \hfill {\mathcal{C}}^1& =G\left(y\right)-c_{1}hx,{\mathcal{C}}^2=M\left(x\right)+d_1=0.\hfill \end{array}$$

Under these conditions, Equations (52) and (53) give the corresponding conserved quantities

$$\begin{array}{cc}\hfill {\mathit{Q}}^x& =G\left(y\right)-c_{1}hx-\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-wh\right)(b_1+b_{2}x)-{\displaystyle \frac{1}{2}}(c_1-(b_1+b_{2}x)w_x-(a_1-b_{2}y)w_y)w_x{w}_{yy},\hfill \\ \hfill {\mathit{Q}}^y& =M\left(x\right)+d_1-\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-wh\right)(a_1-b_{2}y)-{\displaystyle \frac{1}{2}}(c_1-(b_1+b_{2}x)w_x-(a_1-b_{2}y)w_y)w_y{w}_{xx},\hfill \end{array}$$

herein, $b_j$, $a_j,$ $d_1$, and $c_1$ are constants, where $j=1,2$. Thus, associated with this case, four independent conserved quantities are derived.

• Subcase 2.2: $({\displaystyle \frac{h}{h_w}}{)}_{ww}=0$

Now, we have

$$({\displaystyle \frac{h}{h_w}}{)}_{ww}=0.$$

Twice integrating it with respect to w, we have

$${\displaystyle \frac{h}{h_w}}=kw+k_1.$$

To advance our analysis, we turn our attention to two additional cases:

• Subcase 2.2.1: $k\ne 0$

Equations (57) and (58) lead to the following outcomes

$$\begin{array}{c}\hfill h\left(w\right)=r{(w+n)}^m,\varphi =c_1,a_2=-b_2.\end{array}$$

Consequently, Equations (52) and (53) give rise to the following conserved quantities:

$$\begin{array}{c}{\mathit{Q}}^x={\mathcal{C}}^1-(b_1+b_{2}x)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-{\displaystyle \frac{r}{m+1}}{(w+n)}^{m+1}\right)-\hfill \\ \hfill {\displaystyle \frac{1}{2}}(c_1-(b_1+b_{2}x)w_x-(a_1-b_{2}y)w_y)w_x{w}_{yy},\end{array}$$

$$\begin{array}{c}{\mathit{Q}}^y={\mathcal{C}}^2-(a_1-b_{2}y)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-{\displaystyle \frac{r}{m+1}}{(w+n)}^{m+1}\right)-\hfill \\ \hfill {\displaystyle \frac{1}{2}}(c_1-(b_1+b_{2}x)w_x-(a_1-b_{2}y)w_y)w_y{w}_{xx}.\end{array}$$

For $m=-4$, we have

$$\begin{array}{cc}\hfill h\left(w\right)& =r{(w+n)}^{-4},{\tau }^1=b_1+b_{2}x,\hfill \\ \hfill \varphi & =c_2(w+n),a_2=-b_2,\hfill \\ \hfill {\tau }^2& =a_1+(3c_2-b_2)y.\hfill \end{array}$$

Therefore, the following conserved quantities arise from Equations (52) and (53):

$$\begin{array}{c}{\mathit{Q}}^x={\mathcal{C}}^1-(b_1+b_{2}x)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)+{\displaystyle \frac{1}{3}}r{(u+n)}^{-3}\right)-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \frac{1}{2}}(c_2(u+n)-(b_1+b_{2}x)w_x-(a_1+(3c_2-b_2)y)w_y)w_x{w}_{yy},\end{array}$$

$$\begin{array}{c}{\mathit{Q}}^y={\mathcal{C}}^2-(a_1+(3c_2-b_2)y)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)+{\displaystyle \frac{1}{3}}r{(w+n)}^{-3}\right)-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \frac{1}{2}}(c_2(w+n)-(b_1+b_{2}x)w_x-(a_1+(3c_2-b_2)y)w_y)w_y{w}_{xx},\end{array}$$

herein, $b_j$, $a_j,$ and $c_j$ represent constants, where $j=1,2.$

• Subcase 2.2.2: $k=0$

Equations (57) and (58) lead to the following outcomes:

$$\begin{array}{c}\hfill h\left(w\right)=\sigma e^{\delta w},\varphi =0,a_2=-b_2.\end{array}$$

Following this, the conserved quantities derived from Equations (52) and (53) are as follows:

$$\begin{array}{cc}\hfill {\mathit{Q}}^x& ={\mathcal{C}}^1-(b_1+b_{2}x)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-{\displaystyle \frac{\sigma }{\delta }}{e}^{\delta w}\right)+{\displaystyle \frac{1}{2}}((b_1+b_{2}x)w_x+(a_1-b_{2}y)w_y)w_x{w}_{yy},\hfill \\ \hfill {\mathit{Q}}^y& ={\mathcal{C}}^2-(a_1-b_{2}y)\left({\displaystyle \frac{1}{4}}\left(w_y^2{w}_{xx}+w_x^2{w}_{yy}\right)-{\displaystyle \frac{\sigma }{\delta }}{e}^{\delta w}\right)+{\displaystyle \frac{1}{2}}((b_1+b_{2}x)w_x+(a_1-b_{2}y)w_y)w_y{w}_{xx}\hfill \end{array}$$

where, $b_j$, $a_1$ are constants and $j=1,2$.

There are quite interesting applications of higher-order conservation laws derived from the second-order Lagrangian. For instance, higher-order conservation laws for the Monge–Ampère equation are crucial for various reasons, particularly to understand the mathematical understanding of the system. They might be helpful in various aspects such as the following:

• Following Noether’s theorem, which says there is a one-to-one correspondence between symmetries and conservation laws of a variational system, one can construct higher-order symmetries using these conservation laws, which may aid in identifying new exact solutions or soliton solutions.
• Moreover, in some cases, they can be reduced to first-order forms, indicating some fundamental physical principles.
• In the domains of fluid dynamics and nonlinear wave equations, such conservation laws are often linked to soliton-like behavior, revealing the broader physical applications. While first-order conservation laws are only related to fundamental physical principles, higher-order ones may describe more complex conserved quantities, such as higher-order stress tensors or non-local effects.
• In numerical schemes, these conservation laws are useful in the development of structure-preserving algorithms for solving differential equations that ensure numerical accuracy and stability in computational models.

Further applications of higher-order conservation laws can be found in the works of Ibragimov [27] and Khabirov [28].

6. Conclusions

The nonhomogeneous Monge–Ampère Equation (2) represents an important class of fully nonlinear partial differential equations observed in various scientific disciplines, including optical transport, fluid dynamics and differential geometry. The application of Lie symmetry methods and the derivation of conservation laws provides a powerful framework for understanding the solutions and qualitative behavior defined by this equation. In this study, the Lie symmetry method was utilized to derive Lie symmetries and particular forms of the arbitrary function $h\left(w\right)$. A detailed classification was conducted, which led to the extension of principal Lie algebra. Then, to perform the symmetry reductions of Equation (2), the similarity transformation approach was used, which reduced this equation to equivalent Odes. Moreover, the optimal system for each case was derived to perform the symmetry reductions of this equation. Several invariant solutions were also obtained, and conservation laws were constructed using the Noether approach.

In summary, analyzing Equation (2) using the Lie symmetry method and conservation laws offered valuable tools to simplify the equation, grasp its structure, and construct meaningful solutions. Future directions include the following:

• Derivation of non-classical symmetries, generalizations of this equation in higher dimensions, and the exploration of higher-order symmetries.
• Applying Lie symmetry methods to study more nonlinear models appearing in fields such as geometric optics, fluid dynamics, and machine learning.
• Reductions of higher-order conservation laws into the first order.
• Identification of equivalence transformations of Equation (2) to further classify the invariant solutions, following the renowned methods discussed in [5,29].