Abstract
This review discusses two triatomic Hamiltonians and their applications to some non-adiabatic spectroscopic and collision problems. Carter and Handy in 1984 presented the first Hamiltonian in bond lengths–bond angle coordinates, that is here applied for studying the NO2 spectroscopy: vibronic states, internal dynamics, and interaction with the radiation due to the 2A′(A1)−2A′(B2) conical intersection. The second Hamiltonian was reported by Tennyson and Sutcliffe in 1983 in Jacobi coordinates and is here employed in the study of the Kr + OH(A2Σ+) electronic quenching due to conical intersection and Renner–Teller interactions among the 12A′, 22A′, and 12A″ electronic species. Within the non-relativistic approximation and the expansion method in diabatic electronic representations, the formalism is exact and allows a unified study of various non-adiabatic interactions between electronic states. The rotation, inversion, and nuclear permutation symmetries are considered for defining rovibronic representations, which are symmetry adapted for ABC and AB2 molecules, and the matrix elements of the Hamiltonians are then computed.
1. Introduction
Let us consider a laboratory-fixed (LF) frame, an isolated and polyatomic molecule, and a space-fixed (SF) frame with the origin at some point of the molecule, e.g., at the nuclear center of mass. The LF, electrostatic, and non-relativistic Hamiltonian is then equal to the translational one plus an internal SF term, with fully separated coordinates. We thus consider only the SF Hamiltonian with an exact separation of the translation.
Because commutes with the total spinless angular momentum , the molecule is referred to as a body-fixed (BF) frame, thus achieving an approximate separation of the rotation. In 1981, Sutcliffe [1] presented a general BF Hamiltonian , equal to the sum of rotational, electronic, and vibrational terms [Equations (3.18) and (3.20)],
where is the electronic orbital angular momentum, Q are nuclear vibrational coordinates, and q are those electronic and Cartesians. Contrary to [1], and according to [2], here satisfies non-standard commutation rules (a. u. everywhere, unless otherwise specified), whereas fulfills the standard ones. contains the total nuclear mass Mnucl and the polarization term, due to the removal of the translation. Because Mnucl is much larger than the electron mass, it can be safely removed from the electronic Hamiltonian that thus assumes the usual form.
The representation on the electronic states gives rise to rovibronic non-adiabatic (NA) Renner-Teller (RT) couplings , , and . The Q-depending term that multiplies diverges when the molecule is linear along z, and this singularity must be removed by a suitable rotational representation.
On the other hand, and depend on and , and the electronic representation yields vibronic couplings and associated with NA conical-intersection (CI) effects. These couplings are very difficult to compute and diverge at the intersection locus of two adiabatic potential energy surfaces (PESs) . It is then better a diabatic electronic representation, coupled by , whose vibronic couplings divided by the reduced masses are negligible with respect to other terms. More in general, a NA coupling is identically equal to zero if it does not contain a vibrational irreducible representation of the permutation-inversion symmetry group.
Non-relativistic effects in any molecule can be investigated with this Hamiltonian, which is however very complicated, and many approximations are necessary, e.g., separation between linear and non-linear molecules, small vibrations with respect to equilibrium nuclear geometries, point-group symmetries, and normal coordinates. This is discussed in detail by Wilson et al. [3], following Kemble [4].
Exact triatomic Hamiltonians, however, have been well known for many years, and two of them will be discussed in the next sections, with emphasis on non-adiabatic interactions among electronic states.
2. Carter-Handy Hamiltonian
Using the general theory of Sutcliffe [1], this Hamiltonian was obtained in 1984 [5]. In the BF frame, an A−B−C molecule is described by the A−B R1 and B−C R2 bond lengths, by the AC bond angle θ, and lies in the (z,x) plane with x bisecting θ, and xA and xB ≥ 0. is then equal to
where are reduced masses, and is
is represented on the eigenstates labeled by the helicity quantum number. Therefore, in the matrix elements , we have K′ = K, K′ = K ± 1, and K′ = K ± 2, that is Coriolis couplings up to ΔK = ±2. contains the cross term also, because the coordinates are not orthogonal, but improves the convergence of the levels and their assignments. This Hamiltonian can be easily employed for investigating spectroscopic and internal-dynamics problems, but it is not suitable for studying the collision dynamics.
Using the variational theory, much better than the perturbation one, we have applied the vibrational Hamiltonian for investigating the NO2 vibronic spectroscopy and the photo-induced dynamics due to the 2A′(A1)−2A′(B2) CI, where A1 and B2 denote diabatic electronic states. This Hamiltonian has been previously employed in the spectroscopic study of CO2 and SO2 [6], [7], and [7].
Figure 1 [8] shows the following: (1) a photon absorption by a vibrational-rotation state of the ground species A1 creates a Franck-Condon (FC) wave-packet (WP) on the excited B2 PES; (2) the WP propagates in space and time on B2; (3) a spontaneous emission of one photon brings back the WP on the A1 PES.
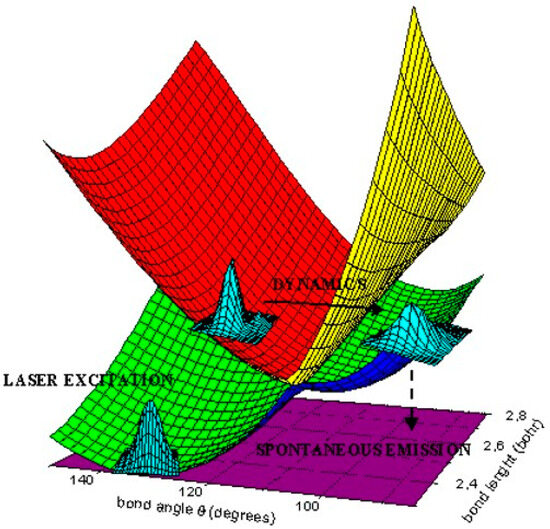
Figure 1.
Spectroscopy and photo-induced dynamics.
Our work began with the calculation of a diabatic representation [9] and of NA states and levels [10] up to about 19,000 cm−1, by using primitive, optimized, and Born–Oppenheimer (BO) vibrational basis functions. The practical implementation in [9] involved the ab-initio configuration-interaction method, the analytical fitting of the configuration-interaction data, and a diabatization method based on the electronic dipole-moment matrix. In [10], we used primitive, optimized, and Born-Oppenheimer basis functions, and the diabatic potentials were optimized with respect to 191 observed bands up to 10,000 cm−1, thus converging 1060 non-adiabatic levels up 17,000 cm−1, within 4.4 cm−1, with 6117 basis functions per symmetry.
Figure 2 [11] shows the CI onset, between 8500 and 12,500 cm−1. The first and third columns report the vibrational levels of A1 and B2, respectively, together their assignments: symmetric stretching, bending, and anti-symmetric stretching. The second column shows the NA levels En. For example, the weights of the highest diabatic states A1 (0,14,1) and B2 (0,3,0) are 37% and 23% in the associated NA species, and 32% is the B2 electronic weight of the last. NA-CI effects begin at ~9500 cm−1 with the coupling A1 (0,11,1) + B2 (0,0,0) and then increase with the energy: above 16,000 cm−1, they are very strong and yield a nearly chaotic spectrum, as we shall see below.
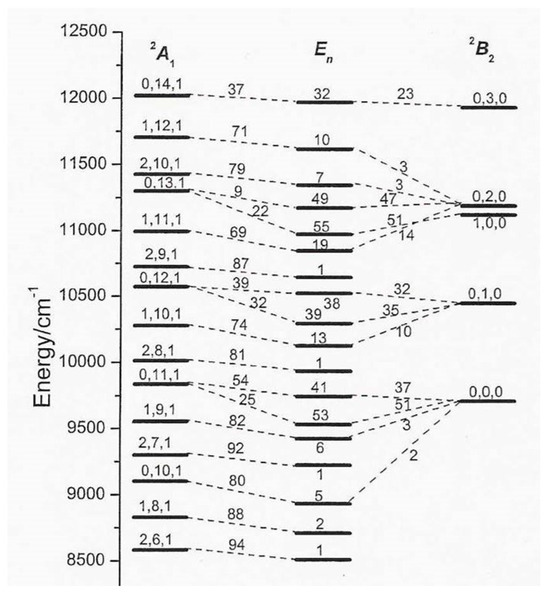
Figure 2.
Diabatic and NA levels. See the text for further details. Adapted with permission from: Absorption, Emission, and Photoelectron continuous-wave spectra. A. Lami, C. Petrongolo, and F. Santoro. Copyright@2004, World Scientific Publishing [11].
The agreement with experimental data is good up to 16,000 cm−1 [10], but it worsens at higher energies owing to inaccuracies of the PESs and coupling.
The calculation of the FC absorption spectrum does not present any problem, and Figure 3 thus reports this spectrum [11], showing v1 and v2. We pass from a strong and regular diabatic spectrum to a weak and irregular NA one, because the CI coupling mixes dark A1 and bright B2 states. These results thus explain the beginning and the development of the CI effects, from the regular far-infrared region up to the chaotic yellow portion of the spectrum. This figure shows also the differences between calculated and observed data.
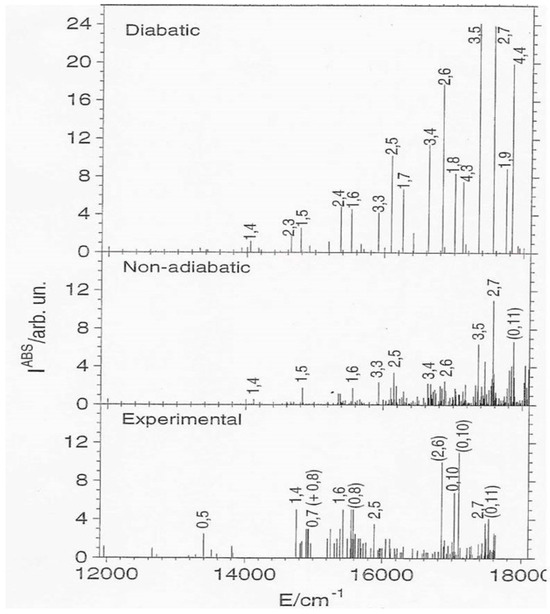
Figure 3.
Absorption intensities. Adapted with permission from: Absorption, Emission, and Photoelectron continuous-wave spectra. A. Lami, C. Petrongolo, and F. Santoro. Copyright@2004, World Scientific Publishing [11].
The left panel of Figure 4 confirms these findings, showing the Fourier transformation of the absorption spectrum from energy to the time domain. This is the survival probability of the FC state and points out the differences between the regular B2 bending recurrences and the irregular NA ones. The electronic populations of the right panel of Figure 4 show again these NA bending recurrences.
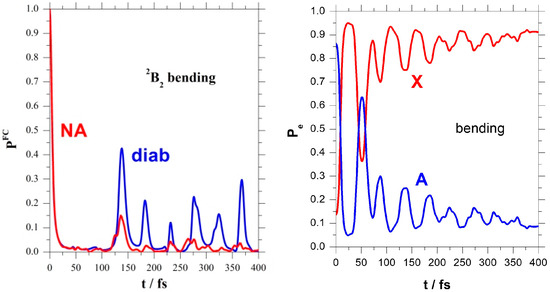
Figure 4.
FC survival probability and electronic populations.
Finally, Figure 5 [8] presents six snapshots at different times of the WP photo-induced propagation, from the initial absorption up to the final fluorescence. Here, Q+ is the symmetric stretching coordinate and the anti-symmetric stretching is equal to zero. This completes the internal dynamics shown schematically in Figure 1.
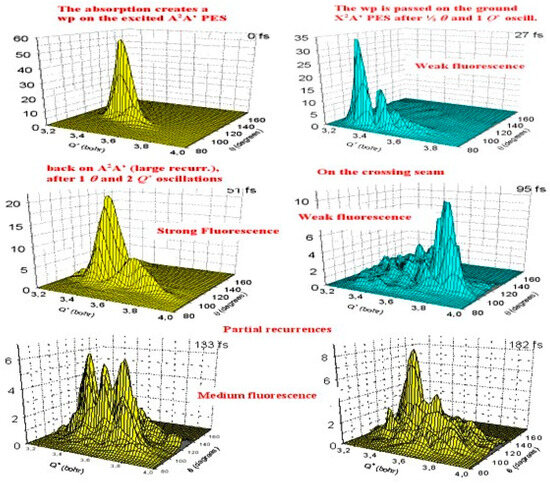
Figure 5.
WP photo-induced propagation.
3. Tennyson-Sutcliffe Hamiltonian
By the general theory of Sutcliffe [1], this Hamiltonian was obtained in 1983 [12] and then rearranged in [13]. In the BF frame, an A−B−C molecule is described by the Jacobi coordinates R (distance A–BC center of mass), r (distance B–C), and γ (included angle), and lies in the (z,x) plane with z parallel to r. This Hamiltonian is better than the CarterHandy one for investigating A + BC collisions. Following [13], we write
where the first term includes only and is equal to
with b = 1/(2μrr2) and B = 1/(2μRR2). Both and are present in the second term,
and we have ΔK = ±1 only.
The vibrational Hamiltonian is simply equal to
because the Jacobi coordinates are orthogonal. The and factors in these equations imply that this Hamiltonian is very large near the linearity.
This Hamiltonian is simpler than the previous one and can be easily applied to collision-dynamics problems, but presents many difficulties in spectroscopy. Therefore, it was employed in many atom + diatom collisions, in particular for investigating the NA quenching Kr + OH(A2Σ+) → Kr + OH(X2Π) due to CI and RT interactions among the 12A′, 22A′, and 12A″ adiabatic electronic species, with OH(A2Σ+) in the ground vibrational-rotational state [13]. We again employ the variational theory for computing PESs and NA couplings, the reaction probabilities are obtained via the real WP formalism [14], and the Hamiltonian is used in many works, e.g., in [15].
Figure 6 reports R cuts of the adiabatic PESs and of the diabatic ones labeled by Σ+(1), Π′(2), and Π″(3), where γ = 180° corresponds to the direction from H to O. The NA couplings CI12, RT12, RT13, and RT23 are shown schematically and yield the electronic quenching, forbidden in the BO approximation.
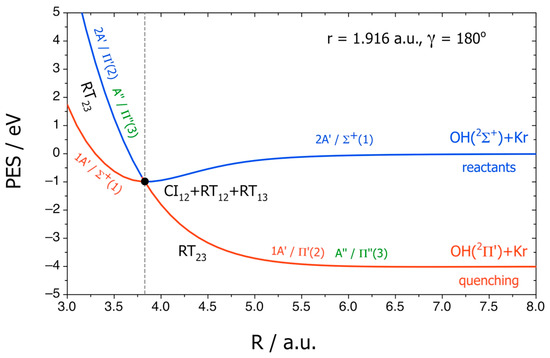
Figure 6.
R cuts of PESs for OH(A2Σ+) + Kr → OH(X2Π) + Kr. Adiabatic states 1A′, 2A′, and A″. Diabatic states Σ+(1), Π′(2), and Π″(3). The black dot labels the CI12 conical intersection. Adapted with permission from [16].
Three NA couplings are plotted in Figure 7 at r = 1.916: CI12 = ,
and
with the z axis along R and at J = 70.
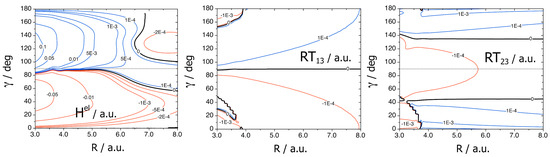
Figure 7.
r = 1.916. Conical intersection coupling CI12 = <Σ+||Π′ >. J = 70. RT13 and RT23. Adapted with permission from [16].
We see that CI12 is larger than RT13, and RT23 and is much larger than RT12 too. The strength of the NA interactions is thus CI12 >> RT23 > RT13 > RT12 and the quenching should be essentially due to the 1A′–2A′ conical intersection, but symmetry implies that Renner–Teller terms are necessary to populate Π″(3).
Initial-state-resolved quenching probabilities are obtained propagating time-dependent WPs up to J = 140, with the formalism of [14] and performing a time-to-energy Fourier transform at the end of the propagation. This is a multi-state approach, requiring about 80,000 s per J on Barcelona computers.
The quenching mechanism on the coupled diabatic PESs is shown in Figure 8, which presents electronic norms and snapshots at five times t of the probability densities of the WP at J = 70, where j labels the Legendre polynomials.
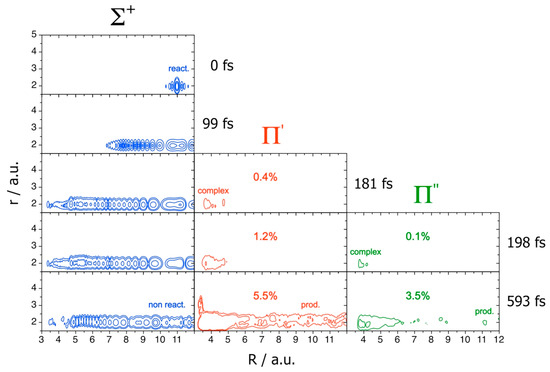
Figure 8.
J = 70. WP norms and probability densities. Adapted with permission from [16].
At the beginning, the WP remains on the Σ+ PES and the quenching is closed. At ~180 fs, part of the WP jumps on the Π′ PES owing to the Σ+-Π′ conical intersection, forming KrOH metastable complexes. At ~200 fs, also the Π″ surface is populated, and the complexes reveal their full NA nature, spreading on all the PESs. At larger times, we finally see both the non-reactive WP on Σ+, due to recrossing of the CI seam, and the reactive densities on Π′ and Π″, together with the formation of the quenching products resolved on these final states.
Quenching probabilities, cross sections, and rate constants confirm the above findings, based on the analysis of the couplings and of the WP. Figure 9 reports CI, RT, and CI + RT probabilities versus the collision energy Ecol, for the formation of both Π states at J = 70: CI and CI + RT results are nearly equal, whereas those RT are much smaller.
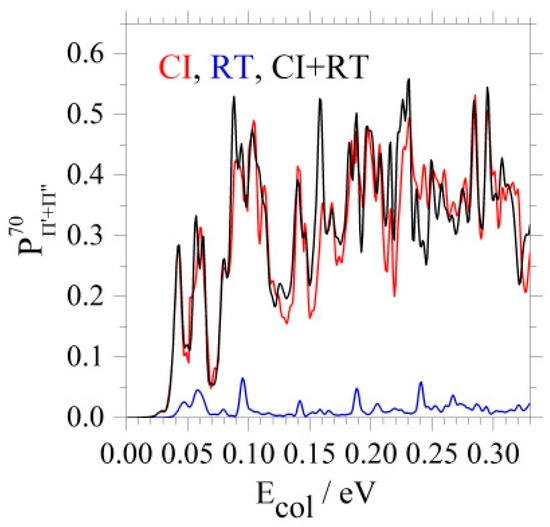
Figure 9.
J = 70. CI, RT, and total probabilities for the total quenching to Π′ and Π″. Adapted with permission from [16].
The cross sections σ of Figure 10 point out a strongly preferred Π′ channel at low Ecol, in agreement with the CI12-induced quenching and the reaction probabilities. Larger energies then enhance the Π″ weight owing to the RT13 and RT23 couplings. The total σ(Ecol = 0.039 eV) is 14.1 Å2, and the thermally averaged <σ(300 K)> is 11.6 Å2, in acceptable agreement with previous experimental results equal to 17.2 ± 0.4 and 10 ± 1 Å2. These differences are due to the limits of the PESs and couplings, as is usual. Finally, the rate constants confirm the cross-section results.
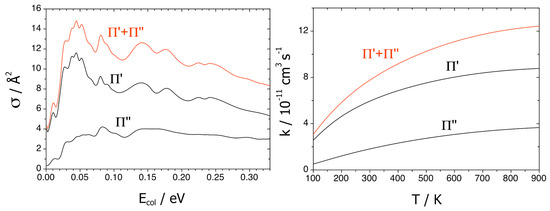
Figure 10.
Cross section and rate constants. Adapted with permission from [16].
4. Conclusions
The vibrational part of the Carter-Handy Hamiltonian is applied to the spectroscopy of NO2. With respect to the BO absorption spectrum, the CI line density increases, the NA spectrum is weaker and borrows its intensity from that BO, with many progressions being more irregular. CI effects also extend to the whole spectrum above their beginning.
The Tennyson–Sutcliffe Hamiltonian is applied to the Kr + OH quenching dynamics, finding that CI effects are much larger than those RT which open the Π″(3) channel. In fact, CI is due to the bare electronic Hamiltonian, whereas all RT operators are multiplied by the small factor B = 1/(2μRR2) of Equations (8) and (9) depending on the large Kr mass. The different magnitude of these couplings is also due to the different PES regions where NA effects are important: CI in bent geometries and RT near the linearity. CI rules the dynamics that is modulated by RT, these effects are non-additive but in competition, and the former is counterbalanced by the latter. All these findings are similar to those of the H2O [17,18] and CO2 [19] photo-dissociations. Finally, CI effects are large in both NO2 and Kr + OH because the CI minimum geometry is near to that of the B2 and Σ+ PES, respectively.
Funding
This research received no external funding.
Acknowledgments
I am very grateful to F. J. Aoiz, R. J. Buenker, P. Gamallo, A. Lami, E. Leonardi, F. Santoro, and A. Zanchet for their past collaboration on these results. I also thank the Dipartimento di Chimica e Chimica Industriale, Università di Pisa, Italy, the Dipartimento di Biotecnologie, Chimica e Farmacia, Università di Siena, Italy, and the Departament de Ciència de Materials i Química Física, Universitat de Barcelona, Spain, for invaluable computing resources.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sutcliffe, B.T. Some problems in defining a nuclear motion Hamiltonian and their relation to the problem of the molecular shape. In Current Aspects of Quantum Chemistry 1981; Carbò, R., Ed.; Elsevier: Amsterdam, The Netherlands, 1982; Volume 21, p. 99. [Google Scholar]
- Davydov, A.S. Quantum Mechanics, 2nd ed.; Pergamon: Oxford, UK, 1976; p. 175. [Google Scholar]
- Wilson, E.B., Jr.; Decius, J.C.; Cross, P.C. Molecular Vibrations, the Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill: New York, NY, USA, 1955; pp. 273–284. [Google Scholar]
- Kemble, E.C. The Fundamental Principles of Quantum Mechanics with Elementary Applications; Dover: New York, NY, USA, 1937; pp. 237–240. [Google Scholar]
- Carter, S.; Handy, N.C. A variational method for the calculation of ro-vibronic levels of any orbitally degenerate (Renner-Teller) triatomic molecule. Molec. Phys. 1984, 52, 1367. [Google Scholar] [CrossRef]
- Carter, S.; Handy, N.C. An efficient procedure for the calculation of the vibrational energy levels of any triatomic molecule. Molec. Phys. 1986, 54, 175. [Google Scholar] [CrossRef]
- Carter, S.; Handy, N.C.; Rosmus, P.; Chambaud, G. A variational method for the calculation of spin-rovibronic levels of Renner-Teller triatomic molecules. Molec. Phys. 1990, 71, 605. [Google Scholar] [CrossRef]
- Santoro, F. 2A1/2B2 Conical Intersection Effects on the Absorption Spectrum and the Intramolecular Dynamics of NO2. Ph.D. Thesis, Universities of Perugia and Siena, Perugia, Italy, 1998. [Google Scholar]
- Hirsch, G.; Buenker, R.J.; Petrongolo, C. Ab initio study of NO2 Part II: Non-adiabatic coupling between the two lowest 2A′ states and construction of a diabatic representation. Molec. Phys. 1990, 70, 835. [Google Scholar] [CrossRef]
- Leonardi, E.; Petrongolo, C.; Hirsch, G.; Buenker, R.J. Ab initio study of NO2. V. Non adiabatic vibronic states and levels of the 2A1/2B2 conical intersection. J. Chem. Phys. 1966, 105, 9051. [Google Scholar] [CrossRef]
- Lami, A.; Petrongolo, C.; Santoro, F. Absorption, emission, and photoelectron continuous-wave spectra. Adv. Ser. Phys. Chem. 2004, 15, 699. [Google Scholar]
- Tennyson, J.; Sutcliffe, B.T. Variational exact ro-vibrational levels of the floppy C molecule. J. Mol. Spectrosc. 1983, 101, 71. [Google Scholar] [CrossRef]
- Petrongolo, C. Nonadiabatic theory of triatomics: General formalism and application to Renner-Teller and conical-intersection effects. J. Chem. Phys. 1988, 89, 1297. [Google Scholar] [CrossRef]
- Gray, S.K.; Balint-Kurti, G.G. Quantum Dynamics with Real Wave Packets, Including Application to Three-Dimensional (J = 0) D + H2→HD + H Reactive Scattering. J. Chem. Phys. 1998, 108, 950. [Google Scholar] [CrossRef]
- Gamallo, P.; González, M.; Petrongolo, C. Quantum Dynamics of Nonadiabatic Renner-Teller Effects in Atom + Diatom Colli-sions. J. Phys. Chem. A 2021, 125, 6637. [Google Scholar] [CrossRef] [PubMed]
- Gamallo, P.; Zanchet, A.; Aoiz, F.J. Non-adiabatic quantum dynamics of the electronic quenching OH(A2∑+)+Kr. Phys. Chem. Chem. Phys. 2020, 22, 17091. [Google Scholar] [CrossRef] [PubMed]
- Mordaunt, D.H.; Ashfold, M.N.R.; Dixon, R.N. Dissociation Dynamics of H2O (D2O) Following Photoexcitation at the Lyman-α Wavelength (121.6 nm). J. Chem. Phys. 1994, 100, 7360. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, B.; Xie, D.; Guo, H. State-to-State Photodissociation Dynamics of H2O in the B-Band: Competition between Two Coexisting Nonadiabatic Pathways. J. Phys. Chem. A 2013, 117, 6940. [Google Scholar] [CrossRef] [PubMed]
- Grebenshchikov, S.Y. Communication: Multistate Quantum Dynamics of Photodissociation of Carbon Dioxide between 120 nm and 160 nm. J. Chem. Phys. 2012, 137, 021101. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).