Abstract
This article aims to study parallelizable random dynamical systems by examining them through the terms of dissipation and stochastic Lyapunov functions. It is demonstrated that any random variable that is not a random fixed point admits a tube, and every non-wandering point is within one. The Lyapunov function is employed to characterize the asymptotic stability of compact and closed random sets. The section of a random dynamical system is used to define the parallelizable random dynamical system, and it is proven that a random dynamical system is parallelizable if and only if it admits a section. Furthermore, the principle of Lyapunov used this characterization to study the parallelizability of random dynamical systems. The concept of symmetry is defined, and then its impact on the behavior of stochastic dynamic systems, particularly the Lorenz system, is discussed. In addition, by using an appropriate stochastic Lyapunov function, we have shown that the random Lorenz system is parallelizable.
1. Introduction
The parallelizability in dynamical systems refers to the ability to solve a system of equations in parallel by dividing the problem into smaller and independent tasks that can be treated concurrently. Therefore, the concept of parallelism plays a fundamental role in various fields, such as complex systems analysis, numerical simulation, and high-performance computing. Many dynamical systems, particularly complicated ones, need extensive computations and enormous datasets. For instance, it can take a lot of processing resources to solve nonlinear differential equations in a high-dimensional phase space. By dividing the problem among several processors or machines, parallelizing the calculations makes it possible to model and solve these systems more effectively.
At last, parallelizability improves the analysis and use of dynamical systems, especially for challenging and computationally intensive issues. Large-scale dataset management, real-time solutions, and faster simulations are made possible by effectively dividing the task.
This article focuses on studying the parallelism in random dynamical systems and analyzing its effects on the system behavior.
The parallelism is an important concepts in the study of dynamical systems due to its close connection with the concepts of dispersibility and stability. This concept has been studied extensively for deterministic dynamical systems by many researchers. J. Dugundji and H. Antosiewicz ([1], Theorem 3) proved that, on a locally compact separable metric space, a deterministic dynamical system is parallelizable if and only if it is dispersive.
In ref. [2], T. Jenkins and W. Johnson provided the necessary and sufficient condition for parallelizability in a locally compact separable space.
In ref. [3,4], T. Ura defined numerous kinds of isomorphisms for local dynamical systems, addressing the concept of parallelizability in the sense mentioned in ref. [1] and using the condition “the final limit set of the prolongational limit set is an empty set” to show that the parallelizability corresponding to type-n isomorphisms (n = 1, 2) are equivalent.
In ref. [5], O. H’ajek generalized the Dugundji–Antosiewicz theorem by removing the separation condition and interchanging the local compactness condition with the Lindelöfness condition.
In ref. [6], J. Egawa completed the discussion of the results presented in refs. [1,2,3], and [5]. He studied the global parallelizability of local dynamical systems.
In ref. [7], T. Ura and J. Egawa re-examined the parallelizability of local dynamical systems from the definite point of view and categorized parallel drifts on homeomorphic phase spaces by isomorphism.
In refs. [8,9,10], B. Garay proved that dispersive dynamical systems may not be parallelizable. Also, he investigated the connection between parallelizability and asymptotic stability. Moreover, he constructed a parallelizable dynamical system with uniformly bounded trajectories.
In refs. [11,12], Z. Le’sniak studied the parallelizability of flows of free mappings; he proved that the boundary of every equivalence class of a certain equivalence relation is a union of orbits, and that at most two of the boundary orbits of a class can be contained in this class.
In ref. [13], J. Souza, T. Pacífico, and H. Tozatti presented a note on the parallelizability of local dynamical systems. They provided an improvement to the classical theory presented in ref. [5] by eliminating all topological assumptions.
Here, we mention some works involving different applications for stochastic Lyapunov function. This principle is used to describe many dynamic properties.
In ref. [14], X. Mao reviews the uses of Lyapunov’s second method in the study of numerous properties of stochastic differential equations. His article emphasizes the original thoughts and methods industrialized lately.
In ref. [15], L. Arnold and B. Schmalfuss used the stochastic Lyapunov function to study the stability of random sets in random dynamics.
In ref. [16] (see also the references therein), the stochastic Lyapunov function was used to study the attractor–repeller pair decomposition and Morse decomposition for compact metric space in the random setting.
In ref. [17], A. Hmissi, F. Hmissi, and M. Hmissi used the stochastic Lyapunov function to describe the gradient RDSs.
In ref. [18], F. Visentin introduced the conditions that were sufficient to apply Lyapunov theory for differential equations to stochastic stability in probability.
In ref. [19], X. Ju, Ailing Qi, and Jintao Wang studied the Strong Morse–Lyapunov functions for Morse decompositions of attractors of random dynamical systems.
In ref. [20], E. Üçer studied the Lyapunov function-based criteria for ship rolling in random beam seas.
In ref. [21], I.J. Kadhim and M. Imran used the stochastic Lyapunov function to study the asymptotic stability, uniformly stable, compact asymptotically stable of random sets in random dynamics.
We also refer to some references through which Lyapunov stability was studied. For example, see refs. [22,23,24].
The main aim of this article is to study the parallelizability for random dynamical systems in a new and different way from the methods used in the aforementioned sources, by using stochastic Lyapunov functions and asymptotic stability on one hand, and the principle of dispersion and prolongational limit sets on the other hand.
This work is organized into six main sections. In Section 2, some prerequisites and facts about RDSs are stated. In Section 3, the notion “section” of random dynamical systems is defined and studied. It is shown that a section of RDSs is closed random, and it cannot be written as a union of disjoint random closed sets if the phase space is connected and vice versa. Also, we prove that any random variable that is not a random fixed point admits a tube. In Section 4, the stochastic Lyapunov function is used to study the stability of random sets. Two important results are proven in this section. The first one, an invariant random compact set is asymptotically stable if and only if there exists a Lyapunov function defined on this random set. The second result, an invariant random closed set is asymptotically stable if and only if there exists a Lyapunov function defined on this random set which satisfies the conditions (i) and (ii) of Theorem 9. In Section 5, parallelizable random dynamical systems are studied by using the dissipation and the stochastic Lyapunov function. Several main results are proven in this section. A random dynamical system is parallelizable if and only if it admits a section. The parallelizability and dispersivity are equivalent when the phase space is a locally compact, separable Banach space. However, in general, parallelizability is not implied by dispersivity. Finally, parallelizability is preserved by an isomorphism. In Section 6, the concept of symmetry in random dynamic systems is studied, and the applications of symmetry are also discussed.
In Section 7, the random Lorenz system is introduced as an application of the parallelizable RDS; this fact is proved by using the stochastic Lyapunov function.
2. Basic Facts About Random Dynamical Systems
In this section, some essential facts about random dynamical systems that are related to our work are given. Let the triple represent the probability space where is a non-empty, be a algebra on , is the probability measure on , and represent to a Banach space. We will denote the open (closed) ball centered at the set with radius by the symbol (respectively, ). The set of random variables from to is denoted by .
Definition 1
([24,25]). The 5-tuple (or just ) is said to be a metric dynamical system (MDS) if is measurable action of on and , for every ,
Definition 2
([24,25]). A random dynamical system (RDS) over an MDS is a mapping , which is measurable, and the mappings form a cocycle over ., i.e., they satisfy for all , and for all , . An RDS is denoted by
Definition 3
([25,26,27]).
- (a)
- The random set is a set-valued function such that the function defined by is measurable for every
- (b)
- For some and some random variable , consider the set. A random set is called tempered ifand is called tempered random variable (TRV); this means
Definition 4
([24,28,29]). The random set is called the trajectory of a random set .
Definition 5
([24,25]). A random fixed point of is the measurable function such that, for all , we have . The set of all random fixed points will be denoted by .
Definition 6
([28]). The random set is called invariant if
Definition 7
([27,28,29,30]). The omega limit set of a random set is defined as follows:
For more details about the Omega limit set (in random case), refer to refs. [27,31].
The definition that follows is in line with what was stated in ref. [20]. Here, the phase space will be regarded as a Banach space.
Definition 8
([32]). Let be a random set in RDS .
- (a)
- The first prolongational limit set of is the random set with the property that if and only if there exist sequences in and in with such that
- (b)
- The first prolongation of a random set is the random set with the property that if and only if there exist sequences in and in such that
Definition 9
([32]). A random variable is said to be non-wandering if .
Definition 10
([32]). Consider an RDS . A random variable is said to be wandering if , for for some random ball centered at .
Definition 11
([32]). Consider the RDS . If for every random variables there exist random balls centered at , respectively, such that , for , then will said to be dispersive.
Theorem 1
([32]). The RDS is dispersive if and only if, for each , is empty.
Theorem 2
([32]). The RDS is dispersive if and only if, for each ,and there are no random periodic trajectories or random fixed points.
Theorem 3
([32]). Let be a closed random set in the RDS . If is invariant and asymptotically stable, then
- (a)
- for each
- (b)
- for each .
3. The Section and the Tube for Random Dynamical Systems
For the study of parallelizable dynamical systems, the two concepts, section and tube, are essential resources. Consequently, we study them for RDSs in this section. The wandering points are used to prove the sufficient condition for the existence of the section. Additionally, we demonstrate that any random variable does not represent a random fixed point for RDSs which is called a tube.
Definition 12.
A section of the RDS is a random set with the property that, for every , there exists a mapping , such that
Lemma 1.
If is a section of such that is continuous for every , then
- (i)
- is a closed random set in
- (ii)
- cannot be written as a union of disjoint random closed sets if and only if is connected.
Proof of (i).
Fix . If is a sequence in and . Since is continuous for every , then for every . Since is continuous for every and every then for every and every . In particular, for every . Since for each , we get . Thus, by the definition of and , we have . So, is a closed random set in . □
Proof of (ii).
Suppose that is connected. Assume the contrary, that is disconnected. So, can be written as a union of two random closed sets, say, , such that . As , then . Note that . To show that and are closed. If , then there exists a net in , such that . Since is continuous, then . Since and are continuous, then we have . Since is a net in and is closed, then . Then .
Therefore, is closed. In a similar way we can show that . Thus is not connected, and this implies a contradiction. The converse can be proven in a similar way. □
Definition 13.
A random open set in will be called a tube if there exists an open neighborhood of and a random subset , such that
- (i)
- , and
- (ii)
- there is a function , with , with .
Remark 1.
Since implies , then . Therefore is an -tube with section and write , and called an -section of the tube .
Lemma 2.
Let be a -tube with section . If is a compact random set, then for every , the function is continuous on for any compact subset of .
Proof.
If is a sequence in and , then . Note that, for every sequence, is in . Since is compact, then this sequence can be assumed to be convergent. Moreover, if is in , then it is bounded; hence, is convergent. Thus, suppose that , and . Since , thus . Since is continous for every , then . Therefore, . This means that . Since , we have by uniqueness. □
Lemma 3.
If is locally compact and is a wandering point of an RDS , then for some random set containing , we have is open and is -section with is continuous on .
Proof.
Let and be the neighborhoods according to which is wandering, and let be a tubular neighborhood of with continuous on . Thus, , and if for some and , then or . We may assume ; otherwise, we need only replace by , which is also open in . If no exists, then for every , there is an and a , such that . Since is wandering, for each hereafter, we may assume that . This implies that , and so because is not closed. Thus, for a sufficiently large , which is absurd. Therefore, there exists a set such that if , the intersects solely at . Since is open in , is open in . Thus, is open. To show that, is continuous on , let and let be a neighborhood of . Then, is a neighborhood of , such that to every there corresponds a unique for which . Since is continuous on , continuity of on follows. □
Theorem 4.
Any random variable that is not a random fixed point admits a tube.
Proof.
Suppose that , then , for some . Consider the function . It follows that
Further, the function is continuous in , with
is continuous. Since
there is a TRV such that for . Define such that
Then, in particular, . Now choose TRV such that
and such that for we have , and for , we have . Finally, determine TRV such that if , then , and whenever . We show that, if , then there is exactly one , , such that . This follows from the fact that is a strictly increasing function of , and . Consider now the open set , and set
We claim that is -section. For this, we need prove that if , then there is a unique , , such that . Indeed, for any , we have , where for some , and for , we have , for some , . Thus, , where , and . Now, let it be possible that there are two numbers, , , , , such that and , and let , where , and where . Then
and
so that
Now, , and , and for , i.e., is strictly increasing for . Hence, , or . □
The following theorem can be now proven as a more general result.
Theorem 5.
Let . Let be given, restricted only by if the motion is periodic with least period . Then there exists a tube containing with a -section .
Theorem 6.
If is a point in a locally compact space such that , then there exists a tube containing , with an -section , and is continuous for every .
Proof.
In fact, there exists a tube of such that a -section of a random set , and is continuous for every . Since is a wandering, we claim that there is a TRV with , which is an -section of the random open set , which is an -tube containing . As there exists a TRV such that every trajectory with intersect only at the point (i.e., if , then ). Otherwise, there will be a sequence in , , and a sequence in , , such that , i.e., either or . However, this is a contradiction because is wandering. Thus, for some TRV , is an -section of the random open set . Furthermore, is open, and the continuity of follows from continuity; it is continuity on , and continuity of the . □
Definition 14.
Given an open -tube with section and a continuous function , and given a random set , satisfying, , where is open in and is compact, we will call the random compactly tube over . Then indeed is continuous forevery .
Theorem 7.
If is locally compact and separable, and if every is a wandering point, then there exists a countable collection of compactly tubes which form a covering of , with continuous on for every and
Proof.
The proof follows from Theorem 5 and the separability of . □
Lemma 4.
A compactly -tube with section of a dispersive dynamical system is a closed random set in
Proof.
Let . For any sequence in , there are sequences and in and , respectively, with . Since is compact, we may assume that . Now, if , then is bounded, so that . For otherwise, if contains an unbounded subsequence , say , then clearly , which is absurd as for each by Theorem 1. □
Lemma 5.
Let , be compactly tubes of a dispersive RDS with sections , , and continuous mappings , , respectively. If , then is a compactly tube with a section and a continuous mapping .Moreover, if the distance of time between and along trajectories in is less than (), the distance of time between and along trajectories in is also less than
Proof.
and are invariant and random closed. Therefore is invariant and closed. Further, is compact and non-empty. Set and . Any trajectory in meets , and therefore , in precisely one point, and therefore meets and in precisely one point. Therefore, for every , we have . This is because and
and there are no random periodic trajectories or random fixed points. The continuous function on a compact set can be extended to a continuous function defined on in which for . Further, if for , we can have on . Notice now that , and is continuous. Since is compact, then so is . Now set
and define , where
as follows
is continuous for every . We need only verify that if , then
4. Stability for the Random Sets via Stochastic Lyapunov Function
This section focuses on studying the stochastic version of Lyapunov stability theory. The principle of Lyapunov stability will be used to complete our study in the later sections. In ref. [24], L. Arnold and B. Schmalfuss studied the stability of random sets by using the stochastic Lyapunov functions. They assumed that the state space of the RDS is the Euclidean space . In this article, the infinite-dimensional Banach space will be considered instead of .
The following definition is mentioned in ref. [30], but in this article, the phase space is Banach space.
Definition 15.
Let be an RDS defined over the infinite dimensional Banach space, and be a random compact set which is invariant under
- (i)
- is called stable under if for any there exists a random compact set which is a neighborhood of (i.e., is a neighborhood of for all ), such that
- is forward invariant under
- (ii)
- is called a (global) attractor of if for any random variable
- (iii)
- is called (globally) asymptotically stable if it is stable and is an attractor.
Definition 16.
Let be an RDS in , and be a random compact set which is invariant under . A function is called a Lyapunov function for (under ) if it has the following properties:
- (i)
- is measurable for each , and is continuous for each ;
- (ii)
- is uniformly unbounded, i.e., for all ;
- (iii)
- is positive-definite, i.e., for , and for ;
- (iv)
- is strictly decreasing along orbits of , i.e.,
Theorem 8.
Let be an RDS in , and let be a random compact set which is invariant under . Then, is asymptotically stable if and only if there exists a Lyapunov function for . If is asymptotically stable, then the Lyapunov function can be chosen to satisfy
on a -invariant set of full measure.
Proof.
For the proof, see ref. [13]. Corollary 2 only replaces the phase space with infinite-dimensional Banach space rather than . □
Theorem 9.
Let be a closed random set. Then, is asymptotically stable if and only if there is a function which satisfies both the condition (i)–(iii) of Definition 16 and the following conditions
- (i)
- there exist strictly increasing functions , defined for , such that
- (ii)
- for all , for all , , and if there is a TRV such that if , but then
Proof of i.
Sufficiency. Given set . By Definition 16 (iii), . Then, for , there is a tempered random variable such that for . This is also possible by Definition 16 (i) and (iii). We claim that ; otherwise, there is and such that . But then, on one hand by Theorem 9 (iii), and also
as , that is . This contradiction proves the result.
Proof of ii.
Necessity. Let be stable. Define
This is defined on . The theorem is proven. □
Remark 2.
Condition (ii) in the Theorem 9 is equivalent to the requirement that for every , there is a tempered random variable , such that
also, for any sequence ,
5. Dispersive and Parallelizability for Random Dynamical Systems
The parallelizable RDSs is given [16] as a special case of gradient-like, where the authors proved that the following statements are equivalents:
- (1)
- is a gradient-like RDS.
- (2)
- possesses a continuous random section
- (3)
- possesses a continuous and strict Lyapunov function.
- (4)
- The backward RDS associated to is gradient-like.
In this section, some new properties of parallelizable RDS are given, and the parallelizable RDS is characterized using dispersive RDS, which is given in ref. [31].
Definition 17.
Let be an RDS. If there is a random set and a mapping satisfy the following conditions:
- (i)
- is measurable.
- (ii)
- is a homeomorphism for every .
- (iii)
- .
- (iv)
- for every and .Then is called parallelizable.
Theorem 10.
An RDS is parallelizable if and only if it admits a section such that is continuous for every
Proof.
Suppose that is parallelizable, then by Definition 17, there is a random set and a function , which satisfies
- (i)
- is measurable.
- (ii)
- is homeomorphism for every .
- (iii)
- .
- (iv)
- for every and .
To show that is a section. Let , then . Thus, for some and , we have , so that . Define by . Then , and hence is a section of . Suppose that has a section with is continuous for every . Then . Now, define by . Then, is for every . Since and are continuous, then is continuous for every . Define by . It is easy to show that the inverse of is the function . Also, is continuous for every . Therefore, is a homeomorphism for every . Consequently, is parallelizable. □
Theorem 11.
For the RDS the parallelizable and dispersive are equivalent when the phase space is locally compact separable Banach space.
Proof.
Only the sufficiency part needs proof. By Theorem 10, it is enough to show that admits a section such that is continuous for every . Theorem 7 implies that there exists a countable cover of by compactly tubes , with as a section and continuous functions . We construct a compactly tube cover as follows. Set , and . Beginning with and , we use Lemma 5 to extend to a compact set , hence finding the compactly tube with is continuous for every . This guarantees is an invariant. After we found the , choose it with , and create likewise with and continuous for every . Now set then , and the function defined by for and is continuous on for every , with the property that . Moreover, is unique for each and . Thus, admits a section such that is continuous for every . The RDS is parallelizable. □
Corollary 1.
If is RDS with the phase space is locally compact separable Banach space, then the following holds:
- (1)
- The RDS is parallelizable if and only if the prolongation limit set for every x ∈ X.
- (2)
- Let be an asymptotically stable closed invariant random set. The set is parallelizable if it is locally compact and covers a countable dense set.
Proof.
The proof follows from Theorem 3 and Theorem 10. □
Example 1.
Consider the stochastic differential system
To put the system (1) in the framework of RDS, we model white noise as a metric dynamical system as follows: Let be the space of continuous functions , which satisfy , let be the Borel sigma-algebra induced by the compact-open topology of , and let be the Wiener measure on , i.e., the distribution on of a standard Wiener process with two-sided time. The shift is defined by . Then, is an ergodic metric dynamical system ‘‘driving’’ the stochastic differential system (1), and . We refer to ref. [4] for details. The solution of the system (1) can be explicitly given by
Then, is defined by
which forms a cocycle over . Thus is the RDS generated by the system (1). Let . Since is invariant, we can restrict on to provide a new RDS in which . Now, since for every , then by Theorem 1 (with and ), is dispersive RDS. Since the space is a locally compact separable metric space, then by Theorem 11, is parallelizable.
Example 2.
Consider the system of stochastic differential equations
where is continuous. Furthermore, when , assume that if and otherwise. Let , where . Note that is not locally compact. Now consider the RDS generated from the given system on over an MDS . This RDS is dispersive but not parallelizable.
Example 3.
Consider Example 3 with ( is locally compact); then, for every x ∈ X. Then, by Corollary 1 (1), the RDS is parallelizable.
Theorem 12.
Let be a closed invariant random set. If is uniformly asymptotically stable, then is parallelizable.
Proof.
Define a function satisfying the properties of Theorem 9 because is uniformly asymptotically stable. Also, there is an so that , and such that for any , there is a with the property that for every , where . Now, let . Indeed, . Consider now any set . We claim that if , then is a section of the flow in such that there is a unique continuous function , mapping into , such that for each . Then, by Corollary 1, is parallelizable. To show that, admits the above enunciated properties, consider the set . Indeed, and . Any trajectory in can meet the set at a single point at most because, if a trajectory in admits two points , on , then we may assume that where . However, since , and , which is a contradiction. To show that any trajectory in meets , if , there exists a with . But . However, . If , then we claim that there exists with ; otherwise, . Thus, we can put , and . By uniform asymptotic stability, it can be assumed that such that implies . Thus, , but , which is a contradiction, and any trajectory in meets at a single point. Define by the requirement that for . We claim that is uniquely defined and is continuous for every . For any , and , the point .·There is, therefore, a neighborhood of such that . The set forms a neighborhood of x and for each . Again, . Note that is open. Hence, there exists a neighborhood of so that . Then is a neighborhood of , and note that, for each , we have . Thus, if is in the neighborhood of , we have . Thus, is continuous on . We claim that for every , as , . Otherwise, there is a and a sequence in , with and . Since the sequence is bounded, it has a convergent subsequence. Therefore, it can be assumed that for every , where . Then, by the continuity of (This function is continuous because is Banach space, and hence it is smooth manifold, see ref. [6].) we have . As is invariant, ; on the other hand, . which is compact. Therefore, but ; this is a contradiction. Define by
Then this function is continuous on . It is positive for and
Finally, to show that, is uniformly unbounded, since
The sets are compact and positively invariant random sets for every . Observe that, if for each , then , so that . □
6. Symmetry of Random Dynamical Systems
This section is dedicated to discussing the concept of symmetry in random dynamical systems. The symmetry of random dynamical systems is a generalization of the symmetry of deterministic dynamical systems. We will illustrate during the discussion the types of symmetry used in the research and their significance to the posed problem. Additionally, we will discuss the applications of symmetry. This field has been the subject of extensive research recently. We make reference to several recent advancements [33,34,35,36,37].
Symmetry will be defined in a manner similar to that mentioned in ref. [26].
Definition 18.
The two RDSs, and (with phase spaces and , respectively), are said to be symmetric and written as , if there is a function such that
- (i)
- The function , is diffeomor-phism for every
- (ii)
- The function → is bi-measurable for every .
- (iii)
- ; for every .
If , then the RDS is called symmetry. The function is called a function of symmetry. Any property that is invariant under the influence of a symmetry function is called a symmetry property.
Proposition 1.
Let . If is a parallelizable RDS, then so is
Proof.
If is parallelizable RDS, then there is a random set and a function satisfying the conditions of Definition 17. It is easy to show that and , satisfying the Definition 17, where and . □
Proposition 2.
Let . If is an dispersive RDS, then so is
Proof.
Suppose that is a dispersive RDS. Then, by Theorem 1, for every . Since
then is an dispersive. □
Proposition 3.
Let . If is an asymptotically stable compact (closed) random set in , then is an asymptotically stable compact (closed) random set in
Proof.
Suppose that is an asymptotically stable compact (closed) random set in . First note that, because is diffeomorphism (and hence homeomorphism), then the set is a compact (closed) random set in . Now, since is asymptotically stable compact (closed), then there exists a function which satisfies the hypothesis of Theorem 8 (Theorem 9). Define by for every . It is not difficult to show that satisfies the hypothesis of Theorem 8 (Theorem 9). Consequently, is a compact (closed) random set in . □
Corollary 2.
The parallelizability, dissipativity, and asymptotic stability are symmetry properties.
Proof.
The proof follows from Propositions 1, 2, and 3, respectively.
7. Application
Consider the (deterministic) system of ordinary differential equations
This system is referred to as “the Lorenz deterministic system” (one can see, for example, [38]), where
- represents time.
- represents the intensity of convection motion.
- represents the temperature difference between uphill and downhill currents.
- represents the misrepresentation (from linearity) of the vertical temperature profile.
The constants in (3) are defined as follows: called the Brandt number, , , a constant associated with the given space. Here, as in ref. [38], is a number associated with the concerned region, is the Rayleigh number, and .
Suppose that the real noises are perturbing the parameters and , i.e.,
Assume that the perturbed parameters are still positive and almost surely. Thus, the random ODE corresponding to deterministic ODE (3) is given by
or, in a compact form , where defined by
Then the perturbed random ordinary differential equations generate an RDS, and we denote it by ; see ref. [5] for details. Consider the function defined by and define the random set
is thus obviously a random compact set. Furthermore, throughout the orbits of , the derivative of with respect to is
whenever by the assumption , where , , and with . Therefore, for every and every we have , i.e., . Consequently, is the Lyapunov function. Thus, possesses a continuous and strict Lyapunov function. Hence, we conclude that is parallelizable RDS [16].
It is worth mentioning that the Lorenz system is symmetry. This can be demonstrated by choosing to be such that
To clarify the ideas presented in this section, we will provide a numerical simulation with some graphs. Note that the parameter will be represented by the order triplet for every figure. If not specified, and are fixed at and .
MatLab’s ODE45 (version 2020) is utilized for every simulation, with an error allowed of . A black point indicates where the initial conditions are in each graph. Unless otherwise indicated, is the time interval displayed for every graph.
For different initial conditions and , a number of tests demonstrate global convergence. One can see the bifurcation as increases from to . For , the origin is no longer stable.
Figure 1 illustrates how a small alteration to the starting condition can result in a significant shift in the trajectory. The -coordinate versus time is shown on the right side of 6.1. Up until roughly , the trajectory is almost stable.
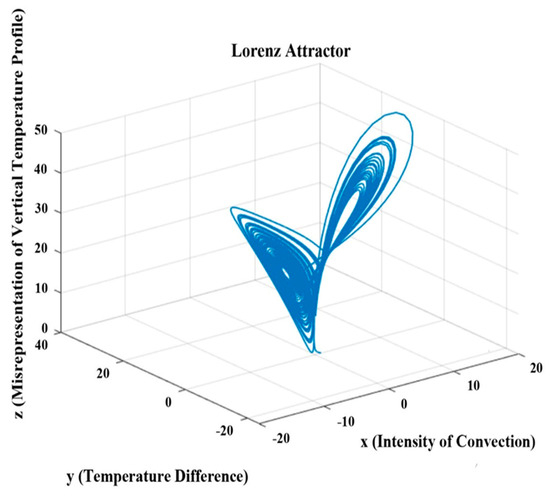
Figure 1.
, . .
In Figure 2, we observe from the graphs that, when the equation includes a random element, sudden changes in long-term patterns can be noticed. The graph shows stability for a certain period, followed by a sudden change in behavior due to random fluctuations. Additionally, irregular fluctuations appear. Consequently, these fluctuations are unpredictable, which can make the movement more erratic. The graph illustrates how the paths continuously change due to randomness.
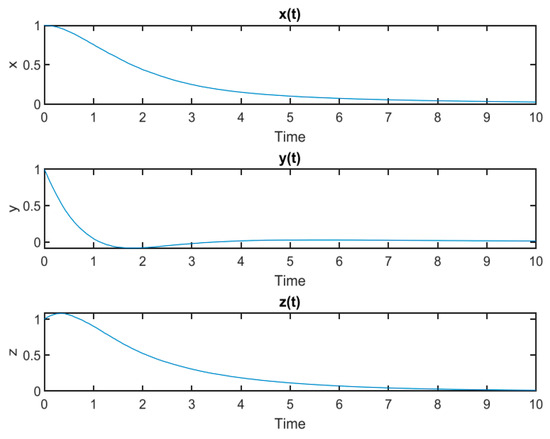
Figure 2.
Simulation of Lorenz Random system.
8. Conclusions
In this article, the parallelism in stochastic dynamics was studied through random Lyapunov function, dispersion, and prolongational limit set. A number of new results were reached, highlighting the impact of parallelism on the long-term behavior of stochastic dynamical systems. We review some of them here. Any random variable that is not a random fixed point admits a tube. The relationship between the concepts, a prolongational limit set and a section, is discussed, and we came to the conclusion stated in Theorem 6. Also, we prove that a closed random set is asymptotically stable if and only if there is a Lyapunov function that satisfies the conditions (i) and (ii) of Theorem 9. A characterization of the concept of parallelizable RDS is given in the sense of the concept of the RDS section, and this is explained in Theorem 10. Theorem 11 shows that for any RDS, the parallelizable and dispersive are equivalent when the phase space is a locally compact separable Banach space. However, in general, parallelizability is not implied by dispersivity. The relationship between the parallelizable property of RDS and the prolongational limit set and the prolongation set, on the one hand, and the relationship of the parallelism property to the dispersion property contained in ref. [21], on the other hand, has been shown. In addition, we find the relationship between the parallelizable and the region of attraction of the asymptotically stable closed invariant random set; this is stated in Corollary 1. One of the important results we have reached during this research is the relationship between parallelizable RDS and the region of attraction of the uniformly asymptotically stable closed invariant random set. This is stated in Theorem 12.
Also, we show that the parallelizability, dispersivity, and asymptotic stability are invariant under symmetry.
Finally, by using an appropriate stochastic Lyapunov function, we conclude that the RDS generated by the random Lorenz system is parallelizable.
The study demonstrates, through the introduction of the random Lorenz system, that there are significant applications for the notion of parallelism. Looking at the future prospects, upcoming research may contribute to the development of the theoretical foundation of the parallelism, in addition to developing effective and important practical models. This may be possible through the study of the parallelizability for RDSs defined on the plane as phase space and proving that such an RDS is either parallelizable, or it has a single random fixed point, which is a global Poincaré center, or the set of all random fixed points is equal to the plane.
Author Contributions
Conceptualization, I.J.K. and A.A.Y.; methodology, I.J.K.; software, A.A.Y.; validation, I.J.K. and A.A.Y.; formal analysis, I.J.K.; investigation, A.A.Y.; resources, I.J.K.; data curation, I.J.K.; writing—original draft preparation, I.J.K.; writing—review and editing, I.J.K.; visualization, A.A.Y.; supervision, I.J.K.; project administration, A.A.Y.; funding acquisition, I.J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dugundji, J.; Antosiewicz, H. Parallelizable Flows and Lyapunov’s Second Method. Ann. Math. 1961, 73, 543–555. [Google Scholar] [CrossRef]
- Jenkins, T.; Johnson, W. Parallelizability of Dynamical Systems. Monatshefte Math. 1965, 69, 323–325. [Google Scholar] [CrossRef]
- Ura, T. Local Isomorphisms and Local Parallelizability in Dynamical Systems Theory. Math. Syst. Theory 1969, 3, 1–16. [Google Scholar] [CrossRef]
- Ura, T. Isomorphisms and local characterization of local dynamical systems. Funkc. Ekvacioj 1969, 12, 99–122. [Google Scholar]
- Hajek, O. Parallelizability Revisited. Proc. Am. Math. Soc. 1971, 27, 77–84. [Google Scholar] [CrossRef]
- Egawa, J. Global Parallelizability of Local Dynamical Systems. Math. Syst. Theory 1972, 6, 133–144. [Google Scholar] [CrossRef]
- Ura, T.; Egawa, J. Isomorphism and Parallelizability in Dynamical Systems Theory. Math. Syst. Theory 1973, 7, 250–263. [Google Scholar] [CrossRef]
- Garay, B. Parallelisability in Banach spaces: A parallelisable dynamical system with uniformly bounded trajectories. Proc. R. Soc. Edinb. 1988, 108A, 371–378. [Google Scholar] [CrossRef]
- Garay, B. Parallelizability in Banach Spaces: Parallelizable Dynamical Systems with Bounded Trajectories. Banach Cent. Publ. 1989, 23, 25–31. Available online: http://eudml.org/doc/265690 (accessed on 10 February 2025). [CrossRef][Green Version]
- Garay, B. Parallelizability in Banach spaces: Applications of negligibility theory. Acta Math. Hung. 1989, 53, 3–22. [Google Scholar] [CrossRef]
- Leśniak, Z. On parallelizability of flows of free mappings. Aequationes Math 2006, 71, 280–287. [Google Scholar] [CrossRef]
- Leśniak, Z. On Boundaries of Parallelizable Regions of Flows of Free Mappings. In Abstract and Applied Analysis; Hindawi Publishing Corporation: London, UK, 2007; Volume 2007, 8p. [Google Scholar] [CrossRef]
- Souza, J.; Pacifico, T.; Tozatti, H. A Note on Parallelizable Dynamical Systems. Electron. Res. Announc. Math. Sci. 2017, 24, 64–67. [Google Scholar] [CrossRef][Green Version]
- Mao, X. Lyapunov’s Second Method for Stochastic Differential Equations. Equadiff 2000, 99, 136–141. [Google Scholar] [CrossRef]
- Arnold, L.; Schmalfuss, B. Lyapunov’s Second Method for Random Dynamical Systems. J. Differ. Equ. 2001, 177, 235–265. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, S.; Su, M. Attractor-Repeller Pair, Morse Decomposition and Lyapunov Function for Random Dynamical Systems. Stoch. Dyn. 2008, 8, 625–641. [Google Scholar] [CrossRef]
- Hmissi, A.; Hmissi, F.; Hmissi, M. On Gradient-Like Random Dynamical Systems. Proceedings 2012, 36, 217–228. [Google Scholar] [CrossRef]
- Visentin, F. A Survey on Stability for Stochastic Differential Equations. Sci. Math. Jpn. 2013, 76, 147–152. [Google Scholar]
- Ju, X.; Qi, A.; Wang, J. Strong Morse–Lyapunov functions for Morse decompositions of attractors of random dynamical systems. Stoch. Dyn. 2018, 18, 1850012. [Google Scholar] [CrossRef]
- Üçer, E. Lyapunov Function Based Criteria for Ship Rolling in Random Beam Seas. Pol. Marit. Res. 2019, 26, 6–14. [Google Scholar] [CrossRef]
- Kadhim, I.J.; Imran, M. Stability and Asymptotic Stability of Closed Random Sets. J. Phys. Conf. Ser. 2020, 1664, 012049. [Google Scholar] [CrossRef]
- Elbaz, I.M. Stability Analysis of Stochastic and Random Systems in The Lyapunov Sense. Results Control Optim. 2021, 5, 100060. [Google Scholar] [CrossRef]
- Almutairi, A.; El-Metwally, H.; Sohaly, M.A.; Elbaz, I.M. Lyapunov Stability Analysis for Nonlinear Delay Systems under Random Effects and Stochastic Perturbations with Applications in Finance and Ecology. Adv. Differ. Equ. 2021, 2021, 186. [Google Scholar] [CrossRef]
- Lukashiv, T.; Litvinchuk, Y.; Malyk, I.V.; Golebiewska, A.; Nazarov, P.V. Stabilization of Stochastic Dynamical Systems of a Random Structure with Markov Switches and Poisson Perturbations. Mathematics 2023, 11, 582. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; corrected 2nd printing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Chueshov, I. Monotone Random Systems Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Molchanov, I. Theory of Random Sets; Springer: London, UK, 2005. [Google Scholar]
- ALkhrayfawee, N.G.; Kadhim, I.J.; ALbukhuttar, A.N. P- Omega Limit Set in Random Dynamical Systems. J. Phys. Conf. Ser. 2022, 2322, 012041. [Google Scholar] [CrossRef]
- Abdullah, N.; Kadhim, I.J.; Kadhim, A.N. Attraction Properties and Asymptotically Equivalent of Random Dynamical System. Int. J. Mech. Eng. 2022, 7, 3674–3680. [Google Scholar]
- Yasir, A.A.; Kadhim, I.J. Dissipative Random Dynamical Systems and Levinson Center. Nonlinear Funct. Anal. Appl. 2023, 28, 521–535. [Google Scholar] [CrossRef]
- Kadhim, I.J. On Dispersive and Completely Unstable Random Dynamical Systems. Int. J. Acad. Appl. Res. IJAAR 2023, 7, 71–78. [Google Scholar]
- Ahmad, H. Dynamical Systems of Characteristic 0+. Pac. J. Math. 1970, 32, 561–574. [Google Scholar] [CrossRef][Green Version]
- Bhatia, N.; Szego, G. Stability Theory of Dynamical System; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1970. [Google Scholar]
- Bihlo, A. Symmetry Methods in the Atmospheric Sciences. Ph.D. Thesis, Universitat Wien, Vienna, Austria, 2010. [Google Scholar]
- Cao, Z.; Lin, Y. Lie Point Symmetries, Conservation Laws, and Solutions of a Space Dependent Reaction-Diffusion Equation. Appl. Math. Comput. 2014, 248, 386–398. [Google Scholar] [CrossRef]
- Johannssen, A.; Chukhrova, N.; Zhu, Q. Symmetrical and Asymmetrical Distributions in Statistics and Data Science. Symmetry 2023, 15, 2140. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Generating Chaos in Dynamical Systems: Applications, Symmetry Results, and Stimulating Examples. Symmetry 2024, 16, 938. [Google Scholar] [CrossRef]
- Gulick, D. Encounters with Chaos and Fractals, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).