Simultaneous Generation of Linear- and Circular-Polarization Vortex Based on Symmetrical Metallic Quasi-Metasurface
Abstract
1. Introduction
2. Fundamental Theory
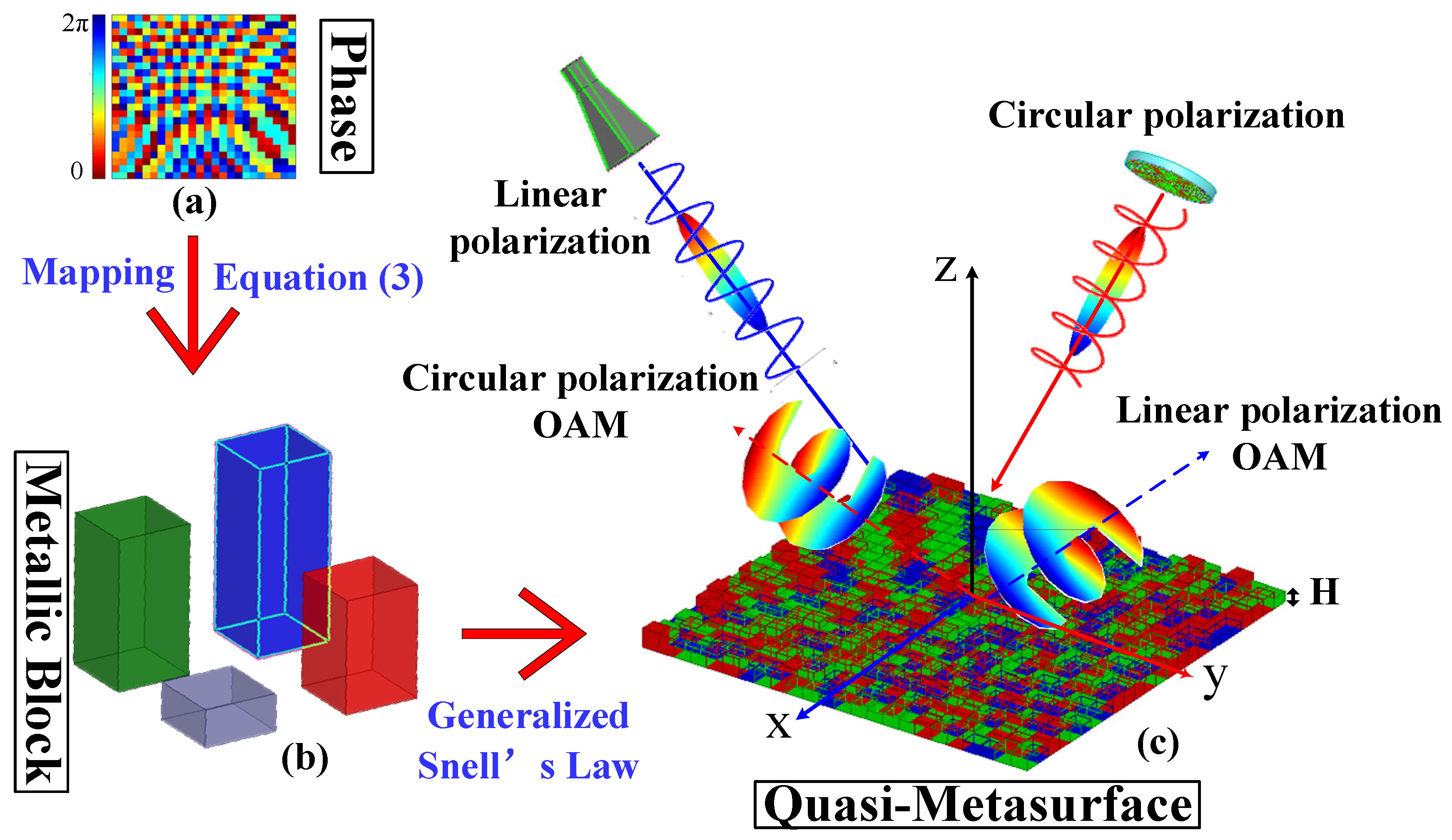
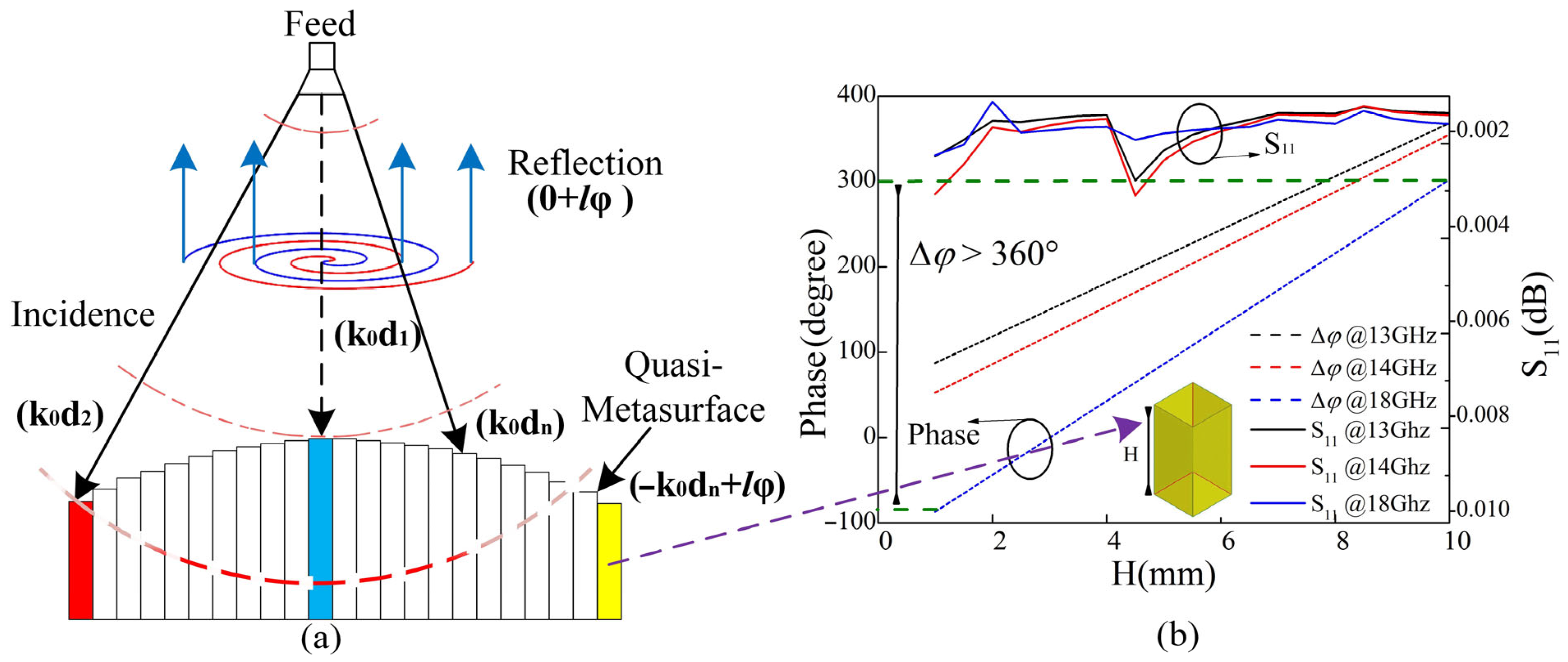
2.1. Generalized Snell’s Law (GSL) and Orbital Angular Momentum (OAM)
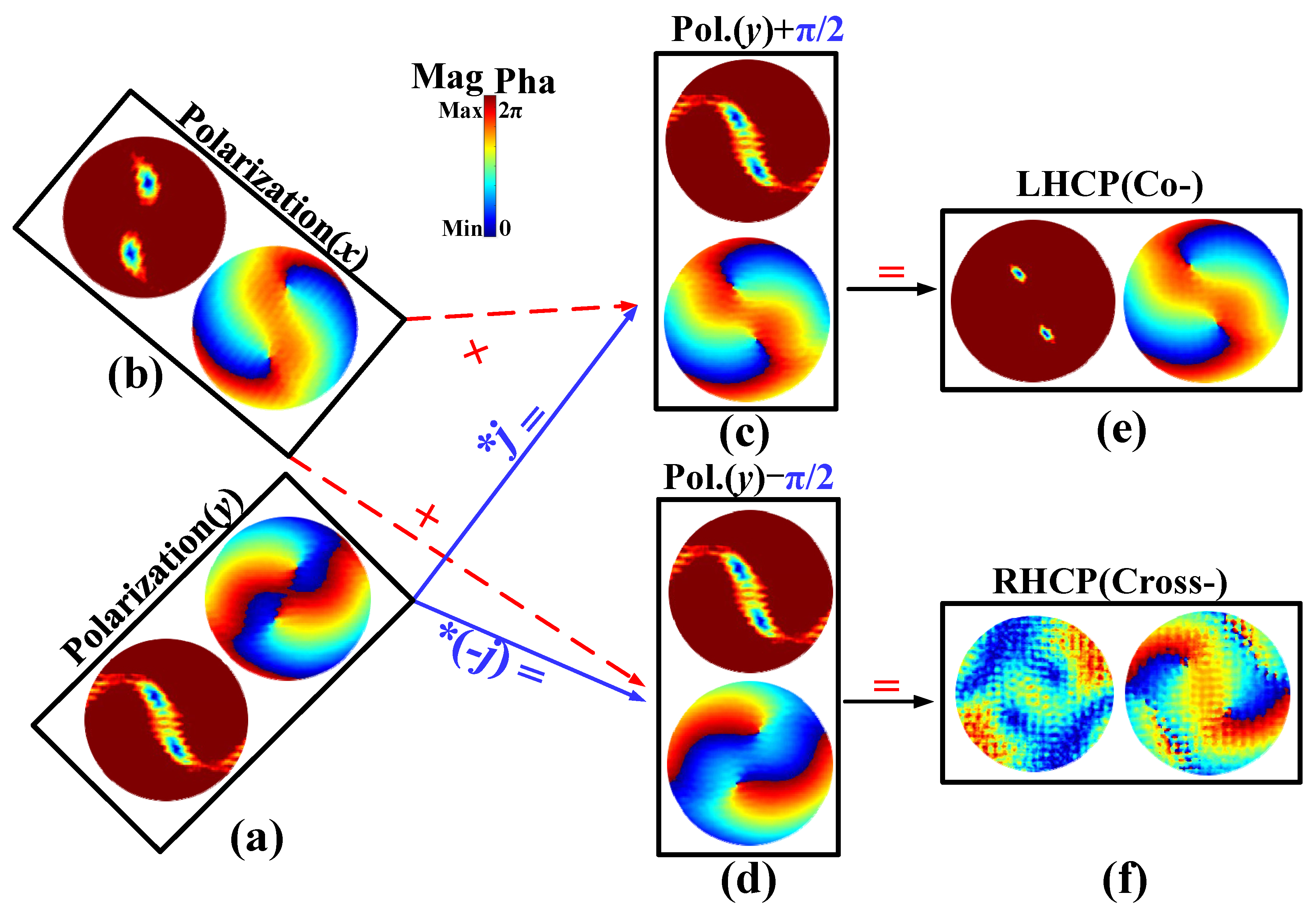
2.2. Synthesis of Circular-Polarization Wave from Linear-Polarization Wave
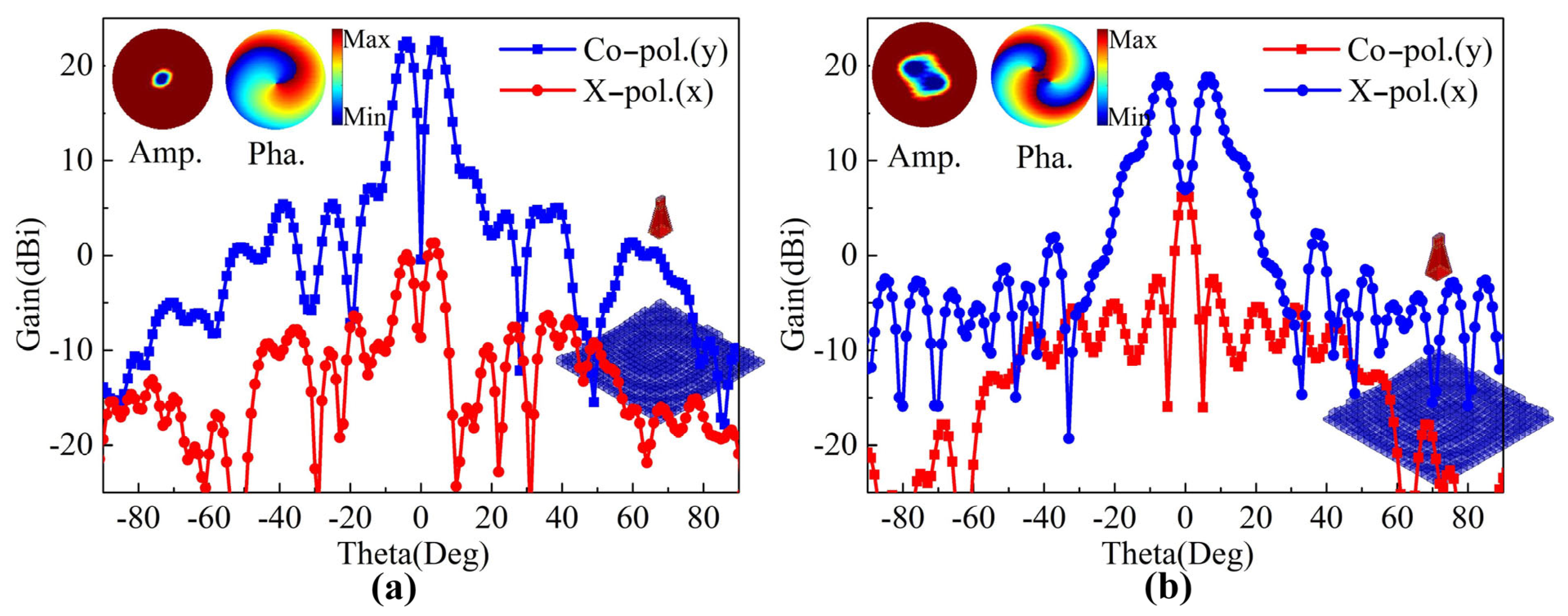
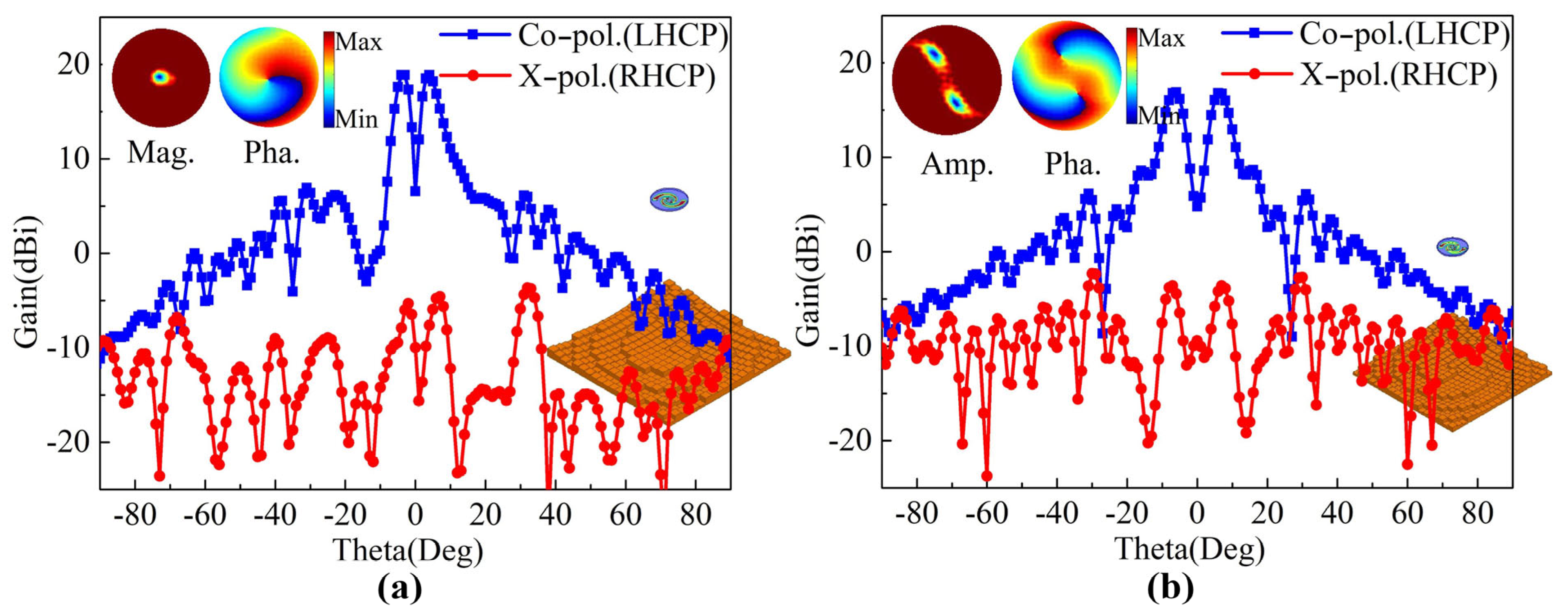
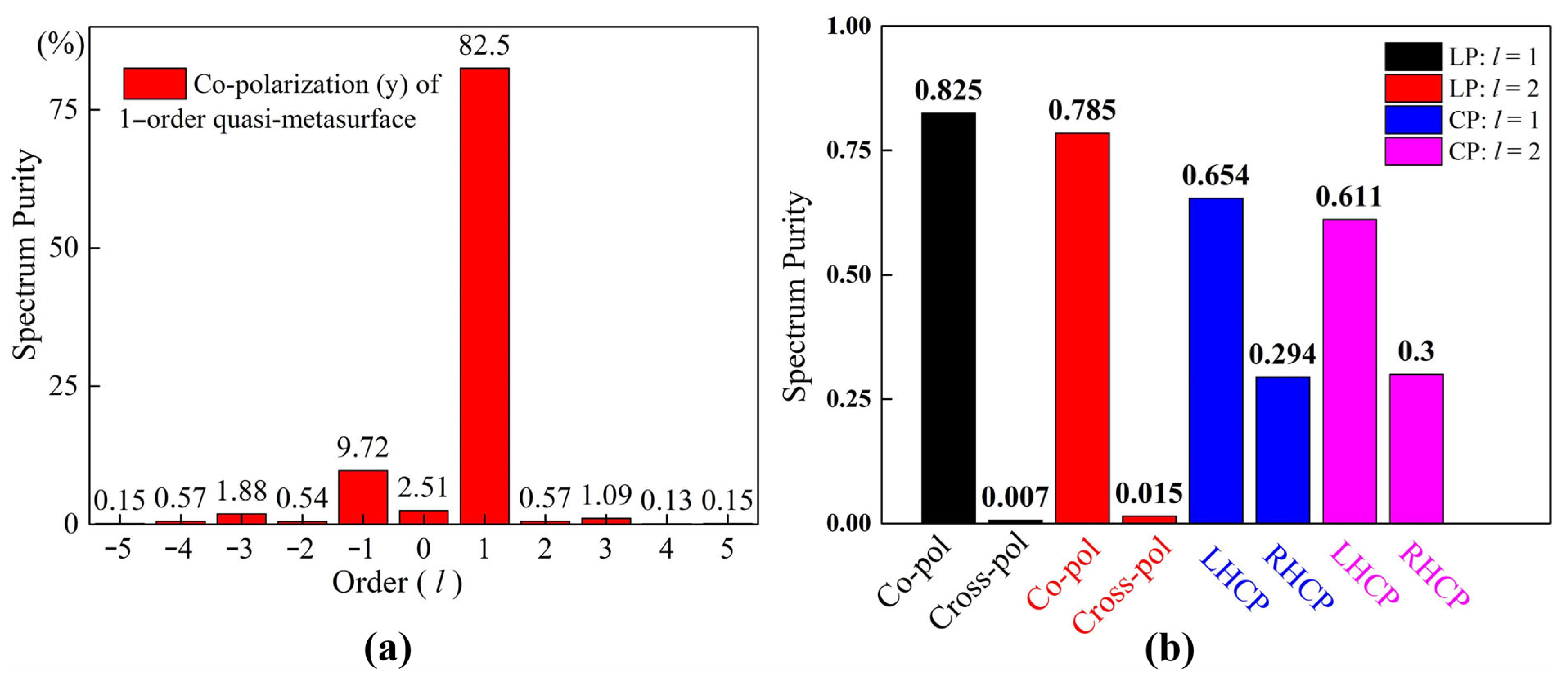
3. Performance Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OAM | Orbital Angular Momentum |
| PB | Pancharatnam–Berry |
| HFSS | High-Frequency Structure Simulator |
| GSL | Generalized Snell’s Law |
| RHCP | Right-Hand Circular Polarization |
| LHCP | Left-Hand Circular Polarization |
References
- Chen, P.; Ren, J.; Zhang, T.; Zheng, Q.; Pang, X. An orbital angular momentum metasurface antenna with broadband radar cross section reduction. Int. J. Electron. Commun. 2024, 177, 1179–1186. [Google Scholar] [CrossRef]
- Al-Nuaimi, M.K.T.; Huang, G.-L.; Whittow, W.G.; Chen, R.-S.; Wong, S.-W. Realization of Single-Layer Fourier Phased Metasurfaces for Wideband RCS Reduction. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1179–1183. [Google Scholar] [CrossRef]
- Ding, X.; Guan, C.; Wang, Z.; Liu, S.; Zhang, K.; Gu, X.; Wu, Q.; Jin, M. Metasurface for Bending the Reflected Wave Under Oblique Incidence. IEEE Trans. Magn. 2019, 55, 1109–1116. [Google Scholar] [CrossRef]
- Yang, C.; Yang, C.; Zhang, C.; Feng, J.; Xu, C.; Li, H. Wideband Lorenz Resonance Reconfigurable Metasurface for 5G+ Communications. Electronics 2022, 11, 4105. [Google Scholar] [CrossRef]
- Wang, K.; Shao, W.; Ding, X.; Wang, B.-Z.; Jiang, B. Design of High-Gain Metasurface Antenna Based on Characteristic Mode Analysis. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 661–665. [Google Scholar] [CrossRef]
- Faenzi, M.; Gonzalez-Ovejero, D.; Petraglia, G.; D’Alterio, G.; Pascariello, F.; Vitiello, R.; Maci, S. A Metasurface Radar Monopulse Antenna. IEEE Trans. Antennas Propag. 2022, 70, 2571–2579. [Google Scholar] [CrossRef]
- Yang, D.; Yuan, Y.; Wu, Q.; Zhang, K. High-Gain OAM Antenna with Low Profile Utilizing Integrated Reflective Metasurface. IEEE Antennas Wirel. Propag. Lett. 2023, 23, 294–298. [Google Scholar] [CrossRef]
- Ishfaq, M.; Li, X.; Qi, Z.; Zhao, W.; Aziz, A.; Qiu, L.; Memon, S. A Transmissive Metasurface Generating Wideband OAM Vortex Beam in the Ka-Band. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1675–1679. [Google Scholar] [CrossRef]
- Qi, Y.; Li, H.; Su, M.; Wang, X. Terahertz Metasurface: Non-Diffracting OAM Generation, Multidimensional Multiplexing, and SA-RCS Reduction. J. Light-Wave Technol. 2024, 42, 1620–1625. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, S.; Zhang, H.; He, T.; Li, N.; Yang, Z.; Lyu, Z.; He, Y.; Zhang, L.; Yu, X. A Reflective Metasurface for OAM and Polarization Multiplexing Communication in the W-Band. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 1124–1128. [Google Scholar] [CrossRef]
- Brennan, C.; Trinh, D.; Pham, V.; Condon, M.; Mittra, R. Full-wave analysis of electromagnetic wave propagation over terrain using the Improved Tabulated Interaction Method. Radio Sci. 2015, 50, 355–364. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, R.; Deng, Y.; Zhang, B.; Wang, N.; Li, N.; Wang, P. Generation and Transmission of OAM-Carrying Vortex Beams Using Circular Antenna Array. IEEE Trans. Antennas Propag. 2017, 65, 2940–2949. [Google Scholar] [CrossRef]
- Fayyaz, U.; Niazi, S.A.; Zhang, X.; Aziz, A.; Aljaloud, K.; Hussain, R. Effective Realization of Higher Order Circular Polarized OAM Mode Circular Patch Antenna. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1989–1993. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, S.; Li, Y.; Hui, X.; Jin, X.; Chi, H.; Zhang, X. A Flat-Lensed Spiral Phase Plate Based on Phase-Shifting Surface for Generation of Millimeter-Wave OAM Beam. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1156–1158. [Google Scholar] [CrossRef]
- Yang, W.; Chen, S.; Che, W.; Xue, Q.; Meng, Q. Compact High-Gain Metasurface Antenna Arrays Based on Higher-Mode SIW Cavities. IEEE Trans. Antennas Propag. 2018, 66, 4918–4923. [Google Scholar] [CrossRef]
- Xin, H.; Yang, J.; Tang, M.-C.; Zhang, H.; Zhang, Z.; Qu, M. Broadband electrically controlled reflective metasurface for reconfigurable circularly polarized wavefront manipulation. Opt. Express 2023, 31, 13518–13527. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.; Ding, T. Ultrathin dual-mode vortex beam generator based on anisotropic coding metasurface. Sci. Rep. 2021, 11, 5766–5774. [Google Scholar] [CrossRef]
- Nadi, M.; Sedighy, S.H.; Cheldavi, A. Multimode OAM beam generation through 1-bit programmable metasurface antenna. Sci. Rep. 2021, 13, 15603. [Google Scholar] [CrossRef]
- Hui, Y.; Cui, Z.; Guo, S.; Han, Y. Propagation dynamics of vortex electromagnetic waves in dispersive left-handed materials. Waves Random Complex Media 2023, 33, 122–136. [Google Scholar] [CrossRef]
- Ding, G.; Chen, S.; Luo, X.-Y.; Wang, S.-Y.; Chen, K. Ultrathin Single-Substrate Pancharatnam–Berry Phase Metasurface With High Transmission Efficiency. IEEE Trans. Antennas Propag. 2023, 70, 9571–9580. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, Y.; Cui, X.; Zhang, J.; Xu, P.; Ji, X. Generation of dual-polarization orbital angular momentum vortex beams with reflection-type metasurface. Opt. Commun. 2023, 553, 130107. [Google Scholar] [CrossRef]
- Lv, H.-H.; Huang, Q.-L.; Yi, X.-J.; Hou, J.-Q.; Shi, X.-W. Low-Profile Transmitting Metasurface Using Single Dielectric Substrate for OAM Generation. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 881–885. [Google Scholar] [CrossRef]
- Liu, B.; Li, Y.; Rashid, A.K.; Jiang, X.; Wong, S.-W.; Zhang, X.; Tam, K.W.; Zhang, Q. High-Gain Broadband Millimeter-Wave Multidimensional Metasurface for Generating Two Independent Vortex Waves. IEEE Trans. Antennas Propag. 2022, 70, 8195–8203. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, D.; Liu, Q.; Yan, M.; Wang, X. Multi-mode vortex beams generation with single-layer transmissive metasurface. Phys. Scr. 2023, 98, 125530. [Google Scholar] [CrossRef]
- Deng, R.; Yang, F.; Xu, S.; Li, M. A 100-GHz Metal-Only Reflectarray for High-Gain Antenna Applications. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 178–181. [Google Scholar] [CrossRef]
- Nayeri, P.; Liang, M.; Sabory-Garcıa, R.A.; Tuo, M.; Yang, F.; Gehm, M.; Xin, H.; Elsherbeni, A.Z. 3D Printed Dielectric Reflectarrays: Low-Cost High-Gain Antennas at Sub-Millimeter Waves. IEEE Trans. Antennas Propag. 2014, 62, 2000–2008. [Google Scholar] [CrossRef]
- Bahramipour, S.S.; Afrooz, K.; Honari, M.M.; Mirzavand, R.; Mousavi, P. Gradient and Huygens’ Metasurface Design and Analysis Based on Transmission Line Theory. IEEE Trans. Antennas Propag. 2020, 68, 6752–6763. [Google Scholar] [CrossRef]
- Yang, L.-J.; Sun, S.; Sha, W.E.I. Ultrawideband Reflection-Type Metasurface for Generating Integer and Fractional Orbital Angular Momentum. IEEE Trans. Antennas Propag. 2019, 68, 2166–2175. [Google Scholar] [CrossRef]
- Qin, F.; Zeng, L.; Liu, S.; Gu, C.; Liu, X.; Zhang, H. Dual-Mode High-gain OAM array based on Nested Metasurface with Simplified Feeding Network. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 59–63. [Google Scholar] [CrossRef]
- Ilić, A.Ž.; Vojnović, N.M.; Savić, S.V.; Grass, E.; Ilić, M.M. Optimized planar printed UCA configurations for OAM waves and the associated OAM mode content at the receiver. Int. J. Commun. Syst. 2023, 36, 5623. [Google Scholar] [CrossRef]
| Ref. | Frequency (GHz) | Polarization | Gain (dBi) | Principle |
|---|---|---|---|---|
| [24] | 7.8 | Circular | >15 | PB |
| [23] | 28 | Circular | 23.8 and 28.7 | PB |
| [7] | 10 | Linear | 17.6 | Resonant |
| [22] | 18 | Linear | 18.45 | Resonant |
| [21] | 15 | Linear | Null | Resonant |
| Our work | 18 | Linear and circular | 16–20 | wavefront difference |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Yang, X.; Han, L.; Yan, J. Simultaneous Generation of Linear- and Circular-Polarization Vortex Based on Symmetrical Metallic Quasi-Metasurface. Symmetry 2025, 17, 274. https://doi.org/10.3390/sym17020274
Zhu D, Yang X, Han L, Yan J. Simultaneous Generation of Linear- and Circular-Polarization Vortex Based on Symmetrical Metallic Quasi-Metasurface. Symmetry. 2025; 17(2):274. https://doi.org/10.3390/sym17020274
Chicago/Turabian StyleZhu, Daoheng, Xiaokun Yang, Lingbo Han, and Jian Yan. 2025. "Simultaneous Generation of Linear- and Circular-Polarization Vortex Based on Symmetrical Metallic Quasi-Metasurface" Symmetry 17, no. 2: 274. https://doi.org/10.3390/sym17020274
APA StyleZhu, D., Yang, X., Han, L., & Yan, J. (2025). Simultaneous Generation of Linear- and Circular-Polarization Vortex Based on Symmetrical Metallic Quasi-Metasurface. Symmetry, 17(2), 274. https://doi.org/10.3390/sym17020274






