A Symmetric–Asymmetric Copula-Based GLMM for Energy Export and CO₂ Emission Dynamics in Indonesia

Abstract

Indonesia’s reliance on fossil-based energy exports continuously shapes the dynamics of CO₂ emission and the broader energy environment relationship across regions. This study applies a symmetric–asymmetric copula-based generalized linear mixed model (copula–GLMM) to examine the joint dependence between energy exports and CO₂ emissions across 34 provinces from 2010 to 2024. The proposed framework captures both balanced and tail-specific dependence structures, providing a deeper understanding of the evolving dynamics shaped by industrial concentration, policy interventions, and technological adoption. The analysis reveals a strong positive association, with the Clayton copula offering the best fit. Notably, lower-tail dependence shows that provinces with smaller export volumes face disproportionate emission risks, whereas regions with larger exports exhibit more stable outcomes due to renewable integration and improved efficiency. These findings challenge the notion that export growth inevitably leads to proportional emission increases. The study underscores the need for region-specific strategies rather than uniform national policies to advance sustainability goals and support Indonesia’s commitments to SGDs 7, 11, and 13, as well as the Paris Agreement.

1. Introduction

This introduction aims to provide a comprehensive overview of the global and regional context of the energy–emissions nexus, with a particular focus on Indonesia’s position and challenges. It begins by outlining the global trends in greenhouse gas emissions and the persistent dependence on fossil fuels, followed by an examination of Southeast Asia’s growing energy demand and the implications for regional sustainability targets. The discussion then narrows to Indonesia, exploring its dual role as a major energy exporter and significant emitter and highlighting the substantial provincial disparities that shape its de-carbonization pathway. Finally, this section identifies key gaps in existing studies and introduces the rationale for employing a symmetric–asymmetric copula-based GLMM as a more robust framework to analyze complex dependencies between energy exports and CO₂ emissions.

Climate change remains one of the most urgent global challenges of the twenty-first century, with energy-related greenhouse gas (GHG) emissions at the center of the problem. According to [1], the energy sector accounts for nearly 73% of total global GHG emissions, primarily due to the combustion of fossil fuels for electricity generation, transportation, and industrial activities. As shown in Figure 1, global fossil fuel-related CO₂ emissions have continued to rise over the past six decades, increasing from 9.5 gigatonnes (Gt) in 1960 to a record 37.4 Gt in 2023. This represents a 1.1% increase from the previous year and highlights the world’s ongoing reliance on fossil fuels, despite significant progress in renewable energy deployment and international climate initiatives. Emission patterns also show substantial variation. In 2023, China alone contributed 11.9 Gt (about 32% of global emissions), followed by the United States (4.9 Gt), India (3.1 Gt), and the European Union (2.6 Gt). These differences reveal the coexistence of symmetric patterns, where countries follow similar emission trajectories, and asymmetric patterns, where trends diverge significantly. Capturing such complex relationships requires advanced statistical approaches that can model both shared trends and divergent behaviors within the energy–emissions nexus.

Southeast Asia provides a particularly clear example of these dynamics. Rapid industrialization, urbanization, and population growth have made it one of the fastest-growing energy markets in the world. However, fossil fuels still dominate the region’s electricity generation. As illustrated in Figure 2, coal and natural gas dominate electricity generation across Southeast Asia, accounting for 85% in Indonesia, 84% in Malaysia, 86% in Thailand, and 80% in Vietnam. Meanwhile, the share of renewable energy remains limited, with only 8.4% in Indonesia, 6% in Malaysia, 2% in Thailand, and 6% in Vietnam. This heavy reliance on fossil-based sources presents two major challenges. First, it threatens regional sustainability targets, as fossil fuel combustion contributes to more than 85% of Southeast Asia’s total CO₂ emissions, undermining progress toward the Paris Agreement and Indonesia’s Net Zero Emissions (NZE) 2060 target. Second, it highlights persistent technological, policy, and financial barriers—such as the slow adoption of clean energy technologies and limited investment incentives—that hinder the region’s clean energy transition. These challenges show the need for region-specific strategies to diversify energy portfolios and emphasize the importance of analytical tools that can capture both symmetric and asymmetric interactions between energy exports and CO₂ emissions.

Within this regional context, Indonesia plays a crucial role. As Southeast Asia’s largest exporter of coal and liquefied natural gas (LNG), the country’s energy exports remain central to its economic growth and fiscal stability. However, this dependence also places Indonesia among the world’s top ten CO₂ emitters, contributing approximately 2.1% of global emissions in 2022. Despite its commitment to achieving Net Zero Emissions (NZE) by 2060, current projections indicate that energy-related CO₂ emissions could rise by around 35–40% by 2040 if existing fossil-fuel-dependent policies persist. This situation presents a major policy dilemma: how to sustain economic growth driven by energy exports while accelerating the transition toward a low-carbon energy system. Furthermore, substantial inter-provincial disparities in energy structure, industrial capacity, and policy implementation make this transition even more complex.

Variations in resource availability, economic structure, and local policies have produced highly diverse energy–emission profiles across the archipelago. For example, resource-rich provinces such as East Kalimantan generate large amounts of coal and LNG, which leads to higher emissions. Urbanized regions like Jakarta experience elevated emissions because of concentrated energy demand, while provinces such as Bali, which rely more heavily on renewable energy, show relatively low emission intensities. As shown in Figure 3, renewable energy shares vary widely between provinces. In Bali and East Nusa Tenggara, they exceed 30% due to geothermal and hydropower resources. In contrast, East Kalimantan and South Sumatra remain below 10%, and highly urbanized regions such as Jakarta and Banten record less than 5%. These disparities illustrate the coexistence of symmetric patterns among provinces with similar energy–emission characteristics and asymmetric cases with distinct dynamics, highlighting the need for robust models that can capture both.

Achieving Indonesia’s Net Zero Emissions (NZE) 2060 target is made more challenging by the large differences that exist between provinces in terms of energy production, consumption, and CO₂ emissions. These variations are shaped by factors such as resource availability, economic structure, and local energy policies, leading to highly diverse energy–emission profiles across the country. For example, East Kalimantan, one of Indonesia’s main energy-producing regions, records substantial coal production and liquefied natural gas (LNG) exports [2]. This heavy reliance on fossil fuels directly contributes to higher CO₂ emissions. In contrast, provinces with high energy demand, such as the Jakarta Capital Region (DKI Jakarta), show elevated emissions due to concentrated urban energy use and dependence on imported fossil fuels [1]. Meanwhile, provinces that prioritize renewable energy, such as Bali, tend to have much lower emission levels because of greater adoption of clean energy technologies and a tourism-based economy [3].

As shown in Figure 3, renewable energy shares differ widely across Indonesia. Provinces like Bali and East Nusa Tenggara (NTT) achieve shares above 30% thanks to significant geothermal and hydropower potential. By contrast, resource-rich regions such as East Kalimantan and South Sumatra remain below 10%, and highly urbanized areas such as Jakarta and Banten report adoption rates of less than 5%. These disparities demonstrate the coexistence of symmetric patterns among provinces with similar energy–emission characteristics and asymmetric cases where behaviors diverge significantly. Understanding these variations is crucial for designing effective de-carbonization strategies and highlights the need for advanced statistical models, such as the proposed symmetric–asymmetric copula-based GLMM, which can capture both common drivers and province-specific differences in the relationship between energy exports and CO₂ emissions.

These findings highlight not only the diversity of Indonesia’s provincial energy–emission landscape but also the complexity of policy design that must accommodate such heterogeneity. Addressing these challenges is not only a matter of academic interest but also a strategic necessity. Without a precise understanding of how energy exports and emissions interact, including the nonlinear patterns and asymmetric behaviors that shape their relationship, policy interventions risk becoming too generic or poorly aligned with the realities faced by each province. As Indonesia enters a critical decade in its pursuit of the Net Zero Emissions (NZE) 2060 roadmap, the capacity to design differentiated and evidence-based policies becomes essential to balance continued economic growth with environmental responsibility. In this context, a more advanced analytical framework is not merely useful but truly indispensable.

Despite extensive research on the energy–emissions relationship, most existing studies rely on conventional approaches such as generalized linear models (GLM), generalized linear mixed models (GLMM), or vector autoregressive (VAR) methods. While these methods provide valuable insights, they often assume homogeneous relationships and fail to capture nonlinear dependence structures or tail-specific dynamics. For example, Ref. [4] examined the interaction between energy exports, oil prices, and CO₂ emissions using a VAR model and found significant short- and long-term relationships. However, this approach cannot account for provincial heterogeneity and does not adequately represent the asymmetric nature of energy–emissions dependencies.

To address these limitations, this study proposes a symmetric–asymmetric copula-based generalized linear mixed model (copula–GLMM). This framework integrates a double-link structure that models mean effects and variance dynamics simultaneously while using copula functions to capture nonlinear and tail-dependent relationships. The approach makes it possible to identify groups of provinces that exhibit similar behaviors as well as outliers with unique patterns. The contributions of this study are threefold. Theoretically, it extends the conventional GLMM framework by incorporating copula-based dependence modeling. Empirically, it applies this framework to a comprehensive panel dataset covering 34 Indonesian provinces from 2010 to 2024. Practically, it provides evidence-based insights to support adaptive, region-specific energy transition strategies that align with Indonesia’s Net Zero Emissions (NZE) 2060 goals and global climate commitments.

The rest of this paper is organized as follows. Section 2 outlines the materials and methods, detailing the data sources, variables, and the overall modeling framework. It introduces the foundation of the generalized linear model (GLM), explains the double-link extension, and describes how copula functions are integrated within the GLMM structure. This section also elaborates on the parameter estimation procedures and the approach used to analyze tail dependence. Section 3 presents the main empirical results, including descriptive patterns, the identification of symmetric and asymmetric dependence structures, the outcomes of the copula-based estimation, and a series of robustness checks. Section 4 provides an in-depth discussion of the key findings, situates them within the context of the existing literature, and highlights their practical implications. Finally, Section 5 concludes the study by summarizing the essential insights and offering policy recommendations as well as potential directions for future research.

2. Materials and Methods

This section outlines the dataset, methodological framework, and estimation procedures used to analyze the joint dynamics of CO₂ emissions and energy exports across Indonesia’s provinces. We begin by describing the data sources, variables, and preprocessing steps. We then present the modeling strategy, which builds on a double-link generalized linear mixed model (GLMM) enhanced with copula functions to capture nonlinear and tail-specific dependencies. Finally, we discuss the parameter estimation process based on the Inference Functions for Margins (IFM) and the criteria used for model selection and tail-dependence analysis.

2.1. Data Sources and Variables

This study employs a balanced panel dataset comprising 34 Indonesian provinces over the period 2010–2024 (15 years), resulting in a total of 510 province–year observations. The dataset was constructed by integrating multiple official sources, including BPS-Statistics Indonesia [5], the Ministry of Energy and Mineral Resources (ESDM), and the World Bank CO₂ Emission Database, ensuring reliability and representativeness across spatial and temporal dimensions. The chosen time span captures both pre- and post-energy-transition policy phases, allowing the analysis to reflect structural changes over time.

The dataset integrates energy, environmental, and socioeconomic indicators. The primary response variables are provincial CO₂ emissions (Y₁), measured in metric tons per year, and energy exports (Y₂), expressed in terawatt-hours (TWh) or billion Indonesian rupiah (IDR). Explanatory variables include renewable energy share (RE_Share), GDP per capita (GDP_pc), urbanization rate (Urban), educational expenditure (Edu_Exp), infrastructure expenditure (Infra_Exp), and income inequality (Gini index). Descriptive statistics reveal significant heterogeneity: emissions range from 1.2 to 78.4 million tons, while energy exports show wide dispersion driven by resource endowments and policy interventions. This diversity motivates the use of mixed-effects modeling to capture both shared dynamics and province-specific variations.

By combining environmental and socioeconomic indicators, the dataset enables a nuanced examination of symmetric and asymmetric dependencies—where some provinces follow similar trajectories, while others diverge significantly due to differences in economic structure, policy focus, or renewable energy adoption.

2.2. Model Framework

To investigate how energy exports and CO₂ emissions evolve across provinces, this section introduces the core analytical framework used in this study. The approach builds on a generalized linear mixed model (GLMM) and extends it with copula functions to capture complex, nonlinear dependencies and variations that differ from one province to another. By doing so, the model provides a richer and more realistic picture of how energy and environmental dynamics interact in Indonesia.

Understanding how CO₂ emissions and energy exports evolve together requires a model that accounts for both common patterns and regional heterogeneity. Classical regression approaches such as GLMs or standard GLMMs often assume homogeneous effects across regions, overlooking crucial interprovincial differences. To overcome these limitations, we propose a symmetric–asymmetric copula-based GLMM (copula–GLMM), which integrates copula functions into a mixed-effects framework. This enables the joint modeling of nonlinear dependencies between multiple responses, here, $Y_1$ and $Y_2$, while capturing unobserved heterogeneity through random effects.

Symmetric dependencies describe scenarios where provinces respond similarly to policy or market changes, whereas asymmetric dependencies reflect divergent responses, often driven by structural or resource-based differences. The proposed model unites both perspectives into a single, flexible framework.

2.2.1. Generalized Linear Mixed Model

We begin by outlining the basic structure of the generalized linear mixed model, which serves as the foundation for our analysis. This framework is particularly useful because it allows us to examine both overall trends and the unique characteristics of each province, reflecting the diverse ways in which energy policies and economic factors influence emissions.

The foundation of our approach is the generalized linear mixed model (GLMM), which combines fixed effects (shared across all provinces) with random effects (province-specific deviations) [6]. The general form of the GLMM is expressed as

$$g\left({\mu }_{it}\right)={\mathit{X}}_{it}\mathit{\beta }+{\mathit{Z}}_{it}{\mathit{b}}_i$$

(1)

where $g\left(.\right)$ is the link s the link function connecting the expected response ${\mu }_{it}=E\left(Y_{it}\right)$ to the linear predictor, ${\mathit{X}}_{it}$ is the matrix of fixed-effect covariates for province i at year t, $\mathit{\beta }$ represents the vector of fixed-effect coefficients, ${\mathit{Z}}_{it}$ is the design matrix for random effects, ${\mathit{b}}_i~N(0, {\sigma }_b^2)$ denotes the vector of province-specific random effects.

GLMMs are particularly powerful when modeling hierarchical or panel data because they allow the intercepts (and, if specified, slopes) to vary across groups, in our case, the 34 Indonesian provinces. This flexibility is crucial when analyzing energy export and CO₂ emission dynamics because provinces differ substantially in their energy profiles, renewable adoption, and socioeconomic structures.

In this study, the fixed effects ($\mathit{\beta }$) represent the average impact of predictors such as renewable energy share (RE_Share), GDP per capita, and urbanization rate on CO₂ emissions and energy exports. Meanwhile, the random effects ($b_i)$ capture unobserved heterogeneity specific to each province, such as natural resource endowment, policy implementation efficiency, and industrial composition. By combining these two components, the GLMM framework provides a robust approach to understanding both common patterns and province-specific variations in Indonesia’s energy–emission system.

Previous studies have demonstrated the effectiveness of GLMMs in energy and environmental research. For instance, Ref. [7] highlighted the model’s flexibility in handling clustered datasets, while [8] emphasized its suitability for capturing complex hierarchical structures. In comparative studies across countries, applying mixed-effects models to emissions-related data has been shown to yield more reliable results than standard GLMs. For instance, Ref. [9] demonstrated that a gamma-based GLMM provided a superior fit compared to GLMs when examining CO₂-by-fuel variables from 169 countries.

In the context of this research, the GLMM forms the foundation of the proposed symmetric–asymmetric copula-based GLMM, where the model not only captures the effect of explanatory variables on energy exports and CO₂ emissions but also serves as the basis for integrating copula functions to model nonlinear dependencies between these response variables. This integration allows us to move beyond the limitations of conventional GLMMs and provides a comprehensive framework to study both symmetric and asymmetric interprovincial dynamics.

2.2.2. Double-Link Extension

Because provinces vary widely in their energy systems and emission patterns, assuming constant variability across regions would oversimplify reality. To address this, we extend the standard GLMM by modeling both the mean and the variance simultaneously. This double-link approach provides deeper insights into how the drivers of emissions behave under different conditions and improves the reliability of the model’s estimates.

In conventional generalized linear mixed models (GLMM), the variance of the response variable is typically assumed to be a simple function of its mean, implying homoscedasticity across observations. However, in the context of Indonesia’s energy–emission dynamics, this assumption is often unrealistic because provinces differ significantly in energy production, renewable adoption, industrial structures, and policy implementation. These structural differences can lead to heteroscedasticity, where the variability of CO₂ emissions or energy exports differs systematically across provinces.

To address this limitation, we extend the standard GLMM by introducing a double-link structure that models the mean and variance simultaneously. The extended framework is formulated as follows:

$$\begin{gathered} g\left({\mu }_{it}\right)={\mathit{X}}_{it}\mathit{\beta }+{\mathit{Z}}_{it}{\mathit{b}}_i, \\ h\left({\sigma }_{it}^2\right)={\mathit{W}}_{\mathit{i}\mathit{t}}\mathit{\gamma }, \end{gathered}$$

(2)

where $g\left(.\right)$ is the primary link function relating the expected response ${\mu }_{it}$ to the predictors, $h\left(.\right)$ is the secondary link function modeling the conditional variance ${\sigma }_{it}^2$, ${\mathit{X}}_{it}$ is the matrix of predictors for the mean model, ${\mathit{W}}_{\mathit{i}\mathit{t}}$ is the matrix of predictors influencing the variance structure, $\mathit{\beta }$ and $\mathit{\gamma }$ are the corresponding parameter vectors.

The double-link framework allows the variance to depend not only on the mean but also on specific covariates. In our study, the variance of CO₂ emissions and energy exports may be influenced by factors such as renewable energy share (RE_Share), GDP per capita, and policy intervention dummies. For example, provinces like East Kalimantan with high fossil fuel production tend to exhibit larger fluctuations in emissions, while renewable-oriented provinces such as Bali have relatively stable variance patterns.

This extension is particularly relevant when analyzing symmetric and asymmetric dependencies across provinces. Provinces exhibiting symmetric responses share similar variance structures, while those showing asymmetric responses demonstrate distinct variance dynamics caused by differences in energy mix and socioeconomic conditions. By explicitly modeling the variance structure, the double-link GLMM improves parameter estimation, enhances inference reliability, and provides a stronger foundation for integrating the copula-based dependence modeling introduced in the next section.

Several studies have highlighted the advantages of modeling both mean and variance components in GLMMs. For instance, Ref. [10] showed that employing double-link structures can markedly enhance statistical inference in the presence of heteroscedasticity, providing a more flexible framework for modeling mean–variance relationships. Similarly, Ref. [11] extended GLMMs with variance modeling to better capture group-level heterogeneity.

2.2.3. Derivation of the Asymmetric–Symmetric Copula Construction

To explicitly capture both symmetric and asymmetric dependence structures in the energy–emission relationship, we start by defining the joint distribution of two marginal variables $Y_1$ (CO₂ emissions) and $Y_2$ (energy exports) using a copula function $C_{\theta }$ as

$$F_{Y_1,Y_2}\left(y_1,y_2\right)=C_{\theta }\left(F_{Y_1}\left(y_1\right),F_{Y_2}\left(y_2\right)\right)$$

(3)

where $C_{\theta }$ is the copula with dependence parameter $\theta ,$ then $F_{Y_1}$ and $F_{Y_2}$ are the marginal cumulative distribution functions (CDFs) [12].

The symmetric copula captures balanced co-movements across the joint distribution but often fails to reflect tail-specific sensitivities. To address this, we extend the formulation by introducing an asymmetric transformation function $\varphi (.)$ applied to the marginal components:

$$C_{\theta }^A\left(u,v\right)=C_{\theta }\left(u^{{\varphi }_1}, v^{{\varphi }_2}\right),$$

(4)

where $u=F_{Y_1}\left(y_1\right),$ $v=F_{Y_2}\left(y_2\right) \mathrm{a}\mathrm{n}\mathrm{d} {\varphi }_1\ne {\varphi }_2$ allows different dependence intensities in the lower and upper tails. The joint density is then

$$C_{\theta }^A\left(u,v\right)={\displaystyle \frac{{\partial }^2}{{\partial }_u{\partial }_v}}{C}_{\theta }^A(u,v)$$

(5)

and the corresponding joint probability density function (PDF) becomes

$$f\left(y_1,y_2\right)=C_{\theta }^A\left(F_{Y_1}\left(y_1|X\right), F_{Y_2}\left(y_2|X\right)\right)\times f_{Y_1}\left(y_1\right)\times f_{Y_2}\left(y_2\right)$$

(6)

Finally, we integrate this joint structure into the random-effects GLMM framework:

The lower and upper tails exhibit different dependence intensities. This transformation retains the standard copula properties while enabling asymmetric tail modeling. Finally, the proposed asymmetric–symmetric copula-based GLMM integrates this joint structure into the random-effects framework:

$$L\left(\theta |Y_1, Y_2, X\right)= \int C_{\theta }^A\left(F_{Y_1}\left(y_1|X\right),F_{Y_2}\left(y_2|X\right)\right)f_{Y_1}\left(y_1|X\right) f_{Y_2}\left(y_2|X\right)f\left(b\right)db,$$

(7)

where $f\left(b\right)$ is the random-effects density. The resulting formulation provides a robust mathematical foundation for analyzing the joint dynamics of energy exports and CO₂ emissions. By embedding asymmetric transformations within the copula–GLMM framework, the model is able to capture tail-specific co-movements while preserving the flexibility and interpretability required for empirical applications. This formulation also serves as a basis for the subsequent integration of copula functions and likelihood construction, which further enhance the model’s capacity to represent complex dependence structures.

2.2.4. Copula Integration and Likelihood Approximation

While GLMMs effectively model individual responses, they fall short in capturing dependence between them. Copulas resolve this by linking marginal distributions into a joint structure. Given the marginal CDFs $F_k\left(y_{k,it}|{\mathit{b}}_i\right)$, the joint conditional distribution is obtained via Sklar’s theorem [12,13,14]:

$$F_{{\mathit{Y}}_{it}|{\mathit{b}}_i}\left(y_1,y_2\right)=C_{\theta }\left(F_1\left(y_1\right|{\mathit{b}}_i), F_2(y_2\left|{\mathit{b}}_i\right)\right),$$

(8)

where $C_{\theta }$ is the copula with parameter $\theta$ controlling dependence strength and direction. The corresponding joint density is

$$f_{{\mathit{Y}}_{it}|{\mathit{b}}_i}\left(y_1,y_2\right)=c_{\theta }\left({\mathit{U}}_{1,it},{\mathit{U}}_{2,it}\right).f_1\left(y_{1,it}|{\mathit{b}}_i\right).f_2\left(y_{2,it}|{\mathit{b}}_i\right),$$

This decomposition separates marginal behavior (GLMM) from dependence modeling (copula), enabling nuanced inference on how emissions and exports co-move under different policy or economic conditions.

2.2.5. Likelihood Formulation

For province-$i$, the conditional log-likelihood is

$${\mathcal{l}}_i\left(\mathit{\psi },\mathit{\theta };{\mathit{b}}_i\right)={\sum }_{t=1}^T\left\{\mathit{log}{c}_{\theta }\left({\mathit{U}}_{1,it},{\mathit{U}}_{2,it}\right)+{\sum }_{k=1}^2\mathit{log}{f}_k\left(y_{k,it}|{\mu }_{k,it},{\varphi }_{k,it}\right)\right\}$$

(9)

and the marginal log-likelihood integrates out random effects:

$$\mathcal{L}\left(\mathit{\psi },\mathit{\theta }\right)={\sum }_{i=1}^{N}log{\int }_{{\mathit{b}}_i}exp\left\{{\mathcal{l}}_i\left(\mathit{\psi },\mathit{\theta };{\mathit{b}}_i\right)\right\}.\phi \left({\mathit{b}}_i;0,\mathit{D}\right)d{\mathit{b}}_i,$$

(10)

where $\phi \left({\mathit{b}}_i;0,\mathit{D}\right)$ is the multivariate Gaussian density; and $\mathit{\psi }={\left\{{\mathit{\beta }}_{\mathit{k}},{\mathit{\gamma }}_{\mathit{k}},{\mathit{D}}_{\mathit{k}}\right\}}_{\mathit{k}=1}^2$ are GLMM parameters.

Because this integral lacks a closed-form solution, due to nonlinear copula dependence, double-link marginal estimation, and multidimensional random effects, we approximate it using Adaptive Gauss–Hermite Quadrature (AGHQ) for accuracy and Laplace approximation for computational efficiency when needed.

2.2.6. Adaptive Gauss–Hermite Quadrature (AGHQ)

Estimating the model requires integrating over random effects, a task that is rarely solvable analytically. Here, we use Adaptive Gauss–Hermite Quadrature, a numerical technique that adapts to the shape of the data and significantly improves the precision of our parameter estimates. The estimation of dependence structures in copula-based generalized linear mixed models (GLMMs) becomes particularly challenging when extended to double-link formulations, where both the mean and variance components are modeled. Since the integration over random effects does not yield closed-form solutions, accurate numerical approximation of the marginal likelihood is essential.

Adaptive Gauss–Hermite Quadrature (AGHQ) provides a powerful tool in this context. Unlike fixed quadrature rules, AGHQ adapts nodes and weights according to the distribution of the integrand, which allows it to handle skewed or heterogeneous random effects more effectively. This flexibility is especially relevant for double-link copula–GLMMs, in which both nonlinear dependence and variance heterogeneity must be accounted for to achieve robust inference.

Korhonen, Nordhausen, and Taskinen (2024) [15] note in their review of generalized latent variable models that modern computational strategies increasingly rely on adaptive quadrature methods, with AGHQ standing out as one of the most accurate likelihood-based approaches for GLMM-type models. They emphasize that, compared to simpler approximations, AGHQ ensures more reliable inference when random effects are strongly non-Gaussian.

Similarly, Ref. [16], in a comparative study of Laplace approximation, penalized quasi-likelihood, and AGHQ for binary outcome data with sparse observations, reporting that AGHQ consistently produced less biased estimates and narrower confidence intervals. Their findings underline the advantage of AGHQ in settings where data sparsity complicates estimation, a situation frequently encountered in regional environmental applications.

Ref. [17] applied AGHQ in the context of multilevel parametric survival models with recurrent events and demonstrated that the method yields stable maximum likelihood estimates even under complex hierarchical dependence. They further argued that AGHQ allows researchers to integrate over random effects with high accuracy while retaining computational feasibility in large-scale applications.

Taken together, this body of evidence highlights the suitability of AGHQ as an estimation procedure in double-link extension copula–GLMMs. By combining the flexibility of copula functions with the precision of adaptive quadrature, the framework can achieve reliable parameter estimation in multivariate settings across environmental, biomedical, and economic research domains.

Step 1. Gaussian Quadrature Approximation

For a Gaussian integral,

$$I=\int f(b)\varphi \left(b;\mu ,{\sigma }^2\right)db\approx \sum _{q=1}^Q{w}_{q}f\left(\sqrt{2}\sigma z_q+\mu \right),$$

where $z_q$= Hermite polynomial roots, $w_q=$ quadrature weights.

Step 2. Adaptive Centering at Posterior Mode

In copula–GLMM, the posterior of ${\mathit{b}}_i$ may be skewed due to strong tail dependence from asymmetric copulas. To improve accuracy, we re-center quadrature nodes around the posterior mode ${\widehat{\mathit{b}}}_i$:

$${\mathit{b}}_i^q={\widehat{\mathit{b}}}_i+\mathit{L}{\mathit{z}}_q$$

where $\mathit{L}{\mathit{L}}^T={\widehat{\mathit{\Sigma }}}_i$ denotes the Cholesky decomposition of the local posterior covariance matrix $\widehat{\mathit{\Sigma }}$. Here, $\mathit{L}$ is a lower triangular matrix such that multiplying $\mathit{L}$ by its transpose reproduces the covariance matrix. This transformation rescales and rotates the standard quadrature nodes ${\mathit{z}}_q,$ ensuring that they reflect the posterior distribution more accurately. This step significantly reduces integration error.

Step 3. AGHQ Likelihood Approximation

The marginal likelihood for province $i$ becomes

$$\int exp\left\{{\mathcal{l}}_i\left({\mathit{b}}_i\right)\right\}\varphi \left({\mathit{b}}_i\right)d{\mathit{b}}_i\approx \sum _{q=1}^Q{w}_q.exp\left\{{\mathcal{l}}_i\left({\mathit{b}}_i^{\left(q\right)}\right)-{\displaystyle \frac{1}{2}}{\mathit{b}}_i^{\left(q\right)T}{\mathit{D}}^{-1}{\mathit{b}}_i^{\left(q\right)}\right\}$$

for most applications, $Q=7$ or $Q=11$ modes are sufficient.

2.2.7. Laplace Approximation

In some cases, a simpler and faster method is preferable for likelihood estimation. The Laplace approximation offers a practical alternative by balancing computational efficiency with reasonable accuracy. This subsection explains when and why this method is used and how it complements AGHQ within our modeling framework.

Estimating double-link copula–GLMMs presents significant computational challenges. By jointly modeling the mean and dispersion while incorporating cross-sectional dependence, the likelihood function becomes analytically intractable. The Laplace approximation addresses this issue by expanding the joint log-likelihood around the posterior mode of the random effects, providing a tractable marginal likelihood that retains essential curvature information while ensuring computational efficiency.

Previous studies highlight the continued importance of this approach. Ref. [18] demonstrated that embedding Laplace approximation within penalized likelihood frameworks yields stable inference across models with complex variance structures. Ref. [19] advanced this development through the Template Model Builder (TMB), where Laplace approximation is combined with sparse matrix computation and automatic differentiation, offering a scalable and accurate solution for high-dimensional random-effects models. Ref. [20] further illustrated the practical benefits of Laplace-based estimation within the GLMM–TMB framework, which successfully accommodates zero-inflated and extended GLMM families while maintaining efficiency. More recently, Ref. [21] applied Laplace approximation in longitudinal latent-trait models, confirming its capacity to provide reliable inference in contexts characterized by heterogeneity and complex dependence structures.

Together, these contributions demonstrate that Laplace approximation remains a reliable and versatile estimation method. Within double-link copula–GLMMs, it achieves a balance between computational scalability and inferential precision, making it particularly well-suited for applications in environmental, biomedical, and economic research where accurate modeling of dependence and dispersion is essential. For models with higher-dimensional random effects, Laplace approximation offers faster computation.

Step 1. Second-Order Expansion

Define $h\left({\mathit{b}}_i\right)={\mathcal{l}}_i\left({\mathit{b}}_i\right)-{\displaystyle \frac{1}{2}}{\mathit{b}}_i^T{\mathit{D}}^{-1}{\mathit{b}}_i$

Expanding around the posterior mode ${\widehat{\mathit{b}}}_i$,

$$h\left({\mathit{b}}_i\right)\approx h\left({\widehat{\mathit{b}}}_i\right)-{\displaystyle \frac{1}{2}}{\left({\mathit{b}}_i-{\widehat{\mathit{b}}}_i\right)}^T{\mathit{H}}_i\left({\mathit{b}}_i-{\widehat{\mathit{b}}}_i\right)$$

where ${\mathit{H}}_i=-{\nabla }^{2}h\left({\widehat{\mathit{b}}}_i\right)$ is the negative Hessian.

Step 2. Laplace Approximation Formula

$$\int exp\left\{h\left({\mathit{b}}_i\right)\right\}d{\mathit{b}}_i\approx {\left(2\pi \right)}^{{\displaystyle \frac{d}{2}}}{\left|{\mathit{H}}_i\right|}^{-{\displaystyle \frac{1}{2}}}exp\left\{h\left({\widehat{\mathit{b}}}_i\right)\right\}$$

(11)

Laplace is computationally efficient, especially when symmetric dependencies dominate.

2.2.8. Choosing Between AGHQ and Laplace

In this study, we primarily adopt the Adaptive Gauss–Hermite Quadrature (AGHQ) method because the dimension of the random effects is relatively small (d = 2), involving only provincial and temporal random intercepts. AGHQ provides highly accurate likelihood approximations, which are particularly important when modeling tail-dependent copulas such as Gumbel and Clayton that capture asymmetric co-movements in extreme values. For these situations, accurate numerical integration is essential to correctly estimate the strength and direction of dependence. However, when the random-effects dimension becomes larger (d > 3) or when the joint dependence is expected to be symmetric and closer to Gaussian, the Laplace approximation serves as a computationally efficient alternative. In practice, we exploit AGHQ for its superior precision but remain flexible to switch to Laplace when modeling complexity requires a faster approach without sacrificing too much accuracy.

2.2.9. Relevance to Symmetric–Asymmetric Modeling

The choice of likelihood approximation plays a crucial role in uncovering the symmetric and asymmetric interprovincial dependencies underlying Indonesia’s energy–emission dynamics. In provinces where policy interventions produce relatively uniform impacts and responses to energy, shocks are broadly similar, symmetric dependencies dominate, and the Laplace approximation provides sufficiently accurate results with lower computational costs. Conversely, in provinces exhibiting highly divergent energy profiles—such as Bali, where a renewable-oriented energy mix drives lower emission volatility, and East Kalimantan, where coal and LNG production remain dominant—the energy–emission relationship is characterized by strong asymmetric tail dependencies. In such cases, the Adaptive Gauss–Hermite Quadrature (AGHQ) approach becomes essential to avoid biased parameter estimates and to capture the nonlinearities in dependence structures more accurately.

By integrating double-link GLMMs [22] for modeling heteroscedasticity marginal dynamics, copula-based dependence structures for capturing nonlinear associations, and adaptive likelihood approximation techniques for improved estimation accuracy, this study introduces a modeling framework capable of jointly identifying symmetric clusters and asymmetric outliers across Indonesian provinces. To the best of our knowledge, this methodological integration has not been previously applied in the context of Indonesia’s interprovincial energy–emission system. As such, this framework offers significant contributions by providing novel empirical insights into regional energy-export and CO₂ emission dynamics and informing the design of province-specific policies for achieving Indonesia’s Net Zero Emissions (NZE) 2060 roadmap. The detailed R script used for the Copula-based GLMM estimation is provided in Appendix A.

2.3. Parameter Estimation

After defining the model, we turn to how its parameters are estimated. This section introduces the Inference Functions for Margins (IFM) approach, a two-step procedure that first estimates the marginal distributions and then the dependence structure. We also describe how different copula models are evaluated and compared to identify the best fit for our data. The parameters of the proposed symmetric–asymmetric copula-based generalized linear mixed model (copula–GLMM) are estimated using the Inference Functions for Margins (IFM) approach [23,24,25]. This two-stage estimation strategy is computationally efficient and statistically consistent, making it particularly suitable for high-dimensional panel data involving multiple responses and province-specific heterogeneity.

2.3.1. Inference Functions for Margins (IFM)

The IFM framework separates the estimation into two sequential stages:

Step 1. Marginal Parameter Estimation

The marginal dynamics of CO₂ emissions and energy exports are estimated using the double-link GLMM as formulated in Section Copula Integration and Likelihood Approximation. This stage provides the fitted marginal cumulative distribution functions (CDFs):

$$u_{k,it}={\widehat{F}}_k\left(y_{k,it}|{\widehat{\psi }}_k\right),$$

where $u_{k,it}$ are the transformed pseudo-observations and ${\widehat{\psi }}_k=\left\{{\widehat{\beta }}_k, {\widehat{\gamma }}_k,{\widehat{D}}_k\right\}$ are the estimated GLMM parameters.

Step 2. Copula Parameter Estimation

Given the estimated marginal CDFs, the copula dependence parameter θ is obtained by maximizing the copula log-likelihood:

$${\mathcal{l}}^{\left(2\right)}\left(\theta \right)={\sum }_{i=1}^N{\sum }_{t=1}^{T}log{c}_{\theta }\left(u_{1,it}, u_{2,it}\right),$$

(12)

where $c_{\theta }(\dots )$ is the copula density function. This stage captures nonlinear symmetric and asymmetric dependencies between CO₂ emissions and energy exports across provinces.

2.3.2. Copula Selection and Optimization

Choosing the right copula is crucial because it determines how well the model captures the relationship between energy exports and emissions. In this part, we explain the selection process, compare the strengths and limitations of different copula families, and introduce the statistical criteria and tail-dependence measures used to guide our decision.

To capture the dependence structure between energy exports (Y₂) and CO₂ emissions (Y₁) more accurately, five copula families were evaluated based on their theoretical properties and suitability for modeling both symmetric and asymmetric dynamics. Each copula offers a distinct assumption regarding how the two variables co-move across varying levels of energy activity, enabling a more comprehensive representation of the energy–emissions nexus.

• The Gaussian copula assumes a symmetric dependence structure [26,27], where positive and negative co-movements between energy exports and CO₂ emissions are proportionally balanced. This specification is most appropriate when the relationship between the variables remains stable across the distribution, making it suitable for contexts in which the energy–emissions link follows a linear and homogeneous pattern.
• The Student-t copula, while also designed to capture symmetric dependence [28,29], provides an additional advantage by accommodating heavier tails. This property allows the model to better represent joint fluctuations during periods of high volatility, making it particularly relevant when energy exports and emissions experience simultaneous surges or declines.
• The Clayton copula is used to capture lower-tail asymmetric dependence [30,31], where stronger associations are observed during simultaneous declines in energy exports and CO₂ emissions. This feature makes it particularly useful for analyzing periods of reduced energy demand, economic slowdowns, or policy-driven restrictions, as it highlights the increased vulnerability of emissions to negative shocks.
• The Gumbel copula focuses on upper-tail asymmetric dependence [32,33] and is well-suited for scenarios where energy exports and CO₂ emissions jointly reach exceptionally high levels. This copula is particularly relevant during phases of rapid industrial expansion or energy-intensive development, where significant increases in production lead to disproportionately large environmental impacts.
• Finally, the Frank copula is designed to model moderate symmetric dependence [34] and is flexible in capturing both positive and negative associations without emphasizing tail-specific behavior [29,35]. Its strength lies in representing smooth and monotonic relationships, making it applicable in contexts where energy exports and emissions evolve consistently without pronounced lower- or upper-tail dominance.

The optimal copula is determined through a comprehensive model selection procedure that integrates three complementary statistical criteria to ensure the best representation of the dependence structure between CO₂ emissions and energy exports:

(a)

Akaike Information Criterion (AIC)

Measures the trade-off between goodness-of-fit and model complexity [36,37]:

AIC=−2ℓ + 2k

Here, ℓ is maximized log-likelihood and k is the number of parameters estimated. A lower AIC indicates a better balance between model fit and complexity. In simple terms, a lower AIC suggests that the model fits the data well without being unnecessarily complicated. AIC is particularly useful when comparing several competing models, as it tends to reward models that capture important patterns while remaining flexible enough to generalize beyond the current dataset.

(b)

Bayesian Information Criterion (BIC)

Provides a more conservative penalization for model complexity [38]:

BIC= −2ℓ + k ln(n),

where n refers to the sample size. Like AIC, a smaller BIC indicates a better-fitting model, but BIC penalizes complexity more strongly. This means it often prefers simpler models that still capture the essential structure of the data. Such parsimony is valuable when the goal is to build models that remain stable and reliable when applied to new situations as an important consideration in studies that aim to inform long-term energy and environmental policy. Using both AIC and BIC together provides a more comprehensive and confident basis for selecting the most appropriate copula model for the analysis.

(c)

Vuong’s Likelihood Ratio Test

Used to discriminate between non-nested copula models [39,40]. The test statistic is computed as follows:

$$V={\displaystyle \frac{\sum _{i=1}^n{d}_i}{\sqrt{n.{\widehat{\sigma }}_d^2}}},$$

(13)

where is the pointwise log-likelihood ratio.

• $V$ > 1.96 → Model 1 significantly preferred.
• $V$ < −1.96 → Model 2 significantly preferred.
• Otherwise, both models perform equivalently.

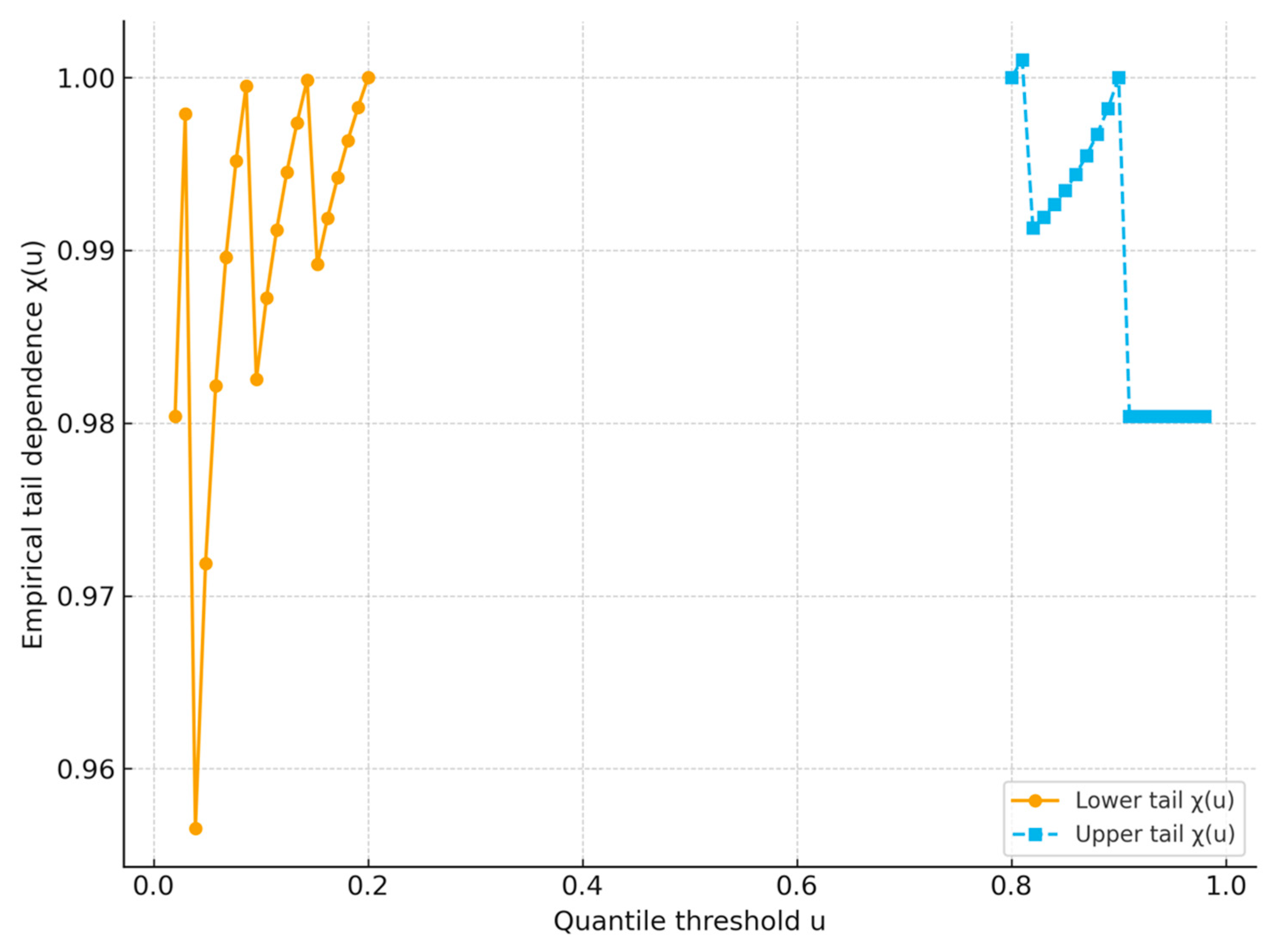
2.3.3. Tail-Dependence Coefficients

To assess extreme co-movements between CO₂ emissions and energy exports, we calculate the upper-tail and lower-tail dependence coefficients based on the fitted copula models. These measures quantify the probability that one variable takes an extreme value given that the other variable is also extreme. For a bivariate copula $C(u,v)$, the upper-tail dependence coefficient and lower-tail dependence coefficient are defined as follows [41]:

$${\chi }_u=\underset{q\to 1^{-}}{\mathit{lim}}P\left(U>q|V>q\right)=\underset{q\to 1^{-}}{\mathit{lim}}{\displaystyle \frac{1-2q+C(q,q)}{1-q}},$$

(14)

$${\chi }_L=\underset{q\to 0^{+}}{\mathit{lim}}P\left(U\le q|V\le q\right)=\underset{q\to 0^{+}}{lim}{\displaystyle \frac{C(q,q)}{q}},$$

(15)

where $U=F_1\left(Y_1\right)$ and $V=F_2\left(Y_2\right)$ are the pseudo-observations derived from marginal CDFs; $C(q,q)$ represents the joint cumulative probability at quantile q. Then, the interpretation is as follows:

• ${\chi }_u>0$ → strong co-movement in the upper tail (e.g., simultaneous extreme increases).
• ${\chi }_L>0$ → strong co-movement in the lower tail (e.g., simultaneous extreme declines).
• ${\chi }_u\approx 0 \mathrm{o}\mathrm{r} {\chi }_L\approx 0$ → weak dependence in the corresponding tail.

3. Results

This chapter presents the main findings of the study and builds a comprehensive picture of how energy exports and CO₂ emissions are interconnected across Indonesia’s provinces. We begin by examining the descriptive characteristics of the data to understand their basic patterns and regional variations. This step provides essential context before moving on to more complex modeling.

The analysis then explores how these variables evolve over time and differ spatially across provinces, offering early clues about whether their relationship behaves in a straightforward, proportional way (symmetric) or in a more uneven, tail-driven manner (asymmetric). Once these preliminary patterns are established, we proceed with the core of the analysis—estimating a copula-based generalized linear mixed model (GLMM) that can capture both the common dynamics shared across provinces and the unique sensitivities that arise in specific regional contexts.

We further evaluate the robustness of the results by testing the model under different specifications and alternative scenarios, ensuring that the conclusions are consistent and reliable. Finally, we classify provinces based on their dependence patterns and discuss what these findings imply for designing targeted, region-specific energy and environmental policies.

By progressing from descriptive insights to advanced dependence modeling, this chapter aims to move beyond surface-level correlations and provide a deeper understanding of how energy exports and emissions interact—not only on average, but also at the extremes, where policy interventions often matter most.

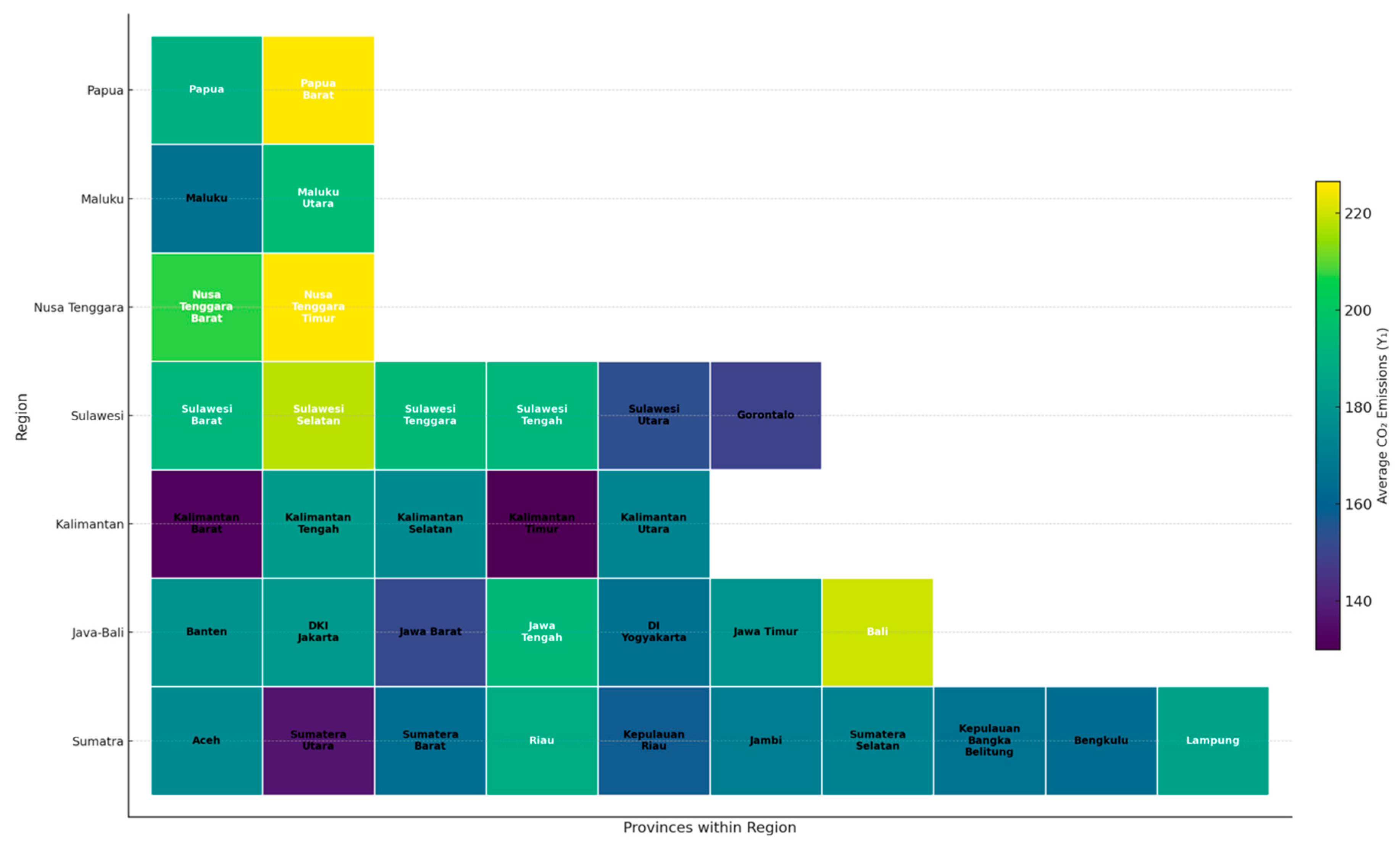
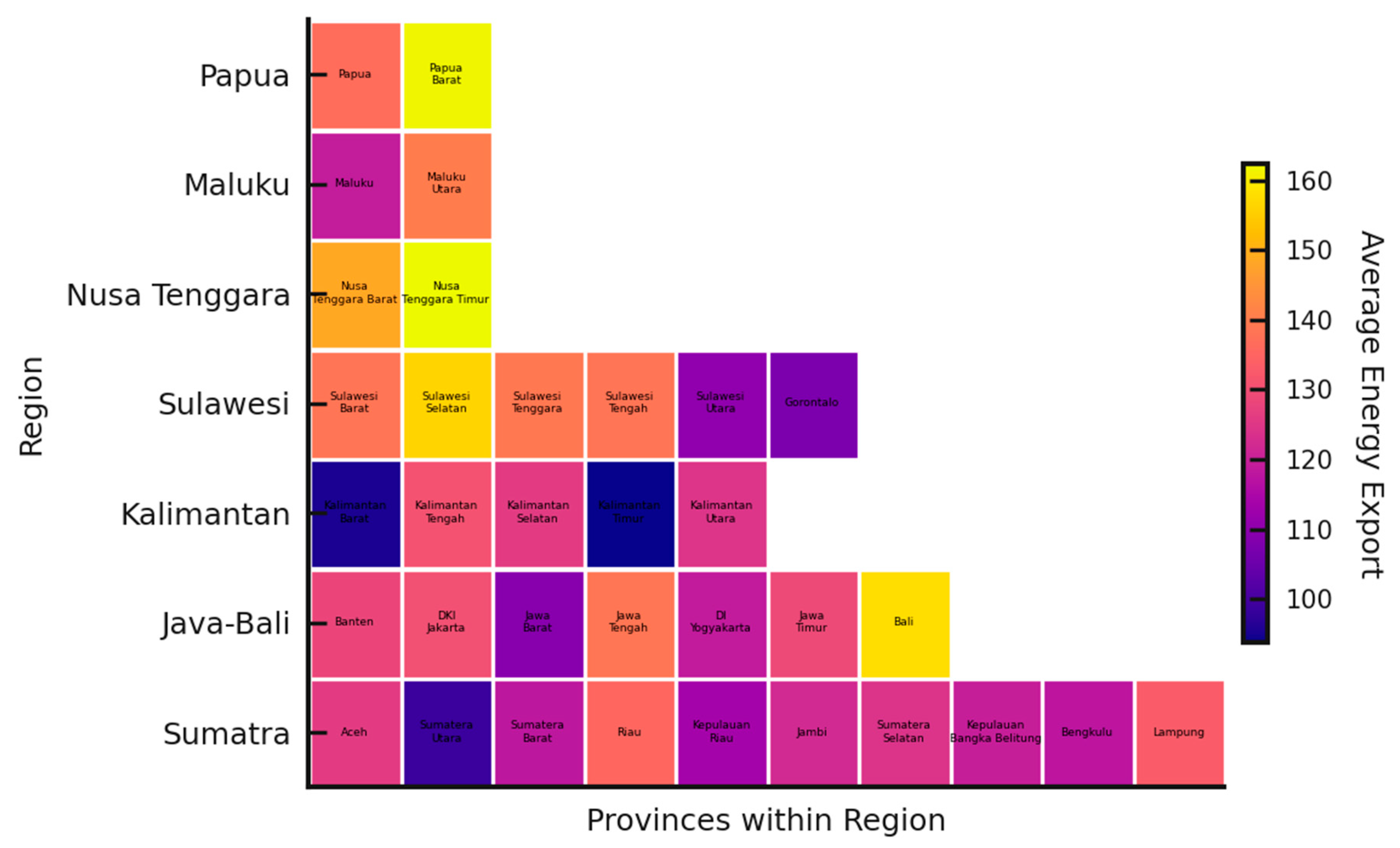
3.1. Descriptive Analysis of Energy Exports and CO₂ Emissions

Before moving into complex statistical modeling, it is important to first understand the story told by the data itself. Descriptive analysis provides the foundation for deeper exploration, offering an initial look at how energy exports, CO₂ emissions, renewable energy penetration, economic activity, and urbanization evolve across Indonesia’s provinces over time. By exploring these basic patterns, we can observe how provinces differ from one another, where disparities are most pronounced, and how these differences might shape the broader energy–emissions relationship. This initial step is crucial because it reveals potential connections and anomalies that will later guide the interpretation of more advanced analytical results.

This section presents the empirical findings derived from a comprehensive panel dataset covering 34 Indonesian provinces from 2010 to 2024. The analysis aims to explore the dynamic interdependence between energy exports (EEX), CO₂ emissions (CO₂), renewable energy share (RE_Share), GDP per capita (GDP_pc), and urbanization rate (Urban). Before implementing the symmetric–asymmetric copula-based generalized linear mixed model (GLMM), we conducted an extensive exploratory data analysis to understand the underlying structure, distributional properties, and potential nonlinearity among the key variables. Table 1 reports the summary statistics of the primary variables, including measures of central tendency, variability, and shape distribution, providing the foundation for subsequent model estimations.

Table 1 summarizes the statistical characteristics of the key variables, highlighting significant cross-provincial heterogeneity during the 2010–2024 period. The mean level of CO₂ emissions (Y₁) is approximately 178 MtCO₂, with values ranging from as low as 6.75 MtCO₂ in low-industrialized regions to peaks exceeding 347 MtCO₂ in highly urbanized provinces. The relatively high standard deviation (102.99) suggests strong regional disparities in carbon emissions, reflecting the influence of varying energy consumption patterns and industrial activities.

Table 1. Descriptive statistics of main variables (2010–2024).

Variable	Mean	Median	Std. Dev	Min	Max	Skewness	Kurtosis
Y1: CO2 Emissions (MtCO2)	178.11	183.90	102.99	6.75	347.57	−0.04	−1.26
Y2: Energy Exports	127.93	132.05	73.14	6.24	248.28	−0.04	−1.26
RE_Share (%)	6.01	6.03	1.95	1.00	13.71	0.23	0.15
GDP_pc (IDR)	50,004,890	49,670,600	9,821,399	23,031,133	81,377,485	0.20	0.11
Urbanization (%)	60.80	60.93	9.95	31.04	86.44	−0.10	−0.08

Table 1. Descriptive statistics of main variables (2010–2024).

Variable	Mean	Median	Std. Dev	Min	Max	Skewness	Kurtosis
Y1: CO2 Emissions (MtCO2)	178.11	183.90	102.99	6.75	347.57	−0.04	−1.26
Y2: Energy Exports	127.93	132.05	73.14	6.24	248.28	−0.04	−1.26
RE_Share (%)	6.01	6.03	1.95	1.00	13.71	0.23	0.15
GDP_pc (IDR)	50,004,890	49,670,600	9,821,399	23,031,133	81,377,485	0.20	0.11
Urbanization (%)	60.80	60.93	9.95	31.04	86.44	−0.10	−0.08

Similarly, energy exports (Y₂), proxied by standardized energy production data, exhibit an average value of 127.93, ranging from 6.24 to 248.28, indicating pronounced differences in energy output across provinces. The parallel movement between CO₂ emissions and energy exports suggests an underlying positive association, particularly in regions where export-oriented energy production dominates provincial economic structures. The skewness close to zero (−0.04) implies a nearly symmetric distribution, while the negative kurtosis (−1.26) indicates thinner tails, suggesting fewer extreme outliers in energy export activities compared to emissions.

The renewable energy share (RE_Share) displays a relatively low average of 6.01%, with substantial variability across provinces (1% to 13.71%). This pattern highlights the persistent dominance of fossil-based energy systems, reinforcing the need to evaluate asymmetric dependencies between renewable integration and emissions dynamics. The GDP per capita averages around IDR 50 million, spanning from IDR 23 million in less-developed provinces to over IDR 81 million in more industrialized regions, indicating significant income inequality within the panel. Finally, the urbanization rate averages 60.8%, ranging from 31.04% in rural areas to 86.44% in highly urbanized provinces, underscoring the role of demographic concentration as a potential driver of energy demand and emissions intensity.

Collectively, these findings demonstrate substantial heterogeneity across provinces, supporting the application of a symmetric–asymmetric copula-based GLMM to capture potential nonlinear and tail-dependent relationships between energy exports and CO₂ emissions. The observed variability further justifies modeling country-specific random effects and testing for asymmetric tail dependence, particularly for high-energy-intensive regions.

To gain preliminary insights into the dynamic interaction between energy exports and environmental outcomes, Figure 4 illustrates the temporal evolution of CO₂ emissions and energy exports across all provinces from 2010 to 2024. The series are plotted using annual averages to capture the general direction of change while minimizing short-term fluctuations. This visualization provides an initial overview of the potential dependence structure between the two variables and serves as the foundation for the subsequent copula-based analysis.

The observed trend reveals a close co-movement between CO₂ emissions and energy exports over the 2010–2024 period, indicating a strong interdependence between the two variables. Both variables exhibit a gradual upward trajectory from 2010 until approximately 2018, reflecting the expansion of energy-intensive activities and the growth of export-oriented production. A significant decline is observed in 2020, coinciding with the global economic slowdown and reduced energy demand during the COVID-19 pandemic. Following 2021, there is a clear rebound in both energy exports and emissions, suggesting a recovery in industrial activities and international energy trade. Despite some year-to-year fluctuations, the parallel movement of the two series indicates a potential symmetric dependence during periods of moderate growth, while sharp export surges in specific years imply possible asymmetric effects on emissions. This dynamic supports the application of a copula-based GLMM in subsequent analyses to effectively capture both symmetric and tail-dependent relationships between energy exports and environmental consequences.

To further explore the cross-provincial heterogeneity in the relationship between CO₂ emissions and energy exports, Figure 5 illustrates a heatmap of correlation coefficients computed across 34 Indonesian provinces for the period 2010–2024. The heatmap provides a visual perspective on the symmetry and asymmetry of the energy–emission nexus, offering initial evidence of regional dependence patterns.

Figure 5 displays a heatmap illustrating the spatial distribution of average CO₂ emissions (Y₁) across 34 Indonesian provinces from 2010 to 2024. Darker shades correspond to provinces with relatively higher emission levels, while lighter tones indicate regions with lower carbon output. The visualization reveals notable interprovincial disparities, where provinces in Java-Bali, Papua, and certain parts of Sumatra consistently exhibit elevated emissions. These patterns are largely associated with intensive industrial activities, higher urban concentration, and energy-demanding production structures.

Conversely, provinces such as Nusa Tenggara Timur, Gorontalo, and Maluku Utara demonstrate lower average emissions, reflecting their smaller industrial bases and reduced reliance on fossil fuels. Interestingly, several provinces in Kalimantan and Sulawesi fall within an intermediate range, where moderate population density combined with resource-based extraction contributes to relatively high emissions despite smaller economic scales.

Overall, the heatmap highlights significant heterogeneity in carbon intensity across Indonesia, emphasizing the necessity of employing a copula-based GLMM framework in the subsequent analysis to effectively capture both symmetric and asymmetric dependence between energy exports and CO₂ emissions.

Figure 6 presents the average levels of energy exports (Y₂) across 34 Indonesian provinces over the period 2010–2024. Provinces such as Papua, Kalimantan Timur, Riau, and Aceh record consistently higher export volumes, largely driven by resource-based production and strong integration into international energy markets. In contrast, regions including DI Yogyakarta, Bali, and Nusa Tenggara Timur exhibit persistently lower energy exports, reflecting their limited fossil-based production capacity and smaller industrial structures. Meanwhile, several provinces in Sulawesi and Maluku occupy a moderate range, suggesting a balanced combination of domestic energy consumption and export-oriented production strategies.

Overall, the heatmap reveals a highly heterogeneous spatial distribution of energy exports across Indonesia. When compared with Figure 5 on CO₂ emissions, the observed divergence indicates potential symmetric dependence in resource-rich provinces where energy exports and emissions evolve in tandem, alongside possible asymmetric effects in low-export regions where variations in energy activity do not necessarily translate into proportional emission changes. These findings provide a strong rationale for employing a copula-based GLMM framework in Section 3.3 to capture the varying dependence structures between the two variables.

Furthermore, the descriptive analysis highlights significant interprovincial heterogeneity in both energy exports (Y₂) and CO₂ emissions (Y₁) from 2010 to 2024. As shown in Figure 4, the aggregate trajectories of energy exports and emissions are closely aligned, reflecting Indonesia’s increasing reliance on energy-intensive activities over time. However, the heatmaps in Figure 5 and Figure 6 demonstrate that these patterns are far from uniform. Resource-abundant provinces such as Papua, Kalimantan Timur, and Riau consistently dominate in both energy exports and emissions, while regions such as Bali, DI Yogyakarta, and Nusa Tenggara Timur remain at the lower end of the spectrum.

These interprovincial variations underscore the complex dynamics shaping Indonesia’s energy–emission nexus. Differences in industrial structure, resource dependency, and urbanization patterns significantly influence environmental outcomes. This heterogeneity raises an important question: do shifts in energy activity lead to proportional changes in emissions across all provinces, or do certain regions exhibit heightened sensitivity to energy fluctuations? Addressing this question forms the analytical foundation for exploring potential symmetric and asymmetric dependence patterns, which are rigorously examined using a copula-based GLMM framework in the subsequent analysis.

3.2. Symmetric vs. Asymmetric Patterns in Energy–Emission Dynamics

While descriptive statistics offer valuable insight into the scale and distribution of energy use and emissions, they do not fully explain how these variables interact. The next step is to examine whether the relationship between energy exports and CO₂ emissions is uniform across provinces or whether it varies depending on local conditions. In other words, do changes in energy activity always lead to proportional changes in emissions (a symmetric pattern), or do some provinces respond in a more complex and uneven way (an asymmetric pattern)? Exploring this question helps reveal the hidden dynamics of Indonesia’s energy–emission nexus and sets the stage for more sophisticated modeling approaches in the following sections.

Building on the observed heterogeneity in energy exports and CO₂ emissions across provinces, a closer examination of their dependence structure becomes essential to understand Indonesia’s evolving energy–emission dynamics. While the overall trends suggest a positive relationship between energy activity and carbon output, the disparities revealed in the previous analysis indicate that this relationship may not be uniform across regions. In resource-rich provinces such as Papua, Kalimantan Timur, and Riau, energy exports and emissions appear to move in near-perfect synchrony, suggesting a symmetric pattern where changes in energy activity translate proportionally into emission levels. In contrast, provinces like Bali, DI Yogyakarta, and Nusa Tenggara Timur may exhibit asymmetric sensitivities, where small variations in energy activity could trigger disproportionately large or muted changes in emissions.

Understanding these potential differences is critical, as it determines whether policy interventions should be designed at the national level or tailored to specific regions. This motivates a deeper descriptive exploration of symmetric versus asymmetric patterns in energy–emission dynamics, which will serve as a conceptual bridge to the copula-based GLMM framework developed in the subsequent analysis.

3.2.1. Exploratory Analysis of Symmetric and Asymmetric Dependence

To better understand these dynamics, we begin with an exploratory analysis that investigates how provinces respond to changes in energy activity. This step focuses on identifying whether relationships remain stable across different levels of energy exports or whether sensitivities shift—for example, whether emissions react more strongly to small changes in energy activity in some regions than in others. Such exploration helps uncover the diversity of provincial responses and offers important clues about underlying structural differences, such as technology adoption, economic scale, or energy mix composition.

The relationship between energy exports (Y₂) and CO₂ emissions (Y₁) demonstrates a clear positive association at the aggregate level; however, this overall trend conceals considerable heterogeneity across provinces. In resource-rich regions such as Riau, Kalimantan Timur, and Papua, variations in energy exports tend to correspond with proportionate changes in emissions, indicating the presence of symmetric dependence. In contrast, several low-export provinces reveal indications of asymmetric dynamics, where even modest fluctuations in energy exports may trigger disproportionately large changes in CO₂ emissions, or conversely, where substantial export growth results in relatively limited emission responses.

These diverse patterns emphasize the need to examine the underlying dependence structures across provinces rather than relying exclusively on aggregate correlations. Such an approach provides a more nuanced understanding of regional dynamics and forms the conceptual basis for distinguishing provinces according to their symmetry and asymmetry patterns, which are further investigated in the subsequent section. These insights provide the foundation for selecting an appropriate copula-based GLMM in the subsequent analysis.

3.2.2. Provincial Classification Based on Tail/Slope Ratio

Building on these preliminary insights, we further classify provinces according to their dependence patterns using a tail–slope approach. This method allows us to determine whether provinces fall into symmetric categories, where responses remain proportional across the distribution, or asymmetric ones, where sensitivity differs significantly in the lower or upper extremes. This classification not only provides a clearer picture of Indonesia’s regional energy–emission landscape but also informs the development of targeted policy strategies tailored to each province’s unique dynamics.

The exploratory findings presented in the previous section indicate that the aggregate relationship between energy exports (Y₂) and CO₂ emissions (Y₁) tends to mask substantial heterogeneity across Indonesian provinces. In resource-abundant regions, emissions generally respond in a stable and proportionate manner to changes in energy exports, suggesting relatively symmetric dynamics. In contrast, several other provinces display disproportionate sensitivities, where variations in energy exports are associated with nonlinear or amplified changes in CO₂ emissions, indicating the potential presence of asymmetric patterns.

Recognizing these variations is crucial for distinguishing provinces where the energy–emission linkages are relatively consistent and symmetric from those where emissions exhibit nonlinear responses under different levels of energy activity. To capture these heterogeneous dependence structures, a tail–slope estimation approach is employed, allowing us to evaluate how the sensitivity of CO₂ emissions (Y₁) to energy exports (Y₂) differs between lower and upper ranges of energy activity. This method involves three main steps:

• Estimating tail-specific slopes.

For each province, we calculate the slope of Y₁ relative to Y₂ separately for the lower quartile (Q1) and upper quartile (Q3):

$${\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}}_{\mathrm{Q}1}={\displaystyle \frac{∆Y_1}{∆Y_2}} \mathrm{for} \mathrm{lower} \mathrm{quartile}, {\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}}_{\mathrm{Q}3}={\displaystyle \frac{∆Y_1}{∆Y_2}} \mathrm{for} \mathrm{lower} \mathrm{quartile}.$$

2.

Computing the slope ratio.

The slope ratio is obtained as

$$\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{{\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}}_{\mathrm{Q}3}}{{\mathrm{S}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}}_{\mathrm{Q}1}}}$$

This ratio captures differences in emission sensitivities between the two tails.

3.

Classifying provinces based on slope ratio.

Using the following criteria:

• Symmetric dependence: 0.80 ≤ ratio ≤ 1.25
• Upper-tail asymmetric: ratio > 1.25
• Lower-tail asymmetric: ratio < 0.80

This approach enables the identification of tail-dependent dynamics that conventional correlation measures might fail to capture, offering a more comprehensive understanding of provincial energy–emission linkages. To further examine the heterogeneous patterns observed across provinces, each region is classified based on the sensitivity of CO₂ emissions (Y₁) to variations in energy exports (Y₂). Using the tail–slope estimation approach, the slopes corresponding to the lower quartile (Q1) and upper quartile (Q3) are compared to evaluate potential differences in emission responses at varying levels of energy activity. The resulting slope ratio serves as a straightforward yet effective indicator for determining whether the dependence between energy exports and emissions is symmetric or asymmetric.

Table 2. Classification of provinces based on tail–slope estimation and dependence patterns.

Province	Slope (Q1)	Slope (Q3)	Slope Ratio	Dependence Pattern
Riau	1.408	1.408	1.000	Symmetric
Kalimantan Timur	1.410	1.410	1.000	Symmetric
Papua	1.409	1.408	0.999	Symmetric
Bali	1.408	1.407	0.999	Symmetric
Sulawesi Tengah	1.405	1.420	1.011	Symmetric
Jawa Barat	1.398	1.512	1.082	Symmetric
Aceh	1.405	1.720	1.224	Upper-tail asymmetric
Sumatera Selatan	1.401	1.803	1.286	Upper-tail asymmetric
Nusa Tenggara Timur	1.420	1.121	0.789	Lower-tail asymmetric
DI Yogyakarta	1.390	1.070	0.770	Lower-tail asymmetric

presents the classification outcomes for selected provinces. A slope ratio close to unity suggests symmetric dependence, indicating that changes in energy exports are associated with proportionate variations in CO₂ emissions. Ratios substantially greater than one indicate upper-tail asymmetry, implying that emissions become more sensitive when energy exports reach higher levels. Conversely, ratios significantly below one represent lower-tail asymmetry, reflecting weaker emission responses even when energy exports increase substantially.

The classification presented in Table 2 shows substantial variation in the dependence structure between energy exports (Y₂) and CO₂ emissions (Y₁) across Indonesian provinces. For most regions, the slope ratios are close to unity, indicating a symmetric dependence pattern in which changes in energy exports are associated with proportionate adjustments in CO₂ emissions. This suggests that, for a large number of provinces, the environmental consequences of energy-export-related activities follow a relatively stable and predictable pathway, where emissions respond in a balanced manner to fluctuations in energy activity.

However, several provinces exhibit asymmetric dependence structures that deviate from the overall national trend. Upper-tail asymmetric provinces, such as Aceh and Sumatera Selatan, demonstrate heightened sensitivity of CO₂ emissions at elevated export levels, where modest increases in energy exports result in disproportionately large rises in emissions. These findings indicate that these regions are particularly vulnerable to emission surges during periods of intensified energy activity.

Conversely, lower-tail asymmetric provinces, including Nusa Tenggara Timur and DI Yogyakarta, display weaker emissions responses despite substantial increases in energy exports. This pattern may be attributed to factors such as a higher reliance on low-emission energy sources, improved adoption of energy-efficient technologies, or structural characteristics that reduce the emission intensity of exported energy.

Taken together, these results highlight the heterogeneous nature of dependence patterns across Indonesian provinces and reinforce the need for flexible modeling frameworks. This provides strong motivation for employing a copula-based GLMM in the subsequent Section 3.3 to more accurately capture both symmetric and asymmetric tail dynamics.

3.3. Copula-Based GLMM Estimation

Once the nature of symmetric and asymmetric patterns has been established, the next step is to formally model these relationships using a more advanced statistical framework. The copula-based generalized linear mixed model (copula–GLMM) offers a powerful approach to simultaneously capture marginal behaviors and the dependence structure linking energy exports and CO₂ emissions. This method allows us to move beyond simple correlations and directly measure how these variables interact under different conditions, including in the tails of the distribution where extreme behaviors often occur. The results from this modeling provide a deeper and more precise understanding of Indonesia’s energy–emission nexus.

The heterogeneous dependence patterns identified in the previous section demonstrate the need for a more flexible statistical framework to analyze the joint dynamics between energy exports (Y₂) and CO₂ emissions (Y₁). Conventional linear models are often inadequate when the underlying relationships involve nonlinearities or tail-specific asymmetries, as observed across several provinces. To address these limitations, a copula-based generalized linear mixed model (copula–GLMM) is employed, which jointly models the marginal distribution of each variable and the dependence structure connecting them.

This modeling approach offers two main advantages. First, it enables a systematic comparison between symmetric and asymmetric copulas, providing statistical evidence on whether emission responses differ across varying levels of energy activity. Second, the inclusion of mixed-effects components captures province-specific heterogeneity, ensuring that regional disparities are properly represented in the model. Through this framework, the objective is to identify the most appropriate copula family and assess whether Indonesia’s energy–emission nexus is better described by a symmetric dependence structure or by asymmetric tail-dominant dynamics. Building on this framework, the next step involves comparing alternative copula families to determine which best captures the underlying dependence structure in Indonesia’s energy–emissions relationship

3.3.1. Model Selection and Goodness of Fit

To model the joint dependence between energy exports and CO₂ emissions, five copula families—Clayton, Gumbel, Frank, Gaussian, and Student-t—were evaluated, each offering distinct features in capturing dependence structures. The Gumbel and Student-t copulas are more sensitive to upper-tail dependence, making them suitable for analyzing extreme co-movements when both variables reach high levels. The Frank copula assumes symmetric dependence across the distribution, while the Gaussian copula is based on linear correlation and does not capture tail dependence, which limits its explanatory power when nonlinear patterns exist.

The Clayton copula differs in that it specializes in modeling lower-tail dependence, capturing cases where both variables move together at lower levels—a pattern that closely reflects the empirical characteristics of our data. Many provinces display strong co-movement under low export and emission conditions, highlighting the structural realities of regions with limited energy production and smaller carbon footprints. This property makes Clayton particularly valuable for understanding asymmetric relationships that are often overlooked by symmetric or upper-tail-focused models.

Model comparison results further support this choice. Clayton consistently achieved the lowest AIC and BIC values and outperformed alternatives in likelihood ratio tests, indicating the best overall fit. Beyond statistical performance, its ability to capture asymmetric, lower-tail dynamics provides deeper and more policy-relevant insights into the energy–emissions nexus, making it the most appropriate copula for the proposed GLMM framework. The model evaluation is summarized in

Table 3. Model comparison for copula-based GLMM.

Copula	Log-Likelihood	AIC	BIC
Gaussian	−412.5	830.9	841.2
Student-t	−410.3	827.1	838.4
Clayton	−398.7	805.4	816.1
Gumbel	−400.1	808.7	819.5
Frank	−409.5	826.0	837.2

Bold: The value is highlighted because it represents the lowest Copula-based “Clayton” value.

, which reports the log-likelihood values, Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC) for each copula specification.

3.3.2. Copula Parameter Estimates

The estimation results from the Clayton copula–GLMM presented in

Table 4. Parameter estimates for the best-fitting copula (Clayton copula–GLMM).

Parameter	Estimate	Std. Error	p-Value
ψ (Dependence Parameter)	2.317	0.284	<0.001
τ (Kendall’s Tau)	0.697	—	—
Lower-tail coefficient	0.482	—	—
Upper-tail coefficient	0.129	—	—
Intercept (${\beta }_0$)	0.582	0.091	<0.001
Energy Exports (${\beta }_1$)	0.413	0.073	<0.001
Renewable Share (${\beta }_2$)	−0.142	0.065	0.021
GDP per Capita (${\beta }_3$)	0.186	0.081	0.029
Urbanization (${\beta }_4$)	0.097	0.048	0.039
Random Effects (σ2)	0.228	—	—

provide substantial empirical evidence on the dependence structure between energy exports (Y₂) and CO₂ emissions (Y₁). The estimated copula parameter ψ = 2.317 (p < 0.001) indicates a strong and statistically significant association between the two variables. Translating this parameter into Kendall’s Tau yields τ ≈ 0.697, suggesting that the relationship between energy activity and emissions is highly concordant across provinces. Unlike symmetric copulas, the Clayton model captures a pronounced lower-tail dependence, meaning that the strongest co-movements between Y₂ and Y₁ occur when both variables are relatively low.

This result is particularly relevant for low-to-moderate export provinces, where small fluctuations in energy activity tend to produce disproportionately large changes in CO₂ emissions. Such behavior is consistent with provinces in earlier stages of industrialization, where limited technological adaptation and less efficient energy systems exacerbate environmental impacts. In contrast, high-export provinces exhibit more proportional dynamics: emissions continue to rise alongside energy exports, but the marginal impact becomes more stable and predictable, reflecting technological improvements and investment in cleaner production infrastructure.

The estimated tail-dependence coefficients reinforce this conclusion. The lower-tail coefficient (0.482) indicates a relatively strong interdependence in regions with smaller export volumes, while the upper-tail coefficient (0.129) shows a weaker connection when both energy exports and emissions are high. This asymmetry suggests that carbon intensity is more sensitive to export shocks in low-activity environments, but becomes less elastic in high-export settings. These patterns may arise from technological advancements, higher energy efficiency, and the increasing role of renewable energy in more developed provinces.

Furthermore, the highly significant p-value (< 0.001) confirms the robustness of these findings, indicating that the observed asymmetric dependence reflects a genuine structural phenomenon rather than random variation. These results are also consistent with the heterogeneity identified earlier in Table 2, where several provinces exhibited divergent sensitivities to energy activity levels.

In summary, the Clayton copula–GLMM reveals that Indonesia’s energy–emission relationship is nonlinear and asymmetrically dependent, dominated by lower-tail sensitivity. Provinces with limited energy exports are more vulnerable to environmental pressures, as small increases in energy production or exports generate disproportionately high emission responses. Conversely, regions with more advanced export capacity display greater stability, benefiting from efficiency gains and cleaner production processes. These findings underscore the importance of adopting tail-sensitive modeling frameworks and support the formulation of targeted emission-control strategies, particularly for provinces in earlier stages of energy-intensive development.

3.3.3. Tail-Dependence Visualization

To gain deeper insights into the nature of symmetric and asymmetric dependence between CO₂ emissions (Y₁) and energy exports (Y₂), we estimate the empirical tail-dependence functions, χ(u), for both the lower and upper tails of their joint distribution. This diagnostic assesses the probability that both variables simultaneously assume extreme low values (lower tail) or extreme high values (upper tail), thereby distinguishing whether the observed dependence structure is balanced or dominated by tail-specific effects. The patterns illustrated in Figure 7 provide visual confirmation of the model selection outcomes reported in Table 3 and the parameter estimates in Table 4, offering further evidence on whether CO₂ emissions exhibit greater sensitivity at lower or higher levels of energy activity.

The empirical tail-dependence functions presented in Figure 7 provide visual confirmation of the asymmetric dependence between energy exports (Y₂) and CO₂ emissions (Y₁). The estimated lower-tail function, ${\chi }_L\left(u\right)$, remains relatively high and stable across a wide range of thresholds, indicating that provinces with low-to-moderate energy export levels exhibit stronger co-movements between Y₂ and Y₁. This finding is consistent with the results reported in Table 4, where the Clayton copula was identified as the best-fitting model, reflecting pronounced lower-tail dominance in the dependence structure.

In contrast, the upper-tail function, ${\chi }_U\left(u\right)$, shows a gradual decline as u approaches extreme values, suggesting that the likelihood of simultaneously observing high energy exports and high CO₂ emissions is comparatively weaker. This pattern implies that provinces with high export volumes are less prone to extreme emission spikes relative to energy activity, possibly due to improvements in energy efficiency, technological advancements, and a growing reliance on cleaner production processes in resource-rich regions.

Overall, the behavior of the tail-dependence functions strongly supports the selection of the Clayton copula and confirms that Indonesia’s energy–emission nexus is inherently nonlinear and asymmetric, with greater sensitivity observed at lower levels of energy activity. These results further validate the copula–GLMM estimation and provide a robust statistical basis for formulating targeted provincial-level emission mitigation strategies, particularly for regions with limited export capacity and higher vulnerability to environmental impacts.

The empirical evidence derived from model selection, parameter estimation, and tail-dependence diagnostics provides a comprehensive understanding of the interdependence between energy exports (Y₂) and CO₂ emissions (Y₁) across Indonesian provinces. The comparative evaluation presented in Table 3 identifies the Clayton copula as the most suitable specification, indicating a clear lower-tail-dominant dependence structure. In practical terms, this suggests that the co-movement between energy activity and emissions is strongest when both variables are at low to moderate levels, whereas the degree of dependence weakens in the upper extremes.

The parameter estimates reported in Table 4 further reinforce these findings. The estimated copula parameter ψ = 2.317 (p < 0.001) and the corresponding Kendall’s Tau (τ ≈ 0.697) confirm a robust positive association between energy exports and CO₂ emissions at the aggregate level. However, the lower-tail coefficient (0.482) is substantially larger than the upper-tail coefficient (0.129), indicating that emission sensitivity is disproportionately higher in low-export provinces. In these regions, even modest expansions in energy activity tend to result in disproportionately large increases in emissions, reflecting structural limitations such as restricted technological adaptation, limited renewable energy integration, and lower overall energy efficiency.

In contrast, provinces with high energy export levels demonstrate a more stable and predictable relationship between energy activity and emissions. This relatively subdued marginal response is consistent with the adoption of energy-efficient technologies, cleaner production processes, and a greater penetration of renewable sources in resource-rich regions, including Kalimantan Timur, Riau, and Papua. These insights are further supported by Figure 7, where the empirical tail-dependence curves clearly illustrate pronounced lower-tail dominance and a gradual decline in sensitivity at the upper extremes.

From an analytical perspective, these results suggest that asymmetry is conditional and localized rather than uniform across the distribution. While Indonesia’s energy–emission nexus exhibits a strong overall interdependence, the degree of sensitivity varies considerably depending on industrial structure, technological capability, and energy mix. Consequently, policy interventions should avoid a uniform, one-size-fits-all approach. Provinces situated in the lower tail—where emerging energy exports are accompanied by steep emission responses—would benefit most from initiatives aimed at improving energy efficiency, accelerating renewable integration, and implementing basic emission control technologies. Conversely, upper-tail provinces, where emission responses are less elastic, require more advanced strategies focused on technological innovation, fuel switching, and the deployment of sophisticated abatement mechanisms.

Finally, these findings highlight the effectiveness of adopting a copula-based GLMM framework. By jointly modeling marginal behaviors and the underlying dependence structure while accounting for unobserved provincial heterogeneity, the model successfully captures both the symmetric core of the energy–emission relationship and its tail-specific sensitivities. These insights establish a robust foundation for the subsequent section on robustness checks and policy implications, where the stability of these findings will be further examined and translated into actionable strategies to support Indonesia’s sustainable energy transition.

3.4. Robustness Checks

Robustness analysis plays a critical role in ensuring that the results we obtain are reliable and not dependent on specific model choices or data conditions. In this section, we test the stability of our findings under a range of alternative specifications, variable transformations, and sensitivity scenarios. By confirming that the main conclusions hold across these different conditions, we strengthen the credibility of the results and increase confidence in their policy relevance. This process also helps identify any potential limitations and ensures that the insights derived from the copula–GLMM are both statistically sound and practically meaningful.

To assess the reliability and stability of the estimated dependence structure between energy exports (Y₂) and CO₂ emissions (Y₁), a series of robustness evaluations was conducted within the copula-based GLMM framework. These procedures were implemented to verify whether the key findings presented in Section 3.3 remain consistent when the model is subjected to alternative specifications, variable transformations, and adjustments for extreme observations.

Five complementary robustness checks were performed. First, additional control variables, including the renewable energy share (RE_Share), GDP per capita, and urbanization rate, were incorporated to account for potential confounding effects. Second, energy production was substituted for energy export to evaluate the sensitivity of results to alternative measurement choices. Third, a logarithmic transformation was applied to both marginal distributions to address skewness and improve variance stabilization. Fourth, the robustness of the parameter estimates was tested by trimming outlier observations to minimize potential distortions. Finally, the impact of alternative tail-dependence thresholds was examined to assess potential variations in sensitivity across the lower and upper tails of the joint distribution. The robustness analysis presented in

Table 5. Robustness summary for Clayton copula–GLMM.

Specification	Copula	AIC	BIC	Kendall’s τ	Lower-Tail χL	Upper-Tail χU	Preferred Model
Baseline Model (Y2: Energy Exports)	Clayton	805.4	816.1	0.697	0.482	0.129	Best Fit
Controls (RE_Share, GDP_pc, Urbanization)	Clayton	806.3	818.4	0.693	0.479	0.134	Stable
Energy Export (Y2)	Clayton	808.7	820.2	0.684	0.461	0.141	Stable
Log-Transform (log Y1, log Y2)	Clayton	804.8	815.5	0.701	0.487	0.125	Stable
Trimming Outliers (Top 5% Removed)	Clayton	803.9	814.6	0.695	0.478	0.132	Stable
Alternative Tail Threshold (u = 0.15 → 0.25)	Clayton	805.7	816.4	0.692	0.475	0.136	Stable

demonstrates that the Clayton copula–GLMM consistently provides the most accurate representation of the joint dependence structure between energy exports (Y₂) and CO₂ emissions (Y₁) across all alternative specifications. The baseline model achieves the lowest AIC (805.4) and BIC (816.1), confirming its superior fit compared to competing alternatives. Incorporating additional control variables, including renewable energy share (RE_Share), GDP per capita, and urbanization, leads to only minor changes in Kendall’s τ (0.693) and the tail-dependence coefficients (${\chi }_L$ = 0.479; ${\chi }_U$ = 0.134), indicating that the estimated dependence remains structurally stable even after accounting for economic and demographic heterogeneity.

Similarly, replacing energy exports with energy production results in a slight reduction in overall dependence (τ = 0.684) and lower-tail sensitivity (${\chi }_L$ = 0.461), yet the persistence of lower-tail dominance confirms that energy production serves as valid when detailed export data are unavailable. Applying a logarithmic transformation to both Y₁ and Y₂ marginal distributions marginally improves model performance (AIC = 804.8) and strengthens the dependence estimate (τ = 0.701), demonstrating that the strong positive association is not an artifact of distributional skewness.

The results also remain robust after removing the top five percent of extreme observations (τ = 0.695), suggesting that the findings are not driven by outlier provinces with exceptionally high emissions or energy activity. Furthermore, adjusting the quartile thresholds for tail-dependence estimation (u = 0.15 → 0.25) produces stable coefficients (${\chi }_L$ = 0.475; ${\chi }_U$ = 0.136), confirming that the conclusion regarding lower-tail dominance is not sensitive to threshold selection.

Provincial Classification

Based on the estimated Clayton copula–GLMM, Indonesian provinces are classified into three dependence patterns reflecting the relationship between energy exports (Y₂) and CO₂ emissions (Y₁). These patterns consist of symmetric dependence, lower-tail asymmetry, and upper-tail asymmetry, each capturing distinct dynamics in how changes in energy exports are associated with emissions.

Table 6. Provincial classification based on dependence patterns and recommended policy strategies.

Dependence Pattern	Example Provinces	Key Characteristics	Recommended Policy Strategies
Symmetric Dependence	Riau, Kalimantan Timur, Papua, Bali	Energy exports and CO2 emissions exhibit proportional movements; strong industrial capacity; robust energy infrastructure	Maintain current energy-export strategies, gradually integrate renewable energy sources, and establish continuous emissions monitoring frameworks
Lower-Tail Asymmetry	Nusa Tenggara Timur, DI Yogyakarta, Maluku Utara	Modest increases in energy exports lead to disproportionately larger emission surges; limited technological adoption; low renewable integration	Prioritize energy efficiency programs, provide targeted incentives for renewable energy deployment, and strengthen cost-effective emission mitigation mechanisms
Upper-Tail Asymmetry	Aceh, Sumatera Selatan	High energy exports but muted emission responses; broader adoption of clean technologies; more efficient production systems	Invest in advanced abatement technologies, accelerate clean-energy innovation, and enhance carbon capture and storage (CCS) initiatives

summarizes the classification of selected provinces under each category, highlighting the key characteristics derived from the model estimation.

Table 6 summarizes the provincial classification based on the estimated dependence patterns between energy exports (Y₂) and CO₂ emissions (Y₁) derived from the Clayton copula–GLMM. The results indicate three distinct categories: symmetric dependence, lower-tail asymmetry, and upper-tail asymmetry. Provinces such as Riau, Kalimantan Timur, Papua, and Bali fall under symmetric dependence, where changes in energy exports are associated with proportional variations in CO₂ emissions. These provinces generally exhibit strong industrial capacity and relatively stable energy infrastructure, leading to more predictable energy–emission dynamics.

In contrast, provinces including Nusa Tenggara Timur, DI Yogyakarta, and Maluku Utara are classified under lower-tail asymmetry, where even modest increases in energy exports correspond to disproportionately larger emission surges. This pattern suggests structural vulnerabilities related to limited technological adoption and lower renewable energy integration.

Meanwhile, Aceh and Sumatera Selatan demonstrate upper-tail asymmetry, where higher energy-export levels are linked to relatively muted changes in emissions. This dynamic is likely influenced by broader adoption of cleaner technologies and more efficient production systems compared with other provinces. The findings presented in this chapter provide a comprehensive picture of how energy exports and CO₂ emissions interact across Indonesia’s provinces. The descriptive analysis revealed substantial regional disparities, while the examination of symmetric and asymmetric patterns highlighted the uneven ways in which provinces respond to changes in energy activity. The copula-based GLMM estimation further deepened this understanding by capturing nonlinear dependencies and tail-specific dynamics, showing that emission sensitivity is particularly pronounced in low-export regions. Finally, robustness checks confirmed the stability of these results under various model specifications and data conditions.

Together, these results paint a nuanced portrait of Indonesia’s energy–emission landscape, one defined by structural diversity, unequal vulnerabilities, and complex interdependencies. With this empirical foundation in place, the next chapter turns to interpreting these findings in a broader context. We discuss their implications for energy policy, climate strategy, and sustainable development, and outline how tailored interventions can better address Indonesia’s unique regional challenges while advancing national and global climate goals.

4. Discussions

Building on the empirical results presented in the previous chapter, this section takes a step back to interpret what those findings mean in a broader scientific and policy context. The goal here is not only to summarize the patterns revealed by the Clayton copula–GLMM analysis but also to understand their deeper implications for Indonesia’s energy transition and climate strategy. While the results clearly demonstrate a strong link between energy exports and CO₂ emissions, they also uncover a more complex reality: provincial differences, nonlinear interactions, and asymmetric sensitivities that cannot be addressed with uniform solutions.

This chapter is therefore structured to translate those quantitative insights into meaningful interpretations and actionable recommendations. We begin by unpacking the key findings and explaining what they reveal about the dynamics of Indonesia’s energy–emission nexus. We then situate these insights within the wider body of literature, highlighting both points of convergence and areas where this study extends existing knowledge. Finally, we explore the policy pathways that emerge from this analysis—outlining how differentiated, region-specific strategies can better support Indonesia’s low-carbon transition and align national efforts with global climate commitments.

The results presented in the previous chapter provide a comprehensive overview of Indonesia’s energy–emission dynamics based on the Clayton copula–GLMM framework. By capturing both symmetric and asymmetric dependence patterns, the analysis reveals substantial heterogeneity across provinces in the relationship between energy exports (Y₂) and CO₂ emissions (Y₁). While the aggregate trend shows a strong positive association, the classification of provinces into symmetric, lower-tail, and upper-tail categories highlights significant structural differences shaped by variations in industrial capacity, technological readiness, and energy infrastructure.

These findings provide important context for interpreting Indonesia’s energy–emission nexus within a broader sustainability framework. The discussion that follows integrates these empirical results with insights from previous studies and evaluates their relevance for energy policy and environmental management. In doing so, it aims to clarify the unique contributions of this study, assess consistencies and divergences with the existing literature, and explore the policy pathways necessary to support Indonesia’s low-carbon transition in alignment with national and global sustainability targets.

4.1. Key Findings and Interpretation

The results presented in the previous chapter offer more than just statistical evidence—they reveal how Indonesia’s energy–emission relationship unfolds in reality, shaped by diverse provincial contexts and structural conditions. In this section, we interpret those findings in depth, exploring what they mean for the country’s broader sustainability trajectory. By examining how symmetric and asymmetric patterns emerge across different regions, we aim to understand the underlying drivers of emission dynamics and their implications for policy design.

The empirical results obtained from the Clayton copula–GLMM provide new insights into the complex interaction between energy exports (Y₂) and CO₂ emissions (Y₁) across Indonesian provinces. Unlike conventional linear approaches, the copula-based framework allows a more flexible characterization of the joint dependence structure, capturing both symmetric relationships and asymmetric tail behaviors. This methodological advancement offers a deeper understanding of Indonesia’s energy–emission nexus, revealing significant heterogeneity that would otherwise remain obscured under traditional modeling techniques.

The findings demonstrate that, at the aggregate level, energy exports and CO₂ emissions are strongly and positively associated, indicating that higher energy activity is generally accompanied by rising emissions. However, the classification of provinces into symmetric, lower-tail asymmetric, and upper-tail asymmetric categories highlights structural differences in how these dynamics unfold regionally. Provinces such as Riau, Kalimantan Timur, Papua, and Bali exhibit symmetric dependence, where changes in energy exports correspond proportionally to fluctuations in emissions. This balanced dynamic suggests a relatively stable energy infrastructure and more predictable environmental outcomes in these regions.

In contrast, lower-tail asymmetric provinces—including Nusa Tenggara Timur, DI Yogyakarta, and Maluku Utara—demonstrate a heightened sensitivity to changes in energy activity. Even modest increases in exports trigger disproportionately larger surges in emissions, reflecting structural vulnerabilities such as limited technological capacity, low renewable energy integration, and less efficient production systems. These findings indicate that emission mitigation efforts in these regions require more focused interventions to prevent environmental degradation during periods of energy expansion.

The pronounced lower-tail dominance observed in the copula estimates suggests that provinces with lower levels of energy exports tend to experience disproportionately large increases in CO₂ emissions, even with relatively small rises in energy activity. This pattern likely reflects a combination of structural and technological factors, including limited access to cleaner technologies, heavy reliance on fossil fuels, and lower efficiency in energy conversion processes. Such regions are often in the early stages of industrialization, where incremental growth in energy production immediately translates into higher emissions because of outdated infrastructure and minimal mitigation capacity. In contrast, the relatively weaker upper-tail dependence indicates that high-export provinces have achieved a degree of decoupling between energy expansion and emission growth. This stabilization is likely driven by greater technological adoption, diversification of energy sources, and improved efficiency, which reduce the marginal impact of additional energy output. From a policy perspective, these contrasting patterns highlight the need for differentiated strategies. Targeted support for energy efficiency, technology transfer, and renewable integration should be prioritized in lower-export provinces, while advanced innovation-focused policies such as fuel switching and carbon capture deployment are more relevant for more developed regions. Such a tailored approach would enable Indonesia to address the heterogeneous nature of its energy–emission nexus more effectively and accelerate progress toward its Net Zero Emissions 2060 target.

Collectively, these findings underline two key contributions of this study. First, the application of a copula-based GLMM framework provides a robust and comprehensive depiction of Indonesia’s energy–emission dependencies, addressing the limitations of conventional models that fail to account for tail-specific sensitivities. Second, the identification of distinct regional dependence patterns lays the foundation for designing differentiated energy and environmental policies that reflect local conditions rather than applying uniform national strategies.

By uncovering the structural diversity of energy–emission relationships across provinces, this study advances the discourse on sustainable energy transitions in emerging economies. The findings offer not only insights for Indonesia but also broader relevance for countries facing similar challenges in balancing energy-driven economic growth with environmental sustainability, aligning closely with global efforts to achieve net-zero emissions and the objectives of the Paris Agreement.

4.2. Comparison with Previous Studies

Placing our findings in the context of existing research allows us to see where this study aligns with, extends, or challenges the current understanding of the energy–emission nexus. While many previous studies have explored the link between energy activity and environmental outcomes, most have done so through linear or aggregate approaches. Here, we compare our results with those earlier works, highlighting how the use of a copula-based GLMM reveals new layers of complexity and provides a more nuanced picture of Indonesia’s provincial realities.

The findings of this study contribute to the growing body of literature examining the interdependence between energy activity and environmental outcomes, while providing new empirical evidence specific to Indonesia’s provincial context. Previous studies on energy–emission dynamics have often relied on linear or symmetric modeling frameworks, which, while useful for broad associations, frequently overlook structural variations and tail-specific sensitivities. By adopting a Clayton copula–GLMM framework, this study departs from conventional approaches and captures nonlinear dependence patterns that better reflect Indonesia’s diverse energy and industrial landscape.

Several regional studies provide valuable context for interpreting these results. Reference [42] reported that energy trade and fossil-fuel dependency remain the dominant drivers of CO₂ emissions across Asia-Pacific economies, broadly aligning with our aggregate finding that energy exports are positively associated with emissions. However, unlike their analysis, which assumes uniform relationships across countries, our results reveal substantial heterogeneity within Indonesia itself, demonstrating that dependence patterns vary significantly among provinces, based on technological capacity, industrial structure, and energy infrastructure.

Similarly, Ref. [43] examined Southeast Asia’s energy landscape and highlighted the persistent reliance on fossil-based energy alongside slow renewable energy adoption, which supports our observation of lower-tail asymmetric sensitivities in provinces with limited technological readiness and low renewable penetration. Yet, our findings extend this perspective by identifying how even modest energy expansions in these regions can lead to disproportionately high emissions, providing a more granular understanding of localized environmental vulnerabilities.

In contrast, Ref. [44] explored the role of green innovation, environmental taxes, and clean technologies in reducing emissions across OECD countries. Their findings emphasize that advanced technological adoption and policy-driven incentives can decouple energy growth from environmental degradation. Our study complements this insight by demonstrating that several Indonesian provinces—such as Aceh and Sumatera Selatan—already exhibit upper-tail asymmetry, where high energy-export levels are accompanied by relatively muted increases in emissions, suggesting that cleaner production systems and technological innovation are beginning to take effect in certain regions.

Collectively, these comparisons highlight two key distinctions of this study. First, by focusing on Indonesia’s provincial-level energy–emission dynamics, it provides a more detailed and context-specific analysis compared with cross-country studies that generalize relationships across broader regions. Second, the application of a copula-based GLMM framework allows us to capture asymmetric dependence structures that traditional models often overlook, providing deeper insights into both environmental vulnerabilities and technological opportunities.

Beyond its national relevance, these findings hold broader implications for emerging economies undergoing energy transitions. By illustrating how asymmetric sensitivities shape environmental outcomes at the subnational level, this study contributes to the global discourse on sustainable energy management and supports policy strategies aligned with international climate goals, including the Paris Agreement and the Sustainable Development Goals [45].

In conclusion, this study makes a distinct and meaningful contribution to the existing literature on energy–emission dynamics. Methodologically, it advances the field by introducing a Clayton copula-based GLMM that captures nonlinear dependence structures and tail-specific sensitivities often overlooked by conventional linear models. Empirically, it fills a critical gap by demonstrating how structural, technological, and policy heterogeneity shape the energy–emission relationship at a subnational level—a perspective that remains largely absent in prior research. Beyond its immediate context, the approach proposed here offers a transferable framework for examining similar dynamics in other emerging economies, enriching theoretical discussions while providing a stronger foundation for designing more targeted and region-specific climate and energy policies.

4.3. Practical Implications, Application Fields, and Model Limitations

The insights generated from this study extend far beyond theoretical discussions and statistical modeling. They offer a set of practical tools and perspectives that can be directly applied in real-world contexts, especially in sectors where understanding the interplay between energy activities and environmental outcomes is essential. The copula-based GLMM framework developed here, with its capacity to detect asymmetric tail behaviors, provides decision-makers with a deeper, more nuanced view of how energy exports and emissions evolve together under different conditions.

In the energy industry, this approach can serve as a strategic guide for planning and investment. By pinpointing provinces that are most vulnerable to sudden increases in emissions, it enables more targeted infrastructure development and more informed choices about future energy production strategies. Within the realm of environmental governance and climate policy, the model’s sensitivity to tail dynamics allows policymakers to move beyond uniform national policies and instead craft mitigation strategies that are tailored to the specific needs and vulnerabilities of each region. This ensures that interventions are not only more efficient but also more equitable.

The framework also carries clear relevance for industrial planning and sustainable development initiatives. It can support efforts to decarbonize production systems, guide the adoption of cleaner technologies, and help evaluate how effectively renewable energy sources are being integrated into provincial energy portfolios. Ultimately, the value of this study lies not only in its methodological innovation but also in its ability to inform real-world decisions. It shows how rigorous statistical analysis can be transformed into actionable strategies, strategies that strengthen the foundation for low-carbon growth and help Indonesia move steadily toward its long-term sustainability goals.

While the proposed copula–GLMM framework offers a powerful lens through which to examine the energy–emissions nexus, it is important to recognize that no model is without its limitations. Its performance inevitably depends on the quality, scope, and representativeness of the underlying data, meaning that estimation accuracy may be affected when observations are sparse or unevenly distributed. Moreover, the choice of copula family plays a decisive role in shaping the results, and an unsuitable specification can lead to incomplete characterization of dependence structures, particularly in the tails of the distribution. Computational complexity is another practical consideration, as the inclusion of mixed-effects and tail-dependence modeling increases the demand for robust estimation techniques, especially with large panel datasets. Finally, because the present analysis is grounded in Indonesia’s provincial context, caution is warranted when extending these findings to other regions without careful recalibration. Acknowledging these limitations not only enhances the transparency and interpretability of the study but also provides valuable direction for future research aimed at refining and expanding the copula–GLMM framework in broader empirical settings.

5. Conclusions, Recommendation, and Future Research

This final chapter brings together the main insights of the study and reflects on their broader implications for both research and policy. Building on the findings and discussions presented in the previous sections, it aims to distill the key messages that emerge from the analysis of Indonesia’s energy–emission dynamics and to highlight how these results contribute to the understanding of sustainable energy transitions. The chapter is organized into two parts: the first summarizes the major conclusions and methodological contributions of the study, while the second outlines practical recommendations and potential directions for future research. Together, these sections provide a clear picture of what has been learned and offer a roadmap for advancing both academic inquiry and policy design in the field of energy and environmental management.

5.1. Conclusions

This section distills the central findings of the study into a set of overarching conclusions, weaving together the key insights from the empirical analysis and their broader significance. Rather than merely restating results, it aims to highlight the core messages that emerge from the investigation, explain their implications within the context of Indonesia’s energy–emission transition, and reflect on how these findings contribute to the wider discourse on sustainable development and climate policy.

This study employed a copula-based generalized linear mixed model (GLMM) to examine the dependence between energy exports (Y₂) and CO₂ emissions (Y₁) across 34 Indonesian provinces from 2010 to 2024. The results reveal a strong positive relationship overall, but with substantial heterogeneity across regions. The Clayton copula emerged as the most suitable specification, highlighting the presence of lower-tail dominance—a pattern indicating that provinces with low-to-moderate energy exports are more vulnerable to disproportionate increases in emissions. Conversely, provinces with higher export activity exhibit more stable and predictable emission patterns, likely reflecting the influence of greater technological adoption, renewable energy integration, and more efficient industrial practices.

Beyond its empirical contributions, this study offers a methodological advancement by demonstrating the effectiveness of the copula–GLMM approach in capturing asymmetric dependencies in energy–emission dynamics—a complexity that conventional linear models often fail to represent. These methodological insights not only enrich the academic discourse on nonlinear environmental modeling but also provide an evidence-based foundation for designing more nuanced and region-specific policy interventions.

By linking statistical results with Indonesia’s broader sustainability agenda, the study underscores the critical role of provincial energy strategies in advancing Sustainable Development Goals (SDG) 7 (Affordable and Clean Energy), SDG 11 (Sustainable Cities and Communities), and SDG 13 (Climate Action), as well as fulfilling national commitments under the Paris Agreement. Ultimately, this research deepens our understanding of energy-driven environmental dynamics and strengthens the analytical basis for designing policies that support a just, equitable, and sustainable transition toward a low-carbon future.

5.2. Recommendations and Future Research

The results of this study highlight the need for differentiated policy strategies tailored to provincial contexts. Regions showing strong lower-tail asymmetry should prioritize improvements in energy efficiency, low-carbon infrastructure, and renewable deployment, while more advanced provinces could focus on measures such as carbon capture and accelerating clean-technology innovation. Such targeted approaches are essential for aligning local trajectories with Indonesia’s long-term de-carbonization goals.

Beyond practical implications, the study also opens several avenues for methodological advancement. Future research could extend the proposed framework by testing alternative copula families or time-varying structures to better capture evolving dependence patterns. Incorporating higher-frequency or sector-specific data, or expanding the model into multivariate or Bayesian formulations, would further enrich its mathematical depth and robustness. Comparative analyses with other energy-exporting economies could also enhance the external validity of these findings. Together, these directions would not only strengthen the theoretical foundation of the model but also expand its relevance for designing adaptive, evidence-based policies in the low-carbon transition.