Two-Degree-of-Freedom Digital RST Controller Synthesis for Robust String-Stable Vehicle Platoons

Abstract

Cooperative and Autonomous Vehicle (CAV) platoons offer significant potential for improving road safety, traffic efficiency, and energy consumption, but maintaining precise inter-vehicle spacing and synchronized velocity under disturbances while ensuring string stability remains challenging. This paper presents a fully decentralized two-layer architecture for homogeneous platoons whose identical vehicle dynamics and information flow produce an inherent symmetrical system structure. Operating under a predecessor-following topology with a constant time headway policy, the upper layer generates a smooth velocity reference based on local spacing and relative-velocity errors, while the lower layer employs a two-degree-of-freedom (2-DOF) digital RST controller designed through discrete-time pole placement and sensitivity-function shaping. The 2-DOF structure enables independent tuning of tracking and disturbance-rejection dynamics and provides a computationally lightweight solution suitable for embedded automotive platforms. The paper develops a stability analysis demonstrating internal stability and $L_2$ string stability within this symmetrical closed-loop architecture. Simulations confirm string-stable behavior with attenuated spacing and velocity errors across the platoon during aggressive leader maneuvers and under input disturbances. The proposed method yields smooth control effort, fast transient recovery, and accurate spacing regulation, offering a robust and scalable control strategy for real-time longitudinal motion control in connected and automated vehicle platoons.

1. Introduction

1.1. Motivation

Rapid urbanization is placing unprecedented pressure on transportation networks, evident in persistent congestion, heightened crash risk, and growing environmental burdens. Within the broader smart city agenda, intelligent transportation systems (ITS) are widely regarded as a foundational lever to relieve these stresses by fusing sensing, connectivity, and automation to coordinate traffic at scale [1,2]. In this context, longitudinal vehicle platooning denotes coordinated strings of vehicles that maintain prescribed gaps and synchronized velocity using onboard sensing, vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) communication, and appropriately designed control strategies [3,4]. The enabling mechanism is Cooperative Adaptive Cruise Control (CACC), an extension of Adaptive Cruise Control (ACC) that shares real-time kinematic states over V2V and V2X links, thereby improving disturbance rejection and supporting shorter, safer headways than sensor-only ACC [3,5,6].

Platooning benefits across traffic flow, energy and emissions, and safety are supported by simulations and experiments. Converting a high-occupancy vehicle (HOV) lane to a dedicated CACC lane reduces corridor travel time and delay once roughly 40–50% of vehicles are CACC-equipped [7]. Reduced aerodynamic drag yields about 10–15% follower fuel savings and about 3–5% for the leader, with two-truck combined savings around 7% under representative speeds, gaps, and masses [8,9]. Fleet-scale analyses indicate proportional ${\mathrm{CO}}_2$ cuts [8,9]. Safety improves as CACC trials lower rear-end risk surrogates, such as time-to-collision, through disturbance attenuation [10]. These combined benefits underscore the critical need for robust and reliable platoon-control systems, which are essential for translating this potential into real-world practice.

1.2. Related Works

Platoon-control architectures are commonly grouped as centralized, decentralized, or distributed [3]. Centralized strategies can optimize network-level objectives but face scalability limits and single-point-of-failure risk. Decentralized schemes are robust and self-contained yet may under-coordinate at the string level. A distributed approach, in which each vehicle regulates itself using neighbor information over V2X, offers a pragmatic balance of coordination, robustness, and scalability, and it aligns with the networked-control view of connected and automated vehicles (CAVs) [3,4].

Across architectures, string stability is the central requirement. Spacing and velocity disturbances must attenuate rather than amplify as they propagate upstream [11,12]. Meeting this requirement requires coordinated choices in three areas: spacing policy, information flow topology (ITF), and controller design and tuning. First, consider the spacing policy. A constant distance (CD) policy keeps a fixed physical gap regardless of speed, which is simple but prone to string instability in long platoons. A constant time headway (CTH) policy keeps a fixed time gap so distance scales with speed and, with appropriate headway and a matched controller, typically limits disturbance growth relative to CD [3,4]. Nonlinear distance (NLD) policies adapt the desired gaps using nonlinear functions of speed, relative speed, acceleration, and context to improve performance under varying regimes [4]. Second, the information flow topology (ITF) dictates how vehicles share state information, thereby determining disturbance propagation, leader preview availability, noise amplification, admissible time headways, and delay margins. Typical structures are predecessor-following (PF), predecessor leader-following (PLF), bidirectional (BD), and multi-predecessor-following (MPF), each trading preview against noise sensitivity and achievable headways [4,13,14]. Third, controller design and tuning must be co-designed with the spacing policy and the information flow topology, explicitly accounting for measurement and communication delays, actuator limits, and model uncertainty, and ensuring robustness, disturbance attenuation, string stability, and bounded control effort across the platoon [3,4,12,13,15]. Surveys from networked control and CAV perspectives converge on this three-way co-design as essential for achieving throughput, energy, and safety goals under real-world constraints, including transitional maneuvers such as join, split, and lane change [3,4,13,14,15,16].

Grounded in this co-design perspective, a wide range of controllers has been explored, from low-complexity schemes to robustness-oriented formulations. Classical proportional-integral-derivative (PID) controllers are widely adopted for simplicity and low computational cost. A study developed a two-layer PID for truck platoons with low computational burden and robust tracking [17]. Authors in [18] propose a PID-based inter-vehicle distance controller with anti-windup and actuator-delay compensation, demonstrating stable gaps under sensor noise and drag variations. Authors in [19] show a decentralized PID with observer-based feedforward aerodynamic drag compensation that tightly tracks extremum-seeking-optimized spacing. Practical tuning rules for PD gains in cooperative CACC that guarantee both individual-vehicle stability and string stability under a constant time headway (CTH) policy with a predecessor-following (PF) topology are provided [20]. Nevertheless, PID strategies are typically limited in handling delays, constraints, or switching topologies unless augmented with robust or observer layers.

Beyond fixed-gain PID, a distributed model-reference adaptive controller (DMRAC) embeds a closed-loop reference model and an adaptive law to counter matched uncertainties under a CD policy [21]. Linear Quadratic Regulator (LQR) control offers a systematic, lightweight controller to balance state error and control effort. Typical applications include disturbance rejection and velocity consensus under external perturbations [22]. Comparative studies against learning-based designs for heavy-duty electric-truck CACC report competitive comfort and efficiency when communication is reliable [23]. Analysis that maps Nyquist-based gain regions for string stability with an LQR spacing-error regulator under CTH is presented in [24]. Such methods often assume full-state feedback and ideal linear models, which can limit practicality in nonlinear, constrained settings. Model predictive control (MPC) and distributed MPC (DMPC) handle constraints, compensate delays, and adapt to topology. In linear platoons, centralized MPC and cooperative distributed MPC with an alternating-direction coordinator achieve collision-free spacing, stable speed tracking, and full constraint satisfaction [25]. A min–max robust MPC that accounts for model uncertainties and feedback delays maintains stability and robustness [26]. Hierarchical designs place a DMPC upper layer for string stability and terminal consensus over an inverse-dynamics lower layer with feedforward and proportional–integral–derivative (PID) throttle–brake regulation [27]. Tube-based MPC with event-triggered updates guarantees string stability under bounded disturbances and actuator limits in discrete time while reducing computation and inter-vehicle communication [28]. Sliding-mode control (SMC) targets nonlinearities and matched disturbances. An SMC-based longitudinal controller enforces safety gaps by fusing position, gap, speed, and acceleration of the current and preceding vehicles [29]. Fixed-time integral terminal SMC with prescribed performance enforces explicit transient and steady-state bounds via transformed error dynamics [30]. More recently, a dual-layer scheme pairing adaptive spacing policy switching with distributed exponential SMC addresses changing traffic conditions and communication interruptions [31]. In parallel, $H_{\infty }$ control minimizes worst-case gain from disturbance to output. A controller-synthesis method for CACC embeds string-stability requirements directly into the design by exploiting $L_2$ string-stability conditions for linear cascaded systems [12]. Related multi-objective formulations balance control effort and robustness while guaranteeing string stability [32]. Static output feedback for PLF platoons, robust to vehicle heterogeneity including mass uncertainty and using limited measurements, is demonstrated in [33].

RST digital controllers have emerged for applications that require high performance, strong disturbance rejection, and explicit sensitivity shaping. An RST structure provides two degrees of freedom with separate regulation and tracking [34]. A comparative study indicates advantages over PI in wind-energy systems [35], and RST achieves voltage regulation with zero steady-state error in converter applications [36]. Moreover, RST was coupled with a machine learning (ML)-based inverse hysteresis compensator, built from hysteresis operators, for piezoelectric nanopositioning, yielding robust, high-precision tracking superior to PID baselines [37]. These studies highlight RST modularity, ease of discrete-time implementation, robustness to time delays and model uncertainties, and strong disturbance attenuation via sensitivity-function shaping.

Despite extensive work, current platoon-control designs face a persistent trade-off between robust performance and the computational feasibility required for scalable, real-time platooning. Classical PID controllers remain popular [17,18,19,20], but their single degree of freedom couples tracking and disturbance rejection, forcing a compromise between performance and robustness. Advanced controllers such as MPC, SMC, and $H_{\infty }$ can deliver higher performance, yet each introduces implementation barriers [12,25,26,27,28,29,30,31,32,33].

MPC demands substantial online computation and complicates real-time deployment on embedded controllers [25,26,27,28]. SMC can induce chattering and elevated high-frequency control effort, which stresses actuators [29,30,31]. $H_{\infty }$ control requires careful selection of weighting functions, making design and tuning complex and often yielding higher-order controllers [12,32,33].

This highlights the need for a practical balance among robust performance, smooth control action, computational feasibility, and ease of implementation. The two-degree-of-freedom digital RST controller is well suited to fill this gap. Its structure inherently decouples tracking from regulation, addressing PID’s core limitation and enabling systematic pole placement and sensitivity shaping. In practice, conservative pole placement provides strong robustness to moderate modeling errors and common disturbances such as grade and wind, while shaping the sensitivity function lets RST allocate robustness where it matters. At the same time, RST avoids the discontinuous, chattering control actions typical of sliding-mode control, delivering smooth actuator commands. Crucially, RST is implemented as simple difference equations with a small memory footprint and no online optimization, unlike MPC and some high-order $H_{\infty }$ realizations, which support straightforward deployment on automotive processors.

Although widely used in other high-performance applications, RST has not, to our knowledge, been designed and applied to vehicle platooning. Architecturally, most existing designs also fuse spacing logic into the low-level loop rather than separating spacing and velocity via a modular velocity-reference layer, and actuator saturation is often unmodeled or handled by clipping rather than with systematic anti-windup. Taken together, the benefits of vehicle platooning and persistent control gaps establish the central goal of this work.

1.3. Contributions

This work advances robust longitudinal control for Connected and Autonomous Vehicle (CAV) platoons by developing a design that leverages the platoon’s homogeneous and symmetrical structure. The key contributions are as follows:

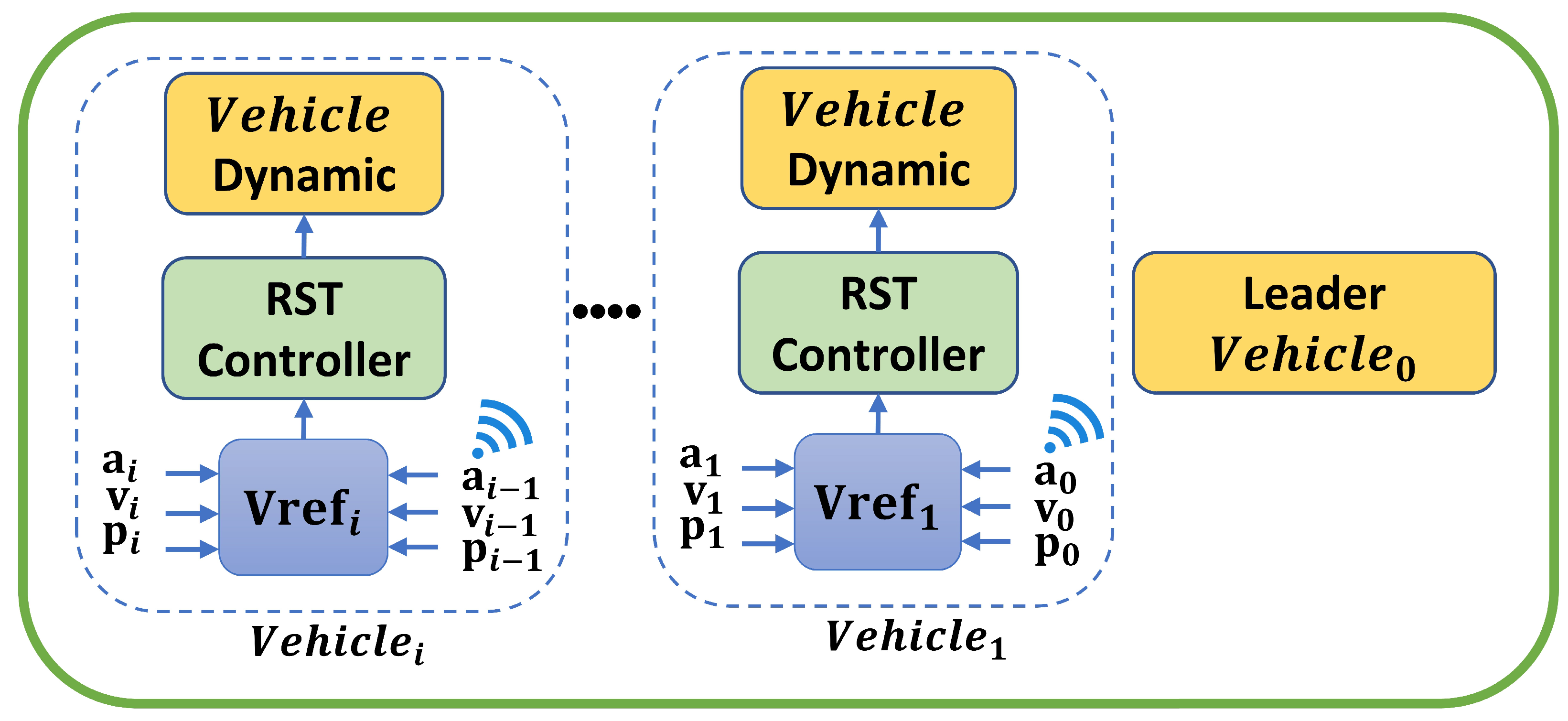
• We propose a fully decentralized two-layer platoon-control architecture that integrates modular velocity-reference generation with a two-degree-of-freedom (2-DOF) RST controller.
• We design a discrete-time two-degree-of-freedom (2-DOF) digital RST controller tailored to this symmetrical structure. Using pole placement and sensitivity shaping, the controller enables independent tuning of tracking and disturbance rejection while remaining lightweight for embedded implementation.
• We develop a stability analysis showing that the proposed architecture ensures internal stability and satisfies $L_2$ string stability under the constant time-headway policy.
• We provide a comparative analysis against another controller proposed in the literature. The proposed method achieves better tracking, faster recovery, and smoother actuation, demonstrating clear performance advantages.

These contributions advance the state of the art in robust digital control for vehicle platoons, offering a scalable, decentralized solution that ensures safety and performance under realistic operating conditions.

1.4. Organization

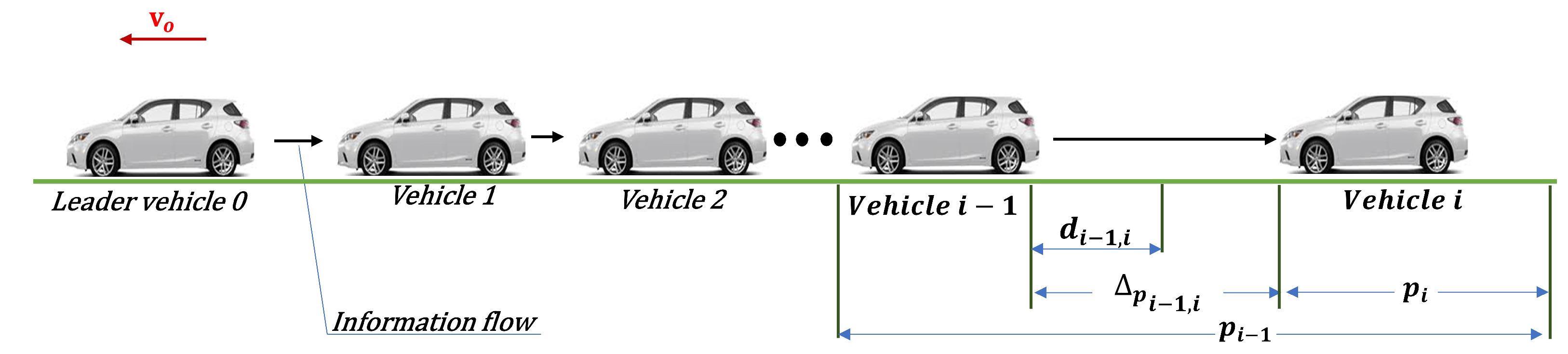
The remainder of the paper is organized as follows: Section 2 introduces the system model and control objectives. Section 3 details the velocity-reference generation. Section 4 presents the digital RST controller architecture, sensitivity functions, and design procedure. Section 5 applies the RST design to the vehicle model. Section 6 establishes internal and $L_2$ string stability. Section 7 presents numerical results and a comparison with a PD-based controller, and Section 8 concludes this paper.

2. System Model

A vehicle platoon refers to a coordinated string of connected and automated vehicles that travel together while maintaining a prescribed inter-vehicle spacing and synchronized velocity through communication and distributed control mechanisms. In this work, we consider a homogeneous platoon composed of $N+1$ Cooperative and Autonomous Vehicles (CAVs) moving along a straight and level road. The vehicle indexed by $i=0$ serves as the leader, while the vehicles indexed by $i=1,2,\dots ,N$ act as followers. The leader vehicle defines the desired velocity and trajectory of the platoon. Each follower adjusts its speed and position based solely on its own state and the state of its immediate predecessor, using decentralized control laws. Homogeneity implies structural symmetry in the platoon’s longitudinal dynamics and actuation characteristics. Each vehicle is modeled as a third-order linear time-invariant (LTI) system capturing position, velocity, and acceleration, with actuator lag included to reflect realistic dynamics. The state vector of the ith vehicle is defined by

$$x_i^{\top }\left(t\right)=\left[\begin{array}{ccc}{p}_i\left(t\right)& v_i\left(t\right)& a_i\left(t\right)\end{array}\right]$$

(1)

where $p_i\left(t\right)$, $v_i\left(t\right)$, and $a_i\left(t\right)$ denote the position, velocity, and acceleration of vehicle i, respectively. The continuous-time state-space model is given by

$${\dot{x}}_i\left(t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right),y_i\left(t\right)=C{x}_i\left(t\right)$$

(2)

with $u_i\left(t\right)\in \mathbb{R}$ representing the net propulsion or braking force.

The system matrices are

$$A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& -\frac{1}{\tau }\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ \frac{1}{\tau }\end{array}\right],C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$$

(3)

where $\tau >0$ denotes the actuator lag time constant. The corresponding open-loop transfer function from $u_i\left(t\right)$ to $p_i\left(t\right)$ is

$$G\left(s\right)={\displaystyle \frac{1}{s^2(\tau s+1)}}$$

(4)

The platoon follows a predecessor-following (PF) communication topology. Each follower accesses information only from its immediate predecessor. This communication structure is modeled by a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{0,1,\dots ,N\}$ is the set of nodes and $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ represents communication links. An edge $(i-1,i)\in \mathcal{E}$ signifies that vehicle i receives data from vehicle $i-1$, as shown in Figure 1.

Communication is assumed to be ideal, being free of delays and losses. The adjacency matrix $A\in {\mathbb{R}}^{(N+1)\times (N+1)}$ is

$$A=\left[\begin{array}{cccc}0& 0& \dots & 0\\ 1& 0& \dots & 0\\ 0& 1& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & 1\end{array}\right]$$

(5)

The control objective of the platoon operating under the predecessor-following (PF) topology is threefold: (i) to ensure that the velocity of each follower vehicle converges to that of the leader, (ii) to maintain a constant prescribed spacing from the immediate predecessor, and (iii) to guarantee $L_2$ string stability, ensuring that disturbances do not amplify as they propagate downstream. The first objective guarantees coordinated motion across the entire formation, while the second preserves the desired inter-vehicular gap for safety and traffic flow efficiency. The third objective ensures robustness of the platoon against disturbance amplification, which is critical for scalability.

In the absence of communication imperfections, the desired performance can be expressed as

$$\underset{t\to \infty }{lim}\left|v_{i-1}\left(t\right)-v_i\left(t\right)\right|=0,\forall i\in \{1,\dots ,N\}$$

(6)

$$\underset{t\to \infty }{lim}\left|p_{i-1}\left(t\right)-p_i\left(t\right)-d_s\left(t\right)\right|=0,\forall i\in \{1,\dots ,N\}$$

(7)

Here, $v_i\left(t\right)$ and $p_i\left(t\right)$ denote the longitudinal velocity and position of the ith follower, $v_{i-1}\left(t\right)$ and $p_{i-1}\left(t\right)$ refer to its immediate predecessor, and $d_s\left(t\right)$ is the desired spacing between vehicles $i-1$ and i. Together with the string-stability requirement:

$$\underset{\omega \in [0,\pi ]}{sup}\left|{\Gamma }_v\left(e^{j\omega }\right)\right|\le 1,\underset{\omega \to 0}{lim}\left|{\Gamma }_v\left(e^{j\omega }\right)\right|=1$$

(8)

where ${\Gamma }_v\left(z\right)={\displaystyle \frac{v_i\left(z\right)}{v_{i-1}\left(z\right)}}$ denotes the transfer of velocity from neighbor to neighbor.

To robustly fulfill the aforementioned control objectives in a fully decentralized manner, each follower vehicle adopts a two-layer control architecture, as illustrated in Figure 2.

• An Upper-Layer Velocity Reference Generation: This layer computes a desired velocity reference $V_{\mathrm{ref},i}\left(t\right)$ for each follower vehicle based on relative measurements of position, velocity, and acceleration with respect to its immediate predecessor. This design decouples the spacing policy from the underlying tracking control, resulting in a modular and flexible architecture that enables independent tuning of both spacing and velocity tracking performance.
• A Lower-Layer RST-Based Tracking and Regulation Control: A discrete-time, two-degree-of-freedom RST controller is implemented to track the velocity reference. This structure allows for independent tuning of regulation and tracking behavior by explicitly shaping the sensitivity functions. Proper shaping improves disturbance rejection, enhances robustness to modeling uncertainties and actuator lag, and ensures a favorable transient response throughout the platoon.

The proposed layered architecture enhances robustness against measurement noise, external disturbances, and dynamic uncertainties, while delivering high-fidelity tracking and stable inter-vehicle coordination across the entire platoon.

3. Velocity Reference Generation

Under the PF communication topology, each follower i constructs a local velocity reference from measurements of its immediate predecessor $(i-1)$. With the constant time headway (CTH) policy, the desired spacing is

$$d_s\left(t\right)=d_0+h{v}_i\left(t\right),d_0>0,h>0$$

(9)

where $d_0$ is the standstill distance and h is the headway time. We define the spacing and relative-velocity errors as

$$e_{p,i}\left(t\right)=p_{i-1}\left(t\right)-p_i\left(t\right)-\left(d_0+h{v}_i\left(t\right)\right)$$

(10)

$$e_{v,i}\left(t\right)=v_{i-1}\left(t\right)-v_i\left(t\right)$$

(11)

The velocity reference is computed as

$$v_{\mathrm{ref},i}\left(t\right)=v_{i-1}\left(t\right)+k_1{e}_{p,i}\left(t\right)+k_2{e}_{v,i}\left(t\right)+k_3{a}_{i-1}\left(t\right)-k_4{a}_i\left(t\right)$$

(12)

with gains $k_1,k_2,k_3,k_4\ge 0$. Gains $k_1$ and $k_2$ weight spacing regulation and speed matching, respectively. Gain $k_3$ scales the predecessor’s acceleration to provide anticipatory feedforward, enabling prompt response to upstream speed changes. Gain $k_4$ scales self-acceleration feedback to add damping, penalizing rapid changes in the follower’s acceleration (jerk). To ensure physical feasibility and safety, the commanded reference is saturated within operational bounds:

$$v_{\mathrm{ref},i}\left(t\right)=min\left\{V_{\mathrm{set}},max\left\{0,v_{\mathrm{ref},i}\left(t\right)\right\}\right\}$$

(13)

where $V_{\mathrm{set}}>0$ is the maximum allowable velocity. This formulation ensures coordinated and stable motion using only local measurements and predecessor information, consistent with the PF communication topology.

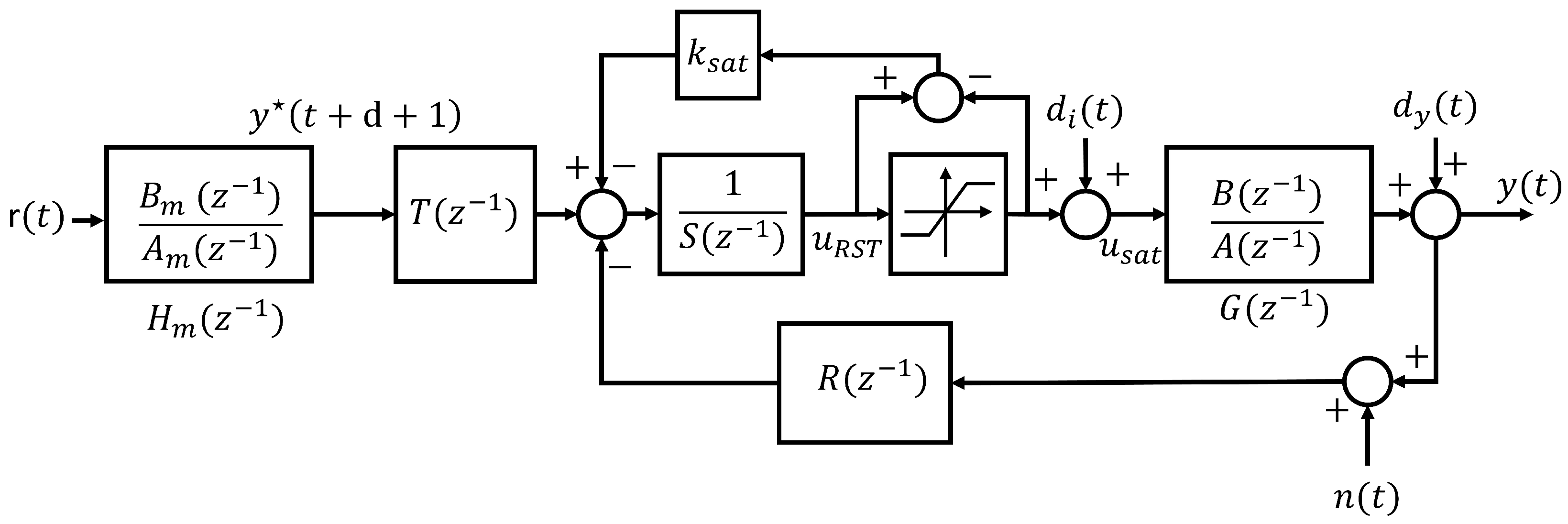
4. RST Digital Controller Design

4.1. RST Controller Architecture

The RST digital controller provides a structured and adaptable approach for designing discrete-time feedback control systems. In contrast to traditional PID controllers, which handle tracking and regulation within a single control loop, the RST structure is based on a two-degree-of-freedom (2DOF) configuration. This separation allows independent tuning of reference tracking and disturbance rejection, leading to improved transient behavior and better steady-state performance. The design is based on pole placement and sensitivity shaping, following the methodology introduced by Landau [34]. The control architecture, depicted in Figure 3, features the polynomials $R\left(z^{-1}\right)$, $S\left(z^{-1}\right)$, and $T\left(z^{-1}\right)$, which operate alongside the plant model $G\left(z^{-1}\right)$ and a reference model $H_m\left(z^{-1}\right)$ to shape the overall system response.

The direct implementation of the RST controller can generate control signals that exceed the actuator’s physical limits. To ensure that the actual control input remains within acceptable bounds $[u_{min},u_{max}]$, the control structure is augmented with an anti-windup mechanism. This mechanism introduces a corrective feedback term based on the difference between the saturated and unsaturated control signals, scaled by a gain $k_{\mathrm{sat}}$, effectively mitigating integrator windup and improving transient performance when saturation occurs [38].

The plant is modeled in discrete time as

$$G\left(z^{-1}\right)={\displaystyle \frac{z^{-d}B\left(z^{-1}\right)}{A\left(z^{-1}\right)}}$$

(14)

where $z^{-1}=e^{-s{T}_s}$ is the backward shift operator corresponding to the sampling period $T_s$. The parameter d is an integer with $d\ge 0$ and represents the number of discrete-time steps in the plant’s input delay. The polynomials $A\left(z^{-1}\right)$ and $B\left(z^{-1}\right)$ are defined as

$$\begin{array}{cc}\hfill A\left(z^{-1}\right)& =1+a_1{z}^{-1}+\cdots +a_{n_A}{z}^{-n_A}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill B\left(z^{-1}\right)& =b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_{n_B}{z}^{-n_B}\hfill \end{array}$$

(16)

Considering the plant model and controller polynomials, the open-loop transfer function is given by:

$$H_{OL}\left(z^{-1}\right)={\displaystyle \frac{z^{-d}B\left(z^{-1}\right)R\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)}}$$

(17)

The control law implemented by the RST controller, incorporating anti-windup compensation via back-calculation, is defined as

$$S\left(z^{-1}\right)u_{RST}\left(t\right)=T\left(z^{-1}\right)y*(t+d+1)-R\left(z^{-1}\right)y\left(t\right)-k_{\mathrm{sat}}\left(u_{RST}\left(t\right)-u_{\mathrm{sat}}\left(t\right)\right)$$

(18)

where $u_{RST}\left(t\right)$ is the unsaturated control input, $y\left(t\right)$ is the measured plant output, and $y*(t+d+1)$ is the one-step-ahead reference signal.

The reference model is defined as

$$\begin{array}{cc}\hfill H_m\left(z^{-1}\right)& ={\displaystyle \frac{B_m\left(z^{-1}\right)}{A_m\left(z^{-1}\right)}},y^{*}(t+d+1)=H_m\left(z^{-1}\right)r\left(t\right)\hfill \end{array}$$

(19)

where $r\left(t\right)$ is the external reference input.

The saturated control signal applied to the plant is

$$u_{\mathrm{sat}}\left(t\right)=\left\{\begin{array}{cc}{u}_{max},\hfill & \mathrm{if}{u}_{RST}\left(t\right)>u_{max}\hfill \\ u_{RST}\left(t\right),\hfill & \mathrm{if}{u}_{min}\le u_{RST}\left(t\right)\le u_{max}\hfill \\ u_{min},\hfill & \mathrm{if}{u}_{RST}\left(t\right)<u_{min}\hfill \end{array}\right.$$

(20)

The resulting closed-loop transfer function from the reference $y*\left(t\right)$ to the plant output $y\left(t\right)$ is

$$H_{CL}\left(z^{-1}\right)={\displaystyle \frac{T\left(z^{-1}\right)B\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+z^{-d}B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(21)

Define the closed-loop characteristic polynomial as

$$P\left(z^{-1}\right)=A\left(z^{-1}\right)S\left(z^{-1}\right)+z^{-d}B\left(z^{-1}\right)R\left(z^{-1}\right)=P_D\left(z^{-1}\right)·P_F\left(z^{-1}\right)$$

(22)

where $P_D\left(z^{-1}\right)$ represents the desired dominant closed-loop poles, and $P_F\left(z^{-1}\right)$ contains auxiliary poles used to shape the frequency response, reduce actuator effort, and enhance robustness.

The controller polynomials are defined as

$$\begin{array}{cc}\hfill R\left(z^{-1}\right)& =r_0+r_1{z}^{-1}+\dots +r_{n_R}{z}^{-n_R}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill S\left(z^{-1}\right)& =s_0+s_1{z}^{-1}+\dots +s_{n_S}{z}^{-n_S}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill T\left(z^{-1}\right)& =t_0+t_1{z}^{-1}+\dots +t_{n_T}{z}^{-n_T}\hfill \end{array}$$

(25)

To meet requirements such as disturbance rejection and elimination of steady-state error, selected factors of $R\left(z^{-1}\right)$ and $S\left(z^{-1}\right)$ are specified a priori. In particular, to guarantee zero steady-state error for step disturbances, $S\left(z^{-1}\right)$ is assigned the factor $(1-z^{-1})$. This yields the decomposition:

$$\begin{array}{cc}\hfill R\left(z^{-1}\right)& =R\prime \left(z^{-1}\right)H_R\left(z^{-1}\right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill S\left(z^{-1}\right)& =S\prime \left(z^{-1}\right)H_S\left(z^{-1}\right)\hfill \end{array}$$

(27)

where $H_R$ and $H_S$ are fixed polynomial components, and $R^{\prime }$, $S^{\prime }$ are to be computed. Substituting into Equation (22) yields the Bézout equation:

$$P\left(z^{-1}\right)=A\left(z^{-1}\right)H_S\left(z^{-1}\right)S\prime \left(z^{-1}\right)+z^{-d}B\left(z^{-1}\right)H_R\left(z^{-1}\right)R\prime \left(z^{-1}\right)$$

(28)

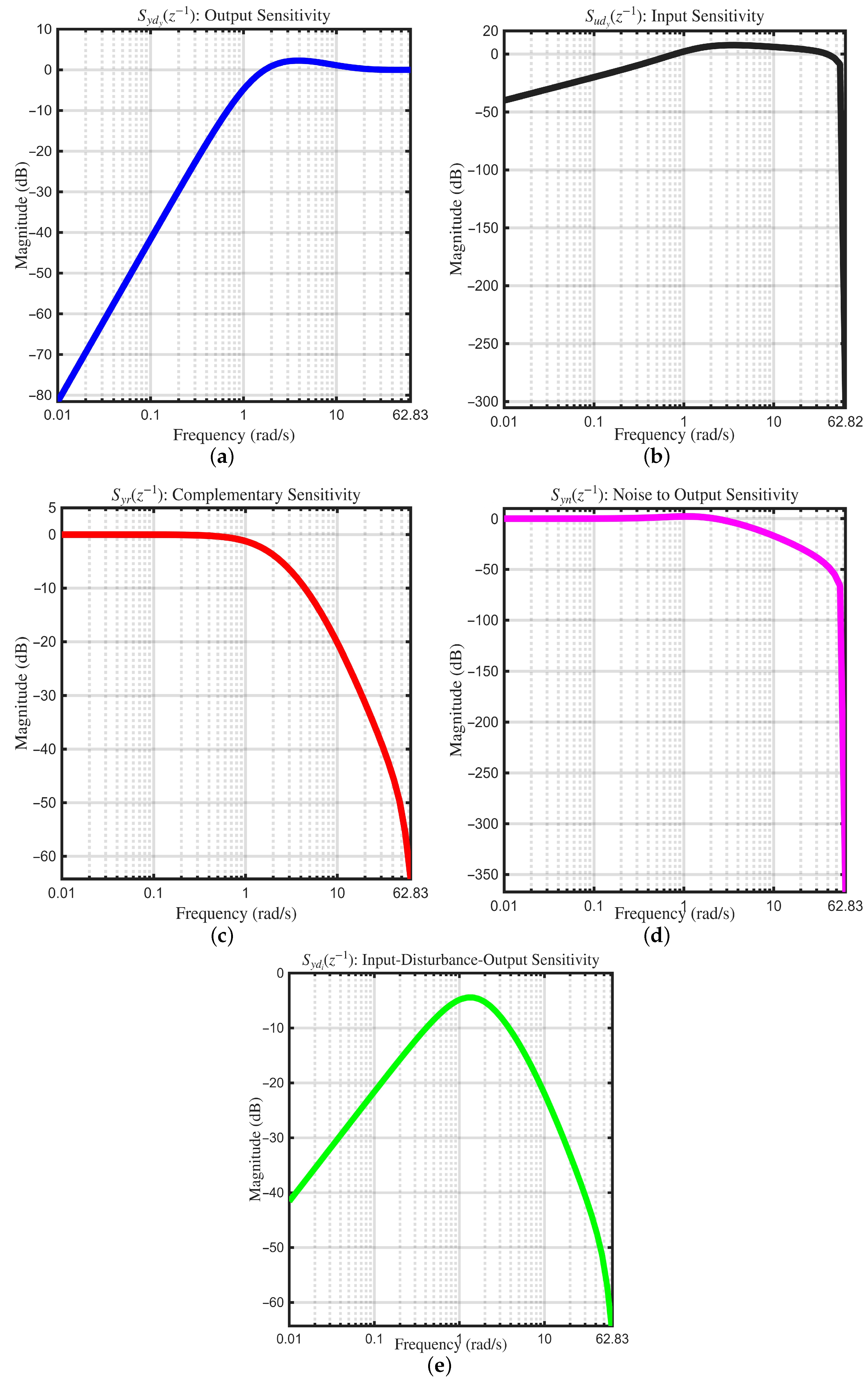
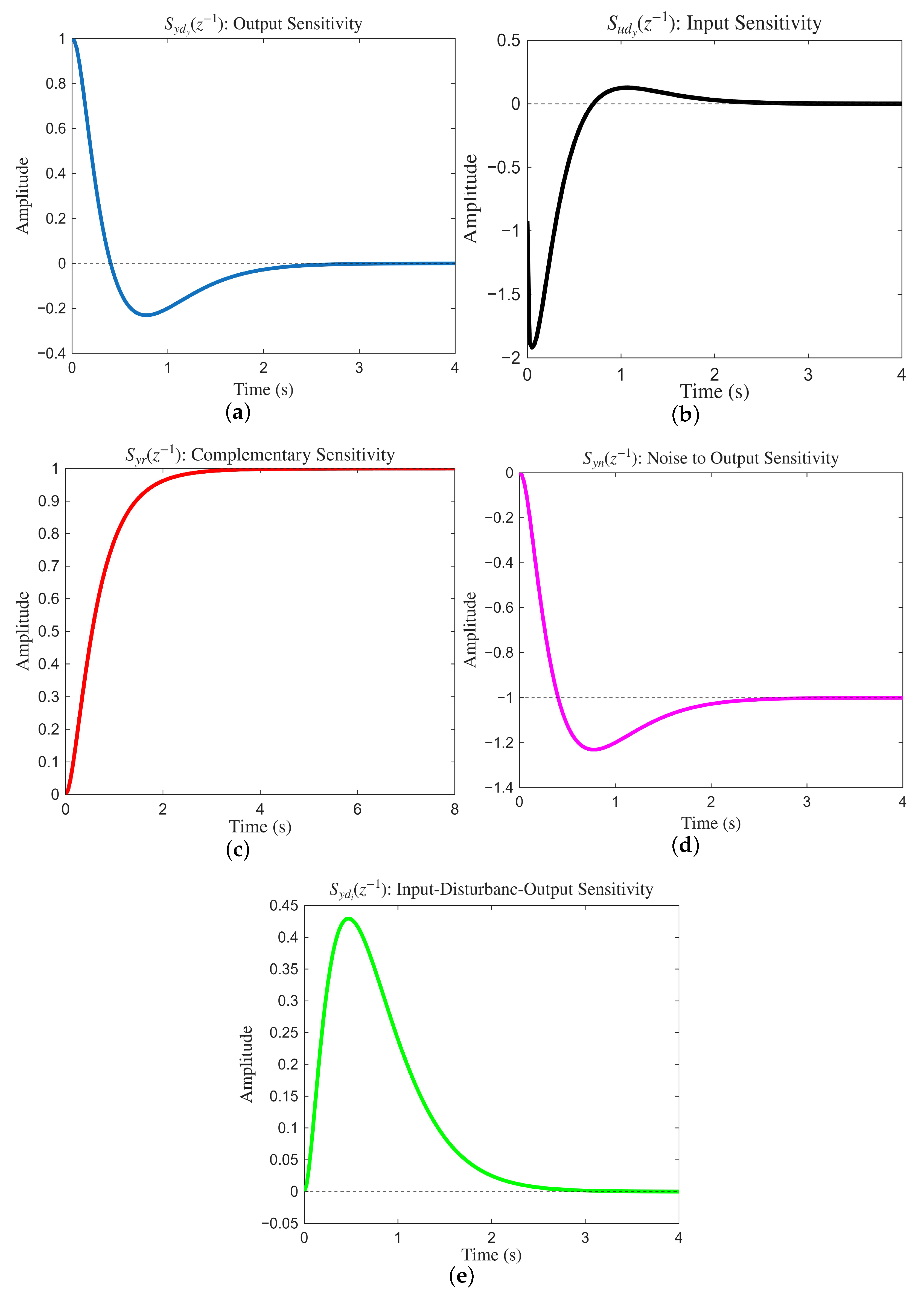
4.2. The Sensitivity Functions

The goal of the digital controller design is to find the polynomials $R\left(z^{-1}\right)$, $S\left(z^{-1}\right)$, and $T\left(z^{-1}\right)$ in order to obtain the closed-loop transfer functions, with respect to the reference and disturbance signals, satisfying the desired performance. In the presence of disturbances and noise (see Figure 3), there are five important sensitivity functions to consider, relating the disturbance and noise to the output and the input of the plant.

The transfer function from the output disturbance $d_y\left(t\right)$ to the system output $y\left(t\right)$, known as the output sensitivity function, is given by

$$S_{y{d}_y}\left(z^{-1}\right)={\displaystyle \frac{A\left(z^{-1}\right)S\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(29)

The transfer function from the output disturbance $d_y\left(t\right)$ to the plant input $u\left(t\right)$, referred to as the input sensitivity function, is given by

$$S_{u{d}_y}\left(z^{-1}\right)={\displaystyle \frac{-A\left(z^{-1}\right)R\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(30)

When measurement noise $n\left(t\right)$ is present in the system output, its impact on the plant output $y\left(t\right)$ can be analyzed using the noise-output sensitivity function, defined as

$$S_{yn}\left(z^{-1}\right)={\displaystyle \frac{-B\left(z^{-1}\right)R\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(31)

The transfer function from the reference input $r\left(t\right)$ to the output $y\left(t\right)$, known as the complementary sensitivity function, is given by

$$S_{yr}\left(z^{-1}\right)={\displaystyle \frac{B\left(z^{-1}\right)T\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(32)

Another relevant transfer function captures the effect of an input-side disturbance $d_i\left(t\right)$ on the output $y\left(t\right)$, referred to as the input-disturbance-output sensitivity function:

$$S_{y{d}_i}\left(z^{-1}\right)={\displaystyle \frac{B\left(z^{-1}\right)S\left(z^{-1}\right)}{A\left(z^{-1}\right)S\left(z^{-1}\right)+B\left(z^{-1}\right)R\left(z^{-1}\right)}}$$

(33)

4.3. Design Procedure for Pole Placement and Sensitivity Shaping

The RST controller design is carried out using a structured stepwise design procedure that combines pole placement with sensitivity-function shaping in order to guarantee robust performance. This procedure follows the methodology of Landau [8,34], in which the output and input sensitivity functions are shaped so that they satisfy prescribed robustness and control–effort constraints for specified sensitivity templates.

The main steps are as follows:

Initialize: Choose the dominant closed-loop poles $P_D\left(z^{-1}\right)$ and the fixed parts of $R\left(z^{-1}\right)$ and $S\left(z^{-1}\right)$ so that the nominal performance specifications are met.

Design loop:

• SOLVE: Compute the R–S controller polynomials by solving the Bézout Equation (28).
• Check: Evaluate the sensitivity functions $S_{y{d}_y}$ and $S_{u{d}_y}$, and verify whether they are consistent with their target robustness templates.
  • If yes→ Proceed to Finalization.
  • If no→ Identify the specific violation and apply the following correction rules:

    -

    Peak in $S_{y{d}_y}$ near the desired bandwidth → add complex zeros to $H_S$.

    -

    $S_{y{d}_y}$ too large at high frequencies → add real high-frequency poles to $P_F$.

    -

    Large $S_{u{d}_y}$ at frequencies where the plant gain is low → add complex zeros to $H_R$.

Return to Step 1 with the updated controller parameters.

Remark 1. 

The procedure is repeated until the sensitivity functions achieve an acceptable compromise with respect to the specified sensitivity templates and the overall performance and robustness requirements. Further details on the selection of the poles and zeros can be found in [8,34].

Finalize: Once the regulator (R-S) is found to meet all sensitivity specifications, design the prefilter $T\left(z^{-1}\right)$ to achieve the desired tracking response:

$$T\left(z^{-1}\right)=K_T{P}_D\left(z^{-1}\right)$$

(34)

with

$$K_T=\left\{\begin{array}{cc}{\displaystyle \frac{P_F\left(1\right)}{B\left(1\right)}},\hfill & \mathrm{if}B\left(1\right)\ne 0,\hfill \\ 1,\hfill & \mathrm{if}B\left(1\right)=0.\hfill \end{array}\right.$$

(35)

The prefilter T shapes the reference tracking response without affecting the regulation properties achieved by the R-S controller, completing the RST digital controller design.

5. RST Controller Design for Vehicle Platooning

The discrete-time vehicle model was obtained by discretizing the continuous-time transfer function in (4) using a Zero-Order Hold (ZOH) method, with actuator time constant $\tau =0.1\mathrm{s}$, sampling time $T_s=0.05\mathrm{s}$, and zero input delay $d=0$. The resulting polynomials are

$$A\left(z^{-1}\right)=1-1.6065z^{-1}+0.6065z^{-2}$$

(36)

$$B\left(z^{-1}\right)=0.0107z^{-1}+0.0090z^{-2}$$

(37)

The dominant closed-loop poles were selected to achieve the regulation dynamics: rise time $t_r=2.0$ s, natural frequency $f_n=0.254$ Hz, and damping ratio $\zeta =0.965$. The selection of damped $\zeta$ is critical for platoon control, as it eliminates overshoot, which is essential for safety, and guarantees the fastest non-oscillatory response. The chosen rise time of $t_r=2.0$ s represents an explicit engineering trade-off to balance rapid disturbance rejection with the necessity of generating smooth acceleration profiles for passenger comfort. This configuration ensures stable disturbance rejection and precise inter-vehicle spacing, while minimizing transient oscillations, reducing actuator workload, and enhancing both safety and energy efficiency.

The auxiliary poles were placed at $P_{F1}=0.912$ and $P_{F2}=0.723$. The placement of these auxiliary poles is chosen to reduce the peaks of the output sensitivity function and to reduce the peak of the input sensitivity function, thereby decreasing actuator stress and improving robustness margins.

For tracking dynamics, a slower response was selected to enhance passenger comfort and yield smoother, more fuel-efficient platoon operation. The reference model parameters were $t_r=2.5\mathrm{s}$, $f_n=0.319\mathrm{Hz}$, and  $\zeta =0.802$. This choice decouples tracking from regulation and deliberately makes the tracking response less aggressive than the vehicle-regulation dynamics, smoothing the velocity command to reduce peak control effort and jerk. The resulting polynomials are

$$A_m\left(z^{-1}\right)=1-1.8423z^{-1}+0.8516z^{-2}$$

(38)

$$B_m\left(z^{-1}\right)=0.0048z^{-1}+0.0045z^{-2}$$

(39)

The fixed parts of the controller were defined as

$$H_S\left(z^{-1}\right)=1-z^{-1}$$

(40)

which introduces an integrator to guarantee zero steady-state error for step disturbances, as well as

$$H_R\left(z^{-1}\right)=1+z^{-1}$$

(41)

which imposes a fixed real zero at $z=-1$ to reduce input sensitivity near the Nyquist frequency, thereby mitigating actuator excitation at high frequencies. The design process was guided by the following predefined sensitivity templates:

• Output Sensitivity Function $S_{y{d}_y}\left(z^{-1}\right)$:

  $$\parallel S_{y{d}_y}\left(e^{j\omega }\right){\parallel }_{\infty }<6\mathrm{dB},\forall \omega$$

  (42)

  to ensure adequate stability margins and robustness.
• Input Sensitivity Function $S_{u{d}_y}\left(z^{-1}\right)$:

  $$\parallel S_{u{d}_y}\left(e^{j\omega }\right){\parallel }_{\infty }\le 8\mathrm{dB},\forall \omega$$

  (43)

  to maintain control accelerations within $\pm 2.5{\mathrm{m}/\mathrm{s}}^2$ for passenger comfort.
• Complementary Sensitivity Function $S_{yr}\left(z^{-1}\right)$:

  $$\parallel S_{yr}\left(e^{j\omega }\right){\parallel }_{\infty }\le 3.5\mathrm{dB},\forall \omega$$

  (44)

to preserve stability and robustness margins in the tracking loop. Solving Equation (28) with the above specifications yielded the controller polynomials:

$$\begin{array}{cc}\hfill R\left(z^{-1}\right)& =0.9227-0.7766z^{-1}-0.9191z^{-2}+0.7802z^{-3}\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill S\left(z^{-1}\right)& =1-1.8902z^{-1}+0.9018z^{-2}-0.0116z^{-3}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill T\left(z^{-1}\right)& =1.2385-2.2934z^{-1}+1.0621z^{-2}\hfill \end{array}$$

(47)

The designed controller achieved modulus margin $\Delta M=0.7700$, gain margin $\Delta G=11.38$, phase margin $\Delta \Phi =54.{42}^{\circ }$, gain-crossover frequency ${\omega }_{\mathrm{CR}}=0.0967\mathrm{rad}/\mathrm{sample}$, and delay margin $9.8233$ samples ($0.4912\mathrm{s}$ at $T_s=0.05\mathrm{s}$). These values satisfy the standard robustness margins ($\Delta G\ge 2$, ${30}^{\circ }\le \Delta \Phi \le {60}^{\circ }$, $\Delta M\ge 0.5$, and $\Delta \tau \ge T_s$) from [34], indicating strong robustness to gain uncertainty, phase lag, and additional pure delay. The closed-loop performance resulting from this RST design was evaluated in the frequency domain. Figure 4 presents the five sensitivity functions, providing a comprehensive frequency-domain assessment of the RST-controlled system. The output sensitivity $S_{y{d}_y}\left(j\omega \right)$ (blue) shows strong low-frequency attenuation with a slight peak of about $2\mathrm{dB}$ near the 2–$3\mathrm{rad}/\mathrm{s}$ crossover, indicating effective disturbance rejection. The input sensitivity $S_{u{d}_y}\left(j\omega \right)$ (red) remains flat at low frequencies and smoothly attenuates, reflecting balanced control effort. The noise sensitivity $S_{yn}\left(j\omega \right)$ (black) achieves excellent high-frequency rejection, with magnitudes dropping below $-60\mathrm{dB}$ beyond $10\mathrm{rad}/\mathrm{s}$. The complementary sensitivity $S_{yr}\left(j\omega \right)$ (magenta) maintains near-$0\mathrm{dB}$ gain in the mid-frequency range, ensuring good reference tracking while suppressing high-frequency amplification. The plant disturbance transfer function $S_{y{d}_y}\left(j\omega \right)$ (green) exhibits a modest peak of about 0–$5\mathrm{dB}$ near crossover, consistent with practical designs and indicative of stable disturbance handling across the operational bandwidth.

6. Stability Analysis

This section presents the stability analysis conducted for the proposed platoon-control architecture. First, we examine the internal stability of the closed-loop vehicle dynamics under the RST controller. Then, we develop the string-stability analysis following established results from the $L_2$ string-stability framework, adapted to the proposed decentralized design.

6.1. Internal Stability Analysis

The internal stability of the closed-loop vehicle–RST system shown in Figure 3 is established by analyzing the sensitivity functions defined in Section 4.2. This analysis is included for completeness and to provide a clear link between the RST design procedure and the closed-loop properties of the proposed architecture.

The asymptotic internal stability of the system is maintained if and only if all sensitivity functions are asymptotically stable [34].

This stability condition follows directly from the fundamental property that, in an RST-controlled system, all closed-loop transfer functions, including the sensitivity functions, share the same characteristic denominator $P\left(z^{-1}\right)$. This polynomial is obtained by solving the Bézout Equation (28) within the pole placement method. In the proposed controller design, $P\left(z^{-1}\right)$ is explicitly constructed to be Schur, meaning that all of its roots lie strictly inside the unit circle. Consequently, each sensitivity function inherits the stable closed-loop poles defined by $P\left(z^{-1}\right)$ and is therefore asymptotically stable.

This stable behavior is illustrated in Figure 5, where the unit-step responses of the sensitivity functions exhibit bounded transients with finite overshoot and rapidly converge to steady-state values.

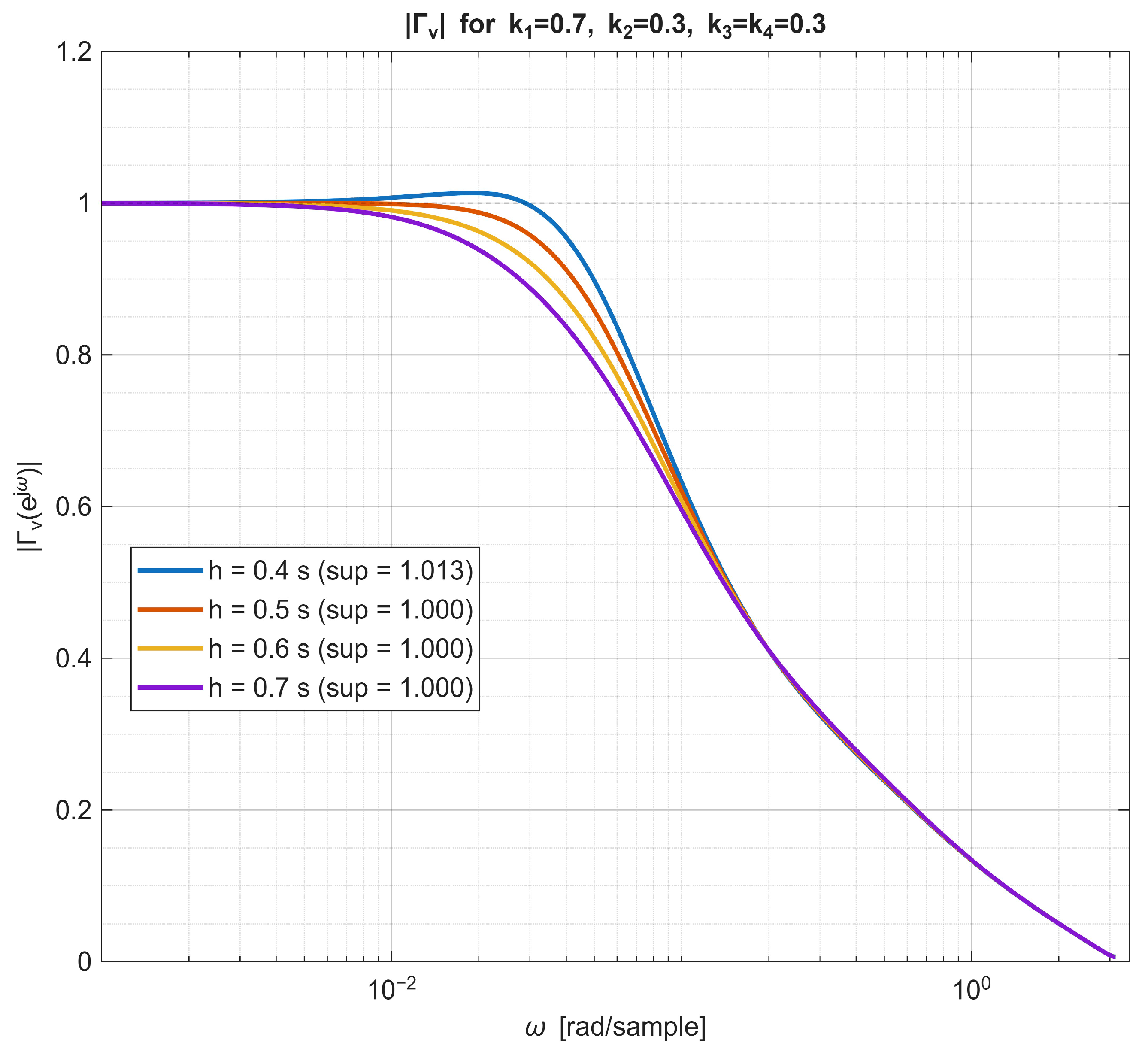
6.2. String-Stability Analysis

String stability is assessed using the $L_2$ framework of Ploeg et al. [11] for linear, unidirectional cascades, adapted here to the homogeneous predecessor-following (PF) topology. Let $P_i$ denote the leader-to-vehicle-i transfer, and define the string complementary sensitivity:

$${\Gamma }_i\left(s\right)=P_i\left(s\right)P_{i-1}{\left(s\right)}^{-1}.$$

(48)

A linear, unidirectional platoon is $L_2$ string-stable if the following are satisfied:

(i)

${\parallel P_1\left(j\omega \right)\parallel }_{\infty }$ exists;

(ii)

${\parallel {\Gamma }_i\left(j\omega \right)\parallel }_{\infty }\le 1$ for all $i\ge 2$.

In the scalar, homogeneous case, these conditions are also necessary for strict $L_2$ string stability [11]. The internal stability and causality of the closed-loop vehicle dynamics were established earlier, which implies that ${\parallel P_1\left(j\omega \right)\parallel }_{\infty }<\infty$ exists, satisfying Ploeg’s condition (i). Velocity is propagated along the string, i.e., $y_i=v_i$. The neighbor map is defined as

$${\Gamma }_v\left(z\right)={\displaystyle \frac{v_i\left(z\right)}{v_{i-1}\left(z\right)}}.$$

(49)

For the constant time headway (CTH) policy in Equation (10), the z-domain spacing error is

$$e_{p,i}\left(z\right)=I\left(z\right)\left(v_{i-1}\left(z\right)-v_i\left(z\right)\right)-h{v}_i\left(z\right),$$

(50)

where $I\left(z\right)={\displaystyle \frac{T_s{z}^{-1}}{1-z^{-1}}}$ is a discrete-time integrator. The velocity reference in the z-domain is

$$v_{\mathrm{ref},i}\left(z\right)=v_{i-1}\left(z\right)+k_1{e}_{p,i}\left(z\right)+k_2\left(v_{i-1}\left(z\right)-v_i\left(z\right)\right)+k_3{a}_{i-1}\left(z\right)-k_4{a}_i\left(z\right),$$

(51)

with $a_j\left(z\right)=\Delta \left(z\right)v_j\left(z\right)$ for $j\in \{i-1,i\}$, where $\Delta \left(z\right)={\displaystyle \frac{1-z^{-1}}{T_s}}$ is a discrete-time differentiator. Substituting $e_{p,i}\left(z\right)$ and $a_j\left(z\right)$ into Equation (51) and collecting the coefficients of $v_{i-1}$ and $v_i$ gives

$$v_{\mathrm{ref},i}\left(z\right)=\left(1+k_2+k_{1}I\left(z\right)+k_3\Delta \left(z\right)\right)v_{i-1}\left(z\right)-\left(k_{1}I\left(z\right)+k_{1}h+k_2+k_4\Delta \left(z\right)\right)v_i\left(z\right).$$

(52)

Let $H_{\mathrm{CL}}\left(z\right)$ denote the single-vehicle closed-loop transfer from $v_{\mathrm{ref},i}$ to $v_i$. Closing the loop via $v_i\left(z\right)=H_{\mathrm{CL}}\left(z\right)v_{\mathrm{ref},i}\left(z\right)$ and solving for $v_i/v_{i-1}$ yields the neighbor map

$${\Gamma }_v\left(z\right)={\displaystyle \frac{H_{\mathrm{CL}}\left(z\right)\left(1+k_2+k_{1}I\left(z\right)+k_3\Delta \left(z\right)\right)}{1+H_{\mathrm{CL}}\left(z\right)\left(k_{1}I\left(z\right)+k_{1}h+k_2+k_4\Delta \left(z\right)\right)}}.$$

(53)

Since the platoon is homogeneous and SISO, the structural symmetry of the system implies that every neighbor map is identical, so ${\Gamma }_i\left(z\right)={\Gamma }_v\left(z\right)$ for all $i\ge 2$. Evaluated on the unit circle $z=e^{j\omega }$ with $\omega \in [0,\pi ]$, condition (ii) reduces to the single ${\mathcal{H}}_{\infty }$ bound:

$${\parallel {\Gamma }_v\parallel }_{\infty }\le 1,{\parallel {\Gamma }_v\parallel }_{\infty }=\underset{\omega \in [0,\pi ]}{sup}\left|{\Gamma }_v\left(e^{j\omega }\right)\right|.$$

(54)

With appropriately chosen positive headway $h>0$ and appropriately chosen positive gains $k_1,k_2,k_3,k_4$, the condition in Equation (54) is satisfied.

Remark 2. 

On selection of gains $k_1,k_2,k_3,k_4$ for string stability.

For the closed-loop RST vehicle dynamics we have

$$\underset{\left|z\right|=1}{max}\left|H_{\mathrm{CL}}\left(z\right)\right|\approx 1,$$

(55)

thus, the neighbor transfer function in Equation (53) simplifies to

$${\Gamma }_v\left(z\right)\approx {\displaystyle \frac{1+k_2+k_{1}I\left(z\right)+k_3\Delta \left(z\right)}{1+k_{1}I\left(z\right)+k_{1}h+k_2+k_4\Delta \left(z\right)}}.$$

(56)

For a small sampling time $T_s$, the discrete-time system can be approximated in continuous time using the mappings $I\left(z\right)\approx 1/s$ and $\Delta \left(z\right)\approx s$, yielding

$${\Gamma }_v\left(s\right)\approx {\displaystyle \frac{k_3{s}^2+(1+k_2)s+k_1}{k_4{s}^2+(1+k_{1}h+k_2)s+k_1}}.$$

(57)

First, let $k_3=k_4=0$. The neighbor map then reduces to

$${\Gamma }_v\left(s\right)\approx {\displaystyle \frac{(1+k_2)s+k_1}{(1+k_{1}h+k_2)s+k_1}}.$$

We require $|{\Gamma }_v\left(\mathrm{j}\omega \right)|\le 1$ for all $\omega \ge 0$. As $\omega \to 0$,

$$\underset{\omega \to 0}{lim}\left|{\Gamma }_v\left(\mathrm{j}\omega \right)\right|=\left|{\displaystyle \frac{k_1}{k_1}}\right|=1,$$

confirming unity DC gain for any $k_1\ne 0$ with $k_1>0$ chosen for stability. As $\omega \to \infty$,

$$\underset{\omega \to \infty }{lim}\left|{\Gamma }_v\left(\mathrm{j}\omega \right)\right|=\left|{\displaystyle \frac{1+k_2}{1+k_{1}h+k_2}}\right|\le 1.$$

This condition is guaranteed if $h>0$, $k_1>0$, and $k_2\ge 0$.

Now, let $k_3,k_4>0$. Equation (57) can be rewritten as

$${\Gamma }_v\left(s\right)={\displaystyle \frac{k_3+{\displaystyle \frac{1+k_2}{s}}+{\displaystyle \frac{k_1}{s^2}}}{k_4+{\displaystyle \frac{1+k_{1}h+k_2}{s}}+{\displaystyle \frac{k_1}{s^2}}}}.$$

Then,

$$\underset{\omega \to \infty }{lim}\left|{\Gamma }_v\left(\mathrm{j}\omega \right)\right|=\left|{\displaystyle \frac{k_3}{k_4}}\right|\le 1,$$

which is ensured by $k_4\ge k_3\ge 0$.

Combined with the previously established conditions, a sufficient set of conditions for string stability is

$$h>0,k_1>0,k_2\ge 0,k_4\ge k_3\ge 0.$$

In practice, larger $k_1$ tightens spacing but may cause velocity overshoot and should be balanced by $k_2$, which smooths transients and improves speed matching but can make the control overly aggressive if too large. Likewise, larger $k_3$ speeds up the response to predecessor maneuvers but increases sensitivity to high-frequency noise, whereas larger $k_4$ attenuates such components and smooths the control input at the cost of a slower response. A practical tuning procedure is to first set $k_3=k_4=0$ and adjust $k_1$ and $k_2$ to achieve acceptable spacing and speed tracking. Then, $k_3$ and $k_4$ are increased jointly to enhance anticipatory behavior while maintaining smooth control action.

Figure 6 shows $\left|{\Gamma }_v\left(e^{j\omega }\right)\right|$ for $h\in \{0.4,0.5,0.6,0.7\}$ with $k_1=0.7$, $k_2=0.3$, $k_3=k_4=0.3$. For these gains, the minimum headway that satisfies the string-stability condition is $h=0.5\mathrm{s}$.

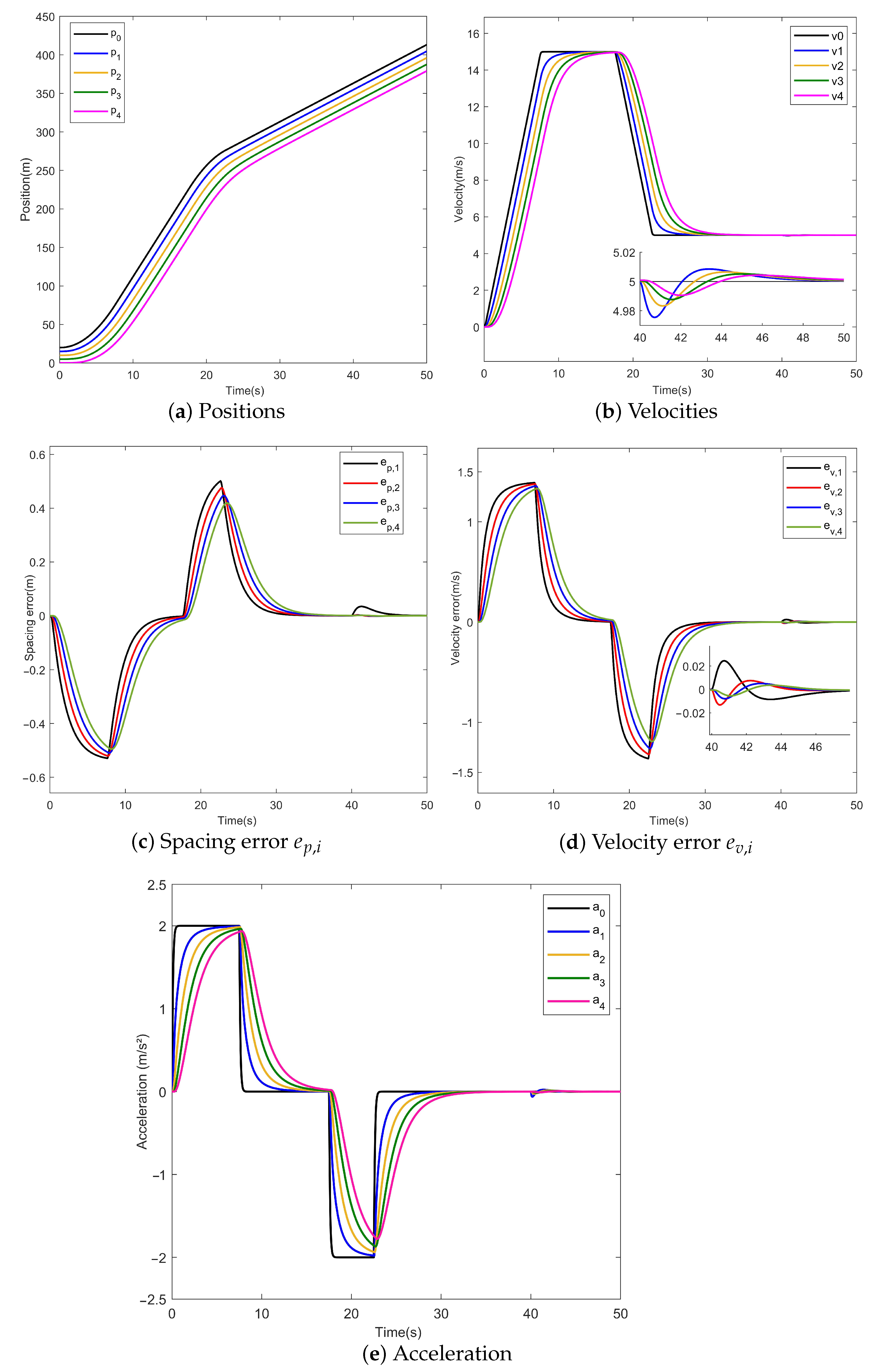
7. Numerical Results

This section presents numerical simulations to evaluate the effectiveness of the proposed platoon-control scheme. The test scenario, illustrated in (Figure 1), is a five-vehicle platoon with one leader and four followers traveling on a straight road. In addition, a simplified configuration with one leader and one follower is used to compare the proposed controller with a PD feedforward compensation controller developed in [20].

7.1. Simulation Setting

Simulations are conducted in MATLAB R2024b for 50 s on a PC with an Intel Core i7-3370 CPU, 16 GB RAM, and a 1 TB SSD. For the controller parameters, the upper-layer (velocity-reference) controller uses gains $k_1=0.7$, $k_2=0.3$, $k_3=0.3$, and $k_4=0.3$ under a CTH policy with standstill distance $d_0=5$ m and headway $h=0.7$ s. The lower-layer RST controller is described in Section 5. For anti-windup back-calculation, the gain is set to $k_{\mathrm{sat}}=1$, and the actuator command is saturated at $u\in [u_{min},u_{max}]=[-2,2]\mathrm{m}/{\mathrm{s}}^2$.

For the test scenario, the leader’s drive cycle consists of an acceleration from rest to 15 m/s, followed by braking and cruising at 5 m/s. Specifically,

$$v_0\left(t\right)=\left\{\begin{array}{cc}2t,\hfill & 0\le t<7.5\mathrm{s},\hfill \\ 15,\hfill & 7.5\le t<17.5\mathrm{s},\hfill \\ 15-2(t-17.5),\hfill & 17.5\le t<22.5\mathrm{s},\hfill \\ 5,\hfill & t\ge 22.5\mathrm{s},\hfill \end{array}\right.(\mathrm{m}/\mathrm{s}).$$

The platoon starts from rest with zero initial spacing and velocity errors. To test disturbance rejection, a step disturbance of magnitude $0.2$ is injected into the input of vehicle 1 at $t=40$ s.

7.2. Discussion

Under the PF topology with a constant time headway policy, $h=0.7\mathrm{s}$ and $d_0=5\mathrm{m}$, the proposed controller maintains vehicle ordering and safe gaps throughout the maneuver. The position profiles in Figure 7a confirm close leader-to-follower tracking without trajectory crossings, indicating that rear-end safety is maintained throughout the maneuver. Spacing errors $e_{p,i}$ in Figure 7c remain bounded during the accelerate-to-brake transient and decay toward zero, and peak magnitudes decrease monotonically with vehicle index. For vehicle 1, the maximum absolute spacing error equals $0.529\mathrm{m}$ at $t=7.6\mathrm{s}$. Sampling all followers at this time shows downstream attenuation of error propagation. After the step disturbance at $t=40\mathrm{s}$, the spacing error of vehicle 1 shows a small transient with amplitude less than $0.035\mathrm{m}$ and settles within about $2.9\mathrm{s}$. Velocity profiles and the corresponding errors are shown in Figure 7b and Figure 7d, respectively. The vehicles accelerate to $15\mathrm{m}/\mathrm{s}$, then decelerate and cruise at $5\mathrm{m}/\mathrm{s}$. The follower profiles closely track the leader without overshoot, and peak error magnitudes decrease downstream. Among the followers, the largest velocity-error magnitude during the transient occurs for vehicle 1. The extrema are $+1.391\mathrm{m}/\mathrm{s}$ at $t=7.5\mathrm{s}$ during acceleration and $-1.363\mathrm{m}/\mathrm{s}$ at $t=22.5\mathrm{s}$ during deceleration, with slightly smaller peaks downstream. The injected disturbance produces only a small, well-damped oscillation about $5\mathrm{m}/\mathrm{s}$ cruise speed with amplitude less than $0.03\mathrm{m}/\mathrm{s}$, and the error returns to zero within a few seconds. The disturbance settling time of $e_{v,1}$ is about $1.15\mathrm{s}$, while $e_{v,2}$, $e_{v,3}$, and $e_{v,4}$ settle immediately. Acceleration profiles in Figure 7e show that each follower closely tracks the leader, with responses bounded by $\pm 2.00{\mathrm{m}/\mathrm{s}}^2$ and with monotonic peak attenuation along the string. The disturbance produces a slight and rapidly vanishing perturbation, and vehicle 1 settles in $1.80\mathrm{s}$, after which the acceleration returns to zero.

The performance of the proposed controller is evaluated in a simplified one-leader, one-follower scenario and compared with the PD feedforward compensation controller developed in [20].

Table 1. Performance comparison of the proposed controller and the PD feedforward controller in [20].

Performance Metric	Proposed Controller	Work [20]
Overall Transient
Peak Position Error (m)	0.529	0.586
RMS Position Error (m)	0.228	0.307
Peak Velocity Error (m/s)	1.391	1.403
RMS Velocity Error (m/s)	0.628	0.724

summarizes the key performance metrics for both approaches. The proposed controller achieves smaller RMS position and velocity errors, with an RMS position error of 0.2288 m and an RMS velocity error of 0.628 m/s, whereas the PD controller yields 0.307 m and 0.724 m/s, respectively, indicating improved tracking.

In summary, the controller preserves safe inter-vehicle spacing without trajectory crossings, yields spacing and velocity errors that attenuate with vehicle index, and rejects a step disturbance with only minor and rapidly decaying transients, which is consistent with string-stable behavior across the platoon.

8. Conclusions

This paper demonstrates robust string stability in CAV platooning using a fully decentralized two-layer architecture with a predecessor-following topology and a constant time headway policy. The upper layer generates a smooth velocity reference from local V2V signals, while the lower layer employs a two-degree-of-freedom digital RST controller designed via pole placement with sensitivity-function shaping. The resulting closed loop achieves a phase margin of $54.4^{\circ }$, a modulus margin of $0.77$, and a delay margin of $0.49\mathrm{s}$, supporting real-time embedded implementation. The proposed closed-loop architecture ensures internal stability and $L_2$ string stability. Simulations confirm rapid recovery and attenuated error propagation. The first follower’s peak spacing error is $0.529\mathrm{m}$, which is about $3.4\%$ of the desired gap, and the error decays along the platoon. Under step disturbances, pre-settling deviations remain below $0.41\%$ for spacing and $0.6\%$ for velocity. The first follower’s velocity tracking settles in about $1.15\mathrm{s}$, after which all errors converge to zero. The approach is computationally lightweight, robust, and scalable, making it suitable for large platoons. Future work will incorporate realistic V2V and V2X effects, including time-varying delays and packet-loss heterogeneity, and a robust state observer. Further extensions include scheduled RST for nonlinear vehicle dynamics and consensus-based methods for distributed coordination in heterogeneous platoons.