Abstract
This paper considers the scheduling problem of uniform parallel machines. The objective is to minimize the makespan. This problem holds practical significance and is inherently NP-hard. Therefore, solutions of the exact formulation are limited to small-sized instances. As the problem size increases, the exact formulation struggles to find optimal solutions within a reasonable time. To address this challenge, an arc flow formulation is proposed, aiming to solve larger instances. The arc flow formulation creates a pseudo-polynomial number of variables, with its size being significantly influenced by the problem’s bounds. Therefore, bounds from the literature are utilized, and symmetry-breaking rules are applied to reduce the size of the arc flow graph. To test the effectiveness of the proposed arc flow formulation, it was compared with a mathematical formulation from the literature on small instances with up to 30 jobs. Computational results showed that the arc flow formulation outperforms the mathematical formulation from the literature, solving all cases within a few seconds. Additionally, on larger benchmark instances, the arc flow formulation solved 84.27% of the cases to optimality. The maximum optimality gap does not exceed 0.072% for the instances not solved to optimality.
1. Introduction
The manufacturing industry faces increasing pressure to optimize operations, reduce costs, and minimize environmental impact. Effective scheduling is crucial to addressing these challenges by optimizing resource allocation and production efficiency. Given the industry’s significant energy consumption [1], particularly in regions like China, where it accounts for approximately 70% of total emissions [2], scheduling also plays a vital role in enhancing energy efficiency.
This paper addresses the uniform parallel machine scheduling problem, aimed at minimizing makespan. This problem is denoted as Q||Cmax, in Graham’s three-field notation [3]. In the uniform parallel machine, a set of machines M = {1, 2, …, m, …, w}, which may differ in their processing speed vmm, is used to schedule a set of n independent jobs J = {1, 2, …, j, …, n}. The machines are ordered by increasing speed such that , where machine 1 is the slowest and machine w is the fastest.
Each job has a processing time, defined based on the slowest machine (i.e., machine 1). The jobs are ordered in non-increasing order of processing times, i.e., . The processing time of job j on machine m is then computed as
Accordingly, the machine speed can be computed from any job j, assuming j = 1, as
Alternatively, if the processing times pj are defined based on the fastest machine (i.e., machine w), the processing times of each job j on machine m can be expressed using a slowness factor , which represents how much slower machine m is compared to the fastest machine w. In this case,
Here, the slowness factor satisfies and .
Each job is assumed to be available at the beginning of scheduling, and no preemption is allowed.
Minimizing makespan in the Q||Cmax problem is a fundamental challenge in operations research with significant applications across various industries where machines have different processing capabilities [4]. Its inherent computational complexity classifies it as NP-hard [5], making the development of exact solution methods particularly challenging for solving larger problem sizes. While heuristic and metaheuristic approaches have been widely explored to obtain near-optimal solutions, the pursuit of exact algorithms remains crucial for obtaining provably optimal schedules. This paper develops an exact solution approach by proposing a novel adaptation of arc flow formulation, originally developed for the identical parallel machine scheduling problem [6,7], to address the uniform parallel machine scheduling problem. By leveraging the strengths of arc flow modeling, we aim to tackle the computational challenges associated with this NP-hard problem.
The following sections of this paper are as follows: Section 2 provides a review of the relevant literature on uniform parallel machine scheduling. The methodology proposed for solving the problem is detailed in Section 3. Section 4 discusses the computational results of the proposed approach. Finally, Section 5 provides a conclusion and suggestions for future work.
2. Literature Review
The scheduling problem of uniform parallel machines involves assigning a set of independent jobs to a group of parallel machines with different speeds to minimize the makespan. This problem is NP-hard [5], implying that achieving optimality for large-scale instances is computationally intractable. While heuristic and metaheuristic algorithms can produce solutions relatively quickly, their ability to guarantee optimal solutions is limited. Consequently, there is a continued need for an effective exact formulation capable of optimally solving larger problem instances.
The longest processing time (LPT) rule is a fundamental and simple heuristic for identical parallel machine scheduling. Introduced by Graham [8], it prioritizes jobs based on their longer processing times, assigning each job to the least loaded machine. For uniform parallel machines, the LPT rule is adapted to consider machine speeds. Jobs are sorted in descending order of processing times, and each job is assigned to a machine that completes it earlier [9].
Despite its simplicity, the LPT rule has limitations in terms of solution quality. For identical parallel machines, Graham [8] established a worst-case bound of 4/3 − 1/3w. Subsequent research by Della Croce and Scatamacchia [10] improved upon this bound to (4/3 − 1/(3(w − 1))) when the total number of machines . In the context of uniform machines, a worst-case bound for the adapted LPT rule is no more than twice the optimal solution, as demonstrated by Gonzalez et al. [9]. Friesen [11] improved the worst-case ratio to be within (1.52, 1.67). Moreover, other studies have investigated the LPT rule, resulting in various performance bounds for different machine configurations [12,13,14,15].
Beyond the LPT rule, various heuristics have addressed makespan minimization in uniform parallel machine scheduling. Li and Zhang [16] introduced the LPT-LRD rule, which prioritizes jobs based on a combination of the LPT rule and the largest release date. The authors further enhance the solution quality by developing a variable neighborhood search algorithm. Sivasankaran et al. [17] developed a heuristic method and assessed its efficiency against a mathematical model on small instances. Li and Yang [18] addressed the uniform parallel machine scheduling with heads and tails and a makespan objective, developing heuristic algorithms to solve it. De Giovanni et al. [19] focused on modifying the LPT rule and combined it with an iterated local search algorithm. Song et al. [20] extended the problem to a green manufacturing context, incorporating energy consumption constraints. They aimed to minimize two objectives, namely the makespan and the maximum job lateness, while adhering to an energy budget.
To obtain better solutions, metaheuristics often enhance heuristic solutions by exploring a wider solution space and escaping local optima, leading to improved overall performance. Senthilkumar and Narayanan [21] compared various genetic algorithms and simulated annealing approaches for the uniform parallel machine scheduling problem. Balin [22] studied the makespan minimization in non-identical parallel machine scheduling and introduced a genetic algorithm (GA), which was evaluated on a small-scale instance involving four machines and nine jobs. Building upon this work, Noman et al. [23] introduced a tabu search (TS) algorithm and compared its performance with Balin’s GA [22] using the same example. Recently, Bamatraf and Gharbi [24] introduced two variants of a variable neighborhood search (VNS) algorithm differentiated by their initial solution generation strategy for Q| |Cmax. The VNS algorithm was compared with the GA [22] and TS [23] algorithms from the literature, demonstrating competitive performance. Additionally, the two versions of the VNS algorithms were evaluated on randomly generated instances with larger problem sizes, comparing their performance to optimal solutions for smaller problems and a lower bound for larger ones. The results demonstrated that one version of the VNS achieved the optimal solutions for 90.19% of the small instances, with an average gap of approximately 0.15% compared to the lower bound for larger problem sizes.
As mentioned earlier, due to the NP-hard nature of the Q||Cmax scheduling problem, the development of exact algorithms is particularly challenging. However, it is still applied to achieve optimal solutions for small to medium-sized instances. As the problem size increases, the time required to obtain an optimal solution remains a computational challenge. Therefore, researchers attempt to develop exact algorithms capable of solving larger instances. Among the researchers who developed exact formulations for this problem, Horowitz and Sahni [25] employed dynamic programming followed by De and Morton’s [26] mathematical formulation and branch and bound algorithm, which was effective for small-scale instances. Liao and Lin [27] proposed an optimal algorithm for this problem with only two uniform parallel machines and tested it on instances with up to 1000 jobs. Building upon this, Lin and Liao [28] extended the optimal algorithm to be capable of solving multiple uniform parallel machines, incorporating techniques to identify quasi-optimal solutions, improve the lower bound, and accelerate the search process. Their algorithm was evaluated on instances with three to five machines and a maximum of 1000 jobs. Other researches include Popenko et al.’s [29] optimality sufficient condition, Berndt et al.’s [30] improved integer linear program (ILP) bounds for faster approximation algorithm, and Mallek and Boudhar’s [31] mixed-integer linear program (MILP) formulation for uniform parallel machines with conflict graphs. For further studies on parallel machine scheduling, consider exploring the works cited in references [32,33].
In recent years, an arc flow model that enables establishing pseudo-polynomial variables and constraints has emerged as a valuable tool for solving classical optimization problems. It has been successfully implemented in solving various optimization problems, such as a cutting stock problem [34], a bin packing problem [35], and a two-dimensional strip-cutting problem [36]. In the field of scheduling, the work of Mrad and Souayah [6] introduced an arc flow formulation for minimizing the makespan in identical parallel machine scheduling. Their proposed arc flow model significantly outperformed existing methods, efficiently solving the most challenging benchmark instances to optimality within seconds. However, the arc flow model struggles to achieve optimality for some instances within the time limit, particularly those with a relatively larger number of jobs and a job-to-machine ratio of at least 2.25. Recently, Gharbi and Bamatraf [7] improved the arc flow formulation presented by Mrad and Souayah [6] by proposing a variable neighborhood search algorithm to provide an upper bound, utilizing three lower bounds from existing literature, and applying a method to minimize the graph’s size. Computational results on the instances generated by Mrad and Souayah [6] showed the outperformance of the improved arc flow formulation over the arc flow formulation proposed by Mrad and Souayah [6] in finding the optimal solution for 99.97% of the instances and achieving an 87% reduction in CPU time. Other research on scheduling problems that applied arc flow formulation includes minimizing the total weighted completion time for the identical parallel machine scheduling [37], and it is extended to include release times [38]. Additionally, the arc flow formulation has been applied to single and parallel batch-processing machine scheduling with unequal sizes of jobs and capacities of machines [39,40].
From the literature, we have noticed that mathematical formulations such as the formulation proposed by De and Morton [26] for the Q||Cmax problem provide an optimal solution for small instances. As the problem size increases, this mathematical model struggles to find the optimal solution within a reasonable computational time due to the rapid growth of the number of variables and constraints. This scalability limitation highlights the need for an efficient mathematical formulation capable of solving larger instances.
To address this gap, this study extends the applicability of the arc flow formulation to the uniform parallel machine scheduling problem, aiming to improve scalability and solution efficiency. The proposed arc flow formulation applied tight bounds and symmetry-breaking rules to reduce the number of variables in the arc flow model, thereby enhancing scalability and allowing the arc flow formulation to solve larger instances efficiently.
Unlike the arc flow for identical parallel machine scheduling, where a single graph is constructed to represent all machines, the proposed arc flow model constructs a separate graph for each machine. In the proposed arc flow formulation, the bounds for the problem are utilized from the literature, and a novel arc reduction technique was proposed. This technique identifies the minimum completion time on each machine and prevents the creation of job arcs whose cumulative processing times are insufficient to reach this minimum completion time threshold.
The combination of this graph reduction technique, along with symmetry-breaking rules and the proposed bounds, allows for a reduction in the arcs of the constructed graph, thereby enhancing scalability and computational performance.
To summarize, the uniform parallel machine scheduling problem has many applications in industries. The proposed arc flow formulation offers solutions for optimizing resource allocation and minimizing the makespan. It also serves as a benchmark for evaluating the performance of heuristic and metaheuristic algorithms for real-world scheduling scenarios.
3. Research Methodology
To solve the uniform parallel machine scheduling problem with the makespan objective using an arc flow formulation, the following methodological steps are proposed:
- (1)
- Calculate the bounds of the problem.
- (2)
- Construct a graph for the arc flow model.
- (3)
- Develop a mathematical formulation for the constructed graph and present a mathematical formulation from the literature.
- (4)
- Implement the bounding algorithms and mathematical formulations using an optimization solver.
- (5)
- Validate the arc flow model on a numerical example
- (6)
- Evaluate the performance of the arc flow formulation against a mathematical formulation from the literature and a lower bound on randomly generated instances.
- (7)
- Analyze the computational results.
Efficient bounds play a crucial role in improving the performance of the arc flow model. This was obvious in the performance of the improved arc flow model proposed by Gharbi and Bamatraf [7] compared to the arc flow model proposed by Mrad and Souayah [6]. Therefore, in step 1, we calculate three lower bounds from the literature and select the best one. Additionally, the variable neighborhood search (VNS) algorithm proposed by Bamatraf and Gharbi [24] is utilized as an upper bound.
In the second step, a graph consisting of arcs and nodes is constructed, where each machine has its own graph. In these graphs, each arc represents the potential start and end times for jobs on each machine. In the arc flow graph, we provide symmetry-breaking rules and an equation to determine the minimum completion time for each machine, enabling us to further reduce the graph size by omitting arcs that end before this time.
Following this, in the third step, we provide the mathematical formulation of the arc flow model. Then we present a mathematical formulation from the literature [26] that is used to evaluate the performance of the arc flow model.
In the fourth step, the bounding algorithms and the mathematical formulation are implemented in C++ with the optimization library of Cplex 12.10.
In the fifth step, a numerical example is presented to illustrate and validate the graph construction process.
In the sixth step, the performance of the arc flow formulation is evaluated against the mathematical formulation by De and Morton [26] on small-sized problems with up to 30 jobs. For larger instances, we only test the performance of the arc flow formulation against the lower bound.
Finally, in the seventh step, an analysis of the computational results is presented and discussed.
The following subsections detail the lower bounds applied, the graph construction of the arc flow model, the mathematical formulations, and the numerical example.
3.1. Definition of the Problem Bounds
3.1.1. Lower Bounds
This paper utilizes three different lower bounds. The first lower bound (LB1) assumes the workload is balanced among all machines and is equal to the sum of the jobs’ processing times of the slowest machine () divided by the total speeds of the machines (), assuming the first machine to be the slowest. LB1 is illustrated as follows:
The other bound of the problem, denoted by LB2, represents the longest processing time required by a job when assigned to the fastest machine, as illustrated in Equation (5) as follows:
The third lower bound (LB3), as presented by Lin and Liao [28], is an attempt to improve LB1 using quasi-optimal allocations. The authors determined an upper bound (CLPT) from the LPT schedule. Then, they determined each machine’s maximum workloads () that limit the final job’s completion time to LB1, such that
After that, the authors identified the quasi-optimal solutions by assigning workloads to each machine without exceeding CLPT, such that
Then, they calculated the possible quasi-optimal solutions () as follows:
The improved lower bound was then found by sorting these solutions along with LB1 in increasing order and selecting the one at position Tp-WL, where WL is the total assigned workload.
From the above-mentioned lower bounds, the maximum lower bound is considered the best, as follows:
3.1.2. Upper Bound
Having established the lower bounds, we now turn our attention to the upper bound. This study employs the VNS algorithm, which was proposed by Bamatraf and Gharbi [24], as the upper bound. For reproducibility, we describe the VNS algorithm.
The VNS algorithm starts with an initial solution generated by the longest processing time (LPT) rule. The algorithm then iteratively explores five neighborhood structures to search for better solutions from the current best schedule. These neighborhood structures are applied to two sets of machines: problem machines S_pm (those with completion time equal to the makespan) and non-problem machines S_npm (the remaining machines).
These neighborhood structures are as follows:
- (1)
- Move: Move a job from a machine in S_pm to a machine in S_npm.
- (2)
- Exchange (1-1): Exchange one job from a machine in S_pm with one job from a machine in S_npm.
- (3)
- Exchange (2-1): Exchange two jobs from a machine in S_pm with one job from a machine in S_npm.
- (4)
- Exchange (1-2): Exchange one job from a machine in S_pm with two jobs from a machine in S_npm.
- (5)
- Exchange (2-2): Exchange two jobs from a machine in S_pm with two jobs from a machine in S_npm.
The proposed neighborhood structures attempt to alter the current schedule to reduce the completion time of problem machines. Starting from the first neighborhood structure (k = 1), if there is an improvement in makespan when applying a neighborhood structure, the makespan and both the problem and non-problem machines are updated, and the search restarts from the first neighborhood structure. However, if there is no improvement, the search proceeds to the next neighborhood structure (k + 1).
The algorithm terminates under three conditions: (1) it finds a solution with a makespan equal to the lower bound, (2) when no further improvements can be made by these neighborhood structures, (3) all machines have the same completion time. The steps of the VNS algorithm are presented in Algorithm 1, and for more details about the VNS algorithm, the reader is referred to the work of Bamatraf and Gharbi [24].
| Algorithm 1: VNS algorithm for uniform parallel machine scheduling. |
| Initialize: Maximum number of iterations (MaxIter)←1, Maximum number of neighborhood structures (kmax)←5, Best makespan (mksp), Best lower bound (LB), i←0, Upper bound (UB) For (i = 0; i < MaxIter; i++) do Generate an initial schedule (S) using the LPT rule and compute the makespan (Makspan(S)) mksp = Makespan(S) If (mksp = LB) Break. //Exit out of the loop “for(i = 0; i < MaxIter; i++)” Else: Create one list for machines with makespan equal makespan (S_pm[]) and another list for the remaining machines (S_npm[]). Initialize r←0 and q←0 While (r < size of S_pm & Makespan(S) ! = LB) do While (q < size of S_npm & Makespan(S) ! = LB) do Initialize: pm1 = S_pm[r], npm1 = S_npm[q], k = 0 While (k < kmax) do Apply neighborhood structure k for pm1 and npm1 to get a new schedule (S’) If (Makespn(S’) < Makespan(S)) Update: S←S’, S_pm[], S_npm[], and mksp = Makesapn(S) If (size of S_npm! = 0 & mksp! = LB) Initialize: r,q,k = 0, pm1 = S_pm[r], and npm1 = S_npm[q] Else: Break. //Exit out of the loop “While (k < kmax)” Else: k←k + 1 End-while q←q + 1 End-while r←r + 1 End-while End-for output: UB←mksp. |
3.2. Graph Construction
To create the graph of the arc flow model for minimizing the makespan in the uniform parallel machine scheduling problem (Q| |Cmax), a graph is established for each machine with several disjoint arcs for each job. The arcs A and vertices V define each graph G, G = (V, A). Each vertex represents the start or end time of a job, , whereas the set of arcs A is a combination of both job arcs (Aj), where j = {1,…,n}, and loss arcs (A0), i.e., . Each arc of a job j (Aj) represents the job starting and ending processing times at vertices v1 and v2, respectively. Therefore, the processing time for each job j on each machine m is pmj = v2 − v1. On the other hand, for each machine m, each loss arc (A0) starts from each candidate vertex to the vertex with the maximum completion time on that machine (MaxVm). The procedures for graph construction are illustrated in Algorithm 2 and visually explained in a flowchart in Figure 1.
| Algorithm 2: Graph construction for the arc flow model. |
| Initialize: V [0,…,w − 1][0,…UB], NewV [0,…,w − 1][], , , JobArcs, LossArcs and TotalArcs. For to do // Loop through each machine. V[m][0] MinV[m] End for CumP[n−1]p [0][n−1]; For down to do // Loop through jobs from index n−2 to index 0. CumP[j]CumP[j + 1]+p [0][j]; End for For to do For to do // Loop through each job. For to do // Loop through each added vertex. If(V[m][v]= 1 AND AND JobArcs End if End for For // Loop through the new vertices. End for End for End for For to do For to do If(V[m][v] = 1) End if End for End for For to do For to do // Loop through the vertices of the graph. If( End if End for End for |
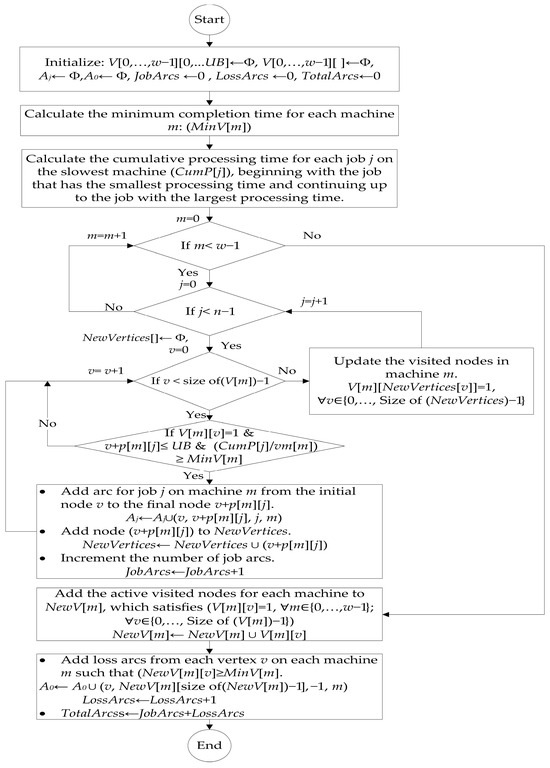
Figure 1.
Flowchart illustrating the graph construction for the arc flow model.
In constructing the graph, the job arcs and loss arcs are characterized by four terms, namely a starting time at vertex v1, an ending time at vertex v2, a job index j, and a machine index m, such that
The job arcs () were constructed by establishing a directed arc for each machine m that connects two vertices and given that if and does not exceed the upper bound, i.e., . These job arcs () can be reduced through several ways as follows:
- High-quality upper bound:
A tight upper bound obtained by the VNS algorithm proposed by Bamatraf and Gharbi [24] is used to limit the range of completion times, thereby preventing the establishment of job arcs that would exceed this bound. As a result, the number of vertices and arcs in a graph will be reduced, and the solver’s computational efficiency will be improved.
- 2.
- Symmetry-breaking rule:
To eliminate redundant solutions, symmetry-breaking rules are applied during graph construction. These symmetry-breaking rules, as proposed by Mrad and Souayah [6], are as follows:
- Jobs are listed from longest to shortest processing times.
- A job arc () is created only from vertex 0 or from vertices created by other jobs.
- 3.
- Minimum completion time on each machine:
In addition to the above symmetry-breaking rules, we propose a method to further reduce the number of job arcs and vertices of the graph by identifying the potential arcs of jobs to be established from each created vertex. This involves calculating the cumulative processing time for each job j on the slowest machine (denoted as CumPj), starting from the job with the minimum processing time and ending with the job with the maximum processing time.
Next, we determine the minimum completion time (MinVm) for each machine, ensuring that the lower bound of the remaining processing times on the remaining machines is no more than the upper bound. To find the minimum completion time (MinVm) for each machine m, we exclude that machine from the calculation of the lower bound (LB1) by subtracting its minimum completion time () and its speed from the total processing time (Tp) and the total speeds (Tvm), respectively. Thus, MinVm is the minimum value that makes the obtained lower bound not exceed the upper bound, as illustrated in the following equation:
Rearranging this equation, we get the following expression for MinVm:
Then, for each graph of a machine m, an arc of job j is established from vertex v1 if v1 is previously created on the graph, and the following equations are satisfied:
The loss arcs (A0) are only created from vertices between the vertex MinVm and the vertex immediately preceding the maximum vertex on each machine, directed toward the vertex with the maximum completion time on that machine.
3.3. Mathematical Formulation
This section introduces the mathematical formulation of the proposed arc flow model for Q| |Cmax and reviews the existing formulation by De and Morton [26] for the same scheduling environment.
3.3.1. Mathematical Formulation of the Arc Flow Model
To present a mathematical formulation for the graph of the arc flow model, Table 1 lists the parameters, sets, and decision variables used in the mathematical model. In the following sections, the arc flow formulation will be denoted as AF.

Table 1.
Sets, parameters, and decision variables of the arc flow model.
Objective function:
Constraints:
Equation (16) presents the makespan minimization objective. The constraint in Equation (17) ensures that the makespan () is at least as large as the completion time of the last job on any machine. Equation (18) ensures that each machine has an arc that starts from a vertex at time 0. The flow conservation constraint is shown in Equation (19). Equation (20) ensures that only one arc is selected for each job. The type of decision variables is presented in Equation (21). Equation (22) represents the bounds of the makespan.
3.3.2. Mathematical Formulation of De and Morton [26]
In this section, the mathematical formulation proposed by De and Morton [26] for the Q| |Cmax problem will be presented. In the following sections, the De and Morton [26] formulation will be denoted as D&M. This formulation serves as a benchmark for evaluating the effectiveness of the proposed arc flow formulation. Due to the NP-hard nature of the problem, the computational time for De and Morton’s mathematical formulation [26] grows rapidly even with medium-sized instances. Therefore, only small instances were solved by this formulation. The parameters and decision variables are listed in Table 2.

Table 2.
De and Morton’s Model [26] parameters, sets, and decision variables.
Objective function:
Constraints:
The makespan minimization objective is illustrated in Equation (23). This makespan, as presented in Equation (24), is at least the maximum of the sum of processing times of jobs on any machine. Equation (25) states that each job is scheduled on only one machine. The type of decision variables is illustrated in Equation (26).
Equation (27) is introduced to the mathematical formulation to provide a valid bound for the makespan.
3.4. Numerical Example
Consider 3 uniform parallel machines to be used to process 9 jobs. The speed of the machines, the time taken to process each job on every machine, and the cumulative processing times of jobs on the slowest machine (CumPj) are presented in Table 3.

Table 3.
Data of the numerical example.
The following steps illustrate the process of graph construction:
- Compute machine parameters.From Table 3,
- The total speed of machines (Tvm) = 1109/225.
- The sum of the slowest machine’s processing times (Tp) = 22,032.
- Determine lower and upper bounds.
- Equation (9) is applied to find the best lower bounds.
- The LPT rule obtains an upper bound of 4725, which the VNS algorithm improves to 4600. Therefore, UB = 4600.
- Calculate the minimum completion time for each machine.
- Using Equation (13), the minimum completion time for machine 1 is
- In the same manner, = 4069.85.
- = 4364.38
- Calculate the cumulative processing time.
The cumulative processing time for each job on the slowest machine (CumPj) is listed in Table 3.
- 5.
- Construct the graph for each machine.
- Initialize the first vertex v = 0 as visited in each machine to allow establishing arcs from that vertex.
- For each job and vertex in each machine, an arc is created if
- New vertices are added whenever a valid arc is established.
- 6.
- Constructing the graph for machine 1.
- Job 1: An arc is not added since v1 + p11 > UB.
- Job 2: An arc is added from vertex 0 to a new vertex 4080.
- Job 3: An arc is added only from vertex 0. However, from vertex 4080, the completion time exceeds the upper bound.visited vertices: V [1][] = {0, 4080}.
- Job 4: An arc is added only from vertex 0 to a new vertex 3264. → V [1][] = {0, 4080, 3264}.
- Job 5: An arc is added only from vertex 0 to a new vertex 2720.The remaining jobs cannot create arcs from vertex 0 since CumP[j] < .
- Job 6: An arc from vertex 2720 to vertex 4352.
- Job 7: Two arcs each from vertices 2720 and 3264 to 3808 and 4352, respectively.
- Jobs 8 and 9 have the same processing time, and two arcs can be created for each job from vertices 3808 and 4080 to vertices 4080 and 4352, respectively.
Thus, V [1][] = {0, 2720, 3260, 3808, 4080, and 4352}. Only one loss arc (dashed) can be created from vertex 4080 to vertex 4352 since v ≥ MinV[m]
The graph construction for machine 1 is shown in Figure 2.
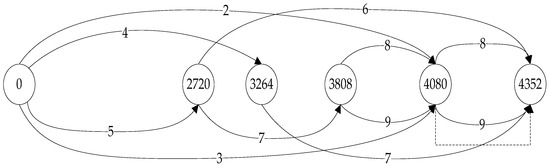
Figure 2.
Arc flow graph for machine 1.
- 7.
- Repeat for the remaining machines.
Similarly, the procedures were performed for machines 2 and 3, and the resulting graphs are shown in Figure 3 and Figure 4, respectively.
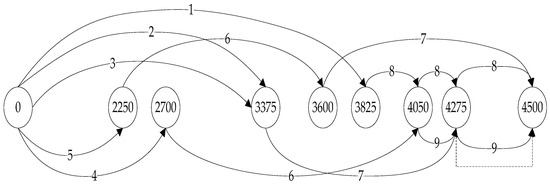
Figure 3.
Arc flow graph for machine 2.
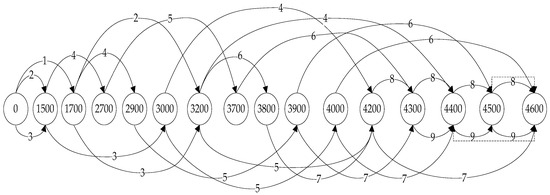
Figure 4.
Arc flow graph for machine 3.
- 8.
- Optimal solution.
- The arc flow formulation achieved an optimal solution of 4500.
The optimal arcs selected for both machines, with a machine name included for each arc, are shown combined in Figure 5. Furthermore, the Gantt chart schedule of the optimal solution is presented in Figure 6. It is worth noting that indexing starts from 1 for both jobs and machines to enhance the readability of the figures.
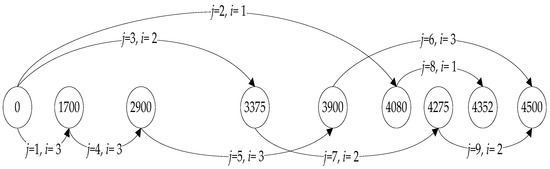
Figure 5.
Optimal solution of the arc flow model.
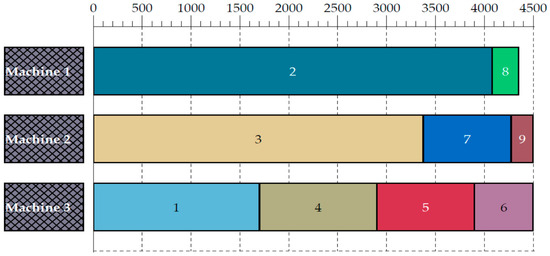
Figure 6.
Gantt chart schedule for the optimal solution.
4. Results and Discussion
The arc flow formulation and the mathematical formulation by De and Morton [26] were implemented in C++ with the optimization library of Cplex 12.10. We conducted the experiments using an Intel® Core i7-4930 k CPU @ 3.40 GHz and 32.0 GB of RAM. To evaluate the effectiveness of the proposed arc flow formulation, we tested it on a set of instances generated by Bamatraf and Gharbi [24]. To recap, the generated instances considered four key parameters:
- Total number of machines (w): Four sizes were selected: .
- Ratio of jobs () to machines (w), : Seven ratios were considered: .
- Processing time for each job (j) on the speediest machine (w), : A discrete uniform distribution, , is applied to generate the processing times with three levels for : .
- The slowness of each machine to the fastest machine : Generated with a uniform distribution with three levels for : . values were rounded to two decimal digits. For each combination of these parameters (), 10 instances were generated, for a total of 2520 instances.
In the following subsection, we first compare the arc flow model (AF) with the mathematical formulation proposed by De and Morton (D&M) [26]. For a fair comparison, both the proposed arc flow formulation and the De and Morton (D&M) formulation [26] were implemented under the same solver parameters and computational settings. The same lower and upper bounds were used in both cases. Moreover, the upper bound obtained by the VNS algorithm was provided as an MIP start to both formulations. No preprocessing steps were applied beyond the solver’s default setting. A time limit of 3600 s is set for both formulations as a termination condition. For the instances that are not solved to optimality within the time limit, the solver returns the best solution obtained so far along with the gap from the best lower bound. The comparison between the two mathematical formulations is limited to instances with a maximum of 30 jobs. We begin by comparing the number of optimal solutions. Next, we examine the gap for instances that do not reach optimality within the given time limit of 3600 s. Finally, we compare the CPU times for each mathematical formulation. Additionally, we present the results of the arc flow formulation for the remaining set of instances.
4.1. Comparison of the Arc Flow and De & Morton Formulations [26]
In this section, we conduct a comparative analysis of the proposed AF formulation and the D&M formulation [26]. Table 4 presents the number of optimal solutions achieved by each algorithm across various job and machine sets, as well as intervals of the slowness of machines and processing times.

Table 4.
The number of optimal solutions obtained by the AF and D&M mathematical formulations.
Table 4 clearly shows that the AF formulation achieves the optimal solution across all instances. In contrast, the D&M formulation finds the optimal solution only in cases with 20 jobs or fewer. For instances with more than 20 jobs, such as m = 10, n = 30 or m = 5, n = 25, the D&M formulation fails to reach optimality across all slowness and processing time intervals. In the case where m = 3, n = 30, with a ratio n/m = 10, the D&M formulation demonstrates better performance by achieving optimality in certain combinations of slowness and processing time intervals such as Sm ~ [1,3] with p ~ [1,25], and Sm ~ [1,7] with both p ~ [1,25] and p ~ [1,100]. Figure 7 illustrates the percentage of the average optimality gap for both the AF and D&M formulations across each interval of slowness and processing time. The figure shows that the AF formulation consistently achieves an average gap of 0%, while the average gap for the D&M formulation ranges from 0.008% to 0.067%. Although this gap is small, it highlights that D&M falls short of AF’s performance, particularly in instances with a larger number of jobs.
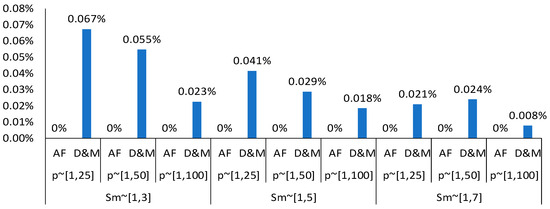
Figure 7.
Percentage of average optimality gap.
In addition to comparing the total optimal solutions achieved by the AF and D&M formulations and the average RPD, it is crucial to consider the computational efficiency of each approach. Table 5 illustrates the CPU time each formulation requires to reach the optimal solution, with a maximum time of 3600 s. If a formulation does not achieve the optimal solution within this time, it returns the best available solution.

Table 5.
Average CPU time for the AF and D&M mathematical formulations.
From Table 5, it is evident that for instances with fewer than 20 jobs, both formulations achieve the optimal solution in under a second, with the AF formulation slightly outperforming in most cases. However, for instances with 20 or more jobs, the time of D&M formulations increases significantly, especially in cases with ratios (n/w) of 3 and 5. In these instances, the D&M often reaches the maximum time limit without achieving optimality, as presented in the previous table (Table 4) of the number of optimal solutions obtained by the AF and D&M formulations.
The arc flow formulation demonstrates a significant advantage in terms of both consistency and efficiency as the problem size increases. Unlike the D&M formulation, which struggles and often reaches the maximum time limit. The arc flow formulation maintains a remarkable level of performance. Even in more challenging scenarios where the number of jobs is 20 or more and the ratios of n/m reach 3 or 5, the arc flow formulation efficiently solves every instance in less than 4 s. This consistent efficiency highlights the robustness of the arc flow approach, making it a preferable choice for large and complex problem instances where minimizing computational time is crucial. The overall average CPU time for every pair of slowness interval and processing time interval also demonstrates the superior performance of the arc flow formulation compared to the D&M formulation. The highest average computational time recorded for the AF formulation is less than 0.5 s, whereas the average CPU time for the D&M formulation ranges from 252.45 to 658.92 s. The average CPU time is presented graphically as shown in Figure 8.
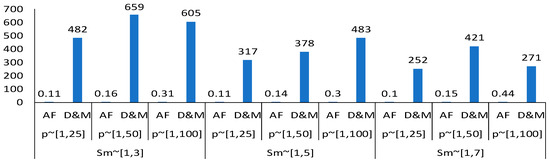
Figure 8.
Average CPU time for the AF and D&M formulations with instances with n 30.
Compared to the De & Morton formulation, the AF formulation showed outperformance and superior scalability, particularly in instances with a high job-to-machine ratio. Unlike the De & Morton formulation, which explicitly considers job-to-machine assignment and sequencing of jobs, leading to a rapid growth of variables and constraints as the problem size increases, the arc flow incorporates arc reduction techniques during graph construction. The combined use of an upper bound obtained by the VNS algorithm, symmetry-breaking rules, minimum completion time for each machine, and arranging jobs in descending order of processing times during graph construction, since the job order on each machine has no influence on makespan for the Q||Cmax problem, significantly reduced the number of variables and constraints. Furthermore, the tight lower and upper bounds narrow the search space of the solver. As a consequence, they improve pruning efficiency and reduce computational time.
Statistical Analysis of the AF and D&M Formulations
This section investigates the statistical significance of the average CPU time of the arc flow formulation against the D&M formulation. The tests were conducted on Minitab 18 statistical software. A normality test of the difference in average CPU times using a Kolmogorov–Smirnov test with a significance level resulted in a p-value < 0.010, indicating that the difference is not normal. Therefore, a one-sample Wilcoxon signed-rank test will be used with the following hypotheses:
H0: Median of differences in average CPU times (D&M-AF) = 0.
H1: Median of differences in average CPU times (D&M-AF) ≠ 0.
Results show that the Wilcoxon statistic = 7529.00 and p-value = 0.000, indicating a statistical significance in the average CPU time. The 95% confidence interval (0.215, 7.11) suggests that the AF has faster CPU time than the D&M formulation.
Since the D&M formulation struggled significantly with instances involving up to 30 jobs, often failing to find optimal solutions efficiently, whereas the proposed arc flow formulation demonstrates superior performance, it was deemed impractical to test this method for even larger problem sizes. Consequently, for instances with more than 30 jobs, we focused exclusively on the arc flow formulation, which had already demonstrated superior performance. This decision was made to ensure that our analysis remained focused on effective and practical solutions.
4.2. Performance of the Arc Flow Formulation for Larger Instances
The performance of the AF formulation for larger instances with more than 30 jobs is illustrated in this section. Table 6 presents the total optimal solutions achieved by the arc flow formulation and the percentage of solved instances for each combination of (Sm, p).

Table 6.
Number of optimal solutions obtained by the arc flow formulation.
From the results presented in Table 6, it is obvious that the arc flow formulation can optimally solve instances comprising up to 60 jobs across all combinations of slowness and processing time intervals. However, as both the total jobs and the ratio n/m increase, the efficiency of the AF formulation in solving all instances gradually declines. Out of a total of 360 instances for each ratio n/m = 20 and n/m = 30, the minimum number of solved instances occurs at a ratio of 30, with only 247 instances solved, compared to 300 instances solved when the ratio n/m = 20. The table also shows that, for each slowness interval, the total number of solved instances decreases as the interval of processing time increases, as also shown in Figure 9 with the decreased percentage of solved instances for each value of Sm as the processing time interval increases. The minimum number of solved instances occurs at the largest processing time interval, i.e., p ~ [1,100].
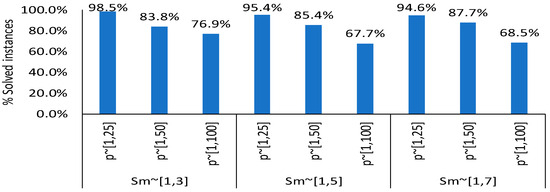
Figure 9.
Percentage of solved instances across combinations of (Sm, p).
The percentage of solved instances is 84.27%, which increases to 92.70% when considering both large and small instances together. Despite these limitations for unsolved instances, the AF formulation exhibits strong performance, with a maximum optimality gap of only 0.072% for unsolved instances.
Table 7 presents the average CPU time required by the AF formulation to solve the instances listed in Table 6. For the instances with up to 60 jobs, the average CPU time ranges from 0.33 to 56.17 s. The minimum average CPU time of 0.33 s is observed for the instance with w = 4, n = 40, Sm ~ [1,3], and p ~ [1,25]. In contrast, the maximum average CPU time of 56.17 s is recorded for the instance with w = 10, n = 50, Sm ~ [1,7], and p ~ [1,100].

Table 7.
The average CPU time for the arc flow formulation.
For the instances with more than 60 jobs, the average CPU time varies depending on whether all instances in each combination of w, n, Sm, and p are solved to optimality. When all instances in a combination are solved to optimality, the average CPU time ranges from 2.27 to 419.88 s. However, for combinations with at least one unsolved instance, the average CPU time increases significantly, reaching up to 3245.15 s. This occurs at n/w = 30 with w = 4, n = 120, Sm ~ [1,7], and p ~ [1,100]. This combination showed the worst performance due to only one instance being solved to optimality.
The overall average CPU time is presented in Figure 10, which shows that, for each speed interval, the overall average CPU time increases as the processing time interval expands.
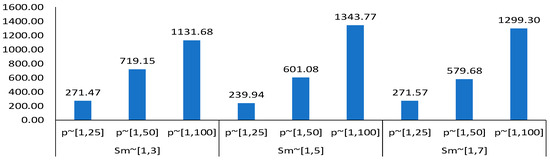
Figure 10.
Average CPU time for the arc flow with instances with n > 30.
5. Conclusions and Future Work
This paper proposes an arc flow formulation for makespan minimization in a uniform parallel machine scheduling problem. This problem is considered in the literature as an NP-hard problem. The proposed arc flow formulation incorporates a variable neighborhood search from the literature to provide an efficient upper bound, as well as symmetry-breaking rules to minimize the graph size when constructing the graph that is used in the arc flow formulation. The performance of the arc flow formulation is first evaluated against a well-known mathematical formulation from the literature on small instances with up to 30 jobs. Computational results demonstrate that the arc flow formulation outperforms the existing formulation in terms of both solution optimality and computational time. Moreover, the arc flow formulation is evaluated against a lower bound for larger instances with more than 30 jobs. According to the results, the arc flow formulation solves about 84.27% of the instances to optimality. The maximum optimality gap does not exceed 0.072% for the instances not solved to optimality.
Future work will focus on further improving the arc flow formulation by exploring additional symmetry-breaking rules. Another promising avenue is to consider multi-objective optimization, rather than focusing on a single scheduling criterion. Real-world scheduling problems often involve multiple, sometimes conflicting, objectives such as minimizing makespan, total completion time, and tardiness. Extending the current models to capture these trade-offs would provide more flexible and realistic decision support.
Author Contributions
Conceptualization, K.B. and A.G.; methodology, K.B. and A.G.; software, K.B.; validation, K.B. and A.G.; formal analysis, K.B. and A.G.; investigation, K.B. and A.G.; resources, K.B. and A.G.; data curation, K.B. and A.G.; writing—original draft preparation, K.B.; writing—review and editing, K.B. and A.G.; visualization, K.B. and A.G.; supervision, A.G.; project administration, A.G.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ongoing Research Funding program (ORF-2025-1039), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
The data are available upon request from the corresponding author.
Acknowledgments
The authors extend their appreciation to the Ongoing Research Funding program (ORF-2025-1039), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lee, J.-H.; Jang, H. Uniform parallel machine scheduling with dedicated machines, job splitting and setup resources. Sustainability 2019, 11, 7137. [Google Scholar] [CrossRef]
- Huang, J.; Wu, J.; Tang, Y.; Hao, Y. The influences of openness on China’s industrial CO2 intensity. Environ. Sci. Pollut. Res. 2020, 27, 15743–15757. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. In Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar]
- Li, K.; Leung, J.-T.; Cheng, B.-Y. An agent-based intelligent algorithm for uniform machine scheduling to minimize total completion time. Appl. Soft Comput. 2014, 25, 277–284. [Google Scholar] [CrossRef]
- Garey, M.R. Computers and Intractability: A Guide to the Theory of Np-Completeness; Freeman: San Francisco, CA, USA, 1979; Volume 174. [Google Scholar]
- Mrad, M.; Souayah, N. An arc-flow model for the makespan minimization problem on identical parallel machines. IEEE Access 2018, 6, 5300–5307. [Google Scholar] [CrossRef]
- Gharbi, A.; Bamatraf, K. An Improved Arc Flow Model with Enhanced Bounds for Minimizing the Makespan in Identical Parallel Machine Scheduling. Processes 2022, 10, 2293. [Google Scholar] [CrossRef]
- Graham, R.L. Bounds on multiprocessing timing anomalies. SIAM J. Appl. Math. 1969, 17, 416–429. [Google Scholar] [CrossRef]
- Gonzalez, T.; Ibarra, O.H.; Sahni, S. Bounds for LPT schedules on uniform processors. SIAM J. Comput. 1977, 6, 155–166. [Google Scholar] [CrossRef]
- Della Croce, F.; Scatamacchia, R. The longest processing time rule for identical parallel machines revisited. J. Sched. 2020, 23, 163–176. [Google Scholar] [CrossRef]
- Friesen, D.K. Tighter bounds for LPT scheduling on uniform processors. SIAM J. Comput. 1987, 16, 554–560. [Google Scholar] [CrossRef]
- Mireault, P.; Orlin, J.B.; Vohra, R.V. A parametric worst case analysis of the LPT heuristic for two uniform machines. Oper. Res. 1997, 45, 116–125. [Google Scholar] [CrossRef][Green Version]
- Koulamas, C.; Kyparisis, G.J. A modified LPT algorithm for the two uniform parallel machine makespan minimization problem. Eur. J. Oper. Res. 2009, 196, 61–68. [Google Scholar] [CrossRef]
- Massabò, I.; Paletta, G.; Ruiz-Torres, A.J. A note on longest processing time algorithms for the two uniform parallel machine makespan minimization problem. J. Sched. 2016, 19, 207–211. [Google Scholar] [CrossRef]
- Mitsunobu, T.; Suda, R.; Suppakitpaisarn, V. Worst-case analysis of LPT scheduling on a small number of non-identical processors. Inf. Process. Lett. 2024, 183, 106424. [Google Scholar] [CrossRef]
- Li, K.; Zhang, S.-c. Heuristics for uniform parallel machine scheduling problem with minimizing makespan. In Proceedings of the 2008 IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; pp. 273–278. [Google Scholar]
- Sivasankaran, P.; Ravi Kumar, M.; Senthilkumar, P.; Panneerselvam, R. Heuristic to minimize makespan in uniform parallel machines scheduling problem. Udyog Pragati 2009, 33, 1–15. [Google Scholar]
- Li, K.; Yang, S. Heuristic algorithms for scheduling on uniform parallel machines with heads and tails. J. Syst. Eng. Electron. 2011, 22, 462–467. [Google Scholar] [CrossRef]
- De Giovanni, D.; Ho, J.C.; Paletta, G.; Ruiz-Torres, A.J. Heuristics for Scheduling Uniform Machines. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, 14–16 March 2018. [Google Scholar]
- Song, J.; Miao, C.; Kong, F. Uniform-machine scheduling problems in green manufacturing system. Math. Found. Comput. 2024, 8, 689–700. [Google Scholar] [CrossRef]
- Senthilkumar, P.; Narayanan, S. GA Based Heuristic to Minimize Makespan in Single Machine Scheduling Problem with Uniform Parallel Machines. Intell. Inf. Manag. 2011, 3, 204–214. [Google Scholar] [CrossRef]
- Balin, S. Non-identical parallel machine scheduling using genetic algorithm. Expert Syst. Appl. 2011, 38, 6814–6821. [Google Scholar] [CrossRef]
- Noman, M.A.; Alatefi, M.; Al-Ahmari, A.M.; Ali, T. Tabu Search Algorithm Based on Lower Bound and Exact Algorithm Solutions for Minimizing the Makespan in Non-Identical Parallel Machines Scheduling. Math. Probl. Eng. 2021, 2021, 1856734. [Google Scholar] [CrossRef]
- Bamatraf, K.; Gharbi, A. Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling. Systems 2024, 12, 221. [Google Scholar] [CrossRef]
- Horowitz, E.; Sahni, S. Exact and approximate algorithms for scheduling nonidentical processors. J. ACM 1976, 23, 317–327. [Google Scholar] [CrossRef]
- De, P.; Morton, T.E. Scheduling to minimize makespan on unequal parallel processors. Decis. Sci. 1980, 11, 586–602. [Google Scholar] [CrossRef]
- Liao, C.-J.; Lin, C.-H. Makespan minimization for two uniform parallel machines. Int. J. Prod. Econ. 2003, 84, 205–213. [Google Scholar] [CrossRef]
- Lin, C.-H.; Liao, C.-J. Makespan minimization for multiple uniform machines. Comput. Ind. Eng. 2008, 54, 983–992. [Google Scholar] [CrossRef]
- Popenko, V.; Sperkach, M.; Zhdanova, O.; Kokosiński, Z. On Optimality Conditions for Job Scheduling on Uniform Parallel Machines. In Proceedings of the International Conference on Computer Science, Engineering and Education Applications, Sanya, China, 22–24 October 2019; pp. 103–112. [Google Scholar]
- Berndt, S.; Brinkop, H.; Jansen, K.; Mnich, M.; Stamm, T. New support size bounds for integer programming, applied to makespan minimization on uniformly related machines. arXiv 2023, arXiv:2305.08432. [Google Scholar] [CrossRef]
- Mallek, A.; Boudhar, M. Scheduling on uniform machines with a conflict graph: Complexity and resolution. Int. Trans. Oper. Res. 2024, 31, 863–888. [Google Scholar] [CrossRef]
- Mokotoff, E. Parallel machine scheduling problems: A survey. Asia-Pac. J. Oper. Res. 2001, 18, 193. [Google Scholar]
- Senthilkumar, P.; Narayanan, S. Literature review of single machine scheduling problem with uniform parallel machines. Intell. Inf. Manag. 2010, 2, 457–474. [Google Scholar] [CrossRef][Green Version]
- de Carvalho, J.V. Exact solution of cutting stock problems using column generation and branch-and-bound. Int. Trans. Oper. Res. 1998, 5, 35–44. [Google Scholar] [CrossRef]
- Valério de Carvalho, J. Exact solution of bin-packing problems using column generation and branch-and-bound. Ann. Oper. Res. 1999, 86, 629–659. [Google Scholar] [CrossRef]
- Mrad, M.; Alı, T.G.; Balma, A.; Gharbı, A.; Samhan, A.; Louly, M. The Two-Dimensional Strip Cutting Problem: Improved Results on Real-World Instances. Eurasia Proc. Educ. Soc. Sci. 2021, 22, 1–10. [Google Scholar] [CrossRef]
- Kramer, A.; Dell’Amico, M.; Iori, M. Enhanced arc-flow formulations to minimize weighted completion time on identical parallel machines. Eur. J. Oper. Res. 2019, 275, 67–79. [Google Scholar] [CrossRef]
- Kramer, A.; Dell’Amico, M.; Feillet, D.; Iori, M. Scheduling jobs with release dates on identical parallel machines by minimizing the total weighted completion time. Comput. Oper. Res. 2020, 123, 105018. [Google Scholar] [CrossRef]
- Trindade, R.S.; de Araújo, O.C.B.; Fampa, M. Arc-flow approach for single batch-processing machine scheduling. Comput. Oper. Res. 2021, 134, 105394. [Google Scholar] [CrossRef]
- Trindade, R.S.; de Araújo, O.C.; Fampa, M. Arc-flow approach for parallel batch processing machine scheduling with non-identical job sizes. In Proceedings of the International Symposium on Combinatorial Optimization, Montreal, QC, Canada, 4–6 May 2020; pp. 179–190. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).