Positive Periodic Solutions of Non-Autonomous Predator-Prey System with Stage-Structured Predator on Time Scales

Abstract

In this note, we investigate the existence and asymptotic property of positive periodic solutions to non-autonomous predator-prey system with stage-structured predator on time scales. Via Schauder’s fixed theorem, easily verifiable sufficient existence conditions of positive periodic solutions for the considered system are obtained. We also study asymptotic property of positive periodic solutions on the basis of existence conditions. Due to the symmetry of periodic solutions, the results of this paper have a certain impact on the study of symmetry. It should be pointed out that the system we are studying is built on arbitrary time scale, so our results generalize the results of existing continuous or discrete systems. Furthermore, we develop Schauder’s fixed theorem for studying the delay system on time scales.

1. Introduction

In 2011, Zeng [1] studied a predator-prey system with stage structure for predator on time scales as follows:

$$\begin{array}{cc}\hfill u_1^{\Delta }\left(t\right)& =r\left(t\right)-a\left(t\right)e^{u_1(t-\gamma \left(t\right))}-{\displaystyle \frac{b_1\left(t\right)e^{u_1\left(t\right)+u_2\left(t\right)}}{m^2\left(t\right)e^{2u_2\left(t\right)}+e^{2u_1\left(t\right)}}}-{\displaystyle \frac{b_2\left(t\right)e^{u_3\left(t\right)}}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)e^{u_1\left(t\right)}+{\alpha }_3\left(t\right)e^{u_3\left(t\right)}}}\hfill \\ \hfill u_2^{\Delta }\left(t\right)& ={\displaystyle \frac{c_1\left(t\right)e^{2u_1(t-\gamma \left(t\right))}}{m^2\left(t\right)e^{2u_2(t-\gamma \left(t\right))}+e^{2u_1(t-\gamma \left(t\right))}}}-d_1\left(t\right)-f\left(t\right)\hfill \\ \hfill u_3^{\Delta }\left(t\right)& =f\left(t\right)e^{u_2\left(t\right)-u_3\left(t\right)}+{\displaystyle \frac{c_2\left(t\right)e^{u_1(t-\gamma \left(t\right))}}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)e^{u_1(t-\gamma \left(t\right))}+{\alpha }_3\left(t\right)e^{u_3(t-\gamma \left(t\right))}}}-d_2\left(t\right),\hfill \end{array}$$

(1)

where $t\in \mathbb{T}$ which is a time scale. In [1], using Mawhin’s continuation theorem and inequality techniques, the authors obtained the existence of positive periodic solutions for system (1). Choose $\mathbb{T}=\mathbb{R}$. If we set $z_i\left(t\right)=exp\left(u_i\left(t\right)\right),i=1,2,3$, then system (1) reduces to

$$\begin{array}{cc}\hfill z_1^{\prime }\left(t\right)& =r\left(t\right)z_1\left(t\right)-a\left(t\right)z_1\left(t\right)z_1(t-\gamma \left(t\right))-{\displaystyle \frac{b_1\left(t\right)z_1^2\left(t\right)z_2\left(t\right)}{m^2\left(t\right)z_2^2\left(t\right)+z_1^2\left(t\right)}}-{\displaystyle \frac{b_2\left(t\right)z_1\left(t\right)z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1\left(t\right)+{\alpha }_3\left(t\right)z_3\left(t\right)}}\hfill \\ \hfill z_2^{\prime }\left(t\right)& =-[d_1\left(t\right)+f\left(t\right)]z_2\left(t\right)+{\displaystyle \frac{c_1\left(t\right)z_1^2(t-\gamma \left(t\right))z_2\left(t\right)}{m^2\left(t\right)z_2^2(t-\gamma \left(t\right))+z_1^2(t-\gamma \left(t\right))}}\hfill \\ \hfill z_3^{\prime }\left(t\right)& =-d_2\left(t\right)z_3\left(t\right)+f\left(t\right)z_2\left(t\right)+{\displaystyle \frac{c_2\left(t\right)z_1(t-\gamma \left(t\right))z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1(t-\gamma \left(t\right))+{\alpha }_3\left(t\right)z_3(t-\gamma \left(t\right))}}.\hfill \end{array}$$

(2)

We find that if system (1) exists a periodic solution $u_i\left(t\right)$, then system (2) exists a periodic solution $z_i\left(t\right)=exp\left(u_i\left(t\right)\right),i=1,2,3$. However, the positive periodic solution of system (2) is represented by e exponential functions, not general positive functions. A natural question is how to obtain the general form of the positive periodic solution for system (2)? Therefore, this paper is aim to study the following predator-prey system with stage-structured predator on time scales:

$$\begin{array}{cc}\hfill z_1^{\Delta }\left(t\right)& =r\left(t\right)z_1\left(\sigma \left(t\right)\right)-a\left(t\right)z_1\left(t\right)z_1(t-\gamma \left(t\right))-{\displaystyle \frac{b_1\left(t\right)z_1^2\left(t\right)z_2\left(t\right)}{m^2\left(t\right)z_2^2\left(t\right)+z_1^2\left(t\right)}}-{\displaystyle \frac{b_2\left(t\right)z_1\left(t\right)z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1\left(t\right)+{\alpha }_3\left(t\right)z_3\left(t\right)}}\hfill \\ \hfill z_2^{\Delta }\left(t\right)& =-[d_1\left(t\right)+f\left(t\right)]z_2\left(\sigma \left(t\right)\right)+{\displaystyle \frac{c_1\left(t\right)z_1^2(t-\gamma \left(t\right))z_2\left(t\right)}{m^2\left(t\right)z_2^2(t-\gamma \left(t\right))+z_1^2(t-\gamma \left(t\right))}}\hfill \\ \hfill z_3^{\Delta }\left(t\right)& =-d_2\left(t\right)z_3\left(\sigma \left(t\right)\right)+f\left(t\right)z_2\left(t\right)+{\displaystyle \frac{c_2\left(t\right)z_1(t-\gamma \left(t\right))z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1(t-\gamma \left(t\right))+{\alpha }_3\left(t\right)z_3(t-\gamma \left(t\right))}},\hfill \end{array}$$

(3)

where $t\in \mathbb{T}$ which is a periodic time sale (see Definitions 3 and 4), $\Delta$ is the delta (or Hilger) derivative, all the parameters are rd-continuous positive $\omega -$periodic functions, the delay $\gamma :\mathbb{T}\to {\mathbb{T}}^{+}={[0,\infty )}_{\mathbb{T}}$ is rd-continuous $\omega -$periodic function. $z_1,z_2$ and $z_3$ denote the densities of prey, immature and mature predators, respectively; r denotes the prey intrinsic growth rate; ${\displaystyle \frac{r}{a}}$ is the carrying capacity of the prey; $b_i,c_i$ and $d_i$ denote the capture rate, the conversion rate and the death rate of immature and mature predators, respectively, where $i=1,2$; m denotes half capturing saturation; f is the transformation of juveniles to adults; ${\displaystyle \frac{b_1\left(t\right)z_1^2\left(t\right)z_2\left(t\right)}{m^2\left(t\right)z_2^2\left(t\right)+z_1^2\left(t\right)}}$ is called Holling III functional response; ${\displaystyle \frac{b_2\left(t\right)z_1\left(t\right)z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1\left(t\right)+{\alpha }_3\left(t\right)z_3\left(t\right)}}$ stands for Beddington-DeAngelis response. Obviously, for $\mathbb{T}=\mathbb{R}$, if system (3) exists a positive periodic solution $z\left(t\right)={(z_1\left(t\right),z_2\left(t\right),z_3\left(t\right))}^T$, then system (1) exists a positive periodic solution $u\left(t\right)={(ln{z}_1\left(t\right),ln{z}_2\left(t\right),ln{z}_3\left(t\right))}^T$.

Generally, the continuity theorem based on Gaines and Mawhin’ coincidence degree theory can easily obtain the existence of periodic solutions to system (3), but cannot conveniently obtain the existence of positive periodic solutions. This paper is devoted to study the existence of positive periodic solutions to system (3) by using Schauder’s fixed theorem.

In the previous works, many researchers deal with the existence of periodic solutions to continuous or discrete predator-prey systems. In [2], based on the bifurcation theory and the slow-fast analysis method, the authors explored the existence and the equilibrium of the autonomous predator-prey model. For predator-prey systems with Holling functional response, see [3,4,5,6]; for predator-prey systems with Beddington-DeAngelis response, see [7,8,9,10,11]; for predator-prey systems with stage-structure, see [12,13,14,15,16]. In recent years, the predator-prey systems on time scales have been concerned by many authors, see [17,18,19,20,21].

The main contributions of this paper are listed as follows:

(1)

We first consider a predator-prey system with stage-structured predator on time scales and obtain the existence of positive periodic solutions which are general positive functions, which is different from corresponding ones in [1].

(2)

We develop Schauder’s fixed-point theorem for investigating dynamic systems on time scales.

(3)

System (3) unifies discrete and continuous systems which can improve and generalize the existing results.

The remaining structure of the paper are organized as follows: Section 2 gives the basic definitions and theories for time scales. In Section 3, some existence results of positive periodic solution of system (3) are given. In Section 4 we examines asymptotic property of system (3). Section 5 contains an example for verifying the main results. Finally, we provide some conclusions.

2. Preliminaries

A time scale $\mathbb{T}$ is a nonempty closed subset of $\mathbb{R}.$ The specific meanings of the following symbols can be found in book [22]: backward jump operator $\rho$, the forward jump operator $\sigma$ and the graininess function $\mu \left(t\right)$. A function $f:\mathbb{T}\to \mathbb{R}$ is regressive if $1+\mu \left(t\right)f\left(t\right)\ne 0$ for all $t\in {\mathbb{T}}^k$ holds. The set of regressive and rd-continuous functions f is denoted by $\mathcal{R}(\mathbb{T},\mathbb{R})$. A function $f:\mathbb{T}\to \mathbb{R}$ is positive regressive if $1+\mu \left(t\right)f\left(t\right)>0$ for all $t\in {\mathbb{T}}^k$ holds. The set of positive regressive and rd-continuous functions f is denoted by ${\mathcal{R}}^{+}(\mathbb{T},\mathbb{R})$. The interval ${[x,y]}_{\mathbb{T}}$ means $[x,y]\cap \mathbb{T}$. The intervals ${(x,y]}_{\mathbb{T}},{(x,y)}_{\mathbb{T}}$ and ${[x,y)}_{\mathbb{T}}$ are defined similarly. $C_{rd}\left({[a,\infty )}_{\mathbb{T}}\right)$ denotes the set of all rd-continuous functions on ${[a,\infty )}_{\mathbb{T}}$. For $s,t\in \mathbb{T}$, the exponential function $e_{\delta }(t,s)$ is defined by $e_{\delta }(t,s)=exp\left({\int }_s^t{\xi }_{\mu \left(\tau \right)}\left(\delta \left(\tau \right)\right)\Delta \tau \right)$, where

$${\xi }_{\mu \left(\tau \right)}\left(\delta \left(\tau \right)\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\mu \left(\tau \right)}}Log(1+\mu \left(\tau \right)\delta \left(\tau \right)),\mu \left(\tau \right)>0,\hfill \\ \delta \left(\tau \right),\mu \left(\tau \right)=0.\hfill \end{array}\right.$$

Lemma 1

([22]). Let $\varphi ,\psi \in \mathcal{R}.$ Then

[1] 

$e_0(t,s)\equiv 1$ and $e_{\varphi }(t,t)\equiv 1;$

[2] 

$e_{\varphi }(\rho \left(t\right),s)=(1-\mu \left(t\right)\varphi \left(t\right))e_{\varphi }(t,s);$

[3] 

$e_{\varphi }(t,s)e_{\psi }(t,s)=e_{\varphi \oplus \psi }(t,s).$

[4] 

$e_{\varphi }(t,s)={\displaystyle \frac{1}{e_{\varphi }(s,t)}}=e_{\ominus \varphi }(s,t);$

[5] 

$e_{\varphi }(t,s)e_{\varphi }(s,r)=e_{\varphi }(t,r),$

where for all $t\in {\mathbb{T}}^k$,

$$(\varphi \oplus \psi )\left(t\right)=\varphi \left(t\right)+\psi \left(t\right)+\mu \left(t\right)\varphi \left(t\right)\psi \left(t\right)$$

and

$$(\ominus \varphi )\left(t\right)=-{\displaystyle \frac{\varphi \left(t\right)}{1+\mu \left(t\right)\varphi \left(t\right)}}.$$

Definition 1

([22]). Assume that $f:\mathbb{T}\to \mathbb{R}$ is a function. For $t\in \mathbb{T}$, define $f^{\Delta }\left(t\right)$ to be the number (provided it exists) with the property that given any $\epsilon >0$, there is a neighborhood U of t such that

$$|f\left(\sigma \left(t\right)\right)-f\left(s\right)-f^{\Delta }\left(t\right)(\sigma \left(t\right)-s)|\le \epsilon |\sigma \left(t\right)-s|\mathrm{for}\mathrm{all}s\in U.$$

In this case, $f^{\Delta }\left(t\right)$ is called the delta (or Hilger) derivative.

Definition 2

([22]). A function $\mathcal{G}:\mathbb{T}\to \mathbb{R}$ is called a delta-antiderivative of $g:\mathbb{T}\to \mathbb{R}$ if ${\mathcal{G}}^{\Delta }\left(t\right)=g\left(t\right)$ holds for all $t\in {\mathbb{T}}^k$. For this case we define the integral of g by

$${\int }_a^{t}g\left(s\right)\Delta s=\mathcal{G}\left(t\right)-\mathcal{G}\left(a\right).$$

Definition 3

([23]). A time scale $\mathbb{T}$ is periodic if there exists $\omega >0$ for each $v\in \mathbb{T}$ such that $v\pm \omega \in \mathbb{T}$. For $\mathbb{T}\ne \mathbb{R}$, the smallest positive ω is the period of time scale.

Definition 4

([23]). Let $\mathbb{T}\ne \mathbb{R}$ be a periodic time scale with the period ω. The function $f:\mathbb{T}\to \mathbb{R}$ is periodic with period T if there exists a natural number n such that $T=n\omega ,f(v\pm T)=f\left(v\right)$ for each $v\in \mathbb{T}$. When $\mathbb{T}=\mathbb{R}$, f is a periodic function if κ is the smallest positive number such that $f(v\pm \kappa )=f\left(v\right)$ for each $v\in \mathbb{T}$.

Obviously, if $\mathbb{T}$ is a periodic time scale with period $\omega$, then $\sigma (t+n\omega )=\sigma \left(t\right)+n\omega ,$ where $n\in \mathbb{Z}$. Thus, the graininess function $\mu$ satisfies $\mu (t+n\omega )=\sigma (t+n\omega )-(t+n\omega )=\sigma \left(t\right)-t=\mu \left(t\right)$ and so $\mu$ is a periodic function with period $\omega$.

Lemma 2

([24]). For a nonnegative function g, where $-g\in {\mathcal{R}}^{+}$, we have

$$1-{\int }_s^{t}g\left(u\right)\Delta u\le e_{-g}(t,s)\le exp\left\{-{\int }_s^{t}g\left(u\right)\Delta u\right\}\mathrm{for}\mathrm{all}t\ge s.$$

For a nonnegative function g, where $g\in {\mathcal{R}}^{+}$, we have

$$1+{\int }_s^{t}g\left(u\right)\Delta u\le e_g(t,s)\le exp\left\{{\int }_s^{t}g\left(u\right)\Delta u\right\}\mathrm{for}\mathrm{all}t\ge s.$$

Lemma 3

(Schauder’s fixed point theorem [25]). Let $\mathcal{K}$ be a closed, convex and nonempty subset of Banach space $\mathbb{B}$. Let ${\rm Y}:\mathcal{K}\to \mathcal{K}$ be a continuous mapping such that ${\rm Y}\mathcal{K}$ is a relatively compact subset of $\mathbb{B}$. Then Υ has at least one fixed point in $\mathcal{K}$.

3. Existence of Positive Periodic Solutions

Let $P_{\omega }=\{{(u_1,u_2,u_3)}^T:{(u_1,u_2,u_3)}^T(t+\omega )={(u_1,u_2,u_3)}^T\left(t\right)\}$, where $u_1,u_2$ and $u_3$ are $rd-$continuous functions on $\mathbb{T}$ endowed with the norm

$$\left|\right|{(u_1,u_2,u_3)}^T\left|\right|=max\{\underset{t\in {[0,\omega ]}_{\mathbb{T}}}{sup}|u_i\left(t\right)|,i=1,2,3\}.$$

For $L_1,L_2>0$, let

$$P_{\omega }(L_1,L_2)=\{z={(z_1,z_2,z_3)}^T\in P_{\omega }:L_1\le z_i\left(t\right)\le L_2,i=1,2,3,t\in \mathbb{T}\}.$$

Obviously, $P_{\omega }(L_1,L_2)$ is bounded, closed, and convex subset of $P_{\omega }$.

Lemma 4.

Assume that $r\left(t\right)=r_1\left(t\right)+r_2\left(t\right)$, where $r_1\left(t\right),r_2\left(t\right)>0$ are $rd-$continuous $\omega -$periodic functions. Let $-r_1,-d_1,-d_2\in {\mathcal{R}}^{+}$, and $z={(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$. System (1.3) exists a periodic solution $z={(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$ if only if

$$\begin{array}{cc}\hfill z_1\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-r_1)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[a\left(s\right)z_1\left(s\right)z_1(s-\gamma \left(s\right))+{\displaystyle \frac{b_1\left(s\right)z_1^2\left(s\right)z_2\left(s\right)}{m^2\left(s\right)z_2^2\left(s\right)+z_1^2\left(s\right)}}\hfill \\ & +{\displaystyle \frac{b_2\left(s\right)z_1\left(s\right)z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1\left(s\right)+{\alpha }_3\left(s\right)z_3\left(s\right)}}-r_2\left(t\right)z_1\left(\sigma \left(s\right)\right)]e_{\ominus (-r_1)}(t,s)\Delta s,\hfill \\ \hfill z_2\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-d_1)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[(2d_1\left(s\right)+f\left(s\right))z_2\left(\sigma \left(s\right)\right)-\hfill \\ & {\displaystyle \frac{c_1\left(s\right)z_1^2(s-\gamma \left(s\right))z_2\left(s\right)}{m^2\left(s\right)z_2^2(s-\gamma \left(s\right))+z_1^2(s-\gamma \left(s\right))}}]e_{\ominus (-d_1)}(t,s)\Delta s,\hfill \\ \hfill z_3\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-d_2)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[2d_2\left(s\right)z_3\left(\sigma \left(s\right)\right)-f\left(s\right)z_2\left(s\right)\hfill \\ & -{\displaystyle \frac{c_2\left(s\right)z_1(s-\gamma \left(s\right))z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1(t-\gamma \left(s\right))+{\alpha }_3\left(s\right)z_3(s-\gamma \left(s\right))}}]e_{\ominus (-d_2)}(t,s)\Delta s.\hfill \end{array}$$

(4)

Proof. 

The proof of Lemma 4 is similar to the proof of Lemma 3.2 in [26]. For the convenience of readers, we provide a simple proof. Let

$$F\left(t\right)=-a\left(t\right)z_1\left(t\right)z_1(t-\gamma \left(t\right))-{\displaystyle \frac{b_1\left(t\right)z_1^2\left(t\right)z_2\left(t\right)}{m^2\left(t\right)z_2^2\left(t\right)+z_1^2\left(t\right)}}-{\displaystyle \frac{b_2\left(t\right)z_1\left(t\right)z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1\left(t\right)+{\alpha }_3\left(t\right)z_3\left(t\right)}}.$$

From the first equation of system (3), we have

$$z_1^{\Delta }\left(t\right)-r_1\left(t\right)z_1\left(\sigma \left(t\right)\right)=r_2\left(t\right)z_1\left(\sigma \left(t\right)\right)+F\left(t\right).$$

Multiply both sides of the above equation by $e_{r_1}(t,0)$ and then integrate from $t-\omega$ to t, then

$${\int }_{t-\omega }^t{\left[e_{-r_1}(s,0)z_1\left(s\right)\right]}^{\Delta }\Delta s={\int }_{t-\omega }^t[r_2\left(s\right)z_1\left(\sigma \left(t\right)\right)+F\left(s\right)]e_{-r_1}(s,0)\Delta s.$$

Thus,

$$e_{-r_1}(t,0)z_1\left(t\right)-e_{-r_1}(t-\omega ,0)z_1(t-\omega )={\int }_{t-\omega }^t[r_2\left(s\right)z_1\left(\sigma \left(t\right)\right)+F\left(s\right)]e_{-r_1}(s,0)\Delta s.$$

Dividing both sides of the above equation by $e_{-r_1}(t,0)$, we have

$$z_1\left(t\right)={\displaystyle \frac{1}{e_{\ominus (-r_1)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[-r_2\left(s\right)z_1\left(\sigma \left(t\right)\right)-F\left(s\right)]e_{\ominus (-r_1)}(t,s)\Delta s.$$

The proof of $z_2\left(t\right)$ and $z_3\left(t\right)$ is similar to the above proof. □

Remark 1.

Since $\ominus (-r_1)={\displaystyle \frac{r_1}{1-\mu r_1}}>0$, by Lemma 2, we have $e_{\ominus (-r_1)}(t,t-\omega )-1>0$. Similarly, we can obtain that

$$e_{\ominus (-d_1)}(t,t-\omega )-1>0\mathrm{and}{e}_{\ominus -\left(d_2\right)}(t,t-\omega )-1>0.$$

Remark 2.

We claim that $e_{\ominus p}(t,t-\omega )$ does not depend on t, where $p\in {\mathcal{R}}^{+}.$ In fact, from the definition of $e_{\ominus p}(t,s)$, we have

$$\begin{array}{cc}\hfill e_{\ominus p}(t,t-\omega )& =exp\left({\int }_{t-\omega }^t{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s\right)\hfill \\ & =exp({\int }_{t-\omega }^0{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s+{\int }_0^{\omega }{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s\hfill \\ & +{\int }_{\omega }^t{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s).\hfill \end{array}$$

Using the periodicity of p and μ, let $s=u-\omega$, we have

$$\begin{array}{c}\hfill {\int }_{t-\omega }^0{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s=-{\int }_t^{\omega }{\displaystyle \frac{log(1+(\ominus p\left(u\right)\left)\mu \right(u\left)\right)}{\mu \left(u\right)}}\Delta u.\end{array}$$

Thus,

$$e_{\ominus p}(t,t-\omega )=exp\left({\int }_0^{\omega }{\displaystyle \frac{log(1+(\ominus p\left(s\right)\left)\mu \right(s\left)\right)}{\mu \left(s\right)}}\Delta s\right).$$

Therefore, $e_{\ominus p}(t,t-\omega )$ does not depend on t.

Remark 3.

For all $t\ge s$ and $s\in {[t-\omega ,t]}_{\mathbb{T}}$, by Lemma 2 we have

$$\begin{array}{cc}\hfill e_{\ominus (-r_1)}(t,s)& \le exp\left({\int }_s^t{\displaystyle \frac{r_1\left(u\right)}{1-\mu \left(u\right)r_1\left(u\right)}}\Delta u\right)\hfill \\ & \le exp\left({\int }_0^{\omega }{\displaystyle \frac{r_1\left(u\right)}{1-\mu \left(u\right)r_1\left(u\right)}}\Delta u\right)={\eta }_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_{\ominus (-r_1)}(t,s)& \ge 1+{\int }_s^t{\displaystyle \frac{r_1\left(u\right)}{1-\mu \left(u\right)r_1\left(u\right)}}\Delta u\hfill \\ & \ge 1+{\int }_0^{\omega }{\displaystyle \frac{r_1\left(u\right)}{1-\mu \left(u\right)r_1\left(u\right)}}\Delta u={\eta }_1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_{\ominus (-d_1)}(t,s)& \le exp\left({\int }_s^t{\displaystyle \frac{d_1\left(u\right)}{1-\mu \left(u\right)d_1\left(u\right)}}\Delta u\right)\hfill \\ & \le exp\left({\int }_0^{\omega }{\displaystyle \frac{d_1\left(u\right)}{1-\mu \left(u\right)d_1\left(u\right)}}\Delta u\right)={\eta }_3,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_{\ominus (-d_1)}(t,s)& \ge 1+{\int }_s^t{\displaystyle \frac{d_1\left(u\right)}{1-\mu \left(u\right)d_1\left(u\right)}}\Delta u\hfill \\ & \ge 1+{\int }_0^{\omega }{\displaystyle \frac{d_1\left(u\right)}{1-\mu \left(u\right)d_1\left(u\right)}}\Delta u={\eta }_4,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_{\ominus (-d_2)}(t,s)& \le exp\left({\int }_s^t{\displaystyle \frac{d_2\left(u\right)}{1-\mu \left(u\right)d_2\left(u\right)}}\Delta u\right)\hfill \\ & \le exp\left({\int }_0^{\omega }{\displaystyle \frac{d_2\left(u\right)}{1-\mu \left(u\right)d_2\left(u\right)}}\Delta u\right)={\eta }_5,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_{\ominus (-d_2)}(t,s)& \ge 1+{\int }_s^t{\displaystyle \frac{d_2\left(u\right)}{1-\mu \left(u\right)d_2\left(u\right)}}\Delta u\hfill \\ & \ge 1+{\int }_0^{\omega }{\displaystyle \frac{d_2\left(u\right)}{1-\mu \left(u\right)d_2\left(u\right)}}\Delta u={\eta }_6.\hfill \end{array}$$

Let $a\left(t\right)\in C_{rd}(\mathbb{T},\mathbb{R})$ be a bounded function, denote

$$a^{+}=\underset{t\in \mathbb{T}}{sup}\left|a\left(t\right)\right|,a^{-}=\underset{t\in \mathbb{T}}{inf}\left|a\left(t\right)\right|.$$

Throughout this paper, we need the following assumption:

(H₁) For $z={(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$, the below inequalities are satisfied

$$r_2\left(t\right)z_1\le a^{+}{L}_2^2+{\displaystyle \frac{b_1^{+}{L}_2^2}{m_1^{-}{L}_1^2+L_1^2}}+{\displaystyle \frac{b_2^{+}{L}_2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}-{\displaystyle \frac{L_2}{{\lambda }_1\omega {\eta }_2}},$$

$$r_2\left(t\right)z_1\ge a^{-}{L}_1^2+{\displaystyle \frac{b_1^{+}{L}_1^2}{m_1^{+}{L}_2^2+L_2^2}}+{\displaystyle \frac{b_2^{-}{L}_1}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}-{\displaystyle \frac{L_1}{{\lambda }_1\omega {\eta }_1}}>0,$$

$$(2d_1\left(t\right)+f\left(t\right))z_2\le {\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+{\displaystyle \frac{L_1}{{\lambda }_2\omega {\eta }_3}},$$

$$(2d_1\left(t\right)+f\left(t\right))z_2\ge {\displaystyle \frac{c_1^{-}{L}_1^3}{{\left(m^{+}\right)}^2{L}_2^2+L_2^2}}+{\displaystyle \frac{L_2}{{\lambda }_2\omega {\eta }_4}},$$

$$2d_2\left(t\right)z_3\le f^{+}{L}_2+{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+{\displaystyle \frac{L_1}{{\lambda }_3\omega {\eta }_5}},$$

$$2d_2\left(t\right)z_3\ge f^{-}{L}_1+{\displaystyle \frac{c_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}+{\displaystyle \frac{L_2}{{\lambda }_3\omega {\eta }_6}},$$

where ${\eta }_i,i=1,2,\cdots ,6$ is defined by Remark 3, ${\lambda }_i,i=1,2,3$ is defined by (6). For assumption ($H_1$), it indicates that $z\in P_{\omega }(L_1,L_2)$ must satisfy certain constraints, which are determined by the coefficients of the system (3), so that system (3) has a positive periodic solution.

For $z={(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$, define the mapping $\mathcal{F}:P_{\omega }(L_1,L_2)\to P_{\omega }$ by

$$\left(\mathcal{F}z\right)\left(t\right)={(\left(\mathcal{F}{z}_1\right)\left(t\right),\left(\mathcal{F}{z}_2\right)\left(t\right),\left(\mathcal{F}{z}_3\right)\left(t\right))}^T,t\in \mathbb{T},$$

(5)

where

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_1\right)\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-r_1)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[a\left(s\right)z_1\left(s\right)z_1(s-\gamma \left(s\right))+{\displaystyle \frac{b_1\left(s\right)z_1^2\left(s\right)z_2\left(s\right)}{m^2\left(s\right)z_2^2\left(s\right)+z_1^2\left(s\right)}}\hfill \\ & +{\displaystyle \frac{b_2\left(s\right)z_1\left(s\right)z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1\left(s\right)+{\alpha }_3\left(s\right)z_3\left(s\right)}}-r_2\left(t\right)z_1\left(\sigma \left(s\right)\right)]e_{\ominus (-r_1)}(t,s)\Delta s,\hfill \\ \hfill \left(\mathcal{F}{z}_2\right)\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-d_1)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[(2d_1\left(s\right)+f\left(s\right))z_2\left(\sigma \left(s\right)\right)-\hfill \\ & {\displaystyle \frac{c_1\left(s\right)z_1^2(s-\gamma \left(s\right))z_2\left(s\right)}{m^2\left(s\right)z_2^2(s-\gamma \left(s\right))+z_1^2(s-\gamma \left(s\right))}}]e_{\ominus (-d_1)}(t,s)\Delta s,\hfill \\ \hfill \left(\mathcal{F}{z}_3\right)\left(t\right)& ={\displaystyle \frac{1}{e_{\ominus (-d_2)}(t,t-\omega )-1}}{\int }_{t-\omega }^t[2d_2\left(s\right)z_3\left(\sigma \left(s\right)\right)-f\left(s\right)z_2\left(s\right)\hfill \\ & -{\displaystyle \frac{c_2\left(s\right)z_1(s-\gamma \left(s\right))z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1(t-\gamma \left(s\right))+{\alpha }_3\left(s\right)z_3(s-\gamma \left(s\right))}}]e_{\ominus (-d_2)}(t,s)\Delta s.\hfill \end{array}$$

Theorem 1.

Suppose that assumption (H₁) holds. Then system (3) has at least one positive $\omega -$periodic solution on $P_{\omega }(L_1,L_2)$, where $L_1$ and $L_2$ are given positive constants satisfying assumption (H₁).

Proof. 

From Remarks 1 and 2, let

$${\displaystyle \frac{1}{e_{\ominus (-r_1)}(t,t-\omega )-1}}={\lambda }_1,{\displaystyle \frac{1}{e_{\ominus (-d_1)}(t,t-\omega )-1}}={\lambda }_2,{\displaystyle \frac{1}{e_{\ominus (-d_2)}(t,t-\omega )-1}}={\lambda }_3,$$

(6)

where ${\lambda }_i>0$ are constants, $i=1,2,3$. It is clear from Lemma 4 that $\left(\mathcal{F}{z}_i\right)(t+\omega )=\left(\mathcal{F}{z}_i\right)\left(t\right)(i=1,2,3)$. Therefore, $\left(\mathcal{F}z\right)(t+\omega )=\left(\mathcal{F}z\right)\left(t\right)$. For $z={(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$, in view of system (5) and assumption (H₁), we have

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_1\right)\left(t\right)& \le {\lambda }_1\omega {\eta }_2(a^{+}{L}_2^2+{\displaystyle \frac{b_1^{+}{L}_2^3}{m_1^{-}{L}_1^2+L_1^2}}+{\displaystyle \frac{b_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}\hfill \\ & -a^{+}{L}_2^2-{\displaystyle \frac{b_1^{+}{L}_2^2}{m_1^{-}{L}_1^2+L_1^2}}-{\displaystyle \frac{b_2^{+}{L}_2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+{\displaystyle \frac{L_2}{{\lambda }_1\omega {\eta }_2}})\hfill \\ & =L_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_1\right)\left(t\right)& \ge {\lambda }_1\omega {\eta }_1(a^{-}{L}_1^2+{\displaystyle \frac{b_1^{+}{L}_1^2}{m_1^{+}{L}_2^2+L_2^2}}+{\displaystyle \frac{b_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}\hfill \\ & -a^{-}{L}_1^2-{\displaystyle \frac{b_1^{+}{L}_1^2}{m_1^{+}{L}_2^2+L_2^2}}-{\displaystyle \frac{b_2^{-}{L}_1}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}+{\displaystyle \frac{L_1}{{\lambda }_1\omega {\eta }_1}})\hfill \\ & =L_1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_2\right)\left(t\right)& \le {\lambda }_2\omega {\eta }_4\left({\displaystyle \frac{c_1^{-}{L}_1^3}{{\left(m^{+}\right)}^2{L}_2^2+L_2^2}}+{\displaystyle \frac{L_2}{{\lambda }_2\omega {\eta }_4}}-{\displaystyle \frac{c_1^{-}{L}_1^3}{{\left(m^{+}\right)}^2{L}_2^2+L_2^2}}\right)\hfill \\ & =L_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_2\right)\left(t\right)& \ge {\lambda }_2\omega {\eta }_3\left({\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+{\displaystyle \frac{L_1}{{\lambda }_2\omega {\eta }_3}}-{\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}\right)\hfill \\ & =L_1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_3\right)\left(t\right)& \le {\lambda }_3\omega {\eta }_6\left(f^{-}{L}_1+{\displaystyle \frac{c_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}+{\displaystyle \frac{L_2}{{\lambda }_3\omega {\eta }_6}}-f^{-}{L}_1+{\displaystyle \frac{c_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2={\alpha }_3^{+}{L}_2}}\right)\hfill \\ & =L_2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \left(\mathcal{F}{z}_3\right)\left(t\right)& \ge {\lambda }_3\omega {\eta }_5\left(f^{+}{L}_2+{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+{\displaystyle \frac{L_1}{{\lambda }_3\omega {\eta }_5}}-f^{+}{L}_2-{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}\right)\hfill \\ & =L_1.\hfill \end{array}$$

Thus, $\mathcal{F}$ maps $P_{\omega }(L_1,L_2)$ into itself, i.e., $\mathcal{F}\left(P_{\omega }(L_1,L_2)\right)\subset P_{\omega }(L_1,L_2)$. Now we show that $\mathcal{F}$ is continuous. Let $\left\{{(z_1^l,z_2^l,z_3^l)}^T\right\}$ be a sequence in $P_{\omega }(L_1,L_2)$ such that

$$\underset{l\to \infty }{lim}\left|\right|{(z_1^l,z_2^l,z_3^l)}^T-{(z_1,z_2,z_3)}^T\left|\right|=0.$$

(7)

Since $P_{\omega }(L_1,L_2)$ is closed, then ${(z_1,z_2,z_3)}^T\in P_{\omega }(L_1,L_2)$. Then by the definition of $\mathcal{F}$ we have

$$\begin{array}{cc}& \left|\right|\mathcal{F}{(z_1^l,z_2^l,z_3^l)}^T-\mathcal{F}{(z_1,z_2,z_3)}^T\left|\right|\hfill \\ & =max\{sup|\left(\mathcal{F}{z}_i^l\right)\left(t\right)-\left(\mathcal{F}{z}_i\right)\left(t\right)|,i=1,2,3,t\in {[0,\omega ]}_{\mathbb{T}}\}.\hfill \end{array}$$

(8)

From (5) and (7), we have

$$\begin{array}{cc}& |\left(\mathcal{F}{z}_1^l\right)\left(t\right)-\left(\mathcal{F}{z}_1\right)\left(t\right)|\hfill \\ & \le {\lambda }_1{\eta }_2{\int }_{t-\omega }^t|a\left(s\right)z_1^l\left(s\right)z_1^l(s-\gamma \left(s\right))-a\left(s\right)z_1\left(s\right)z_1(s-\gamma \left(s\right))|\Delta s\hfill \\ & +{\lambda }_1{\eta }_2{\int }_{t-\omega }^t|{\displaystyle \frac{b_1\left(s\right){\left(z_1^l\right)}^2\left(s\right)z_2^l\left(s\right)}{m^2\left(s\right){\left(z_2^l\right)}^2\left(s\right)+{\left(z_1^l\right)}^2\left(s\right)}}-{\displaystyle \frac{b_1\left(s\right)z_1^2\left(s\right)z_2\left(s\right)}{m^2\left(s\right)z_2^2\left(s\right)+z_1^2\left(s\right)}}|\Delta s\hfill \\ & +{\lambda }_1{\eta }_2{\int }_{t-\omega }^t|{\displaystyle \frac{b_2\left(s\right)z_1^l\left(s\right)z_3^l\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1^l\left(s\right)+{\alpha }_3\left(s\right)z_3^l\left(s\right)}}\hfill \\ & -{\displaystyle \frac{b_2\left(s\right)z_1\left(s\right)z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1\left(s\right)+{\alpha }_3\left(s\right)z_3\left(s\right)}}|\Delta s+{\lambda }_1{\eta }_2{\int }_{t-\omega }^t|r_2\left(s\right)-z_1^l\left(\sigma \left(s\right)\right)-r_2\left(s\right)-z_1\left(\sigma \left(s\right)\right)|\Delta s\hfill \\ & \to 0\mathrm{as}l\to \infty .\hfill \end{array}$$

(9)

Similar to the above proof, we have

$$|\left(\mathcal{F}{z}_2^l\right)\left(t\right)-\left(\mathcal{F}{z}_2\right)\left(t\right)|\to 0\mathrm{as}l\to \infty$$

(10)

and

$$|\left(\mathcal{F}{z}_3^l\right)\left(t\right)-\left(\mathcal{F}{z}_3\right)\left(t\right)|\to 0\mathrm{as}l\to \infty .$$

(11)

It follows by (8)–(11) that

$$\left|\right|\mathcal{F}{(z_1^l,z_2^l,z_3^l)}^T-\mathcal{F}{(z_1,z_2,z_3)}^T\left|\right|\to 0\mathrm{as}l\to \infty .$$

This proves that $\mathcal{F}$ is a continuous map. To show that the map $\mathcal{F}$ is completely continuous, we will prove that $\mathcal{F}\left(P_{\omega }(L_1,L_2)\right)$ is relatively compact. We have proved that $\mathcal{F}\left(P_{\omega }(L_1,L_2)\right)$ is uniformly bounded. It is easy to see that $|{\left(\mathcal{F}{z}_i\right)}^{\Delta }\left(t\right)|\le D,$ where $i=1,2,3$ and $D>0$ is a constant. Therefore, $\mathcal{F}\left(P_{\omega }(L_1,L_2)\right)$ is equicontinuous, and by Arzela-Ascoli’s theorem, it is relatively compact. Based on Schauder’s fixed point theorem, $\mathcal{F}$ has at least one fixed point on $P_{\omega }(L_1,L_2)$ and these fixed points are positive periodic solutions of system (3). □

4. Asymptotic Property of Positive Periodic Solutions

In this section, we will give the boundary of the difference between the two positive periodic solutions of system (3).

Theorem 2.

If all the conditions of Theorem 1 hold, and for given positive constant ε, there exists a positive constant $\delta =\delta \left(\epsilon \right)$ such that $\left|\right|z\left(0\right)-\tilde{z}\left(0\right)\left|\right|\le \delta$. Then, we have

$$\left|\right|z\left(t\right)-\tilde{z}\left(t\right)\left|\right|\le \epsilon \mathrm{for}\mathrm{all}t\in {[0,\infty )}_{\mathbb{T}},$$

where $\epsilon >{\Lambda }_1^{*}$ and ${\Lambda }_1^{*}$ is defined by (20), $z\left(t\right)={(z_1\left(t\right),z_2\left(t\right),z_3\left(t\right))}^T$ is a positive periodic solution of system (3), $\tilde{z}\left(t\right)={({\tilde{z}}_1\left(t\right),{\tilde{z}}_2\left(t\right),{\tilde{z}}_3\left(t\right))}^T$ is another solution of system (3).

Proof. 

Since all the conditions of Theorem 1 hold, system (3) exists a positive periodic solution $z\left(t\right)={(z_1\left(t\right),z_2\left(t\right),z_3\left(t\right))}^T\in P_{\omega }(L_1,L_2)$. Let $\tilde{z}\left(t\right)={({\tilde{z}}_1\left(t\right),{\tilde{z}}_2\left(t\right),{\tilde{z}}_3\left(t\right))}^T\in P_{\omega }(L_1,L_2)$ be another solution of system (3). Using Theorem 1, we obtain that

$$\begin{array}{cc}\hfill |z_1\left(t\right)-{\tilde{z}}_1\left(t\right)|& \le {\lambda }_1{a}^{+}{\eta }_2{\int }_{t-\omega }^t|z_1\left(s\right)z_1(s-\gamma \left(s\right))-{\tilde{z}}_1\left(s\right){\tilde{z}}_1(s-\gamma \left(s\right))|\Delta s\hfill \\ & +{\lambda }_1{b}_1^{+}{\eta }_2{\int }_{t-\omega }^t|{\displaystyle \frac{z_1^2\left(s\right)z_2\left(s\right)}{m^2\left(s\right)z_2^2\left(s\right)+z_1^2\left(s\right)}}-{\displaystyle \frac{{\tilde{z}}_1^2\left(s\right){\tilde{z}}_2\left(s\right)}{m^2\left(s\right){\tilde{z}}_2^2\left(s\right)+{\tilde{z}}_1^2\left(s\right)}}|\Delta s\hfill \\ & +{\lambda }_1{b}_2^{+}{\eta }_2{\int }_{t-\omega }^t|{\displaystyle \frac{z_1\left(s\right)z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1\left(s\right)+{\alpha }_3\left(s\right)z_3\left(s\right)}}\hfill \\ & -{\displaystyle \frac{{\tilde{z}}_1\left(s\right){\tilde{z}}_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right){\tilde{z}}_1\left(s\right)+{\alpha }_3\left(s\right){\tilde{z}}_3\left(s\right)}}|\Delta s+{\lambda }_1{r}_2^{+}{\eta }_2{\int }_{t-\omega }^t|z_1\left(\sigma \left(s\right)\right)-{\tilde{z}}_1\left(\sigma \left(s\right)\right)|\Delta s.\hfill \end{array}$$

(12)

In view of assumption (H₁), we get

$$\begin{array}{cc}& |z_1\left(s\right)z_1(s-\gamma \left(s\right))-{\tilde{z}}_1\left(s\right){\tilde{z}}_1(s-\gamma \left(s\right))|\Delta s\hfill \\ & \le 2L_2^2+2L_2+|z_1\left(0\right)-{\tilde{z}}_1\left(0\right)|,\hfill \end{array}$$

(13)

$$\begin{array}{cc}& |{\displaystyle \frac{z_1^2(s-\gamma \left(s\right))z_2\left(s\right)}{m^2\left(s\right)z_2^2(s-\gamma \left(s\right))+z_1^2(s-\gamma \left(s\right))}}-{\displaystyle \frac{{\tilde{z}}_1^2(s-\gamma \left(s\right)){\tilde{z}}_2\left(s\right)}{m^2\left(s\right){\tilde{z}}_2^2(s-\gamma \left(s\right))+{\tilde{z}}_1^2(s-\gamma \left(s\right))}}|\hfill \\ & \le {\displaystyle \frac{2L_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+2L_2+|z_1\left(0\right)-{\tilde{z}}_1\left(0\right)|,\hfill \end{array}$$

(14)

$$\begin{array}{cc}& |{\displaystyle \frac{z_1\left(s\right)z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1\left(s\right)+{\alpha }_3\left(s\right)z_3\left(s\right)}}-{\displaystyle \frac{{\tilde{z}}_1\left(s\right){\tilde{z}}_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right){\tilde{z}}_1\left(s\right)+{\alpha }_3\left(s\right){\tilde{z}}_3\left(s\right)}}|\hfill \\ & \le {\displaystyle \frac{2L_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+2L_2+|z_1\left(0\right)-{\tilde{z}}_1\left(0\right)|,\hfill \end{array}$$

(15)

$$|z_1\left(\sigma \left(s\right)\right)-{\tilde{z}}_1\left(\sigma \left(s\right)\right)|\le 4L_2+|z_1\left(0\right)-{\tilde{z}}_1\left(0\right)|.$$

(16)

From (12)–(16), we have

$$|z_1\left(t\right)-{\tilde{z}}_1\left(t\right)|\le {\Lambda }_1+{\Lambda }_2|z_1\left(0\right)-{\tilde{z}}_1\left(0\right)|,$$

(17)

$$\begin{array}{cc}\hfill {\Lambda }_1& ={\lambda }_1{a}^{+}{\eta }_2\omega (2L_2^2+2L_2)+{\lambda }_1{b}_1^{+}{\eta }_2\omega \left({\displaystyle \frac{2L_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+2L_2\right)\hfill \\ & +{\lambda }_1{b}_2^{+}{\eta }_2\omega \left({\displaystyle \frac{2L_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+2L_2\right)+4L_2{\lambda }_1{r}_2^{+}{\eta }_2\omega ,\hfill \end{array}$$

$${\Lambda }_2={\lambda }_1{a}^{+}{\eta }_2\omega +{\lambda }_1{b}_1^{+}{\eta }_2\omega +{\lambda }_1{b}_2^{+}{\eta }_2\omega +{\lambda }_1{r}_2^{+}{\eta }_2\omega .$$

We also have

$$\begin{array}{cc}\hfill |z_2\left(t\right)-{\tilde{z}}_2\left(t\right)|& \le {\lambda }_2{\eta }_4{\int }_{t-\omega }^t|{\displaystyle \frac{c_1\left(s\right)z_1^2(s-\gamma \left(s\right))z_2\left(s\right)}{m^2\left(s\right)z_2^2(s-\gamma \left(s\right))+z_1^2(s-\gamma \left(s\right))}}\hfill \\ & -{\displaystyle \frac{c_1\left(s\right){\tilde{z}}_1^2(s-\gamma \left(s\right)){\tilde{z}}_2\left(s\right)}{m^2\left(s\right){\tilde{z}}_2^2(s-\gamma \left(s\right))+{\tilde{z}}_1^2(s-\gamma \left(s\right))}}|\Delta s\hfill \\ & +{\lambda }_2{\eta }_4{\int }_{t-\omega }^t|(2d_1\left(s\right)+f\left(s\right))z_2\left(\sigma \left(s\right)\right)-(2{\tilde{d}}_1\left(s\right)+\tilde{f}\left(s\right)){\tilde{z}}_2\left(\sigma \left(s\right)\right)|\Delta s\hfill \\ & \le {\Lambda }_3+{\Lambda }_4|z_2\left(0\right)-{\tilde{z}}_2\left(0\right)|,\hfill \end{array}$$

(18)

where

$${\Lambda }_3=2{\lambda }_2{\eta }_4\omega \left({\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+2L_2+(2d_1^{+}+f^{+})L_2\right),{\Lambda }_4=2{\lambda }_2{\eta }_4\omega ,$$

and

$$\begin{array}{cc}\hfill |z_3\left(t\right)-{\tilde{z}}_3\left(t\right)|& \le {\lambda }_3{\eta }_6{\int }_{t-\omega }^t|f\left(s\right)z_2-f\left(s\right){\tilde{z}}_2|\Delta s+{\lambda }_3{\eta }_6{\int }_{t-\omega }^t|2d_2\left(s\right)z_3\left(\sigma \left(s\right)\right)-2{\tilde{d}}_2\left(s\right){\tilde{z}}_3\left(\sigma \left(s\right)\right)|\Delta s\hfill \\ & +{\lambda }_3{\eta }_6{\int }_{t-\omega }^t|{\displaystyle \frac{c_2\left(s\right)z_1(s-\gamma \left(s\right))z_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right)z_1(t-\gamma \left(s\right))+{\alpha }_3\left(s\right)z_3(s-\gamma \left(s\right))}}\hfill \\ & -{\displaystyle \frac{c_2\left(s\right){\tilde{z}}_1(s-\gamma \left(s\right)){\tilde{z}}_3\left(s\right)}{{\alpha }_1\left(s\right)+{\alpha }_2\left(s\right){\tilde{z}}_1(t-\gamma \left(s\right))+{\alpha }_3\left(s\right){\tilde{z}}_3(s-\gamma \left(s\right))}}|\Delta s\hfill \\ & \le {\Lambda }_5+{\Lambda }_6|z_3\left(0\right)-{\tilde{z}}_3\left(0\right)|,\hfill \end{array}$$

(19)

where

$${\Lambda }_5=2{\lambda }_3{\eta }_6\omega \left(f^{+}{L}_2+3L_2+{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+d_2^{+}{L}_2\right),{\Lambda }_6=3{\lambda }_3{\eta }_6\omega .$$

From (17)–(19), we have

$$\left|\right|z\left(t\right)-\tilde{z}\left(t\right)\left|\right|\le {\Lambda }_1^{*}+{\Lambda }_2^{*}\left|\right|z\left(0\right)-\tilde{z}\left(0\right)\left|\right|,$$

where

$${\Lambda }_1^{*}=max\left\{{\Lambda }_1,{\Lambda }_3,{\Lambda }_5\right\},{\Lambda }_2^{*}=max\left\{{\Lambda }_2,{\Lambda }_4,{\Lambda }_6\right\}.$$

(20)

Choosing $\delta \le {\displaystyle \frac{\epsilon -{\Lambda }_1^{*}}{{\Lambda }_2^{*}}}$, we have

$$\left|\right|z\left(t\right)-\tilde{z}\left(t\right)\left|\right|\le \epsilon \mathrm{for}\mathrm{all}t\in {[0,\infty )}_{\mathbb{T}}.$$

□

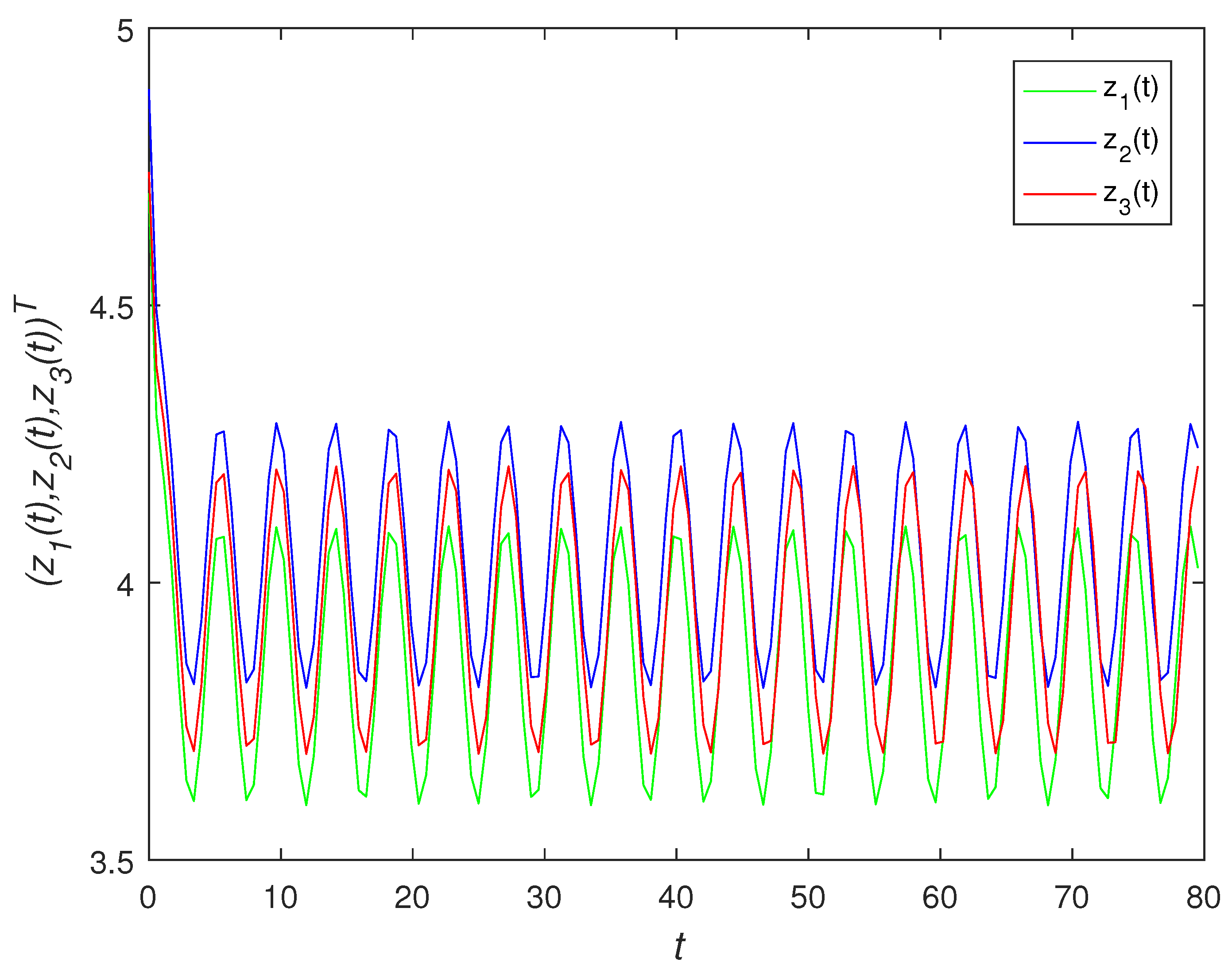
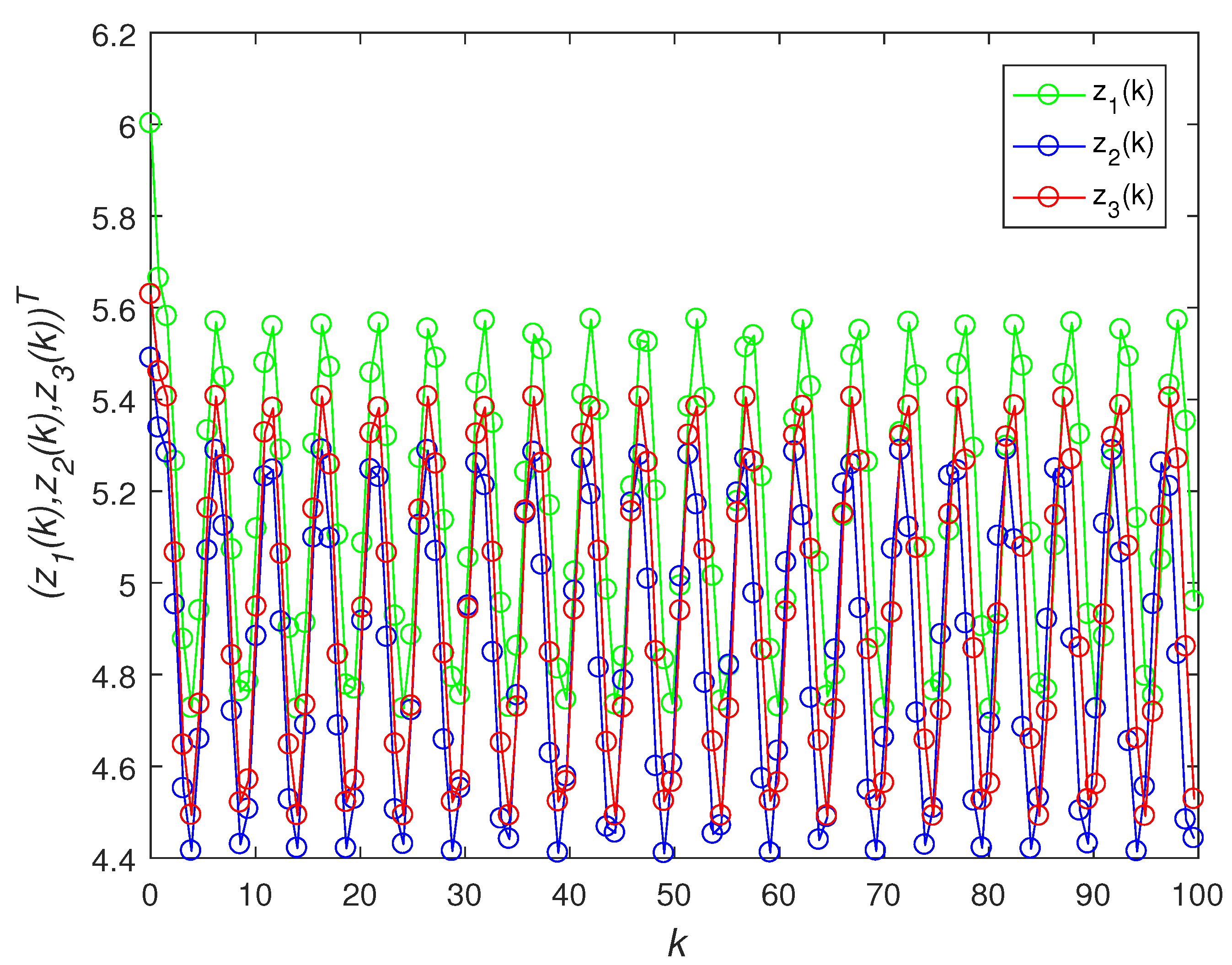
5. An Example

When $\mathbb{T}=\mathbb{R}$, then system (3) is changed into the following system:

$$\begin{array}{cc}\hfill z_1^{\prime }\left(t\right)& =r\left(t\right)z_1\left(t\right)-a\left(t\right)z_1\left(t\right)z_1(t-\gamma \left(t\right))-{\displaystyle \frac{b_1\left(t\right)z_1^2\left(t\right)z_2\left(t\right)}{m^2\left(t\right)z_2^2\left(t\right)+z_1^2\left(t\right)}}-{\displaystyle \frac{b_2\left(t\right)z_1\left(t\right)z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1\left(t\right)+{\alpha }_3\left(t\right)z_3\left(t\right)}}\hfill \\ \hfill z_2^{\prime }\left(t\right)& =-[d_1\left(t\right)+f\left(t\right)]z_2\left(t\right)+{\displaystyle \frac{c_1\left(t\right)z_1^2(t-\gamma \left(t\right))z_2\left(t\right)}{m^2\left(t\right)z_2^2(t-\gamma \left(t\right))+z_1^2(t-\gamma \left(t\right))}}\hfill \\ \hfill z_3^{\prime }\left(t\right)& =-d_2\left(t\right)z_3\left(t\right)+f\left(t\right)z_2\left(t\right)+{\displaystyle \frac{c_2\left(t\right)z_1(t-\gamma \left(t\right))z_3\left(t\right)}{{\alpha }_1\left(t\right)+{\alpha }_2\left(t\right)z_1(t-\gamma \left(t\right))+{\alpha }_3\left(t\right)z_3(t-\gamma \left(t\right))}},\hfill \end{array}$$

(21)

where $t\in \mathbb{R}$. Let

$$r\left(t\right)=r_1\left(t\right)+r_2\left(t\right),r_1\left(t\right)=4.5+sin{\displaystyle \frac{20\pi }{7}}t,r_2\left(t\right)=4.5+cos{\displaystyle \frac{20\pi }{7}}t,a\left(t\right)=1+0.5sin{\displaystyle \frac{20\pi }{7}}t,$$

$$b_1\left(t\right)=0.5+0.2cos{\displaystyle \frac{20\pi }{7}}t,b_2\left(t\right)=0.4+0.1sin{\displaystyle \frac{20\pi }{7}}t,$$

$$d_1\left(t\right)=f\left(t\right)=0.2+0.1cos{\displaystyle \frac{20\pi }{7}}t,c_1\left(t\right)=c_2\left(t\right)=0.7+0.2cos{\displaystyle \frac{20\pi }{7}}t,m\left(t\right)=0.5+0.3sin{\displaystyle \frac{20\pi }{7}}t,$$

$$d_2\left(t\right)=0.3+0.1sin{\displaystyle \frac{20\pi }{7}}t,{\alpha }_1\left(t\right)={\displaystyle \frac{5+sin\frac{20\pi }{7}t}{100}},{\alpha }_2\left(t\right)={\displaystyle \frac{3+sin\frac{20\pi }{7}t}{100}},$$

$${\alpha }_3\left(t\right)={\displaystyle \frac{4+sin\frac{20\pi }{7}t}{100}},\gamma \left(t\right)=10+2cos{\displaystyle \frac{20\pi }{7}}t.$$

By simple calculation, we have

$$\omega =0.7,{\lambda }_1\approx 0.04,{\lambda }_2\approx 6.67,{\lambda }_3\approx 4.17,$$

$${\eta }_1\approx 4.15,{\eta }_2\approx 23.34,{\eta }_3\approx 1.14,{\eta }_4\approx 1.15,{\eta }_5\approx 1.21,{\eta }_6\approx 1.24,$$

$$a^{+}=1.5,a^{-}=0.5,b_1^{+}=0.7,b_1^{-}=0.5,b_2^{+}=0.5,b_2^{-}=0.3,$$

$$c_1^{+}=c_2^{+}=0.9,c_1^{-}=c_2^{-}=0.5,m^{+}=0.8,m^{-}=0.2,d_1^{+}=f^{+}=0.3,d_1^{-}=f^{-}=0.1,$$

$${\alpha }_1^{+}=0.06,{\alpha }_1^{-}=0.04,{\alpha }_2^{+}=0.04,{\alpha }_2^{-}=0.02,{\alpha }_3^{+}=0.05,{\alpha }_3^{-}=0.03.$$

Choosing $L_1=20,L_2=100$, we get

$$r_2\left(t\right)z_1\le a^{+}{L}_2^2+{\displaystyle \frac{b_1^{+}{L}_2^2}{m_1^{-}{L}_1^2+L_1^2}}+{\displaystyle \frac{b_2^{+}{L}_2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}-{\displaystyle \frac{L_2}{{\lambda }_1\omega {\eta }_2}}\approx 1.67\times {10}^4,$$

$$r_2\left(t\right)z_1\ge a^{-}{L}_1^2+{\displaystyle \frac{b_1^{+}{L}_1^2}{m_1^{+}{L}_2^2+L_2^2}}+{\displaystyle \frac{b_2^{-}{L}_1}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}-{\displaystyle \frac{L_1}{{\lambda }_1\omega {\eta }_1}}\approx 42,$$

$$(2d_1\left(t\right)+f\left(t\right))z_2\le {\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+{\displaystyle \frac{L_1}{{\lambda }_2\omega {\eta }_3}}\approx 1.89\times {10}^3,$$

$$(2d_1\left(t\right)+f\left(t\right))z_2\ge {\displaystyle \frac{c_1^{-}{L}_1^3}{{\left(m^{+}\right)}^2{L}_2^2+L_2^2}}+{\displaystyle \frac{L_2}{{\lambda }_2\omega {\eta }_4}}\approx 18.52,$$

$$2d_2\left(t\right)z_3\le f^{+}{L}_2+{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+{\displaystyle \frac{L_1}{{\lambda }_3\omega {\eta }_5}}\approx 9.05\times {10}^3,$$

$$2d_2\left(t\right)z_3\ge f^{-}{L}_1+{\displaystyle \frac{c_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}+{\displaystyle \frac{L_2}{{\lambda }_3\omega {\eta }_6}}\approx 70.02.$$

So all conditions of Theorems 1 and 2 are satisfied, then system (21) has a positive periodic solution. From Figure 1, we find that system (21) exists a positive periodic solution with the period $\omega =0.7$.

When $\mathbb{T}=\mathbb{Z}$, then system (3) is changed into the following system:

$$\begin{array}{cc}\hfill \Delta z_1\left(k\right)& =r\left(k\right)z_1(k+1)-a\left(k\right)z_1\left(k\right)z_1(k-\gamma \left(k\right))-{\displaystyle \frac{b_1\left(k\right)z_1^2\left(k\right)z_2\left(k\right)}{m^2\left(k\right)z_2^2\left(k\right)+z_1^2\left(k\right)}}-{\displaystyle \frac{b_2\left(k\right)z_1\left(k\right)z_3\left(k\right)}{{\alpha }_1\left(k\right)+{\alpha }_2\left(k\right)z_1\left(k\right)+{\alpha }_3\left(k\right)z_3\left(k\right)}}\hfill \\ \hfill \Delta z_2\left(k\right)& =-[d_1\left(k\right)+f\left(k\right)]z_2(k+1)+{\displaystyle \frac{c_1\left(k\right)z_1^2(k-\gamma \left(k\right))z_2\left(k\right)}{m^2\left(k\right)z_2^2(k-\gamma \left(k\right))+z_1^2(k-\gamma \left(k\right))}}\hfill \\ \hfill \Delta z_3\left(k\right)& =-d_2\left(k\right)z_3(k+1)+f\left(k\right)z_2\left(k\right)+{\displaystyle \frac{c_2\left(k\right)z_1(k-\gamma \left(k\right))z_3\left(k\right)}{{\alpha }_1\left(k\right)+{\alpha }_2\left(k\right)z_1(k-\gamma \left(k\right))+{\alpha }_3\left(k\right)z_3(k-\gamma \left(k\right))}},\hfill \end{array}$$

(22)

where $k\in \mathbb{Z},\Delta z_i\left(k\right)=z_i(k+1)-z_i\left(k\right),i=1,2,3$. Let

$$r\left(k\right)=r_1\left(k\right)+r_2\left(k\right),r_1\left(k\right)=4+sin{\displaystyle \frac{20\pi }{9}}k,r_2\left(k\right)=4+cos{\displaystyle \frac{20\pi }{9}}k,a\left(k\right)=1.2+0.6cos{\displaystyle \frac{20\pi }{9}}k,$$

$$b_1\left(k\right)=0.4+0.2cos{\displaystyle \frac{20\pi }{9}}k,b_2\left(k\right)=0.3+0.1sin{\displaystyle \frac{20\pi }{9}}k,$$

$$d_1\left(k\right)=f\left(k\right)=0.3+0.1sin{\displaystyle \frac{20\pi }{9}}k,c_1\left(k\right)=c_2\left(k\right)=0.6+0.2sin{\displaystyle \frac{20\pi }{9}}k,m\left(k\right)=0.4+0.3cos{\displaystyle \frac{20\pi }{9}}k,$$

$$d_2\left(k\right)=0.2+0.1cos{\displaystyle \frac{20\pi }{9}}k,{\alpha }_1\left(k\right)={\displaystyle \frac{4+sin\frac{20\pi }{9}k}{100}},{\alpha }_2\left(k\right)={\displaystyle \frac{3+sin\frac{20\pi }{9}k}{100}},$$

$${\alpha }_3\left(k\right)={\displaystyle \frac{2+cos\frac{20\pi }{9}k}{100}},\gamma \left(k\right)=5+2cos{\displaystyle \frac{20\pi }{9}}k.$$

By simple calculation, we have

$$\omega =0.9,{\lambda }_1\approx 0.03,{\lambda }_2\approx 5.27,{\lambda }_3\approx 4.54,$$

$${\eta }_1\approx 4.6,{\eta }_2\approx 36.6,{\eta }_3\approx 1.27,{\eta }_4\approx 1.31,{\eta }_5\approx 1.18,{\eta }_6\approx 1.19,$$

$$a^{+}=1.8,a^{-}=0.6,b_1^{+}=0.6,b_1^{-}=0.2,b_2^{+}=0.4,b_2^{-}=0.2,$$

$$c_1^{+}=c_2^{+}=0.8,c_1^{-}=c_2^{-}=0.4,m^{+}=0.7,m^{-}=0.1,d_1^{+}=f^{+}=0.4,d_1^{-}=f^{-}=0.2,$$

$${\alpha }_1^{+}=0.05,{\alpha }_1^{-}=0.03,{\alpha }_2^{+}=0.04,{\alpha }_2^{-}=0.02,{\alpha }_3^{+}=0.01,{\alpha }_3^{-}=0.01.$$

Choosing $L_1=15,L_2=100$, we get

$$r_2\left(k\right)z_1\le a^{+}{L}_2^2+{\displaystyle \frac{b_1^{+}{L}_2^2}{m_1^{-}{L}_1^2+L_1^2}}+{\displaystyle \frac{b_2^{+}{L}_2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}-{\displaystyle \frac{L_2}{{\lambda }_1\omega {\eta }_2}}\approx 1.81\times {10}^4,$$

$$r_2\left(k\right)z_1\ge a^{-}{L}_1^2+{\displaystyle \frac{b_1^{+}{L}_1^2}{m_1^{+}{L}_2^2+L_2^2}}+{\displaystyle \frac{b_2^{-}{L}_1}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}-{\displaystyle \frac{L_1}{{\lambda }_1\omega {\eta }_1}}\approx 10.25,$$

$$(2d_1\left(k\right)+f\left(k\right))z_2\le {\displaystyle \frac{c_1^{+}{L}_2^3}{{\left(m^{-}\right)}^2{L}_1^2+L_1^2}}+{\displaystyle \frac{L_1}{{\lambda }_2\omega {\eta }_3}}\approx 3.52\times {10}^3,$$

$$(2d_1\left(k\right)+f\left(k\right))z_2\ge {\displaystyle \frac{c_1^{-}{L}_1^3}{{\left(m^{+}\right)}^2{L}_2^2+L_2^2}}+{\displaystyle \frac{L_2}{{\lambda }_2\omega {\eta }_4}}\approx 16.07,$$

$$2d_2\left(k\right)z_3\le f^{+}{L}_2+{\displaystyle \frac{c_2^{+}{L}_2^2}{{\alpha }_1^{-}+{\alpha }_2^{-}{L}_1+{\alpha }_3^{-}{L}_1}}+{\displaystyle \frac{L_1}{{\lambda }_3\omega {\eta }_5}}\approx 1.67\times {10}^4,$$

$$2d_2\left(k\right)z_3\ge f^{-}{L}_1+{\displaystyle \frac{c_2^{-}{L}_1^2}{{\alpha }_1^{+}+{\alpha }_2^{+}{L}_2+{\alpha }_3^{+}{L}_2}}+{\displaystyle \frac{L_2}{{\lambda }_3\omega {\eta }_6}}\approx 25.03.$$

So all conditions of Theorems 1 and 2 are satisfied, then system (22) has a positive periodic solution. From Figure 2, we find that system (22) exists a positive periodic solution with the period $\omega =0.9$.

6. Conclusions

The predator-prey system is a well-known differential dynamic system. The research of the dynamic behaviour and properties of this system can provide a theoretical and practical basis for population biology. In this paper, we deal with a non-autonomous predator-prey system with stage-structured predator on time scales. Firstly, using Schauder’s fixed theorem and the theory of calculus on time scales, we obtain existence of positive periodic solution. Then, by some inequalities technique, the asymptotic property of the positive periodic solution is obtained. Finally, we give an numerical example for verifying the correctness of our results. In the future, we will explore the dynamic properties for neutral-type predator-prey system with stage-structured predator on time scales.