A Dual-Layer Symmetric Multi-Robot Path Planning System Based on an Improved Neural Network-DWA Algorithm

Abstract

Path planning for multi-robot systems in complex dynamic environments is a key issue in autonomous robotics research. In response to the challenges posed by such environments, this paper proposes a dual-layer symmetric path planning algorithm that integrates an improved Glasius bio-inspired neural network (GBNN) and an enhanced dynamic window approach (DWA). This algorithm enables real-time obstacle avoidance for multi-robots in dynamic environments while effectively addressing robot-to-robot conflict issues. First, to address the low global optimization capability of the GBNN algorithm in the first layer, a signal waveform propagation model for single-neuron signals is established, enhancing the global optimization ability of the algorithm. Additionally, a path optimization function is developed to remove redundant points along the path, improving its efficiency. In the second layer, based on the global path, a reward function is introduced into the DWA. The Score function within the DWA algorithm is also modified to enable symmetric path adjustments, effectively reducing detour paths and minimizing the probability of deviation from the planned trajectory while ensuring real-time obstacle avoidance under the condition of maintaining the global path’s optimality. Next, to address conflicts arising from multi-robot encounters, a dynamic priority method based on distance is proposed. Finally, through multi-dimensional comparative experiments, the superiority of the proposed method is validated. Experimental results show that, compared with other algorithms, the improved neural network-DWA algorithm significantly reduces path length and the number of turns. This research contributes to enhancing the efficiency, adaptability, and safety of multi-robot systems.

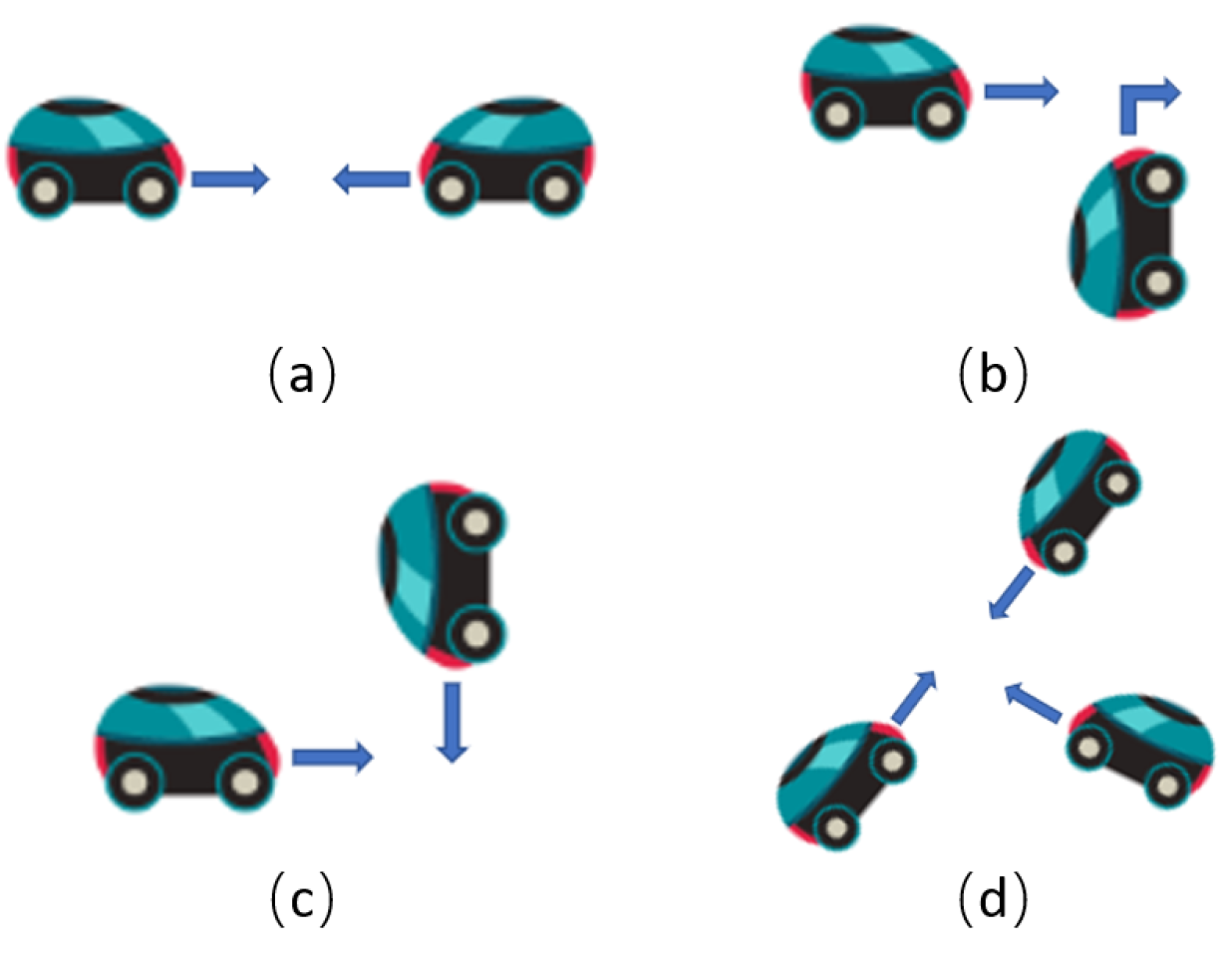
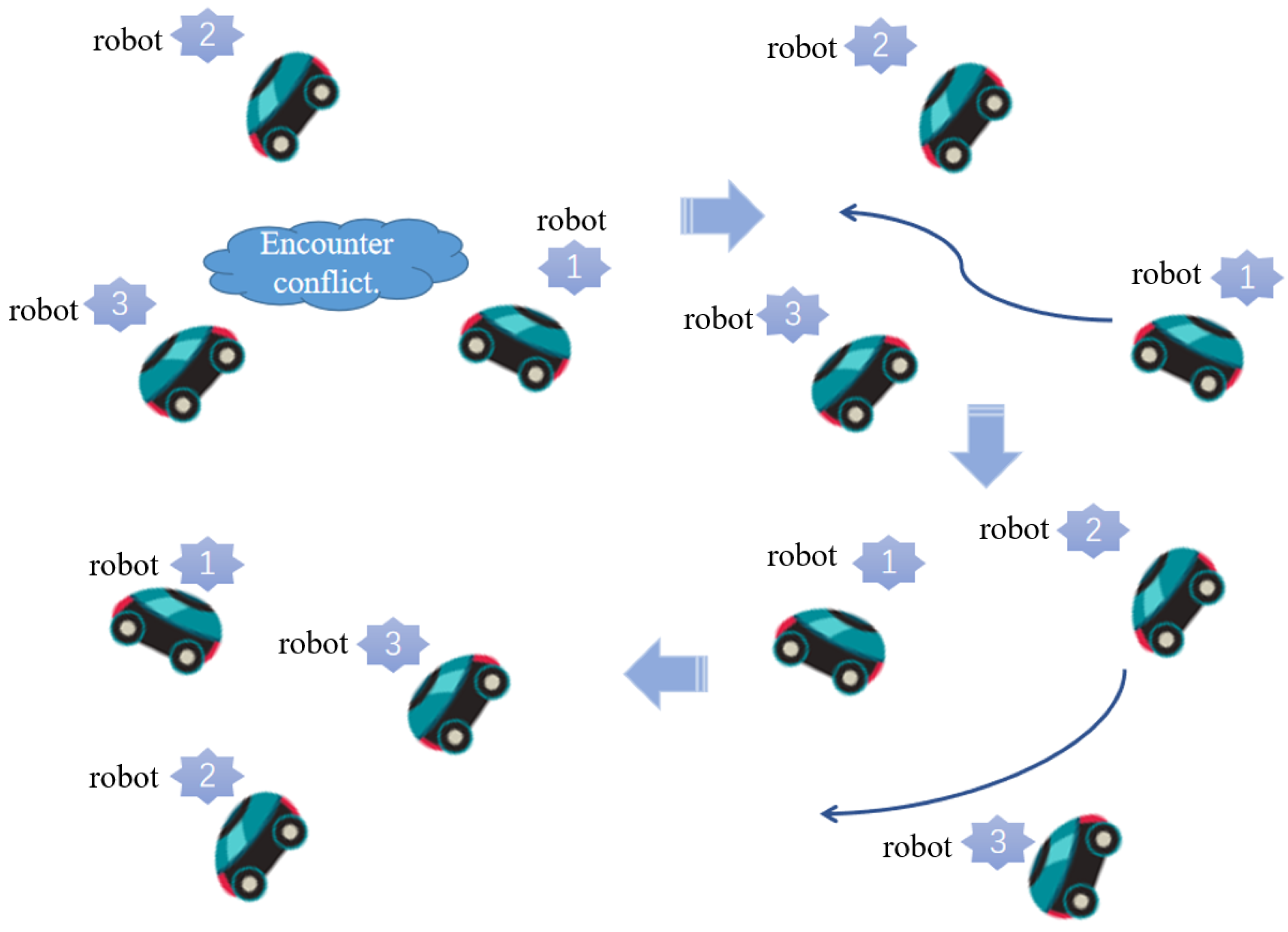
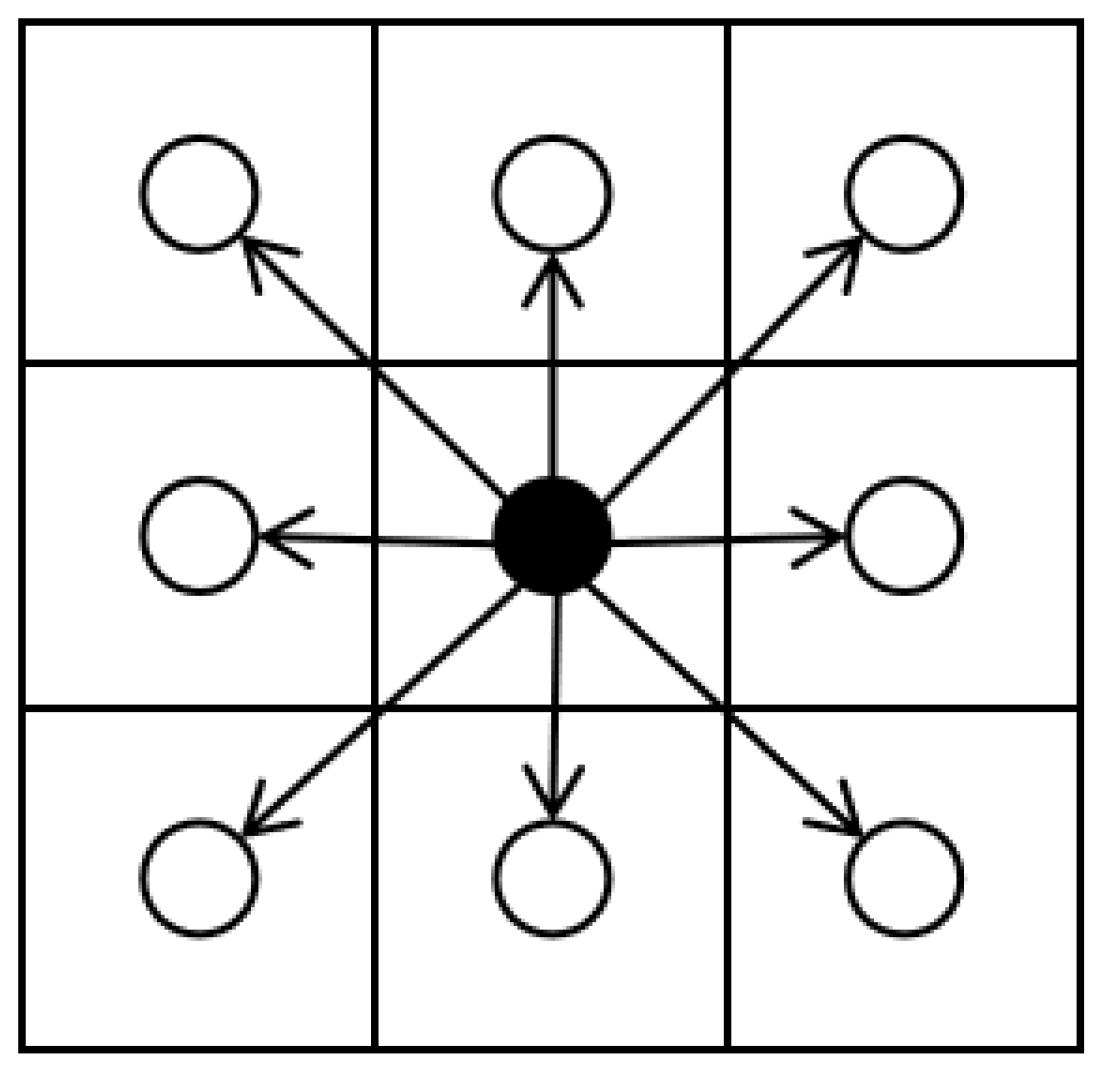
1. Introduction

With the development of intelligent robotics technology, multi-robot systems are increasingly applied in fields such as industry, logistics, agriculture, and rescue operations. In modern logistics warehouses, multiple autonomous robots often need to collaborate to complete tasks such as goods handling and sorting. These robots must not only avoid shelves and walls but also navigate in real-time to avoid other robots and workers. In modern agriculture, robots frequently move efficiently in complex field environments to perform tasks such as crop monitoring, fertilizing, and spraying. However, path planning for multi-robot systems in complex dynamic environments remains a challenging research problem. Path planning not only needs to ensure that robots can successfully reach their target points but also must address a series of issues, such as avoiding unknown obstacles, real-time avoidance of dynamic obstacles, and coordination of robot-to-robot conflicts. Traditional path planning algorithms, such as the A* algorithm [1], genetic algorithms [2], ant colony optimization [3], zebra optimization algorithm [4], grey wolf optimization [5,6], and whale optimization algorithms [7,8], excel in static environments but exhibit limitations in dynamic settings. They struggle to effectively manage real-time obstacle avoidance and multi-robot coordination. In such ever-changing environments, planning algorithms must also possess the robust capability to counter various uncertainties [9,10].

Yang et al. [11,12,13] were the pioneers in applying the Shunting neural network model to mobile robot path planning, proposing a bio-inspired neural network algorithm. This algorithm, which does not require any neural network learning or training process, has demonstrated good real-time performance and has found widespread application. Building on the foundation of bio-inspired neural networks, Tang [14] introduced the template model method and jump point search algorithm to address the original algorithm’s inability to fully cover and lock adjacent obstacles. Luo [15] incorporated the multi-scale mapping method into bio-inspired neural networks, reducing the time cost and mathematical complexity of the path planning algorithm. Han et al. [16] proposed a novel CCPP strategy, where the planned path of the robot depends not only on neuron activity but also on the distribution of obstacles in the environment map. They used a proposed path backtracking algorithm to reduce path redundancy. Qu et al. [13] addressed the issue of neuron signals being confined to local propagation by proposing a method to propagate neuron waveforms, linking the propagation distance to signal strength. Wang [16] tackled the problem of low neuron activity values near boundaries and obstacles by proposing an improved BINN, effectively optimizing the movement paths of multiple robots. Analysis reveals that past research has, to varying degrees, improved the neural network algorithm’s tendency to fall into local optima. However, these improvements have not adequately balanced the algorithm’s local and global optimization capabilities, and in complex environments, the algorithm fails when dynamic obstacles appear.

The Dynamic Window Approach (DWA) algorithm, introduced by Fox et al. [17], is a classic method that ingeniously transforms the problem of positional constraints into a velocity constraint problem, thus converting obstacle avoidance into an optimal velocity execution issue. Xu et al. [18] proposed a Parameter-Adaptive DWA (PA-DWA) algorithm, addressing the limitations of the traditional DWA in complex environments with numerous obstacles, where fixed parameters fail to balance safety and speed effectively. Gong et al. [19] improved the original DWA by enhancing the speed cost function and adding a distance cost function for the target point, enabling the robot to continuously adjust and adapt to unknown environments. Chang et al. [20] modified and expanded the existing evaluation function by introducing two new evaluation functions to enhance global navigation performance. Liu et al. [21] addressed the poor adaptability of fixed DWA evaluation function weights in complex environments by designing a fuzzy controller to improve the algorithm’s adaptability. Mai et al. [22] introduced an obstacle density-related evaluation factor into the evaluation function for environments with dense obstacles, further enhancing the efficiency of the DWA in complex settings, though it still falls short of achieving globally optimal paths. Currently, the standalone DWA algorithm struggles with processing complex maps and is prone to falling into “traps” and local optima.

The existing research has improved neural network algorithms and the DWA algorithm from different perspectives. However, studies that simultaneously consider environmental information, obstacle avoidance capabilities, and coordination between multiple robots in multi-robot path planning are relatively scarce. To address these challenges, this paper proposes a dual-layer symmetric path planning method based on an improved neural network-DWA algorithm. This method not only enables robots to achieve more efficient and real-time path planning in complex dynamic environments but also significantly enhances the collaborative capabilities and safety of multi-robot systems. The main contributions of this paper are as follows:

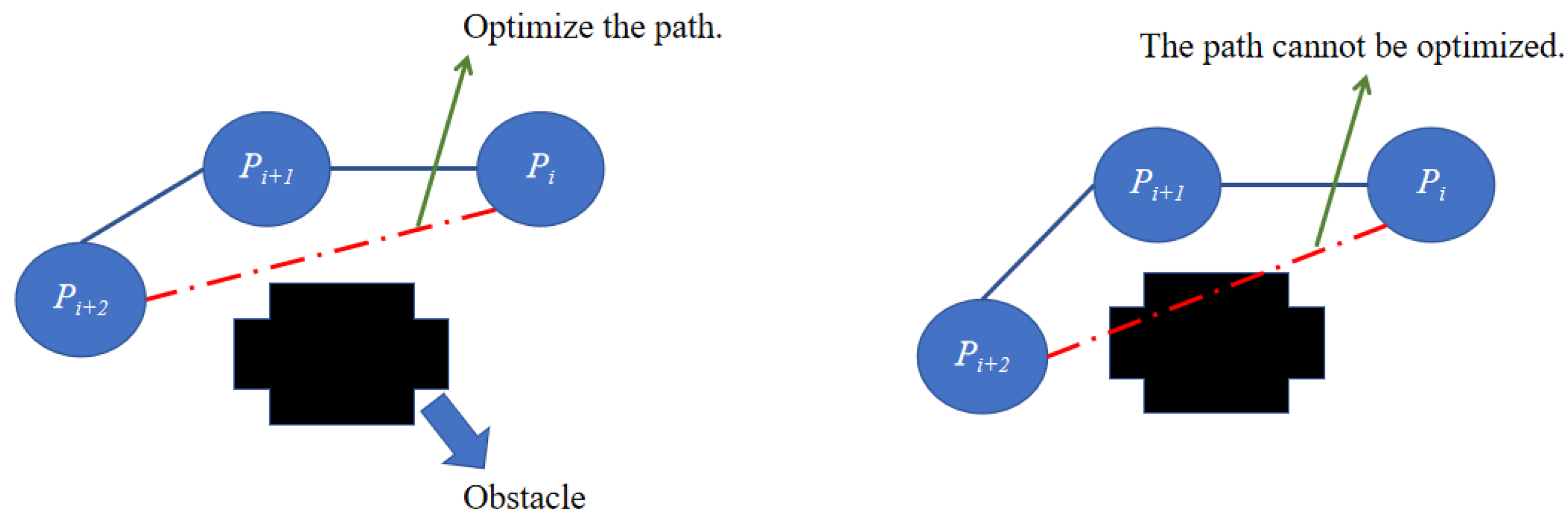
(1) In the traditional GBNN algorithm, the propagation of neuronal activation signals is typically limited to a local range, causing the algorithm to easily fall into local optima and fail to effectively explore the global space, resulting in low global optimization capability. To address this issue, we introduce the concept of single-neuron signal waveform propagation. The signals from the target neuron propagate like waves across the global space, allowing the activation signals to span a larger area and influence more neurons. This expands the search range, enhances the global optimization ability, and establishes a path optimization function to remove redundant points from the path, improving its smoothness.

(2) To address the obstacle avoidance requirements in complex dynamic environments, a reward function is introduced to improve the traditional Score function in the DWA algorithm. This effectively reduces detour paths and minimizes the probability of deviation from the planned trajectory, ensuring real-time obstacle avoidance while maintaining the optimality of the global path.

(3) When multiple robots encounter each other, traditional priority assignment methods usually rely on static rules, which can lead to low-priority robots waiting for long periods or result in unreasonable path planning. To address this issue, the dynamic priority rule proposed in this paper adjusts the priority in real-time based on the robot’s distance to the target point. Robots closer to the target point are assigned higher priority and are given tasks first. When two robots are at the same distance from the target point, the robot with the smaller ID will have a higher priority, indicating a more urgent task. This allows robots to flexibly adjust their travel order based on the actual situation, effectively avoiding conflicts between robots and improving the overall efficiency and coordination of the system.

(4) This paper proposes an improved dual-layer symmetric path planning algorithm based on the improved GBNN algorithm and the enhanced DWA, enabling multi-robots to achieve real-time obstacle avoidance in dynamic environments while effectively addressing the conflicts between robots.

For the multi-robot path planning problem, this paper employs a dual-layer symmetric path planning method based on an improved neural network-DWA algorithm. First, a signal waveform propagation model for single-neuron signals is established. Then, the Score function of the DWA algorithm is improved. Next, a dynamic priority rule is applied to effectively resolve conflicts between robots. Finally, the improved GBNN algorithm is combined with the enhanced DWA.

The structure of the rest of this paper is as follows: Section 2 introduces the conflict model for multi-robot systems and the improved priority algorithm. Section 3 presents the improved global path planning method. Section 4 introduces the improved local path planning method. Section 5 discusses the proposed method. Section 6 provides the experimental simulation results. Section 7 concludes with the conclusion and outlook.

2. Conflict Model for Multi-Robot Systems

When in multi-robot systems, the establishment of a conflict model is pivotal for ensuring system coordination and stability. Each robot must not only develop precise obstacle avoidance strategies based on the movement trajectories and dynamic states of obstacles but also effectively resolve coordination and cooperation issues with other robots. This ensures the overall operational efficiency and safety of the system. We categorize the conflicts encountered between multiple robots into four main types: reverse conflicts (a), same-direction conflicts (b), crossing conflicts (c), and complex crossing conflicts (d), as illustrated in Figure 1.

In multi-robot systems, the priority method is a classic conflict resolution strategy initially proposed by Erdmann. In multi-robot path planning, robot priority is a strategy used to coordinate conflicts and competition among multiple robots. When conflicts arise, the robot with higher priority is granted the right of way, while the robot with lower priority must yield or automatically brake. However, traditional priority methods rely on predefined static rules, which can lead to excessive waiting times for low-priority robots and complicate local path planning, thus affecting the overall path optimization.

This paper introduces a dynamic priority rule to address path conflicts in multi-robot systems. This method dynamically adjusts robot priorities by comparing the distance of each robot from its current position to its target point. Robots closer to their target point are assigned higher priority, while those farther away must yield to higher priority robots. If two robots are equidistant from their target points, priority is determined by the urgency of their tasks; the smaller the robot’s number, the more urgent its task, thereby assigning it a higher priority, as illustrated in Figure 2. This dynamic adjustment mechanism aims to reduce the waiting time for low-priority robots and enhance overall path planning efficiency.

3. Global Path Planning

3.1. Neural Network Algorithm

To address the issues of prolonged learning time, complex training processes, and high computational demands in artificial neural network algorithms, Canadian scholar Simon X. Yang proposed a biologically inspired neural network algorithm that requires no prior knowledge and has a reduced computational load. This model was subsequently applied to the path planning of mobile robots.

Based on predefined grid coordinates, a two-dimensional neural network model is constructed in a two-dimensional grid coordinate system, with each cell corresponding to a neuron in the neural network. For instance, the i-th cell represents the i-th neuron. Within the receptive field shown in Figure 3, each neuron can transmit its information to its eight neighboring neurons. In other words, once a neuron is activated (Filled circle), its eight adjacent neurons will also be activated and receive the corresponding information (Hollow circles).

The GBNN algorithm is a discrete, biologically inspired neural network. Its core concept involves the target neuron continuously transmitting excitation signals through the topological space, while obstacles exert an inhibitory effect on these signals. This process ultimately forms a neural network activity field within the topological space, as illustrated in Figure 4.

The GBNN model is described by Equations (1)–(3):

$$x_i(t+1)=g(\sum _{j=1}^M{w}_{ij}{\left[x_j\left(t\right)\right]}^{+}+I_i)$$

(1)

$$w_{ij}=\left\{\begin{array}{cc}{e}^{-{(i-j)}^2},\hfill & |i-j|⩽r\hfill \\ 0,\hfill & |i-j|>r\hfill \end{array}\right.$$

(2)

$$|i-j|=\sqrt{{\left(x_{ix}-x_{jx}\right)}^2+{\left(x_{iy}-x_{jy}\right)}^2}$$

(3)

where $x_i$ represents the input activity value of neuron i; $x_j$ denotes the neurons within the half-price radius r; |i − j| and $w_{ij}$ are the Euclidean distance and connection weight between neurons i and j, respectively. $I_i$ is the external excitation for neuron i.

The mathematical model for $I_i$ is given by Equation (4):

$$I_i=\left\{\begin{array}{cc}G,\hfill & \mathrm{destination}\mathrm{grid}\hfill \\ -G,\hfill & \mathrm{obstacle}\mathrm{grid}\hfill \\ 0,\hfill & \mathrm{free}\mathrm{grid}\hfill \end{array}\right.$$

(4)

where G is a positive number greater than 0.

The transformation function model is given by Equation (5):

$$g\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<0\hfill \\ k_{g}x,\hfill & 0<x<1\hfill \\ 1,\hfill & x>1\hfill \end{array}\right.$$

(5)

Here, $k_g$ is constrained within the range of 0 to 1.

3.2. Enhancing the Neural Network Algorithm

To address the weak global optimization capability of the traditional GBNN algorithm in path planning, this paper introduces a wave propagation method. By propagating the activation values of target neurons in waves, we establish a relationship between these values and the distances to global neurons. The wave propagation model for target neurons is as follows:

$$G_{t_1}=\{\left(G_{t_0}+1\right)\cup \left(G_{t_0}+\sqrt{2}\right)\}$$

(6)

$$G_{t_0}=unique\left(G_{t_1}\right)$$

(7)

In Equations (6) and (7), $G_{t_0}$ represents the base array for each iteration, initialized to 0. $G_{t_1}$ denotes the array of distances to the target neurons. The term unique refers to removing duplicate values from the array and sorting the remaining values in ascending order.

The calculation formula for the activation values of neurons is given by Equations (8) and (9):

$$x_i=I_i$$

(8)

$$l_i=\left\{\begin{array}{cc}G,\hfill & \mathrm{destination}\mathrm{grid}\hfill \\ -G,\hfill & \mathrm{obstacle}\mathrm{grid}\hfill \\ {\displaystyle \frac{1}{G_{t_0}}}\hfill & \mathrm{free}\mathrm{grid}\hfill \end{array}\right.$$

(9)

In Equations (8) and (9), $x_i$ represents the input activation value of neuron i, and $I_i$ denotes the external stimulation of neuron i.

Through waveform propagation, the activation value’s magnitude of the target neuron is effectively correlated with the propagation distance. The waveform propagation method of the target neuron and the distribution of its activation values are illustrated in Figure 5.

Due to environmental obstacles and the local optimal choices of neural network algorithms, robots often generate paths with unnecessary turns, leading to increased path length and potentially affecting overall task efficiency. To address these issues, this paper incorporates a path optimization function into the improved neural network model, removing redundant points to simplify the path and enhance navigation smoothness.

The path optimization function proposed in this paper is based on geometric analysis. Firstly, as the algorithm traverses the path points, it detects whether each intermediate point plays a crucial role in avoiding obstacles within the current segment. If the detection indicates that the path can still avoid obstacles after removing the point, it is considered redundant and thus removed. The set of path points planned by the improved neural network algorithm is denoted as P.

$$P=\{P_1,P_2,\dots ,P_n\}$$

(10)

where $P_i=\begin{array}{c}(x_i,y_i)\end{array}$.

The perpendicular distance from the obstacle point $(x_{obs},y_{obs})$ to the line $\overrightarrow{P_i{P}_{i+2}}$ is calculated as distance:

$$\mathrm{distance}=\frac{|(y_{i+2}-y_i)·x_{obs}-(x_{i+2}-x_i)·y_{obs}+x_{i+2}·y_i-y_{i+2}·x_i|}{\sqrt{{(y_{i+2}-y_i)}^2+{(x_{i+2}-x_i)}^2}}$$

(11)

$$\left\{{\displaystyle \frac{distance<ϵ,\mathrm{intersects}\mathrm{with}\mathrm{the}\mathrm{obstacle}}{distance>ϵ,\mathrm{does}\mathrm{not}\mathrm{intersect}\mathrm{with}\mathrm{the}\mathrm{obstacle}}}\right\}$$

(12)

If the obstacle point does not intersect with the straight line $\overrightarrow{P_i{P}_{i+2}}$, then point $P_{i+1}$ can be deleted, and it can be determined whether $\overrightarrow{P_i{P}_{i+2}}$ can substitute the path segments $\overrightarrow{P_i{P}_{i+1}}$ and $\overrightarrow{P_{i+1}{P}_{i+2}}$. If the obstacle intersects with $\overrightarrow{P_i{P}_{i+2}}$, the intermediate point $P_{i+1}$ must be retained, as illustrated in Figure 6. The optimized path can be expressed as:

$$\begin{array}{c}\hfill {\mathit{P}}_{\mathit{optimized}}=\left\{P_1\right\}\cup \left\{P_i\right|\exists (x_{obs},y_{obs})\in \mathit{O},\mathrm{distance}(P_i,P_{i+2},(x_{obs},y_{obs}))<ϵ\}\cup \left\{P_n\right\}\end{array}$$

(13)

Here, $P_{optimized}$ represents the set of optimized paths, $P_1$ and $P_n$ represent the starting and ending points of the path, respectively, O represents the set of obstacles.

The blue solid line represents the original path, and the red dashed line represents the optimized path.

4. Local Path Planning

4.1. DWA Algorithm

The traditional Dynamic Window Approach (DWA) is an obstacle avoidance algorithm grounded in local path planning, widely utilized in the navigation of mobile robots. The essence of the DWA algorithm lies in its real-time dynamic sampling of the robot’s velocity space, generating a set of potential velocity pairs (linear and angular velocities). From this set, the algorithm selects the most optimal velocity pair, ensuring that the robot can advance towards its target while deftly circumventing obstacles.

Within a specified time window, the DWA algorithm initially samples the velocity space based on the robot’s current speed, generating multiple candidate velocity pairs. This velocity space is constrained by the robot’s maximum acceleration, deceleration, and current speed limitations.

$$\begin{array}{cc}\hfill {\nu }_{min}& \le \nu \left(t\right)\le {\nu }_{max},\hfill \\ \hfill {\omega }_{min}& \le \omega \left(t\right)\le {\omega }_{max}.\hfill \end{array}$$

(14)

Here, $v_{min}$ and $v_{max}$ represent the robot’s minimum and maximum linear velocities, respectively.

Following the sampling of the velocity space, the DWA algorithm predicts trajectories for each velocity pair (v, w), simulating the robot’s motion over a future time interval T. The robot’s trajectory can be described by the following differential equations:

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=v\left(t\right)·cos\left(\theta \left(t\right)\right)\\ \hfill \dot{y}\left(t\right)=v\left(t\right)·sin\left(\theta \left(t\right)\right)\\ \hfill \dot{\theta }\left(t\right)=\omega \left(t\right)\end{array}$$

(15)

Here, $\left(x\right(t),y(t\left)\right)$ denote the robot’s coordinates at time t, while $\theta \left(t\right)$ represents the robot’s orientation angle. After conducting a search and sampling within the velocity space, the DWA algorithm simulates several feasible trajectories corresponding to multiple velocity combinations (v, $\omega$). Subsequently, each trajectory is assessed using a scoring function. The traditional DWA evaluation function encompasses three criteria: the goal orientation function, the obstacle clearance function, and the velocity function, expressed as follows:

Objective function:

$$G(v,\omega )=\mathrm{distance}\mathrm{to}\mathrm{goal}(v,\omega )$$

(16)

Obstacle avoidance function:

$$O(v,\omega )=\mathrm{distance}\mathrm{to}\mathrm{nearest}\mathrm{obstacle}(v,\omega )$$

(17)

Velocity smoothness function:

$$V(v,\omega )=|v-v_{\mathrm{preferred}}|+|\omega -{\omega }_{\mathrm{preferred}}|$$

(18)

Comprehensive evaluation function:

$$\mathrm{Score}(v,\omega )=\alpha ·G(v,\omega )+\beta ·O(v,\omega )+\gamma ·V(v,\omega )$$

(19)

Here, $\alpha$, $\beta$, and $\gamma$ serve as weighting parameters to balance the significance of various evaluation metrics.

The DWA algorithm assigns scores to all possible speed pairs (v, $\omega$) using the evaluation function and selects the pair with the highest score as the control input for the robot’s movement at the next moment.

$$(v^{*},{\omega }^{*})=\underset{(v,\omega )}{\mathrm{maxScore}}(v,\omega )$$

(20)

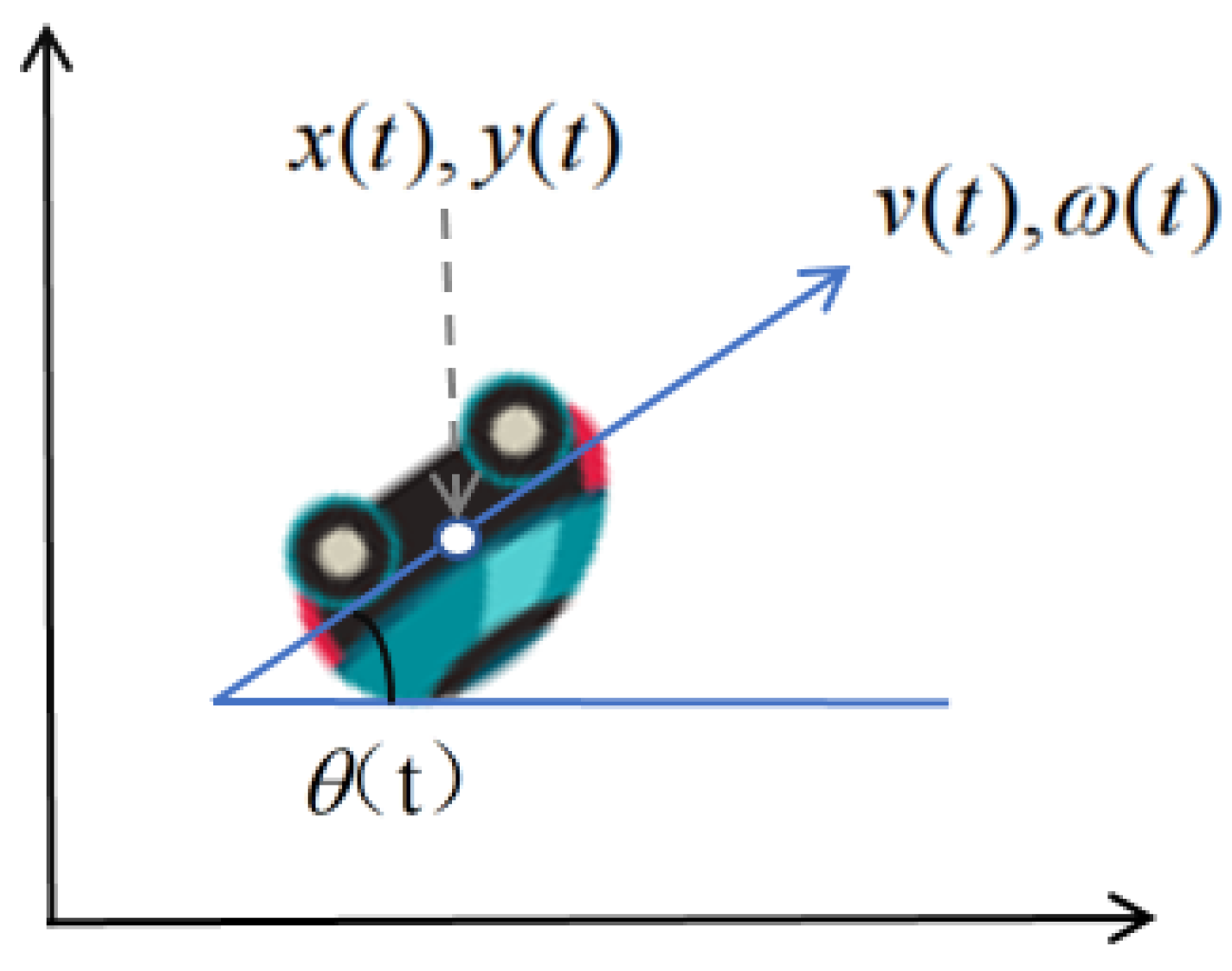
This study focuses on non-holonomic mobile robots, which are restricted to forward movement, turning, and waiting in place. As illustrated, we assume that the robot’s trajectory can be segmented into multiple time slices. Within each time slice $\Delta t$, the robot can be approximated as moving in uniform straight-line motion, and its kinematic model can be expressed as follows:

$$\left\{\begin{array}{c}x\left(t\right)=x(t-1)+v\left(t\right)\Delta tcos\left(\theta \right(t-1\left)\right)\hfill \\ y\left(t\right)=y(t-1)+v\left(t\right)\Delta tsin\left(\theta \right(t-1\left)\right)\hfill \\ \theta \left(t\right)=\theta (t-1)+\omega \left(t\right)\Delta t\hfill \end{array}\right.$$

(21)

As depicted in Figure 7, the variables $x\left(t\right)$, $y\left(t\right)$, and $\theta \left(t\right)$ represent the robot’s position along the x and y axes and its orientation at time t, respectively. The range of linear velocity $v\left(t\right)$ is contingent upon the robot’s closest distance to obstacles and its maximum linear deceleration. Meanwhile, the variation in angular velocity $\omega \left(t\right)$ is determined by both the robot’s proximity to obstacles and its maximum angular deceleration.

4.2. Enhanced DWA Algorithm

The conventional DWA algorithm’s comprehensive evaluation function primarily takes into account the distance to the target, obstacle avoidance capability, and smoothness of velocity. However, this approach can lead the robot to opt for longer detours or excessive and unnecessary maneuvers in complex environments, thereby diminishing the efficiency of path planning.

In path planning, factors such as the shortest route and minimal turns should be considered. This paper’s reward function is based on an improved neural network algorithm for static path planning. Specifically, during local path tracking, we establish a search circle with a radius r around the robot’s current position ($x_{robot}$, $y_{robot}$). If the path point generated by the neural network ($x_{NN}$, $y_{NN}$) lies within this search circle, the robot receives a reward score for that local path. This reward mechanism effectively guides the robot to prioritize movement along the static planned path, thereby reducing the likelihood of deviating from the optimal route and minimizing the occurrence of detours and unnecessary turns. The reward function can be expressed as

$$R(v,\omega )=\lambda ·\delta (\sqrt{{(x_{\mathrm{robot}}-x_{\mathrm{NN}})}^2+{(y_{\mathrm{robot}}-y_{\mathrm{NN}})}^2}\le r)$$

(22)

Here, $\lambda$ represents the reward weight parameter, which adjusts the influence of the reward score within the comprehensive evaluation function; $\delta (·)$ is the indicator function, taking a value of 1 when the neural network path point ($x_{NN}$, $y_{NN}$) is within the search circle, and 0 otherwise. The final comprehensive evaluation function can be expressed as:

$$\mathrm{Score}(\nu ,\omega )=\alpha ·G(\nu ,\omega )+\beta ·O(\nu ,\omega )+\gamma ·V(\nu ,\omega )+\eta R(\nu ,\omega )$$

(23)

$G(v,\omega )$ represents the distance score, indicating the robot’s progression towards the target point. $O(v,\omega )$ denotes the obstacle avoidance score, $V(v,\omega )$ signifies the velocity smoothness score, and $R(v,\omega )$ is the newly introduced reward function, designed to encourage the robot to advance along a more optimal path. The parameters $\alpha$, $\beta$, $\gamma$, and $\eta$ serve as weights for these four evaluation functions, balancing the influence of various factors on path selection.

5. Improved Neural Network-DWA Dual-Layer Symmetric Path Planning Algorithm

While the standalone improved neural network algorithm can effectively generate a collision-free path from the starting point to the target, its performance often falls short when confronted with dynamic or unknown obstacles in the environment. Furthermore, in maps characterized by complex static obstacles, relying solely on the DWA algorithm for local path planning may lead the robot to become trapped in local optima, ultimately preventing it from reaching its destination.

To address this shortcoming, this paper presents a method that integrates the improved neural network algorithm with the enhanced DWA algorithm, leveraging the strengths of both approaches. In this hybrid algorithm, the improved neural network is tasked with global path planning, ensuring the generation of a collision-free route in static environments, while the enhanced DWA algorithm focuses on dynamic obstacle avoidance, managing moving or unknown obstacles in real-time settings. With the support of this integrated approach, the robot can not only rely on the global path provided by the neural network but also benefit from the dynamic adjustments of the DWA algorithm, enabling a responsive navigation through complex environments.

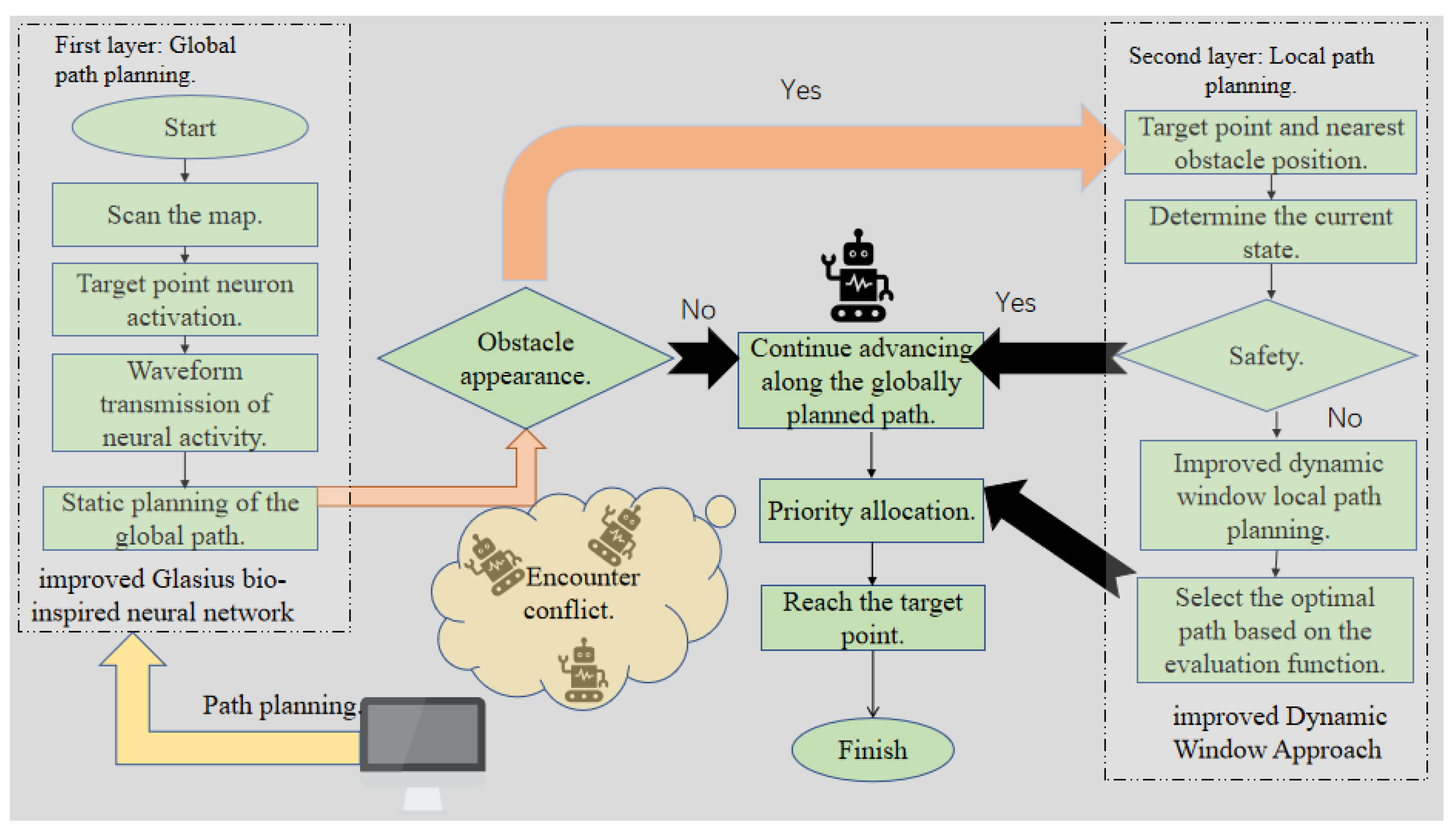
The specific algorithm flow is shown in Figure 8. In the first layer of path planning, the robot first models the complex static environment using a grid-based method. Then, after the target neuron is activated, the waveform propagates the neuron activity. Using the neural network algorithm, a global collision-free shortest path is planned for the robot, which it will follow to start moving. The waveform propagation model of the target neuron is represented by Equations (6)–(9), and the optimal path point set is defined by Equation (13). During the robot’s movement along the global path, if dynamic obstacles are encountered, the process transitions to the second layer of path planning—local path planning based on the improved DWA algorithm. First, the robot determines its current state, and then selects the trajectory with the optimal evaluation function value based on its current state. Once the robot determines that the distance to the obstacle has reached a safe range, it exits the second layer of path planning and continues moving along the global path toward the target point. The final comprehensive evaluation function is defined by Equation (23). If the robot encounters conflicts due to interactions with other robots during movement, a priority allocation is performed, and the robot continues moving toward the target point.

6. Experiments

To validate the path planning method of the improved neural network and DWA algorithm under complex road conditions and to better illustrate the algorithm’s performance, this paper conducts simulation experiments from three perspectives. The first direction focuses on performance analysis, which includes a comparative study of the algorithm’s effectiveness before and after improvements in a static environment, as well as comparisons with other algorithms to confirm its overall superiority. The second direction examines dynamic environments, assessing the flexibility of this method in addressing robot collision conflicts and encountering unknown or dynamic obstacles. The third direction explores complex environments, where the introduction of more intricate known obstacles, unknown obstacles, and dynamic obstacles within a multi-robot system demonstrates the comprehensive advantages of this algorithm in tackling complex challenges. The simulations were conducted using MATLAB R2022B on a Windows 11 platform.

6.1. Algorithm Performance Experiments

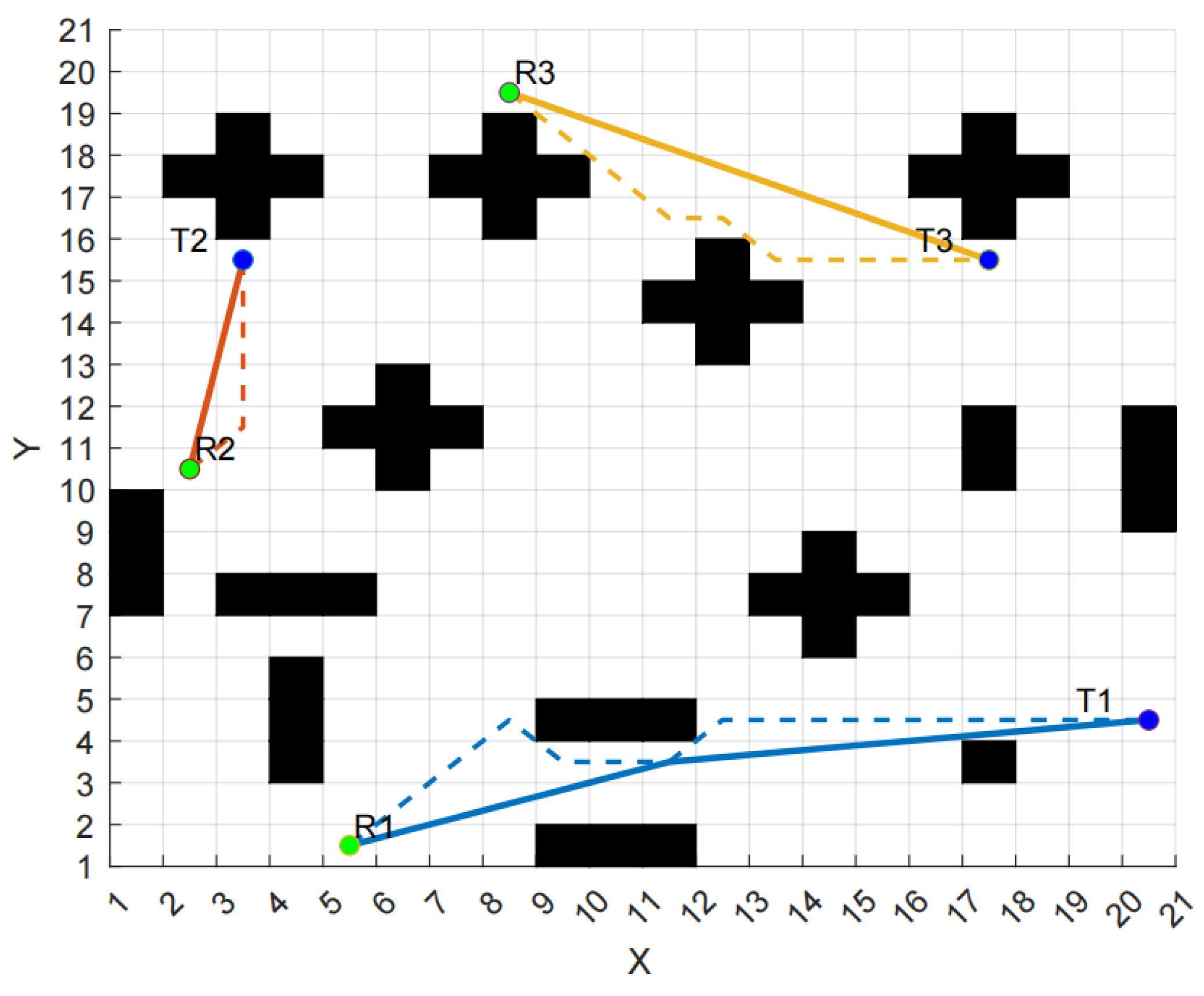
Due to the limitations of traditional neural network algorithms, robots often generate excessive turns in complex environments, resulting in increased path lengths. As illustrated in Figure 9, the dashed line represents the path planned by the improved neural network model proposed in this paper, while the solid line denotes the path planned using the optimized function incorporated into the improved neural network model. The experimental setup comprises a 21 × 21 grid map with 51 obstacles and 3 robots.

R1–R3 represent the starting points of each robot, T1–T3 represent the target points of each robot, the dashed lines represent the original paths of the robots, and the solid lines represent the optimized paths.By analyzing Figure 9, we can obtain the data presented in

Table 1. Performance data before and after the integration of the optimization function in the improved neural network.

R	Number of Turns			Path Distance
	Before Optimization	After Optimization	Enhancement	Before Optimization	After Optimization	Enhancement
R1	4	1	75%	17.07	15.38	10%
R2	1	0	100%	5.41	5.10	6%
R3	3	0	100%	10.66	9.85	8%

.

Through Table 1, we observe that the improved neural network optimization demonstrates an increase in turning frequency of as much as 100% and no less than 75% compared to the previous optimization. The path distance shows a maximum enhancement of 10% and a minimum of 6%, significantly enhancing both the smoothness and length of the path.

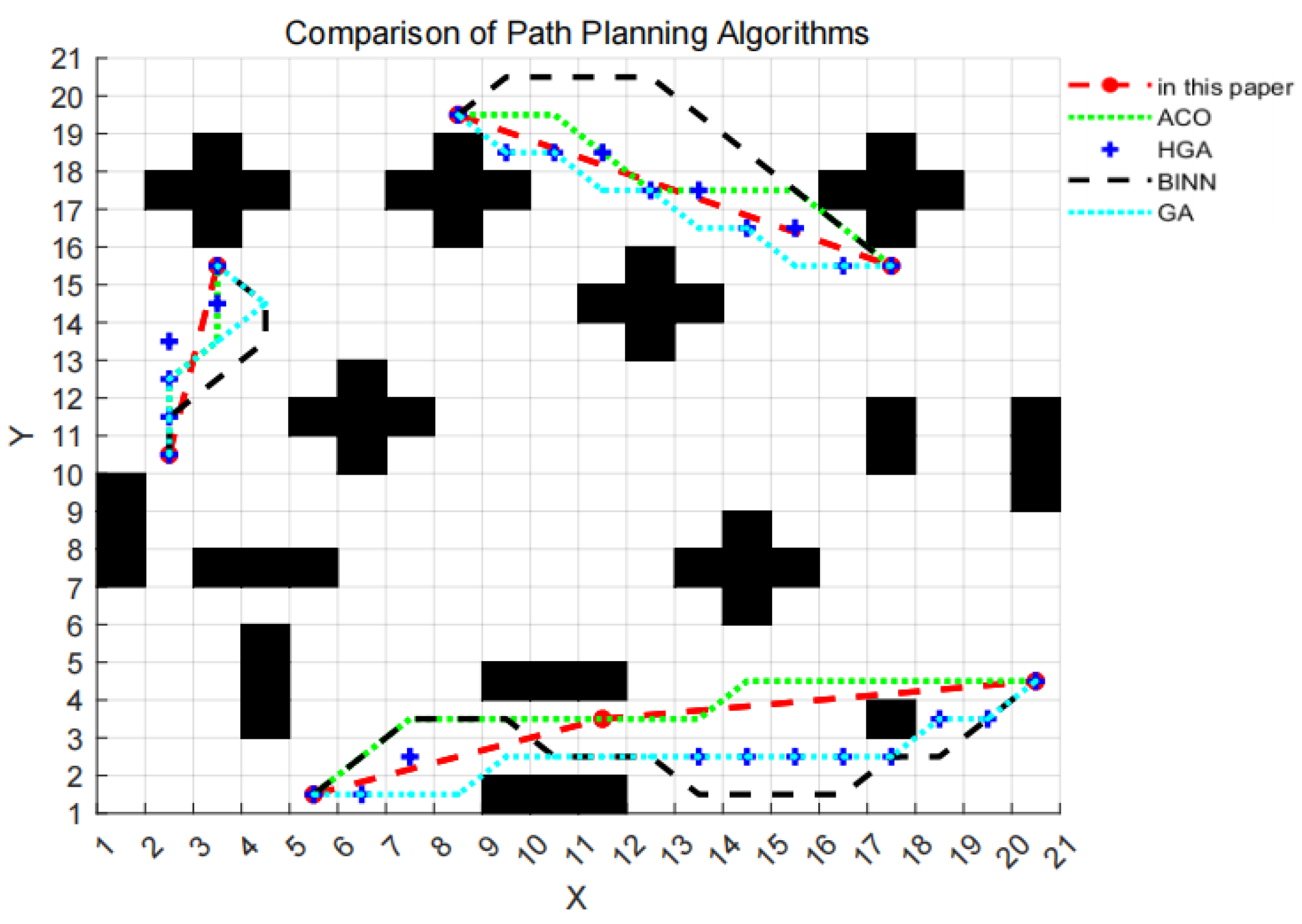
To validate the performance of the improved neural network—DWA algorithm, we compared it with traditional approaches such as the Genetic Algorithm (GA), Ant Colony Optimization (ACO), Hybrid Genetic Algorithm (HGA), and Bio-inspired Neural Network Algorithm (BINN). The results are shown in Figure 10.

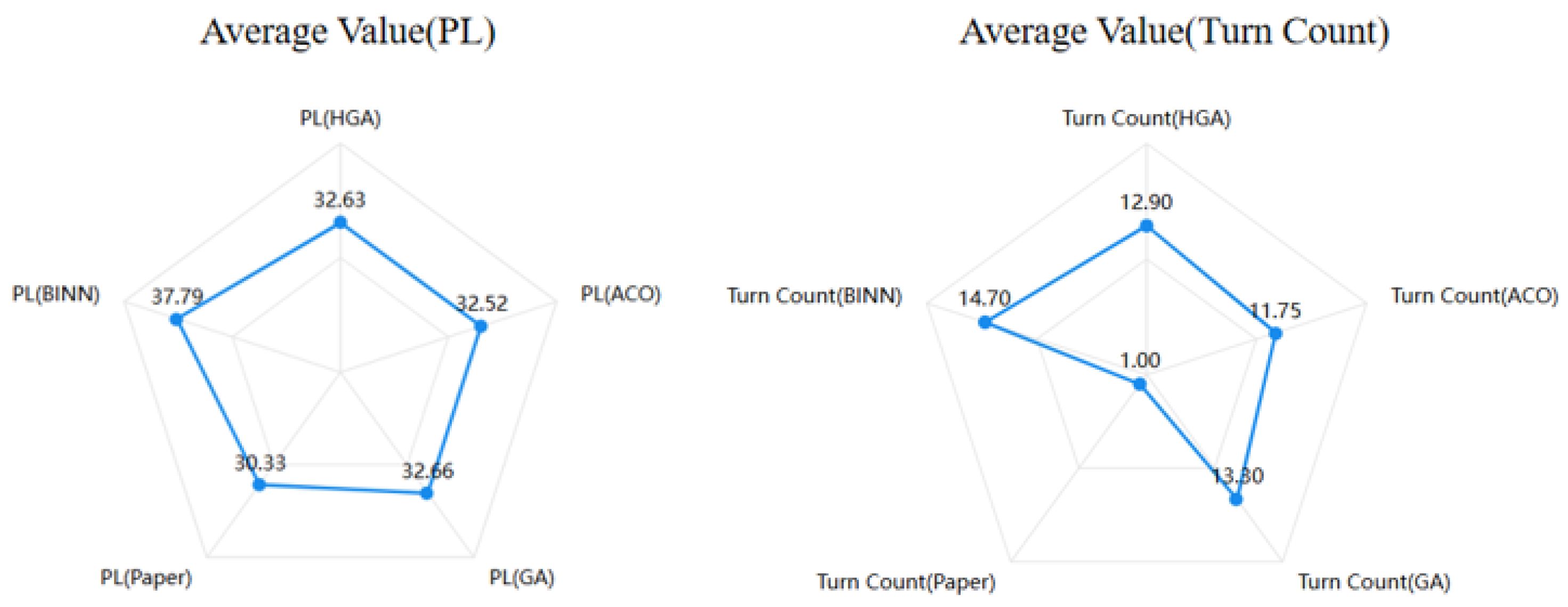
From Figure 10, it is evident that the path planned by our method significantly outperforms those generated by other algorithms in terms of path distance and turning frequency. To mitigate the effects of randomness and ensure the accuracy of our results, we conducted 20 repeated simulation experiments. The analyzed experimental data is presented in Figure 11 and

Table 2. Analysis of repeated experimental data for different algorithms.

Algorithm	Type	Average Value	Variance	Standard Error	IQR	CV	Enhancement
GA	PL (m)	32.659	0.372	0.136	0.830	1.868%	7.13%
	Turn Count	13.300	1.905	0.309	1.000	10.378%	92.48%
ine ACO	PL (m)	32.518	0.136	0.082	0.623	1.134%	6.72%
	Turn Count	11.750	3.355	0.414	2.750	15.589%	91.48%
ine HGA	PL (m)	32.630	0.164	0.091	0.830	1.242%	7.07%
	Turn Count	12.900	3.989	0.447	2.000	15.483%	92.24%
ine BINN	PL (m)	37.790	1.083	0.233	1.453	2.754%	19.74%
	Turn Count	14.700	5.379	0.519	2.750	15.777%	93.19%
ine Paper	PL (m)	30.330	0.000	0.000	0.000	0.000%
	Turn Count	1.000	0.000	0.000	0.000	0.000%

.

Through the repeated experimental data presented in Table 2, we found that the paths planned using the proposed method achieve the shortest path length and the lowest total number of turns compared to other methods. In terms of path length, the proposed method demonstrates improvements of up to 19.74% over other algorithms, and in terms of the number of turns, improvements reach up to 93.17%. Additionally, in the repeated experiments, the variance, standard error, interquartile range (IQR), and coefficient of variation (CV) of the proposed method are all zero. Compared to other methods, the proposed method significantly improves path quality while exhibiting excellent robustness and stability.

6.2. Experiments in Dynamic Environments

In dynamic environments, robots must navigate various uncertainties, such as encountering conflicts, unknown obstacles, and dynamic barriers. These challenges are particularly pronounced in multi-robot systems. The improved neural network proposed in this paper—the DWA algorithm—introduces a dynamic priority mechanism, enabling robots to automatically slow down, brake, or change direction when approaching other robots, unknown obstacles, or dynamic barriers, thereby preventing collisions.

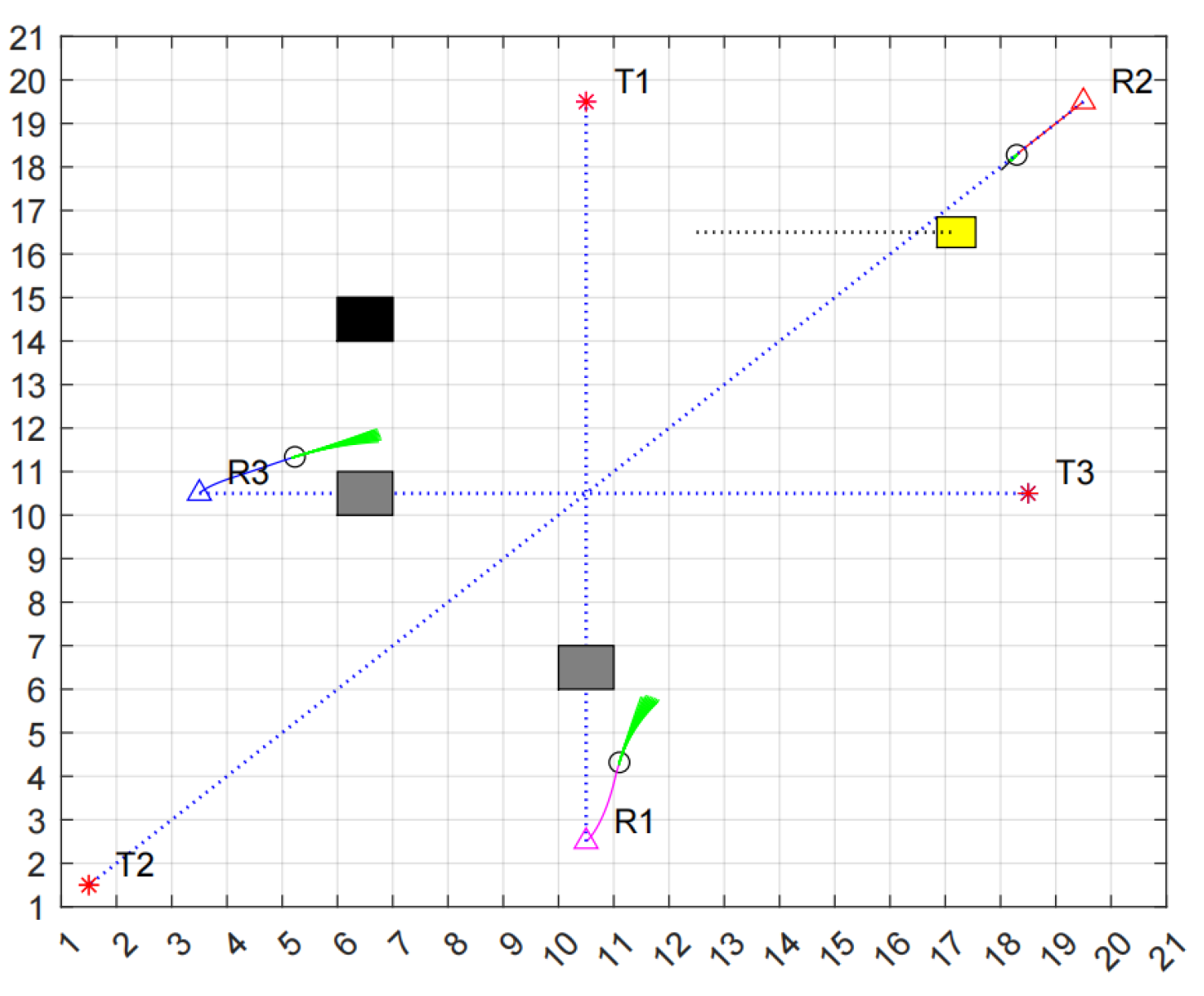
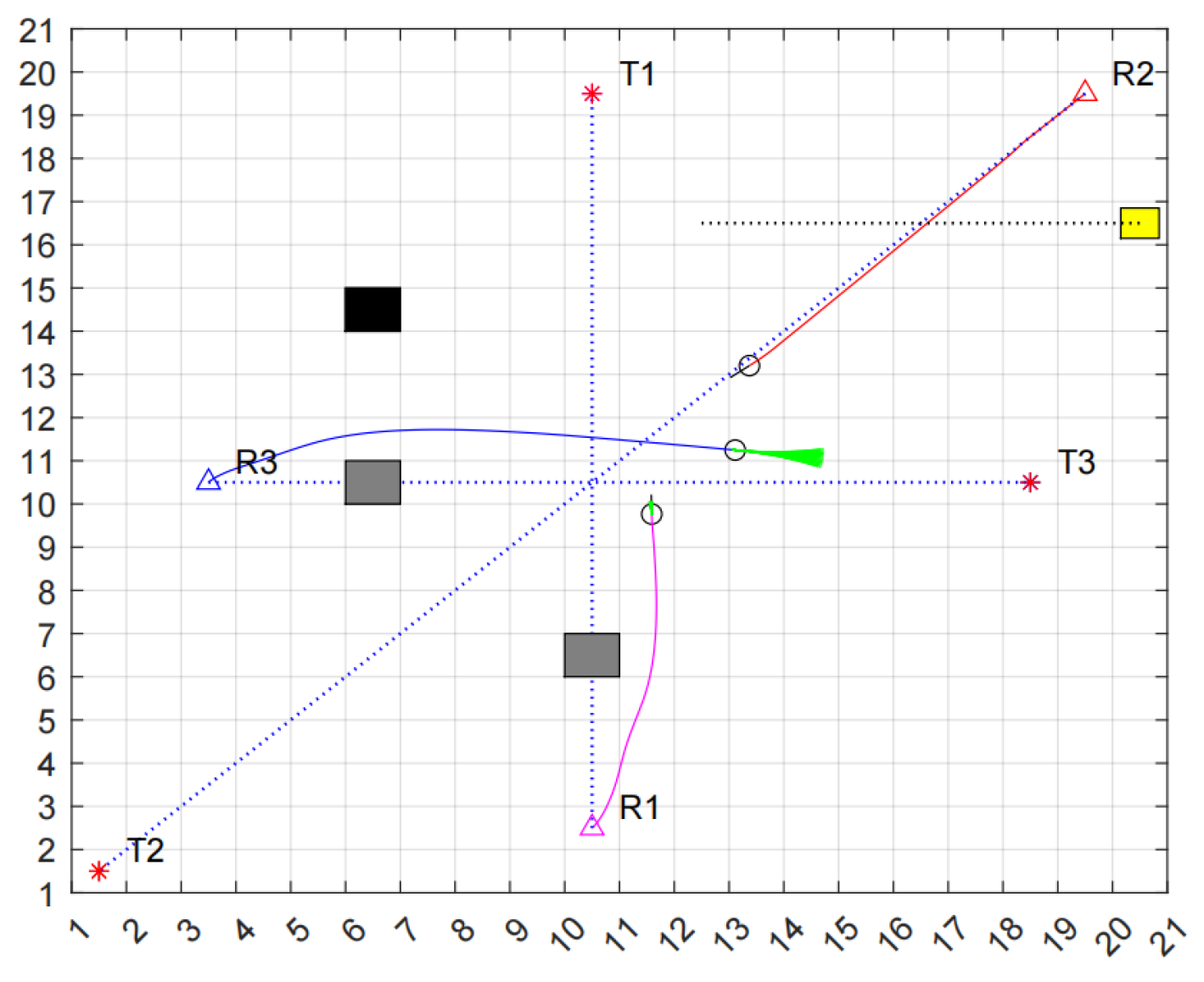
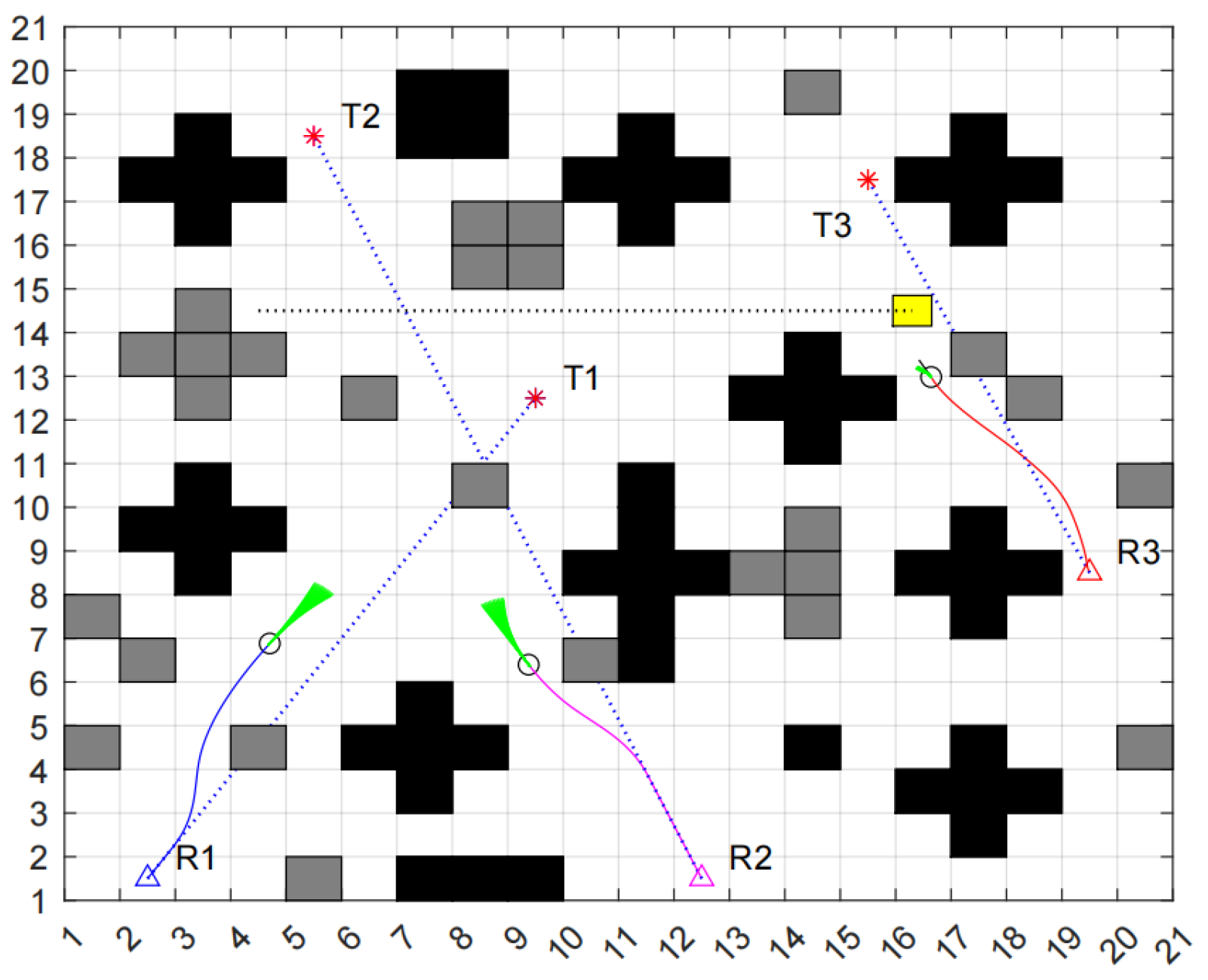
In the experimental environment, we designate black as known obstacles, gray as unknown obstacles, yellow as dynamic obstacles, and the blue dashed line represents the global path planned by the robot in a static environment, triangles represent the starting points of the robots, and asterisks represent the target points of the robots. As illustrated in Figure 12, at time t = t0, Robot 1 (R1) and Robot 3 (R3) encounter an unknown obstacle. Utilizing the improved DWA algorithm, both robots executed turning maneuvers, successfully avoiding the obstacle and continuing toward their target. A dynamic obstacle suddenly appeared in the path of Robot 2 (R2), moving to the right at a certain speed. To prevent a collision with this dynamic obstacle, R3 automatically activated its braking mechanism as it approached, temporarily halting its movement.

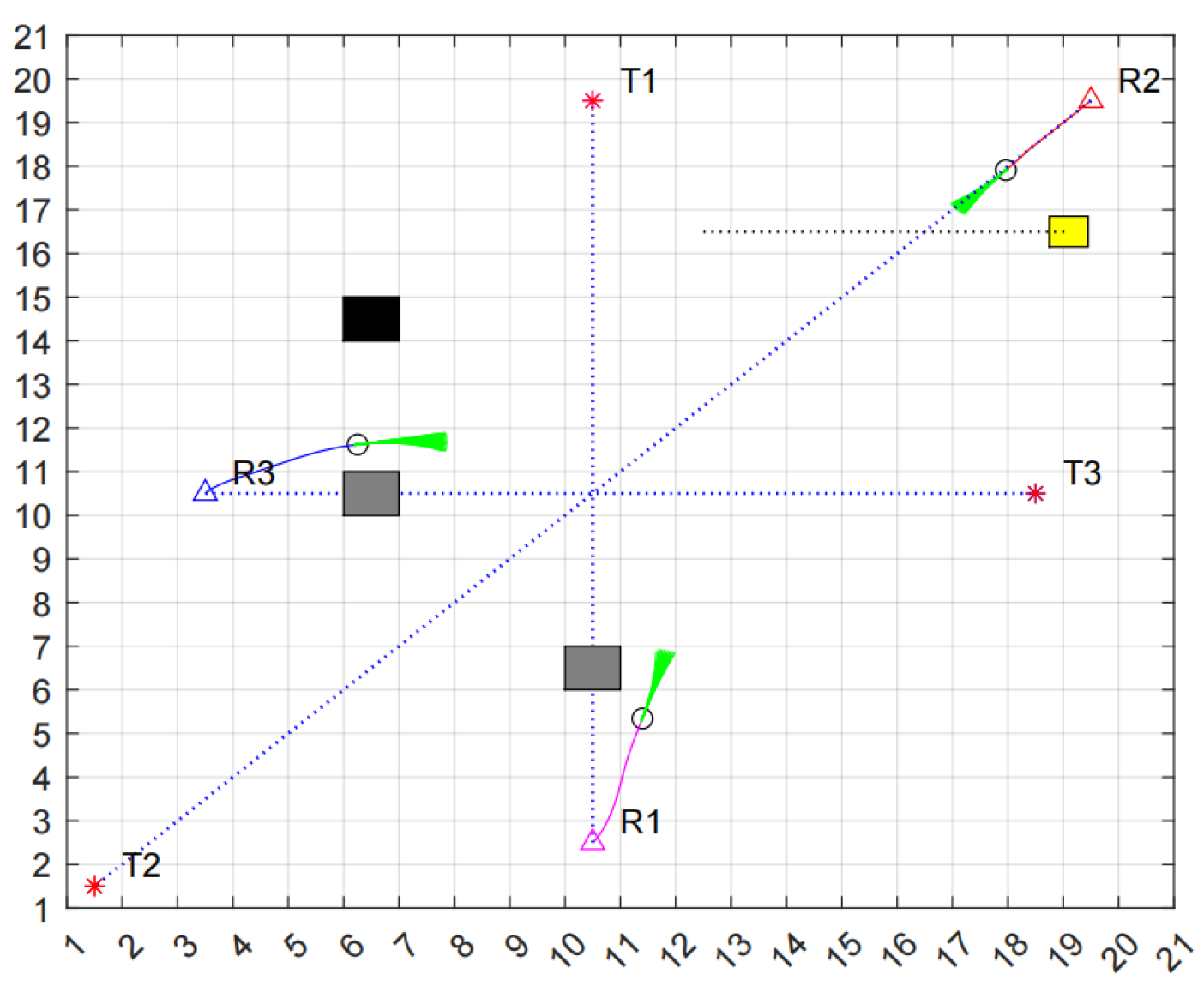
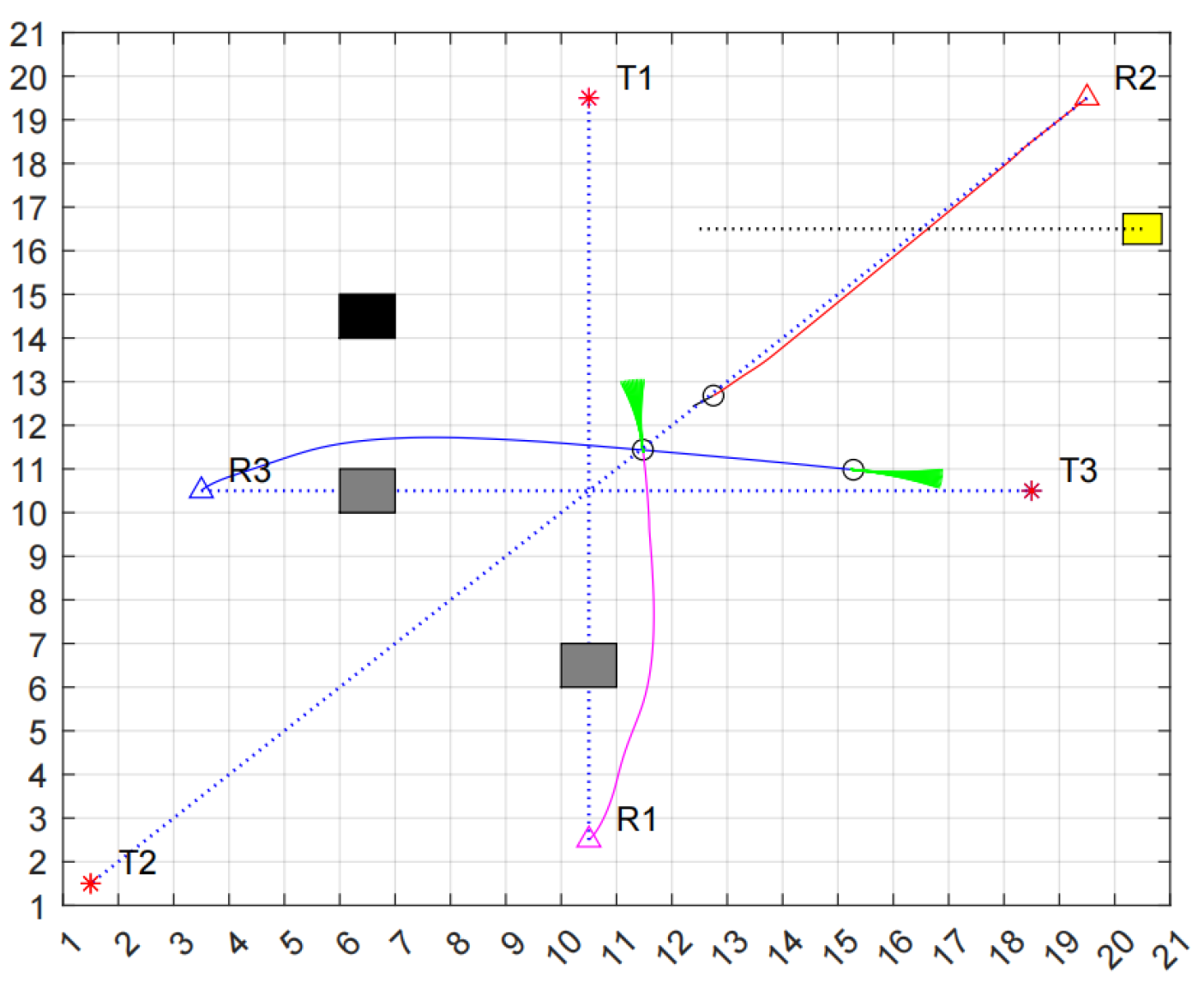
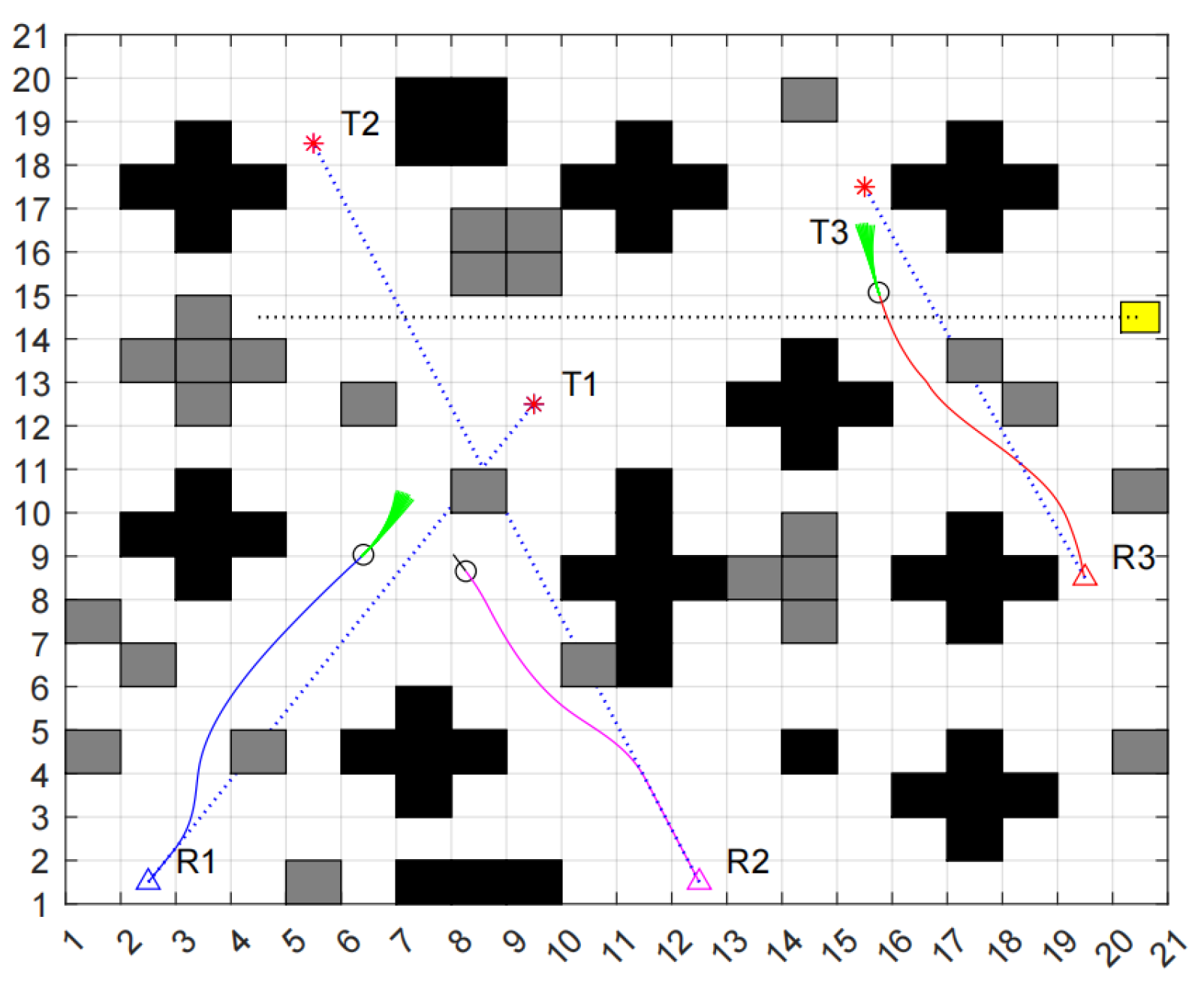
As depicted in Figure 13, at time t = t1, R2 has successfully navigated around the dynamic obstacle and continues to advance toward the target point along its planned path.

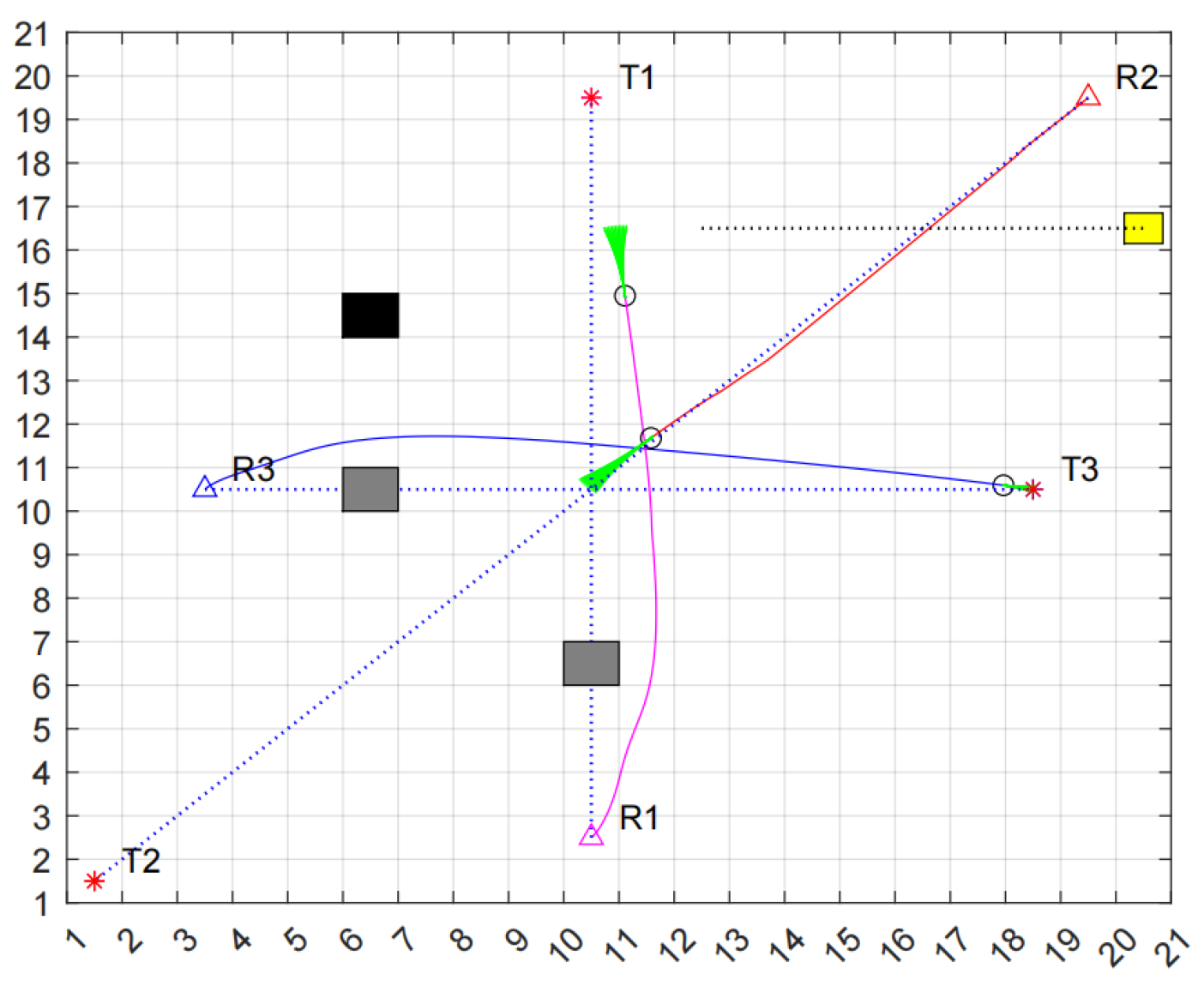
As illustrated in Figure 14, at time t = t2, the three robots converge, with their current distances from the target point as follows: R3 < R1 < R2. Consequently, the dynamic priority among the robots is established as R3 > R1 > R2. R1 and R2 automatically engage their braking mechanisms, momentarily halting their movements, while R3 proceeds toward the target point.

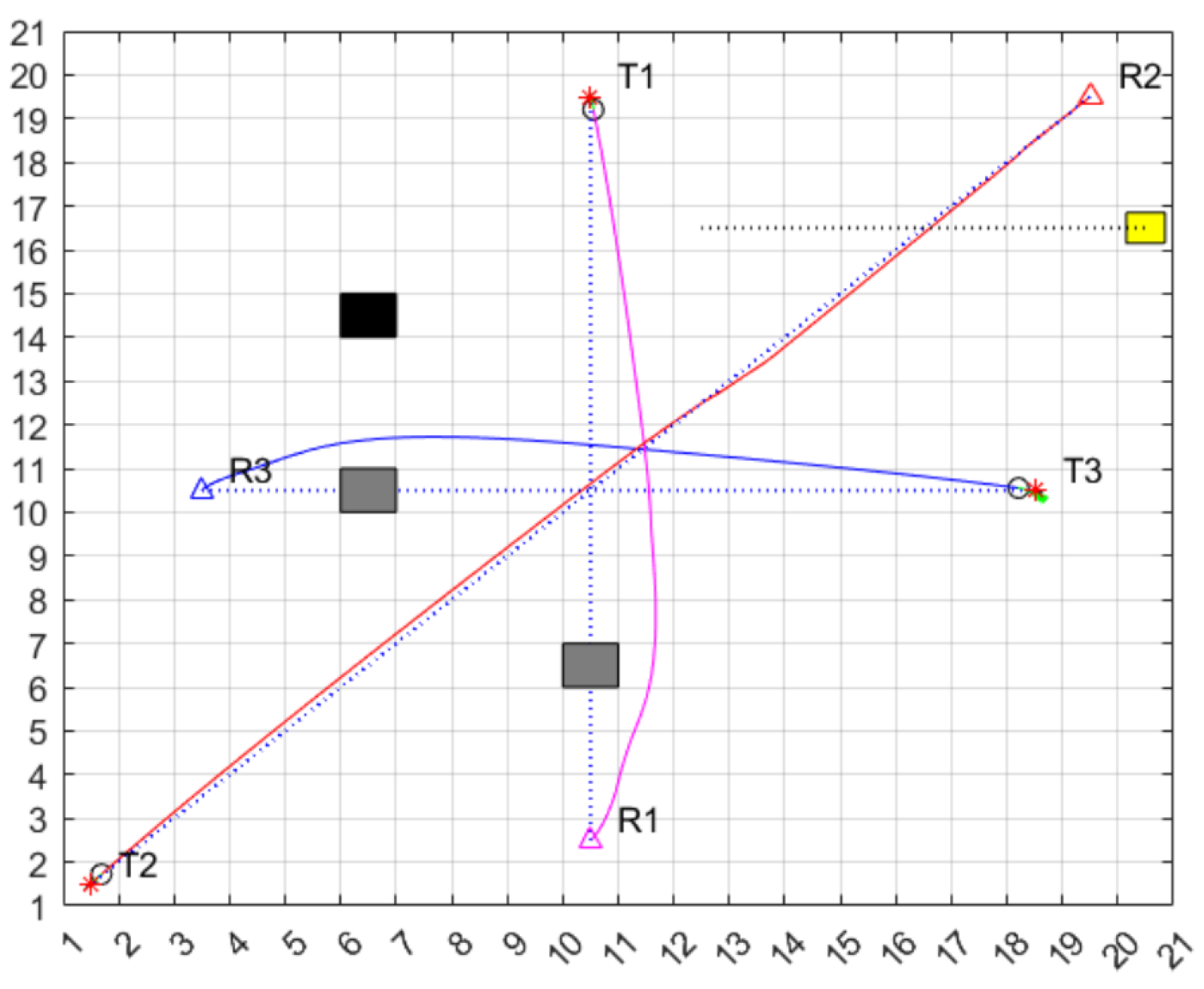
As depicted in Figure 15, at time t = t3, the dynamic priority is established as R1 > R2. To prevent a collision with R1, R2 automatically activates its braking mechanism, temporarily halting its movement, while R1 and R3 continue their advance toward the target.

As illustrated in Figure 16 and Figure 17, at time t = t4, the three robots have successfully navigated around all obstacles and adeptly managed any potential conflicts during their encounters. They continue their journey toward the target point and arrive there at time t = t5.

6.3. Experiments in Complex Environments

To further verify the practicality and reliability of the proposed method, an in-depth study was conducted in a complex environment. In this study, several unknown static obstacles were placed in a known complex environment, and dynamic obstacles were also introduced, further increasing the complexity and risk of the environment. Finally, the proposed method was validated using three mobile robots, labeled as R1, R2, and R3, with their movements illustrated in Figure 18, Figure 19, Figure 20 and Figure 21. In the figures, gray represents temporarily added unknown obstacles, and yellow represents dynamic obstacles moving to the right.

Table 3. Kinematic parameter settings.

Kinematic Parameters	Setting
Maximum speed	1.5 m/s
Maximum rotational speed	20 rad/s
Acceleration	0.2 m/s2
Rotational acceleration	50 rad/s2
Speed resolution	0.02 m/s
Rotational speed resolution	1 rad/s

shows the kinematic parameters of the mobile robots.

As shown in Figure 18, at time t = t0, R1, R2, and R3 are moving toward their target points along the paths planned by the improved neural network algorithm.

Robots R1, R2, and R3 travel along their pre-planned paths. When a robot detects unknown obstacles during its movement, it will automatically replan a local path to avoid the unknown obstacles. As shown in Figure 19, at time t = t1, robots R1, R2, and R3 successfully avoid static unknown obstacles by replanning their local paths. After avoiding the obstacles, they continue along their original paths toward their target points. Meanwhile, when robot R3 detects a dynamic obstacle, it triggers the automatic braking function. R3 stops briefly by braking and resumes movement after detecting that the dynamic obstacle has moved away, thereby avoiding the dynamic obstacle and improving the safety of the mobile robot’s operation.

During the movement of multiple robots, conflict issues may arise when robots encounter each other. We determine the dynamic priority of the robots based on their current distance from their target points. As shown in Figure 20, at time t = t2, R1 and R2 encounter each other. The current distance to the target point is R1 < R2, and therefore, the dynamic priority is R1 > R2. R1 continues its movement, while R2 triggers the automatic braking function, stopping briefly. Once R2 detects that R1 has left, it resumes moving forward, thereby resolving the conflict issue when multiple robots meet.

As shown in Figure 21, at time t = t3, R1, R2, and R3 have all successfully reached their target points, successfully avoiding both dynamic and unknown obstacles. Additionally, the coordination issues between the robots have been successfully resolved.

In summary, the experimental results demonstrate that the dual-layer symmetric path planning algorithm, which integrates the improved neural network algorithm and the DWA, can efficiently and effectively plan global paths for robots in complex dynamic environments. Furthermore, when dynamic or unknown obstacles appear on the path, robots can bypass these obstacles using local path planning and braking mechanisms, ensuring their safety. Finally, for conflict issues arising from encounters between multiple robots, the proposed method resolves these conflicts based on the dynamic priority rule. The experimental results indicate that the proposed algorithm is well-suited for complex dynamic environments, enabling robots to plan collision-free paths and significantly improving the adaptability and safety performance of multi-robot systems.

7. Conclusions

This paper proposes a dual-layer symmetric path planning method that combines an improved neural network and an enhanced DWA algorithm to address the path planning challenges of multi-robot systems in complex dynamic environments. By introducing a single-neuron signal waveform propagation model and a path optimization function, the global optimization capacity of the neural network is significantly enhanced. Additionally, the DWA algorithm’s local path planning efficiency is improved through the implementation of a reward function. The study effectively navigates both static and dynamic obstacles, incorporating a dynamic priority mechanism to resolve conflicts during robot encounters, thereby ensuring overall system efficiency and safety. To validate the superiority and reliability of the proposed method, performance experiments, dynamic environment tests, and complex environment assessments were conducted. The results indicate that, compared to traditional methods, the proposed algorithm offers notable advantages in path length and turning frequency, with turning frequency improvements reaching up to 100%. Furthermore, the method demonstrated zero variance, standard error, interquartile range (IQR), and coefficient of variation (CV) in repeated experiments, effectively confirming its accuracy and reproducibility. This research not only enhances the collaborative operational capabilities and safety of multi-robot systems but also provides a novel solution for robot path planning in complex environments. Future work will focus on further improving the algorithm’s performance and conducting physical validations in real-world settings.