Macroscopic Mechanical Properties of Periodic Nanocomposites Containing Arbitrarily-Shaped Inclusions
Abstract
1. Introduction
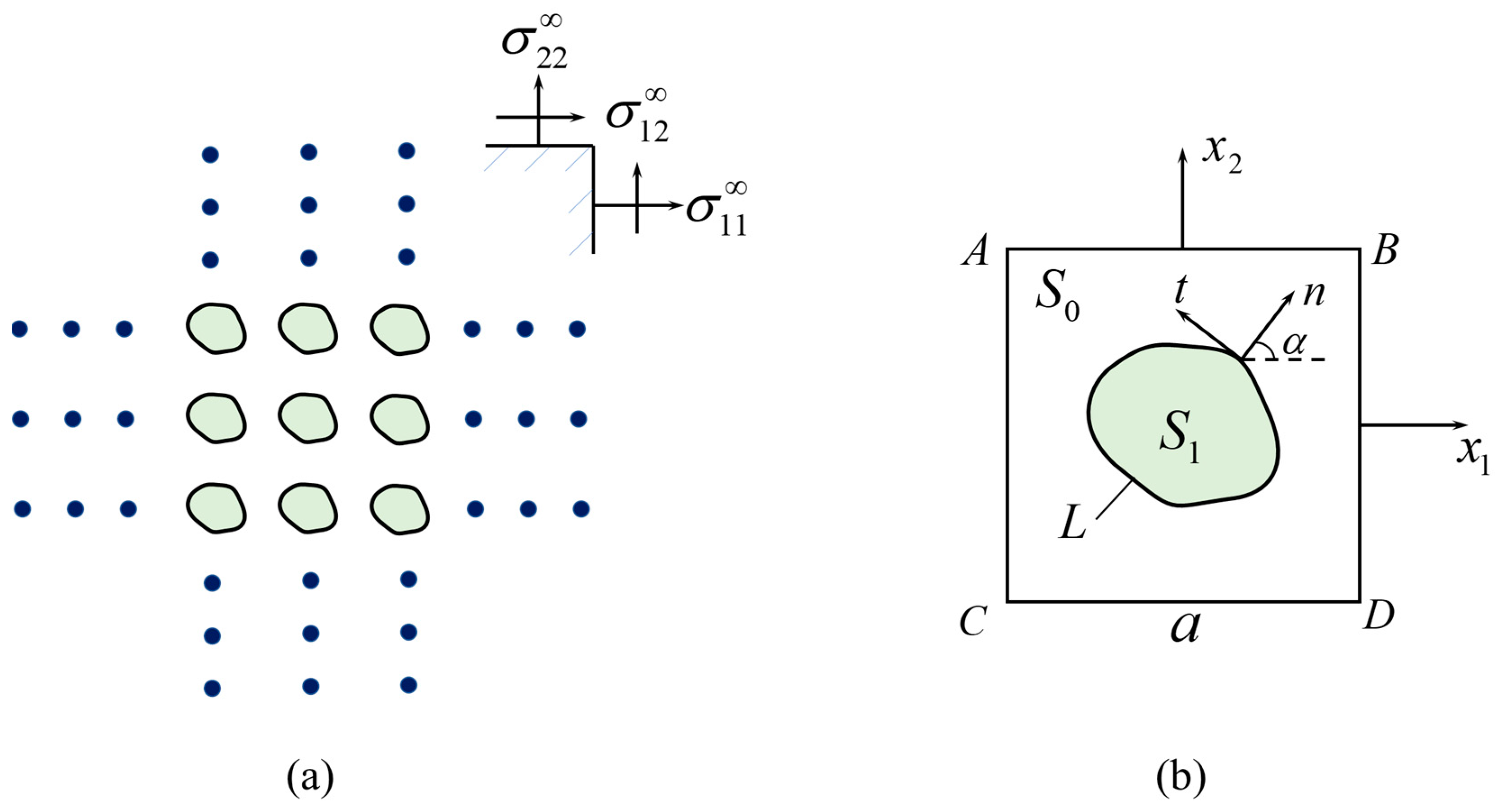
2. Problem Formulation and the Boundary Conditions
3. Solution to the Problem Using the Complex Variable Method
4. Numerical Examples and Discussion
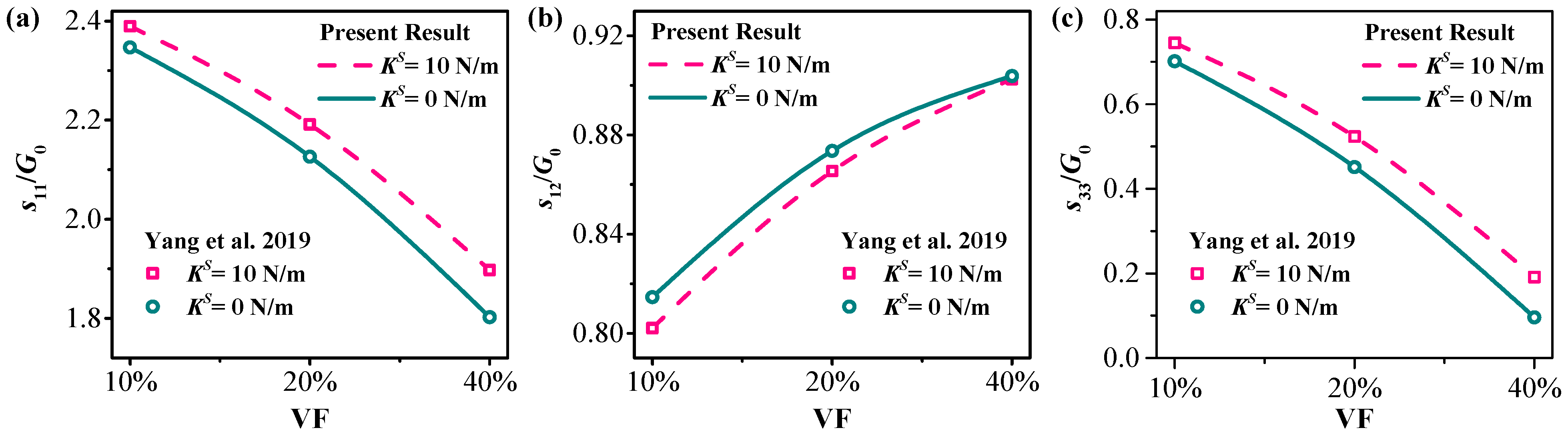
4.1. Verification of the Present Solution
4.2. Numerical Investigations of the Effective Stiffness of Periodic Nanocomposites
4.2.1. Investigation on the Influence of Volume Fraction (VF)
4.2.2. Investigation on the Influence of Inclusion Size
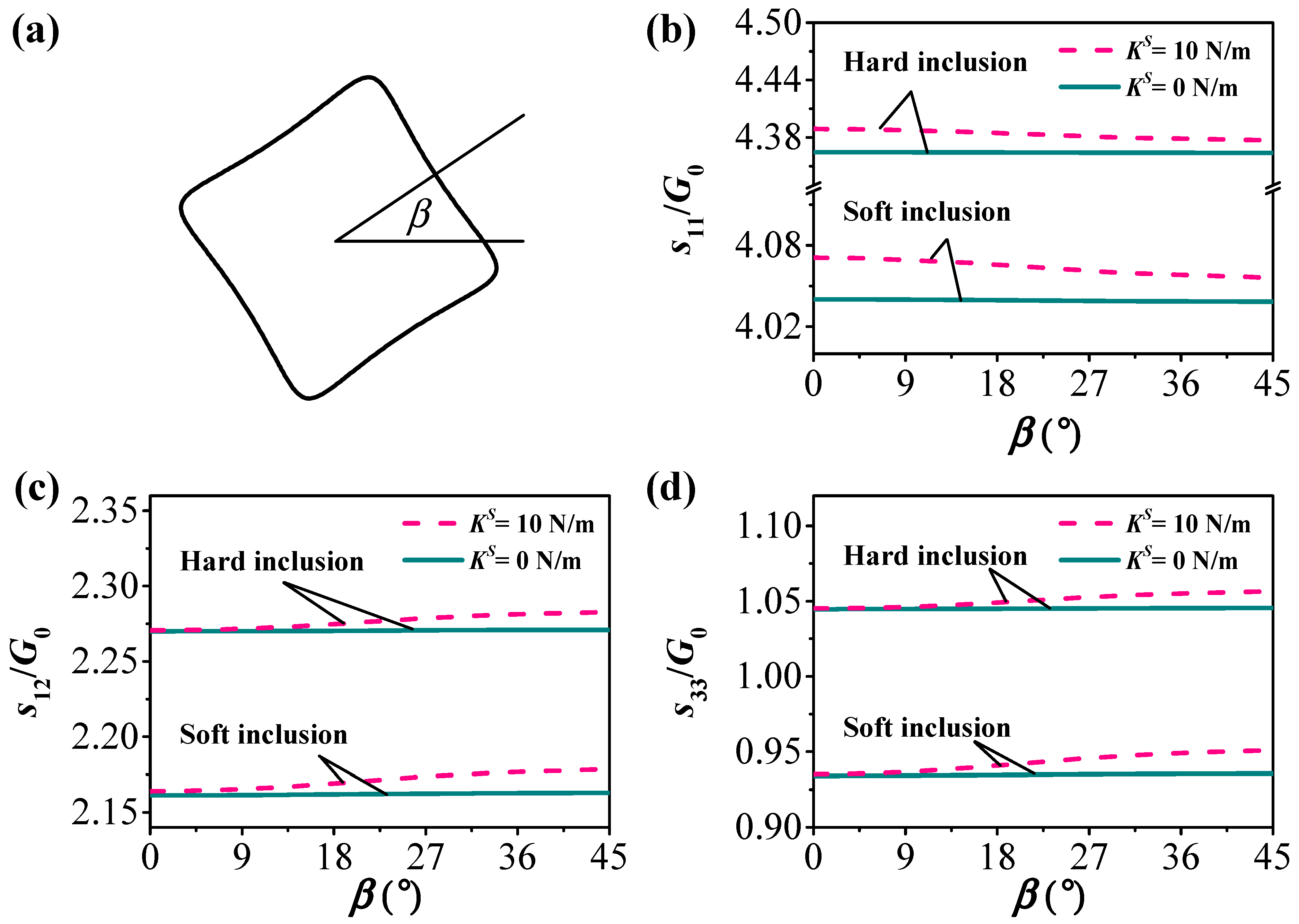
4.2.3. Investigation on the Influence of Orientation Angle
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wong, E.W.; Sheehan, P.E.; Lieber, C.M. Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar] [CrossRef]
- Naganuma, T.; Kagawa, Y. Effect of particle size on the optically transparent nano meter-order glass particle-dispersed epoxy matrix composites. Compos. Sci. Technol. 2002, 62, 1187–1189. [Google Scholar] [CrossRef]
- Cui, Y.; Lieber, C.M. Functional nanoscale electronic devices assembled using silicon nanowire building blocks. Science 2001, 291, 851–853. [Google Scholar] [CrossRef] [PubMed]
- Pour, G.B.; Ashourifar, H.; Aval, L.K.; Solaymani, S. CNTs-Supercapacitors: A Review of Electrode Nanocomposites Based on CNTs, Graphene, Metals, and Polymers. Symmetry 2023, 15, 1179. [Google Scholar] [CrossRef]
- Wang, Z.L.; Song, J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Algarou, N.A.; Slimani, Y.; Klygach, D.S.; Baykal, A.; Korkmaz, A.D.; Zubar, T.I.; Silibin, M.V.; Vakhitov, M.G.; UI-Hamid, A.; et al. Structure, magnetic and electrodynamic properties of SrInxFe12-xO4/Ni0.5Zn0.5Fe2O4 composites at low temperature. J. Am. Ceram. Soc. 2024, 107, 4936–4948. [Google Scholar] [CrossRef]
- Matzui, L.Y.; Trukhanov, A.V.; Yakovenko, O.S.; Vovchenko, L.L.; Zagorodnii, V.V.; Oliynyk, V.V.; Borovoy, M.O.; Trukhanova, E.L.; Astapovich, K.A.; Karpinsky, D.V.; et al. Functional magnetic composites based on hexaferrites: Correlation of the composition, magnetic and high-frequency properties. Nanomaterials 2019, 9, 1720. [Google Scholar] [CrossRef] [PubMed]
- Trukhanov, S.V.; Fedotova, V.V.; Trukhanov, A.V.; Szymczak, H.; Botez, C.E. Cation ordering and magnetic properties of neodymium-barium manganites. Tech. Phys. 2008, 53, 49–54. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Kostishyn, V.G.; Panina, L.V.; Turchenko, V.A.; Kazakevich, I.S.; Trukhanov, A.V.; Trukhanova, E.L.; Natarov, V.O.; Balagurov, A.M. Thermal evolution of exchange interactions in lightly doped barium hexaferrites. J. Magn. Magn. Mater. 2017, 426, 554–562. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Kostishyn, V.G.; Zabeivorota, N.I.; Panina, L.V.; Trukhanov, A.V.; Turchenko, V.A.; Trukhanova, E.L.; Oleynik, V.V.; Yakovenko, O.S.; et al. High-frequency absorption properties of gallium weakly doped barium hexaferrites. Philos. Mag. 2019, 99, 585–605. [Google Scholar] [CrossRef]
- Poncharal, P.; Wang, Z.; Ugarte, D.; de Heer, W.A. Electrostatic deflections and electromechanical resonances of carbon nanotubes. Science 1999, 283, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmüller, J.; Larche, F. A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Miller, R.E.; Shenoy, V.B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology 2000, 11, 139–147. [Google Scholar] [CrossRef]
- Shenoy, V.B. Size-dependent rigidities of nanosized torsional elements. Int. J. Solids Struct. 2002, 39, 4039–4052. [Google Scholar] [CrossRef]
- Sharma, P.; Ganti, S.; Bhate, N. Effect of surfaces on the size-dependent elastic state of nano-inhomogeneities. Appl. Phys. Lett. 2003, 82, 535–537. [Google Scholar] [CrossRef]
- Sharma, P.; Ganti, S. Interfacial elasticity corrections to size-dependent strain-state of embedded quantum dots. Phys. Status Solidi B Basic Solid State Phys. 2002, 234, 10–12. [Google Scholar] [CrossRef]
- Duan, H.L.; Wang, J.; Huang, Z.P.; Karihaloo, B.L. Size-dependent effective elastic constants of solids containing nano-inhomogeneities with interface stress. J. Mech. Phys. Solids 2005, 53, 1574–1596. [Google Scholar] [CrossRef]
- Chen, T.; Dvorak, G.J.; Yu, C.C. Size-dependent elastic properties of unidirectional nano-composites with interface stresses. Acta Mech. 2007, 188, 39–54. [Google Scholar] [CrossRef]
- Xiao, J.H.; Xu, Y.L.; Zhang, F.C. Evaluation of effective electroelastic properties of piezoelectric coated nano-inclusion composites with interface effect under antiplane shear. Int. J. Eng. Sci. 2013, 69, 61–68. [Google Scholar] [CrossRef]
- Wang, G.F.; Feng, X.Q.; Yu, S.W.; Nan, C.W. Interface effects on effective elastic moduli of nanocrystalline materials. Mater. Sci. Eng. A 2003, 363, 1–8. [Google Scholar] [CrossRef]
- Chen, H.; Hu, G.; Huang, Z. Effective moduli for micropolar composite with interface effect. Int. J. Solids Struct. 2007, 44, 8106–8118. [Google Scholar] [CrossRef][Green Version]
- Huang, Z.P.; Sun, L. Size-dependent effective properties of a heterogeneous material with interface energy effect: From finite deformation theory to infinitesimal strain analysis. Acta Mech. 2007, 190, 151–163. [Google Scholar] [CrossRef]
- Doan, T.; Le-Quang, H.; To, Q.-D. Effective elastic stiffness of 2D materials containing nanovoids of arbitrary shape. Int. J. Eng. Sci. 2020, 150, 103234. [Google Scholar] [CrossRef]
- Mogilevskaya, S.G.; Crouch, S.L.; Stolarski, H.K.; Benusiglio, A. Equivalent inhomogeneity method for evaluating the effective elastic properties of unidirectional mult-phase composites with surface/interface effects. Int. J. Solids Struct. 2010, 47, 407–418. [Google Scholar] [CrossRef]
- Wang, H.W.; Zhou, H.W.; Peng, R.D.; Mishnaevsky, L. Nanoreinforced polymer composites: 3D FEM modeling with effective interface concept. Compos. Sci. Technol. 2011, 71, 980–988. [Google Scholar] [CrossRef]
- Yvonnet, J.; Quang, H.L.; He, Q.C. An XFEM/level set approach to modelling surface/interface effects and to computing the size-dependent effective properties of nanocomposites. Comput. Mech. 2008, 42, 119–131. [Google Scholar] [CrossRef]
- Dai, M.; Schiavone, P.; Gao, C.F. A new method for the evaluation of the effective properties of composites containing unidirectional periodic nanofibers. Arch. Appl. Mech. 2017, 87, 647–665. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1953. [Google Scholar]
- Tian, L.; Rajapakse, R.K.N.D. Elastic field of an isotropic matrix with a nanoscale elliptical inhomogeneity. Int. J. Solids Struct. 2007, 44, 7988–8005. [Google Scholar] [CrossRef]
- Yang, H.B.; Wang, S.; Yu, C. Effective in-plane stiffness of unidirectional periodic nanoporous materials with surface elasticity. Z. Für Angew. Math. Phys. 2019, 70, 129. [Google Scholar] [CrossRef]
- Wang, S.; Dai, M.; Ru, C.Q.; Gao, C.F. Stress field around an arbitrarily shaped nanosized hole with surface tension. Acta Mech. 2014, 225, 3453–3462. [Google Scholar] [CrossRef]
- Dai, M.; Gao, C.F.; Ru, C.Q. Surface tension-induced stress concentration around a nanosized hole of arbitrary shape in an elastic half-plane. Meccanica 2014, 49, 2847–2859. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Z. Void initiation from interfacial debonding of spherical silicon particles inside a silicon-copper nanocomposite: A molecular dynamics study. Model. Simul. Mater. Sci. Eng. 2017, 25, 025007. [Google Scholar] [CrossRef]
| Inclusion Shape | Schematic | Conformal Mapping |
|---|---|---|
| Ellipse |  | |
| Square |  |
| Phase | Material | Lame Constants | VF | R | ||||
|---|---|---|---|---|---|---|---|---|
| Matrix | Al | 58.17 | 26.13 | 1.62 | 0.1, 0.2, 0.3 | 0 N/m, 10 N/m | 5 nm, 10 nm, 20 nm | 0°, 5°, 15°, 30°, 45° |
| Soft inclusion | InAs | 50.66 | 19 | 1.55 | ||||
| Hard inclusion | GaAs | 64.43 | 32.9 | 1.68 | ||||
| Inclusion Type | VF | KS = 0 N/m | KS = 10 N/m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Soft inclusion | 0.1 | 4.134 | 2.194 | 4.128 | 0.967 | 4.150 | 2.197 | 4.133 | 0.970 |
| 0.2 | 4.046 | 2.161 | 4.034 | 0.934 | 4.046 | 2.161 | 4.034 | 0.934 | |
| 0.3 | 3.962 | 2.129 | 3.943 | 0.902 | 3.962 | 2.129 | 3.943 | 0.902 | |
| Hard inclusion | 0.1 | 4.296 | 2.248 | 4.293 | 1.022 | 4.307 | 2.250 | 4.296 | 1.024 |
| 0.2 | 4.368 | 2.270 | 4.361 | 1.045 | 4.392 | 2.274 | 4.367 | 1.048 | |
| 0.3 | 4.443 | 2.292 | 4.431 | 1.067 | 4.480 | 2.298 | 4.440 | 1.073 | |
| Inclusion Type | VF | KS = 0 N/m | KS = 10 N/m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Soft inclusion | 0.1 | 4.131 | 2.194 | 4.131 | 0.967 | 4.147 | 2.195 | 4.131 | 0.967 |
| 0.2 | 4.040 | 2.161 | 4.040 | 0.934 | 4.071 | 2.164 | 4.071 | 0.935 | |
| 0.3 | 3.952 | 2.130 | 3.952 | 0.903 | 3.997 | 2.134 | 3.997 | 0.904 | |
| Hard inclusion | 0.1 | 4.294 | 2.248 | 4.294 | 1.022 | 4.306 | 2.249 | 4.306 | 1.022 |
| 0.2 | 4.365 | 2.270 | 4.365 | 1.045 | 4.389 | 2.271 | 4.389 | 1.045 | |
| 0.3 | 4.437 | 2.292 | 4.437 | 1.068 | 4.474 | 2.293 | 4.474 | 1.068 | |
| Inclusion Type | R | KS = 0 N/m | KS = 10 N/m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Soft inclusion | 5 nm | 4.046 | 2.161 | 4.034 | 0.934 | 4.077 | 2.167 | 4.044 | 0.940 |
| 10 nm | 4.046 | 2.161 | 4.034 | 0.934 | 4.062 | 2.164 | 4.039 | 0.937 | |
| 20 nm | 4.046 | 2.161 | 4.034 | 0.934 | 4.054 | 2.163 | 4.037 | 0.936 | |
| Hard inclusion | 5 nm | 4.368 | 2.270 | 4.361 | 1.045 | 4.392 | 2.274 | 4.367 | 1.048 |
| 10 nm | 4.368 | 2.270 | 4.361 | 1.045 | 4.380 | 2.272 | 4.365 | 1.046 | |
| 20 nm | 4.368 | 2.270 | 4.361 | 1.045 | 4.374 | 2.271 | 4.363 | 1.045 | |
| Inclusion Type | R | KS = 0 N/m | KS = 10 N/m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Soft inclusion | 5 nm | 4.040 | 2.161 | 4.040 | 0.934 | 4.071 | 2.164 | 4.071 | 0.935 |
| 10 nm | 4.040 | 2.161 | 4.040 | 0.934 | 4.056 | 2.163 | 4.056 | 0.935 | |
| 20 nm | 4.040 | 2.161 | 4.040 | 0.934 | 4.048 | 2.162 | 4.048 | 0.934 | |
| Hard inclusion | 5 nm | 4.365 | 2.270 | 4.365 | 1.045 | 4.389 | 2.271 | 4.389 | 1.045 |
| 10 nm | 4.365 | 2.270 | 4.365 | 1.045 | 4.377 | 2.270 | 4.377 | 1.045 | |
| 20 nm | 4.365 | 2.270 | 4.365 | 1.045 | 4.371 | 2.270 | 4.371 | 1.045 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Jia, X.; Cheng, M.; Li, H.; Yu, C.; Yang, H. Macroscopic Mechanical Properties of Periodic Nanocomposites Containing Arbitrarily-Shaped Inclusions. Symmetry 2025, 17, 39. https://doi.org/10.3390/sym17010039
Wang S, Jia X, Cheng M, Li H, Yu C, Yang H. Macroscopic Mechanical Properties of Periodic Nanocomposites Containing Arbitrarily-Shaped Inclusions. Symmetry. 2025; 17(1):39. https://doi.org/10.3390/sym17010039
Chicago/Turabian StyleWang, Shuang, Xin Jia, Ming Cheng, Hongyuan Li, Chuanbin Yu, and Haibing Yang. 2025. "Macroscopic Mechanical Properties of Periodic Nanocomposites Containing Arbitrarily-Shaped Inclusions" Symmetry 17, no. 1: 39. https://doi.org/10.3390/sym17010039
APA StyleWang, S., Jia, X., Cheng, M., Li, H., Yu, C., & Yang, H. (2025). Macroscopic Mechanical Properties of Periodic Nanocomposites Containing Arbitrarily-Shaped Inclusions. Symmetry, 17(1), 39. https://doi.org/10.3390/sym17010039






