1. Introduction
Fuzziness plays a vital role in several real-world applications, such as data mining, decision-making, management science, computer science, and pattern recognition. Often, the information available in these fields contains uncertainty or inherent ambiguity, which can lead to insufficient understanding. Effectually managing this lack of clarity is vital for making informed choices, identifying meaningful patterns, and gaining valuable insights. Addressing these uncertainties and indecisions allows for better decision-making. Ultimately, handling vagueness is vital for unlocking the full perspective of the data at hand. To address these challenges, Zadeh [
1] presented the notion of a fuzzy set (FS). This idea provides a framework for dealing with vagueness and uncertainty in numerous contexts. FS contains only one element called the degree of satisfaction (DOS). So, it fails to handle data that contains the degree of satisfactory and unsatisfactory (DOUS) information of interest. Overcoming this faintness, Atanassov [
2] presented the idea of the intuitionistic fuzzy set (IFS). In IFS, each element can be written as:
with
. The theory of Pythagorean fuzzy set (PyFS) was presented by Yager [
3] to extend the classical notion of FS and IFSs by relaxing the restriction of IFS, such as
to
. Yager [
4] presented the concept of q-rung orthopair fuzzy set (q-ROFS) to further extend PyFS. In q-ROFS, the constraint
to
, allowing more flexibility for DOS and DOUS. They are employed in modeling and decision-making, commonly in situations involving imprecision or uncertainty in the data. They are an extension of orthopair fuzzy sets and represent a more refined and expressive way of dealing with uncertainty and imprecision. This extension offers decision-makers greater elasticity when considering alternative preferences. These concepts are well-established. Previous existing studies have primarily focused on the use of DOS and DOUS, overlooking the importance of neutral degrees, which also play a vital role in decision-making problems. Senapati and Yager [
5] introduced a fermatean fuzzy set (FFS). Representation of each element in FFS as
with
. FFS is more powerful than IFS and PyFS. For example, if
, then for IFS and PyFS, we have
,
. Thus, IFS and PyFS both fail in this case. Now for FSS:
. This example demonstrates the effectiveness and reliability of the FFS in achieving its intended outcomes. Its consistent performance highlights its dependability in various scenarios. See
Figure 1 for comparison of IFS, PyFs and FFS.
The above models fail miserably to produce the expected result since there are many real-world issues where the computation of a degree of neutral membership is crucial. Cuong et al. [
6] presented the idea of a picture fuzzy set (PcFS) to deal with the occurring problems. In PcFS, each element can be presented mathematically as
, where
,
, and
are called degrees of satisfactory, neutral, and unsatisfactory with condition:
. So, a PcFS extends a fuzzy set by incorporating degrees of satisfactory, neutral, and unsatisfactory. This model allows for a more nuanced representation of ambiguity and uncertainty in data. It is particularly useful in scenarios where information is incomplete or subjective. Ashraf et al. [
7,
8] introduced the idea of the spherical fuzzy set (SpFS), which relaxes the limitation of PcFS, such as
to
. They also introduced several operators based on spherical fuzzy numbers (SpFNs). This approach allows for a more comprehensive and inclusive representation of uncertainty in decision-making problems. It is particularly valuable in fields requiring nuanced evaluations, including decision analysis and artificial intelligence. Beg et al. [
9] explored the notion of a Polytopic fuzzy set (PFS), which reduces the restriction of SpFS, such as
to
. They provide a more advanced and nuanced method for modeling uncertainty and can be particularly valuable in scenarios where traditional fuzzy sets may not capture the complexity of the problem.
The existing sets discussed above fail to capture the partial unfamiliarity of the data and how it changes over time. As a result, none of these FS theories or their extensions can efficiently handle periodic information. In complex datasets, vagueness, ambiguity, and variations in data periodicity often coexist. Particularly, such datasets may include critical data from areas like facial recognition, health diagnostics, image analysis, biometric analysis, and audio processing. These databases, while rich in information, often suffer from a lack of entirety and clarity. To circumvent these circumstances, Ramot et al. [
10] introduced a complex fuzzy set (CFS), which is an extension of the traditional fuzzy set that introduces complex-valued membership grades to handle multidimensional data. Alkouri and Salleh [
11] presented a complex intuitionistic fuzzy set (CIFS) in which the element is expressed as
with conditions
and
. Ullah et al. [
12] introduced complex Pythagorean fuzzy set (CPyFS), which reduces the limitation of CIFS, such as
to
and
to
, respectively. Liu et al. [
13] introduced complex q-rung orthopair fuzzy set (Cq-ROFS), which reduces the restriction of CPyFS, such as
to
and
to
, respectively. Cq-ROFS combines q-ROFS with complex values to model and handle contradictory information or ambiguous and imprecise information more effectively in decision-making. Akram et al. [
14] introduced a complex picture fuzzy set (CPcFS), offering a more innovative and effective tool than previous models. In CPcFS, each element is mathematically presented as
with conditions
and
. This new model enhances the ability to handle imprecision and uncertainty in data analysis. Naeem et al. [
15] introduced a complex spherical fuzzy set (CSFS) to overcome the limitations found in CPcFS, such as
to
and
to
. Rahman [
16] introduced a complex Polytopic fuzzy set (CPFS) and developed new methods using algebraic operational laws. In CPFS, each element can be written as
with
and
. These innovations offer advanced techniques for managing and analyzing fuzzy data, enhancing the precision and applicability of fuzzy set theory.
1.1. Comprehensive Review of Operators in Literature
Aggregation operators play an essential role in combining multiple input values into a single output, facilitating the synthesis of information from several sources. They are widely used in data analysis, decision-making, and optimization to simplify complex data and reach a combined conclusion. Several different operators are designed to effectively handle information from various environments, ensuring more reliable and accurate outcomes in complex consequences. Tesic and Bozanic [
17] presented the FUCOM-EWAA COPRAS-G model, while Komazec and Jankovic [
18] introduced a comprehensive decision-making algorithm tailored for risk management. Zhang et al. [
19] and Hadzikadunic et al. [
20] presented Koopman and Bonferroni operators, respectively, while several scholars, such as Wang and Liu [
21,
22], Iqbal and Kalsoom [
23], Kenani et al. [
24], Rahman et al. [
25], Li and Sun [
26], Hao et al. [
27], Chen et al. [
28], and Ma et al. [
29] have contributed to the development of numerous operators based on intuitionistic fuzzy information. These operators are designed to handle vagueness and uncertainty in decision-making problems efficiently. These innovations enhance the ability to aggregate complex data in diverse contexts and improve the robustness of decision support systems. Garg [
30,
31], Hussain et al. [
32], Liu et al. [
33], Rahman and Ali [
34], and Sajad et al. [
35] offered numerous aggregation operators based on Pythagorean fuzzy information to address vagueness in decision-making. These approaches offer more consistent and reliable solutions in complex environments where fuzzy approaches may fall short. Khan and Wang [
36], Jana and Nunic [
37], Choudhar et al. [
38], and Qiu and Choudhar et al. [
39] have introduced various operators tailored to fuzzy frameworks, including FFNs, PcFNs, and SFNs. These techniques have been effectively, excellently, and efficiently applied to decision-making processes, showcasing their utility in handling imprecise, hesitation, and uncertain information. Their contributions significantly enhance the efficiency and flexibility of decision-making models in complex situations. Ma et al. [
40], Dick et al. [
41], Liu and Zhang [
42], Rani and Garg [
43], Garg and Reni [
44], Kumer and Bajej [
45], and Ahmed et al. [
46] presented various approaches using CIF-information. These developments enhance the applicability of fuzzy logic in diverse decision-making and logical contexts. Rahman et al. [
47], Hezam et al. [
48], Akram et al. [
49], Liu et al. [
50], and Jin et al. [
51] presented various methods within the context of the CPyF-environment. These operators offer more accurate and flexible solutions for real-world problems involving uncertain data.
Ali et al. [
52] and Jan et al. [
53] introduced several operators, along with their structure properties, based on CFFNs, providing valuable tools for handling complex, ambiguous, and uncertain data. Building on this foundation, Rahman [
54] introduced various techniques utilizing CPF information, further enhancing the versatility, flexibility, and applicability of fuzzy aggregation methodologies.
1.2. Motivation of the Study
Motivated by [
16], where the author introduced the concept of a complex Polytopic fuzzy set and developed some aggregation operators based on algebraic t-norm and t-conorm, such as CPFWAA, CPFOWAA, and CPFHAA operators. However, the Einstein t-norm and t-conorm are good alternatives to the algebraic t-norm and t-conorm. In this paper, we introduce Einstein t-norm and t-conorm specifically for complex Polytopic fuzzy numbers. Using these norms, we develop new aggregation operators and analyze their structural properties, including idempotency, boundedness, and monotonicity. These operators are tailored to handle complex decision-making processes. Compared to the algebraic aggregation operators, our proposed aggregation operators provide enhanced accuracy and adaptability, making them particularly useful in practical decision-making applications. This work highlights the potential of Einstein-based approaches to improve the overall performance and robustness of fuzzy aggregation techniques.
1.3. Contributions of the Study
This paper significantly advances the field by exploring various aspects of CPFS and introducing novel techniques. Each contribution enhances the precision and applicability of fuzzy decision-making methodologies.
- (i)
Einstein Operational Laws: The paper introduces Einstein’s operational laws in a complex Polytopic fuzzy environment.
- (ii)
Aggregation Operators: The paper introduces a set of operators, namely (CPFEWA, CPFEOWA, CPFEHA) operators
- (iii)
Algorithm for Decision-Making: The paper makes a significant contribution by introducing an algorithm tailored to the innovative CPFS-based model.
- (iv)
Ensuring Reliability and Visibility in Decision-Making: The paper validates its contributions by demonstrating the visibility and reliability of the newly developed methods through a descriptive example. This real-world application proves the efficiency of the approaches in improving the decision-making algorithm process.
1.4. Structure of the Study
The rest of the paper is scheduled as follows:
Section 2 provides an inclusive review of existing studies related to our research.
Section 3 presents central Einstein laws formulated using complex polytopic fuzzy information, emphasizing the integration of uncertainty in relativistic principles.
Section 4 presents some novel approaches, namely CPFEWA, CPFEOWA, and CPFEHA operators.
Section 5 presents the application of the novel methods.
Section 6 presents a descriptive example to demonstrate the efficiency of the new methods.
Section 7 focuses on analyzing the sensitivity of the proposed models and conducting a comparative analysis.
Section 8 outlines the limitations of the new proposed model, including challenges in scalability and adaptability across diverse contexts. The paper concludes with
Section 9, summarizing the key findings, contributions, and implications of the research. See
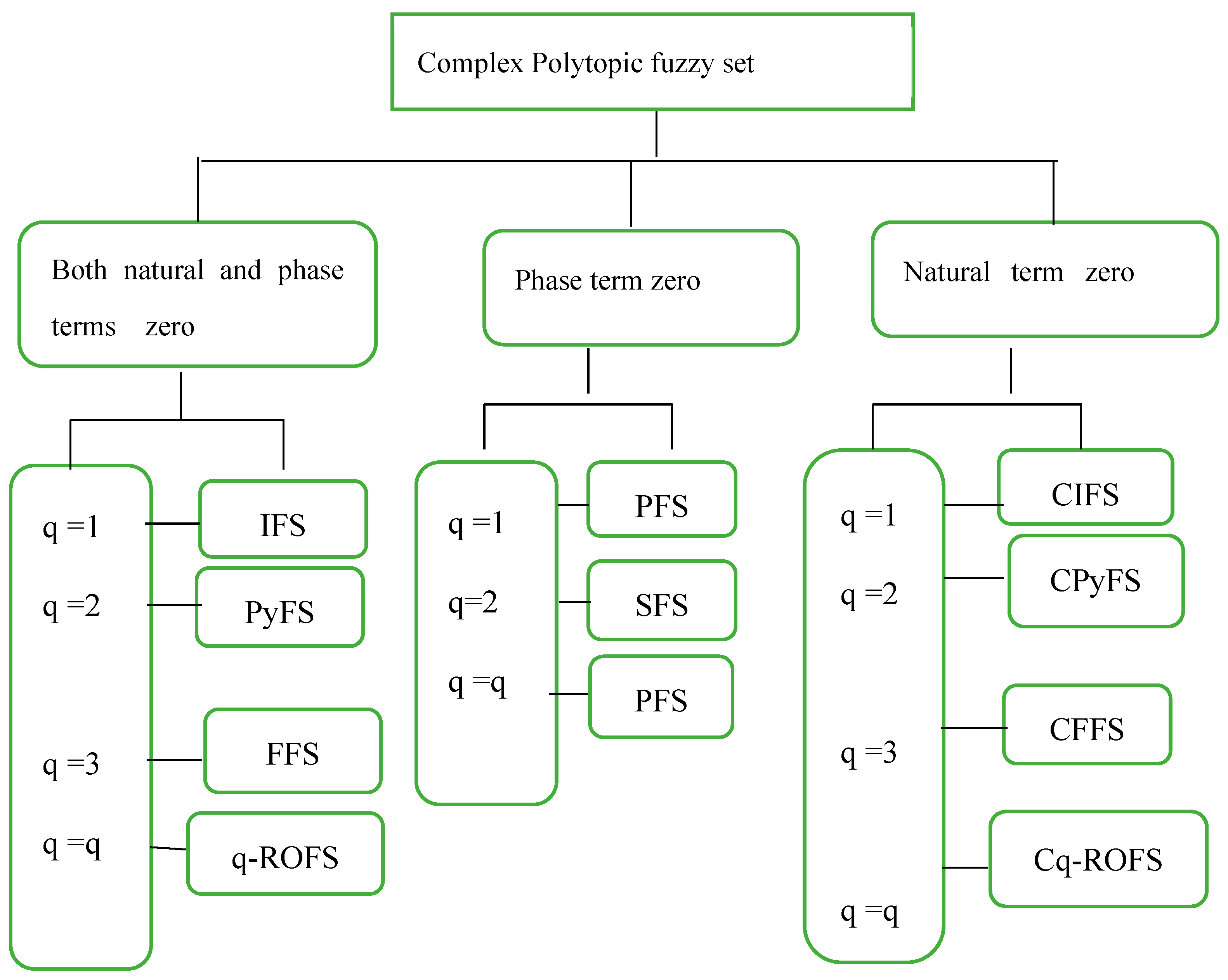
Figure 2 for different cases of CPFS.
2. Preliminaries
In this unit, we define main concepts such as PcFS, SFS, and PFS within complex environments. Moreover, we present the notions of score and accuracy degrees, which are essential for calculating the performance of fuzzy systems. These definitions provide the basis for the subsequent analysis and study of our work.
Definition 1 [14]. Let be a universal set, be a CPcFS, and then can be presented aswhere , , with condition . Moreover, , , with .
Definition 2 [15]. Let be a universal set, be a CSFS, and then can be presented aswhere , , , , , with conditions and .
Definition 3 [16]. Let be a universal set, be a CPFS, and then can be defined aswhere , , , , , with and .
A CPFS is an advanced extension of FSs and their derivation that incorporates multiple dimensions and parameters to address and control complex vagueness. It combines the ideas of polytopic and fuzzy logic, allowing for more precise modeling of complex systems with varying degrees of truth across multiple criteria. The flexibility of CPFS allows the representation of intricate relationships in uncertain environments, improving decision-making processes. CPFS is more powerful than CPcFS and CSFS. For example, if
, then
,
. Again. Both PcFS and SFS fail in this case. Now if
, then
. This example demonstrates the effectiveness and reliability of the CPFS. See
Figure 3 for Comparison of CPFS, CSFS, CPcFS.
Definition 4 [16]. Let be a CPFN, and then its and can be expressed as and , respectively.
Definition 5 [16]. Let are CPFNs, and then the following conditions hold:
- (i)
If,
- (ii)
If,
- (iii)
If, , then
- (a)
If,
- (b)
If,
- (c)
3. Exploring Some Basic Laws for CPF-Model Based on Einstein’s Norms
In this section, we present Einstein t-conorm and t-norm, specifically within the framework of CPFNs. We utilize these norms to develop operational laws that help in developing many aggregation operators. They are crucial for efficiently managing and integrating fuzzy information in complex Polytopic environments. See
Figure 4 for Structure of this section.
Definition 6. The generalized union and intersection for CPFNs can be defined as follows:
- (i)
- (ii)
- (iii)
where represents the t-norm and represents the t-conorm, with examples being the Einstein product and Einstein sum, respectively. Mathematically, can be presented as follows: T-conorms and T-norms are important tools in FS theory, providing a vigorous framework for combining fuzzy values in both disjunctive and conjunctive contexts. These tools offer flexibility in handling vagueness and methods in numerous applications, such as fuzzy logic, control systems, decision-making, and reasoning under fuzziness, ensuring logical stability and supporting complex decision-making processes.
The following are some t-norms and t-conorms for CPFS, such as the product T
P and the probabilistic sum S
P, the minimum T
M and the maximum S
M, and the Dombi sum and the Dombi product, where each pair is associated by the De Morgan duality.
Based on the Einstein t-norm and t-conorm within the context of complex information, we introduce essential operational laws. These laws form the basis for presenting novel Einstein operators tailored for complex Polytopic fuzzy information.
Definition 7. Let are CPFNs and , then
- (i)
- (ii)
Definition 8. A function: is ETN, if , then the following properties satisfied:
- (i)
Symmetry property:.
- (ii)
Monotonicity property:.
- (iii)
Associativity property:.
- (iv)
Unit identity property:.
Definition 9. A function: is ETCN, if , then the following properties satisfied:
- (i)
Symmetry property:.
- (ii)
Monotonicity property:.
- (iii)
Associativity property:.
- (iv)
Zero identity property:.
Definition 10. Let are any two CPFSs, then the Einstein sum , and Product mathematically can be presented as follows:
- (i)
- (ii)
4. Einstein-Based Approaches in Complex Polytopic Fuzzy Settings
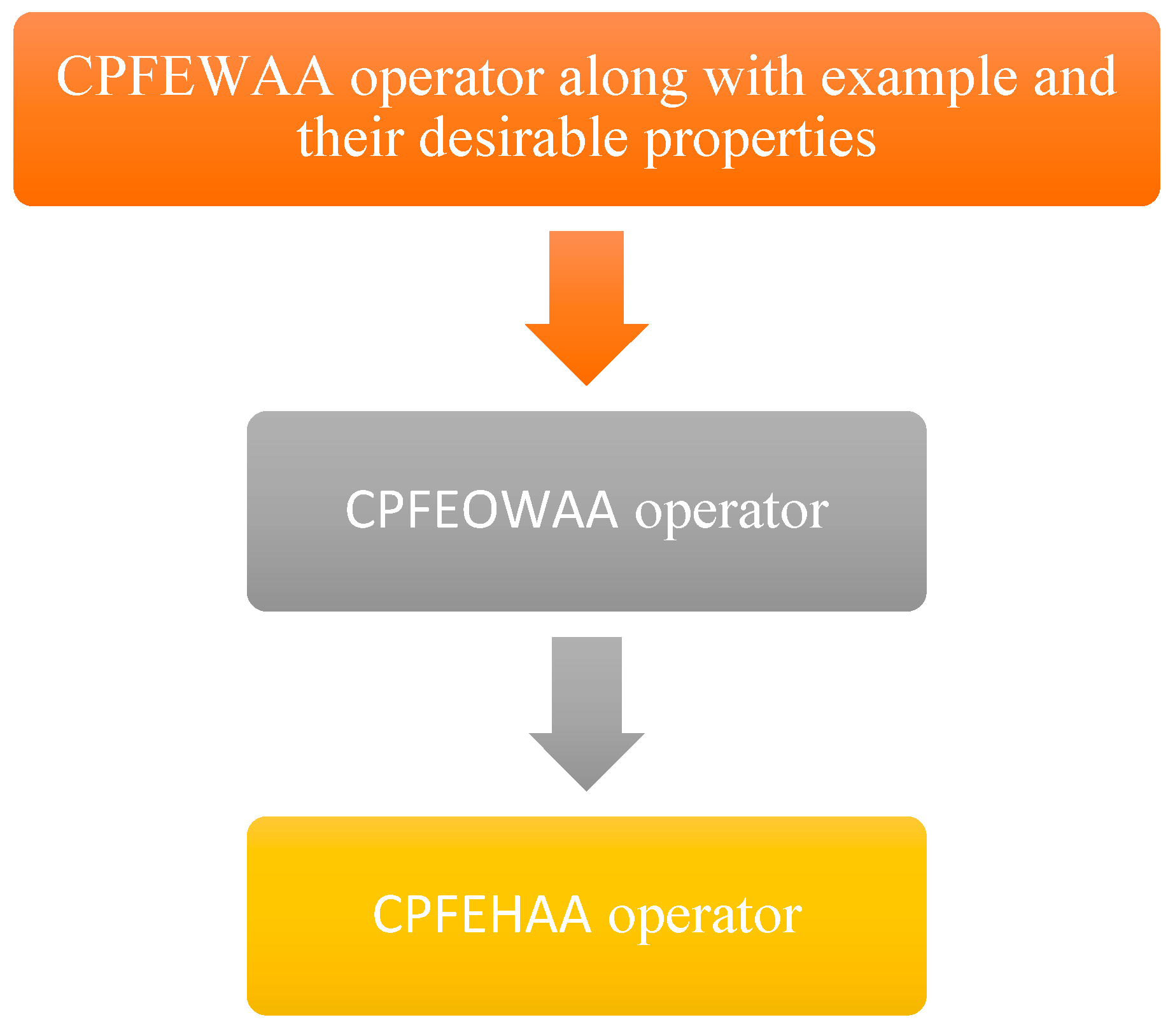
In this unit, we develop three advanced Polytopic fuzzy operators planned for complex fuzzy information aimed at effectively synthesizing multiple data points into a coherent representative value. Using ETN and ETCN, we present the CPFEWAA operator, CPFEOWAA operator, and CPFEHAA operator. These approaches are not only versatile but also possess important properties, such as idempotency, monotonicity, and boundedness, enhancing their applicability across several domains. By leveraging these properties, we can ensure that the aggregation process remains robust and reliable, making these operators appreciated tools for data analysis and decision-making in complex scenarios. This comprehensive framework positions our novel proposed aggregation operators as essential in the realm of fuzzy logic applications, providing a strong foundation for future research and practical implementations. See
Figure 5 for Structure of proposed method.
Definition 11. Let are CPFNs, and be their corresponding known weighted vector under conditions:
and . Then CPFEWAA operator mathematically can be expressed as follows: Example 1. Let there are four CPFNs:and their weights , Next, we have to compute the required values for further analysis. These values will be used in the succeeding steps. Next, utilizing the CPFEWAA operator with the above-calculated values, we obtain the following results
The properties of Einstein aggregation operators, such as idempotency, boundedness, and monotonicity, significantly influence the decision-making process by shaping the way individual inputs are combined and evaluated. Here is an explanation of their effects as follows:
Idempotency: The idempotency property ensures that if all inputs to the aggregation operator are equal, the output is the same as the common input value. This property preserves the consistency of decision-making when uniform data is provided, ensuring that the aggregation process does not distort identical inputs. For decision-making, this fosters fairness and reliability, as no unnecessary bias or variation is introduced when all inputs agree.;
Boundedness: Boundedness guarantees that the result of the aggregation lies within a fixed range, typically between the minimum and maximum input values. This ensures that the decision outcome remains realistic and does not exceed the range of feasible values defined by the data. In decision-making, boundedness prevents extreme or illogical outcomes, maintaining the relevance of results to the problem at hand.
Monotonicity: Monotonicity implies that if an input value increases (or decreases) while others remain constant, the aggregated result reflects a corresponding increase (or decrease). This property ensures that the aggregation process respects the natural order of the data, leading to correct and rational outcomes intuitively. For decision-making, monotonicity ensures that better (or worse) inputs lead to better (or worse) outcomes, which enhances trust and transparency in the decision process.
Theorem 1. Let are CPFNs, with weights under condition: , then Theorem 2. Let
are CPFNs, and let with conditions: , , , , On the same way with , , , , , , then Theorem 3. Let two CPFNs, such as: and with , , , , , , then Definition 12. Let be a family of CPFNs,
be their corresponding weights under limitation, such as ,, and be any rearrangement of with . Then CPFEOWAA operator can be defined mathematically as:
Next, we present hybrid operators that impeccably integrate elements from various traditional operators, nuanced data summarization, and offer greater flexibility. These methods are particularly valuable in data analysis and decision-making, as they effectively capture complex relationships within datasets. By combining different methods, hybrid operators enhance the ability to model real-world scenarios, making them indispensable tools for tackling multilayered problems. Their flexibility ensures a more comprehensive understanding of the underlying data dynamics. See Figure 6 for Space of CPFS. Definition 13. Let be a group of CPFNs, and
be associated vector under conditions, such as belong to one and their sum is equal to 1. Let be their weights such as belong to one and their sum is equal to 1. Also , where be the greatest value and n used for balancing and called balancing coefficient. If tendes to , then approaches to . Then the CPFEHAA operator mathematically can be presented as: 5. An Application of the Proposed Approaches
Decision-making is the process of choosing a solution from among numerous alternatives. It is an essential and essential aspect of human life and is crucial in business, computer science, mathematics, and numerous other fields. This is the point at which you select one choice over the others. Trust your judgment, but also be open to seeking advice or input from others if necessary. CPFS can be used in MCGDM to calculate and rank alternatives based on multiple interrelated criteria. This is particularly useful in situations where decision-makers need to consider complex, multidimensional factors. We develop a decision-making process using the complex Polytopic fuzzy information and their corresponding operators: CPFEWAA operator, CPFEOWAA operator, and CPFEHAA operator. In this process, we consider a fixed group of m alternatives , a fixed group of n attributes with , a fixed group of e experts whose weights is . The key steps are as follows:
Step 1: In this step, we present information about each decision-maker in the form of a matrix with attributes and alternatives:
Step 2: In this 2nd step, combine all individual matrices into a single matrix using the CPFEWAA approach. This results in a combined matrix for further study.
Step 3: Next, calculate all the preference values, such as , using all new approaches. These values are then used for further evaluation.
Step 4: The preference values are utilized to calculate their corresponding score function. This score function is then utilized for further selection analysis.
Step 5: The scores are ranked, and the highest score is selected as the most suitable alternative. This choice represents the optimal option for the given criteria.
6. Illustrative Example
Solar energy is a vital renewable resource with applications across industries, but selecting the right solar panel system can be challenging due to the variety of available options. An enterprise must carefully evaluate factors like needs, objectives, and performance to identify the optimal solution. A thorough, well-informed decision-making process ensures sustainable and effective energy solutions. The goal of this decision-making is to choose the most stable alternative among three alternatives {A1, A2, A3}. For this enterprise, make a group of three experts for the decision of different brands, whose weighted vectors are . The experts considered the three alternatives listed as follows:
Trina solar A1: Trina Solar is a leading global supplier of solar energy solutions, known for its high-efficiency solar panels and pioneering technologies. The company focuses on sustainability and aims to drive the acceptance of clean energy worldwide through its progressive products and services.
Chilwee A2: Chilwee is a prominent manufacturer specializing in progressive lead-acid batteries and energy storage solutions. The company emphasizes advance and sustainability, providing reliable power storage for several applications, including renewable energy systems and electric vehicles.
Samil A3: Samil Power is a leading manufacturer of solar inverters and energy management solutions known for its obligation to efficiency and quality. The company offers a range of products designed to optimize solar energy alteration and enhance system performance for residential and commercial applications.
To determine the most suitable and valuable solar panel system, experts/decision-makers will consider the following criteria:
Safety Performance C1: This criterion assesses the safety features of the solar panel system, including electrical safety standards, fire resistance, and compliance with safety regulations to protect users and property.
Economic Performance C2: This assesses the financial aspects, such as return on investment, payback period, initial cost of the system, maintenance costs, and rebates or available incentives, to ensure the system is economically feasible for users.
Durability C3: This evaluates the resilience and lifespan of the solar panels under numerous environmental conditions, including extreme temperatures, hail, wind, and UV exposure, ensuring they can withstand the test of time.
Applicable Performance C4: This criterion focuses on the efficiency and effectiveness of solar panels in converting sunlight into usable energy, including their performance under different weather conditions and their suitability for numerous systems.
Step 1: In the first step, a comprehensive compilation of information about all the experts is meticulously presented in
Table 1,
Table 2 and
Table 3. These tables are designed to systematically organize and display key details about each expert in a clear matrix format, ensuring that all relevant information is easily accessible and comprehensible.
Step 2: Using CPFEWAA operator, where
and
(
Table 4).
Step 3: Again, using the CPFEWAA operator, with
and get the all preference values as follows:
Step 4: Next, computing the score as below for further selection process:
Step 5: Thus, the more suitable system is .
The following
Table 5 and
Table 6 present the score functions and rankings of various proposed aggregation operators and methods, including CPFEWAA, CPFEOWAA, and CPFEHAA. Moreover,
Figure 7 visually illustrates the rankings derived from these score functions. This comprehensive and complete analysis provides a clear comparison of the aggregation operators, highlighting their respective effectiveness and
Figure 8 illustrates Ranking of all newly proposed approaches. By combining numerical rankings and visual representation, the evaluation enables a deeper understanding of the strengths and weaknesses of each approach. This comparison serves as a valuable tool for systematically assessing and contrasting the performance of the different methods.
7. Comparative and Sensitivity Analysis
Complex Polytopic Fuzzy Sets are an innovative extension of traditional fuzzy sets designed to model complex, higher-dimensional fuzzy information. These sets are particularly valuable in applications requiring the controlling of multidimensional data, such as control, decision-making, and pattern recognition. Unlike FSs, which only represent membership degrees, CPFS can capture both the magnitude and phase of uncertainty using complex numbers. They offer a more nuanced method compared to IFS, PyFS, CFS, CIFS, and CPyFS, each of which has restrictions in handling complex uncertainties and hesitations. Our suggested model is more versatile and adaptable, accommodating complex membership and non-membership degrees and offering greater elasticity compared to existing models, as shown in
Table 7 and
Table 8.
The findings reveal that when utilizing operators such as CPFEWAA, CPFEOWAA, and CPFEHAA, the prime choice can be determined by appropriately adjusting its parameters. Consequently, our proposed aggregation operators offer a versatile tool for decision-makers dealing with complex Polytopic fuzzy MPDA problems. In essence, our complex Polytopic fuzzy Einstein operators not only effectively represent fuzzy information but also enhance the flexibility of the information aggregation process through parameter customization. This distinguishes our proposed operators from existing methods, as they cannot introduce flexibility into the data aggregation procedure. Thus, our innovative operators demonstrate advancements and reliability in the decision-making process involving complex Polytopic fuzzy data, offering decision-makers a more adaptable and superior approach compared to currently available methods.
8. Limitations
The Complex Polytopic Fuzzy Set (CPFS) represents a significant advancement over traditional fuzzy set extensions, such as FSs, IFSs, PyFSs, FFSs, PFSs, and SFSs. CPFSs provide a robust framework for addressing uncertainty and imprecision across a wide array of real-world problems, making them a valuable asset for decision-makers in diverse fields. However, their applicability is constrained by the requirement that the qth power of the membership (m), neutrality (n), and non-membership (ℎ) grades must collectively remain less than or equal to one, i.e., .
However, the limitation of the CPFS lies in its inherent dependency on the balance of its components. Specifically, if any one of the functions membership (m), neutrality (n), and non-membership (ℎ) reaches a value of one, the proposed model fails to function effectively. For example, if we consider . In this case, the proposed model should fail. This constraint highlights a critical weakness in the model’s design, as it depends on a delicate equilibrium among its constituent functions to maintain reliability and accuracy.
9. Conclusions and Implications
Complex Polytopic fuzzy sets offer a powerful framework for handling uncertainty and imprecision in a wide range of real-life problems, making them a valuable tool for decision-makers in various fields. They can be used to model uncertain medical diagnoses. Medical conditions often have overlapping symptoms, making it challenging to arrive at a definitive diagnosis. They can help represent the varying degrees of membership of different symptoms to different medical conditions, providing more accurate and nuanced diagnoses. Thus, in this research, we have explored complex Polytopic fuzzy sets and complex Polytopic fuzzy numbers. We have introduced several novel techniques, such as CPFEWAA, CPFEOWAA, and CPFEHAA, with desirable properties, such as idempotency, monotonicity, and boundedness, based on CPFNs. The new complex Polytopic fuzzy model using Einstein techniques was explained with an illustrative example. Finally, comparison and sensitivity analyses were presented to prove its effectiveness, proficiency, and efficiency.
In the future, we can implement this suggested work in various practical applications, expanding beyond their current scope. This includes applying these approaches to real-world scenarios such as medical diagnosis, pattern recognition, machine learning, and the detection of brain hemorrhages. These applications will involve adapting the techniques to operate it effectively in environment that incorporate fuzzy logic extensions, enhancing their versatility and performance in diverse settings.