Matching Polynomials of Symmetric, Semisymmetric, Double Group Graphs, Polyacenes, Wheels, Fans, and Symmetric Solids in Third and Higher Dimensions
Abstract
1. Introduction
2. Mathematical and Computational Methods Pertinent to Matching Polynomials
3. Results and Discussion
- A.
- Matching Polynomials of the Petersen graph, Chàvatal graph, Grotzsch graph, Star of David graph, Möbius–Kantor graph, Folkman graph, Desargues–Levi graph, Coxeter graph, and Tutte–Coxeter graph
- B.
- Matching Polynomials of three-dimensional polyhedra
- C.
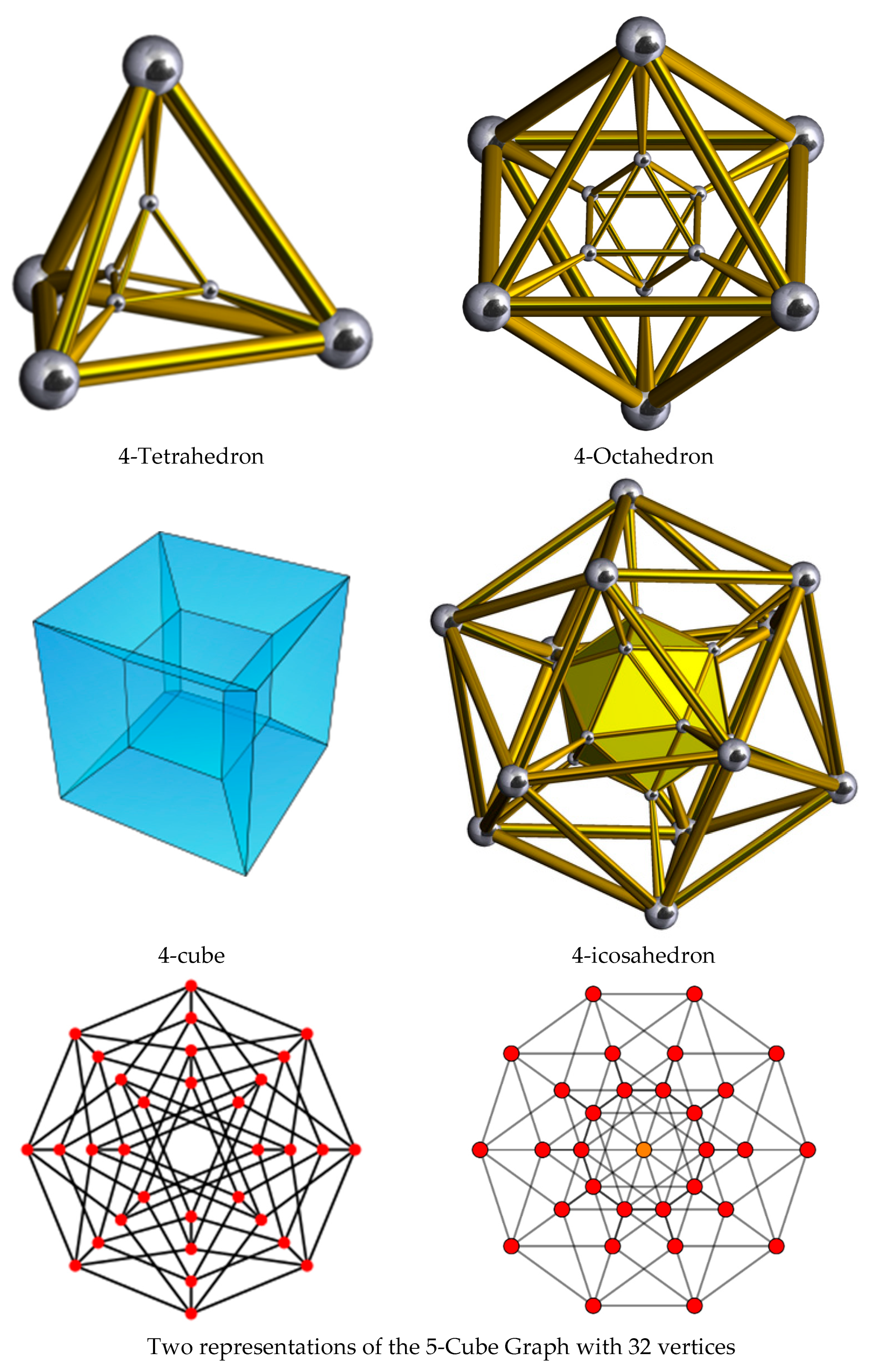
- Matching Polynomials of three-dimensional, 4D, and 5D structures
- D.
- Matching Polynomials of Prism Graphs and circulenes
- E.
- Matching Polynomials of D2h Symmetric Polyacenes
- F.
- Matching Polynomials of Fan and Wheel Graphs
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Balasubramanian, K. Matching Polynomial-Based Similarity Matrices and Descriptors for Isomers of Fullerenes. Inorganics 2023, 11, 335. [Google Scholar] [CrossRef]
- Balasubramanian, K. New Insights into Aromaticity through Novel Delta Polynomials and Delta Aromatic Indices. Symmetry 2024, 16, 391. [Google Scholar] [CrossRef]
- Ramaraj, R.; Balasubramanian, K. Computer Generation of King and Color Polynomials of Graphs and Lattices and Their Applications to Statistical Mechanics. J. Comput. Chem. 1985, 6, 447–454. [Google Scholar] [CrossRef]
- Hosoya, H. Matching and symmetry of graphs. Comput Math. 1986, 12B, 271–290. [Google Scholar]
- Hosoya, H. Aromaticity Index Can Predict and Explain the Stability of Polycyclic Conjugated Hydrocarbons. Monatshefte Für Chem. 2005, 36, 1037–1054. [Google Scholar] [CrossRef]
- Hosoya, H.; Motoyama, A. An effective algorithm for obtaining polynomials for dimer statistics. Application of operator technique on the topological index to two-and three-dimensional rectangular and torus lattices. J. Math. Phys. 1985, 26, 157–167. [Google Scholar] [CrossRef]
- Hosoya, H. On some counting polynomials in chemistry. Discret. Appl. Math. 1988, 19, 239–257. [Google Scholar] [CrossRef]
- Cash, C.G. Relationship between the Hosoya polynomial and the hyper-Wiener index. Appl. Math. Lett. 2002, 15, 893–895. [Google Scholar] [CrossRef]
- Hosoya, H. Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar] [CrossRef]
- Hosoya, H.; Balasubramanian, K. Computational Algorithms for Matching Polynomials of Graphs from the Characteristic Polynomials of Edge-Weighted Graphs. J. Comput. Chem. 1989, 10, 698–710. [Google Scholar] [CrossRef]
- Hosoya, H.; Balasubramanian, K. Exact Dimer Statistics and Characteristic-Polynomials of Cacti Lattices. Theor. Chim. Acta 1989, 76, 315–329. [Google Scholar] [CrossRef]
- Hosoya, H.; Harary, F. On the matching properties of three fence graphs. J. Math. Chem. 1993, 12, 211–218. [Google Scholar] [CrossRef]
- Farell, E.J. An Introduction to Matching Polynomials. J. Comb. Theory Ser. B 1979, 27B, 75–86. [Google Scholar] [CrossRef]
- Gutman, I. A Survey on the Matching Polynomial, in “Graph Polynomials”; Dehmer, M., Shi, Y., Gutman, I., Li, X., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 73–95. [Google Scholar]
- Balasubramanian, K. Tree Pruning Method and Lattice Statistics on Bethe Lattices. J. Math. Chem. 1988, 2, 69–82. [Google Scholar] [CrossRef]
- Balasubramanian, K. Spectra of Matching Polynomials. Chem. Phys. Lett. 1993, 208, 219–224. [Google Scholar] [CrossRef]
- Ramaraj, R.; Balasubramanian, K. Computer Generation of Matching Polynomials of Chemical Graphs and Lattices. J. Comput. Chem. 1985, 6, 122–141. [Google Scholar] [CrossRef]
- Speyer, D.E. Perfect matchings and the octahedron recurrence. J. Algebr. Comb. 2007, 25, 309–348. [Google Scholar] [CrossRef]
- Ohsugi, H.; Tsuchiya, A. Symmetric edge polytopes and matching generating polynomials. arXiv 2020, arXiv:2008.08621. [Google Scholar] [CrossRef]
- Devaraj, J.; Sowmya, S. On matching polynomial in graphs. Bull. Pure Appl. Sci.-Math. Stat. 2014, 33, 75–90. [Google Scholar] [CrossRef]
- Manoharan, M.; Balakrishnarajan, M.; Venuvanalingam, P.; Balasubramanian, K. Topological resonance energy predictions of the stability of fullerene clusters. Chem. Phys. Lett. 1994, 222, 95–100. [Google Scholar] [CrossRef]
- Babić, D.; Ori, O. Matching polynomial and topological resonance energy of C70. Chem. Phys. Lett. 1995, 234, 240–244. [Google Scholar] [CrossRef]
- Liu, J.; Shan, B.Z. The Computation of the Matching Polynomials of Fullerene Graphs. Croat. Chem. Acta. 1997, 70, 971–977. [Google Scholar]
- Aihara, J.I.; Babić, D.; Gutman, I. Matching spectra of fullerenes. MATCH Commun. Math. Comput. Chem. 1996, 33, 7–16. [Google Scholar]
- Herndon, W.C.; Radhakrishnan, T.P.; Zivković, T.P. Characteristic and matching polynomials of chemical graphs. Chem. Phys. Lett. 1988, 152, 233–238. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, C.; Yao, H.; Wang, X. Computing the forcing and anti-forcing numbers of perfect matchings for graphs by integer linear programmings. MATCH Commun. Math. Comput. Chem. 2022, 87, 561–575. [Google Scholar] [CrossRef]
- Salvador, J.M.; Hernandez, A.; Beltran, A.; Duran, R.; Mactutis, A. Fast partial-differential synthesis of the matching polynomial of C72-100. J. Chem. Inf. Comput. Sci. 1988, 38, 1105–1110. [Google Scholar] [CrossRef]
- Kasteleyn, P.W. Graph Theory and Theoretical Physics; Harary, F., Ed.; Academic Press: London, UK, 1967. [Google Scholar]
- Percus, J.K. Combinatorial Methods; Courant Institute of New York University: New York, NY, USA, 1969. [Google Scholar]
- Temperley, H.N.V. Phase Transition and Critical Phenomena; Domb, C., Green, M.S., Eds.; Academic Press: London, UK, 1972; Volume I, p. 227. [Google Scholar]
- Park, J.; Newman, M.E.J. Statistical mechanics of networks. Phys. Rev. B. 2004, 70, 066117. [Google Scholar] [CrossRef]
- Kaatz, F.H.; Bultheel, A. Informational thermodynamic model for nanostructures. J. Math. Chem. 2014, 52, 1563–1575. [Google Scholar] [CrossRef]
- Balasubramanian, K. Matching Polynomials of Fullerene Clusters. Chem. Phys. Lett. 1993, 201, 306–314. [Google Scholar] [CrossRef]
- Balasubramanian, K. Density Functional and Graph Theory Computations of Vibrational, Electronic and Topological Properties of Porous Nanographenes. J. Phys. Org. Chem. 2023, 36, e4435. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/poc.4435 (accessed on 20 November 2024). [CrossRef]
- Aihara, J. Graph theory of aromatic stabilization. Bull. Chem. Soc. Jpn. 2016, 89, 1425–1454. [Google Scholar] [CrossRef]
- Aihara, J. Graph-theoretical formulation of London diamagnetism. J. Am. Chem. Soc. 1979, 101, 5913–5917. [Google Scholar] [CrossRef]
- Aihara, J.; Horikawa, T. Graph-theoretical formula for ring currents induced in a polycyclic conjugated system. Bull. Chem. Soc. Jpn. 1983, 56, 1853–1854. [Google Scholar] [CrossRef]
- Aihara, J. Circuit resonance energy: A key quantity that links energetic and magnetic criteria of aromaticity. J. Am. Chem. Soc. 2006, 128, 2873–2879. [Google Scholar] [CrossRef]
- Aihara, J. Topological resonance energy, bond resonance energy, and circuit resonance energy. J. Phys. Org. Chem. 1979, 21, 79–85. [Google Scholar] [CrossRef]
- Dias, J.R. Valence-bond determination of diradical character of polycyclic aromatic hydrocarbons: From acenes to rectangular benzenoids. J. Phys. Chem. A. 2013, 117, 4716–4725. [Google Scholar] [CrossRef]
- Dias, J.R. The Formula Periodic Table for Benzenoid Hydrocarbons and the Unifying Theory of a Periodic Table Set. Polycycl. Aromat. Compounds. 1994, 4, 87–106. [Google Scholar] [CrossRef]
- Aihara, J.; Makino, M.; Ishida, T.; Dias, J.R. Analytical study of superaromaticity in cycloarenes and related coronoid hydrocarbons. J. Phys. Chem. A 2013, 117, 4688–4697. [Google Scholar] [CrossRef]
- Aihara, J. On the number of aromatic sextets in a benzenoid hydrocarbon. Bull. Chem. Soc. Jpn. 1976, 49, 1429–1430. [Google Scholar] [CrossRef]
- Randić, M. Aromaticity of polycyclic conjugated hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef]
- Aihara, J. Aromaticity and superaromaticity in cyclopolyacenes. J. Chem. Soc. Perkin Trans. 1994, 2, 971–974. [Google Scholar] [CrossRef]
- Randić, M.; Balaban, A.T. Local aromaticity and aromatic sextet theory beyond Clar. Int. J. Quant. Chem. 2018, 118, e25657. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. Long carbon chain molecules in circumstellar shells. Astrophys. J. 1987, 314, 352–355. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.L.; Yuf, C.H. Computations in treating fullerenes and carbon aggregates. Rev. Comput. Chem. 2009, 8, 1. [Google Scholar]
- Ōsawa, E.; Ueno, H.; Yoshida, M.; Slanina, Z.; Zhao, X.; Nishiyama, M.; Saito, H. Combined topological and energy analysis of the annealing process in fullerene formation. Stone–Wales interconversion pathways among IPR isomers of higher fullerenes. J. Chem. Soc. Perkin Trans. 1998, 2, 943–950. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological peripheral shapes and distance-based characterization of fullerenes C20–C720: Existence of isoperipheral fullerenes. Polycycl. Aromat. Compounds. 2022, 42, 1649–1667. [Google Scholar] [CrossRef]
- Balaban, A.T.; Liu, X.; Klein, D.J.; Babić, D.; Schmalz, T.G.; Seitz, W.A.; Randi’c, M. Graph invariants for fullerenes. J. Chem. Inf. Comput. Sci. 1995, 35, 396–404. [Google Scholar] [CrossRef]
- Bača, M.; Horváthová, J.; Mokrišová, M.; Suhányiová, A. On topological indices of fullerenes. Appl. Math. Comput. 2015, 251, 154–161. [Google Scholar] [CrossRef]
- Alizadeh, Y.; Iranmanesh, A.; Mirzaie, S. Computing Schultz polynomial, Schultz index of C60 fullerene by gap program. Dig. J. Nanomater. Biostructures 2009, 4, 7–10. [Google Scholar]
- Ghorbani, M. Connective eccentric index of fullerenes. J. Math. Nanosci. 2011, 1, 43–50. [Google Scholar]
- Walker, P.D.; Maggiora, G.M.; Johnson, M.A.; Petke, J.D.; Mezey, P.G. Shape group analysis of molecular similarity: Shape similarity of six-membered aromatic ring systems. J. Chem. Inf. Comput. Sci. 1995, 35, 568–578. [Google Scholar] [CrossRef]
- Mezey, P.G. Fuzzy electron density fragments in macromolecular quantum chemistry, combinatorial quantum chemistry, functional group analysis, and shape–activity relations. Acc. Chem. Res. 2014, 47, 2821–2827. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, K. Symmetry, Combinatorics, Artificial Intelligence, Music and Spectroscopy. Symmetry 2021, 13, 1850. [Google Scholar] [CrossRef]
- Balasubramanian, K. Orthogonal polynomials through complex matrix graph theory. J. Math. Chem. 2023, 61, 144–165. [Google Scholar] [CrossRef]
- Balasubramanian, K. Enumeration of Internal-Rotation Reactions and Their Reaction Graphs. Theor. Chim. Acta 1979, 53, 129–146. [Google Scholar] [CrossRef]
- Mislow, K. Role of pseudorotation in the stereochemistry of nucleophilic displacement reactions. Acc. Chem. Res. 1970, 3, 321–331. [Google Scholar] [CrossRef]
- Zon, G.; Mislow, K. Studies in phosphorus stereochemistry. In The Chemistry of Organophosphorus Compounds I; Springer: Berlin/Heidelberg, Germany, 2006; pp. 61–94. [Google Scholar]
- Randić, M. Symmetry properties of graphs of interest in chemistry. II. Desargues–Levi graph. Int. J. Quantum Chem. 1979, 15, 663–682. [Google Scholar] [CrossRef]
- Balasubramanian, K. Relativity and the Jahn–Teller, Berry pseudorotations of TBP clusters: Group theory, spin–orbit and combinatorial nuclear spin statistics of TBP Desargues–Levi isomerization graph. J. Math. Chem. 2018, 56, 2194–2225. [Google Scholar] [CrossRef]
- Balasubramanian, K. Nonrigid group theory, tunneling splittings, and nuclear spin statistics of water pentamer:(H2O)5. J. Phys. Chem. A. 2004, 108, 5527–5536. [Google Scholar] [CrossRef]
- Lijnen, E.; Ceulemans, A. Oriented 2-Cell Embeddings of a Graph and Their Symmetry Classification: Generating Algorithms and Case Study of the Möbius-Kantor Graph. J. Chem. Inf. Model. 2004, 44, 1552–1564. [Google Scholar] [CrossRef] [PubMed]
- Herges, R. Topology in chemistry: Designing Möbius molecules. Chem. Rev. 2006, 106, 4820–4842. [Google Scholar] [CrossRef]
- Segawa, Y.; Watanabe, T.; Yamanoue, K.; Kuwayama, M.; Watanabe, K.; Pirillo, J.; Hijikata, Y.; Itami, K. Synthesis of a Möbius carbon nanobelt. Nat. Synth. 2022, 1, 535–541. [Google Scholar] [CrossRef]
- Balasubramanian, K. Relativistic double group spinor representations of nonrigid molecules. J. Chem. Phys. 2004, 120, 5524–5535. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, K. Double group of the icosahedral group (Ih) and its application to fullerenes. Chem. Phys. Lett. 1996, 260, 476–484. [Google Scholar] [CrossRef]
- Balasubramanian, K. Relativistic Effects in Chemistry: Part A Theory & Techniques; John Wiley & Sons: New York, NY, USA, 1997; p. 301. [Google Scholar]
- Judd, B.R.; Lister, G.M.S. Complementary groups in the quark model of the atom. J. Phys. A Math. Gen. 1992, 25, 2615. [Google Scholar] [CrossRef]
- Balasubramanian, K. Enumeration of n-Dimensional Hypercubes, Icosahedra, Rubik’s Cube Dice, Colorings, Chirality, and Encryptions Based on Their Symmetries. Symmetry 2024, 16, 1020. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological Indices, Graph Spectra, Entropies, Laplacians, and Matching Polynomials of n-Dimensional Hypercubes. Symmetry 2023, 15, 557. [Google Scholar] [CrossRef]
- Balasubramanian, K. Symmetry in Chemistry and Indian Religions. In Symmetry in Cultural Context: An Interdisciplinary Workshop; Nagy, D., Ed.; Arizona State University: Tempe, AZ, USA, 1987; Volume 1, pp. 12–15. [Google Scholar]
- Nagarajan, V. Feeding a Thousand Souls: Women, Ritual, and Ecology in India-An Exploration of the Kolam; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Ali, H.; Shafiq, M.; Farahani, M.; Cancan, M.; Aldemir, M. Degree-based topological descriptors of star of David and hexagonal cage networks. Eurasian Chem. Commun. 2020, 2, 1093–1100. [Google Scholar]
- Tesseract. The File is Licensed Under the Creative Commons Attribution-Share Alike 3.0 Unported License. Available online: https://en.wikipedia.org/wiki/File:Hypercube.svg (accessed on 20 November 2024).
- Dwunastościan Ścięty EN:Truncated Dodecahedron. Available online: https://en.wikipedia.org/wiki/Truncated_dodecahedron#/media/File:Dwunasto%C5%9Bcian_%C5%9Bci%C4%99ty.svg (accessed on 20 November 2024).
- Knuth, D.E. Chàyvatal Graph Layout, “The Art of Computer Programming, Volume 4, Fascicle 0: Introduction to Combinatorial Functions and Boolean Functions”; Addison-Wesley: Boston, MA, USA, 2008. [Google Scholar]
- David Eppstein—Own Work, Public Domain. Available online: https://commons.wikimedia.org/w/index.php?curid=2798751 (accessed on 20 November 2024).
- Available online: https://en.wikipedia.org/wiki/Desargues_graph#/media/File:DesarguesGraph.svg (accessed on 20 November 2024).
- Available online: https://commons.wikimedia.org/wiki/File:Groetzsch-graph.svg (accessed on 20 November 2024).
- Available online: https://commons.wikimedia.org/wiki/File:Folkman_Lombardi.svg (accessed on 20 November 2024).
- Genus-2 By Maproom—Own Work, CC BY-SA 4.0. Available online: https://commons.wikimedia.org/w/index.php?curid=143656298 (accessed on 20 November 2024).
- Weisstein, E.W. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/BidiakisCube.html (accessed on 20 November 2024).
- Tom Ruen, Open Source, Copy-Right Free, Public Domain Image. Available online: https://commons.wikimedia.org/wiki/File:5-cube_t0.svg (accessed on 20 November 2024).
- Amamoto, K.; Harada, T.; Nakazaki, M.; Naka, T.; Kai, Y.; Harada, S.; Kasai, N. Synthesis and characterization of [7]circulene. J. Am. Chem. Soc. 1983, 105, 7171–7172. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, A.; Wang, H.; Zhao, W.-T.; Sun, D.-Q. On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution. Mathematics 2019, 7, 472. [Google Scholar] [CrossRef]
- Alotaibi, M.; Alghamdi, A.; Alolaiyan, H. On Laplacian Eigenvalues of Wheel Graphs. Symmetry 2023, 15, 1737. [Google Scholar] [CrossRef]
- “Lucas Polynomial.” From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/LucasPolynomial.html (accessed on 20 November 2024).
- Krishnamurthy, V. Counting of finite topologies and a dissection of Stirling numbers of the second kind. Bull. Austra. Math. Soc. 1975, 12, 111–124. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Z.; Xue, H.; Zhang, L.; He, M.; Yang, Z.; Singh, R.; Chong, Y.; Zhang, B.; Chen, H. Realization of a three-dimensional photonic topological insulator. Nature 2019, 565, 622. [Google Scholar] [CrossRef]
- Yang, Y.; Jing, L.; Zheng, B.; Hao, R.; Yin, W.; Li, E.; Soukoulis, C.M.; Chen, H. Full-polarization 3D metasurface cloak with preserved amplitude and phase. Adv. Mater. 2016, 28, 6866–6871. [Google Scholar] [CrossRef]








| Petersen Graph | |
|---|---|
| Petersen Graph S5 (120) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −15 |
| 4 | 75 |
| 6 | −145 |
| 8 | 90 |
| 10 | −6 |
| Matching Polynomial of the Chàvatal Graph (D4) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −24 |
| 4 | 204 |
| 6 | −752 |
| 8 | 1175 |
| 10 | −628 |
| 12 | 52 |
| Matching Polynomial of the Grotzsch Graph | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −20 |
| 4 | 135 |
| 6 | −365 |
| 8 | 360 |
| 10 | −87 |
| Matching Polynomial of the Star of David Graph | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −18 |
| 4 | 111 |
| 6 | −276 |
| 8 | 255 |
| 10 | −66 |
| 12 | 2 |
| Matching Polynomial of the Möbius–Kantor Graph: Oh2 (Order:96)-Double Group of the Octahedral Group | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −24 |
| 4 | 228 |
| 6 | −1096 |
| 8 | 2826 |
| 10 | −3816 |
| 12 | 2444 |
| 14 | −600 |
| 16 | 33 |
| Matching Polynomial of the Semisymmetric Folkman Graph: S5[S2]: O(3840) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −40 |
| 4 | 660 |
| 6 | −5840 |
| 8 | 30,200 |
| 10 | −93,408 |
| 12 | 170,080 |
| 14 | −172,480 |
| 16 | 86,880 |
| 18 | −17,280 |
| 20 | 768 |
| The Desargues–Levi Graph (S5 × S2) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −30 (2 × 3 × 5) |
| 4 | 375 (3 × 53) |
| 6 | −2540 (22 × 5 × 127) |
| 8 | 10,155 (3 × 5 × 677) |
| 10 | −24,486 (2 × 3 × 7 × 11 × 53) |
| 12 | 34,945 (2 × 29 × 241) |
| 14 | −27,840 |
| 16 | 11,040 |
| 18 | −1720 (23 × 5 × 43) |
| 20 | 60 (22 × 3 × 5) |
| The Levi-30 Graph: | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −45 |
| 4 | 890 |
| 6 | −10,215 |
| 8 | 75,665 |
| 10 | −380,559 |
| 12 | 1,331,660 |
| 14 | −3,268,585 |
| 16 | 5,604,695 |
| 18 | −6,610,695 |
| 20 | 5,213,550 |
| 22 | −2,626,805 |
| 24 | 786,360 |
| 26 | −123,630 |
| 28 | 8040 |
| 30 | −120 |
| Matching Polynomial of the Coxeter Graph: PGL2(7) O:338 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −42 |
| 4 | 777 |
| 6 | −8344 |
| 8 | 57,708 |
| 10 | −269,640 |
| 12 | 868,700 |
| 14 | 1,934,712 (23 × 33 × 132 × 53) |
| 16 | 2,942,247 |
| 18 | −2,970,310 |
| 20 | 1,894,851 |
| 22 | −703,080 |
| 24 | 130,872 |
| 26 | −8904 |
| 28 | 84 |
| Matching Polynomial of the Tutte–Coxeter Graph S6 × S2: O(1440) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −45 |
| 4 | 900 |
| 6 | −10,560 |
| 8 | 80,820 |
| 10 | −424,404 |
| 12 | 1,566,360 |
| 14 | −4,094,280 |
| 16 | 7,541,460 |
| 18 | −9,622,660 |
| 20 | 8,246,160 |
| 22 | −4,517,280 |
| 24 | 1,464,120 |
| 26 | −247,320 |
| 28 | 17,280 |
| 30 | −288 (2 × 122)= |
| Matching Polynomial of Cube | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −12 |
| 4 | 42 |
| 6 | −44 |
| 8 | 9 |
| Matching Polynomial of Octahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −12 |
| 4 | 30 |
| 6 | −8 |
| Matching Polynomial of Icosahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −30 |
| 4 | 315 |
| 6 | −1400 |
| 8 | 2535 |
| 10 | −1482 |
| 12 | 125 |
| Matching Polynomial of Dodecahedron C20 Ih (120) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −30 |
| 4 | 375 |
| 6 | −2540 |
| 8 | 10,155 |
| 10 | −24,474 |
| 12 | 34,805 |
| 14 | −27,300 |
| 16 | 10,260 |
| 18 | −1400 |
| 20 | 36 |
| Matching Polynomial of Bidiakis cube: D4 (8) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −18 |
| 4 | 117 |
| 6 | −336 |
| 8 | 418 |
| 10 | −184 |
| 12 | 12 |
| Matching Polynomial of Bislit Cube (Td: O(24)) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −14 |
| 4 | 55 |
| 6 | −58 |
| 8 | 9 |
| Matching Polynomial of Rhombicuboctahedron Oh (O:48) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −48 |
| 4 | 984 (23 × 3 × 41) |
| 6 | −11,288 |
| 8 | 79,806 |
| 10 | −361,248 |
| 12 | 1,054,328 |
| 14 | −1,951,272 |
| 16 | 2,196,753 |
| 18 | −1,394,608 |
| 20 | 436,608 |
| 22 | −51,552 (25 × 32 × 179) |
| 24 | 1088 (17 × 43) |
| Matching Polynomial of truncated dodecahedron: Ih (O:120) | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −90 |
| 4 | 3825 |
| 6 | −102,100 |
| 8 | 1,920,480 |
| 10 | −27,073,548 |
| 12 | 297,017,670 |
| 14 | −2,599,271,940 |
| 16 | 18,452,804,370 |
| 18 | −107,509,368,860 |
| 20 | 518,092,164,744 |
| 22 | −2,075,424,449,400 |
| 24 | 6,929,555,927,025 |
| 26 | −19,297,656,051,090 |
| 28 | 44,774,805,188,205 |
| 30 | −86,315,702,921,360 |
| 32 | 137,639,652,148,260 |
| 34 | −180,432,784,692,900 |
| 36 | 192,895,567,767,700 |
| 38 | −166,490,504,865,960 |
| 40 | 114,582,353,107,800 |
| 42 | −61,926,709,855,920 |
| 44 | 25,792,171,457,280 |
| 46 | −8,085,072,744,000 |
| 48 | 1,850,294,700,320 |
| 50 | −296,798,234,112 |
| 52 | 31,509,790,080 |
| 54 | −2,030,914,560 |
| 56 | 68,820,480 |
| 58 | −921,600 |
| 60 | 2048 |
| Matching polynomial of 4-tetrahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −16 |
| 4 | 72 |
| 6 | −88 |
| 8 | 16 |
| Matching Polynomial of 4-octahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −30 |
| 4 | 315 |
| 6 | −1404 |
| 8 | 2571 |
| 10 | −1518 |
| 12 | 137 |
| Matching Polynomial of 4-cube | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −32 |
| 4 | 400 |
| 6 | −2496 |
| 8 | 8256 |
| 10 | −14,208 |
| 12 | 11,648 |
| 14 | −3712 |
| 16 | 272 (17 × 24) |
| Matching Polynomial of 4-icosahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −72 |
| 4 | 2196 |
| 6 | −37,160 |
| 8 | 384,060 |
| 10 | −2,517,456 |
| 12 | 10,535,152 |
| 14 | −27,675,936 |
| 16 | 43,782,600 |
| 18 | −38,663,520 |
| 20 | 16,625,760 |
| 22 | −2,632,320 |
| 24 | 66,400 |
| Matching Polynomial of 5-tetrahedron | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −40 |
| 4 | 620 |
| 6 | −4744 |
| 8 | 18,934 |
| 10 | −38,360 |
| 12 | 35,564 |
| 14 | −11,768 |
| 16 | 673 |
| Matching Polynomial of 5-cube a | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −80 |
| 4 | 2840 |
| 6 | −59,120 |
| 8 | 803,580 |
| 10 | −7,517,264 |
| 12 | 49,715,240 |
| 14 | −235,146,480 |
| 16 | 795,862,790 |
| 18 | −1,910,146,160 |
| 20 | 3,190,117,800 |
| 22 | −3,594,554,960 |
| 24 | 2,605,908,220 |
| 26 | −1,129,177,840 |
| 28 | 259,084,440 |
| 30 | −25,108,944 |
| 32 | 589,185 32 × 5 × 13,093 |
| Matching Polynomial of 6-prism | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −18 |
| 4 | 117 |
| 6 | −336 |
| 8 | 420 |
| 10 | −192 |
| 12 | 20 |
| Matching Polynomial of 20-prism | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −60 |
| 4 | 1650 |
| 6 | −27,580 |
| 8 | 313,355 |
| 10 | −2,564,152 |
| 12 | 15,624,200 |
| 14 | −72,305,160 |
| 16 | 256,948,925 |
| 18 | −704,514,900 |
| 20 | 1,489,893,222 |
| 22 | −2,418,300,660 |
| 24 | 2,984,254,025 |
| 26 | −2,759,465,880 |
| 28 | 1,873,096,780 |
| 30 | −907,342,584 |
| 32 | 301,700,575 |
| 34 | −65,197,340 |
| 36 | 8,444,350 |
| 38 | −573,100 |
| 40 | 15,129 |
| Matching Polynomial of [7]Circulene | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −35 |
| 4 | 539 |
| 6 | −4816 |
| 8 | 27,720 |
| 10 | −107,912 |
| 12 | 290,339 |
| 14 | −542,329 |
| 16 | 696,906 |
| 18 | −602,070 |
| 20 | 335,671 |
| 22 | −112,728 |
| 24 | 20,223 |
| 26 | −1540 |
| 28 | 29 |
| Matching Polynomial of Dodecacene (n = 12) C50H28 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −61 |
| 4 | 1736 |
| 6 | −30,626 |
| 8 | 375,366 |
| 10 | −3,395,178 |
| 12 | 23,498,917 |
| 14 | −127,361,785 |
| 16 | 548,705,684 |
| 18 | −1,896,924,530 |
| 20 | 5,290,433,560 |
| 22 | −11,927,625,748 |
| 24 | 21,721,468,366 |
| 26 | −31,840,941,462 |
| 28 | 37,338,708,833 |
| 30 | −34,709,568,941 |
| 32 | 25,258,851,533 |
| 34 | −14,150,729,127 |
| 36 | 5,968,641,194 |
| 38 | −1,839,602,672 |
| 40 | 397,649,627 |
| 42 | −56,858,935 |
| 44 | 4,923,425 |
| 46 | −223,119 |
| 48 | 3991 |
| 50 | −13 |
| Matching Polynomial of Icosadecaacene: C82H44 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −101 |
| 4 | 4892 |
| 6 | −151,318 |
| 8 | 3,358,252 |
| 10 | −56,961,072 |
| 12 | 768,023,033 |
| 14 | −8,453,932,129 |
| 16 | 77,422,745,297 |
| 18 | −598,247,474,531 |
| 20 | 3,941,670,102,182 |
| 22 | −22,323,819,077,892 |
| 24 | 109,352,563,856,004 |
| 26 | −465,483,428,654,996 |
| 28 | 1,727,898,071,519,730 |
| 30 | −5,607,400,985,161,978 |
| 32 | 15,935,046,764,398,403 |
| 34 | −39,690,091,049,676,019 |
| 36 | 86,663,388,278,077,032 |
| 38 | −165,813,129,496,595,054 |
| 40 | 277,691,639,411,066,623 |
| 42 | −406,373,387,911,744,607 |
| 44 | 518,422,953,957,560,676 |
| 46 | −574,807,649,440,327,458 |
| 48 | 551,828,147,671,441,734 |
| 50 | −456,602,133,188,515,554 |
| 52 | 323,842,004,554,570,254 |
| 54 | −195,583,677,627,033,074 |
| 56 | 99,799,512,244,940,281 |
| 58 | −42,623,325,522,793,081 |
| 60 | 15,065,907,534,807,099 |
| 62 | −4,347,541,972,528,117 |
| 64 | 1,007,231,299,977,324 |
| 66 | −183,492,571,858,506 |
| 68 | 25,601,107,765,586 |
| 70 | −2,643,389,537,838 |
| 72 | 192,895,705,906 |
| 74 | −9,324,974,318 |
| 76 | 271,097,321 |
| 78 | −4,043,149 |
| 80 | 22,771 |
| 82 | −21 |
| Matching Polynomial of icosikaihenaacene: C86H46 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −106 |
| 4 | 5399 |
| 6 | −175,982 |
| 8 | 4,124,817 |
| 10 | −74,063,694 |
| 12 | 1,059,798,817 |
| 14 | −12,413,256,034 |
| 16 | 121,312,317,953 |
| 18 | −1,003,323,241,558 |
| 20 | 7,098,532,567,167 |
| 22 | −43,320,026,062,610 |
| 24 | 229,505,620,258,568 |
| 26 | −1,060,826,821,769,124 |
| 28 | 4,294,355,311,546,214 |
| 30 | −15,268,301,022,112,204 |
| 32 | 47,775,302,500,611,115 |
| 34 | −131,736,351,086,317,702 |
| 36 | 320,322,373,771,219,109 |
| 38 | −686,879,644,763,111,634 |
| 40 | 1,298,296,235,256,059,369 |
| 42 | −2,160,812,435,654,172,406 |
| 44 | 3,161,718,641,030,940,101 |
| 46 | −4,058,460,408,832,005,802 |
| 48 | 4,557,683,667,571,399,942 |
| 50 | −4,462,813,454,863,667,224 |
| 52 | 3,794,792,897,456,339,076 |
| 54 | −2,788,519,170,495,778,816 |
| 56 | 1,760,616,669,946,163,818 |
| 58 | −948,642,540,487,223,764 |
| 60 | 432,694,958,770,892,042 |
| 62 | −165,475,778,402,889,628 |
| 64 | 52,453,188,928,638,474 |
| 66 | −13,591,558,098,242,156 |
| 68 | 2,830,490,059,458,396 |
| 70 | −463,880,574,967,916 |
| 72 | 58,254,110,807,545 |
| 74 | −5,414,880,348,970 |
| 76 | 355,639,745,651 |
| 78 | −15,461,753,910 |
| 80 | 403,631,899 |
| 82 | −5,390,418 |
| 84 | 27,049 |
| 86 | −22 |
| Matching polynomial of fan graph:F1,8 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −15 |
| 4 | 57 |
| 6 | −70 |
| 8 | 21 |
| Matching polynomial of fan graph:F1,9 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −17 |
| 4 | 77 |
| 6 | −125 |
| 8 | 65 |
| 10 | −5 |
| Matching polynomial of fan graph:F1,59 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −117 |
| 4 | 4902 |
| 6 | −115,500 |
| 8 | 1,810,215 |
| 10 | −20,556,315 |
| 12 | 177,920,470 |
| 14 | −1,212,786,120 |
| 16 | 6,657,068,250 |
| 18 | −29,886,244,850 |
| 20 | 110,940,604,236 |
| 22 | −343,090,279,272 |
| 24 | 888,273,814,467 |
| 26 | −1,930,565,260,575 |
| 28 | 3,525,156,951,030 |
| 30 | −5,402,923,000,816 |
| 32 | 6,932,619,043,842 |
| 34 | −7,414,579,956,042 |
| 36 | 6,568,660,819,500 |
| 38 | −4,779,873,142,200 |
| 40 | 2,825,853,840,810 |
| 42 | −1,338,323,167,170 |
| 44 | 498,643,637,220 |
| 46 | −142,773,786,000 |
| 48 | 30,457,490,700 |
| 50 | −4,641,936,156 |
| 52 | 476,333,352 |
| 54 | −30,105,712 |
| 56 | 1,011,375 |
| 58 | −13,515 |
| 60 | 30 |
| Matching polynomial of fan graph:F1,85 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −169 (132) |
| 4 | 10,375 (83 × 53) |
| 6 | −364,203 (33 × 7 × 41 × 47) |
| 8 | 8,659,980 (22 × 33 × 5 × 7 × 29 × 79) |
| 10 | −152,147,996 |
| 12 | 2,080,963,885 |
| 14 | −22,933,178,125 |
| 16 | 208,617,123,495 |
| 18 | −1,594,369,711,175 |
| 20 | 10,374,198,391,655 |
| 22 | −58,060,344,219,059 |
| 24 | 281,714,375,014,800 |
| 26 | −1,192,427,220,013,008 |
| 28 | 4,424,260,086,335,960 |
| 30 | −14,442,497,433,011,224 |
| 32 | 41,594,650,278,748,204 |
| 34 | −105,895,397,831,661,900 |
| 36 | 238,617,629,780,678,148 |
| 38 | −476,182,683,153,477,300 |
| 40 | 841,563,020,406,566,640 |
| 42 | −1,316,390,172,750,258,480 |
| 44 | 1,820,371,878,792,109,125 |
| 46 | −2,221,526,893,121,028,885 |
| 48 | 2,386,893,699,264,226,425 |
| 50 | −2,251,111,074,386,846,217 |
| 52 | 1,856,642,490,120,368,853 |
| 54 | −1,333,123,593,620,443,625 |
| 56 | 828,854,313,170,681,336 |
| 58 | −443,360,306,892,355,160 |
| 60 | 202,479,302,558,751,372 |
| 62 | −78,232,205,870,140,140 |
| 64 | 25,294,376,054,504,375 |
| 66 | −6,754,075,658,931,055 |
| 68 | 1,465,618,299,382,825 |
| 70 | −253,359,004,049,445 |
| 72 | 34,025,040,410,564 |
| 74 | −3,436,353,389,300 |
| 76 | 249,909,853,193 |
| 78 | −12,317,366,985 |
| 80 | 375,894,519 (19,383 × 19,393) (3 × 7 × 11 × 13 × 41 × 43 × 71) |
| 82 | −6,122,039 (part of integer sequence A006414 for nonseparable toroidal tree-rooted maps with n + 2 edges and n + 1 vertices. |
| 84 | 39,775 (52 × 37 × 43) |
| 86 | −43 |
| Matching polynomial of wheel graph:W18 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −34 |
| 4 | 374 |
| 6 | −1989 |
| 8 | 5797 |
| 10 | −9537 |
| 12 | 8568 |
| 14 | −3774 |
| 16 | 629 |
| 18 | −17 |
| Matching polynomial of wheel graph:W20 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −38 |
| 4 | 475 |
| 6 | −2945 |
| 8 | 10,374 |
| 10 | −21,736 |
| 12 | 26,961 |
| 14 | −18,810 |
| 16 | 6555 |
| 18 | −874 |
| 20 | 19 |
| Matching polynomial of wheel graph:W86 | |
| Xn−k | Ck |
| 0 | 1 |
| 2 | −170 = × C(2,1)) |
| 4 | 10,540: × S(6,2) × 22 |
| 6 | −374,085: S(9,2) × 163 × 32 |
| 8 | 8,998,100: × 67 × 79 × 52 × 23 |
| 10 | −159,976,817 |
| 12 | 2,214,762,550 |
| 14 | −24,711,381,475 |
| 16 | 227,636,971,275 |
| 18 | −1,762,087,833,500 |
| 20 | 11,615,083,138,744 |
| 22 | −65,865,738,744,845 |
| 24 | 323,880,131,505,840 |
| 26 | −1,389,589,368,548,360 |
| 28 | 5,227,087,399,521,200 |
| 30 | −17,302,653,035,266,792 |
| 32 | 50,541,458,989,916,620 |
| 34 | −130,532,286,306,783,240 |
| 36 | 298,446,755,493,160,560 |
| 38 | −604,444,951,535,743,500 |
| 40 | 1,084,392,669,948,364,560 |
| 42 | −1,722,273,249,878,853,525 |
| 44 | 2,418,792,979,176,641,550 |
| 46 | −29,98,596,873,327,102,075 |
| 48 | 3,273,690,120,802,954,125 |
| 50 | −3,137,999,806,448,287,872 |
| 52 | 2,631,194,427,017,021,040 |
| 54 | −1,921,253,875,028,804,855 |
| 56 | 1,215,086,813,713,908,520 |
| 58 | −66,1347,989,014,027,700 |
| 60 | 307,419,817,142,915,064 |
| 62 | −120,935,396,967,175,700 |
| 64 | 39,824,665,609,048,775 |
| 66 | −10,834,363,223,810,350 |
| 68 | 2,396,195,651,846,500 |
| 70 | −422,340,034,401,579 |
| 72 | 57,851,679,198,620 |
| 74 | −5,961,837,763,765 |
| 76 | 442,600,039,310 |
| 78 | −22,278,193,575 |
| 80 | 694,637,867 |
| 82 | −11,564,420 (43 × 113 × 7 × 22) |
| 84 | 76,840 (× 113 × 23) |
| 86 | −85: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramanian, K. Matching Polynomials of Symmetric, Semisymmetric, Double Group Graphs, Polyacenes, Wheels, Fans, and Symmetric Solids in Third and Higher Dimensions. Symmetry 2025, 17, 133. https://doi.org/10.3390/sym17010133
Balasubramanian K. Matching Polynomials of Symmetric, Semisymmetric, Double Group Graphs, Polyacenes, Wheels, Fans, and Symmetric Solids in Third and Higher Dimensions. Symmetry. 2025; 17(1):133. https://doi.org/10.3390/sym17010133
Chicago/Turabian StyleBalasubramanian, Krishnan. 2025. "Matching Polynomials of Symmetric, Semisymmetric, Double Group Graphs, Polyacenes, Wheels, Fans, and Symmetric Solids in Third and Higher Dimensions" Symmetry 17, no. 1: 133. https://doi.org/10.3390/sym17010133
APA StyleBalasubramanian, K. (2025). Matching Polynomials of Symmetric, Semisymmetric, Double Group Graphs, Polyacenes, Wheels, Fans, and Symmetric Solids in Third and Higher Dimensions. Symmetry, 17(1), 133. https://doi.org/10.3390/sym17010133






