Abstract
The main goal of the paper is to characterize families of -(upper) superporous subsets of , which generalize well-known notions of superporosity and strong superporosity of subsets of . Definitions and properties of -superporosity are symmetric to definitions and properties of superporosity and strong superporosity. The purpose in all cases is to define small subsets of the line using the notion of porosity. Superporous sets preserve positive porosity, and strongly superporous sets preserve strong porosity; i.e., if E is superporous (correspondingly, E is strongly superporous), then for every and for every F such that porosity of F at x is greater than 0 (correspondingly, is equal to 1), porosity of at x is greater than 0 (correspondingly, is equal to 1). Taking arbitrary positive porosity, instead of 0 or 1, we obtain the symmetric definition as follows: -superporosity for transfers s-porosity to r-porosity; i.e., if E is -superporous, then for every and for every F such that porosity of F at x is not less than s, porosity of at x is not less than r. Even though the definition and properties of -superporosity, superporosity and strong superporosity are symmetric and all of them consist of very small sets, the families of these sets are essentially different. In the paper, we focus on relationships between -superporous sets for different indices . Furthermore, we compare -superporosity to superporosity and strong superporosity. We apply the notion of -superporosity to find multipliers and adders of porouscontinuous functions.
Keywords:
porosity; superporosity; strong superporosity; [r, s]-superporosity; multiplier; adder; porouscontinuity MSC:
26A15; 54C08
1. Introduction
In [1,2] V. Kelar and L. Zajíček defined the notions of superporosity and strong superporosity, i.e., sets which preserve some aspects of porosity by taking a union of sets. The basic concept of porosity was introduced by E. P. Dolženko in [3] and is now being considered from very different points of view, see for example [4,5,6]. Properties of superporous and strongly superporous subsets of were intensively studied [1,2,7,8]. In [1,2], using the notion of superporosity, topologies p, s, and are defined. Topologies p and s consist of complements of superporous and strongly superporous sets, respectively, and and consist of sets which are different from elements of p and s, respectively, by a meager set. In [2], L. Zajíček showed that consists of -dense sets.
Some types of generalized continuity connected with the notions of porosity, superporosity and strong superporosity were studied. In [9], J. Borsík and J. Holos defined families of porouscontinuous functions , for and , for . Families of porouscontinuous functions are examples of so-called -continuous functions and path continuous functions with respect to the family . In [10], one can find many examples of generalized continuities and path continuities defined in this way. In the case of porouscontinuous functions, the family is defined in terms of porosity. Using topologies p and s, maximal additive and maximal multiplicative classes for porouscontinuous functions are described [7].
In the paper, we introduce families and of and -superporous sets. These concepts are symmetric to notions of superporosity and strong superporosity. As in the case of superporosity and strong superporosity, the -superporous sets are very small and preserve some aspects of porosity under a union of sets. We also apply -superporous sets to find multipliers and adders for porouscontinuous functions.
2. Preliminaries
As we mentioned before, in [1,2], V. Kelar and L. Zajíček defined the notions of superporosity and strong superporosity, i.e., sets which preserve some aspects of porosity by taking a union of sets. For a set and an interval , let denote the length of the largest open subinterval of I having an empty intersection with A. Then, according to [2,8,9], the right-handed (upper) porosity of the set A at is defined as
the left-handed (upper) porosity of the set A at x is defined as
and the (upper) porosity of A at x is defined as
We say that the set A is porous at if . The set A is called porous if A is porous at each point . We say that A is strongly porous at x if and A is called strongly porous if A is strongly porous at each . Obviously, every strongly porous set is porous, and every porous set is nowhere dense. Moreover, none of the reverse inclusions is true.
In a similar way, taking the lower limit instead of upper limit, we can define lower porosity .
We say that is superporous at if porosity of is positive for every with positive porosity at x. E is superporous if it is superporous at every point. Similarly, we say that is strongly superporous at if porosity of is equal to 1 for every with porosity 1 at x. E is strongly superporous if it is strongly superporous at every point.
J. Borsík and J. Holos defined families of porouscontinuous functions , for and , for . is ()-continuous at if the complement of every pre-image has porosity greater than r (not less than r). Similarly, f is ()-continuous at if there exists such that , () and f restricted to E is continuous at x. Using topologies p and s, maximal additive and maximal multiplicative classes for porouscontinuous functions are described [7]. Porouscontinuous functions are examples of -continuous functions and path continuous functions with respect to the family , , where is a family of "large" subsets of containing x. Then, the continuity of the function at means that pre-image contains an element of for every . Meanwhile, path continuity at means that there is a set such that f restricted to E is continuous in ordinary sense at x. Of course, path continuity with respect to implies -continuity, and sometimes, they are equivalent. In the case of porouscontinuous functions, the family is defined in terms of porosity.
In the paper, we study the properties of and of and -superporous sets. These concepts are close and symmetric to notions of superporosity and strong superporosity; i.e., -superporous sets are very small and preserve some values of porosity under taking a union of sets. Nevertheless, despite symmetric definitions and properties, there are huge differences between -superporosity, superporosity and strong superporosity. The families of and -superporous sets and for form monotone families of subsets of the real line, i.e., and for every and and and for every and . Furthermore, if , then and are trivial, i.e., they consist of all sets with empty derivatives. In the final part of the paper, we use -superporous sets to find multipliers and adders for porouscontinuous functions.
In Section 3, we present basic properties of porosity of subsets of . Moreover, we proved a few technical lemmas used in the sequel.
The main part of the paper, Section 4, is devoted to definition and properties of families and of subset of consisting of -superporous and -superporous sets, respectively. is -superporous at if porosity of is not less than r for every with porosity not less than s at x. Similarly, is -superporous at if porosity of is greater than r for every with porosity greater than s at x. Directly from the definition, r and s play a symmetric role in these definitions, i.e., and for every and . It turned out that and have quite complicated structure, and we focus on investigating relationships between these families for different values of r and s. In Theorem 5, the structures of and are described. If , then and consist of discrete sets, and if , then and contain sets with nonempty derivative. For every and , we have (Theorem 7). Moreover, we show relationships between -superporous sets for different r and s (Theorems 8 and 10). At the end of the section, we present necessary and sufficient conditions for belonging to and formulated in terms of lower porosity, and we show lack of dependencies between superporosity, strong superporosity, -superporosity and -superporosity.
In Section 5, we present definitions and basic properties of porouscontinuous functions, multipliers and adders. Given two families of real function X and Y, we can consider all functions such that the product (the sum ) belongs to X whenever f belongs to Y. Such a function g is said to be a multiplier (an adder) of the set X over the set Y. Multipliers are a generalization of the maximal multiplicative classes, and adders are a generalization of the notion of maximal additive classes of a given family of functions. Theorems 13, 14 and 15 show equalities , and inclusion for every , where and are families of -continuous, where or , respectively, and is a family of path continuous functions with respect to . To find multipliers of porouscontinuous functions, we need to introduce the concept of -continuity for . Theorems 16, 17 and Corollary 3 describe multipliers for porouscontinuous functions.
3. Porosity
Let and denote the set of all positive integers and the set of all real numbers, respectively. By and , we denote a closure and a set of accumulation points of a set . By , we denote the restriction of f to .
Now, we show a few useful technical lemmas connected with porosity.
Theorem 1.
Let , , , and . Then, and .
Proof.
Choose and . If then and if then for some . Similarly, if , then , and if , then for some . Therefore,
and
□
Definition 1.
We say that an open interval is maximal in relation to if and for every .
Theorem 2.
For every and with , there exists a sequence of open intervals maximal in relation to E such that , , and .
Proof.
Let be a family of all open intervals maximal in relation to E such that and . Obviously, consists of pairwise disjoint open intervals and intersects only a finite number of elements of for every . Therefore, , where , for some and for every .
Fix . Take any . If , then , and if , then there exists such that . If , then for some . Hence, for every , we can find such that . Therefore, .
Finally, if is any open interval disjoint from , then . Hence, . □
Lemma 1.
Let , , and . Then, , i.e., .
Proof.
see Figure 1. □
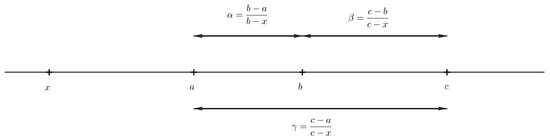

Figure 1.
.
Corollary 1.
- (1)
- Let , and . Then, , i.e., .
- (2)
- Let , , , and . Then, .
- (3)
- Let , , and . Then, .
Lemma 2.
For every and , there exists an open interval such that and . Moreover, and .
Proof.
Fix and . Put and . Then, , and . □
Lemma 3.
Let . For every and every open interval such that and , the following inequality holds. Moreover, if and , then and .
Proof.
Fix and . Put and . Then, , , and . For every open interval such that and , either and or and . □
Lemma 4.
Let be an arbitrary open interval. For every and every open interval such that , and , the following inequality holds. Moreover, if and , then and .
Proof.
Fix and such that and . Put and . Then, , and . For every open interval such that and either and or and . □
4. -Superporosity
We now introduce the main concept of our work, i.e., -superporosity.
Definition 2.
Let . We say that a set is -superporous at if for every containing x, if , then . We say that E is -superporous if it is -superporous at each of its points. The family of all -superporous subsets of we denote by .
Definition 3.
Let . We say that a set is -superporous at if for every containing x, if , then . We say that E is -superporous if it is -superporous at each of its points. The family of all -superporous subsets of we denote by .
The following proposition follows directly from definitions of superporosity and shows the symmetric structure of families and .
Proposition 1.
- (1)
- and for every and .
- (2)
- and for every and .
Theorem 3.
If and is an accumulation point of , then for every , there exists such that and , i.e., .
Proof.
Fix and let . For every , define and , i.e., . Then, by Corollary 1 , . We can find the inductively decreasing sequence such that . Let . Since , by Theorem 1, . On the other hand, . Again by Theorem 1, . □
Theorem 4.
For every , there exists such that
- is an accumulation point of ;
- iff ;
- iff .
Proof.
Fix and . Let , where and , i.e., for . Since , we only need to check -superporosity at x. Choose any . By Theorem 3, we can find such that and . Therefore, if , then .
Assume and let us take any such that . If , then, obviously, . Let . By Theorem 2, there exists a sequence of open intervals maximal in relation to F such that , and . We may assume that , where is such that . Choose . If , then . If contains at least two points, then for some and . Finally, consider the case where for some n. By Lemma 3, contains an interval disjoint from and satisfying . We have shown that every interval contains interval disjoint from and such that . Therefore,
Hence, if , then , and if , then . The proof is complete. □
Directly from Theorems 3 and 4, we obtain characterizations of and .
Theorem 5.
Let .
- (1)
- If , i.e., , then and are trivial, i.e., they consist of sets with empty derivatives.
- (2)
- If , i.e., , then and are nontrivial, i.e., they contain sets with nonempty derivative.
Theorem 6.
For every , there exists such that
- is an accumulation point of ;
- iff and ;
- iff and .
Proof.
Fix and . Let , where and for . Since , we only need to check -superporosity at 0. By Theorem 1, . Taking with , we can conclude for and for . Choose any and . By Theorem 3, we can find such that and . Therefore, if , then .
Assume and . Let us take any such that . If , then, obviously, . Let . By Theorem 2, there exists a sequence of open intervals maximal in relation to F such that , and . Choose . If , then . If contains at least two points, then for some n. Finally, consider the case where for some n. By Lemma 3, contains an interval disjoint from and satisfying . We have shown that every interval contains interval disjoint from and such that . Therefore,
Hence, if and , then , and if and , then . The proof is complete. □
Theorem 7.
for every and .
Proof.
Fix and . Take any and . Assume that E is not -superporous at x. Then, we can find with and . Without loss of generality, we may assume , and moreover, . By Theorem 2, there exists a sequence of open intervals maximal in relation to F such that , and . Inductively, we can find a sequence of open intervals such that , , , and . In particular, all are disjoint from F. Define . Obviously, and . Let . Then, . For , let , i.e., . Let . Then,
Since , . For every , let be a maximal open interval contained in and disjoint from E (if such an interval does not exist, we take and ). Then, and . On the other hand, Therefore,
and
contrary to assumption . Hence, inclusion is proved.
Let for be the set from Theorem 6. Then, for all . The proof is completed. □
Theorem 8.
- (1)
- If and , then and for every .
- (2)
- If and , then and .
Proof.
Both assertions follow directly from Theorem 6. For any , we have for every and . Similarly, for every and . □
Theorem 9.
For every there exists such that
- is an accumulation point of ,
- iff ,
- iff .
Proof.
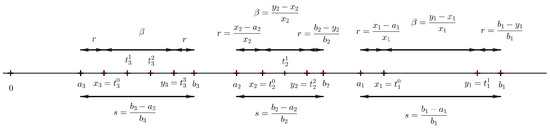
Fix . Inductively, we can find two sequences and , both tending to 0 such that , and for . Next, for every let satisfy for (see Figure 2). Finally, let . Since , we have only to check -superporosity at 0.

Figure 2.
Construction of .
Let .
Clearly, and . Choose any . Let be such that . For every , define and , i.e., . Then, by Corollary 1 , . Let . Obviously, we can find such that for . Similarly as in the proof of Theorem 3, we can show and . Therefore, if , then .
Choose , , and let us take any such that . If , then, obviously, . Let . By Theorem 2, there exists a sequence of open intervals maximal in relation to F such that , and . Choose .
If , then . If intersects at least two different intervals and , then . Finally, consider the case where for some n.
By Lemma 4, contains an interval disjoint from and such that . Therefore,
Hence, if , then , and if , then . The proof is complete. □
Theorem 10.
If and , then and .
Proof.
Inclusions and are obvious. Take . Then, and . By Theorem 9, . □
In the next two theorems, we present connections between -superporosity and the lower porosity.
Theorem 11.
Let , and . If , then E is -superporous at x.
Proof.
Take any such that and . Without loss of generality, we may assume . We can find decreasing sequence tending to x such that . Since , . Obviously, . Therefore,
Hence, if and E is -superporous at x. □
Theorem 12.
Let , and . If E is -superporous at x, then .
Proof.
Let and choose any . We may assume . Let be a decreasing sequence tending to x such that , and . We may assume for every n. For , define such that and . Then, . Let . Obviously, . Let be any open interval disjoint from . Then, for some n. Since , and
Finally, and E is not -superporous at x. The proof is complete. □
In the last part of this section, we discuss relationships between , , superporous sets and strongly superporous sets. Fix any , where . For any , the set belongs to and is not strongly superporous. For any , the set is superporous and belongs neither to nor . For any , the set is strongly superporous and does not belong to . For any , the set belongs to (for sufficiently large s) and is not superporous.
5. Applications
We now apply -superporosity to determine multipliers and adders of porouscontinuous functions. In the theory of real functions, families of functions that are not closed under addition or multiplication are often considered. Therefore, it seems natural for any class of functions X to search for functions g with the property that for each , the product (the sum ) belongs to X as well. Such a family of functions is called a maximal multiplicative (additive) class. The concept of maximal multiplicative class has been generalized in many papers as follows. Given two function classes X and Y, we can identify all functions g such that the product belongs to X whenever f belongs to Y. Such a family of functions is said to be a multiplier of the set X over the set Y. There are many papers devoted to multipliers, see for example [11,12,13,14,15]. Similarly, we can generalize the concept of maximal additive class. Given two families of real function X and Y, we can consider all functions such that the sum belongs to X whenever f belongs to Y. Such a function g is said to be an adder of the set X over the set Y, and it is denoted by .
We now recall the notion of porouscontinuity [9]. Let and . A point will be called a point of -density of the set A if . Let and . A point will be called a point of -density of the set A if . Let . The function will be called
- -continuous at x if there exists such that , x is a point of -density of A and is continuous at x and
- -continuous at x if for each , there exists a set such that , x is a point of -density of A and .
Let . The function will be called
- -continuous at x if there exists such that , x is a point of -density of A and is continuous at x, and
- -continuous at x if for each there exists a set such that , x is a point of -density of A and .
All of these functions are called porouscontinuous functions.
We denote the class of -continuous, -continuous, -continuous, -continuous functions by , , , , respectively. Symbols , , and denote the set of all points at which f is -continuous, -continuous, -continuous and -continuous, respectively.
In [9], the equality for every f and every was proved.
Observe that if f is left-handed or right-handed continuous at some x, then f is porouscontinuous (in each sense) at x.
Let , and . Then, if and only if .
Applying -superporosity, we describe multipliers and adders for porouscontinuous functions.
Definition 4.
Let . We say that is -continuous at if for every , the set is -superporous at x. The set of points at which f is -continuous is denoted by and denotes the family of which are -continuous at every .
Definition 5.
Let . We say that is -continuous at if for every , the set is -superporous at x. The set of points at which f is -continuous is denoted by , and denotes the family of which are -continuous at every .
Definition 6.
Let . We say that is -continuous at if there exists such that , is -superporous at x and f restricted to E is continuous at x. The set of points at which f is -continuous is denoted by and denotes the family of which are -continuous at every .
Theorem 13.
for every . Moreover, for every .
Proof.
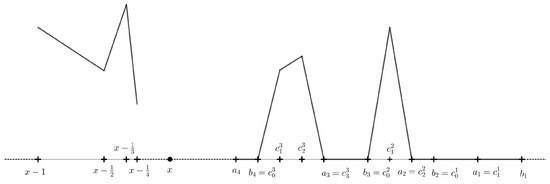
Fix . Take any , , and . Obviously,
Hence,
Since is -superporous and , . Thus, and .
Let . We can find and such that is not -superporous at x. Hence, there is for which and . We may assume . By Theorem 2, we can find a sequence of open intervals such that , , and . For every , let such that . Define (see Figure 3.) by

Figure 3.
Function g.
Clearly, g is continuous at every . Moreover, , and
Hence, . On the other hand,
Therefore,
Finally, and . The proof is complete. □
Theorem 14.
for every .
Proof.
The proof is very similar to the proof of Theorem 13 and we leave it to the reader. □
Theorem 15.
for every .
Proof.
Inclusion was proved in Theorem 13.
Take , and . There exist such that , , , f restricted to E is continuous at x and g restricted to F is continuous at x. Hence, and restricted to is continuous at x. Therefore, . Since x is arbitrary, and . The proof is completed. □
Question 1.
Is either of the equalities or true?
To find multipliers of porouscontinuous functions, we need to introduce the concept of -continuity for .
Definition 7.
Let and . We say that is -continuous at if, for every , the set is -superporous at x.
Definition 8.
Let and . We say that is -continuous at if, for every , the set is -superporous at x.
Definition 9.
Let and . We say that is -continuous at if there exists such that , is -superporous and f restricted to E is continuous at x.
Corollary 2.
Let and . If is -superporous (-superporous) at x, then every function is -continuous (-continuous) at x.
Theorem 16.
Let . if and only if the following two conditions hold:
- (i)
- f is -continuous at every at which ;
- (ii)
- f is -continuous at every at which and .
Moreover, .
Proof.
Fix . Take any , , and . First, consider the case where . Obviously,
Hence,
Because is -superporous at x and , we obtain . Therefore, is -continuous at x.
Consider the second case where . Obviously,
Hence,
Since is -superporous at x and , we obtain . Again, is -continuous at x. Thus, and .
Take any and . Assume that f does not satisfy condition , i.e., and f is not -continuous at x. Repeating constructions and arguments from the proof of Theorem 13, we can construct such that is not -continuous at x. Now, consider the case where f does not satisfy condition . We can find such that is not -superporous at x, and there is for which and . We may assume . By Theorem 2, we can find a sequence of open intervals such that , , and .
For every , there exists a finite set such that for every , we can find for which . Moreover, we can find a decreasing sequence tending to x such that and (we can do it because is not -superporous and ). Define by
Clearly, g is continuous at every . Similarly, as in the proof of Theorem 13, we can check that .
On the other hand,
Therefore,
Hence, and . We have proved that if f does not satisfy or then . The proof is complete. □
Theorem 17.
Let . if and only if the following two conditions hold
- (i)
- f is -continuous at every at which ;
- (ii)
- f is -continuous at every at which and .
Proof.
The proof is very similar to the proof of the previous theorem, and we have omitted it. □
Corollary 3.
for .
6. Conclusions
In this paper, we introduced the concept of and -upper superporosity, which proposes a different perspective on the construction of small subsets of using the properties of porosity. The motivation for these studies were the results relating superporosity and strong superporosity, obtained by L. Zajíček and V. Kelar. Despite similarities in the definition, and -upper superporosity has diametrically different properties than superporosity and strong superporosity. We focused on relationships between -upper superporous sets for different indices . We also showed that there are no inclusions between families of -superporous sets, superporous sets and strong superporous sets. Moreover, we applied the notion of -superporosity to find adders of porouscontinuous functions.
It seems to be an interesting question whether similar properties hold for subsets of the plane or metric space. It is known that porosity and strong superporosity were also studied for subsets of metric space. One can also try to define and investigate and -lower superporosity sets, where in the definitions we use lower porosity instead of the usual one. As shown in [16], as a rule, problems in which upper porosity is replaced by lower porosity are much more difficult, but also more interesting.
Author Contributions
Conceptualization, S.K. and M.T.; methodology, S.K. and M.T.; validation, S.K. and M.T.; formal analysis, S.K. and M.T.; investigation, S.K. and M.T.; resources, S.K. and M.T.; data curation, S.K. and M.T.; writing—original draft preparation, S.K. and M.T.; writing—review and editing, S.K. and M.T.; visualization, S.K. and M.T.; supervision, S.K. and M.T.; project administration, S.K. and M.T.; funding acquisition, S.K. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kelar, V. Topologies generated by porosity and strong porosity. Real Anal. Exch. 1990, 16, 255–267. [Google Scholar] [CrossRef]
- Zajíček, L. Porosity and σ-porosity. Real Anal. Exch. 1987, 13, 314–350. [Google Scholar] [CrossRef]
- Dolženko, E.P. Boundary properties of arbitrary functions. Math. USSR Izv. 1967, 31, 3–14. (In Russian) [Google Scholar] [CrossRef]
- Dymond, M. Porosity phenomena of non-expansive, Banach space mappings. Israel J. Math. 2023, 255, 931–953. [Google Scholar] [CrossRef]
- Ivanova, G.; Domnik, I. On density and σ-porosity in some families of Darboux functions. Real Anal. Exch. 2022, 47, 63–73. [Google Scholar] [CrossRef]
- Klinga, P.; Kwela, A. Porosities of the sets of attractors. J. Math. Anal. Appl. 2022, 514, 126348. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. On topologies generated by lower porosity. Results Math. 2022, 77, 220. [Google Scholar] [CrossRef]
- Zajíček, L. On σ-porous sets in abstract spaces. Abstr. Appl. Anal. 2005, 5, 509–534. [Google Scholar] [CrossRef]
- Borsík, J.; Holos, J. Some properties of porouscontinuous functions. Math. Slovaca 2014, 64, 741–750. [Google Scholar] [CrossRef]
- Bruckner, A.M. Differentiation of Real Functions; Lecture Notes in Mathematics; Springer: New York, NY, USA, 1978; Volume 659. [Google Scholar]
- Bugajewska, D.; Reinwand, S. Some Remarks on Multiplier Spaces 1: Classical Spaces. Z. Anal. Anwend. 2019, 38, 125–142. [Google Scholar] [CrossRef]
- Bugajewska, D.; Reinwand, S. Some Remarks on Multiplier Spaces 2: BV-type Spaces. Z. Anal. Anwend. 2019, 38, 309–327. [Google Scholar] [CrossRef]
- Mařík, J. Multipliers of summable derivatives. Real Anal. Exch. 1982, 8, 486–493. [Google Scholar] [CrossRef]
- Maz’ya, V.; Shaposhnikova, T.O. Theory of Sobolev Multipliers with Applications to Differential and Integral Operators. In Grundlehren der Mathematischen Wissenschaften; Springer: Berlin, Germany, 2009; Volume 337. [Google Scholar]
- Reinwand, S.; Kasprzak, P. Multiplication operators in BV spaces. Ann. Mat. Pura Appl. 2023, 202, 787–826. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. Lower porosity on R2. Symmetry 2021, 13, 1594. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).