Stacking Monotone Polytopes
Abstract
1. Introduction
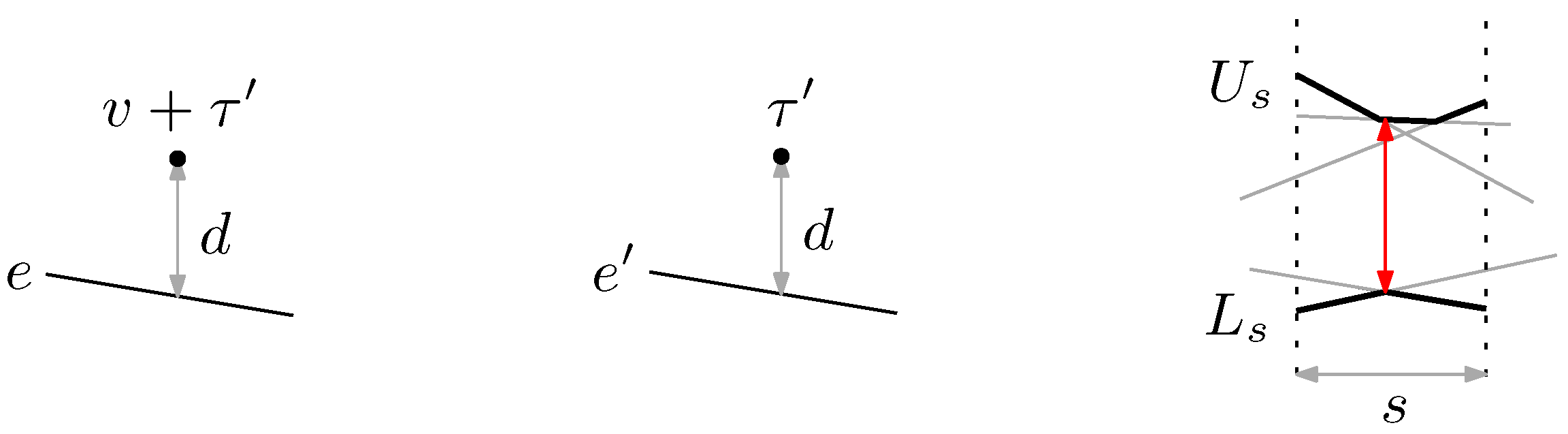
2. Preliminaries
- C1. The domain of is contained in .
- C2. For a vertical line ℓ, any point has the same or larger -coordinate than that of any point .
- C3. P and have a non-empty intersection.
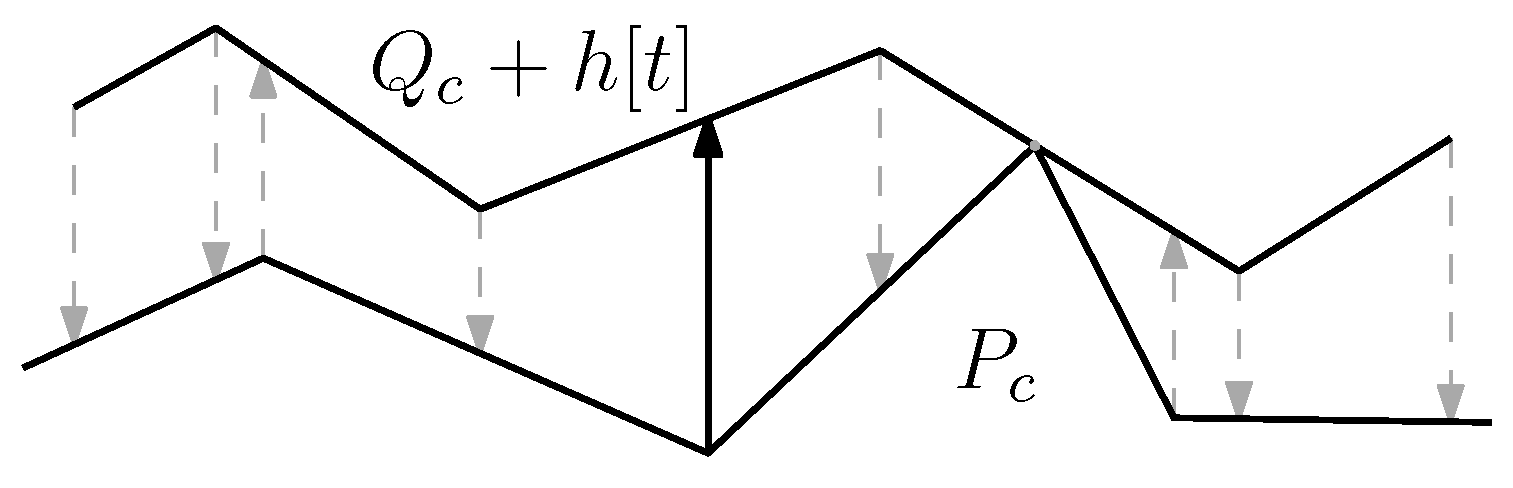
3. Minimizing Scoring Criterion (1)
3.1. The Case When
3.2. The Case When
4. Minimizing Scoring Criterion (2)
4.1. The Case When
4.2. The Case When
5. Minimizing Scoring Criterion (3)
5.1. The Case When
5.2. The Case When
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kepler, J. The Six-Cornered Snowflake; Paul Dry Books: Philadelphia, PA, USA, 2010. [Google Scholar]
- Paterson, M.; Peres, Y.; Thorup, M.; Winkler, P.; Zwick, U. Maximum overhang. Am. Math. Mon. 2009, 116, 763–787. [Google Scholar] [CrossRef]
- Lee, S.J. Efficient Algorithms for Stacking Polytopes. Master’s Thesis, Pohang University of Science and Technology, Pohang, Republic of Korea, 2019. [Google Scholar]
- Ahn, H.K.; Abardia, J.; Bae, S.W.; Cheong, O.; Dann, S.; Park, D.; Shin, C.S. The minimum convex container of two convex polytopes under translations. Comput. Geom. 2019, 77, 40–50. [Google Scholar] [CrossRef]
- Egeblad, J.; Nielsen, B.K.; Brazil, M. Translational packing of arbitrary polytopes. Comput. Geom. 2009, 42, 269–288. [Google Scholar]
- Trivella, A.; Pisinger, D. Bin-Packing Problems with Load Balancing and Stability Constraints. In Proceedings of the INFORMS Transportation and Logistics Society, Chicago, IL, USA, 26–29 July 2017. [Google Scholar]
- Casko, J.S.; Vaden, J.L.; Kokich, V.G.; Damone, J.; James, R.D.; Cangialosi, T.J.; Riolo, M.L.; Owens, S.E.; Bills, E.D. Objective grading system for dental casts and panoramic radiographs. Am. J. Orthod. Dentofac. Orthop. 1998, 114, 589–599. [Google Scholar] [CrossRef] [PubMed]
- Hershberger, J. Finding the upper envelope of n line segments in O(n log n) time. Inf. Process. Lett. 1989, 33, 169–174. [Google Scholar] [CrossRef]
- McMullen, P. The maximum numbers of faces of a convex polytope. Mathematika 1970, 17, 179–184. [Google Scholar] [CrossRef]
- Berg, M.; Cheong, O.; Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Dobkin, D.P.; Kirkpatrick, D.G. A linear algorithm for determining the separation of convex polyhedra. J. Algorithms 1985, 6, 381–392. [Google Scholar] [CrossRef]
- Dobkin, D.P.; Kirkpatrick, D.G. Determining the separation of preprocessed polyhedra—A unified approach. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 1990; pp. 400–413. [Google Scholar]
- Edelsbrunner, H.; Guibas, L.J.; Sharir, M. The upper envelope of piecewise linear functions: Algorithms and applications. Discret. Comput. Geom. 1989, 4, 311–336. [Google Scholar] [CrossRef]
- Agarwal, P.K.; Aronov, B.; Sharir, M. Computing envelopes in four dimensions with applications. In Proceedings of the Tenth Annual Symposium on Computational Geometry, Stony Brook, NY, USA, 6–8 June 1994; pp. 348–358. [Google Scholar]
- Herschberger, J.; Suri, S. Offline maintenance of planar configurations. In Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 28–30 January 1991; pp. 32–41. [Google Scholar]
- Clarkson, K.L. New applications of random sampling in computational geometry. Discret. Comput. Geom. 1987, 2, 195–222. [Google Scholar] [CrossRef][Green Version]
- Edelsbrunner, H.; O’Rourke, J.; Seidel, R. Constructing arrangements of lines and hyperplanes with applications. Siam J. Comput. 1986, 15, 341–363. [Google Scholar] [CrossRef]
- Balaban, I.J. An optimal algorithm for finding segments intersections. In Proceedings of the Eleventh Annual Symposium on Computational Geometry, Vancouver, BC, Canada, 5–7 June 1995; pp. 211–219. [Google Scholar]
- Matoušek, J.; Schwarzkopf, O. Linear optimization queries. In Proceedings of the Eighth Annual Symposium on Computational Geometry, Berlin, Germany, 10–12 June 1992; pp. 16–25. [Google Scholar]
- Chazelle, B. An optimal convex hull algorithm in any fixed dimension. Discret. Comput. Geom. 1993, 10, 377–409. [Google Scholar] [CrossRef]
- Moet, E.; van Kreveld, M.; der Stappen, A.F.v. On realistic terrains. Comput. Geom. 2008, 41, 48–67. [Google Scholar] [CrossRef][Green Version]


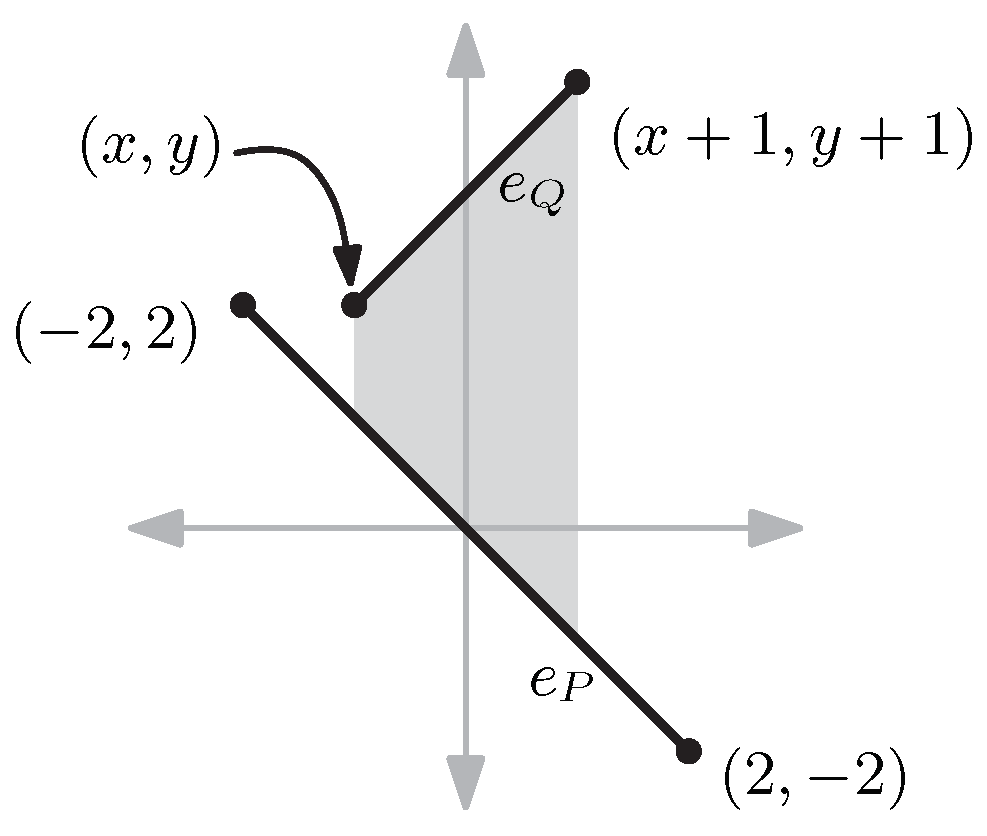
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, H.-K.; Lee, S.J.; Yoon, S.D. Stacking Monotone Polytopes. Symmetry 2024, 16, 1246. https://doi.org/10.3390/sym16091246
Ahn H-K, Lee SJ, Yoon SD. Stacking Monotone Polytopes. Symmetry. 2024; 16(9):1246. https://doi.org/10.3390/sym16091246
Chicago/Turabian StyleAhn, Hee-Kap, Seung Joon Lee, and Sang Duk Yoon. 2024. "Stacking Monotone Polytopes" Symmetry 16, no. 9: 1246. https://doi.org/10.3390/sym16091246
APA StyleAhn, H.-K., Lee, S. J., & Yoon, S. D. (2024). Stacking Monotone Polytopes. Symmetry, 16(9), 1246. https://doi.org/10.3390/sym16091246




