Nuclear Matter and Finite Nuclei: Recent Studies Based on Parity Doublet Model

Abstract

In this review, we summarize recent studies on nuclear matter and finite nuclei based on parity doublet models. We first construct a parity doublet model (PDM), which includes the chiral invariant mass $m_0$ of nucleons together with the mass generated by the spontaneous chiral symmetry breaking. We then study the density dependence of the symmetry energy in the PDM, which shows that the symmetry energy is larger for smaller chiral inavariant mass. Then, we investigate some finite nuclei by applying the Relativistic Continuum Hartree–Bogoliubov (RCHB) theory to the PDM. We present the root-mean-square deviation (RMSD) of the binding energies and charge radii, and show that $m_0=700$ MeV is preferred by the nuclear properties. Finally, we modify the PDM by adding the isovector scalar meson $a_0\left(980\right)$, and show that the inclusion of the $a_0\left(980\right)$ enlarges the symmetry energy of the infinite nuclear matter.

1. Introduction

Spontaneous chiral symmetry breaking plays an important role in low-energy hadron physics, contributing substantially to the generation of hadron masses and the manifestation of mass differences between chiral partners. In recent decades, there has been a growing focus on investigating the restoration of chiral symmetry in hot and dense matter. Nucleon masses will be changed in such extreme conditions, which provides hints for us towards a further understanding to the mass of hadrons and further understanding to the dynamics of the strongly interacting matter.

In the traditional linear sigma model, the entire nucleon mass is generated from the spontaneous chiral symmetry breaking, in which the chiral partner to ordinary nucleon is the nucleon itself. When the chiral symmetry is restored, the nucleon and its chiral partner will be degenerate in mass. However, increasing evidence from the lattice calculations [1,2] show that, with increasing temperature, the mass of negative parity baryon decreases to be degenerate with the mass of positive baryon at the critical temperature.

The Parity Doublet Model (PDM) was proposed in Ref. [3] as an extended linear sigma model with parity doubling structure to model the parity doubling of nucleon. In the PDM, the excited nucleon, such as $N\left(1535\right)$, is regarded as the chiral partner to the ordinary nucleon, in which the spontaneous symmetry breaking generates the mass difference between them. By considering the symmetry properties of the chiral partner, the PDM predicts that the masses of the parity partners are degenerate into a finite mass, the so-called chiral invariant mass $m_0$, when the chiral symmetry is restored. In addition to the lattice simulations mentioned above, a recent analysis based on the QCD sum rules [4] also supports the existence of the chiral invariant mass. Therefore, quantitative and qualitative study of the chiral invariant mass will help us to understand the origin of hadron masses.

Studying the chiral invariant mass $m_0$ is an essential measure to the origin of the mass of a nucleon. There are several analyses to determine the value of $m_0$ by studying the nucleon properties in vacuum. For example, the analysis in Ref. [5] shows that $m_0$ is smaller than 500 MeV using the decay width of $N\left(1535\right)$, while Ref. [6] includes higher derivative interaction, which makes the large $m_0$ consistent with the decay width.

Chiral symmetry is expected to be partially restored in the high density region, the study of which will provide some information on the chiral invariant mass. Actually, the PDM is applied to study high density matter in several analyses, such as in Refs. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Recently, in Refs. [33,35,37,38,40], the EoS of neutron star (NS) matter constructed from an extended PDM [19] was connected to the one from the NJL-type quark model, following Refs. [41,42]. The analysis of Ref. [33] used the observational data of NS given in Refs. [43,44,45,46,47,48] to put a constraint on the chiral invariant mass $m_0$ as 600 MeV $\lesssim m_0\lesssim 900$ MeV, which was updated in Refs. [37,38] to 400 MeV$\lesssim m_0\lesssim 700$ MeV by considering the effect of anomaly, as well as new data analysis [49,50,51]. Ref. [40] showed that $m_0\simeq 850$ MeV with the consideration of central compact object (CCO) within the supernova remnant HESS J1731-347 [52].

In recent decades, increasing attention is paid to the effect of isovector-scalar $a_0$(980) meson (also called the $\delta$ meson) on asymmetric matter such as NS because it accounts for the attractive force in the isovector channel. References [53,54,55,56,57,58,59,60,61,62,63] use Walecka-type relativistic mean-field (RMF) models, and Refs. [64,65] use density-dependent RMF models to study the effect of $a_0$(980) meson to the symmetry energy as well as to the EoS of asymmetric matter. It was pointed that the existence of $a_0$ meson increases the symmetry energy [53,55,56,59,60,61,62,63], and that it stiffens the NS EoS [54,55,56,58,59] and asymmetric matter EoS [65]. Therefore, the $a_0\left(980\right)$ meson is influential for the study of asymmetric matter. Recently, in Ref. [66], the effect of $a_0\left(980\right)$ in neutron star is studied in the PDM and the constraint to the chiral invariant mass is obtained as 580 MeV $\lesssim m_0\lesssim 860$ MeV. In particular, this work shows that the $a_0\left(980\right)$ meson has large influence to the symmetry energy at density larger than saturation density. Therefore, it is expected that further experimental constraints on the symmetry energy will provide hints to the chiral invariant mass and the origin of the mass of a nucleon.

To put an additional constraint on the value of the chiral invariant mass, the properties of stable nuclei were studied in Ref. [67] with the PDM in the frame work of a self-consistent relativistic mean field theory. For the nuclear structure calculations, the Relativistic Continuum Hartree–Bogoliubov (RCHB) theory [68] was employed. It was found in Ref. [67] that the calculated binding energies and charge radii of selected fifteen nuclei are closest to the experimental values when $m_0=700$ MeV.

In this review, we summarize the recent works on the study of chiral invariant mass in infinite nuclear matter in Ref. [66] and finite nuclei in Ref. [67]. In Section 2.1, we introduce a PDM including $a_0$ meson based on the chiral U(2)_L × U(2)_R symmetry with U(1)_A anomaly included. Then, as a first step, we drop the $a_0$ meson and construct the infinite nuclear matter using mean field approximation in Section 2.2, Section 2.3 and Section 2.4. In Section 3, the construction of finite nuclei in mean field model using Relativistic Continuum Hartree–Bogoliubov (RCHB) theory is introduced. After a brief introduction on the construction of finite nuclei, the finite nuclei are constructed using PDM, as in Ref. [67], and the method to constrain the value of chiral invariant mass using experimental data of finite nuclei are discussed. Some results on the specific nuclei, such as the nuclei properties and effective mass of a nucleon in finite nuclei, are also shown. In Section 4, we review an extension of the PDM by including the isovector scalar meson $a_0\left(980\right)$ performed in Ref. [66]. We also compute the results for the extended PDM without vector meson mixing interaction for comparison. The symmetry energy for these models are compared to the PDM without $a_0$ meson introduced in Section 2. Finally, a summary is given in Section 5.

2. Dense Nuclear Matter with Parity Doublet Model

2.1. A Parity Doublet Model with U(2)_L × U(2)_R Symmetry

Here, we introduce the parity doublet model (PDM) based on the U(2)_L × U(2)_R chiral symmetry constructed in Ref. [66]. The Lagrangian is given by

$$\mathcal{L}={\mathcal{L}}_N+{\mathcal{L}}_M+{\mathcal{L}}_V,$$

(1)

where ${\mathcal{L}}_N$ is for the nucleons, ${\mathcal{L}}_M$ for the scalar and pseudoscalar mesons and ${\mathcal{L}}_V$ for the vector mesons.

In ${\mathcal{L}}_M$, the scalar meson field M is introduced as the ${(2,2)}_{-2}$ representation under the SU(2)_L × SU(2)_R × U(1)_A symmetry, which transforms as

$$M\to e^{-2i{\theta }_A}{g}_{L}M{g}_R^{†},$$

(2)

where $g_{R,L}\in \mathrm{SU}{\left(2\right)}_{R,L}$ and $e^{-2i{\theta }_A}\in \mathrm{U}{\left(1\right)}_A$. We parameterize M as

$$M=[\sigma +i\overrightarrow{\pi }·\overrightarrow{\tau }]-[\overrightarrow{a_0}·\overrightarrow{\tau }+i\eta ],$$

(3)

where $\sigma ,\overrightarrow{\pi },\overrightarrow{a_0},\eta$ are fields for the sigma meson, pions, the lightest isovector scalar meson $a_0\left(980\right)$ and $\eta$ meson, respectively, and $\overrightarrow{\tau }$ are the Pauli matrices. The vacuum expectation value (VEV) of M is

$$\begin{array}{c}⟨0\left|M\right|0⟩=\left(\begin{array}{cc}{\sigma }_0& 0\\ 0& {\sigma }_0\end{array}\right),\end{array}$$

(4)

where ${\sigma }_0=⟨0\left|\sigma \right|0⟩$ is the VEV of the $\sigma$ field, which is equal to the pion decay constant $f_{\pi }=93$ MeV in vacuum. The explicit form of the Lagrangian ${\mathcal{L}}_M$ is given by

$${\mathcal{L}}_M={\displaystyle \frac{1}{4}}\mathrm{tr}\left[{\partial }_{\mu }M{\partial }^{\mu }{M}^{†}\right]-V_M,$$

(5)

where $V_M$ is the potential for M. In the present model, $V_M$ is taken as [66]

$$\begin{array}{cc}{V}_M=& -{\displaystyle \frac{{\overline{\mu }}^2}{4}}\mathrm{tr}\left[M^{†}M\right]+{\displaystyle \frac{{\lambda }_{41}}{8}}\mathrm{tr}\left[{\left(M^{†}M\right)}^2\right]\hfill \\ & -{\displaystyle \frac{{\lambda }_{42}}{16}}{\left\{tr\left[M^{†}M\right]\right\}}^2-{\displaystyle \frac{{\lambda }_{61}}{12}}\mathrm{tr}\left[{\left(M^{†}M\right)}^3\right]\hfill \\ & -{\displaystyle \frac{{\lambda }_{62}}{24}}\mathrm{tr}\left[{\left(M^{†}M\right)}^2\right]\mathrm{tr}\left[M^{†}M\right]-{\displaystyle \frac{{\lambda }_{63}}{48}}{\left\{tr\left[M^{†}M\right]\right\}}^3\hfill \\ & -{\displaystyle \frac{m_{\pi }^2{f}_{\pi }}{4}}\mathrm{tr}[M+M^{†}]-{\displaystyle \frac{K}{8}}\{detM+det{M}^{†}\},\hfill \end{array}$$

(6)

where we included all the terms invariant under SU(2)_L × SU(2)_R × U(1)_A symmetry up to the sixth order in M fields. The six-point interaction terms are introduced to reproduce the nuclear saturation properties following Ref. [19]. The term proportional to $m_{\pi }^2$ is the explicit chiral symmetry breaking term due to the non-zero current quark masses, which generates the mass of pion. The last term is introduced to account for the U(1)_A anomaly.

For vector mesons, the iso-triplet $\rho$ meson and iso-singlet $\omega$ meson are included based on the hidden local symmetry (HLS) [69,70,71] to account for the repulsive force in the hadronic matter. The HLS is introduced by performing polar decomposition of the field M as

$$\begin{array}{c}M={\xi }_L^{†}S{\xi }_R,\end{array}$$

(7)

where $S=\sigma +{\displaystyle \sum _{b=1}^3}{a}_0^b{\tau }_b/2$ is the $2\times 2$ matrix field for scalar mesons. The fields ${\xi }_{L,R}$ transform as

$$\begin{array}{c}{\xi }_{L,R}\to h_{\omega }{h}_{\rho }{\xi }_{L,R}{g}_{L,R}^{†}{e}^{\pm i{\theta }_A},\end{array}$$

(8)

with $h_{\omega }\in {\mathrm{U}\left(1\right)}_{\mathrm{HLS}}$ and $h_{\rho }\in {\mathrm{S}\mathrm{U}\left(2\right)}_{\mathrm{HLS}}$. Here, $e^{+i{\theta }_A}$ for ${\xi }_L$ and $e^{-i{\theta }_A}$ for ${\xi }_R$. In the unitary gauge of the HLS, ${\xi }_{L,R}$ are parameterized as

$${\xi }_R={\xi }_L^{†}=exp\left(iP/f_{\pi }\right),$$

(9)

where $P=\eta +{\displaystyle \sum _{a=1}^3}{\pi }^a{\tau }_a/2$ is the $2\times 2$ matrix field for pseudoscalar mesons. In the HLS, vector mesons are introduced as the gauge bosons of the HLS. They transform as

$$\begin{array}{c}{\omega }_{\mu }\to h_{\omega }{\omega }_{\mu }{h}_{\omega }^{†}+{\displaystyle \frac{i}{g_{\omega }}}{\partial }_{\mu }{h}_{\omega }{h}_{\omega }^{†},\end{array}$$

(10)

$$\begin{array}{c}{\rho }_{\mu }\to h_{\rho }{\rho }_{\mu }{h}_{\rho }^{†}+{\displaystyle \frac{i}{g_{\rho }}}{\partial }_{\mu }{h}_{\rho }{h}_{\rho }^{†},\end{array}$$

(11)

where ${\omega }_{\mu }$ and ${\rho }_{\mu }={\displaystyle \sum _{a=1}^3}{\rho }_{\mu }^a{\tau }_a/2$ are the gauge fields for SU(2)_HLS and U(1)_HLS, respectively, and $g_{\omega }$ and $g_{\rho }$ are the corresponding gauge coupling constants.

To construct the Lagrangian invariant under the HLS, it is convenient to define the covariantized Maurer–Cartan 1-forms:

$${\widehat{\alpha }}_{\perp }^{\mu }\equiv {\displaystyle \frac{1}{2i}}[D^{\mu }{\xi }_R{\xi }_R^{†}-D^{\mu }{\xi }_L{\xi }_L^{†}],$$

(12)

$${\widehat{\alpha }}_{\Vert }^{\mu }\equiv {\displaystyle \frac{1}{2i}}[D^{\mu }{\xi }_R{\xi }_R^{†}+D^{\mu }{\xi }_L{\xi }_L^{†}],$$

(13)

where the covariant derivatives of ${\xi }_{L,R}$ are given by

$$\begin{array}{c}{D}^{\mu }{\xi }_L={\partial }^{\mu }{\xi }_L-i{g}_{\rho }{\rho }^{\mu }{\xi }_L-i{g}_{\omega }{\omega }^{\mu }{\xi }_L+i{\xi }_L{\mathcal{L}}^{\mu }-i{\xi }_L{\mathcal{A}}^{\mu },\end{array}$$

(14)

$$\begin{array}{c}{D}^{\mu }{\xi }_R={\partial }^{\mu }{\xi }_R-i{g}_{\rho }{\rho }^{\mu }{\xi }_R-i{g}_{\omega }{\omega }^{\mu }{\xi }_R+i{\xi }_R{\mathcal{R}}^{\mu }+i{\xi }_R{\mathcal{A}}^{\mu },\end{array}$$

(15)

with ${\mathcal{L}}^{\mu }$, ${\mathcal{R}}^{\mu }$ and ${\mathcal{A}}^{\mu }$ being the external gauge fields corresponding to SU(2)_L × SU(2)_R × U(1)_A global symmetry. We note that mesons do not carry the baryon number, so that the external gauge field corresponding to U(1) baryon number does not appear in the above covariant derivative. We also note that the covariant derivative acting on the baryon fields includes the external gauge field ${\mathcal{A}}^{\mu }$).

By using these 1-forms, the HLS-invariant Lagrangian including the interaction terms among the nucleons and the vector mesons is given by

$$\begin{array}{cc}{\mathcal{L}}_V= & a_{VNN}\left[{\overline{N}}_{1l}{\gamma }^{\mu }{\xi }_L^{†}{\widehat{\alpha }}_{\Vert \mu }{\xi }_L{N}_{1l}+{\overline{N}}_{1r}{\gamma }^{\mu }{\xi }_R^{†}{\widehat{\alpha }}_{\Vert \mu }{\xi }_R{N}_{1r}\right]\hfill \\ & +a_{VNN}\left[{\overline{N}}_{2l}{\gamma }^{\mu }{\xi }_R^{†}{\widehat{\alpha }}_{\Vert \mu }{\xi }_R{N}_{2l}+{\overline{N}}_{2r}{\gamma }^{\mu }{\xi }_L^{†}{\widehat{\alpha }}_{\Vert \mu }{\xi }_L{N}_{2r}\right]\hfill \\ & +a_{0NN}{\displaystyle \sum _{i=1,2}}\left[{\overline{N}}_{il}{\gamma }^{\mu }tr\left[{\widehat{\alpha }}_{\Vert \mu }\right]N_{il}+{\overline{N}}_{ir}{\gamma }^{\mu }tr\left[{\widehat{\alpha }}_{\Vert \mu }\right]N_{ir}\right]\hfill \\ & +{\displaystyle \frac{{m_{\rho }}^2}{{g_{\rho }}^2}}\mathrm{tr}\left[{\widehat{\alpha }}_{\Vert }^{\mu }{\widehat{\alpha }}_{\Vert \mu }\right]+\left({\displaystyle \frac{{m_{\omega }}^2}{8{g_{\omega }}^2}}-{\displaystyle \frac{{m_{\rho }}^2}{2{g_{\rho }}^2}}\right)\mathrm{tr}\left[{\widehat{\alpha }}_{\Vert }^{\mu }\right]\mathrm{tr}\left[{\widehat{\alpha }}_{\Vert \mu }\right]-{\displaystyle \frac{1}{8{g_{\omega }}^2}}\mathrm{tr}\left[{\omega }^{\mu \nu }{\omega }_{\mu \nu }\right]-{\displaystyle \frac{1}{2{g_{\rho }}^2}}\mathrm{tr}\left[{\rho }^{\mu \nu }{\rho }_{\mu \nu }\right]\hfill \\ & +{\lambda }_{\omega \rho }{\left(a_{VNN}+a_{0NN}\right)}^2{a}_{VNN}^2\left[{\displaystyle \frac{1}{2}}tr\left[{\widehat{\alpha }}_{\Vert }^{\mu }{\widehat{\alpha }}_{\Vert \mu }\right]tr\left[{\widehat{\alpha }}_{\Vert }^{\nu }\right]tr\left[{\widehat{\alpha }}_{\Vert \nu }\right]-{\displaystyle \frac{1}{4}}{\left\{tr\left[{\widehat{\alpha }}_{\Vert }^{\mu }\right]tr\left[{\widehat{\alpha }}_{\Vert \mu }\right]\right\}}^2\right],\hfill \end{array}$$

(16)

where ${\rho }^{\mu \nu }$ and ${\omega }^{\mu \nu }$ are the field strengths of the $\rho$ meson and the $\omega$ meson, given by

$$\begin{array}{cc}{\rho }_{\mu \nu }=& {\partial }_{\mu }{\rho }_{\nu }-{\partial }_{\nu }{\rho }_{\mu }-i{g}_{\rho }\left[{\rho }_{\mu },{\rho }_{\nu }\right],\hfill \\ {\omega }_{\mu \nu }=& {\partial }_{\mu }{\omega }_{\nu }-{\partial }_{\nu }{\omega }_{\mu }.\hfill \end{array}$$

(17)

We note that the last term in Equation (16) is a mixing term of $\rho$ and $\omega$ mesons, as introduced in Ref. [66] to the $a_0$ model to reduce the slope parameter, following Ref. [37]. As we will show in Section 4.3, when we just add the effect of $a_0\left(980\right)$ meson to the PDM without this vector meson mixing term, the slope parameter becomes too large compared with the recent constraints as summarized in Ref. [72].

Finally, the baryonic Lagrangian ${\mathcal{L}}_N$ based on the parity doubling structure [3,5] is given by

$$\begin{array}{cc}{\mathcal{L}}_{\mathcal{N}} & =\overline{N_1}i{\gamma }^{\mu }{\mathcal{D}}_{\mu }{N}_1+\overline{N_2}i{\gamma }^{\mu }{\mathcal{D}}_{\mu }{N}_2\hfill \\ & -m_0[{\overline{N}}_1{\gamma }_5{N}_2-{\overline{N}}_2{\gamma }_5{N}_1]\hfill \\ & -g_1[{\overline{N}}_{1l}M{N}_{1r}+{\overline{N}}_{1r}{M}^{†}{N}_{1l}]\hfill \\ & -g_2[{\overline{N}}_{2r}M{N}_{2l}+{\overline{N}}_{2l}{M}^{†}{N}_{2r}],\hfill \end{array}$$

(18)

where $N_{ir}={\displaystyle \frac{1+{\gamma }_5}{2}}{N}_i$ ($N_{il}={\displaystyle \frac{1-{\gamma }_5}{2}}{N}_i$) ($i=1,2$) is the right-handed (left-handed) component of the nucleon fields $N_i$, and the covariant derivatives of the nucleon fields are defined as

$$\begin{array}{cc}{\mathcal{D}}^{\mu }{N}_{1l,2r}& =\left({\partial }^{\mu }-i{\mathcal{L}}^{\mu }-i{\mathcal{V}}^{\mu }+i{\mathcal{A}}^{\mu }\right)N_{1l,2r},\hfill \\ {\mathcal{D}}^{\mu }{N}_{1r,2l}& =\left({\partial }^{\mu }-i{\mathcal{R}}^{\mu }-i{\mathcal{V}}^{\mu }-i{\mathcal{A}}^{\mu }\right)N_{1r,2l},\hfill \end{array}$$

(19)

where ${\mathcal{V}}^{\mu }$ is the external gauge field corresponding to the U(1) baryon number. By diagonalizing ${\mathcal{L}}_N$, we obtain two baryon fields $N_{+}$ and $N_{-}$ corresponding to the positive parity and negative parity nucleon fields, respectively. Their masses in vacuum are obtained as [3,5]

$$\begin{array}{c}{m}_{\pm }^{\left(\mathrm{vac}\right)}={\displaystyle \frac{1}{2}}\left[\sqrt{{(g_1+g_2)}^2{\sigma }_0^2+4m_0^2}\pm (g_1-g_2){\sigma }_0\right].\end{array}$$

(20)

In the present work, $N_{+}$ and $N_{-}$ are identified as N(939) and $N\left(1535\right)$, respectively.

2.2. Dense Nuclear Matter in PDM with Mean Field Approximation

To construct the nuclear matter from the model introduced in the previous section, we adopt the mean-field approximation following Ref. [19]. As a first step, we reduce the effect of $a_0\left(980\right)$ meson and vector meson mixing interaction to study the dense nuclear matter. The effect of $a_0\left(980\right)$ meson and vector meson mixing will be studied in Section 4.

The meson fields are then given by

$$\sigma \left(x\right)\to \sigma ,\overrightarrow{\pi }\left(x\right)\to 0,{\overrightarrow{a}}_0\left(x\right)\to 0,\eta \left(x\right)\to 0,$$

(21)

and then, the mean field for M becomes

$$\begin{array}{c}⟨M⟩=\left(\begin{array}{cc}\sigma & 0\\ 0& \sigma \end{array}\right).\end{array}$$

(22)

Now, the potential $V_M$ is written in terms of the meson mean fields as

$$\begin{array}{cc}{V}_M=& -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{\sigma }^2+{\displaystyle \frac{{\lambda }_4}{4}}{\sigma }^4-{\displaystyle \frac{{\lambda }_6}{6}}{\sigma }^6-m_{\pi }^2{f}_{\pi }\sigma .\hfill \end{array}$$

(23)

Here, the parameters are defined as

$$\begin{array}{cc} & {\overline{\mu }}_{\sigma }^2\equiv {\overline{\mu }}^2+{\displaystyle \frac{1}{2}}K,\hfill \\ & {\lambda }_4\equiv {\lambda }_{41}-{\lambda }_{42},\hfill \\ & {\lambda }_6\equiv {\lambda }_{61}+{\lambda }_{62}+{\lambda }_{63}.\hfill \end{array}$$

(24)

In the mean-field approximation, the vector meson fields are taken as

$${\omega }_{\mu }\left(x\right)\to \omega {\delta }_{\mu 0},{\rho }_{\mu }^i\left(x\right)\to \rho {\delta }_{\mu 0}{\delta }_{i3},$$

(25)

according to the rotational symmetry and isospin symmetry. Subsequently, the Lagrangian of the vector mesons is expressed in terms of the mean fields as

$$\begin{array}{c}{\mathcal{L}}_V=-g_{\omega NN}{\displaystyle \sum _{\alpha j}}{\overline{N}}_{\alpha j}{\gamma }^0\omega N_{\alpha j}-g_{\rho NN}{\displaystyle \sum _{\alpha j}}{\overline{N}}_{\alpha j}{\gamma }^0{\displaystyle \frac{{\tau }_3}{2}}\rho N_{\alpha j}+{\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }^2+{\displaystyle \frac{1}{2}}{m}_{\rho }^2{\rho }^2.\end{array}$$

(26)

with

$$\begin{array}{cc}{g}_{\omega NN}& =\left(a_{VNN}+a_{0NN}\right)g_{\omega },\hfill \end{array}$$

(27)

$$\begin{array}{cc}{g}_{\rho NN}& =a_{VNN}{g}_{\rho }.\hfill \end{array}$$

(28)

We note that, as we stated in the beginning of this subsection, we take ${\lambda }_{\omega \rho }=0$ to turn off the vector meson mixing interaction for the moment.

Then, the thermodynamic potential for the nucleons is written as

$$\begin{array}{c}{\mathrm{\Omega }}_N=-2{\displaystyle \sum _{\alpha =\pm ,j=\pm }}{\int }^{k_f}{\displaystyle \frac{d^{3}p}{{\left(2\pi \right)}^3}}\left[{\mu }_j^{*}-{\omega }_{\alpha j}\right],\hfill \end{array}$$

(29)

where $\alpha =\pm$ denotes the parity and $j=\pm$ the iso-spin of nucleons. ${\mu }_j^{*}$ is the effective chemical potential, given by

$$\begin{array}{c}{\mu }_j^{*}\equiv ({\mu }_B-g_{\omega NN}\omega )+{\displaystyle \frac{j}{2}}({\mu }_I-g_{\rho NN}\rho ),\end{array}$$

(30)

and ${\omega }_{\alpha j}$ is the energy of the nucleon defined as ${\omega }_{\alpha j}=\sqrt{{\left(\overrightarrow{p}\right)}^2+{\left(m_{\alpha j}^{*}\right)}^2}$, with $\overrightarrow{p}$ and $m_{\alpha j}^{*}$ being the momentum and the effective mass of the nucleon. The effective mass $m_{\alpha j}^{*}$ is given by

$$\begin{array}{c}{m}_{\alpha j}^{*}={\displaystyle \frac{1}{2}}\left[\sqrt{{(g_1+g_2)}^2{\sigma }^2+4m_0^2}+\alpha (g_1-g_2)\sigma \right].\end{array}$$

(31)

The entire thermodynamic potential for hadronic matter is expressed as

$$\begin{array}{cc} & {\mathrm{\Omega }}_H={\mathrm{\Omega }}_N-{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{\sigma }^2+{\displaystyle \frac{{\lambda }_4}{4}}{\sigma }^4-{\displaystyle \frac{{\lambda }_6}{6}}{\sigma }^6-m_{\pi }^2{f}_{\pi }\sigma -{\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }^2-{\displaystyle \frac{1}{2}}{m}_{\rho }^2{\rho }^2-{\mathrm{\Omega }}_0,\hfill \end{array}$$

(32)

where we subtracted the potential at the vacuum

$$\begin{array}{c}{\mathrm{\Omega }}_0\equiv -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{f}_{\pi }^2+{\displaystyle \frac{{\lambda }_4}{4}}{f}_{\pi }^4-{\displaystyle \frac{{\lambda }_6}{6}}{f}_{\pi }^6-m_{\pi }^2{f}_{\pi }^2.\end{array}$$

(33)

2.3. Nuclear Saturation Properties

Nuclear properties at the saturation density $n_0$ = 0.16 fm⁻³ are very important to be satisfied in nuclear physics. At the saturation, the energy per nucleon of the infinite symmetric nuclear matter is minimized. There are several fundamental nuclear properties at the saturation density: the binding energy $B_0$, the nuclear incompressibility $K_0$, the nuclear symmetry energy $S_0$, and the slope parameter $L_0$. In the present work, the model parameters are determined such that the saturation properties of the nuclear matter are reproduced.

We first obtain the pressure of hadronic matter P from the thermodynamic potential in Equation (86) as

$$P({\mu }_B,{\mu }_I)=-{\mathrm{\Omega }}_H({\mu }_B,{\mu }_H;\sigma ={\sigma }_0,\omega ={\omega }_0,\rho ={\rho }_0),$$

(34)

where ${\mu }_B$ and ${\mu }_I$ are the chemical potentials for the baryon number and the isospin number, and ${\sigma }_0$, ${\omega }_0$ and ${\rho }_0$ are the solutions of the stationary conditions of ${\mathrm{\Omega }}_H$, given by

$${\displaystyle \frac{\partial {\mathrm{\Omega }}_H}{\partial \sigma }}=0,{\displaystyle \frac{\partial {\mathrm{\Omega }}_H}{\partial \omega }}=0,{\displaystyle \frac{\partial {\mathrm{\Omega }}_H}{\partial \rho }}=0.$$

(35)

From the pressure P, we define the baryon number density $n_B$ and the isospin density $n_I$ as

$$n_B={\displaystyle \frac{\partial P}{\partial {\mu }_B}},n_I={\displaystyle \frac{\partial P}{\partial {\mu }_I}}.$$

(36)

They are related to the proton number density $n_p$ and the neutron number density $n_n$ as

$$n_B=n_p+n_n,n_I={\displaystyle \frac{1}{2}}{n}_p-{\displaystyle \frac{1}{2}}{n}_n.$$

(37)

As usual, from these densities and the pressure, we obtain the energy density $ϵ$ via the Legendre transformation as

$$ϵ(n_B,n_I)=-P+{\mu }_B{n}_B+{\mu }_I{n}_I.$$

(38)

It is convenient to define the energy per nucleon as

$$w(x,\delta )\equiv {\displaystyle \frac{ϵ(n_B,n_I)}{n_B}}-m_N,$$

(39)

where

$$x\equiv {\displaystyle \frac{n_B-n_0}{3n_0}},\delta \equiv -{\displaystyle \frac{2n_I}{n_B}}.$$

(40)

At the saturation density $n_B=n_0$, the symmetric nuclear matter ($n_I=0$) forms the most stable state with minimized energy. In other words, $w(x,\delta )$ is stationary when $(x,\delta )=(0,0)$, with $w(0,0)<0$. Then,

$${\displaystyle \frac{\partial w}{\partial \delta }}{|}_{\begin{array}{c}0\end{array}}={\displaystyle \frac{\partial w}{\partial n_B}}{\displaystyle \frac{\partial n_B}{\partial \delta }}+{\displaystyle \frac{\partial w}{\partial n_I}}{\displaystyle \frac{\partial n_I}{\partial \delta }}{|}_{\begin{array}{c}0\end{array}}=-{\displaystyle \frac{1}{2}}{\mu }_I{|}_{\begin{array}{c}0\end{array}}=0,$$

(41)

$${\displaystyle \frac{\partial w}{\partial x}}{|}_{\begin{array}{c}0\end{array}}={\displaystyle \frac{3P}{n_0}}{|}_{\begin{array}{c}0\end{array}}=0,$$

(42)

where ${|}_0$ means that the derivatives are evaluated at $(x,\delta )=(0,0)$. These imply that the pressure P and isospin chemical potential ${\mu }_I$ are zero at the saturation density. The binding energy $B_0$ is obtained as

$$B_0 =-w(0,0)=-{\displaystyle \frac{ϵ}{n_B}}{|}_{\begin{array}{c}0\end{array}}+m_N=-{\mu }_B{|}_{\begin{array}{c}0\end{array}}+m_N.$$

(43)

In this review, we take $B_0=-16$MeV as an input.

Expanding $w(x,\delta )$ around the stationary point $(x,\delta )=(0,0)$, we obtain

$$\begin{array}{cc}w(x,\delta ) & =w(0,0)+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}{|}_{\begin{array}{c}0\end{array}}{x}^2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\delta }^2}}{|}_{\begin{array}{c}0\end{array}}{\delta }^2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{3}w}{\partial x\partial {\delta }^2}}{|}_{\begin{array}{c}0\end{array}}x{\delta }^2+O\left(x^3\right)\hfill \\ & \equiv -B_0+{\displaystyle \frac{1}{2}}{K}_0{x}^2+(S_0+L_{0}x){\delta }^2+O\left(x^3\right),\hfill \end{array}$$

(44)

where $K_0$, $S_0$, and $L_0$ are called as the incompressibility, the symmetry energy, and the slope parameter at the saturation density, respectively.

The incompressibility $K_0$ represents the curvature of $w(x,\delta )$ in the direction of the baryon number density. It corresponds to the rate of increase of the baryon chemical potential ${\mu }_B$ with respect to $n_B$ around the saturation density. $K_0$ is calculated as

$$K_0 \equiv {\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}{|}_{\begin{array}{c}0\end{array}}=9n_0^2{\displaystyle \frac{{\partial }^2}{\partial n_B^2}}\left({\displaystyle \frac{ϵ}{n_B}}\right){|}_{\begin{array}{c}0\end{array}}=9n_0{\displaystyle \frac{\partial {\mu }_B}{\partial n_B}}{|}_{\begin{array}{c}0\end{array}}.$$

(45)

We note that $K_0$ corresponds to the hardness of the (symmetric) matter around the saturation density; the larger $K_0$ corresponds to the larger pressure at high baryon density. Thus, it is called the incompressibility of nuclear matter because a larger $K_0$ corresponds to a matter that is more resistant to compression. The generally accepted values are $K_0=240\pm 40$ (see recent review [73] for detailed discussion and summary of the values of $K_0$). In this review, the results are mainly computed with $K_0$ = 215, 240 MeV for comparison.

The symmetry energy $S_0$ is defined to be the slope of $w(x,\delta )$ in the isospin density direction around $n_0$ as

$$S_0 \equiv {\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}w}{\partial {\delta }^2}}{|}_{\begin{array}{c}0\end{array}}={\displaystyle \frac{n_0^2}{8}}{\displaystyle \frac{{\partial }^2}{\partial n_I^2}}\left({\displaystyle \frac{ϵ}{n_B}}\right){|}_{\begin{array}{c}0\end{array}}={\displaystyle \frac{n_0}{8}}{\displaystyle \frac{\partial {\mu }_I}{\partial n_I}}{|}_{\begin{array}{c}0\end{array}}.$$

(46)

The symmetry energy is the energy that arises from the asymmetry of the matter. If we ignore the $O\left(x^3\right)$ contribution in Equation (44), the symmetry energy at the saturation density $S_0$ can be approximated by

$$S_0\approx w(0,1)-w(0,0),$$

(47)

which is the energy difference between pure neutron matter and symmetric matter. Then, the term $S_0{\delta }^2$ can be seen as the energy arises from the difference of $n_p$ and $n_n$ (the asymmetry of the matter) around the saturation density. For later convenience, we define the symmetry energy at arbitrary baryon density $n_B$ as

$$S\left(n_B\right)\equiv {\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}w(x,\delta )}{\partial {\delta }^2}}{|}_{\delta =0}.$$

(48)

This $S\left(n_B\right)$ approximately corresponds to the energy difference between pure neutron matter and symmetric matter at $n_B$:

$$S\left(n_B\right)\approx w(x,1)-w(x,0).$$

(49)

The value of $S_0$ is well-studied with little ambiguity. In this review, $S_0$ is taken to be 31 MeV.

Finally, the slope parameter $L_0$ is given by

$$\begin{array}{cc}{L}_0 & \equiv {\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{3}w}{\partial x\partial {\delta }^2}}{|}_{\begin{array}{c}0\end{array}}={\displaystyle \frac{\partial S\left(n_B\right)}{\partial x}}{|}_{\begin{array}{c}0\end{array}}=3S_0+{\displaystyle \frac{3n_0^2}{8}}{\displaystyle \frac{{\partial }^2{\mu }_I}{\partial n_B{n}_I}}{|}_{\begin{array}{c}0\end{array}}.\hfill \end{array}$$

(50)

The slope parameter approximates the slope of the symmetry energy in the direction of baryon number density around the saturation density. The larger $L_0$ results in the larger symmetry energy $S\left(n_B\right)$ at higher density. Due to the experimental difficulties, the value of $L_0$ possesses large uncertainty and has been discussed for many years. The recent accepted values are $L_0=57.7\pm 19$ MeV, as summarized in Ref. [72].

2.4. Determination of Model Parameters

In the present model, the model parameters are fitted to reproduce the nuclear saturation properties, as well as physical masses and the decay constant in vacuum. Under the mean field approximation in Section 2.2, there are seven parameters to be determined for a given value of the chiral invariant mass $m_0$:

$$g_1,g_2,{\overline{\mu }}_{\sigma }^2,{\lambda }_4,{\lambda }_6,g_{\omega NN},g_{\rho NN}.$$

(51)

The vacuum expectation value of $\sigma$ is taken to be ${\sigma }_0=f_{\pi }$ with the pion decay constant $f_{\pi }=$ 93 MeV. The Yukawa coupling constants $g_1$ and $g_2$ are determined by fitting them to the nucleon masses in vacuum given in Equation (20), with $m_{+}=m_N=939$ MeV and $m_{-}=m_{N^{*}}=1535$ MeV for fixed value of the chiral invariant mass $m_0$. The values of ${\overline{\mu }}_{\sigma }^2$, ${\lambda }_4$, ${\lambda }_6$, $g_{\omega NN}$, and $g_{\rho NN}$ are determined by the saturation properties shown in Table 1 together with the stationary condition of the potential in vacuum given by

$${\overline{\mu }}_{\sigma }^2{f}_{\pi }-{\lambda }_4{f}_{\pi }^3+{\lambda }_6{f}_{\pi }^5+m_{\pi }^2{f}_{\pi }=0.$$

(52)

For the meson masses, we use the values listed in Table 2. We should note that there is a relatively large uncertainty in the incompressibility, so we use $K_0=215$ and 240 MeV as inputs for studying the dependence. The determined values of the parameters for a fixed value of $m_0$ are summarized in Table 3.

Table 1. Saturation properties that are used to determine the model parameters: saturation density $n_0$, binding energy $B_0$, incompressibility $K_0$, and symmetry energy $S_0$.

${\mathit{n}}_0$ [fm−3]	${\mathit{B}}_0$ [MeV]	${\mathit{K}}_0$ [MeV]	${\mathit{S}}_0$ [MeV]
0.16	16	215, 240	31

Table 2. Values of meson masses and pion decay constant in the vacuum in unit of MeV.

${\mathit{m}}_{\mathit{\pi }}$	${\mathit{m}}_{\mathit{\omega }}$	${\mathit{m}}_{\mathit{\rho }}$	${\mathit{f}}_{\mathit{\pi }}$
140	783	776	93

Table 3. Values of $g_1$, $g_2$, ${\overline{\mu }}_{\sigma }^2,{\lambda }_4,{\lambda }_6,g_{\omega NN},g_{\rho NN}$ for $m_0$ = 600–900 MeV, $K_0=215,240$ MeV.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	$g_1$	8.427	7.762	6.941	5.921
	$g_2$	14.836	14.171	13.349	12.329
	${\overline{\mu }}_{\sigma }^2/f_{\pi }^2$	23.377	20.979	13.346	2.502
	${\lambda }_4$	42.368	38.92	26.128	6.673
	${\lambda }_6{f}_{\pi }^2$	16.79	15.739	10.58	1.969
	$g_{\omega NN}$	8.902	7.055	5.471	3.389
	$g_{\rho NN}$	7.896	8.16	8.314	8.442
$K_0=240$ MeV	$g_1$	8.427	7.762	6.941	5.921
	$g_2$	14.836	14.171	13.349	12.329
	${\overline{\mu }}_{\sigma }^2/f_{\pi }^2$	21.821	18.842	11.692	1.537
	${\lambda }_4$	39.367	34.583	22.577	4.388
	${\lambda }_6{f}_{\pi }^2$	15.344	13.54	8.683	0.649
	$g_{\omega NN}$	9.132	7.305	5.66	3.522
	$g_{\rho NN}$	7.854	8.13	8.298	8.436

The slope parameter $L_0$ is computed as an output, and the resultant values are shown in Table 4. We note that the computed $L_0$ is slightly larger than the recently accepted values $L_0=57.7\pm 19$ MeV, as summarized in Ref. [72]. We also observe that the value of incompressibility has little effect on $L_0$, even with a large $K_0=260$ MeV.

Table 4. Slope parameter $L_0$ computed as a output from the model with $K_0=215,240,260$ MeV. $S_0=31$ MeV.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	$L_0$ [MeV]	85.91	82.87	81.32	80.15
$K_0=240$ MeV	$L_0$ [MeV]	86.25	83.04	81.33	80.08
$K_0=260$ MeV	$L_0$ [MeV]	86.45	83.14	81.33	80.03

The dependence of $L_0$ on $S_0$ is compared in Table 5. We observe that the value of $S_0$ have a relatively large impact on the value of $L_0$.

Table 5. Slope parameter $L_0$ with $S_0=24,31,36$ MeV. $K_0=215$ MeV.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$S_0=24$ MeV	$L_0$ [MeV]	64.91	61.87	60.32	59.15
$S_0=31$ MeV	$L_0$ [MeV]	85.91	82.87	81.32	80.15
$S_0=36$ MeV	$L_0$ [MeV]	100.91	97.87	96.32	95.15

3. Finite Nuclei

In the previous section, we observed that the parity doublet model reproduces reasonably the nuclear matter saturation properties with the chiral invariant nucleon mass $m_0$ in the range of 600–900 MeV. In this section, we study the properties of nuclei in self-consistent relativistic mean field theory to see if the parity doublet model can explain some nuclear properties, and to find out the value of the chiral invariant mass preferred by nuclear structures. As a first step, we use the PDM without the $a_0$ meson, focusing on the properties of stable nuclei. Nuclear properties in the PDM with the $a_0$ meson is being studied and the results will be reported elsewhere.

Before we investigate the properties of nuclei using the PDM, we first describe how one obtains the nuclear energy density functional based on the relativistic mean field theory and the corresponding equation of motion for nucleons and mesons. We also discuss, in brief, how to solve the equation of motion, especially for exotic nuclei in which the continuum effect is important. For this, we closely follow the description in Ref. [68], where a Walecka-type model was adopted. The Relativistic Continuum Hartree–Bogoliubov (RCHB) theory [68] is an extension of the relativistic mean field theory in a self-consistent way with both bound and (discretized) continuum states.

The starting Lagrangian is given by

$$\begin{array}{ccc}\mathcal{L}& =& \overline{\psi }[i{\displaystyle \cancel{\mathit{\partial }}}-M-g_{\sigma }\sigma -g_{\omega }{\displaystyle \cancel{\omega }}-g_{\rho }{\displaystyle \cancel{\rho }}-e{\displaystyle \cancel{A}}{\displaystyle \frac{1-{\tau }_3}{2}}]\psi +{\displaystyle \frac{1}{2}}{\partial }^{\mu }\sigma {\partial }_{\mu }\sigma -U\left(\sigma \right)\hfill \\ & & -{\mathrm{\Omega }}^{\mu \nu }{\mathrm{\Omega }}_{\mu \nu }+U_{\omega }\left({\omega }_{\mu }\right)-{\displaystyle \frac{1}{4}}{\overrightarrow{R}}^{\mu \nu }·{\overrightarrow{R}}_{\mu \nu }+U_{\rho }\left({\overrightarrow{\rho }}_{\mu }\right)-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}_{\mu \nu },\hfill \end{array}$$

(53)

where ${\mathrm{\Omega }}^{\mu \nu }$, ${\overrightarrow{R}}^{\mu \nu }$ and $F_{\mu \nu }$ are the field strength tensors of the $\omega$ meson, $\rho$ meson and electromagnetic field, respectively and

$$\begin{array}{ccc}& & U\left(\sigma \right)={\displaystyle \frac{1}{2}}{m}_{\sigma }^2{\sigma }^2+{\displaystyle \frac{1}{3}}{g}_2{\sigma }^3+{\displaystyle \frac{1}{4}}{g}_3{\sigma }^4,\hfill \\ & & U_{\omega }\left({\omega }_{\mu }\right)={\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }+{\displaystyle \frac{1}{4}}{c}_3{\left({\omega }_{\mu }{\omega }^{\mu }\right)}^2,\hfill \\ & & U_{\rho }\left({\overrightarrow{\rho }}_{\mu }\right)={\displaystyle \frac{1}{2}}{m}_{\rho }^2{\overrightarrow{\rho }}_{\mu }{\overrightarrow{\rho }}^{\mu }+{\displaystyle \frac{1}{4}}{d}_3{\left({\overrightarrow{\rho }}_{\mu }{\overrightarrow{\rho }}^{\mu }\right)}^2,\rho =\overrightarrow{\rho }·\overrightarrow{\tau }.\hfill \end{array}$$

(54)

We refer to Table 2 in Ref. [68] for the value of the masses and coupling constants in the above Lagrangian that were determined by studying the properties of nuclear matter and a few doubly magic nuclei with no-sea and mean-field approximations. After taking the mean field approximation on the above Lagrangian and performing the Legendre transformation, we obtain the corresponding mean field Hamiltonian ${\mathcal{H}}_{\mathrm{RMF}}$ and the energy density functional $E_{\mathrm{RMF}}=⟨\mathrm{\Phi }|{\mathcal{H}}_{\mathrm{RMF}}|\mathrm{\Phi }⟩$. Here, $|\mathrm{\Phi }⟩$ is the ground state of a nucleus with the mass number A, $|\mathrm{\Phi }⟩={\displaystyle \prod _{a=1}^A}{c}_a^{†}|0⟩$, and $c_a^{†}$ is the creation operator of the nucleon field, $\psi \left(x\right)={\displaystyle \sum _a}{\psi }_a\left(x\right)c_a$. Then, the expectation value of the Hamiltonian with the mean field approximation reads

$$\begin{array}{ccc}{E}_{\mathrm{RMF}}(\rho ,\varphi )& =& ⟨\mathrm{\Phi }\left|{\mathcal{H}}_{\mathrm{RMF}}\right|\mathrm{\Phi }⟩\hfill \\ & =& \int d^{3}x\mathrm{Tr}[\beta (\overrightarrow{\gamma }·\overrightarrow{p}+M+g_{\sigma }\sigma +g_{\omega }\beta {\omega }_0+g_{\rho }\beta {\rho }_0^3{\tau }_3+e\cancel{A}{\displaystyle \frac{1-{\tau }_3}{2}})\rho ]\hfill \\ & & +\int d^{3}x[-{\displaystyle \frac{1}{2}}{\partial }^i\sigma {\partial }_i\sigma +U_{\sigma }\left(\sigma \right)+{\displaystyle \frac{1}{4}}{\mathrm{\Omega }}^{ij}{\mathrm{\Omega }}_{ij}-U_{\omega }\left({\omega }_0\right)+{\displaystyle \frac{1}{4}}{\overrightarrow{R}}^{ij}·{\overrightarrow{R}}_{ij}-U_{\rho }\left({\rho }_0^3\right)\hfill \\ & & -{\displaystyle \frac{1}{4}}{F}^{0j}{F}_{0j}],\hfill \end{array}$$

(55)

where $\rho$ is the density matrix, $\varphi$ represents bosonic fields, and ${\gamma }^{\mu }=(\beta ,\beta \overrightarrow{\alpha })$. Here, we assumed that the mean field is time-independent. Also, we have applied the fact that the spatial components of the vector fields are zero in a system with the time reversal symmetry. By performing variations on $E_{\mathrm{RMF}}$ with respect to $\rho$ and $\varphi$, we obtain the equations for the nucleon and bosons [68].

$$\begin{array}{c}{h}_D{\psi }_i\left(\overrightarrow{x}\right)={ϵ}_i{\psi }_i\left(\overrightarrow{x}\right),\end{array}$$

(56)

where the Dirac Hamiltonian $h_D$ is given by

$$h_D=\overrightarrow{\alpha }·\overrightarrow{p}+\beta [M+S\left(\overrightarrow{x}\right)]+V\left(\overrightarrow{x}\right)$$

(57)

with the scalar $S\left(\overrightarrow{x}\right)$ and vector $V\left(\overrightarrow{x}\right)$ potentials given by

$$\begin{array}{cc}S\left(\overrightarrow{x}\right)& =g_{\sigma }\sigma \left(\overrightarrow{x}\right),\hfill \\ V\left(\overrightarrow{x}\right)& =g_{\omega }{\omega }_0\left(\overrightarrow{x}\right)+g_{\rho }{\tau }_3{\rho }_0^3\left(\overrightarrow{x}\right)+{\displaystyle \frac{1}{2}}e(1-{\tau }_3)A_0\left(\overrightarrow{x}\right).\hfill \end{array}$$

In general, the equations of motion for the nucleon moving in the mean field potentials are solved by using the harmonic oscillator basis. However, for exotic nuclei, whose density profile can have a long tail, it is preferable to solve the equations in coordinate space and adopt a basis which can treat the asymptotic behavior of the nucleon wave function. In Ref. [68], the Woods–Saxon basis was used to solve the equations of motion for the nucleon.

Similarly, by doing variations on $E_{\mathrm{RMF}}$ with respect to $\varphi$, we obtain the equations for the bosons [68],

$$\begin{array}{ccc}& & -{\overrightarrow{▿}}^2\sigma +U_{\sigma }^{\prime }\left(\sigma \right)=-g_{\rho }{\rho }_3,\hfill \\ & & -{\overrightarrow{▿}}^2{\omega }_0+U_{\omega }^{\prime }\left({\omega }_0\right)=g_{\omega }{\rho }_{\omega },\hfill \\ & & -{\overrightarrow{▿}}^2{\rho }_0^3+U_{\rho }^{\prime }\left({\rho }_0^3\right)=g_{\rho }{\rho }_3,\hfill \\ & & -{\overrightarrow{▿}}^2{A}_0=e{\rho }_c.\hfill \end{array}$$

(58)

where

$$\begin{array}{ccc}& & {\rho }_s=\mathrm{Tr}\left[\beta \rho \right],\hfill \\ & & {\rho }_{\omega }=\mathrm{Tr}\left[\rho \right],\hfill \\ & & {\rho }_3=\mathrm{Tr}\left[{\tau }_3\rho \right],\hfill \\ & & {\rho }_c=\mathrm{Tr}\left[(1-{\tau }_3)\rho \right].\hfill \end{array}$$

(59)

Using Equation (58) in Equation (55), one can obtain the total energy of the system as

$$\begin{array}{ccc}E& =& \int d^{3}x\mathrm{Tr}[\beta (\overrightarrow{\gamma }·\overrightarrow{p}+M)\rho +{\displaystyle \frac{1}{2}}(g_{\sigma }\beta \sigma +g_{\omega }{\omega }_0+g_{\rho }{\rho }_0^3{\tau }_3+A_0{\displaystyle \frac{1-{\tau }_3}{2}})\rho ]\hfill \\ & & +\int d^{3}x[U_{\sigma }\left(\sigma \right)-U_{\omega }\left({\omega }_0\right)-U_{\rho }\left({\rho }_0^3\right)-{\displaystyle \frac{1}{2}}(\sigma U_{\sigma }^{\prime }\left(\sigma \right)-{\omega }_0{U}_{\omega }^{\prime }\left({\omega }_0\right)-{\rho }_0^3{U}_{\rho }^{\prime }\left({\rho }_0^3\right))].\hfill \end{array}$$

(60)

Now, we move onto the PDM without the $a_0$ meson. To pin down the value of $m_0$, we study the properties of nuclei using the parity doublet model without the $a_0$ meson in the framework of a self-consistent relativistic mean field theory.

Using the Lagrangian of the parity doublet model without the $a_0$ meson in Equation (1), we obtain the equations of motion (EoM) for the stationary mean fields $\sigma$, ${\omega }_0$, ${\rho }_0^3$ and $A_0$ [67],

$$\begin{array}{ccc}\left(-{\overrightarrow{\nabla }}^2+m_{\sigma }^2\right)⟨\sigma \left(\overrightarrow{x}\right)⟩& =& -\overline{N}\left(\overrightarrow{x}\right)N\left(\overrightarrow{x}\right){\left.{\displaystyle \frac{\partial m_N^{*}\left(\sigma \right)}{\partial \sigma }}\right|}_{\sigma =⟨\sigma \left(\overrightarrow{x}\right)⟩}\hfill \\ & & +\left(-3f_{\pi }{\lambda }_4+10f_{\pi }^3{\lambda }_6\right){⟨\sigma \left(\overrightarrow{x}\right)⟩}^2\hfill \\ & & +\left(-{\lambda }_4+10f_{\pi }^2{\lambda }_6\right){⟨\sigma \left(\overrightarrow{x}\right)⟩}^3\hfill \\ & & +5f_{\pi }{\lambda }_6{⟨\sigma \left(\overrightarrow{x}\right)⟩}^4+{\lambda }_6{⟨\sigma \left(\overrightarrow{x}\right)⟩}^5,\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\left(-{\overrightarrow{\nabla }}^2+m_{\omega }^2\right)⟨{\omega }_0\left(\overrightarrow{x}\right)⟩& =& g_{\omega NN}{N}^{†}\left(\overrightarrow{x}\right)N\left(\overrightarrow{x}\right),\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\left(-{\overrightarrow{\nabla }}^2+m_{\rho }^2\right)⟨{\rho }_0^3\left(\overrightarrow{x}\right)⟩& =& g_{\rho NN}{N}^{†}\left(\overrightarrow{x}\right){\displaystyle \frac{{\tau }^3}{2}}N\left(\overrightarrow{x}\right),\hfill \end{array}$$

(63)

$$\begin{array}{ccc}-{\overrightarrow{\nabla }}^2⟨A_0\left(\overrightarrow{x}\right)⟩& =& e{N}^{†}\left(\overrightarrow{x}\right){\displaystyle \frac{1-{\tau }_3}{2}}N\left(\overrightarrow{x}\right).\hfill \end{array}$$

(64)

Note here that we take the shift $\sigma \to f_{\pi }+\sigma$, since the scalar field in the parity doublet model is a chiral partner of the pion field, whose vacuum expectation value in free space is $f_{\pi }$, while that of the widely used scalar field in nuclear structure studies is zero in free space. Since we are interested in finite nuclei, we will not consider the EoM for the parity partner of the nucleon, $N^{*}\left(1535\right)$, which does not form its Fermi sea near the saturation density. In addition, since our primary goal here is to see if the parity doublet model can explain some basic nuclear properties, such as the binding energy with a reasonable value of the chiral invariant mass, we will not consider pairing correlations, which are essential for odd–even staggering in nuclear properties. For instance, according to the semi-empirical mass formula, the contribution from the pairing term to the binding energy per nucleon of ⁵⁸Ni is only about $0.03$ MeV.

The EoM for the nucleon is given by

$$\left[\overrightarrow{\alpha }·\overrightarrow{p}+\beta m_N^{*}\left(⟨\sigma \left(\overrightarrow{x}\right)⟩\right)+V\left(\overrightarrow{x}\right)\right]N_i\left(\overrightarrow{x}\right)={ϵ}_i{N}_i\left(\overrightarrow{x}\right),$$

(65)

where $N_i$ is the single-particle wave function, and

$$V\left(\overrightarrow{x}\right)=g_{\omega NN}⟨{\omega }_0\left(\overrightarrow{x}\right)⟩+g_{\rho NN}⟨{\rho }_0^3\left(\overrightarrow{x}\right)⟩{\displaystyle \frac{{\tau }^3}{2}}+e{\displaystyle \frac{(1-{\tau }_3)}{2}}⟨A_0\left(\overrightarrow{x}\right)⟩.$$

(66)

With assuming the spherical shape of the nucleus, we can solve Equations (61)–(65) simultaneously to obtain the energy

$$E=\int d^{3}x\mathcal{H}\left(\overrightarrow{x}\right).$$

(67)

After subtracting out the vacuum contribution, we write the Hamiltonian density $\mathcal{H}\left(\overrightarrow{x}\right)$ in the mean field approximation as

$$\begin{array}{ccc}\mathcal{H}& =& \overline{N}\left(-i{\gamma }^i{\partial }_i+m_N^{*}\right)N+g_{\omega NN}⟨{\omega }_0⟩N^{†}N+g_{\rho NN}⟨{\rho }_0^3⟩N^{†}{\displaystyle \frac{{\tau }^3}{2}}N+e⟨A_0⟩N^{†}{\displaystyle \frac{1-{\tau }_3}{2}}N\hfill \\ & & -{\displaystyle \frac{1}{2}}{\partial }^i⟨\sigma ⟩{\partial }_i⟨\sigma ⟩+{\displaystyle \frac{1}{2}}{\partial }^i⟨{\omega }_0⟩{\partial }_i⟨{\omega }_0⟩+{\displaystyle \frac{1}{2}}{\partial }^i⟨{\rho }_0^3⟩{\partial }_i⟨{\rho }_0^3⟩+{\displaystyle \frac{1}{2}}{\partial }^i⟨A_0⟩{\partial }_i⟨A_0⟩\hfill \\ & & -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}\left[{\left(f_{\pi }+⟨\sigma ⟩\right)}^2-f_{\pi }^2\right]+{\displaystyle \frac{{\lambda }_4}{4}}\left[{\left(f_{\pi }+⟨\sigma ⟩\right)}^4-f_{\pi }^4\right]-{\displaystyle \frac{{\lambda }_6}{6}}\left[{\left(f_{\pi }+⟨\sigma ⟩\right)}^6-f_{\pi }^6\right]-m_{\pi }^2{f}_{\pi }⟨\sigma ⟩\hfill \\ & & -{\displaystyle \frac{1}{2}}{m}_{\omega }^2{⟨{\omega }_0⟩}^2-{\displaystyle \frac{1}{2}}{m}_{\rho }^2{⟨{\rho }_0^3⟩}^2.\hfill \end{array}$$

(68)

Then, the binding energy (BE) per nucleon is given by

$$\mathrm{BE}/A=-{\displaystyle \frac{E}{A}}+m_N.$$

(69)

To put an additional constraint on the value of the chiral invariant mass, using the model parameters summarized in Table 3, we calculate the binding energies per nucleon and charge radii of selected nuclei: ¹⁶O, ⁴⁰Ca, ⁴⁸Ca, ⁵⁸Ni, ⁷⁰Ge, ⁸²Se, ⁹²Mo, ¹¹²Sn, ¹²⁶Sn, ¹³⁸Ba, ¹⁵⁴Sm, ¹⁷⁰Er, ¹⁸²W, ²⁰²Pb and ²⁰⁸Pb [67]. Before we compare our results for the binding energies and charge radii with the experiments, we show the nucleon density profile, mean-field value and effective nucleon mass in a nucleus with different values of the chiral invariant mass to visualize how the chiral invariant mass affects them. We first plot the nucleon density profile in ¹¹²Sn and ¹²⁶Sn for different values of the chiral invariant mass in Figure 1. It is interesting to see that ¹¹²Sn has a depleted central density and, therefore, can be a candidate of bubble nuclei, which was also observed in the previous studies based on relativistic mean field models; for example, see Ref. [74].

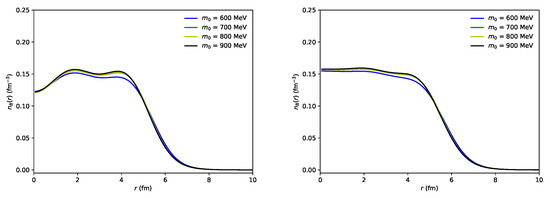
Figure 1. Nucleon density profile in ¹¹²Sn (left) and ¹²⁶Sn (right) calculated with $K_0=215$ MeV.

In Figure 2, we present the value of $⟨\sigma ⟩$ and $⟨{\omega }_0⟩$ in ¹¹²Sn and ¹²⁶Sn for different values of the chiral invariant mass. As expected, the value of $⟨\sigma ⟩$ decreases and $⟨{\omega }_0⟩$ increases as $r\to 0$, from zero density to the saturation density.

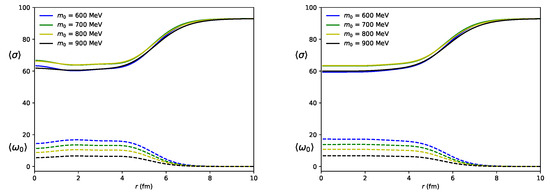
Figure 2. $⟨\sigma ⟩$ and $⟨{\omega }_0⟩$ in ¹¹²Sn (left) and ¹²⁶Sn (right) with $K_0=215$ MeV.

The effective neutron and proton masses in ¹¹²Sn and ¹²⁶Sn are shown in Figure 3, where the effective mass is defined as the energy of the nucleon at rest:

$$\begin{array}{ccc}& & m_n^{\left(\mathrm{eff}\right)}=m_n^{*}+g_{\omega NN}⟨{\omega }_0⟩-{\displaystyle \frac{g_{\rho NN}}{2}}⟨{\rho }_0⟩,\hfill \\ & & m_p^{\left(\mathrm{eff}\right)}=m_p^{*}+g_{\omega NN}⟨{\omega }_0⟩+{\displaystyle \frac{g_{\rho NN}}{2}}⟨{\rho }_0⟩.\hfill \end{array}$$

As observed in Ref. [67], the neutron–proton mass difference becomes larger in a nucleus with larger isospin asymmetry.

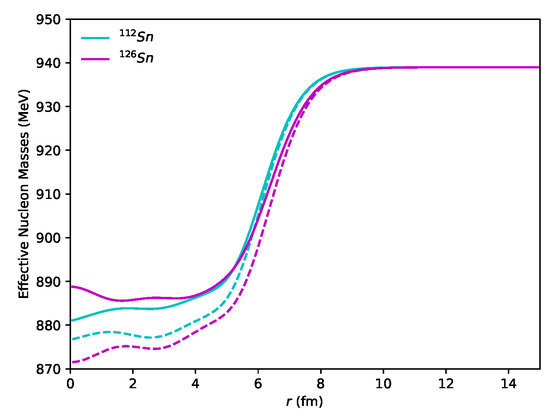
Figure 3. Neutron and proton effective masses in ¹¹²Sn and ¹²⁶Sn with $K_0=215$ MeV. Here, solid (dashed) lines are for the neutron (proton).

Now, as in Ref. [67], we compare our results with experiments to check which value of the chiral invariant mass reproduces the experimental results well. In Table 6 and Table 7, we present the binding energies per nucleon and the charge radii as well as the root-mean-square deviation (RMSD) with $m_0=600$, 700, 800, 900 MeV for selected nuclei: ¹⁶O, ⁴⁰Ca, ⁴⁸Ca, ⁵⁸Ni, ⁷⁰Ge, ⁸²Se, ⁹²Mo, ¹¹²Sn, ¹²⁶Sn, ¹³⁸Ba, ¹⁵⁴Sm, ¹⁷⁰Er, ¹⁸²W, ²⁰²Pb, and ²⁰⁸Pb [67]. It can be seen from Table 6 and Table 7 that the case with $m_0=700$ MeV has the smallest RMS deviation both in the binding energies and charge radii. Therefore, as concluded in Ref. [67], $m_0=700$ MeV is preferred by the nuclear properties of selected isotopes.

Table 6. Binding energy per nucleon and the charge radius ($R_C$) with the parameter set in Table 3 for $K=215$ MeV. The table is taken from Ref. [67].

${\mathit{m}}_0$ (MeV)		600	700	800	900	Exp.
BE/A (MeV)	16O	$7.489$	$7.781$	$7.298$	$5.698$	$7.976$
	40Ca	$8.063$	$8.301$	$7.942$	$6.693$	$8.551$
	48Ca	$7.978$	$8.134$	$7.757$	$6.541$	$8.667$
	58Ni	$7.685$	$7.841$	$7.473$	$6.308$	$8.732$
	70Ge	$8.044$	$8.239$	$7.932$	$6.866$	$8.722$
	82Se	$8.066$	$8.219$	$7.910$	$6.881$	$8.693$
	92Mo	$7.993$	$8.123$	$7.822$	$6.828$	$8.658$
	112Sn	$7.911$	$8.050$	$7.774$	$6.844$	$8.514$
	126Sn	$7.980$	$8.070$	$7.802$	$6.909$	$8.443$
	138Ba	$7.920$	$8.028$	$7.764$	$6.890$	$8.393$
	154Sm	$7.821$	$7.958$	$7.724$	$6.894$	$8.227$
	170Er	$7.733$	$7.837$	$7.618$	$6.830$	$8.112$
	182W	$7.616$	$7.707$	$7.494$	$6.726$	$8.018$
	202Pb	$7.468$	$7.535$	$7.310$	$6.549$	$7.882$
	208Pb	$7.496$	$7.552$	$7.321$	$6.558$	$7.867$
RMS deviation		$0.573$	$0.438$	$0.727$	$1.734$	−
$R_C$ (fm)	16O	$2.845$	$2.763$	$2.772$	$2.796$	$2.699$
	40Ca	$3.546$	$3.469$	$3.473$	$3.479$	$3.478$
	48Ca	$3.585$	$3.521$	$3.525$	$3.527$	$3.478$
	58Ni	$3.912$	$3.848$	$3.856$	$3.863$	$3.776$
	70Ge	$4.085$	$4.013$	$4.013$	$4.008$	$4.041$
	82Se	$4.209$	$4.145$	$4.144$	$4.135$	$4.140$
	92Mo	$4.401$	$4.339$	$4.344$	$4.344$	$4.315$
	112Sn	$4.671$	$4.608$	$4.609$	$4.602$	$4.594$
	126Sn	$4.754$	$4.697$	$4.698$	$4.688$	$4.685$
	138Ba	$4.920$	$4.862$	$4.861$	$4.849$	$4.838$
	154Sm	$5.111$	$5.045$	$5.039$	$5.022$	$5.105$
	170Er	$5.242$	$5.178$	$5.175$	$5.160$	$5.279$
	182W	$5.364$	$5.301$	$5.298$	$5.286$	$5.356$
	202Pb	$5.549$	$5.493$	$5.493$	$5.481$	$5.471$
	208Pb	$5.584$	$5.531$	$5.532$	$5.519$	$5.501$
RMS deviation		$0.082$	$0.046$	$0.049$	$0.056$	−

Table 7. Binding energy per nucleon and the charge radius ($R_C$) with the parameter set in Table 3 for $K=240$ MeV. The table is taken from Ref. [67].

${\mathit{m}}_0$ (MeV)		600	700	800	900	Exp.
BE/A (MeV)	16O	$7.087$	$7.280$	$6.792$	$5.093$	$7.976$
	40Ca	$7.736$	$7.906$	$7.538$	$6.191$	$8.551$
	48Ca	$7.676$	$7.768$	$7.378$	$6.061$	$8.667$
	58Ni	$7.391$	$7.486$	$7.108$	$5.849$	$8.732$
	70Ge	$7.761$	$7.900$	$7.584$	$6.429$	$8.722$
	82Se	$7.799$	$7.899$	$7.580$	$6.462$	$8.693$
	92Mo	$7.741$	$7.821$	$7.507$	$6.424$	$8.658$
	112Sn	$7.668$	$7.760$	$7.474$	$6.460$	$8.514$
	126Sn	$7.757$	$7.801$	$7.516$	$6.536$	$8.443$
	138Ba	$7.695$	$7.758$	$7.482$	$6.526$	$8.393$
	154Sm	$7.596$	$7.691$	$7.447$	$6.540$	$8.227$
	170Er	$7.526$	$7.587$	$7.354$	$6.484$	$8.112$
	182W	$7.418$	$7.466$	$7.237$	$6.387$	$8.018$
	202Pb	$7.277$	$7.303$	$7.062$	$6.221$	$7.882$
	208Pb	$7.306$	$7.322$	$7.075$	$6.232$	$7.867$
RMS deviation		$0.827$	$0.737$	$1.047$	$2.147$	−
$R_C$ (fm)	16O	$2.877$	$2.792$	$2.790$	$2.803$	$2.699$
	40Ca	$3.572$	$3.491$	$3.485$	$3.479$	$3.478$
	48Ca	$3.605$	$3.537$	$3.532$	$3.522$	$3.478$
	58Ni	$3.932$	$3.863$	$3.861$	$3.855$	$3.776$
	70Ge	$4.104$	$4.028$	$4.018$	$4.001$	$4.041$
	82Se	$4.223$	$4.154$	$4.145$	$4.125$	$4.140$
	92Mo	$4.418$	$4.351$	$4.347$	$4.335$	$4.315$
	112Sn	$4.684$	$4.616$	$4.608$	$4.591$	$4.594$
	126Sn	$4.764$	$4.703$	$4.695$	$4.675$	$4.685$
	138Ba	$4.928$	$4.865$	$4.856$	$4.834$	$4.838$
	154Sm	$5.117$	$5.045$	$5.031$	$5.004$	$5.105$
	170Er	$5.250$	$5.181$	$5.169$	$5.144$	$5.279$
	182W	$5.374$	$5.305$	$5.294$	$5.270$	$5.356$
	202Pb	$5.555$	$5.493$	$5.485$	$5.462$	$5.471$
	208Pb	$5.588$	$5.529$	$5.521$	$5.499$	$5.501$
RMS deviation		$0.097$	$0.052$	$0.053$	$0.062$	−

With $m_0=700$ MeV, we try to improve our results of nuclear properties. For this, we use the following nuclear matter properties as inputs,

$$\begin{array}{ccc}& & {\displaystyle \frac{E}{A}}-m_N=-16.3\mathrm{MeV},n_0=0.16{\mathrm{fm}}^{-3},\hfill \\ & & K_0=215\mathrm{MeV},S_0=30\mathrm{MeV},\hfill \end{array}$$

(70)

and determine the model parameters again given in Table 8 [67]. With the new parameter set in Table 8, we calculate the properties of selected nuclei and compare our results with experiments and the ones obtained in RCHB with PC-PK1 [75,76] in Table 9. As in Table 9, our results are in quantitative agreement with experiments. As stated in Ref. [67], pairing correlations are not included in our current results, which will be improved in our future publications.

Table 8. Parameter set with the inputs in Equation (70). All the parameters are dimensionless except $m_{\sigma }$.

${\mathit{g}}_1$	${\mathit{g}}_2$	${\mathit{g}}_{\mathit{\omega }\mathbf{NN}}$	${\mathit{g}}_{\mathit{\rho }\mathbf{NN}}$	${\overline{\mathit{\mu }}}_{\mathit{\sigma }}^2/{\mathit{f}}_{\mathit{\pi }}^2$	${\mathit{\lambda }}_4$	${\mathit{\lambda }}_6{\mathit{f}}_{\mathit{\pi }}^2$	${\mathit{m}}_{\mathit{\sigma }}$ [MeV]
$7.762$	$14.171$	$7.036$	$3.958$	$21.135$	$39.332$	$15.996$	$382.140$

Table 9. Binding energy per nucleon and the charge radius ($R_C$) with the parameters in Table 8.

	BE/A [MeV]			${\mathit{R}}_{\mathit{C}}$ [fm]
	PDM	RCHB	Exp.	PDM	RCHB	Exp.
16O	$8.040$	$7.956$	$7.976$	$2.757$	$2.768$	$2.699$
40Ca	$8.574$	$8.577$	$8.551$	$3.464$	$3.481$	$3.478$
48Ca	$8.419$	$8.654$	$8.667$	$3.517$	$3.494$	$3.478$
58Ni	$8.118$	$8.691$	$8.732$	$3.843$	$3.737$	$3.776$
70Ge	$8.521$	$8.650$	$8.722$	$4.010$	$4.001$	$4.041$
82Se	$8.513$	$8.664$	$8.693$	$4.142$	$4.125$	$4.140$
92Mo	$8.408$	$8.662$	$8.658$	$4.335$	$4.310$	$4.315$
112Sn	$8.339$	$8.489$	$8.514$	$4.605$	$4.582$	$4.594$
126Sn	$8.372$	$8.447$	$8.443$	$4.695$	$4.683$	$4.685$
138Ba	$8.329$	$8.406$	$8.393$	$4.860$	$4.848$	$4.838$
154Sm	$8.263$	$8.149$	$8.227$	$5.042$	$5.062$	$5.105$
170Er	$8.140$	$8.000$	$8.112$	$5.176$	$5.224$	$5.279$
182W	$8.007$	$7.927$	$8.018$	$5.299$	$5.342$	$5.356$
202Pb	$7.837$	$7.869$	$7.882$	$5.491$	$5.490$	$5.471$
208Pb	$7.860$	$7.875$	$7.867$	$5.529$	$5.518$	$5.501$
RMS deviation	$0.204$	$0.05$	−	$0.045$	$0.031$	−

4. Effect of ${\mathbf{a}}_{\mathbf{0}}$ Meson to Nuclear Matter

In the previous sections, we omitted the effect of the $a_0$ meson when we studied nuclear matter and finite nuclei. However, the isovector scalar meson may play an important role in the asymmetric matter, such as neutron star matter and neutron-rich nuclei. In this section, we study the effect of the $a_0$ meson on nuclear properties such as symmetry energy and slope parameter. As we will see, the $a_0$ meson stiffens the matter strongly and causing a large slope parameter $L_0$. We include also the vector meson mixing interaction to effectively reduce the slope parameter and study the effect of it.

4.1. Dense Nuclear Matter with $a_0\left(980\right)$

To construct the nuclear matter with $a_0\left(980\right)$, we adopt the mean-field approximation by taking

$$\sigma \left(x\right)\to \sigma ,\pi \left(x\right)\to 0,a_0^i\left(x\right)\to a{\delta }_{i3},\eta \left(x\right)\to 0.$$

(71)

Then, the mean field for M becomes

$$⟨M⟩=\left(\begin{array}{cc}\sigma -a& 0\\ 0& \sigma +a\end{array}\right).$$

(72)

Now, the potential $V_M$ is written in terms of the meson mean fields as

$$\begin{array}{cc}{V}_M=& -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{\sigma }^2-{\displaystyle \frac{{\overline{\mu }}_a^2}{2}}{a}^2+{\displaystyle \frac{{\lambda }_4}{4}}({\sigma }^4+a^4)+{\displaystyle \frac{{\gamma }_4}{2}}{\sigma }^2{a}^2\hfill \\ & -{\displaystyle \frac{{\lambda }_6}{6}}({\sigma }^6+15{\sigma }^2{a}^4+15{\sigma }^4{a}^2+a^6)+{\lambda }_6^{\prime }({\sigma }^2{a}^4+{\sigma }^4{a}^2)\hfill \\ & -m_{\pi }^2{f}_{\pi }\sigma ,\hfill \end{array}$$

(73)

where the parameters are defined as

$$\begin{array}{cc} & {\overline{\mu }}_{\sigma }^2\equiv {\overline{\mu }}^2+{\displaystyle \frac{1}{2}}K,\hfill \\ & {\overline{\mu }}_a^2\equiv {\overline{\mu }}^2-{\displaystyle \frac{1}{2}}K={\overline{\mu }}_{\sigma }^2-K,\hfill \\ & {\lambda }_4\equiv {\lambda }_{41}-{\lambda }_{42},\hfill \\ & {\gamma }_4\equiv 3{\lambda }_{41}-{\lambda }_{42},\hfill \\ & {\lambda }_6\equiv {\lambda }_{61}+{\lambda }_{62}+{\lambda }_{63},\hfill \\ & {\lambda }_6^{\prime }\equiv {\displaystyle \frac{4}{3}}{\lambda }_{62}+2{\lambda }_{63}.\hfill \end{array}$$

(74)

In the present model, ${\lambda }_6^{\prime }$ is taken as a free parameter to examine the effect of ${\lambda }_{62}$ and ${\lambda }_{63}$ interactions, which are of sub-leading order in the large $N_c$ expansion. Given that the ${\lambda }_6^{\prime }$ term is suppressed by $1/N_c$ compared to the ${\lambda }_6$ term in the large $N_c$ expansion, we assume $|{\lambda }_6^{\prime }|\lesssim |{\lambda }_6|$ holds. Consequently, we consider ${\lambda }_6^{\prime }=0,\pm {\lambda }_6$ to assess the impact of the sub-leading order six-point interactions on the symmetry energy. By default, we first set ${\lambda }_6^{\prime }=0$. In the end of Section 4.3 and Section 4.4, we investigate the impact of ${\lambda }_6^{\prime }$ on the results by comparing the cases with ${\lambda }_6^{\prime }=0,\pm {\lambda }_6$.

In the mean-field approximation, the vector meson fields are taken as

$${\omega }_{\mu }\left(x\right)\to \omega {\delta }_{\mu 0},{\rho }_{\mu }^i\left(x\right)\to \rho {\delta }_{\mu 0}{\delta }_{i3},$$

(75)

according to the rotational symmetry and isospin symmetry. Subsequently, the Lagrangian of the vector mesons is expressed in terms of the mean fields as

$$\begin{array}{cc}{\mathcal{L}}_V=& -g_{\omega NN}{\displaystyle \sum _{\alpha j}}{\overline{N}}_{\alpha j}{\gamma }^0\omega N_{\alpha j}-g_{\rho NN}{\displaystyle \sum _{\alpha j}}{\overline{N}}_{\alpha j}{\gamma }^0{\displaystyle \frac{{\tau }_3}{2}}\rho N_{\alpha j}\hfill \\ & +{\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }^2+{\displaystyle \frac{1}{2}}{m}_{\rho }^2{\rho }^2+{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2{\omega }^2{\rho }^2.\hfill \end{array}$$

(76)

with

$$\begin{array}{cc}{g}_{\omega NN}& =\left(a_{VNN}+a_{0NN}\right)g_{\omega },\hfill \end{array}$$

(77)

$$\begin{array}{cc}{g}_{\rho NN}& =a_{VNN}{g}_{\rho }.\hfill \end{array}$$

(78)

It is crucial to note that ${\lambda }_{\omega \rho }\ge 0$ is required to realize $\omega =\rho =0$ in vacuum. To show it, we start from the vector meson potential in vacuum given as

$$\begin{array}{c}{V}_V\equiv -{\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }^2-{\displaystyle \frac{1}{2}}{m}_{\rho }^2{\rho }^2-{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2{\omega }^2{\rho }^2.\end{array}$$

(79)

The vacuum expectation values of the vector meson fields are chosen at the stationary point of $V_V$ with minimal energy. The stationary conditions are given by

$$\begin{array}{c}{\displaystyle \frac{\partial V_V}{\partial \omega }}=\omega [m_{\omega }^2+2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2{\rho }^2]=0,\\ {\displaystyle \frac{\partial V_V}{\partial \rho }}=\rho [m_{\rho }^2+2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2{\omega }^2]=0,\end{array}$$

(80)

leading to two distinct stationary points,

$$\begin{array}{c}({\omega }^2,{\rho }^2)=(0,0),(-{\displaystyle \frac{m_{\rho }^2}{2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2}},-{\displaystyle \frac{m_{\omega }^2}{2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2}}).\end{array}$$

(81)

Then, the values of potential at stationary points are

$$V_V=\left\{\begin{array}{cc}0,\hfill & \mathrm{for}({\omega }^2,{\rho }^2)=(0,0),\hfill \\ {\displaystyle \frac{m_{\omega }^2{m}_{\rho }^2}{4{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2}},\hfill & \mathrm{for}({\omega }^2,{\rho }^2)=(-{\displaystyle \frac{m_{\rho }^2}{2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2}},-{\displaystyle \frac{m_{\omega }^2}{2{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2}}).\hfill \end{array}\right.$$

(82)

In the present model, vanishing vacuum expectation values of the vector meson fields are required at zero density due to the Lorentz-invariance of the vacuum. Consequently, we must require ${\lambda }_{\omega \rho }\ge 0$ here, such that $({\omega }^2,{\rho }^2)=(0,0)$ minimizes the effective potential $V_V$ in vacuum.

Then, the thermodynamic potential for the nucleons is written as

$$\begin{array}{cc} & {\mathrm{\Omega }}_N=-2{\displaystyle \sum _{\alpha =\pm ,j=\pm }}{\int }^{k_f}{\displaystyle \frac{d^{3}p}{{\left(2\pi \right)}^3}}\left[{\mu }_j^{*}-{\omega }_{\alpha j}\right],\hfill \end{array}$$

(83)

where $\alpha =\pm$ denotes the parity and $j=\pm$ the iso-spin of nucleons ($j=+$ for proton and $j=-$ for neutron). ${\mu }_j^{*}$ is the effective chemical potential given by

$$\begin{array}{c}{\mu }_j^{*}\equiv ({\mu }_B-g_{\omega NN}\omega )+{\displaystyle \frac{j}{2}}({\mu }_I-g_{\rho NN}\rho ),\end{array}$$

(84)

and ${\omega }_{\alpha j}$ is the energy of the nucleon defined as ${\omega }_{\alpha j}=\sqrt{{\left(\overrightarrow{p}\right)}^2+{\left(m_{\alpha j}^{*}\right)}^2}$, where $\overrightarrow{p}$ and $m_{\alpha j}^{*}$ are the momentum and the effective mass of the nucleon. The effective mass $m_{\alpha j}^{*}$ is given by

$$\begin{array}{c}{m}_{\alpha j}^{*}={\displaystyle \frac{1}{2}}\left[\sqrt{{(g_1+g_2)}^2{(\sigma -ja)}^2+4m_0^2}+\alpha (g_1-g_2)(\sigma -ja)\right].\end{array}$$

(85)

We note that the masses of proton and neutron become non-degenerate in the asymmetric matter due to the non-zero mean field of $a_0\left(980\right)$.

The entire thermodynamic potential for hadronic matter is expressed as

$$\begin{array}{cc} & {\mathrm{\Omega }}_H={\mathrm{\Omega }}_N\hfill \\ & -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{\sigma }^2-{\displaystyle \frac{{\overline{\mu }}_a^2}{2}}{a}^2+{\displaystyle \frac{{\lambda }_4}{4}}({\sigma }^4+a^4)+{\displaystyle \frac{{\gamma }_4}{2}}{\sigma }^2{a}^2\hfill \\ & -{\displaystyle \frac{{\lambda }_6}{6}}({\sigma }^6+15{\sigma }^2{a}^4+15{\sigma }^4{a}^2+a^6)+{\lambda }_6^{\prime }({\sigma }^2{a}^4+{\sigma }^4{a}^2)\hfill \\ & -m_{\pi }^2{f}_{\pi }\sigma -{\displaystyle \frac{1}{2}}{m}_{\omega }^2{\omega }^2-{\displaystyle \frac{1}{2}}{m}_{\rho }^2{\rho }^2-{\lambda }_{\omega \rho }{g}_{\omega NN}^2{g}_{\rho NN}^2{\omega }^2{\rho }^2\hfill \\ & -{\mathrm{\Omega }}_0,\hfill \end{array}$$

(86)

where we subtracted the potential at the vacuum

$$\begin{array}{c}{\mathrm{\Omega }}_0\equiv -{\displaystyle \frac{{\overline{\mu }}_{\sigma }^2}{2}}{f}_{\pi }^2+{\displaystyle \frac{{\lambda }_4}{4}}{f}_{\pi }^4-{\displaystyle \frac{{\lambda }_6}{6}}{f}_{\pi }^6-m_{\pi }^2{f}_{\pi }^2.\end{array}$$

(87)

4.2. Determination of Model Parameters

In the present model, there are seven parameters in the meson potential, ${\mu }_{\sigma }^2$, ${\mu }_a^2={\mu }_{\sigma }^2-K$, ${\lambda }_4$, ${\gamma }_4$, ${\lambda }_6$, ${\lambda }_6^{\prime }$, and ${\lambda }_{\omega \rho }$, in addition to the meson masses $m_{\pi }$, $m_{\omega }$, $m_{\rho }$, and the pion decay constant $f_{\pi }$. We also have four parameters, $g_1$, $g_2$, $g_{\omega NN}$, and $g_{\rho NN}$ for the couplings of mesons to baryons. As in Section 2, we use the physical values of three masses $m_{\pi }$, $m_{\omega }$, and $m_{\rho }$, together with the pion decay constant $f_{\pi }$ as listed in Table 2. In addition, we use the masses of $a_0\left(980\right)$ and $\eta$ mesons listed in Table 10 as inputs. Similarly to Section 2, we determine the values of ${\mu }_{\sigma }^2$, ${\lambda }_4$, ${\lambda }_6$ and $g_{\omega NN}$ from the saturation properties: the saturation density $n_0$, the binding energy $B_0$, and the incompressibility $K_0$ summarized in Table 1, combined with the vacuum condition given in Equation (52). $g_1$ and $g_2$ are determined from the vacuum mass of nucleon $N\left(939\right)$ and its parity partner $N^{*}\left(1535\right)$. The resultant values are same as those shown in Table 3. Then, the parameters K and ${\gamma }_4$ are determined from the meson masses and the other parameters as

$$\begin{array}{cc}K=& m_{\eta }^2-m_{\pi }^2,\hfill \\ {\gamma }_4=& {\displaystyle \frac{m_{a_0}^2+(5{\lambda }_6-2{\lambda }_6^{\prime })f_{\pi }^4+{\overline{\mu }}_a^2}{f_{\pi }^2}},\hfill \end{array}$$

(88)

where $m_{\eta }$ and $m_{a_0}$ are the masses of $\eta$ and $a_0$.

Table 10. Values of masses of $a_0\left(980\right)$ and $\eta$ mesons in unit of MeV.

${\mathit{m}}_{{\mathit{a}}_0}$	${\mathit{m}}_{\mathit{\eta }}$
980	550

As we stated in the previous subsection, we take ${\lambda }_6^{\prime }=0$ for a while. The resultant values of ${\overline{\mu }}_a^2$ and ${\gamma }_4$ corresponding to a given $m_0$ are presented in Table 11.

Table 11. Values of parameters ${\overline{\mu }}_a^2$ and ${\gamma }_4$ for several choices of $m_0$ and $K_0$ with ${\lambda }_6^{\prime }=0$.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	${\overline{\mu }}_a^2/f_{\pi }^2$	−9.40	−11.79	−19.43	−30.27
	${\gamma }_4$	185.59	177.94	144.51	90.62
$K_0=240$ MeV	${\overline{\mu }}_a^2/f_{\pi }^2$	−10.95	−13.93	−21.08	−31.24
	${\gamma }_4$	176.81	164.81	133.38	83.05

To demonstrate the effect of $a_0$(980) on the matter, we consider both the $a_0$ model with vector-meson mixing (${\lambda }_{\omega \rho }\ne 0$) and that without the mixing (${\lambda }_{\omega \rho }=0$). In the $a_0$ model without vector meson mixing, parameter $g_{\rho NN}$ is determined from the symmetry energy at the saturation density $S_0$, while the slope parameter $L_0$ is computed from the model as an output.

Table 12 shows the values of $g_{\rho NN}$ together with $L_0$. We note that the slope parameters are much larger than the recently accepted value $L_0=57.7\pm 19$ MeV [72]. We also note that the effect of $K_0$ on the value of $L_0$ is larger when we include the $a_0$ meson into the model. The value of $L_0$ with different $S_0$ is shown in Table 13.

Table 12. The values of $g_{\rho NN}$ and slope parameter $L_0$ in the $a_0$ model without vector meson mixing, for several choices of $m_0$ and $K_0$ with ${\lambda }_6^{\prime }=0$. $S_0=31$ MeV.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	$g_{\rho NN}$	12.52	11.20	9.94	8.90
	$L_0$ [MeV]	120.14	105.21	97.05	87.65
$K_0=240$ MeV	$g_{\rho NN}$	12.47	11.16	9.90	8.86
	$L_0$ [MeV]	126.58	108.78	98.67	87.75
$K_0=260$ MeV	$g_{\rho NN}$	12.43	11.13	9.86	8.83
	$L_0$ [MeV]	131.19	111.45	99.86	87.75

Table 13. Values of $g_{\rho NN}$ and slope parameter $L_0$ in the $a_0$ model without vector meson mixing, for several choices of $m_0$ and $S_0$ with ${\lambda }_6^{\prime }=0$. $K_0=215$ MeV.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$S_0=24$ MeV	$g_{\rho NN}$	11.37	9.9	8.45	7.2
	$L_0$ [MeV]	99.14	84.21	76.05	66.65
$S_0=31$ MeV	$g_{\rho NN}$	12.52	11.2	9.94	8.9
	$L_0$ [MeV]	120.14	105.21	97.05	87.65
$S_0=36$ MeV	$g_{\rho NN}$	13.28	12.04	10.88	9.94
	$L_0$ [MeV]	135.14	120.21	112.05	102.65

For making the slope parameter consistent with $L_0=57.7\pm 19$ MeV, we include the vector meson mixing interaction, which allows us to reduce $L_0$. In the $a_0$ model with vector meson mixing, the parameters $g_{\rho NN}$ and ${\lambda }_{\omega \rho }$ are determined by fitting them to the symmetry energy $S_0$, as well as the slope parameter $L_0$. To reproduce the matter for recent accepted value of $L_0=57.7\pm 19$ MeV, we compute our results for $L_0=40$–80 MeV. The resultant parameters are shown in Table 14 and Table 15. Here, we only show the results for ${\lambda }_6^{\prime }=0$ because the values of the parameters for ${\lambda }_6^{\prime }=\pm {\lambda }_6$ are similar to the values listed in Table 14 and Table 15.

Table 14. Values of $g_{\rho NN}$ for several choices of $m_0$, $L_0$, with ${\lambda }_6^{\prime }$ = 0. Vector meson mixing is considered.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	$L_0=40$ MeV	15.34	13.78	12.59	11.42
	$L_0=50$ MeV	14.88	13.27	11.97	10.72
	$L_0=60$ MeV	14.46	12.81	11.44	10.13
	$L_0=70$ MeV	14.08	12.39	10.97	9.63
	$L_0=80$ MeV	13.72	12.02	10.55	9.19
$K_0=240$ MeV	$L_0=40$ MeV	15.63	13.96	12.68	11.41
	$L_0=50$ MeV	15.14	13.42	12.04	10.7
	$L_0=60$ MeV	14.69	12.94	11.49	10.11
	$L_0=70$ MeV	14.28	12.51	11.0	9.6
	$L_0=80$ MeV	13.9	12.11	10.58	9.16

Table 15. Values of ${\lambda }_{\omega \rho }$ for several choices of $m_0$, $L_0$, with ${\lambda }_6^{\prime }$ = 0. Vector meson mixing is considered.

	${\mathit{m}}_0$ [MeV]	600	700	800	900
$K_0=215$ MeV	$L_0=40$ MeV	0.0254	0.0818	0.3191	2.8164
	$L_0=50$ MeV	0.0222	0.0693	0.2632	2.2253
	$L_0=60$ MeV	0.0191	0.0567	0.2072	1.6342
	$L_0=70$ MeV	0.0159	0.0442	0.1513	1.0431
	$L_0=80$ MeV	0.0127	0.0316	0.0954	0.4519
$K_0=240$ MeV	$L_0=40$ MeV	0.0252	0.0761	0.2914	2.4593
	$L_0=50$ MeV	0.0223	0.065	0.2418	1.9443
	$L_0=60$ MeV	0.0194	0.054	0.1921	1.4293
	$L_0=70$ MeV	0.0165	0.0429	0.1424	0.9142
	$L_0=80$ MeV	0.0135	0.0318	0.0927	0.3992

4.3. Effect of $a_0\left(980\right)$ to Symmetry Energy in Model without Vector Meson Mixing

The $a_0$(980) meson should affect the properties of the matter via the asymmetry of the matter. Therefore, we expect that symmetry energy is essential to study the effect of $a_0$(980) meson to the matter. In the following, we study how the inclusion of the $a_0\left(980\right)$ meson affects the symmetry energy.

In the present model, the symmetry energy S($n_B$) for a given density $n_B$ is expressed as

$$\begin{array}{cc}S\left(n_B\right)& ={\displaystyle \frac{n_B}{8}}{\displaystyle \frac{\partial {\mu }_I}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}\hfill \\ & ={\displaystyle \frac{{\left(k_{+}^{*}\right)}^2}{6{\mu }_{+}^{*}}}+{\displaystyle \frac{n_B}{2}}{\displaystyle \frac{{(g_{\rho NN}/2)}^2}{m_{\rho }^2}}-{\displaystyle \frac{n_B}{4}}{\displaystyle \frac{m_{+}^{*}}{{\mu }_{+}^{*}}}{\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}},\hfill \end{array}$$

(89)

where ${\mu }_{+}^{*}\equiv {\mu }_p^{*}{|}_{\begin{array}{c}{n}_I=0\end{array}}={\mu }_n^{*}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ is the effective chemical potential for $N\left(939\right)$ in the symmetric matter, $k_{+}^{*}\equiv \sqrt{{\left({\mu }_p^{*}\right)}^2-{\left(m_{+p}^{*}\right)}^2}{|}_{\begin{array}{c}{n}_I=0\end{array}}=\sqrt{{\left({\mu }_n^{*}\right)}^2-{\left(m_{+n}^{*}\right)}^2}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ the corresponding Fermi momentum, $m_{+}^{*}\equiv m_{+p}^{*}{|}_{\begin{array}{c}{n}_I=0\end{array}}=m_{+n}^{*}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ the mass. In Equation (89), there are three contributions to the symmetry energy: the nucleon contribution, the $\rho$ meson contribution, and the $a_0$ meson contribution.

The nucleon contribution $S_N\left(n_B\right)$ is given by

$$\begin{array}{c}{S}_N\left(n_B\right)\equiv {\displaystyle \frac{{\left(k_{+}^{*}\right)}^2}{6{\mu }_{+}^{*}}},\end{array}$$

(90)

which arises from the effective kinetic contribution of nucleons. Figure 4 shows $S_N\left(n_B\right)$ for $m_0=600$–900 MeV with $K_0=215$, 240 MeV. It is observed that $S_N\left(n_B\right)$ increases with density, as the effective kinetic energy of nucleons rises with density. Additionally, it is noted that $S_N\left(n_B\right)$ is larger for smaller $m_0$ due to the stiffening of matter for smaller $m_0$. It can be also seen that $S_N\left(n_B\right)$ is larger for larger $K_0$. However, the change in $K_0$ has little effect on $S_N\left(n_B\right)$. We note that, since $S_N\left(n_B\right)$ arises from the effective kinetic contribution of a nucleon, $S_N\left(n_B\right)$ is not affected by the inclusion of $a_0$ meson.

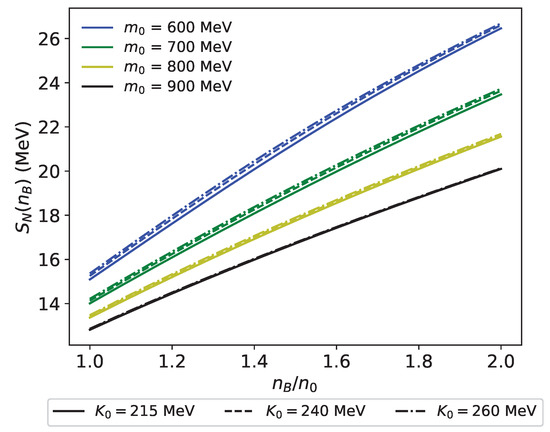
Figure 4. Nucleon contribution $S_N\left(n_B\right)$ for $m_0=600$–900 MeV. Solid, dashed, and dash-dot curves represent $S_N\left(n_B\right)$ with $K_0=215,240,260$ MeV, respectively.

The contribution from the $a_0\left(980\right)$ meson is expressed as

$$\begin{array}{cc}{S}_{a_0}\left(n_B\right)& \equiv -{\displaystyle \frac{n_B}{4}}{\displaystyle \frac{m_{+}^{*}}{{\mu }_{+}^{*}}}{\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}.\hfill \end{array}$$

(91)

Figure 5 shows $S_{a_0}$ computed in the present model. We note that $S_{a_0}$ is negative and, thus, reduces the total symmetry energy $S\left(n_B\right)$. This is because ${\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ is always positive, as shown in Figure 6. Intuitively, this can be understood from the dependence of $m_{+n}^{*}$ on the mean field a given in Equation (85). If we vary the mean field a, $m_{+n}^{*}$ will also change correspondingly. However, the effective chemical potential ${\mu }_n^{*}$ does not depend on the mean field a directly, as we can see from Equation (84). This change in the effective mass $m_{+n}^{*}$ due to the mean field a leads to a change in the momentum of the neutron $k_{+n}=\sqrt{{\left({\mu }_n^{*}\right)}^2-{\left(m_{+n}^{*}\right)}^2}$. When $n_I=(n_p-n_n)/2$ is increased for a fixed $n_B$, the density of the neutron $n_n$ and, thus, the momentum $k_{+n}$ is decreased. Accordingly, the effective mass of the neutron is increasing as $n_I$ increase, causing a positive ${\displaystyle \frac{\partial m_{+n}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}$. Therefore, the $a_0$(980) meson contribution $S_{a_0}\left(n_B\right)$ reduces the total symmetry energy $S\left(n_B\right)$ in the present model. We also find that the $a_0$(980) effect on the symmetry energy is stronger for smaller $m_0$. This is because the coupling constants of $a_0\left(980\right)$ meson to the nucleon, $g_1$ and $g_2$, are larger for smaller $m_0$, as shown in Table 3. As a result, the symmetry energy becomes larger by $a_0\left(980\right)$ meson more when $m_0$ is smaller. In addition, we note that the $a_0\left(980\right)$ effect on the symmetry energy is decreasing as the density increases since ${\displaystyle \frac{\partial m_{+n}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ decreases. We also observe that $K_0$ has a larger effect on $S_{a_0}$ due to the effect of $K_0$ on the coupling constants of $a_0$ meson, as indicated in Table 3 and Table 11. Since the effect of the $a_0$ meson becomes smaller as the density increases, $S_{a_0}$ becomes less negative and spreads at higher densities. We also note that the difference of $S_{a_0}$ with different $K_0$ becomes smaller as $m_0$ increase due to a weaker $a_0$ meson effect. Notice that this contribution does not exist in models without the $a_0$ meson.

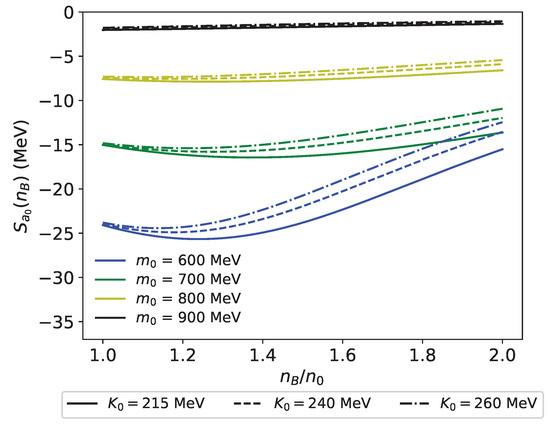
Figure 5. $a_0$ meson contribution to the symmetry energy $S_{a_0}\left(n_B\right)$ for $m_0=600$–900 MeV. Solid, dashed, and dash-dot curves represent $S_{a_0}\left(n_B\right)$ with $K_0=215,240,260$ MeV, respectively.

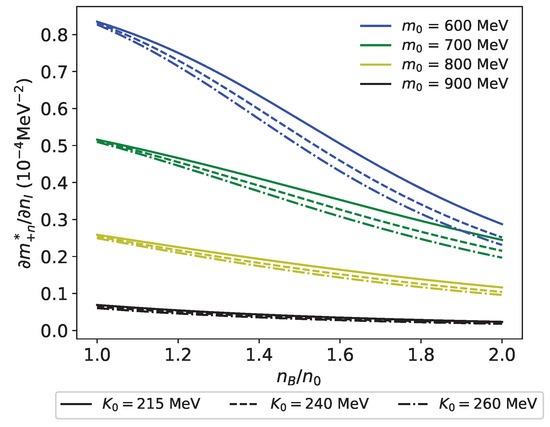
Figure 6. ${\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ for $m_0=600$–900 MeV. Solid, dashed, and dash-dot curves represent ${\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}$ with $K_0=215,240,260$ MeV, respectively.

The $\rho$ meson contribution is given by

$$\begin{array}{c}{S}_{\rho }\left(n_B\right)\equiv {\displaystyle \frac{n_B}{2}}{\displaystyle \frac{{(g_{\rho NN}/2)}^2}{m_{\rho }^2}}.\end{array}$$

(92)

This shows that the contribution is always positive and, thus, provides repulsive force to the matter. Figure 7 shows the behavior of $S_{\rho }\left(n_B\right)$ for $m_0=600$–900 MeV with $K_0=215$, 240 MeV. It is noteworthy that $S_{\rho }\left(n_B\right)$ is directly proportional to the baryon density $n_B$, rendering it an increasing function with density. We also note that $S_{\rho }\left(n_B\right)$ exhibits larger values for heavier $m_0$. This is understood as follows: at the saturation density, the symmetry energy $S_0$ is fixed to be 31 MeV. Since the total symmetry energy is given by Equation (89), a larger $m_0$ corresponds to a smaller $S_N\left(n_0\right)$ and, consequently, a larger $S_{\rho }\left(n_0\right)$. This larger $S_{\rho }\left(n_0\right)$ yields a larger coupling constant $g_{\rho NN}$ for larger $m_0$. As a result, $S_{\rho }\left(n_B\right)$ is larger for larger $m_0$ at density higher than the saturation density. Figure 7 also shows that $K_0$ has little effect on $S_{\rho }$. We note that $S_N$ and $S_{a_0}$ is determined from $K_0$. Then, we obtain $S_{\rho }\left(n_B\right)$ from $S_0$, $S_N$ and $S_{a_0}$. Since $S_N$ and $S_{a_0}$ are larger as $K_0$ increases, these two contributions compensate with $S_{\rho }$ to maintain $S_0=31$ MeV at $n_B=n_0$. Thus, $S_{\rho }$ is smaller as $K_0$ increases, which is opposite to $S_N$ and $S_{a_0}$. We also observe that the value of $S_{\rho }$ for the present model is very large compared with the value of model without $a_0$ meson. This is because the $\rho$ meson coupling is much larger in the present model due to the attractive interaction of $a_0$(980) when comparing to the model without $a_0$ meson.

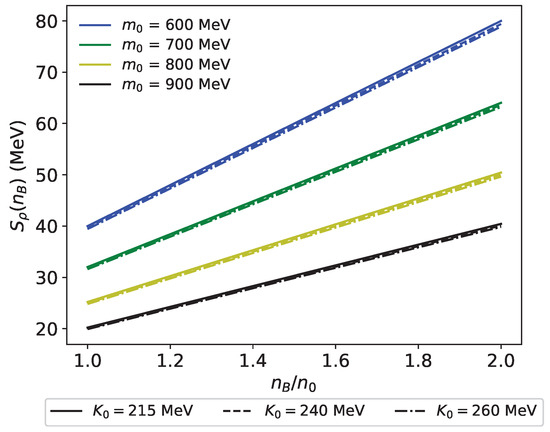
Figure 7. $\rho$ meson contribution $S_{\rho }\left(n_B\right)$ in $a_0$ model for $m_0=600$–900 MeV and ${\lambda }_6^{\prime }=0$. Solid, dashed, and dash-dot curves represent $S_{\rho }\left(n_B\right)$ with $K_0=215,240,260$ MeV, respectively.

Based on the above properties of three contributions, the symmetry energy can be understood as a result of the competition between the repulsive $\rho$ meson interaction and the attractive $a_0$(980) interaction, in addition to the kinetic contribution from the nucleons. On the other hand, in the model without $a_0$ meson, only repulsive contributions exist. Since the symmetry energy at the saturation density is fixed as $S_0=31$ MeV in the both models with and without $a_0\left(980\right)$ meson, the $\rho$ meson coupling $g_{\rho NN}$ is strengthened by the existence of the attractive $a_0\left(980\right)$ contribution in the model with $a_0$ comparing to the model without $a_0$. Actually, it is clear from Table 3 and Table 12 that $g_{\rho NN}$ is larger in the $a_0$ model than in the no-$a_0$ model for a fixed $m_0$. Figure 8 shows the symmetry energy for $m_0=600$–900 MeV and $K_0=215$ MeV, with the results of the model with $a_0$ meson and without $a_0$ meson are shown in solid curve and dashed curve, respectively. We observe that the symmetry energy is indeed stiffened by the existence of $a_0$(980). Furthermore, the difference of the symmetry energy between the models is larger for smaller $m_0$ because the coupling to the $a_0$ meson is stronger, as indicated by Table 3. At $n_B=2n_0$, the symmetry energy $S\left(2n_0\right)$ is enlarged by $a_0\left(980\right)$ meson as large as ∼60% or more in the present model depending on the choice of input parameters.

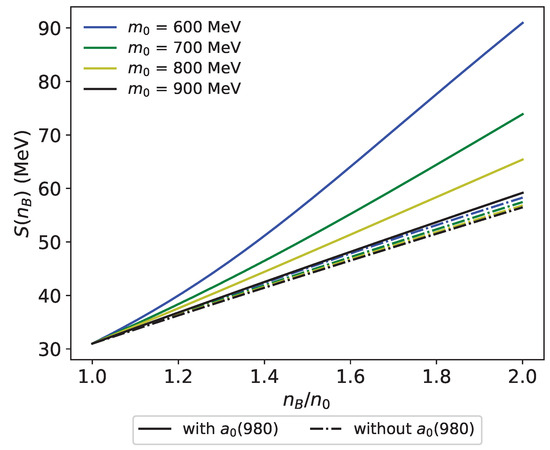
Figure 8. Symmetry energy $S\left(n_B\right)$ for $m_0=600$–900 MeV, $K_0=215$ MeV, and ${\lambda }_6^{\prime }=0$. Solid curves represent the $S\left(n_B\right)$ of the model, including $a_0\left(980\right)$ with ${\lambda }_6^{\prime }$ = 0, while the dash-dot curves show the results of the model without $a_0\left(980\right)$.

In Figure 9, we compare the total symmetry energy with different choices of $K_0$, and the results show that the symmetry energy is not sensitive to the value of $K_0$ because the effect of $K_0$ to the total symmetry energy is canceled by the compensation between $S_N$, $S_{a_0}$, and $S_{\rho }$.

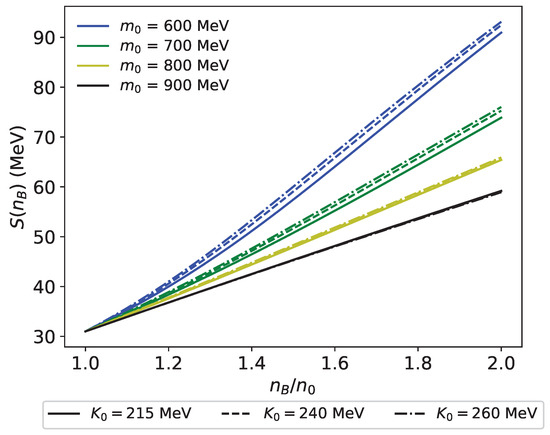
Figure 9. Symmetry energy $S\left(n_B\right)$ for $m_0=600$–900 MeV, ${\lambda }_6^{\prime }=0$, with different choices of $K_0$ compared. Solid, dashed, and dash-dot curves represent $S\left(n_B\right)$ with $K_0=215,240,260$ MeV, respectively.

The effect of $S_0$ to the total symmetry energy $S\left(n_B\right)$ is also studied. Figure 10 shows the difference of the symmetry energy $S\left(n_B\right)-S_0$. We note that $S_0$ has large impact to the symmetry energy, since $S_0$ affects the determination of $g_{\rho NN}$. As expected, larger $S_0$ results in larger $S\left(n_B\right)$.

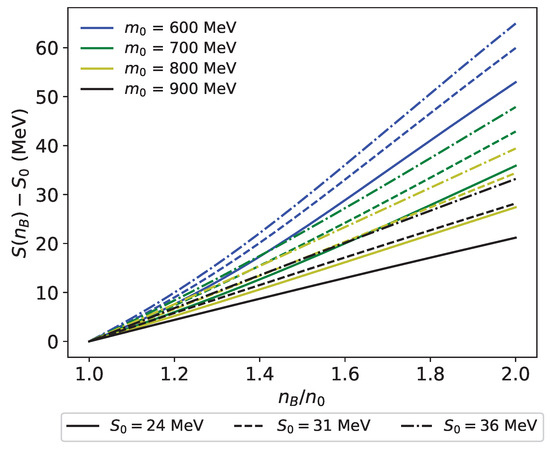
Figure 10. Difference of the symmetry energy $S\left(n_B\right)-S_0$ in $a_0$ model for $m_0=600$–900 MeV and ${\lambda }_6^{\prime }=0$. $K_0=215$ MeV. Solid, dashed, and dash-dot curves represent $S_{\rho }\left(n_B\right)$ with $S_0=24,31, 36$ MeV, respectively.

In addition, we investigate the effect of higher-order terms in the large $N_c$ expansion for the six-point interaction on the symmetry energy by taking ${\lambda }_6^{\prime }=\pm {\lambda }_6$. The results of the symmetry energies with different values of ${\lambda }_6^{\prime }$ are shown in Figure 11. We can see that the difference between the symmetry energies for models with the same $m_0$ is small, which indicates that the effect of ${\lambda }_6^{\prime }$ on the symmetry energy is small. Notice also that the difference becomes smaller for larger $m_0$, due to a smaller $a_0$(980) effect.

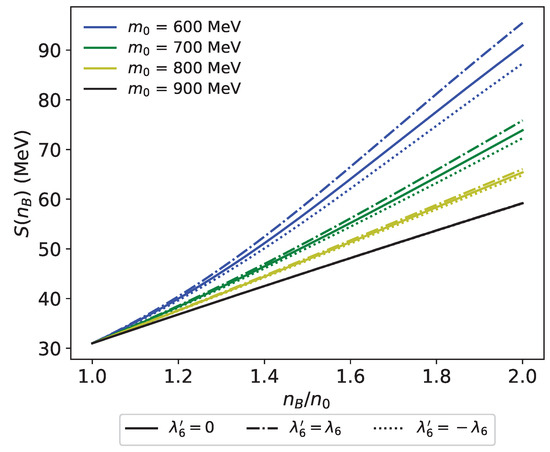
Figure 11. Symmetry energy $S\left(n_B\right)$ for $m_0=600$–900 MeV and $K_0=215$ MeV, with the effect of ${\lambda }_6^{\prime }$ compared. Solid, dash-dot, and dotted curves show the $S\left(n_B\right)$ with ${\lambda }_6^{\prime }=0,{\lambda }_6$, and $-{\lambda }_6$, respectively.

4.4. Symmetry Energy of $a_0$ Model with Vector Meson Mixing

As we see from the previous sections, PDM predicts a rather large slope parameter $L_0$, which does not seem compatible with the recently accepted value of $L_0=57.7\pm 19$ MeV. In particular, the model with $a_0$ meson predicts a very large $L_0$, as well as the symmetry energy at density $n_B>n_0$. In order to soften the matter to reproduce the accepted value of $L_0$, we include the $\omega$-$\rho$ vector mixing term to reduce the stiffness of the matter in our model. In this section, we study the symmetry energy with vector meson mixing interaction.

In the current model, the symmetry energy $S\left(n_B\right)$ for a given density $n_B$ is expressed as follows:

$$\begin{array}{cc}S\left(n_B\right)& ={\displaystyle \frac{n_B}{8}}{\displaystyle \frac{\partial {\mu }_I}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}\hfill \\ & ={\displaystyle \frac{{\left(k_{+}^{*}\right)}^2}{6{\mu }_{+}^{*}}}+{\displaystyle \frac{n_B}{2}}{\displaystyle \frac{{(g_{\rho NN}/2)}^2}{m_{\rho }^2+\left(2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4\right)}}-{\displaystyle \frac{n_B}{4}}{\displaystyle \frac{m_{+}^{*}}{{\mu }_{+}^{*}}}{\displaystyle \frac{\partial m_{+n}^{*}}{\partial n_I}}{|}_{\begin{array}{c}{n}_I=0\end{array}}.\hfill \end{array}$$

(93)

Similarly to Equation (89), the symmetry energy is divided into sum of three contributions: the nucleon contribution $S_N\left(n_B\right)$, $\rho$ meson contribution $S_{\rho }\left(n_B\right)$, and $a_0$ meson contribution $S_{a_0}\left(n_B\right)$. Notably, the nucleon contribution and $a_0$ meson contribution are unaffected by the vector meson mixing, since their related parameters are determined from symmetric matter properties. Therefore, the results of $S_N\left(n_B\right)$ and $S_{a_0}\left(n_B\right)$ are the same as given in Figure 4 and Figure 5.

On the other hand, the $\rho$ meson contribution receives a correction from the vector meson mixing interaction as

$$\begin{array}{c}{S}_{\rho }\left(n_B\right)\equiv {\displaystyle \frac{n_B}{2}}\left[{\displaystyle \frac{{(g_{\rho NN}/2)}^2}{m_{\rho }^2+(2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4)}}\right],\end{array}$$

(94)

where the $\rho$ meson appears to have an effective mass ${\left(m_{\rho }^{*}\right)}^2=m_{\rho }^2+(2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4)$ exhibiting density-dependence. We note that the $\omega$ meson influences the symmetry energy through $2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4$ in the denominator. Given that ${\lambda }_{\omega \rho }>0$, as shown in Section 4.1, the $\omega$-$\rho$ mixing term always reduces the symmetry energy. The density dependence of $S_{\rho }$ is illustrated in Figure 12. It is observed that $S_{\rho }$ increases with rising $n_B$ in the low-density region, but decreases in the high-density region. This is understood as follows: in the low-density region where $m_{\rho }^2\gg 2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4$, the density dependence of $S_{\rho }\left(n_B\right)$ is primarily determined by the pre-factor $n_B$. In the high density region, on the other hand, the denominator is dominated by $2{\lambda }_{\omega \rho }{g}_{\omega NN}^4{g}_{\rho NN}^2{n}_B^2/m_{\omega }^4$, which leads to $S_{\rho }\left(n_B\right)\propto 1/n_B$. As a result, the behavior of $S_{\rho }$ smoothly transforms from $\sim n_B\to \sim 1/n_B$. We also observe that the value of $K_0$ has larger influence to $S_{\rho }\left(n_B\right)$ due to the vector meson mixing. $S_{\rho }\left(n_B\right)$ receives a extra correction from $g_{\omega NN}$ coming from the vector meson mixing as we read from Equation (94). Since the repulsive $g_{\omega NN}$ coupling increase as $K_0$ becomes larger, $S_{\rho }\sim 1/g_{\omega NN}^4$ is smaller with larger $K_0$ and further spread at higher densities.

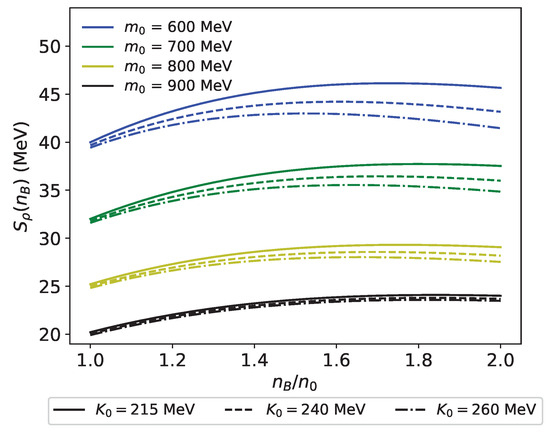
Figure 12. $\rho$ meson contribution $S_{\rho }\left(n_B\right)$ in $a_0$ model for $m_0=600$–900 MeV, ${\lambda }_6^{\prime }=0$, and $L_0=60$ MeV. Solid, dashed, and dash-dot curves represent $S_{\rho }\left(n_B\right)$ with $K_0=215,240,260$ MeV, respectively.

Figure 13 shows the total symmetry energy $S\left(n_B\right)$ for $m_0=600$–900 MeV and $L_0=60$ MeV. For comparison, we also show the results of the no-$a_0$ model with vector meson mixing by dashed curves, as retrieved from Ref. [66]. We note that when the vector meson mixing is included, the slope of the symmetry energy is reduced in the high density region. We also observe that, in most cases, the symmetry energy is stiffened by the existence of $a_0$(980), and the difference of the symmetry energy between two models is larger for smaller $m_0$. In the case of large $m_0$, such as $m_0=900$ MeV where the $a_0$(980) meson effect is small, the softening effect of ${\lambda }_{\omega \rho }$ term overrides the stiffening effect from the $a_0$(980) meson. As a result, the symmetry energy $S\left(n_B\right)$ is reduced even after the inclusion of $a_0$ meson. A similar reduction in the symmetry energy in the intermediate density region was also reported in Ref. [56], which includes both the scalar meson mixing and the vector meson mixing interactions in an RMF model with the presence of isovector-scalar meson.

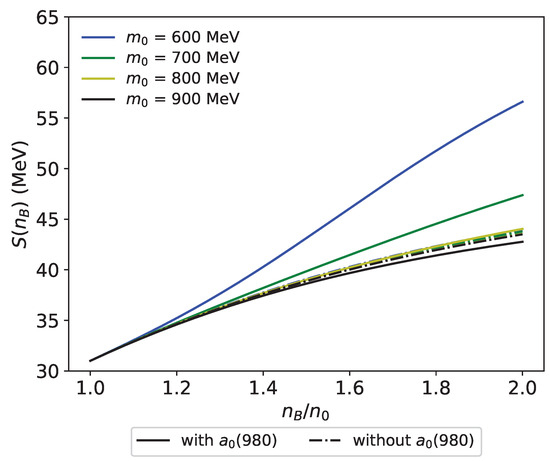
Figure 13. Symmetry energy $S\left(n_B\right)$ in $a_0$ model with vector meson mixing for $m_0=600$–900 MeV, ${\lambda }_6^{\prime }=0$, $K_0=215$ MeV, and $L_0=60$ MeV. Solid curves represent the $S\left(n_B\right)$ of the model, including $a_0\left(980\right)$ with ${\lambda }_6^{\prime }$ = 0, while the dash-dot curves show the results of the model without $a_0\left(980\right)$.

In Figure 14, we study the $K_0$ dependence of the symmetry energy. Similarly to the models introduced in the previous sections, $K_0$ has very little effect to the symmetry energy. Due to the extra correction of the vector meson mixing to $S_{\rho }$, the effect of $K_0$ is further suppressed due to the compensation of the effect of $K_0$ to $S_N$, $S_{a_0}$, and $S_{\rho }$.

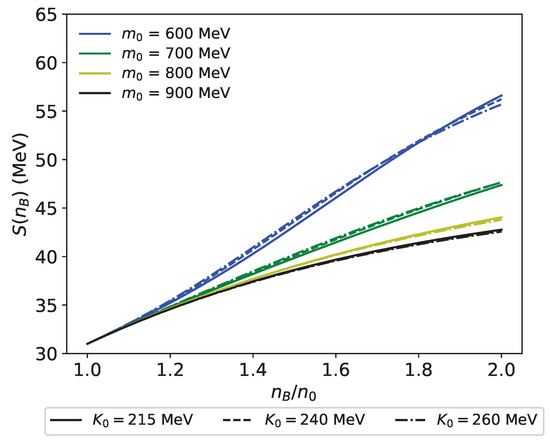
Figure 14. $K_0$ dependence of the symmetry energy $S\left(n_B\right)$ in the $a_0$ model with vector meson mixing for ${\lambda }_6^{\prime }=0$, and $L_0=60$ MeV. Solid, dashed, and dash-dot curves represent $S\left(n_B\right)$ with $K_0=215,240, 260$ MeV, respectively.

In particular, the results of $m_0$ = 700 MeV and $L_0$ = 60 MeV from the present model is compared to the results of other mean field models such as FSU-$\delta$6.7 [56] and B. Liu et al. [63], and density dependent RMF models such as DD-ME$\delta$ [65] in Figure 15. We observe that the vector meson mixing reduces the symmetry energy at high density similarly to the model with density dependent couplings without vector meson mixing interaction. In addition, our $a_0$ model without vector meson mixing predicts a large symmetry energy similarly to the RMF model without vector meson mixing, while the symmetry energy in models with vector meson mixing is effectively reduced.

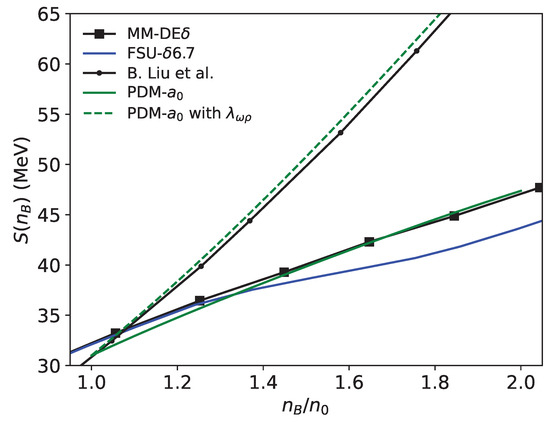
Figure 15. Comparison of the symmetry energy $S\left(n_B\right)$ of the present model with the ones of other models. The results from density dependent RMF model DD-ME$\delta$ [65] and RMF model from B. Liu et al. [63] and FSU-$\delta$6.7 [56] are compared. The results from present model shown in the figure takes the typical value of $m_0=700$ MeV, ${\lambda }_6^{\prime }=0$, $K_0=215$ MeV, and $L_0=60$ MeV for result with vector meson mixing.

Finally, we compare the symmetry energy in the models with different ${\lambda }_6^{\prime }$ in Figure 16. As expected, the effect to symmetry energy is smaller than the effect of $m_0$, because ${\lambda }_6^{\prime }$ interactions are of sub-leading order in large $N_c$ expansion.

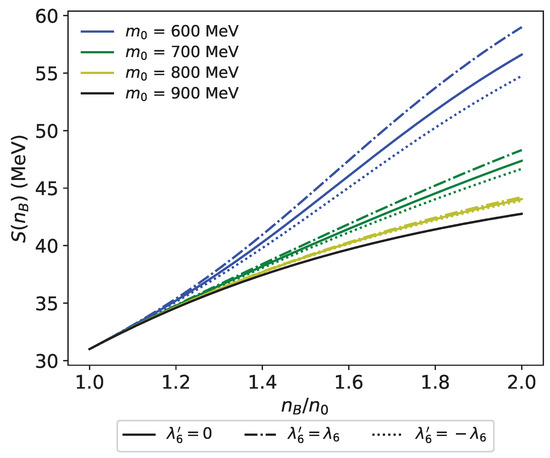
Figure 16. Symmetry energy $S\left(n_B\right)$ for $m_0=600$–900 MeV, $K_0=215$ MeV, and $L_0=60$ MeV with the effect of ${\lambda }_6^{\prime }$ compared. Solid, dash-dot, and dotted curves show the $S\left(n_B\right)$ with ${\lambda }_6^{\prime }=0,\pm {\lambda }_6$.

5. Summary

In this review, we summarized the recent studies on infinite nuclear matter and finite nuclei based on parity doublet models (PDMs). We first introduced a PDM, which is constructed in Ref. [19]. Under the mean field approximation, the nuclear properties such as slope parameter and symmetry energy were computed. In particular, we observed that the slope parameter is relatively larger than the recently accepted value $L_0=57.7\pm 19$ MeV [72]. We also investigated the impact of the value of $K_0$ to the model. We found that the value of $K_0$ has little impact to the matter properties, such as the symmetry energy and slope parameter $L_0$ in the model without $a_0$ meson. We also studied the effect of $S_0$ to the slope parameter $L_0$. We find that the value of $S_0$ will affect the value of $L_0$ significantly.

We then considered the properties of some stable nuclei in the mean field approximation to pin down the value of the chiral invariant mass preferred by the nuclear binding energies and charge radii. We found that our results are closest to the experiments when we take $m_0=700$ MeV. We also calculated the neutron and proton masses in a nucleus and observed, as expected, that the neutron–proton mass difference becomes larger in an isospin asymmetric nucleus.

Then, we studied the effect of isovector scalar meson $a_0\left(980\right)$ to the matter. The isovector scalar meson provides the attractive force in the isovector channel, and is important in the asymmetric matter. We found that the inclusion of $a_0\left(980\right)$ has a very strong influence on the symmetry energy and slope parameter. We observed that the symmetry energy at densities $n_B>n_0$ is largely enhanced by the existence of $a_0\left(980\right)$. By analyzing the different contributions to the symmetry energy, we concluded that this enhancement is originated from the strengthening of the $\rho$ meson coupling $g_{\rho NN}$. The $a_0\left(980\right)$ meson generates the attractive force in the isovector channel, which requires the repulsive force from $\rho$ meson to be larger for reproducing the saturation property. As a result, a larger repulsive $\rho$ interaction increases the symmetry energy at densities $n_B>n_0$. However, we also observed that this stiffening of nuclear matter produces a large slope parameter that is much larger than the recently accepted value suggested by other studies. Therefore, we introduced the $\omega$-$\rho$ mixing interaction to reduce the slope parameter in the model. It was found that the symmetry energy at density $n_B>n_0$ is reduced after the inclusion of $\omega$-$\rho$ mixing interaction. Furthermore, we observed that the $\omega$-$\rho$ mixing interaction modifies the density dependence of the symmetry energy at density $n_B>n_0$. We also observed that the value of $K_0$ has relatively large impact on the $a_0$ contribution to symmetry energy $S_{a_0}$ and $L_0$ due to the effect of $K_0$ to the $a_0$ meson. However, similarly to the case of model without the $a_0$ meson, $K_0$ has limited effect to the total symmetry energy $S\left(n_B\right)$ because of the compensation of the $K_0$ effect between $S_N$, $S_{a_0}$, and $S_{\rho }$. The effect is further suppressed when vector meson mixing effect is included. We also investigated the effect of $S_0$ to the total symmetry energy. As expected, the value of $S_0$ has large impact to the $\rho$ meson coupling $g_{\rho NN}$ and thus the symmetry energy. There are also some microscopic nuclear force models in, e.g., Refs. [77,78,79]. It would be also interesting to compare the result of the present model to the results of these models.

We expect that future experiments on the study of symmetry energy at higher densities will provide further constraints on the chiral invariant mass of the nucleon. We also expect that $a_0\left(980\right)$ will have a significant influence on asymmetric nuclei. It would be interesting to study finite nuclei using the extended PDM including the $a_0\left(980\right)$ meson, which may give new information to constraints on the chiral invariant mass of the nucleon and the behavior of nucleon mass in dense matter. We leave this as future project.