A Channel-Sensing-Based Multipath Multihop Cooperative Transmission Mechanism for UE Aggregation in Asymmetric IoE Scenarios
Abstract
1. Introduction
1.1. Related Works
1.2. Main Contributions
- A new control signaling field is introduced to inform the cooperative transmission strategy of UE and CN through a unicast or groupcast method. The proposed control signaling can reduce the resource consumption of the next-generation node base station (gNB) sending information and better control the status of UE and CN.
- The AOS algorithm is designed to minimize resource consumption through prioritizing neighboring UE of each CN in the cooperative transmission stage. This can optimize the resource consumption of CN to solve the problem of capacity constraints.
- A novel mechanism CSCTM with HARQ for future asymmetric IoE scenarios is proposed in this paper, which determines transmission strategy by channel sensing and allocates optimal RVs for different transmitters. In addition, the CSCTM modifies the signal combination mechanism at the receiving end by employing various combining techniques for data retransmission from different transmitters.
1.3. Organization
2. System Model and Problem Formulation
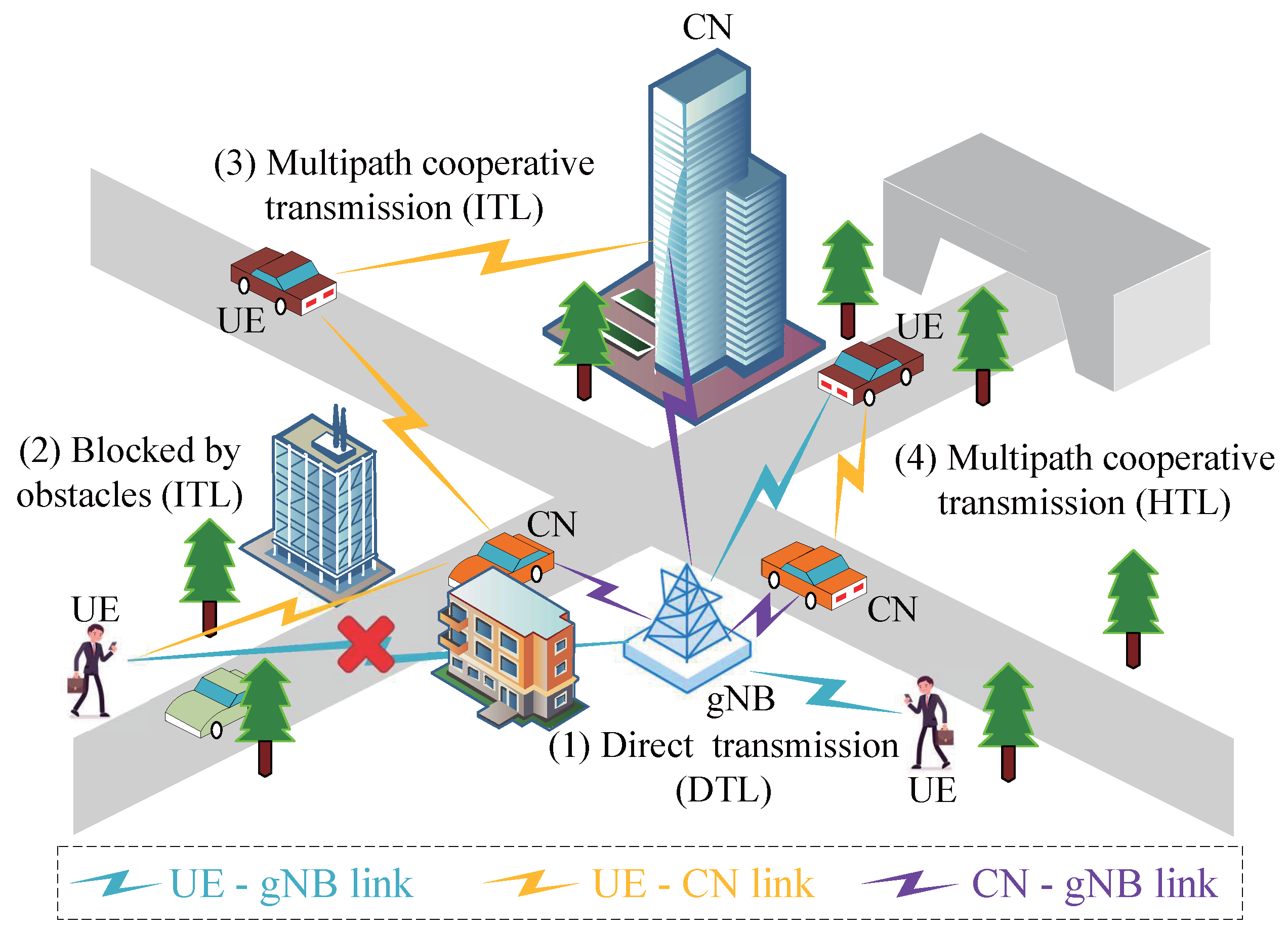
2.1. System Model
- Direct transmission link (DTL): UE transmits data to gNB directly without any assistance. In this case, the channel quality between UE and gNB is good enough to support direct transmission, and UE is located in the coverage range of gNB, resulting in high communication quality characterized by a high SINR between them.
- Indirect transmission link (ITL): UE transmits data to the nearby CN at first, then CN assists UE in transmitting data to gNB after decoding UE information successfully. Moreover, UE will terminate the transmission of information after CN confirms the assistance in transmitting the information. In this situation, the channel quality between UE and gNB is not good enough, which can occur in many scenarios, such as the presence of obstacles or long distances.
- Hybrid transmission link (HTL): The data from UE can be decoded at CN and gNB simultaneously. In general, CN will decode the UE data successfully before gNB, then UE and CN transmit data to gNB jointly. In other words, UE continues transmitting data after CN decoding successfully. At this time, the channel quality between UE and gNB is similar to the channel quality between the nearby CN and gNB.
2.2. Design of Cooperative Transmission Procedure
- Step 1: UE establishes connections with gNB and nearby CNs.
- Step 2: UE informs the gNB when it has packet requests.
- Step 3: gNB determines the transmission strategy (DTL/ITL/HTL) for UE with packet requests by using the CSCTM, based on the channel qualities between the UE, CN, and gNB. The DTL strategy will be employed when the UE is close to the gNB, the ITL strategy will be used when the UE has poorer channel quality, and the HTL strategy will be used otherwise.
- Step 4: UE begins transmitting data to the gNB via the physical channel, such as the physical uplink shared channel (PUSCH) in DTL and HTL strategies, or to the CN in the ITL strategy.
- Step 5: When CN decodes UE data successfully, CN informs gNB that the information of the UE has been decoded successfully.
- Step 6: The AOS and CSCTM algorithms will be executed by CN in the distributed mode, while they will be executed by gNB in the centralized mode. This is the main difference between the distributed mode and the centralized mode. In this situation, CNs communicate with each other through the physical sidelink shared channel (PSSCH) in the distributed mode or gNB sends the relevant instructions to CNs in the centralized mode. The communicated information or relevant instructions involve prioritizing decoded UE using the AOS algorithm and determining different transmission RVs for CNs and UE through CSCTM to achieve maximum decoding efficiency. Due to the limitations in CN-assisted transmission capabilities, not all UE can be assisted immediately after successful decoding by the CN. After that, if a UE still requires further data transmission operations (HTL), the CN will provide the optimal RV for HARQ encoding when the UE retransmits data in the distributed mode. In the centralized mode, the gNB will provide the optimal RV for UE in HTL and for CNs in ITL or HTL.
- Step 7: On the UE side, the UE will continue retransmitting data when gNB does not decode the data successfully and it still has instructions to continue sending messages. On the CN side, CN will assist in transmitting UE data to gNB. Moreover, steps 6 and 7 are repeated until gNB decodes UE data successfully.
- Step 8: gNB sends ACK feedback to the corresponding CNs and UE in the final step, and then the entire process ends.

2.3. Problem Formulation
3. Detailed Design of AOS-Based Channel Sensing for CSCTM
3.1. Theoretical Calculation and Analysis of Latency
3.1.1. Transmission Latency
3.1.2. Propagation Latency
3.1.3. Queuing Latency
3.1.4. Processing Latency
3.1.5. Overall Latency
3.2. Design of Ascending Offset Sort-Based Channel Sensing
| Algorithm 1 Ascending Offset Sort Algorithm |
|
3.3. Channel-Sensing-Based Cooperative Transmission Mechanism
3.3.1. No Cooperative Transmission with
3.3.2. One Cooperative Transmission with
3.3.3. M Cooperative Nodes
| Algorithm 2 Channel-sensing-based cooperative transmission mechanism. |
|
4. Simulation Results and Discussion
4.1. Performance and Results of the AOS Algorithm
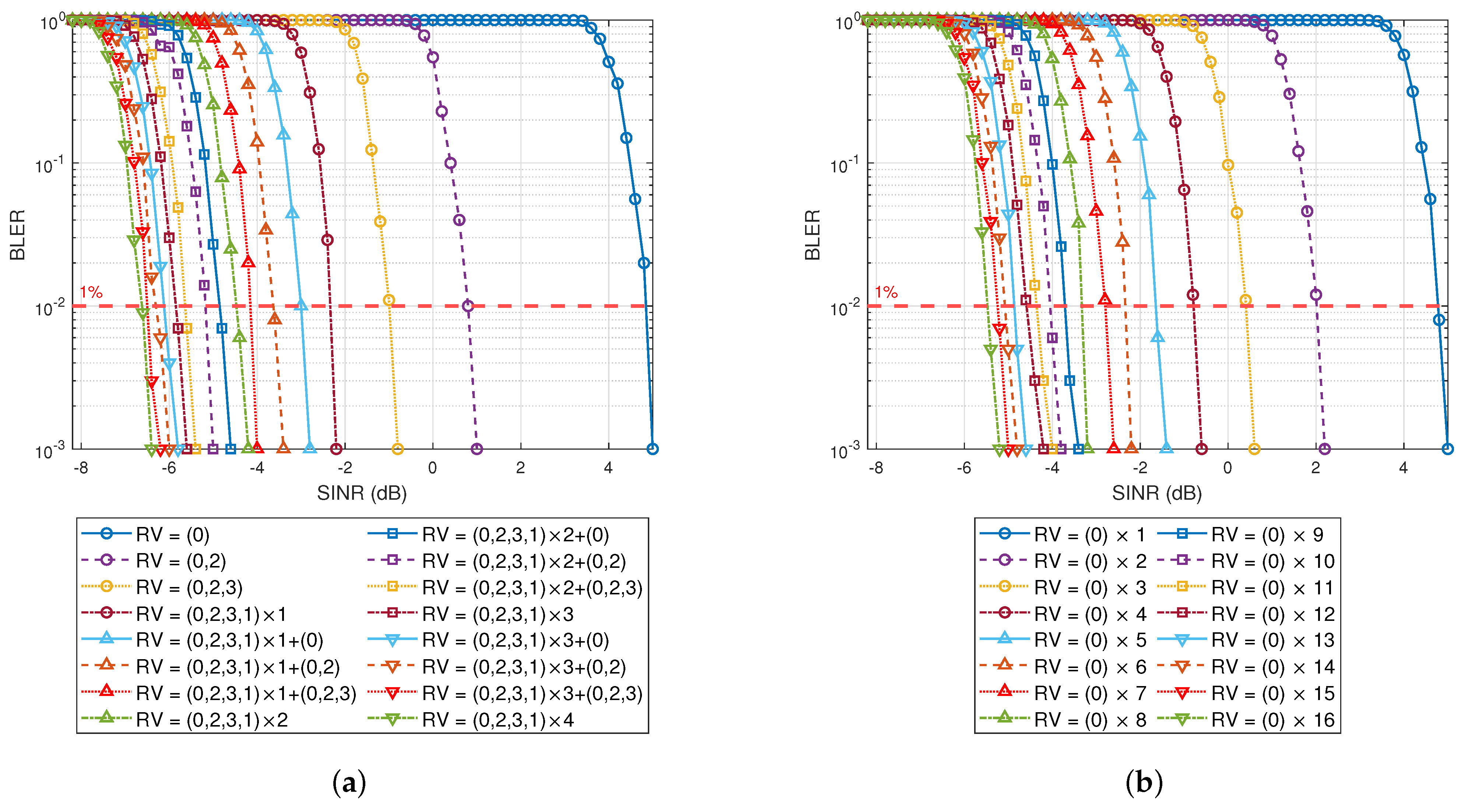
4.2. HARQ Retransmission Performance Analysis
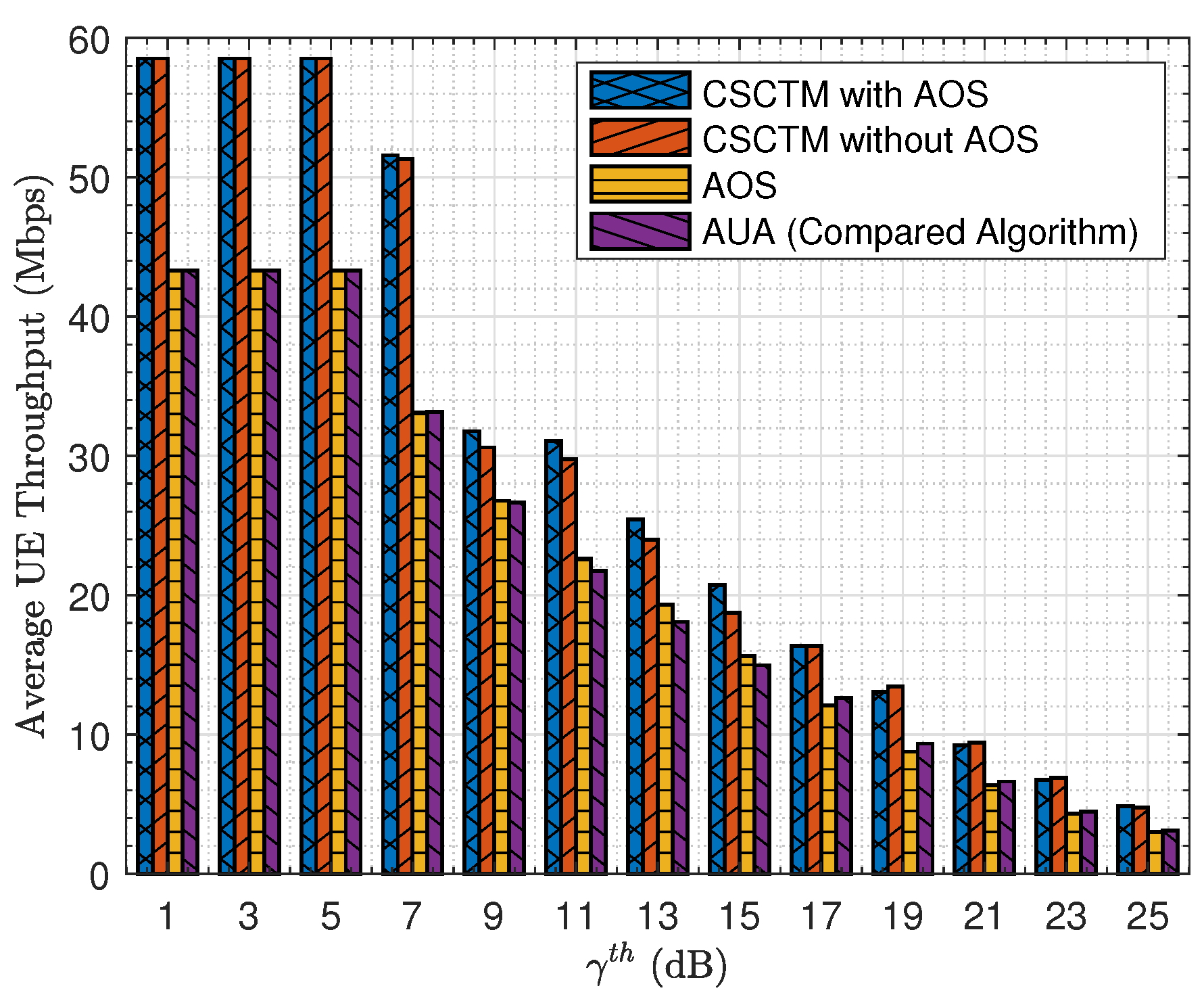
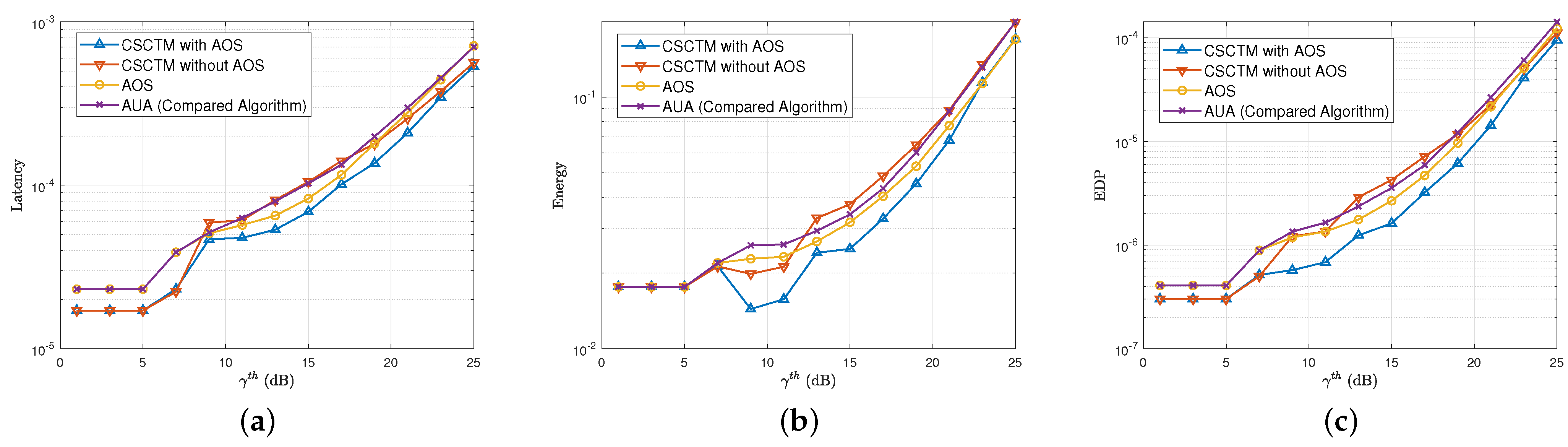
4.3. The Performance Comparison between CSCTM and AOS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | third-generation partnership project |
| 5G NR | fifth-generation new radio |
| 6G | sixth-generation |
| ACK | acknowledgment |
| AOS | ascending offset sort |
| ARQ | automatic repeat request |
| AS | absolute sort |
| AUA | adaptive UE aggregation |
| BLER | block error rate |
| CC-HARQ | chase combining hybrid automatic repeat request |
| CN | cooperative node |
| CP | cyclic prefix |
| CRC | cyclic redundancy check |
| CSCTM | channel-sensing-based cooperative transmission mechanism |
| CSI | channel state information |
| C-SWaP | Cost, size, weight, and power |
| DCI | downlink control information |
| DTL | direct transmission link |
| EDP | energy-delay product |
| gNB | next-generation node base station |
| HARQ | hybrid automatic repeat request |
| HTL | hybrid transmission link |
| IIoT | Industrial Internet of Things |
| IoE | Internet of Everything |
| IR-HARQ | incremental redundancy hybrid automatic repeat request |
| ITL | indirect transmission link |
| LDPC | low-density parity-check code |
| LTE | long-term evolution |
| MCS | modulation and coding scheme |
| MIMO | multiple-input multiple-output |
| MPTCP | multipath transmission control protocol |
| UAV | unmanned aerial vehicle |
| UE | user equipment |
| ProSe | proximity service |
| PDCCH | physical downlink control channel |
| PSSCH | physical sidelink control channel |
| PUSCH | physical uplink shared channel |
| RA | resource allocation |
| RV | redundancy version |
| SINR | signal-to-interference-plus-noise ratio |
References
- Rong, B. 6G: The Next Horizon: From Connected People and Things to Connected Intelligence. IEEE Wirel. Commun. 2021, 28, 8. [Google Scholar] [CrossRef]
- Ren, Q.; Sun, Y.; Wang, T.; Zhang, B. Energy-Efficient Cooperative MIMO Formation for Underwater MI-Assisted Acoustic Wireless Sensor Networks. Remote Sens. 2022, 14, 3641. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Sensviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A Comprehensive Survey. IEEE Internet Things J. 2022, 9, 359–383. [Google Scholar] [CrossRef]
- Vivo Mobile Communications Ltd. Study on UE Aggregation for Industry with Multi-Connectivity. In Proceedings of the 3GPP TSG SA WG2 Electronic Meeting, 18–22 October 2021; Available online: https://www.3gpp.org/ftp/tsg_sa/WG2_Arch/TSGS2_146E_Electronic_2021-08/INBOX/DRAFTS/UE%20Aggregation%20for%20Industry%20with%20Multi-connectivity.pdf (accessed on 23 April 2024).
- Wang, C.-X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the Road to 6G: Visions, Requirements, Key Technologies, and Testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- China Mobile. Motivation of Study for UE Aggregation. In Proceedings of the 3GPP TSG RAN Rel-18 Workshop, RWS-210355, 28 June 2021–2 July 2021; Available online: https://www.3gpp.org/ftp/TSG_RAN/TSG_RAN/TSGR_AHs/2021_06_RAN_Rel18_WS/Docs/RWS-210355.zip (accessed on 24 April 2024).
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Fantacci, R.; Picano, B. End-to-End Delay Bound for Wireless uVR Services Over 6G Terahertz Communications. IEEE Internet Things J. 2021, 8, 17090–17099. [Google Scholar] [CrossRef]
- Ma, S.; Wang, S.; Tsai, W.-T. Delay Analysis of Consensus Communication for Blockchain-Based Applications Using Network Calculus. IEEE Wirel. Commun. Lett. 2022, 9, 1825–1829. [Google Scholar] [CrossRef]
- Verma, S.; Kawamoto, Y.; Fadlullah, Z.M.; Nishiyama, H.; Kato, N. A Survey on Network Methodologies for Real-Time Analytics of Massive IoT Data and Open Research Issues. IEEE Commun. Surv. Tutor. 2017, 19, 1457–1477. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, C.; Zhu, S.; Cheng, N.; Yang, B.; Guan, X. Control Performance Aware Cooperative Transmission in Multiloop Wireless Control Systems for Industrial IoT Applications. IEEE Internet Things J. 2018, 5, 3954–3966. [Google Scholar] [CrossRef]
- Chen, H.; Fang, R.; Chen, T.; Wang, P.; Wang, Z.; Lin, S.; Li, F. A Novel Adaptive UE Aggregation-Based Transmission Scheme Design for a Hybrid Network with Multi-Connectivity. Symmetry 2023, 5, 1766. [Google Scholar] [CrossRef]
- Renzo, M.D.; Zappone, A.; Debbah, M.; Alouini, M.-S.; Yuen, C.; Rosny, J.; Tretyakov, S. Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Renzo, M.D.; AI-Dhahir, N. Reconfigurable Intelligent Surfaces: Principles and Opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Boulogeorgos, A.-A.A.; Alexiou, A. Performance Analysis of Reconfigurable Intelligent Surface-Assisted Wireless Systems and Comparison With Relaying. IEEE Access 2020, 8, 94463–94483. [Google Scholar] [CrossRef]
- More, S.; Naik, U.L. Optimization driven Multipath Routing for the video transmission in the VANET. In Proceedings of the 2018 IEEE Global Conference on Wireless Computing and Networking (GCWCN), Lonavala, India, 23–24 November 2018; pp. 6–10. [Google Scholar]
- Sadi, Y.; Erkucuk, S.; Panayirci, E. Flexible Physical Layer based Resource Allocation for Machine Type Communications Towards 6G. In Proceedings of the 2020 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020; pp. 1–5. [Google Scholar]
- Hu, J.; Liu, G.; Ma, Z.; Xiao, M.; Fan, P. Low-Complexity Resource Allocation for Uplink RSMA in Future 6G Wireless Networks. IEEE Wirel. Commun. Lett. 2024, 13, 565–569. [Google Scholar] [CrossRef]
- Mahmood, N.H.; López, O.A.; Alves, H.; Latva-Aho, M.; Fan, P. A Predictive Interference Management Algorithm for URLLC in Beyond 5G Networks. IEEE Commun. Lett. 2021, 25, 995–999. [Google Scholar] [CrossRef]
- Suyama, S.; Okuyama, T.; Nonaka, N.; Asai, T. Recent Studies on Massive MIMO Technologies for 5G Evolution and 6G. In Proceedings of the 2022 IEEE Radio and Wireless Symposium (RWS), Las Vegas, NV, USA, 16–19 January 2022; pp. 90–93. [Google Scholar]
- Romero-Peña, J.S.; Cardona, N. Diffuse Modular Honeycomb Passive Reflector for Efficient mmWave Propagation in Indoor Environments. In Proceedings of the 2022 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Grenoble, France, 7–10 June 2022; pp. 49–52. [Google Scholar]
- Chirivella-Perez, E.; Salva-Garcia, P.; Ricart-Sanchez, R.; Calero, J.A.; Wang, Q. Intent-Based E2E Network Slice Management for Industry 4.0. In Proceedings of the 2021 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Porto, Portugal, 8–11 June 2021; pp. 353–358. [Google Scholar]
- Makki, B.; Svensson, T.; Zorzi, M. Finite Block-Length Analysis of the Incremental Redundancy HARQ. IEEE Wirel. Commun. Lett. 2014, 3, 529–532. [Google Scholar] [CrossRef]
- Anand, A.; de-Veciana, G. Resource Allocation and HARQ Optimization for URLLC Traffic in 5G Wireless Networks. IEEE J. Sel. Areas Commun. 2018, 36, 2411–2421. [Google Scholar] [CrossRef]
- Khan, F.; Rehma, A.; Zhang, Y.; Mastorrakis, S.; Song, H.; Jan, M.A.; Dev, K. A Secured and Reliable Continuous Transmission Scheme in Cognitive HARQ-Aided Internet of Things. IEEE Internet Things J. 2021, 8, 14835–14844. [Google Scholar] [CrossRef]
- Dosti, E.; Shehab, M.; Alves, H.; Latva-aho, M. Ultra reliable communication via CC-HARQ in finite block-length. In Proceedings of the 2017 European Conference on Networks and Communications (EuCNC), Oulu, Finland, 12–15 June 2017; pp. 1–5. [Google Scholar]
- Zhao, M.-M.; Zhang, G.; Xu, C.; Zhang, H.; Li, R.; Wang, J. An Adaptive IR-HARQ Scheme for Polar Codes by Polarizing Matrix Extension. IEEE Commun. Lett. 2018, 22, 1306–1309. [Google Scholar] [CrossRef]
- Frenger, P.; Parkvall, S.; Dahlman, E. Performance comparison of HARQ with Chase combining and incremental redundancy for HSDPA. In Proceedings of the IEEE 54th Vehicular Technology Conference (VTC), Atlantic City, NJ, USA, 7–11 October 2001; pp. 1829–1833. [Google Scholar]
- Cheng, J.-F. Coding performance of hybrid ARQ schemes. IEEE Trans. Commun. 2006, 54, 1017–1029. [Google Scholar] [CrossRef]
- Avranas, A.; Kountouris, M.; Ciblat, P. Energy-Latency Tradeoff in Ultra-Reliable Low-Latency Communication With Retransmissions. IEEE J. Sel. Areas Commun. 2018, 36, 2475–2485. [Google Scholar] [CrossRef]
- Kim, D.; Jung, B.C.; Lee, H.; Sung, D.K.; Yoon, H. Optimal modulation and coding scheme selection in cellular networks with hybrid-ARQ error control. IEEE Trans. Wirel. Commun. 2008, 7, 5195–5201. [Google Scholar] [CrossRef]
- Nasraoui, L.; Ikki, S. Neighbor Discovery for ProSe and V2X Communications. IEEE Internet Things J. 2021, 8, 7241–7251. [Google Scholar] [CrossRef]
- Ganesan, K.; Mallick, P.B.; Löhr, J. NR Sidelink Enhancement in 3GPP Release 17. J. ICT Stand. 2021, 9, 79–90. [Google Scholar] [CrossRef]
- Ganesan, K. 5G Advanced: Sidelink Evolution. IEEE Commun. Stand. Mag. 2023, 7, 58–63. [Google Scholar] [CrossRef]
- Harounabadi, M.; Soleymani, D.M.; Bhadauria, S.; Leyh, M.; Roth-Mandutz, E. V2X in 3GPP Standardization: NR Sidelink in Release-16 and Beyond. IEEE Commun. Stand. Mag. 2021, 5, 12–21. [Google Scholar] [CrossRef]
- Bazzi, A.; Campolo, C.; Todisco, V.; Bartoletti, S.; Decarli, N.; Molinaro, A.; Berthet, A.O.; Gallacher, R.A. Toward 6G Vehicle-to-Everything Sidelink: Nonorthogonal Multiple Access in the Autonomous Mode. IEEE Veh. Technol. Mag. 2023, 18, 50–59. [Google Scholar] [CrossRef]
- Verma, S.; Kawamoto, Y.; Kato, N. A Network-Aware Internet-Wide Scan for Security Maximization of IPv6-Enabled WLAN IoT Devices. IEEE Internet Things J. 2021, 8, 8411–8422. [Google Scholar] [CrossRef]
- Chen, H.-M.; Wang, J.-B.; Chen, M. Downlink outage probability of distributed antenna systems over shadowed Nakagami-m fading channels with antenna selection. In Proceedings of the 2009 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–4. [Google Scholar]
- Laros III, J.H.; Pedretti, K.; Kelly, S.M.; Shu, W.; Ferreira, K.; Dyke, J.V.; Vaughan, C. Energy-Efficient High Performance Computing; Springer: London, UK, 2012; pp. 51–55. [Google Scholar] [CrossRef]
- Vijaykumar, G.; Pekhimenko, A.; Jog, S.; Ghose, A.; Bhowmick, R.; Ausavarungnirun, C.; Das, M.; Kandemir, T.C.; Mowry, O.M. A Framework for Accelerating Bottlenecks in GPU Execution with Assist Warps; Elsevier: Amsterdam, The Netherlands, 2017; pp. 373–415. [Google Scholar] [CrossRef]
- Ivan, R.; Nikola, B.; Osman, S.; Adrian, C.; Veljko, M. An Overview of Architecture-Level Power- and Energy-Efficient Design Techniques; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–57. [Google Scholar]
- dos Santos, A.; Soares, B.; Fan, C.; Kuipers, M.; Sabino, S.; Grilo, A.M.; Pereira, P.R.B.; Nunes, M.S.; Casaca, A. Characterization of Substation Process Bus Network Delays. IEEE Trans. Ind. Inform. 2018, 14, 2085–2094. [Google Scholar] [CrossRef]
- Hamidi-Sepehr, F.; Nimbalker, A.; Ermolaev, G. Analysis of 5G LDPC Codes Rate-Matching Design. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Elsevier: Burlington, VT, USA; Academic Press: Burlington, VT, USA, 2007. [Google Scholar]
- Lagrange, X. Throughput of HARQ protocols on a block fading channel. IEEE Commun. Lett. 2010, 14, 257–259. [Google Scholar] [CrossRef]






| Notation | Explanation |
|---|---|
| R | The radius of the entire cell |
| r | Distance between CN and gNB |
| The total UE number within the cell | |
| The total CN number within the cell | |
| The transmission number of the ith UE when gNB decodes successfully | |
| SINR threshold | |
| SINR between the ith UE and gNB during the kth transmission | |
| SINR between the ith UE and jth CN during the kth transmission | |
| SINR between the jth CN and gNB during the kth transmission | |
| Whether or not the jth CN needs to assist the ith UE during the kth transmission | |
| Whether or not the ith UE needs to transmit data during the kth transmission | |
| The overall latency of ith UE data successfully decoded at gNB | |
| The overall energy consumption of ith UE data successfully decoded at gNB | |
| The maximum number of UE that can be assisted by a single CN in one time segment | |
| The absolute sort of ith UE and jth CN during the kth transmission | |
| The transmission latency for one time segment | |
| The propagation latency for one time segment | |
| The queuing latency for one time segment | |
| The processing latency for one time segment | |
| Pathloss of the channel | |
| Packet size | |
| Transmission power | |
| Link rate | |
| The average transmission number under assistance from M CNs | |
| q | The probability of transmission failure |
| The probability of transmission failure from UE to gNB | |
| The probability of transmission failure from ith CN to gNB | |
| The probability of transmission failure from UE to jth CN | |
| The processing latency at the symbol level | |
| The processing latency at the bit level | |
| A dynamically adjusted SINR factor | |
| The number of times that the UE waits for the CN to transmit other UE data in the queue | |
| f | The successful transmission flag |
| M | The number of CNs assisting UE in transmission |
| n | The transmission number of specific tasks |
| The main factor values used in transmission strategy determination | |
| Shadowing effect, modeled by a log-normal distribution | |
| I | The interference within devices |
| g | The fast channel fading, following a Nakagami distribution |
| The noise of the system, modeled as a Gaussian random noise with zero mean and variance | |
| The set of positive integers | |
| The absolute operation to the input parameter |
| Tx Number | Previous RV | Current RV | SINR Value | SINR Value Increment | SINR dB Increment |
|---|---|---|---|---|---|
| 1st Tx | RV = (-) | RV = (0) | − | ||
| 2nd Tx | RV = (0) | RV = (0, 2) | 4 dB | ||
| 3rd Tx | RV = (0, 2) | RV = (0, 2, 3) | dB | ||
| 4th Tx | RV = (0, 2, 3) | RV = (0, 2, 3, 1) × 1 | dB | ||
| 5th Tx | RV = (0, 2, 3, 1) × 1 | RV = (0, 2, 3, 1) × 1 + (0) | dB | ||
| 6th Tx | RV = (0, 2, 3, 1) × 1 + (0) | RV = (0, 2, 3, 1) × 1 + (0, 2) | dB | ||
| 7th Tx | RV = (0, 2, 3, 1) × 1 + (0, 2) | RV = (0, 2, 3, 1) × 1 + (0, 2, 3) | dB | ||
| 8th Tx | RV = (0, 2, 3, 1) × 1 + (0, 2, 3) | RV = (0, 2, 3, 1) × 2 | dB |
| Tx Number | Previous RV | Current RV | SINR Value | SINR Value Increment | SINR dB Increment |
|---|---|---|---|---|---|
| 1st Tx | RV = (-) | RV = (0) × 1 | − | ||
| 2nd Tx | RV = (0) × 1 | RV = (0) × 2 | dB | ||
| 3rd Tx | RV = (0) × 2 | RV = (0) × 3 | dB | ||
| 4th Tx | RV = (0) × 3 | RV = (0) × 4 | dB | ||
| 5th Tx | RV = (0) × 4 | RV = (0) × 5 | dB | ||
| 6th Tx | RV = (0) × 5 | RV = (0) × 6 | dB | ||
| 7th Tx | RV = (0) × 6 | RV = (0) × 7 | dB | ||
| 8th Tx | RV = (0) × 7 | RV = (0) × 8 | dB |
| Parameter | Value |
|---|---|
| Cell radius (R) | |
| Distance between cooperation node and gNB (r) | |
| UE number () | 10,000 |
| Cooperation node number () | 32 |
| The maximum assisting number for a single CN () | 16 |
| Transmit power () | |
| Packet size () | |
| Link rate () | |
| Adjusted SINR factor () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-M.; Fang, R.; Wang, S.; Wang, Z.; Sun, Y.; Zheng, Y. A Channel-Sensing-Based Multipath Multihop Cooperative Transmission Mechanism for UE Aggregation in Asymmetric IoE Scenarios. Symmetry 2024, 16, 1225. https://doi.org/10.3390/sym16091225
Chen H-M, Fang R, Wang S, Wang Z, Sun Y, Zheng Y. A Channel-Sensing-Based Multipath Multihop Cooperative Transmission Mechanism for UE Aggregation in Asymmetric IoE Scenarios. Symmetry. 2024; 16(9):1225. https://doi.org/10.3390/sym16091225
Chicago/Turabian StyleChen, Hua-Min, Ruijie Fang, Shoufeng Wang, Zhuwei Wang, Yanhua Sun, and Yu Zheng. 2024. "A Channel-Sensing-Based Multipath Multihop Cooperative Transmission Mechanism for UE Aggregation in Asymmetric IoE Scenarios" Symmetry 16, no. 9: 1225. https://doi.org/10.3390/sym16091225
APA StyleChen, H.-M., Fang, R., Wang, S., Wang, Z., Sun, Y., & Zheng, Y. (2024). A Channel-Sensing-Based Multipath Multihop Cooperative Transmission Mechanism for UE Aggregation in Asymmetric IoE Scenarios. Symmetry, 16(9), 1225. https://doi.org/10.3390/sym16091225







