Three-Dimensional Moran Walk with Resets
Abstract
1. Introduction
2. Definitions and Presentation of the Model
2.1. Definitions
- Let be a discrete walk with three dimensions with and the finite state space.
- We define the probability associated to the discrete process for all by
- The probability-generating function of a discrete variable Y, is given by:for all such that , where is the distribuation of a discrete variable Y.
2.2. Presentation of the Model
3. Main Result
- The expressions of and in Equations (5) and (6) generalize the expressions of the mean and the variance in Theorem 2.1 in [6] for the one-dimensional random walks. Precisely, if we take our model (1), the probability , which means . We start by the closed expression of the meanTaking in Equation (6), we haveandFrom Equation (28), we haveand combining Equations (6) and (10)–(12), we obtainEquations (9) and (13) are the same as the expressions of the mean and the variance in Theorem 2.1 in [6] (taking and ).
- The expressions of and in Equations (5) and (6) generalize the expressions of the mean and the variance in Theorem 2 in [8]. Precisely, if we take our model (1), the probability equals 0, which means . We start by the closed expression of the meanTaking in Equations (7) and (32), we haveandUsing Equation (7), we haveCombining Equations (16) and (17), we obtainwhere , is the correct formula defined when in (p. 20 in [8]). The authors in [8] forgot the following term in the formula (p. 20 in [8]).
- and are two probabilities such that depends only on the initial probability but depends on the initial probabilities .
- Since , then , for . So we deduce from Theorem 2 and Corollary 1 that .
4. Application and Simulations
4.1. Application
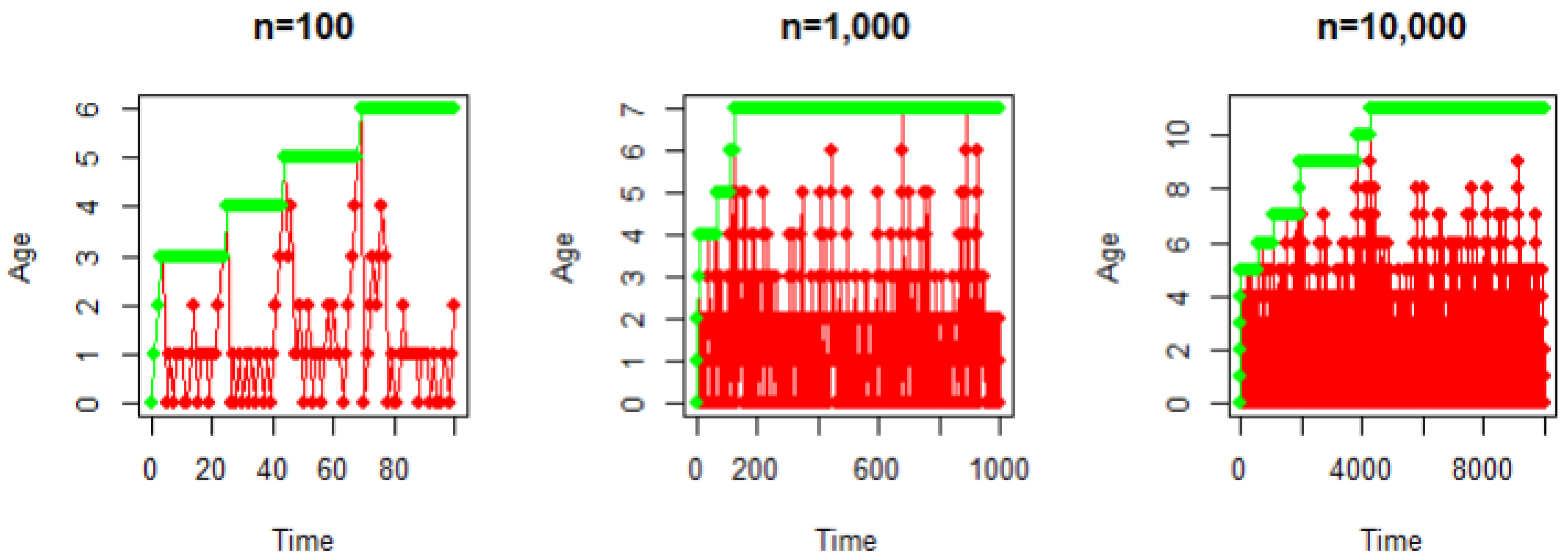
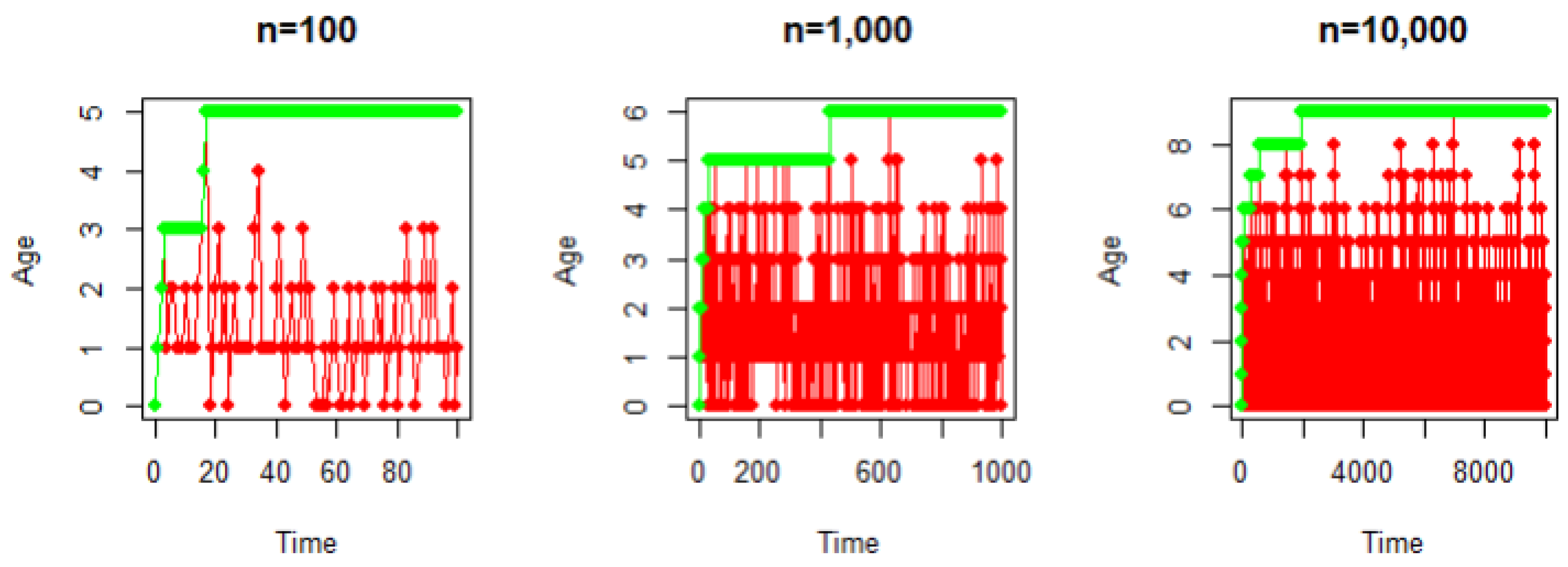
4.2. Simulations
4.2.1. Uniform Case
4.2.2. Non-Uniform Case
5. Recursive Equations
- Case 1: For , denote by and the following events:using the conditional probability, we havesince .
- Case 2: For and , denote by and the following events:using the conditional probability, we have
- Case 5: For , denote by and the following events:and using the conditional probability, we havewe finish the proof.
6. Distribution of ,
7. Proofs
7.1. Proof of Theorem 1
7.2. Proof of Theorem 2
8. Conclusions and Perspectives
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banderier, C. Combinatoire Analytique des Chemins et des Cartes. Ph.D. Thesis, University Paris VI, Paris, France, 2001. [Google Scholar]
- Banderier, C.; Flajolet, P. Basic analytic combinatorics of directed lattice paths. Theor. Sci. 2002, 281, 37–80. [Google Scholar] [CrossRef]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Abdelkader, M.; Aguech, R. Moran random walk with reset and short memory. AIMS Math. 2024, 9, 19888–19910. [Google Scholar] [CrossRef]
- Banderier, C.; Nicodème, P. Bounded discrete walks. In Proceedings of the 2010 Discrete Mathematics and Theoretical Computer Science (DMTCS), Nancy, France, 14–16 June 2010; pp. 35–48. [Google Scholar]
- Aguech, R.; Althagafi, A.; Banderier, C. Height of Walks with Resets and the Moran Model and The Discrete Gumbel Distribution. Lattice Path Comb. Interact. 2023, 87B, 263. [Google Scholar]
- Banderier, C.; Wallner, M. Lattice paths with catastrophes. Discret. Math. Theor. Comput. Sci. 2017, 19, 32. [Google Scholar] [CrossRef][Green Version]
- Althagafi, A.; Abdelkader, M. Two-Dimensional Moran Model. Symmetry 2023, 15, 1046. [Google Scholar] [CrossRef]
- Itoh, Y.; Mahmoud, H.M.; Takahashi, D. A stochastic model for solitons. Random Struct. Algorithms 2004, 24, 51–64. [Google Scholar] [CrossRef]
- Huillet, T.E. Random walk Green kernels in the neutral Moran model conditioned on survivors at a random time to origin. Math. Popul. Stud. 2016, 23, 164–200. [Google Scholar] [CrossRef]
- Huillet, T.; Möhle, M. Duality and asymptotics for a class of nonneutral discrete Moran models. J. Appl. Probab. 2009, 46, 866–893. [Google Scholar] [CrossRef][Green Version]
- Itoh, Y.; Mahmoud, H.M. Age statistics in the Moran population model. Stat. Probab. Lett. 2005, 74, 21–30. [Google Scholar] [CrossRef]
- Moran, P.A.P. Random processes in genetics. Proc. Camb. Philos. Soc. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Moran, P.A.P. The Statistical Processes of Evolutionary Theory; Oxford University Press: Oxford, UK, 1962. [Google Scholar]
- Lieberman, E.; Hauert, C.; Nowak, M.A. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkader, M. Three-Dimensional Moran Walk with Resets. Symmetry 2024, 16, 1222. https://doi.org/10.3390/sym16091222
Abdelkader M. Three-Dimensional Moran Walk with Resets. Symmetry. 2024; 16(9):1222. https://doi.org/10.3390/sym16091222
Chicago/Turabian StyleAbdelkader, Mohamed. 2024. "Three-Dimensional Moran Walk with Resets" Symmetry 16, no. 9: 1222. https://doi.org/10.3390/sym16091222
APA StyleAbdelkader, M. (2024). Three-Dimensional Moran Walk with Resets. Symmetry, 16(9), 1222. https://doi.org/10.3390/sym16091222





