Analytic Theory of Seven Classes of Fractional Vibrations Based on Elementary Functions: A Tutorial Review

Abstract

This paper conducts a tutorial review of the analytic theory of seven classes of fractional vibrations based on elementary functions. We discuss the classification of seven classes of fractional vibrations and introduce the problem statements. Then, the analytic theory of class VI fractional vibrators is given. The analytic theories of fractional vibrators from class I to class V and class VII are, respectively, represented. Furthermore, seven analytic expressions of frequency bandwidth of seven classes of fractional vibrators are newly introduced in this paper. Four analytic expressions of sinusoidal responses to fractional vibrators from class IV to VII by using elementary functions are also newly reported in this paper. The analytical expressions of responses (free, impulse, step, and sinusoidal) are first reported in this research. We dissert three applications of the analytic theory of fractional vibrations: (1) analytical expression of the forced response to a damped multi-fractional Euler–Bernoulli beam; (2) analytical expressions of power spectrum density (PSD) and cross-PSD responses to seven classes of fractional vibrators under the excitation with the Pierson and Moskowitz spectrum, which are newly introduced in this paper; and (3) a mathematical explanation of the Rayleigh damping assumption.

1. Introduction

When a system is with inertial force and restorative one, it may vibrate. Mass is the measure of inertia and stiffness is the measure of restoration. Let m and k be the mass and stiffness of a vibration system, respectively. Denote by x(t) displacement. Then, the inertial force is mx″(t) and restorative force is kx(t).

If a system vibrates with a certain dissipative force, we say that a vibration system has damping. Using the concept of viscous or linear damping, the damping force is cx′(t), where c is called viscous damping coefficient (damping for short). Thus, conventional linear vibration considers a second-order differential equation in the following form

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{2}x(t)}{d{t}^2}}+c{\displaystyle \frac{dx(t)}{dt}}+kx(t)=f(t),\\ x_0=x(0),v_0=x^{\prime }(0),\end{array}\right.$$

where f(t) is the driven force and x₀ and v₀ are the initial conditions. In the above, the expression mx″(t) + cx′(t) + kx(t) = f(t) is called the equation of motion or motion equation of a linear vibration system. Among References [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133], Harris [71] or Palley et al. [72] suffices for the preliminaries about the theory of conventional linear vibration.

The theory of linear vibration is mature. However, fractional vibration remains academic and interesting. By fractional vibration, we mean inertial force may be of fractional order α, that is, $m{\displaystyle \frac{d^{\alpha }x(t)}{d{t}^{\alpha }}},$ or damping force may be of fractional order β, that is, $c{\displaystyle \frac{d^{\beta }x(t)}{d{t}^{\beta }}},$ or restoration force may be of fractional order λ, i.e., $k{\displaystyle \frac{d^{\lambda }x(t)}{d{t}^{\lambda }}}$ (Li [24,25,26]). In this section, we describe the classification of fractional vibrations and brief the related results in Section 1.1, Section 1.2, Section 1.3, Section 1.4, Section 1.5, Section 1.6 and Section 1.7. Problem statements are presented in Section 1.8 and paper organization in Section 1.9.

1.1. Class I Fractional Vibration

Denote by m and k the primary mass and stiffness of a vibration system. Then, the simplest fractional vibration form is expressed by

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_1(t)}{d{t}^{\alpha }}}+k{x}_1(t)=f(t),1<\alpha <3,\\ x_{10}=x_1(0),v_{10}=x_1^{\prime }(0).\end{array}\right.$$

(1)

The above vibration system has a fractional inertial force of order α, zero damping force in form, and standard restoration force. There are rich references about the research of (1), including Equation (3) of Duan [1], Equation (4.2) of Duan et al. [2], Equation (16) of Zurigat [3], Equation (1) of Blaszczyk and Ciesielski [4], Equation (10) of Blaszczyk et al. [5], Blaszczyk [6], Equation (3.1) of Al-rabtah et al. [7], Drozdov [8], Equation (9) of Stanislavsky [9], Equation (1) of Achar et al. [10], Equation (9) of [11], Equation (2) of [12], Equation (2) of Tofighi [13], Equation (1) of Ryabov and Puzenko [14], Equation (1) of Ahmad and Elwakil [15], Chapter 7 of Uchaikin [16], Tavazoei [17], Equation (36) of Sandev and Tomovski [18], Singh et al. [19], Equation (19b) of Rossikhin [20], Equation (1) of Pskhu and Rekhviashvili [21], Equation (1.2) of Aghchi et al. [22], and Equation (2.1) of Čermák and Kisela [23]. A common form of the solution of free response to (1) is given by

$$x_1(t)=x_{10}{E}_{\alpha ,1}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right]+v_{10}t{E}_{\alpha ,2}\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],$$

(2)

where E_a and _b(z) is the generalized Mittag–Leffler function and ${\omega }_n=\sqrt{{\displaystyle \frac{k}{m}}}$ is the primary damping free natural angular frequency. The solution x₁(t) to (1) in the form of (2) is well known in the field (Achar et al. [10,11,12]; Chapter 7 of Uchaikin [16]). For facilitating discussions, we call a system that follows (1) a class I fractional vibrator.

Let h₁(t) be the impulse of a class I fractional vibrator. A common expression of h₁(t), by using the Mittag–Leffler function, is in the form

$$h_1(t)=t^{\alpha -1}{E}_{\alpha ,\alpha }\left[-{\left({\omega }_{n}t\right)}^{\alpha }\right],t\ge 0.$$

(3)

The impulse h₁(t) in (3) is well known in the field (Chapter 7 of Uchaikin [16]).

Recently, Li [24,25,26] introduced a method to express the closed forms of x₁(t) and h₁(t) by using elementary functions. The analytic theory of class I fractional vibrators will be reviewed in Section 3.

1.2. Class II Fractional Vibration

Let m, c, and k be the primary mass, damping, and stiffness of a vibration system, respectively. The following fractional vibrator is widely studied

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_2(t)}{d{t}^{\beta }}}+k{x}_2(t)=f(t),0<\beta <2,\\ x_{20}=x_2(0),v_{20}=x_2^{\prime }(0).\end{array}\right.$$

(4)

The above vibration system is with standard inertial force, fractional damping force of order β, and standard restoration force. There are rich references regarding (4), see, e.g., Equation (2) of Lin et al. [27], Equation (5) of Hermosillo-Arteaga et al. [28], Equation (1a) of Alkhaldi et al. [39], Equation (1) of Dai et al. [30], Equation (1) of Xu et al. [31], Equation (4) of He et al. [32], Equation (2) of Leung et al. [33], Equation (1) of Chen et al. [34], Equation (1) of Deü and Matignon [35], Equation (4) of Drăgănescu et al. [36], Equation (1) of Xie and Lin [37], Equation (1) of Ren et al. [38], Equation (1) of [39], Equation (8) of Yuan et al. [40], Equations (22) and (23) of Shitikova [41], Equation (1) of Lin et al. [42], Equation (1) of Naranjani et al. [43], Equation (1) of Duan and Zhang [44], Matteo et al. [45], Equation (44) of Tomovski and Sandev [46], Equation (2.4) of Zelenev et al. [47], Equation (3) of Rossikhin and Shitikova [48], Equation (2.2.2) of [49], Equation (26a) of [50], Equation (32) of Bagley and Torvik [51], Equation (18) of Spanos and Malara [52], Equation (1) of [53], Equation (1a) of Hu et al. [54], Equation (8) of Cao et al. [55], Equation (8) of [56], Equation (7) of Kaltenbacher and Schlintl [57], and Equation (1.1) of Pang et al. [58]. In order to facilitate discussion, we call a system that obeys (4) a class II fractional vibrator.

Using the Mittag–Leffler function, Pang et al. [58] proposed (5) as the general solution to (4)

$$\begin{array}{l}{x}_2(t)=x_{20}{\displaystyle \sum _{n=0}^{\infty }{(-c)}^n{t}^{(2-\beta )n}{E}_{2,(2-\beta )n+1}^{n+1}(-k{t}^2)}+x_{20}c{\displaystyle \sum _{n=0}^{\infty }{(-c)}^n{t}^{(2-\beta )n-\beta +2}{E}_{2,(2-\beta )n-\beta +3}^{n+1}(-k{t}^2)}\\ +v_{20}{\displaystyle \sum _{n=0}^{\infty }{(-c)}^n{t}^{(2-\beta )n+1}{E}_{2,(2-\beta )n+2}^{n+1}(-k{t}^2)}+{\displaystyle \sum _{n=0}^{\infty }{(-c)}^n{\displaystyle \underset{0}{\overset{t}{\int }}f(t-s)s^{(2-\beta )n+1}{E}_{2,(2-\beta )n+2}^{n+1}(-k{s}^2)ds}}.\end{array}$$

(5)

Note that Li [24,25,26] recently introduced an analytical expression of x₂(t) simply using elementary functions. We will review the analytic theory of class II fractional vibrators in Section 4.

1.3. Class III Fractional Vibration

When the motion equation of a system follows

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_3(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_3(t)}{d{t}^{\beta }}}+k{x}_3(t)=f(t),\\ x_{30}=x_3(0),v_{30}=x_3^{\prime }(0),\end{array}\right.$$

(6)

it is called a class III fractional vibrator, for the purpose of facilitating discussion (Li [24]). The literature regarding (6) includes Gomez-Aguilar [59], Equation (10); Tian et al. [60]; Berman and Cederbaum [61]; Duan et al. [62], Equation (2); Mendiola-Fuentes et al. [63], Equation (4); Morales-Delgado et al. [64], Equation (16); Parovik [65], Equation (1); Ref. [66], Equation (4); and Sene and Aguilar [67], Equation (8). By using the Mittag–Leffler function (Berman and Cederbaum [61]) and specifically when 2β = α, the expression of the general solution to (6) is in the form

$$x_3(t)={\displaystyle \frac{x_{30}A+v_{30}B+C}{2i{\omega }_d}}.$$

(7)

In (7),

$$\begin{array}{l}A=(\varsigma +i{\omega }_d)E_{\beta ,1}\left[(-\varsigma +i{\omega }_d)t^{\beta }\right]-(\varsigma -i{\omega }_d)E_{\beta ,1}\left[(-\varsigma -i{\omega }_d)t^{\beta }\right],\\ B=t(-\varsigma +i{\omega }_d)E_{\beta ,2}\left[(-\varsigma +i{\omega }_d)t^{\beta }\right]-t(-\varsigma -i{\omega }_d)E_{\beta ,2}\left[(-\varsigma -i{\omega }_d)t^{\beta }\right],\\ C=\left\{t^{\beta -1}(-\varsigma +i{\omega }_d)E_{\beta ,\beta }\left[(-\varsigma +i{\omega }_d)t^{\beta }\right]\right\}\ast {\displaystyle \frac{f(t)}{m}}\\ -\left\{t^{\beta -1}(-\varsigma -i{\omega }_d)E_{\beta ,\beta }\left[(-\varsigma -i{\omega }_d)t^{\beta }\right]\right\}\ast {\displaystyle \frac{f(t)}{m}},\\ {\omega }_d={\omega }_n\sqrt{1-{\varsigma }^2}.\end{array}$$

(8)

In (8), $\varsigma ={\displaystyle \frac{c}{2\sqrt{mk}}}$ is the primary damping ratio.

Let G₃(t) be the unit step response to (6). Duan et al. [68] obtained (9) to express G₃(t) for α being independent of β in series form

$$G_3(t)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{l=0}^n\frac{n!{(-k)}^l{(-c)}^{n-l}}{l!(n-l)!}}}{\displaystyle \frac{t^{\alpha l+(\alpha -\beta )(n-l)+1}}{\mathsf{\Gamma }\left[\alpha l+(\alpha -\beta )(n-l)+2\right]}}.$$

(9)

Recently, Li [24,25,26] addressed the analytical expression of the general solution to (6) when α is independent of β by using elementary functions. The analytic theory of class III fractional vibrators will be reviewed in Section 5.

1.4. Class IV Fractional Vibration

For facilitating discussion, a system is called a class IV fractional vibrator when its motion equation is in the form

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_4(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\lambda }{x}_4(t)}{d{t}^{\lambda }}}=f(t),\\ x_{40}=x_4(0),v_{40}=x_4^{\prime }(0),\end{array}\right.$$

(10)

where 0 ≤ λ < 1. The above vibration system is with fractional inertia force of order α, zero damping force in form, and fractional restoration force of order λ. Reports regarding (10) are rarely seen but in the author’s recent work [24,25]. We shall review the analytic theory of class IV fractional vibrators in Section 6.

1.5. Class V Fractional Vibration

We call a system a class V fractional vibrator when its motion equation is in the form

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{x}_4(t)}{d{t}^{\lambda }}}=f(t),\\ x_{50}=x_5(0),v_{50}=x_5^{\prime }(0).\end{array}\right.$$

(11)

The literature regarding (11) is quite scarce. Duan [70] presents (12) as its solution for x₅₀ = 1 and v₅₀ = 1

$$x_5(t)=E_{2-\lambda ,1}(-t^{2-\lambda })+t^{2-\lambda }{E}_{2-\lambda ,3-\lambda }(-t^{2-\lambda })+t{E}_{2-\lambda ,2}(-t^{2-\lambda }).$$

(12)

We will review the analytic theory of class V fractional vibrators using elementary functions in Section 7.

1.6. Class VI Fractional Vibration

When the motion equation of a system follows

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}}=f(t),\\ x_{60}=x_6(0),v_{60}=x_6^{\prime }(0),\end{array}\right.$$

(13)

it is called a class VI fractional vibrator (Li [25,26], Li [69]). The literature regarding (13) is scarce, with only Li [25,26] and Li [69], which give the closed form of the analytical expression of x₆(t) using elementary functions. We shall review the analytic theory of class I fractional vibrators in Section 2.

1.7. Class VII Fractional Vibration

A system is called a class VII fractional vibrator if its motion equation is in the form

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_7(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_7(t)}{d{t}^{\lambda }}}=f(t),\\ x_{70}=x_7(0),v_{70}=x_7^{\prime }(0).\end{array}\right.$$

(14)

Reports about (14) are scarce except for Li [69], which expresses the closed form of x₇(t) using elementary functions. The analytic theory of class VII fractional vibrators will be reviewed in Section 8.

1.8. Problem Statements

We consider five main problems as follows.

(1)

From the perspective of vibration engineering, people are interested in its equivalent mass or damping or stiffness (Harris [71], Palley et al. [72]). However, analytical expressions of equivalent mass, damping, or stiffness with respect to fractional vibrations of classes I–VII are rarely reported. What they are is a problem.

(2)

Equivalent damping-free and damped natural angular frequencies play a key role in vibration engineering. However, their analytical expressions are seldom seen. What they are for class I–VII fractional vibrators is the second problem.

(3)

From an engineering point of view, the logarithmic decrement in a vibration system is essential. However, analytical expressions of equivalent logarithmic decrements in class I–VII fractional vibrators are rarely reported. What they are is a problem.

(4)

The quantity called the Q factor of a vibration system plays a role in engineering. Nonetheless, analytical expressions of Q factors for fractional vibrators of classes I–VII are rarely seen. What Q factors are for class I–VII fractional vibrators is a problem.

(5)

Let B_0.707 be the frequency bandwidth of a vibration system. It is a crucial parameter in describing a vibration system. Nevertheless, analytical expressions of equivalent frequency bandwidths of fractional vibrators of classes I–VII are seldom seen. What they are is a problem

In order to find solutions to the above problems, we study seven classes of fractional vibrations with the focus on explicitly expressing equivalent mass or damping or stiffness. This tutorial review work based on Li [24,25,26,69] gives the solutions to all problems above. Since the solutions are expressed by using elementary functions, we use the term “analytic theory” in this research.

1.9. Paper Organization

In Section 2, we address the analytic theory of class VI fractional vibrations. We expound the analytic theories of fractional vibrations with classes I–V and VII in Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8, respectively. As an application of fractional vibrations, we discuss the closed form of forced response to a multi-fractional damped Euler–Bernoulli beam in Section 9. In Section 10, we propose the analytical expressions of power spectrum density (PSD) and cross-PSD response to fractional vibrations driven by random processes with the Pierson and Moskowitz spectrum as an application case of fractional vibrations in Section 1, Section 2, Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8 to fractionally random vibrations. In Section 11, we address a theory application of fractional vibrations to the mathematical explanation of the Rayleigh damping assumption. Finally, Section 12 gives a summary and the conclusions.

2. Analytic Theory of Class VI Fractional Vibrators

This section gives a tutorial regarding the analytic theory of class VI fractional vibrators in seven parts: (1) the analytical expression of frequency transfer function of class VI fractional vibrator in Theorem 1 in Section 2.1; (2) the equivalent motion equation of class VI vibration systems in Theorem 2 in Section 2.2; (3) the analytical expressions of equivalent parameters of class VI fractional vibrators in Section 2.3; (4) the analytical expressions of responses of class VI fractional vibrators in Theorems 3–6 in Section 2.4, where the sinusoidal response expression is newly introduced; (5) the analytical expression for the equivalent logarithmic decrement in class VI fractional vibrators in Theorem 7 in Section 2.5; (6) the analytical expression of the equivalent quality factor of class VI fractional vibrators in Theorem 8 in Section 2.6; (7) in addition, the analytical expression for the equivalent frequency bandwidth in class VI fractional vibrators is newly reported in Theorem 9 in Section 2.7.

2.1. Frequency Transfer Function of Class VI Fractional Vibrator

Theorem 1 (Frequency transfer function VI). 

Let H₆(ω) be the frequency transfer function of a class VI fractional vibrator [25,26]. Then,

$$H_6(\omega )={\displaystyle \frac{1}{\begin{array}{l}\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}\right)\\ +i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda }\sin \frac{\lambda \pi }{2}\right)+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\end{array}}}.$$

(15)

Proof. 

Denote by F(ω) the Fourier transform of f(t). Let X₆(ω) be the Fourier transform of x₆(t). With (13), performing the Fourier transform on the both sides of $m{\displaystyle \frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}}=f(t)$ yields

$$\left[m{(i\omega )}^{\alpha }+c{(i\omega )}^{\beta }+k{(i\omega )}^{\lambda }\right]X_6(\omega )=F(\omega ).$$

(16)

From (16),

$$\begin{array}{l}{H}_6(\omega )={\displaystyle \frac{1}{m{(i\omega )}^{\alpha }+c{(i\omega )}^{\beta }+k{(i\omega )}^{\lambda }}}\\ ={\displaystyle \frac{1}{\begin{array}{l}\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}\right)\\ +i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda }\sin \frac{\lambda \pi }{2}\right)+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\end{array}}}.\end{array}$$

(17)

From (17), we see that (15) is true. The proof is finished. □

2.2. Equivalent Motion Equation of Class VI Fractional Vibrator

Theorem 2 (Equivalent motion equation VI). 

The motion Equation (13) of class VI fractional vibrators is equivalently equal to

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right){\displaystyle \frac{d^2{x}_6(t)}{d{t}^2}}\\ +\left(m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}\right){\displaystyle \frac{d{x}_6(t)}{dt}}+k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}{x}_6(t)=f(t).\end{array}$$

(18)

Proof. 

Performing the Fourier transform on the both sides of the above equation yields

$$\left[\begin{array}{l}\left(m{\omega }^{\alpha }\cos {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta }\cos {\displaystyle \frac{\beta \pi }{2}}\right)\\ +i\left(m{\omega }^{\alpha }\sin {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta }\sin {\displaystyle \frac{\beta \pi }{2}}+k{\omega }^{\lambda }\sin {\displaystyle \frac{\lambda \pi }{2}}\right)+k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}\end{array}\right]X_6(\omega )=F(\omega ).$$

(19)

The above implies ${\displaystyle \frac{X_6(\omega )}{F(\omega )}}=H_6(\omega ).$ From (19), we see that (18) holds. This finishes the proof. □

2.3. Equivalent Parameters of Class VI Fractional Vibrator

Corollary 1 (Equivalent mass VI). 

Let m_eq6 be the equivalent mass of class VI fractional vibrators [25,26]. Then,

$$m_{\mathrm{eq}6}=-\left(m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right).$$

(20)

Proof. 

The right side of the above expression is the coefficient of ${\displaystyle \frac{d^2{x}_6(t)}{d{t}^2}}$ in (18) and (20) holds. The proof is finished. □

Corollary 2 (Equivalent damping VI). 

Denote by c_eq6 the equivalent damping of class VI fractional vibrators [25,26]. Then,

$$c_{\mathrm{eq}6}=m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}.$$

(21)

Proof. 

Because the right side of the above expression is the coefficient of ${\displaystyle \frac{d{x}_6(t)}{dt}}$ in (18), it is an equivalent damping coefficient of class VI fractional vibrators expressed by (13). Thus, (21) is valid. The proof is finished. □

Corollary 3 (Equivalent stiffness VI). 

Let k_eq6 be the equivalent stiffness of class VI fractional vibrators [25,26]. Then,

$$k_{\mathrm{eq}6}=k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}.$$

(22)

Proof. 

Since the right side of the above expression is the coefficient of x₆(t) in (18), we see that (22) is valid. The proof ends. □

Using m_eq6, c_eq6, and k_eq6 to rewrite (18) produces the equivalent motion equation VI in the form

$$m_{\mathrm{eq}6}{\displaystyle \frac{d^2{x}_6(t)}{d{t}^2}}+c_{\mathrm{eq}6}{\displaystyle \frac{d{x}_6(t)}{dt}}+k_{\mathrm{eq}6}{x}_6(t)=f(t).$$

(23)

Corollary 4 (Equivalent damping ratio VI). 

Denote by ζ_eq6 the equivalent damping ratio for class VI fractional vibrators [25,26]. Define it by

$${\varsigma }_{\mathrm{eq}6}={\displaystyle \frac{c_{\mathrm{eq}6}}{2\sqrt{m_{\mathrm{eq}6}{k}_{\mathrm{eq}6}}}}.$$

(24)

Then,

$${\varsigma }_{\mathrm{eq}6}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(25)

Proof. 

Substituting m_eq6, c_eq6, and k_eq6 into (24) results in (25). This finishes the proof. □

Note that ζ_eq6 > 1 is trivial in vibrations. Thus, we default |ζ_eq6| ≤ 1 in what follows.

Corollary 5 (Equivalent damping free natural angular frequency VI). 

Denote by ω_eqn6 the equivalent damping free natural angular frequency of class VI fractional vibrators [25,26]. Define it by

$${\omega }_{\mathrm{eqn}6}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}6}}{m_{\mathrm{eq}6}}}}.$$

(26)

Then,

$${\omega }_{\mathrm{eqn}6}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}.$$

(27)

Proof. 

Substituting m_eq6 and k_eq6 into (26) produces (27). The proof ends. □

Corollary 6 (Equivalent damped natural angular frequency VI). 

Let ω_eqd6 be the equivalent damped natural angular frequency of class VI fractional vibrators [25,26]. Define

$${\omega }_{\mathrm{eqd}6}={\omega }_{\mathrm{eqn}6}\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2}.$$

(28)

Then,

$$\begin{array}{l}{\omega }_{\mathrm{eqd}6}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}\\ \sqrt{1-{\left({\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}\right)}^2}.\end{array}$$

(29)

Proof. 

Substituting ω_eqn6 and ζ_eq6 into (28) results in (29). The proof is finished. □

Corollary 7 (Equivalent frequency ratio VI). 

Let γ_eq6 be the equivalent frequency ratio of class VI fractional vibrators [25,26]. Define it by

$${\gamma }_{\mathrm{eq}6}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}6}}}.$$

(30)

Then,

$${\gamma }_{\mathrm{eq}6}=\gamma \sqrt{{\displaystyle \frac{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}},$$

(31)

where $\gamma ={\displaystyle \frac{\omega }{{\omega }_n}}.$

Proof. 

Substituting ω_eqn6 into (30) yields (31). The proof is finished. □

2.4. Responses of Class VI Fractional Vibrator

By using m_eq61, ζ_eq6, and ω_eqn6, we rewrite (23) by (32) below

$${\displaystyle \frac{d^2{x}_6(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{\displaystyle \frac{d{x}_6(t)}{dt}}+{\omega }_{\mathrm{eqn}6}^2{x}_6(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}6}}}.$$

(32)

Theorem 3 (Free response VI). 

Let x₆(t) be the free response of a class VI fractional vibrator [25,26]. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}}=0,\\ x_6(0)=x_{60},x_6^{\prime }(0)=v_{60}.\end{array}\right.$$

(33)

Then,

$$x_6(t)=e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}\left(x_{60}\cos {\omega }_{\mathrm{eqd}6}t+{\displaystyle \frac{v_{60}+{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{x}_{60}}{{\omega }_{\mathrm{eqd}6}}}\sin {\omega }_{\mathrm{eqd}6}t\right), t\ge 0.$$

(34)

Proof. 

The solution to (33) is equal to the solution to the following differential equation

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_6(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{\displaystyle \frac{d{x}_6(t)}{dt}}+{\omega }_{\mathrm{eqn}6}^2{x}_6(t)=0,\\ x_6(0)=x_{60},x_6^{\prime }(0)=v_{60}.\end{array}\right.$$

(35)

From (35), we have (34). This completes the proof. □

Figure 1 shows some plots of x₆(t).

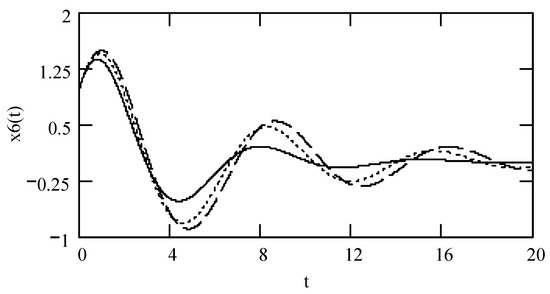
Figure 1. Plots of x₆(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β, λ) = (1.9, 1.9, 0.3) (solid line), (2.1, 1.8, 0.4) (dotted line), and (2.2, 1.7, 0.5) (dashed line).

Theorem 4 (Impulse response VI). 

Let h₆(t) be the impulse response of a class VI fractional vibrator [25,26]. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^{\alpha }{h}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{h}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{h}_6(t)}{d{t}^{\lambda }}}=\delta (t)$$

(36)

with zero initial conditions. Then,

$$h_6(t)={\displaystyle \frac{1}{m_{\mathrm{eq}6}{\omega }_{\mathrm{eqd}6}}}{e}^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}\sin {\omega }_{\mathrm{eqd}6}t, t\ge 0.$$

(37)

Proof. 

The solution to (36) is equivalent to the one in the following differential equation

$${\displaystyle \frac{d^2{h}_6(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{\displaystyle \frac{d{h}_6(t)}{dt}}+{\omega }_{\mathrm{eqn}6}^2{h}_6(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}6}}}.$$

(38)

Equation (38) implies that (37) holds. The proof is finished. □

Some plots of h₆(t) are shown in Figure 2.

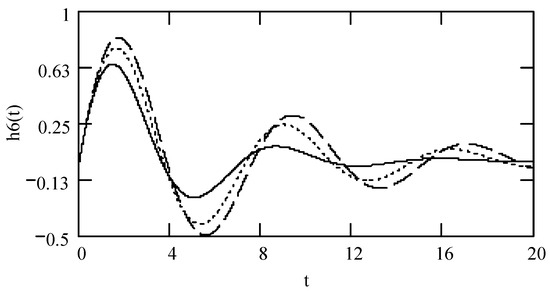
Figure 2. Plots of h₆(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β, λ) = (1.9, 1.9, 0.3) (solid line), (2.1, 1.8, 0.4) (dotted line), and (2.2, 1.7, 0.5) (dashed line).

Theorem 5 (Step response VI). 

Let g₆(t) be the unit step response of a class VI fractional vibrator [25,26]. It is the solution to (39) below

$$m{\displaystyle \frac{d^{\alpha }{g}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{g}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{g}_6(t)}{d{t}^{\lambda }}}=u(t)$$

(39)

with zero initial conditions. Then,

$$g_6(t)={\displaystyle \frac{1}{k_{\mathrm{eq}6}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2}}}\cos \left({\omega }_{\mathrm{eqd}6}t-{\varphi }_6\right)\right], t\ge 0,$$

(40)

where

$${\varphi }_6={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}6}}{\sqrt{1-{\zeta }_{\mathrm{eq}6}^2}}}.$$

(41)

Proof. 

The solution to (39) is equal to the one in the following differential equation

$${\displaystyle \frac{d^2{g}_6(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{\displaystyle \frac{d{g}_6(t)}{dt}}+{\omega }_{\mathrm{eqn}6}^2{g}_6(t)={\displaystyle \frac{u(t)}{m_{\mathrm{eq}6}}}.$$

(42)

From (42), we see that (40) with (41) is sound. This finishes the proof. □

The step response g₆(t) can also be attained from (43) in the form

$$g_6(t)={\displaystyle \underset{0}{\overset{t}{\int }}{h}_6(t)dt}.$$

(43)

Figure 3 indicates some of the plots of g₆(t).

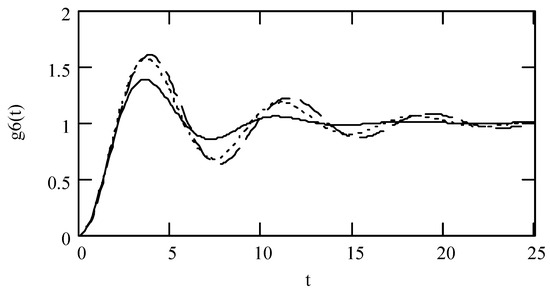
Figure 3. Plots of g₆(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β, λ) = (1.9, 1.9, 0.3) (solid line), (2.1, 1.8, 0.4) (dotted line), and (2.2, 1.7, 0.5) (dashed line).

Theorem 6 (Sinusoidal response VI). 

Denote by x_6zs(t) the sinusoidal response of a class VI fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_{6\mathrm{zs}}(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_{6\mathrm{zs}}(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_{6\mathrm{zs}}(t)}{d{t}^{\lambda }}}=A\cos \omega t,\\ x_{6\mathrm{zs}}(0)=0,x_{6\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(44)

Then,

$$x_{6\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}6}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}6}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}6}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}6}t\\ -\frac{{\varsigma }_{\mathrm{eq}6}}{\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2}}\left({\omega }_{\mathrm{eqn}6}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}6}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}6}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}\omega \right)}^2}}.$$

(45)

Proof. 

The solution to (44) is equal to the solution to (46) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{6\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{\displaystyle \frac{d{x}_{6\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}6}^2{x}_{6\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}6}}},\\ x_{6\mathrm{zs}}(0)=0,x_{6\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(46)

From (46), we see that (45) holds. This finishes the proof. □

Figure 4 indicates some of the plots of x_6zs(t).

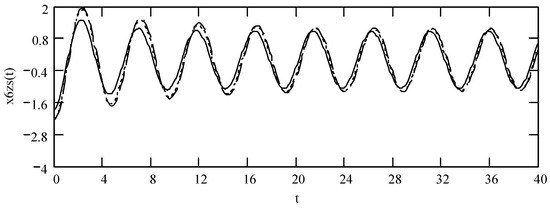
Figure 4. Plots of x_6zs(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β, λ) = (1.9, 1.9, 0.3) (solid line), (2.1, 1.8, 0.4) (dotted line), and (2.2, 1.7, 0.5) (dashed line).

2.5. Equivalent Logarithmic Decrement in Class VI Fractional Vibrators

Theorem 7 (Equivalent logarithmic decrement VI). 

Let t_i and t_i+1 be two successive time points of the free response x₆(t), where x₆(t) reaches its successive peak values of x₆(t_i) and x₆(t_i+1), respectively. Let Δ_eq6 be the equivalent logarithmic decrement in x₆(t) [25,26]. Then,

$${\Delta }_{\mathrm{eq}6}=\ln {\displaystyle \frac{x_6(t_i)}{x_6(t_{i+1})}}={\displaystyle \frac{\pi \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}{\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\right]}}}}.$$

(47)

Proof. 

With the free response x₆(t), we have

$$\ln {\displaystyle \frac{x_6(t_i)}{x_6(t_{i+1})}}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}6}}{\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2}}}.$$

(48)

Substituting ζ_eq6 into (48) results in (47). Thus, Theorem 7 holds. This finishes the proof. □

2.6. Quality Factor of Class VI Fractional Vibrators

Denote by Q_eq6 the equivalent Q factor of class VI fractional vibrators. Equation (32) is the equivalent motion equation of class VI fractional vibrators, that is, in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}6}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}6}}}.$$

(49)

Theorem 8 (Equivalent Q factor VI). 

The quantity Qeq6 is given by

$$Q_{\mathrm{eq}6}={\displaystyle \frac{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}}.$$

(50)

Proof. 

Substituting ζ_eq6 into (49) yields (50) [25,26]. The proof ends. □

2.7. Equivalent Frequency Bandwidth of Class VI Fractional Vibrators

Let B_eq6,0.707 be the equivalent frequency bandwidth of class VI fractional vibrators. Due to (32) being in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}6,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}6}}{2\pi Q_{\mathrm{eq}6}}}.$$

(51)

Theorem 9 (Equivalent frequency bandwidth VI). 

The quantity B_eq6,0.707 is given by

$${\mathrm{B}}_{\mathrm{eq}6,0.707}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\pi \left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}}.$$

(52)

Proof. 

Substituting ω_eqn6 and Q_eq6 into (51) results in (52). The proof ends. □

2.8. More about Frequency Transfer Function of Class VI Fractional Vibrations

By using γ_eq6, ζ_eq6 and k_eq6 [25,26], we have

$$H_6(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}6}\left(1-{\gamma }_{\mathrm{eq}6}^2+i2{\varsigma }_{\mathrm{eq}6}{\gamma }_{\mathrm{eq}6}\right)}}.$$

(53)

In a polar system, we express (53) by H₆(ω) = |H₆(ω)|exp[−φ₆(ω)], where

$$\begin{array}{l}\left|H_6(\omega )\right|={\displaystyle \frac{1}{k_{\mathrm{eq}6}}}{\displaystyle \frac{1}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}6}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}6}{\gamma }_{\mathrm{eq}6}\right)}^2}}}\\ ={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{\begin{array}{l}{\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\gamma }^2{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2\end{array}}}}.\end{array}$$

(54)

Equation (54) designates |H₆(ω)|. Equation (55) below gives the phase of H₆(ω)

$${\phi }_6(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}6}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}6}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}6}{\gamma }_{\mathrm{eq}6}\right)}^2}}}.$$

(55)

Figure 5 demonstrates some of the plots of |H₆(ω)| and φ₆(ω).

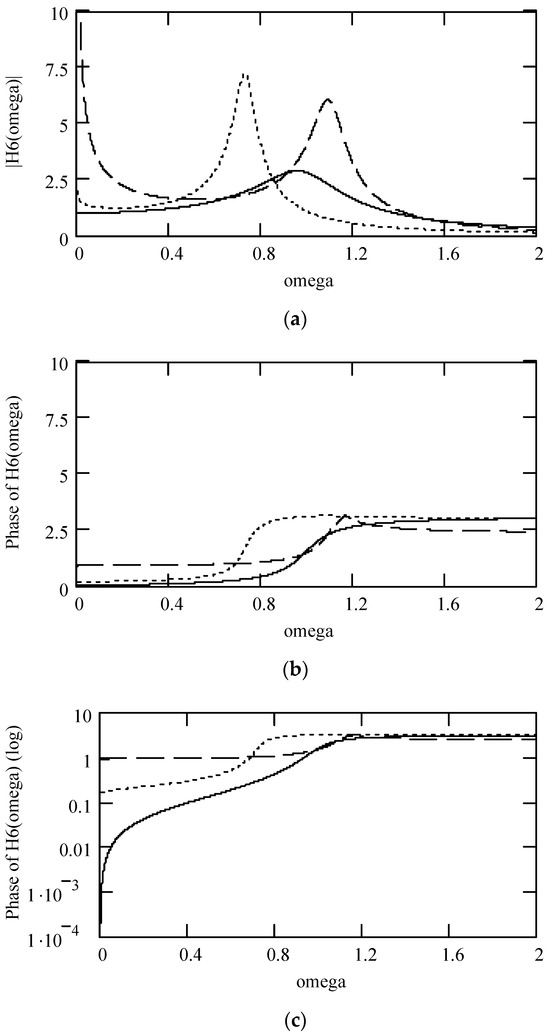
Figure 5. Plots of |H₆(ω)| and φ₆(ω) for m = 1, c = 0.2, and k = 1 when (α, β, λ) = (1.9, 1.0, 0) (solid line), (2.1, 0.8, 0.1) (dotted line), and (2.5, 0.5, 0.6) (dashed line). (a) |H₆(ω)|; (b) φ₆(ω); (c) logφ₆(ω).

3. Representing Analytic Theory of Class I Fractional Vibrators

This section addresses a tutorial with respect to the analytic theory of class I fractional vibrators in seven aspects as follows. (1) The analytical expression of frequency transfer function of class I fractional vibrators in Theorem 10 in Section 3.1. (2) The equivalent motion equation of class I fractional vibrators in Theorem 11 in Section 3.2. (3) The analytical expressions for the equivalent parameters of class I fractional vibrators in Section 3.3. (4) The analytical expressions of responses of class I fractional vibrators in Theorems 12–15 in Section 3.4. (5) The analytical expression of the equivalent logarithmic decrement in class I fractional vibrators in Theorem 16 in Section 3.5. (6) The analytical expression of the equivalent quality factor of class I fractional vibrators in Theorem 17 in Section 3.6. (7) Additionally, we put forward the analytical expression of the equivalent frequency bandwidth for class I fractional vibrators in Theorem 18 in Section 3.7.

3.1. Frequency Transfer Function of Class I Fractional Vibrator

Theorem 10 (Frequency transfer function I). 

Denote by H₁(ω) the frequency transfer function of a class I fractional vibrator. Then,

$$H_1(\omega )={\displaystyle \frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+im{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k}}.$$

(56)

Proof. 

A class I fractional vibrator is a special case of a class VI one when c = 0 and λ = 0. Thus, doing the operation of (57)

$$H_1(\omega )={\left.H_6(\omega )\right|}_{c=0,\lambda =0}$$

(57)

yields (56). The proof is finished. □

3.2. Equivalent Motion Equation of Class I Fractional Vibrator

Theorem 11 (Equivalent motion equation I). 

The motion Equation (1) of a class I fractional vibrators is equivalently expressed by

$$-m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}{\displaystyle \frac{d^2{x}_1(t)}{d{t}^2}}+m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}{\displaystyle \frac{d{x}_1(t)}{dt}}+k{x}_1(t)=f(t).$$

(58)

Proof. 

Because a class I fractional vibrator is a special case of a class VI one when c = 0 and λ = 0, replacing c and λ in (18) with 0 produces (58). This finishes the proof. □

3.3. Equivalent Parameters of Class I Fractional Vibrator

Corollary 8 (Equivalent mass I). 

Let m_eq1 be the equivalent mass of class I fractional vibrators. Then,

$$m_{\mathrm{eq}1}=-m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}.$$

(59)

Proof. 

The right side of the above expression is the coefficient of ${\displaystyle \frac{d^2{x}_1(t)}{d{t}^2}}$ in (58). Thus, (59) is true. This finishes the proof. □

Corollary 9 (Equivalent damping I). 

Let c_eq1 be the equivalent damping of class I fractional vibrators. Then,

$$c_{\mathrm{eq}1}=m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}.$$

(60)

Proof. 

Because the right side of the above expression is the coefficient of $x_1^{\prime }(t)$ in (58), (60) is true. The proof is finished. □

Corollary 10 (Equivalent stiffness I). 

Let k_eq1 be the equivalent stiffness of class I fractional vibrators. Then,

k_eq1= k.

(61)

Proof. 

Since the right side of the above expression is the coefficient of x₁(t) in (58), (61) is true. The proof ends. □

Using m_eq1, c_eq1, and k_eq1 to rewrite (58) yields the equivalent motion equation I in the form of (62) below

$$m_{\mathrm{eq}1}{\displaystyle \frac{d^2{x}_1(t)}{d{t}^2}}+c_{\mathrm{eq}1}{\displaystyle \frac{d{x}_1(t)}{dt}}+k_{\mathrm{eq}1}{x}_1(t)=f(t).$$

(62)

Corollary 11 (Equivalent damping ratio I). 

Let ζ_eq1 be the equivalent damping ratio for a class I fractional vibrator. It is defined by (63) below

$${\varsigma }_{\mathrm{eq}1}={\displaystyle \frac{c_{\mathrm{eq}1}}{2\sqrt{m_{\mathrm{eq}1}{k}_{\mathrm{eq}1}}}}.$$

(63)

Then,

$${\varsigma }_{\mathrm{eq}1}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k}}}.$$

(64)

Proof. 

Substituting c = 0 and λ = 0 in (25) regarding ζ_eq6 yields (64). This finishes the proof. □

Due to ζ_eq1 > 1 being trivial in vibrations, we default |ζ_eq1| ≤ 1 in what follows.

Corollary 12 (Equivalent damping free natural angular frequency I). 

Let ω_eqn1 be the equivalent damping free natural angular frequency of class I fractional vibrators. Define it by (65) below

$${\omega }_{\mathrm{eqn}1}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}1}}{m_{\mathrm{eq}1}}}}.$$

(65)

Then,

$${\omega }_{\mathrm{eqn}1}=\sqrt{{\displaystyle \frac{k}{-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}}.$$

(66)

Proof. 

Substituting c = 0 and λ = 0 in (27) with respect to ω_eqn6 produces (66). The proof ends. □

Corollary 13 (Equivalent damped natural angular frequency I). 

Let ω_eqd1 be the equivalent damped natural angular frequency of class I fractional vibrators. Define

$${\omega }_{\mathrm{eqd}1}={\omega }_{\mathrm{eqn}1}\sqrt{1-{\varsigma }_{\mathrm{eq}1}^2}.$$

(67)

Then,

$${\omega }_{\mathrm{eqd}1}=\sqrt{{\displaystyle \frac{k}{-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}}\sqrt{1-{\left({\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k}}}\right)}^2}.$$

(68)

Proof. 

Substituting ω_eqn1 and ζ_eq1 into (67) results in (68). The proof is finished. □

Corollary 14 (Equivalent frequency ratio I). 

Denote by γ_eq1 the equivalent frequency ratio of class I fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}1}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}1}}}.$$

(69)

Then,

$${\gamma }_{\mathrm{eq}6}=\gamma \sqrt{{\displaystyle \frac{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(70)

Proof. 

Substituting ω_eqn1 into (69) produces (70). This finishes the proof. □

3.4. Responses of Class I Fractional Vibrator

By using m_eq1, ζ_eq1, and ω_eqn1, we rewrite the equivalent motion equation of a class I fractional vibrator by (71) below

$${\displaystyle \frac{d^2{x}_1(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{\displaystyle \frac{d{x}_1(t)}{dt}}+{\omega }_{\mathrm{eqn}1}^2{x}_1(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}1}}}.$$

(71)

Theorem 12 (Free response I). 

Denote by x₁(t) the free response of a class I fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_1(t)}{d{t}^{\alpha }}}+k{x}_1(t)=0,\\ x_1(0)=x_{10},x_1^{\prime }(0)=v_{10}.\end{array}\right.$$

(72)

Then,

$$x_1(t)=e^{-{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}t}\left(x_{10}\cos {\omega }_{\mathrm{eqd}1}t+{\displaystyle \frac{v_{10}+{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{x}_{10}}{{\omega }_{\mathrm{eqd}1}}}\sin {\omega }_{\mathrm{eqd}1}t\right), t\ge 0.$$

(73)

Proof. 

The solution to (72) is equal to the solution to the following differential equation of (74)

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_1(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{\displaystyle \frac{d{x}_1(t)}{dt}}+{\omega }_{\mathrm{eqn}1}^2{x}_1(t)=0,\\ x_1(0)=x_{10},x_1^{\prime }(0)=v_{10}.\end{array}\right.$$

(74)

Then, (73) holds. This completes the proof. □

Figure 6 indicates some of the plots of x₁(t).

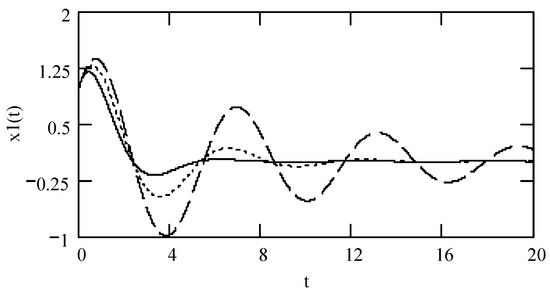
Figure 6. Plots of x₁(t) for ω = 1.3, m = 1, and k = 1 when α = 1.5 (solid line), 1.7 (dotted line), and 1.9 (dashed line).

Theorem 13 (Impulse response I). 

Denote by h₁(t) the impulse response of a class I fractional vibrator. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^{\alpha }{h}_1(t)}{d{t}^{\alpha }}}+k{h}_1(t)=\delta (t)$$

(75)

with zero initial conditions. Then,

$$h_1(t)=e^{-{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}t}{\displaystyle \frac{1}{m_{\mathrm{eq}1}{\omega }_{\mathrm{eqd}1}}}\sin {\omega }_{\mathrm{eqd}1}t, t\ge 0.$$

(76)

Proof. 

The solution to (75) is equivalent to the one in differential Equation (77)

$${\displaystyle \frac{d^2{h}_1(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{\displaystyle \frac{d{h}_1(t)}{dt}}+{\omega }_{\mathrm{eqn}1}^2{h}_1(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}1}}}.$$

(77)

Hence, (76) is true. The proof ends. □

Some plots of h₁(t) are indicated in Figure 7.

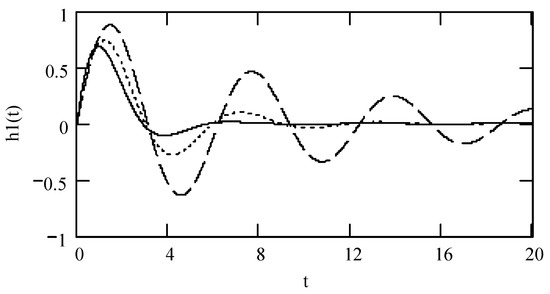
Figure 7. Plots of h₁(t) for ω = 1.3, m = 1, and k = 1 when α = 1.5 (solid line), 1.7 (dotted line), and 1.9 (dashed line).

Theorem 14 (Step response I). 

Denote by g₁(t) the unit step response of a class I fractional vibrator. It is the solution to the following equation

$$m{\displaystyle \frac{d^{\alpha }{g}_1(t)}{d{t}^{\alpha }}}+k{g}_1(t)=u(t)$$

(78)

with zero initial conditions. Then,

$$g_1(t)={\displaystyle \frac{1}{k_{\mathrm{eq}1}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}1}^2}}}\cos \left({\omega }_{\mathrm{eqd}1}t-{\varphi }_1\right)\right],t\ge 0,$$

(79)

where

$${\varphi }_1={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}1}}{\sqrt{1-{\zeta }_{\mathrm{eq}1}^2}}}.$$

(80)

Proof. 

The solution to (78) is equal to the one to differential Equation (81)

$${\displaystyle \frac{d^2{g}_1(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{\displaystyle \frac{d{g}_1(t)}{dt}}+{\omega }_{\mathrm{eqn}1}^2{g}_1(t)={\displaystyle \frac{u(t)}{m_{\mathrm{eq}1}}}.$$

(81)

Thus, (79) with (80) is true. This finishes the proof. □

The step response g₁(t) can also be attained from (82) below

$$g_1(t)={\displaystyle \underset{0}{\overset{t}{\int }}{h}_1(t)dt}.$$

(82)

Figure 8 shows some plots of g₁(t).

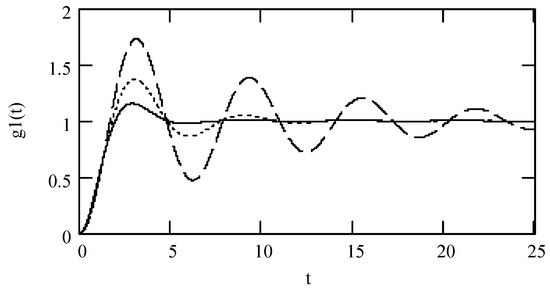
Figure 8. Plots of g₁(t) for ω = 1.3, m = 1, and k = 1 when α = 1.5 (solid line), 1.7 (dotted line), and 1.9 (dashed line).

Theorem 15 (Sinusoidal response I). 

Let x_1zs(t) be the sinusoidal response of a class I fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_{1\mathrm{zs}}(t)}{d{t}^{\alpha }}}+k{x}_{1\mathrm{zs}}(t)=A\cos \omega t,\\ x_{1\mathrm{zs}}(0)=0,x_{1\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(83)

Then,

$$x_{1\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}1}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}1}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}1}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}1}t\\ -\frac{{\varsigma }_{\mathrm{eq}1}}{\sqrt{1-{\varsigma }_{\mathrm{eq}1}^2}}\left({\omega }_{\mathrm{eqn}1}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}1}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}1}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}\omega \right)}^2}}.$$

(84)

Proof. 

The solution to (83) is equal to the one to (85) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{1\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}1}{\omega }_{\mathrm{eqn}1}{\displaystyle \frac{d{x}_{1\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}1}^2{x}_{1\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}1}}},\\ x_{1\mathrm{zs}}(0)=0,x_{1\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(85)

Hence, (84) results. This finishes the proof. □

Figure 9 shows some plots of x_1zs(t).

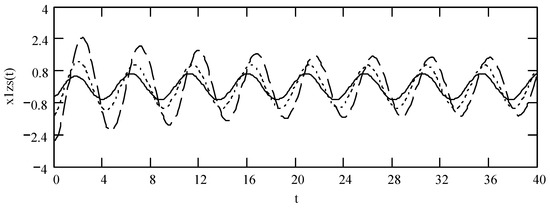
Figure 9. Plots of x_1zs(t) for ω = 1.3, m = 1, and k = 1 when α = 1.5 (solid line), 1.7 (dotted line), and 1.9 (dashed line).

3.5. Equivalent Logarithmic Decrement in Class I Fractional Vibrators

Theorem 16 (Equivalent logarithmic decrement I). 

Let t_i and t_i+1 be two successive time points of the free response x₁(t), where x₁(t) reaches its successive peak values of x₁(t_i) and x₁(t_i+1), respectively. Let Δ_eq1 be the equivalent logarithmic decrement in x₁(t). Then,

$${\Delta }_{\mathrm{eq}1}=\ln {\displaystyle \frac{x_1(t_i)}{x_1(t_{i+1})}}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}1}}{\sqrt{1-{\varsigma }_{\mathrm{eq}1}^2}}}={\displaystyle \frac{\pi \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}}{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k}}}{\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k\right]}}}}.$$

(86)

Proof. 

Substituting c = 0 and λ = 0 in (47) for Δ_eq6 yields (86). This finishes the proof. □

3.6. Quality Factor of Class I Fractional Vibrators

Let Q_eq1 be the equivalent Q factor of class I fractional vibrators. The equivalent motion equation of class I fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}1}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}1}}}.$$

(87)

Theorem 17 (Equivalent Q factor I). 

The quantity Q_eq1 is given by

$$Q_{\mathrm{eq}1}={\displaystyle \frac{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k}}{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}}}.$$

(88)

Proof. 

Substituting ζ_eq1 into (87) produces (88). The proof ends. □

3.7. Equivalent Frequency Bandwidth of Class I Fractional Vibrators

Let B_eq1,0.707 be the equivalent frequency bandwidth of class I fractional vibrators. Owing to the equivalent motion equation of class I fractional vibrators being in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}1,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}1}}{2\pi Q_{\mathrm{eq}1}}}.$$

(89)

Theorem 18 (Equivalent frequency bandwidth I). 

The quantity B_eq1,0.707 is expressed by

$${\mathrm{B}}_{\mathrm{eq}1,0.707}=-{\displaystyle \frac{\omega \sin \frac{\alpha \pi }{2}}{2\pi \cos \frac{\alpha \pi }{2}}}.$$

(90)

Proof. 

Substituting ω_eqn1 and Q_eq1 into (89) yields (90). The proof is finished. □

3.8. More about Frequency Transfer Function of Class I Fractional Vibrators

By using γ_eq1, ζ_eq1, and k_eq1, we write H₁(ω) as (91) below

$$H_1(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}1}\left(1-{\gamma }_{\mathrm{eq}1}^2+i2{\varsigma }_{\mathrm{eq}1}{\gamma }_{\mathrm{eq}1}\right)}}.$$

(91)

When writing H₁(ω) as |H₁(ω)|exp[−φ₁(ω)], we have |H₁(ω)| in the form of (92)

$$\begin{array}{l}\left|H_1(\omega )\right|={\displaystyle \frac{1}{k_{\mathrm{eq}1}}}{\displaystyle \frac{1}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}1}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}1}{\gamma }_{\mathrm{eq}1}\right)}^2}}}\\ ={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{{\left[1+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)\right]}^2+{\gamma }^2{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\right)}^2}}}.\end{array}$$

(92)

The phase of H₁(ω) is given by (93) in the form

$${\phi }_1(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}1}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}1}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}1}{\gamma }_{\mathrm{eq}1}\right)}^2}}}.$$

(93)

Figure 10 indicates some of the plots of |H₁(ω)| and φ₁(ω).

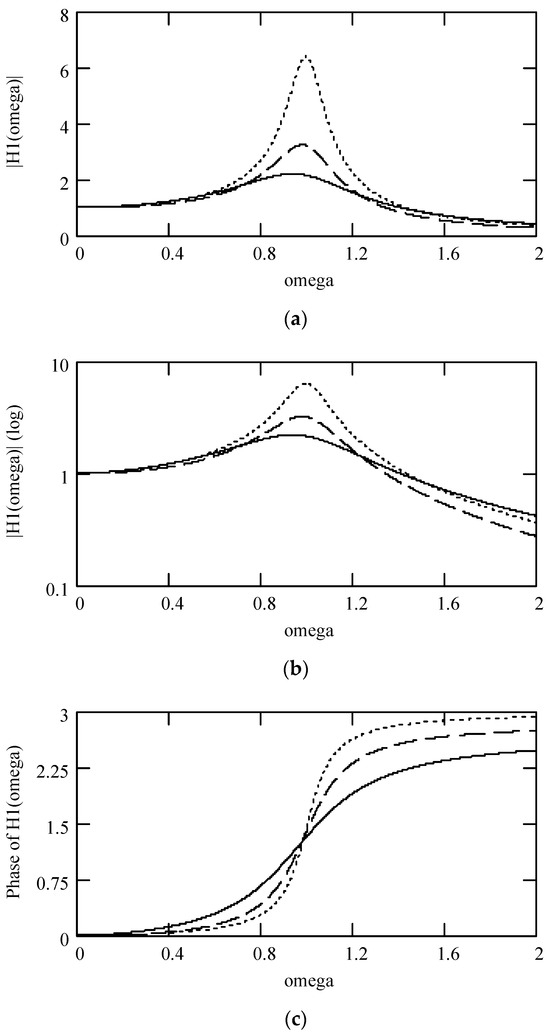
Figure 10. Plots of |H₁(ω)| and φ₁(ω) for m = 1 and k = 1 when α = 1.7 (solid line), 1.9 (dotted line), and 2.2 (dashed line). (a) |H₁(ω)|; (b) log|H₁(ω)|; (c) φ₁(ω).

4. Analytic Theory of Class II Fractional Vibrators

This section explains a tutorial regarding the analytic theory of class II fractional vibrators in seven parts: (1) the analytical expression of frequency transfer function of class II fractional vibrator in Theorem 19 in Section 4.1; (2) the equivalent motion equation of class II fractional vibrators in Theorem 20 in Section 4.2; (3) the analytical expressions for the equivalent parameters of class II fractional vibrators in Section 4.3; (4) the analytical expressions of class II fractional vibrator responses in Theorems 21–24 in Section 4.4; (5) the analytical expression of the equivalent logarithmic decrement in class II fractional vibrators in Theorem 25 in Section 4.5; (6) the analytical expression for the equivalent quality factor of class II fractional vibrators in Theorem 26 in Section 4.6; (7) additionally, we propose an analytical expression for the equivalent frequency bandwidth of class II fractional vibrators in Theorem 27 in Section 4.7.

4.1. Frequency Transfer Function of Class II Fractional Vibrator

Theorem 19 (Frequency transfer function II). 

Let H₂(ω) be the frequency transfer function of a class II fractional vibrator. Then,

$$H_2(\omega )={\displaystyle \frac{1}{-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k+ic{\omega }^{\beta }\sin \frac{\beta \pi }{2}}}.$$

(94)

Proof. 

Since a class II fractional vibrator is a special case of a class VI fractional vibrator for α = 2 and λ = 0, doing the operation of (95)

$$H_2(\omega )={\left.H_6(\omega )\right|}_{\alpha =2,\lambda =0}$$

(95)

produces (94). The proof ends. □

4.2. Equivalent Motion Equation of Class II Fractional Vibrator

Theorem 20 (Equivalent motion equation II). 

The motion equation of class II fractional vibrators is equivalently expressed by

$$m-c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}{\displaystyle \frac{d{x}_2(t)}{dt}}+k{x}_2(t)=f(t).$$

(96)

Proof. 

Because a class II fractional vibrator is a special case of class VI one when α = 2 and λ = 0, substituting α = 2 and λ = 0 in (18) yields (96). The proof is finished. □

4.3. Equivalent Parameters of Class II Fractional Vibrator

Corollary 15 (Equivalent mass II). 

Denote by m_eq2 the equivalent mass of a class II fractional vibrator. Then,

$$m_{\mathrm{eq}2}=m-c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}.$$

(97)

Proof. 

The right side of the above expression is the coefficient of $x_2^{″}(t)$ in (96). Thus, (97) holds. This finishes the proof. □

Corollary 16 (Equivalent damping II). 

Denote by c_eq2 the equivalent damping of a class II fractional vibrator. Then,

$$c_{\mathrm{eq}2}=c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}.$$

(98)

Proof. 

Because the right side of the above expression is the coefficient of  $x_2^{\prime }(t)$ in (96), (98) holds. The proof ends. □

Corollary 17 (Equivalent stiffness II). 

Let k_eq2 be the equivalent stiffness of a class II fractional vibrator. Then,

k_eq2 = k.

(99)

Proof. 

As the right side of the above expression is the coefficient of x₂(t) in (96), (99) is true. The proof ends. □

Using m_eq2, c_eq2, and k_eq2 to rewrite (96) produces the equivalent motion equation II in the form (100) below

$$m_{\mathrm{eq}2}{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+c_{\mathrm{eq}2}{\displaystyle \frac{d{x}_2(t)}{dt}}+k_{\mathrm{eq}2}{x}_2(t)=f(t).$$

(100)

Corollary 18 (Equivalent damping ratio II). 

Denote by ζ_eq2 the equivalent damping ratio for a class II fractional vibrator. Define it by the expression of (101)

$${\varsigma }_{\mathrm{eq}2}={\displaystyle \frac{c_{\mathrm{eq}2}}{2\sqrt{m_{\mathrm{eq}2}{k}_{\mathrm{eq}2}}}}.$$

(101)

Then,

$${\varsigma }_{\mathrm{eq}2}={\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}.$$

(102)

Proof. 

Substituting α = 2 and λ = 0 in ζ_eq6 results in (102). This finishes the proof. □

Due to ζ_eq2 > 1 being trivial in vibrations, we default |ζ_eq2| ≤ 1 in what follows.

Corollary 19 (Equivalent damping free natural angular frequency II). 

Denote by ω_eqn2 the equivalent damping free natural angular frequency of a class II fractional vibrator. Define it by the expression of (103)

$${\omega }_{\mathrm{eqn}2}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}2}}{m_{\mathrm{eq}2}}}}.$$

(103)

Then,

$${\omega }_{\mathrm{eqn}2}=\sqrt{{\displaystyle \frac{k}{m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}}}.$$

(104)

Proof. 

Substituting α = 2 and λ = 0 in ω_eqn6 produces (104). The proof ends. □

Corollary 20 (Equivalent damped natural angular frequency II). 

Denote by ω_eqd2 the equivalent damped natural angular frequency of a class II fractional vibrator. Define

$${\omega }_{\mathrm{eqd}2}={\omega }_{\mathrm{eqn}2}\sqrt{1-{\varsigma }_{\mathrm{eq}2}^2}.$$

(105)

Then,

$${\omega }_{\mathrm{eqd}2}=\sqrt{{\displaystyle \frac{k}{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}\sqrt{1-{\left({\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}\right)}^2}.$$

(106)

Proof. 

Substituting ω_eqn2 and ζ_eq2 into (105) yields (106). The proof ends. □

Corollary 21 (Equivalent frequency ratio II). 

Let γ_eq2 be the equivalent frequency ratio of class II fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}2}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}2}}}.$$

(107)

Then,

$${\gamma }_{\mathrm{eq}2}=\gamma \sqrt{1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}}.$$

(108)

Proof. 

Substituting ω_eqn2 into (107) results in (108). This finishes the proof. □

4.4. Responses of Class II Fractional Vibrator

By using m_eq2, ζ_eq2, and ω_eqn2, we write the motion equation of a class II fractional vibrator by (109) below

$${\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{\displaystyle \frac{d{x}_2(t)}{dt}}+{\omega }_{\mathrm{eqn}2}^2{x}_2(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}2}}}.$$

(109)

Theorem 21 (Free response II). 

Let x₂(t) be the free response of a class II fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_2(t)}{d{t}^{\beta }}}+k{x}_2(t)=0,\\ x_2(0)=x_{20},x_2^{\prime }(0)=v_{20}.\end{array}\right.$$

(110)

Then,

$$x_2(t)=e^{-{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}t}\left(x_{20}\cos {\omega }_{\mathrm{eqd}2}t+{\displaystyle \frac{v_{20}+{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{x}_{20}}{{\omega }_{\mathrm{eqd}2}}}\sin {\omega }_{\mathrm{eqd}2}t\right), t\ge 0.$$

(111)

Proof. 

The solution to (110) equals to the solution to differential Equation (112)

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{\displaystyle \frac{d{x}_2(t)}{dt}}+{\omega }_{\mathrm{eqn}2}^2{x}_2(t)=0,\\ x_2(0)=x_{20},x_2^{\prime }(0)=v_{20}.\end{array}\right.$$

(112)

Then, (111) is true. This completes the proof. □

Figure 11 shows some of the plots of x₂(t).

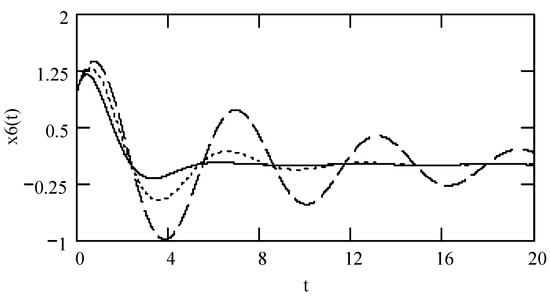
Figure 11. Plots of x₂(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when β = 0.9 (solid line), 1.4 (dotted line), and 1.9 (dashed line).

Theorem 22 (Impulse response II). 

Let h₂(t) be the impulse response of a class II fractional vibrator. It is the solution to the following fractional differential equation

$$m{\displaystyle \frac{d^2{h}_2(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{h}_2(t)}{d{t}^{\beta }}}+k{h}_2(t)=\delta (t)$$

(113)

with zero initial conditions. Then,

$$h_2(t)=e^{-{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}t}{\displaystyle \frac{1}{m_{\mathrm{eq}2}{\omega }_{\mathrm{eqd}2}}}\sin {\omega }_{\mathrm{eqd}2}t, t\ge 0.$$

(114)

Proof. 

The solution to (113) is equivalent to the one to (115)

$${\displaystyle \frac{d^2{h}_2(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{\displaystyle \frac{d{h}_2(t)}{dt}}+{\omega }_{\mathrm{eqn}2}^2{h}_2(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}2}}}.$$

(115)

Thus, (114) holds. The proof ends. □

Some plots of h₂(t) are shown in Figure 12.

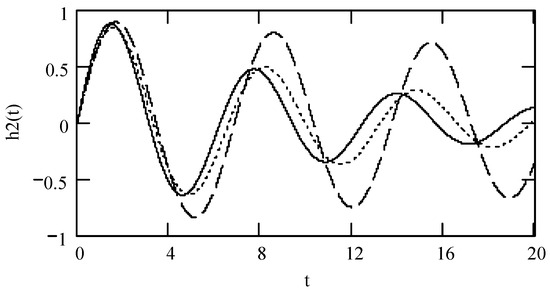
Figure 12. Plots of h₂(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when β = 0.9 (solid line), 1.4 (dotted line), and 1.9 (dashed line).

Theorem 23 (Step response II). 

Denote by g₂(t) the unit step response of a class II fractional vibrator. It is the solution to

$$m{\displaystyle \frac{d^2{g}_2(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{g}_2(t)}{d{t}^{\beta }}}+k{g}_2(t)=u(t)$$

(116)

with zero initial conditions. Then,

$$g_2(t)={\displaystyle \frac{1}{k_{\mathrm{eq}2}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}2}^2}}}\cos \left({\omega }_{\mathrm{eqd}2}t-{\varphi }_2\right)\right],t\ge 0,$$

(117)

where

$${\varphi }_2={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}2}}{\sqrt{1-{\zeta }_{\mathrm{eq}2}^2}}}.$$

(118)

Proof. 

The solution to (116) is equal to the one to (119)

$${\displaystyle \frac{d^2{g}_2(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{\displaystyle \frac{d{g}_2(t)}{dt}}+{\omega }_{\mathrm{eqn}2}^2{g}_2(t)={\displaystyle \frac{u(t)}{m_{\mathrm{eq}2}}}.$$

(119)

Thus, (117) with (118) holds. This finishes the proof. □

Figure 13 indicates some plots of g₂(t).

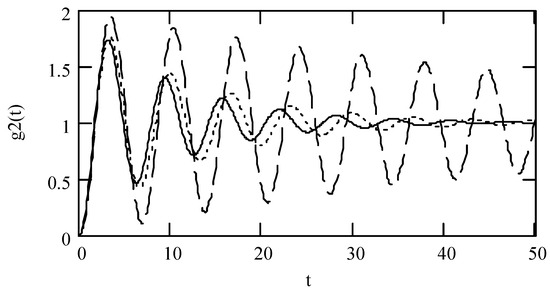
Figure 13. Plots of g₂(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when β = 0.9 (solid line), 1.4 (dotted line), and 1.9 (dashed line).

Theorem 24 (Sinusoidal response II). 

Denote by x_2zs(t) the sinusoidal response of a class II fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_{2\mathrm{zs}}(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_{2\mathrm{zs}}(t)}{d{t}^{\beta }}}+k{x}_{2\mathrm{zs}}(t)=A\cos \omega t,\\ x_{2\mathrm{zs}}(0)=0,x_{2\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(120)

Then,

$$x_{2\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}2}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}2}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}2}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}2}t\\ -\frac{{\varsigma }_{\mathrm{eq}2}}{\sqrt{1-{\varsigma }_{\mathrm{eq}2}^2}}\left({\omega }_{\mathrm{eqn}2}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}2}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}2}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}\omega \right)}^2}}.$$

(121)

Proof. 

The solution to (120) is equal to the one to (122) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{2\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}2}{\omega }_{\mathrm{eqn}2}{\displaystyle \frac{d{x}_{2\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}2}^2{x}_{2\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}2}}},\\ x_{2\mathrm{zs}}(0)=0,x_{2\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(122)

Hence, (121) holds. This finishes the proof. □

Figure 14 indicates some plots of x_2zs(t).

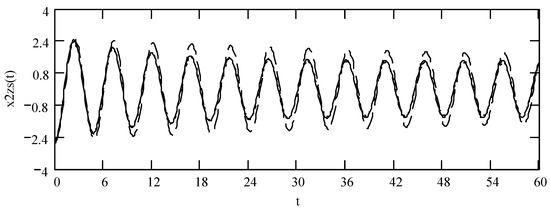
Figure 14. Plots of x_2zs(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when β = 0.9 (solid line), 1.4 (dotted line), and 1.9 (dashed line).

4.5. Equivalent Logarithmic Decrement in Class II Fractional Vibrators

Theorem 25 (Equivalent logarithmic decrement II). 

Let t_i and t_i+1 be two successive time points of the free response x₂(t), where x₂(t) reaches its successive peak values of x₂(t_i) and x₂(t_i+1), respectively. Let Δ_eq2 be the equivalent logarithmic decrement in x₂(t). Then,

$${\Delta }_{\mathrm{eq}2}=\ln {\displaystyle \frac{x_2(t_i)}{x_2(t_{i+1})}}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}2}}{\sqrt{1-{\varsigma }_{\mathrm{eq}2}^2}}}={\displaystyle \frac{\pi \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}{\sqrt{1-\frac{{\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}}.$$

(123)

Proof. 

Substituting α = 2 and λ = 0 in Δ_eq6 yields Δ_eq2 in (123). This finishes the proof. □

4.6. Quality Factor of Class II Fractional Vibrators

Denote by Q_eq2 the equivalent Q factor of class II fractional vibrators. The equivalent motion equation of class II fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}2}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}2}}}.$$

(124)

Theorem 26 (Equivalent Q factor II). 

The quantity Q_eq2 is given by

$$Q_{\mathrm{eq}2}={\displaystyle \frac{\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}}.$$

(125)

Proof. 

Substituting ζ_eq2 into (124) produces (125). The proof ends. □

4.7. Equivalent Frequency Bandwidth of Class II Fractional Vibrators

Let B_eq2,0.707 be the equivalent frequency bandwidth of class II fractional vibrators. Owing to the equivalent motion equation of class II fractional vibrators being in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}2,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}2}}{2\pi Q_{\mathrm{eq}2}}}.$$

(126)

Theorem 27 (Equivalent frequency bandwidth  II). 

The quantity B_eq2,0.707 is expressed by

$${\mathrm{B}}_{\mathrm{eq}2,0.707}={\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\pi \left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(127)

Proof. 

Substituting ω_eqn2 and Q_eq2 into (126) yields (127). The proof ends. □

4.8. More about Frequency Transfer Function of Class II Fractional Vibrators

By using γ_eq2, ζ_eq2, and k_eq2, we have H₂(ω) in the form (128)

$$H_2(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}2}\left(1-{\gamma }_{\mathrm{eq}2}^2+i2{\varsigma }_{\mathrm{eq}2}{\gamma }_{\mathrm{eq}2}\right)}}.$$

(128)

Writing H₂(ω) = |H₂(ω)|exp[−φ₂(ω)] results in |H₂(ω)| in the form of (129)

$$\begin{array}{l}\left|H_2(\omega )\right|={\displaystyle \frac{1}{k_{\mathrm{eq}2}}}{\displaystyle \frac{1}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}2}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}2}{\gamma }_{\mathrm{eq}2}\right)}^2}}}\\ ={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\left|1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{1}{{\omega }_n}2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}\right|}}\end{array}$$

(129)

and φ₂(ω) in the form of (130)

$${\phi }_2(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}2}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}2}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}2}{\gamma }_{\mathrm{eq}2}\right)}^2}}}.$$

(130)

Figure 15 indicates some of the plots of |H₂(ω)| and φ₂(ω).

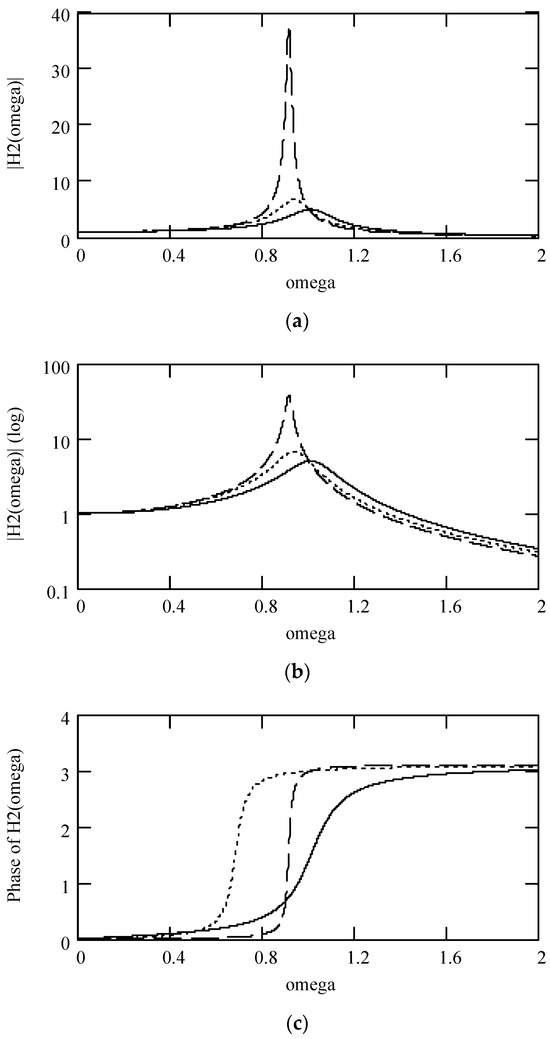
Figure 15. Plots of |H₂(ω)| and φ₂(ω) for m = 1, c = 0.2, and k = 1 when β = 0.9 (solid line), 1.5 (dotted line), and 1.9 (dashed line). (a) |H₂(ω)|; (b) log|H₂(ω)|; (c). φ₂(ω).

5. Representation of Analytic Theory of Class III Fractional Vibrators

We address a tutorial regarding the analytic theory of class III fractional vibrators from seven aspects: (1) the analytical expression of the frequency transfer function for a class III fractional vibrator in Theorem 28 in Section 5.1; (2) the equivalent motion equation of class III fractional vibrators in Theorem 29 in Section 5.2; (3) the analytical expressions for the equivalent parameters of class III fractional vibrators in Section 5.3; (4) the analytical expressions of responses of class III fractional vibrators in Theorems 30–33 in Section 5.4; (5) the analytical expression of the equivalent logarithmic decrement in class III fractional vibrators in Theorem 34 in Section 5.5; (6) the analytical expression of the equivalent quality factor of class III fractional vibrators in Theorem 35 in Section 5.6; (7) moreover, we present an analytical expression for the equivalent frequency bandwidth of class III fractional vibrators in Theorem 36 in Section 5.7.

5.1. Frequency Transfer Function of Class III Fractional Vibrator

Theorem 28 (Frequency transfer function III). 

Let H₃(ω) be the frequency transfer function of a class III fractional vibrator. Then,

$$\begin{array}{l}{H}_3(\omega )={\displaystyle \frac{1}{m{(i\omega )}^{\alpha }+c{(i\omega )}^{\beta }+k}}\\ ={\displaystyle \frac{1}{\left(m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}\right)+k+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta }\sin \frac{\beta \pi }{2}\right)}}.\end{array}$$

(131)

Proof. 

Note that a class III fractional vibrator is a special case of a class VI fractional vibrator for λ = 0. Thus, doing ${H_6(\omega )|}_{\lambda -0}$ yields (131). The proof is finished. □

5.2. Equivalent Motion Equation of Class III Fractional Vibrator

Theorem 29 (Equivalent motion equation III). 

The motion equation of class III fractional vibrators is equivalently expressed by

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right){\displaystyle \frac{d^2{x}_3(t)}{d{t}^2}}\\ +\left(m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}\right){\displaystyle \frac{d{x}_3(t)}{dt}}+k{x}_3(t)=f(t).\end{array}$$

(132)

Proof. 

Because a class III fractional vibrator is a special case of a class VI one for λ = 0, replacing λ with 0 in (18) produces (132). The proof ends. □

5.3. Equivalent Parameters of Class III Fractional Vibrator

Corollary 22 (Equivalent mass III). 

Let m_eq3 be the equivalent mass of class III fractional vibrators. Then,

$$m_{\mathrm{eq}3}=-\left(m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right).$$

(133)

Proof. 

The right side of the above expression is the coefficient of $x_3^{″}(t)$ in (132). Hence, (133) is true. The proof is finished. □

Corollary 23 (Equivalent damping III). 

Denote by c_eq3 the equivalent damping of class III fractional vibrators. Then,

$$c_{\mathrm{eq}3}=m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}.$$

(134)

Proof. 

Because the right side of the above expression is the coefficient of $x_3^{\prime }(t)$ in (132), (134) holds. The proof ends. □

Corollary 24 (Equivalent stiffness III). 

Denote by k_eq3 the equivalent stiffness of class III fractional vibrators. Then,

k_eq3 = k.

(135)

Proof. 

As the right side of the above expression is the coefficient of x₃(t) in (132), (135) holds. The proof is finished. □

By using m_eq3, c_eq3, and k_eq3, we write (132) by the expression of (136)

$$m_{\mathrm{eq}3}{\displaystyle \frac{d^2{x}_3(t)}{d{t}^2}}+c_{\mathrm{eq}3}{\displaystyle \frac{d{x}_3(t)}{dt}}+k_{\mathrm{eq}3}{x}_3(t)=f(t).$$

(136)

Corollary 25 (Equivalent damping ratio III). 

Let ζ_eq3 be the equivalent damping ratio for a class III fractional vibrator. Define it by (137) in the form

$${\varsigma }_{\mathrm{eq}3}={\displaystyle \frac{c_{\mathrm{eq}3}}{2\sqrt{m_{\mathrm{eq}3}{k}_{\mathrm{eq}3}}}}.$$

(137)

Then,

$${\varsigma }_{\mathrm{eq}3}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}.$$

(138)

Proof. 

Substituting λ = 0 in ζ_eq6 produces (138). This finishes the proof. □

Owing to ζ_eq3 > 1 being trivial in vibrations, we default |ζ_eq3| ≤ 1 in what follows.

Corollary 26 (Equivalent damping free natural angular frequency III). 

Let ω_eqn3 be the equivalent damping free natural angular frequency of class III fractional vibrators. Define it by the expression of (139)

$${\omega }_{\mathrm{eqn}3}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}3}}{m_{\mathrm{eq}3}}}}.$$

(139)

Then,

$${\omega }_{\mathrm{eqn}3}=\sqrt{{\displaystyle \frac{k}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}.$$

(140)

Proof. 

Substituting λ = 0 in ω_eqn6 yields (140). The proof ends. □

Corollary 27 (Equivalent damped natural angular frequency III). 

Denote by ω_eqd3 the equivalent damped natural angular frequency of class III fractional vibrators. Define it by (141) below

$${\omega }_{\mathrm{eqd}3}={\omega }_{\mathrm{eqn}3}\sqrt{1-{\varsigma }_{\mathrm{eq}3}^2}.$$

(141)

Then,

$$\begin{array}{l}{\omega }_{\mathrm{eqd}3}=\sqrt{{\displaystyle \frac{k}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}\\ \sqrt{1-{\left({\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}\right)}^2}.\end{array}$$

(142)

Proof. 

Substituting ω_eqn3 and ζ_eq3 into ω_eqd3 results in (142). The proof ends. □

Corollary 28 (Equivalent frequency ratio III). 

Denote by γ_eq3 the equivalent frequency ratio of class III fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}3}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}3}}}.$$

(143)

Then,

$${\gamma }_{\mathrm{eq}3}=\gamma \sqrt{-\left({\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right)}.$$

(144)

Proof. 

Substituting ω_eqn3 into (143) yields (144). This finishes the proof. □

5.4. Responses of Class III Fractional Vibrator

With m_eq3, ζ_eq3, and ω_eqn3, we write the motion equation of a class III fractional vibrator by (145) in the form

$${\displaystyle \frac{d^2{x}_3(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}{\displaystyle \frac{d{x}_3(t)}{dt}}+{\omega }_{\mathrm{eqn}3}^2{x}_3(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}3}}}.$$

(145)

Theorem 30 (Free response III). 

Denote by x₃(t) the free response of a class III fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_3(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_3(t)}{d{t}^{\beta }}}+k{x}_3(t)=0,\\ x_3(0)=x_{30},x_3^{\prime }(0)=v_{30}.\end{array}\right.$$

(146)

Then,

$$x_3(t)=e^{-{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}t}\left(x_{30}\cos {\omega }_{\mathrm{eqd}3}t+{\displaystyle \frac{v_{30}+{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}{x}_{30}}{{\omega }_{\mathrm{eqd}3}}}\sin {\omega }_{\mathrm{eqd}3}t\right), t\ge 0.$$

(147)

Proof. 

The solution to (146) is equal to the one to (148)

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\alpha }{x}_3(t)}{d{t}^{\alpha }}}+2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}{\displaystyle \frac{d{x}_3(t)}{dt}}+{\omega }_{\mathrm{eqn}3}^2{x}_3(t)=0,\\ x_3(0)=x_{30},x_3^{\prime }(0)=v_{30}.\end{array}\right.$$

(148)

Then, (147) holds. This completes the proof. □

Figure 16 indicates some of the plots of x₃(t).

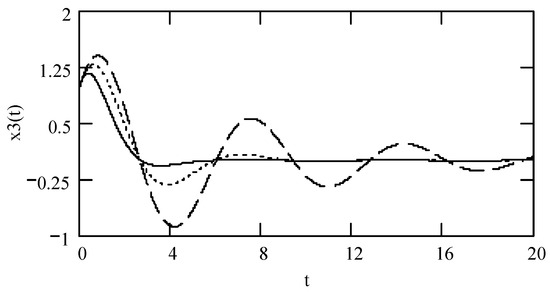
Figure 16. Plots of x₃(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β) = (1.3, 1.9) (solid line), (1.6, 1.8) (dotted line), and (1.9, 1.7) (dashed line).

Theorem 31 (Impulse response III). 

Denote by h₃(t) the impulse response of a class III fractional vibrator. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^{\alpha }{h}_3(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{h}_3(t)}{d{t}^{\beta }}}+k{h}_3(t)=\delta (t)$$

(149)

with zero initial conditions. Then,

$$h_3(t)={\displaystyle \frac{1}{m_{\mathrm{eq}3}{\omega }_{\mathrm{eqd}3}}}{e}^{-{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}t}\sin {\omega }_{\mathrm{eqd}3}t, t\ge 0.$$

(150)

Proof. 

The solution to (149) is equivalent to the one to (151)

$${\displaystyle \frac{d^2{h}_3(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}{\displaystyle \frac{d{h}_3(t)}{dt}}+{\omega }_{\mathrm{eqn}3}^2{h}_3(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}3}}}.$$

(151)

Therefore, (150) is true. The proof ends. □

Some plots of h₃(t) are indicated in Figure 17.

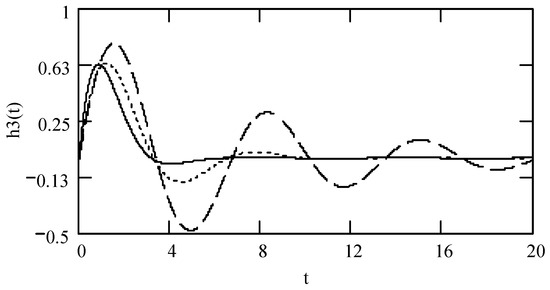
Figure 17. Plots of h₃(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β) = (1.3, 1.9) (solid line), (1.6, 1.8) (dotted line), and (1.9, 1.7) (dashed line).

Theorem 32 (Step response III). 

Denote by g₃(t) the unit step response of a class III fractional vibrator. It is the solution to (152)

$$m{\displaystyle \frac{d^{\alpha }{g}_3(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{g}_3(t)}{d{t}^{\beta }}}+k{g}_3(t)=u(t)$$

(152)

with zero initial conditions. Then,

$$g_3(t)={\displaystyle \frac{1}{k_{\mathrm{eq}3}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}3}^2}}}\cos \left({\omega }_{\mathrm{eqd}3}t-{\varphi }_3\right)\right],t\ge 0,$$

(153)

where

$${\varphi }_3={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}3}}{\sqrt{1-{\zeta }_{\mathrm{eq}3}^2}}}.$$

(154)

Proof. 

Substituting λ = 0 into g₆(t) yields g₃(t) in (153) with (154). This finishes the proof. □

Figure 18 shows some plots of g₃(t).

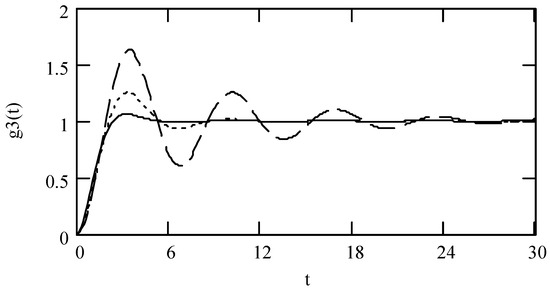
Figure 18. Plots of g₃(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β) = (1.3, 1.9) (solid line), (1.6, 1.8) (dotted line), and (1.9, 1.7) (dashed line).

Theorem 33 (Sinusoidal response III). 

Denote by x_3zs(t) the sinusoidal response of a class III fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_{3\mathrm{zs}}(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_{3\mathrm{zs}}(t)}{d{t}^{\beta }}}+k{x}_{3\mathrm{zs}}(t)=A\cos \omega t,\\ x_{3\mathrm{zs}}(0)=0,x_{3\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(155)

Then,

$$x_{3\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}3}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}3}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}3}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}3}t\\ -\frac{{\varsigma }_{\mathrm{eq}3}}{\sqrt{1-{\varsigma }_{\mathrm{eq}3}^2}}\left({\omega }_{\mathrm{eqn}3}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}3}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}3}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}\omega \right)}^2}}.$$

(156)

Proof. 

The solution to (155) is equal to the one to (157)

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{3\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}3}{\omega }_{\mathrm{eqn}3}{\displaystyle \frac{d{x}_{3\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}3}^2{x}_{3\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}3}}},\\ x_{3\mathrm{zs}}(0)=0,x_{3\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(157)

Hence, (156) holds. This finishes the proof. □

Figure 19 indicates some plots of x_3zs(t).

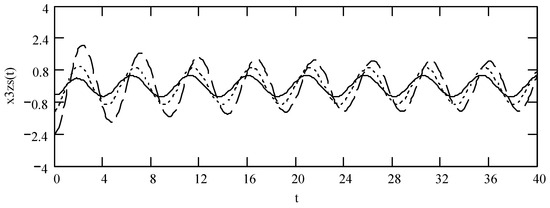
Figure 19. Plots of x_3zs(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (α, β) = (1.3, 1.9) (solid line), (1.6, 1.8) (dotted line), and (1.9, 1.7) (dashed line).

5.5. Equivalent Logarithmic Decrement in Class III Fractional Vibrators

Theorem 34 (Equivalent logarithmic decrement III). 

Let t_i and t_i+1 be two successive time points of the free response x₃(t), where x₃(t) reaches its successive peak values of x₃(t_i) and x₃(t_i+1), respectively. Let Δ_eq3 be the equivalent logarithmic decrement in x₃(t). Then,

$${\Delta }_{\mathrm{eq}3}=\ln {\displaystyle \frac{x_3(t_i)}{x_3(t_{i+1})}}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}3}}{\sqrt{1-{\varsigma }_{\mathrm{eq}3}^2}}}={\displaystyle \frac{\pi \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}}{\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k\right]}}}}.$$

(158)

Proof. 

Substituting λ = 0 into Δ_eq6 produces Δ_eq3 in (158). The proof ends. □

5.6. Quality Factor of Class III Fractional Vibrators

Denote by Q_eq3 the equivalent Q factor of class III fractional vibrators. The equivalent motion equation of class III fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}3}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}3}}}.$$

(159)

Theorem 35 (Equivalent Q factor III). 

The quantity Q_eq3 is given by

$$Q_{\mathrm{eq}3}={\displaystyle \frac{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k}}{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}}.$$

(160)

Proof. 

Substituting ζ_eq3 into (159) yields (160). The proof is finished. □

5.7. Equivalent Frequency Bandwidth of Class III Fractional Vibrators

Let B_eq3,0.707 be the equivalent frequency bandwidth of class III fractional vibrators. Owing to the equivalent motion equation of class III fractional vibrators being in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}3,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}3}}{2\pi Q_{\mathrm{eq}3}}}.$$

(161)

Theorem 36 (Equivalent frequency bandwidth III). 

The quantity B_eq3,0.707 is expressed by

$${\mathrm{B}}_{\mathrm{eq}3,0.707}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}}{2\pi \left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}}.$$

(162)

Proof. 

Substituting ω_eqn3 and Q_eq3 into (161) yields (162). The proof is finished. □

5.8. More about Frequency Transfer Function of Class III Fractional Vibrators

By using γ_eq3, ζ_eq3, and k_eq3, we have the expression of H₃(ω) in the form (163)

$$H_3(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}3}\left(1-{\gamma }_{\mathrm{eq}3}^2+i2{\varsigma }_{\mathrm{eq}3}{\gamma }_{\mathrm{eq}3}\right)}}.$$

(163)

When writing H₃(ω) = |H₃(ω)|exp[−φ₃(ω)], we have the expression of |H₃(ω)| in the form (164)

$$\left|H_3(\omega )\right|={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{\begin{array}{l}{\left[1+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\gamma }^2{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}^2\end{array}}}}.$$

(164)

The phase of H₃(ω) is given by (165) below

$${\phi }_3(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}3}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}3}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}3}{\gamma }_{\mathrm{eq}3}\right)}^2}}}.$$

(165)

Figure 20 indicates some of the plots of |H₃(ω)| and φ₃(ω).

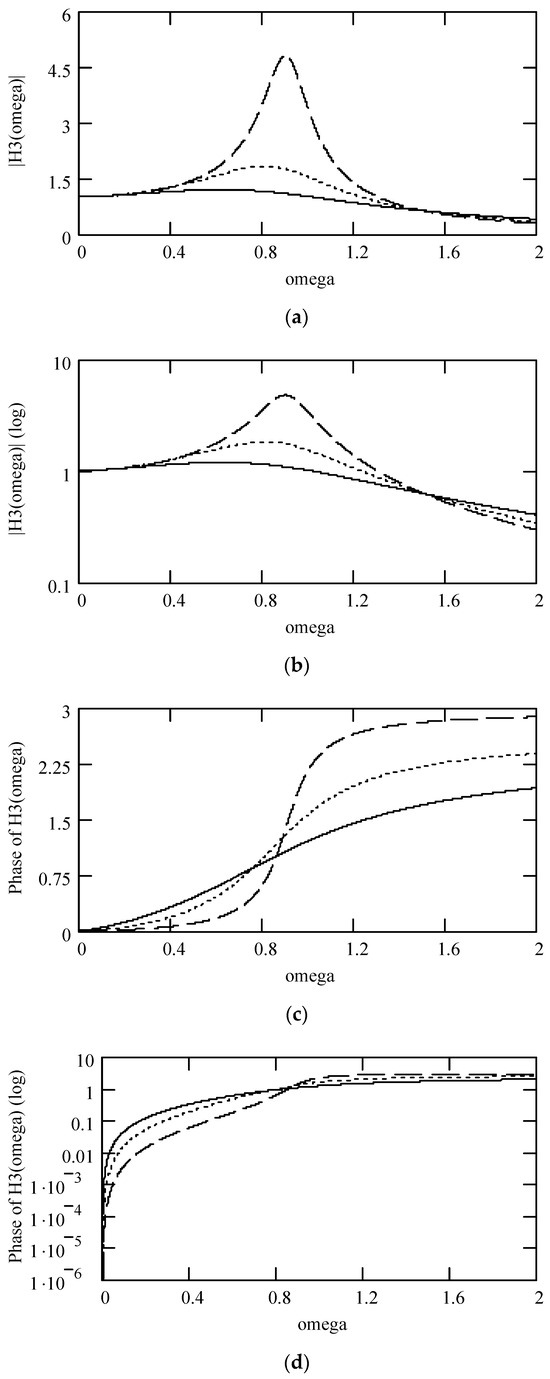
Figure 20. Plots of |H₃(ω)| and φ₃(ω) for m = 1, c = 0.2, and k = 1 when (α, β) = (1.3, 1.9) (solid line), (1.6, 1.8) (dotted line), and (1.9, 1.7) (dashed line). (a) |H₃(ω)|; (b) log|H₃(ω)|; (c) φ₃(ω); (d) logφ₃(ω).

6. Analytic Theory of Class IV Fractional Vibrators

We discuss a tutorial with respect to the analytic theory of class IV fractional vibrators in seven parts: (1) the analytical expression of the frequency transfer function for a class IV fractional vibrator in Theorem 37 in Section 6.1; (2) the equivalent motion equation of class IV fractional vibrators in Theorem 38 in Section 6.2; (3) analytical expressions for the equivalent parameters of class IV fractional vibrators in Section 6.3; (4) the analytical expressions of responses of class IV fractional vibrators in Theorems 39–42 in Section 6.4, where the sinusoidal response expression is newly presented; (5) the analytical expression of the equivalent logarithmic decrement in class IV fractional vibrators in Theorem 43 in Section 6.5; (6) the analytical expression for the equivalent quality factor of class IV fractional vibrators in Theorem 44 in Section 6.6; (7) in addition, we bring forward an analytical expression for the equivalent frequency bandwidth of class IV fractional vibrators in Theorem 45 in Section 6.7.

6.1. Frequency Transfer Function of Class IV Fractional Vibrator

Theorem 37 (Frequency transfer function IV). 

Let H₄(ω) be the frequency transfer function of a class IV fractional vibrator. Then,

$$H_4(\omega )={\displaystyle \frac{1}{m{\omega }^{\alpha }\cos \frac{\alpha \pi }{2}+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+i\left(m{\omega }^{\alpha }\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda }\sin \frac{\lambda \pi }{2}\right)}}.$$

(166)

Proof. 

Note that a class IV fractional vibrator is a special case of a class VI fractional vibrator for c = 0. Thus, substituting c = 0 into H₆(ω) yields the above H₄(ω) in (166). The proof is finished. □

6.2. Equivalent Motion Equation of Class IV Fractional Vibrator

Theorem 38 (Equivalent motion equation IV). 

The motion equation of class IV fractional vibrators is equivalently expressed by

$$\begin{array}{l}-m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}{\displaystyle \frac{d^2{x}_4(t)}{d{t}^2}}+\left(m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}\right){\displaystyle \frac{d{x}_4(t)}{dt}}\\ +k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}{x}_4(t)=f(t).\end{array}$$

(167)

Proof. 

As a class IV fractional vibrator is a special case of a class VI one for c = 0, replacing c with 0 in (18) yields (167). The proof is finished. □

6.3. Equivalent Parameters of Class IV Fractional Vibrator

Corollary 29 (Equivalent mass IV). 

Denote by m_eq4 the equivalent mass of class IV fractional vibrators. Then,

$$m_{\mathrm{eq}4}=-m{\omega }^{\alpha -2}\cos {\displaystyle \frac{\alpha \pi }{2}}.$$

(168)

Proof. 

The right side of the above expression is the coefficient of $x_4^{″}(t)$ in (167). Hence, (168) holds. The proof ends. □

Corollary 30 (Equivalent damping IV). 

Let c_eq4 be the equivalent damping of class IV fractional vibrators. Then,

$$c_{\mathrm{eq}4}=m{\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}.$$

(169)

Proof. 

As the right side of the above expression is the coefficient of $x_4^{\prime }(t)$ in (167), (169) holds. The proof is finished. □

Corollary 31 (Equivalent stiffness IV). 

Denote by k_eq4 the equivalent stiffness of class IV fractional vibrators. Then,

$$k_{\mathrm{eq}4}=k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}.$$

(170)

Proof. 

Because the right side of the above expression is the coefficient of x₄(t) in (167), (170) holds. The proof ends. □

Using m_eq4, c_eq4, and k_eq4 to write (167) yields (171) in the form

$$m_{\mathrm{eq}4}{\displaystyle \frac{d^2{x}_4(t)}{d{t}^2}}+c_{\mathrm{eq}4}{\displaystyle \frac{d{x}_4(t)}{dt}}+k_{\mathrm{eq}4}{x}_4(t)=f(t).$$

(171)

Corollary 32 (Equivalent damping ratio IV). 

Denote by ζ_eq4 the equivalent damping ratio for a class IV fractional vibrator. Define it by (172) in the form

$${\varsigma }_{\mathrm{eq}4}={\displaystyle \frac{c_{\mathrm{eq}4}}{2\sqrt{m_{\mathrm{eq}4}{k}_{\mathrm{eq}4}}}}.$$

(172)

Then,

$${\varsigma }_{\mathrm{eq}4}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(173)

Proof. 

Substituting c = 0 into ζ_eq6 produces the above ζ_eq4 in (173). This completes the proof. □

Because of ζ_eq4 > 1 being trivial in vibrations, |ζ_eq4| ≤ 1 is defaulted in what follows.

Corollary 33 (Equivalent damping free natural angular frequency IV). 

Denote by ω_eqn4 the equivalent damping free natural angular frequency of class IV fractional vibrators. Define it by (174) below

$${\omega }_{\mathrm{eqn}4}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}4}}{m_{\mathrm{eq}4}}}}.$$

(174)

Then,

$${\omega }_{\mathrm{eqn}4}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}}.$$

(175)

Proof. 

Substituting c = 0 into ω_eqn6 produces the above ω_eqn4 in (175). The proof is finished. □

Corollary 34 (Equivalent damped natural angular frequency IV). 

Let ω_eqd4 be the equivalent damped natural angular frequency of class IV fractional vibrators. Define it by (176) below

$${\omega }_{\mathrm{eqd}4}={\omega }_{\mathrm{eqn}4}\sqrt{1-{\varsigma }_{\mathrm{eq}4}^2}.$$

(176)

Then,

$${\omega }_{\mathrm{eqd}4}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}}\sqrt{1-{\left({\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}\right)}^2}.$$

(177)

Proof. 

Substituting ω_eqn4 and ζ_eq4 into ω_eqd4 yields (177). The proof is finished. □

Corollary 35 (Equivalent frequency ratio IV). 

Let γ_eq4 be the equivalent frequency ratio of class IV fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}4}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}4}}}.$$

(178)

Then,

$${\gamma }_{\mathrm{eq}4}=\gamma \sqrt{{\displaystyle \frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(179)

Proof. 

Substituting ω_eqn4 into (178) produces (179). This completes the proof. □

6.4. Responses of Class IV Fractional Vibrator

Based on m_eq4, ζ_eq4, and ω_eqn4, we can write the motion equation of a class IV fractional vibrator by (180) in the form

$${\displaystyle \frac{d^2{x}_4(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}{\displaystyle \frac{d{x}_4(t)}{dt}}+{\omega }_{\mathrm{eqn}4}^2{x}_4(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}4}}}.$$

(180)

Theorem 39 (Free response IV).  

Let x₄(t) be the free response of a class IV fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_4(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\lambda }{x}_4(t)}{d{t}^{\lambda }}}=0,\\ x_4(0)=x_{40},x_4^{\prime }(0)=v_{40}.\end{array}\right.$$

(181)

Then,

$$x_4(t)=e^{-{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}t}\left(x_{40}\cos {\omega }_{\mathrm{eqd}4}t+{\displaystyle \frac{v_{40}+{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}{x}_{40}}{{\omega }_{\mathrm{eqd}4}}}\sin {\omega }_{\mathrm{eqd}4}t\right), t\ge 0.$$

(182)

Proof. 

The solution to (181) is equal to the one to (183) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_4(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}{\displaystyle \frac{d{x}_4(t)}{dt}}+{\omega }_{\mathrm{eqn}4}^2{x}_4(t)=0,\\ x_4(0)=x_{40},x_4^{\prime }(0)=v_{40}.\end{array}\right.$$

(183)

Therefore, (182) is true. This completes the proof. □

Figure 21 shows some plots of x₄(t).

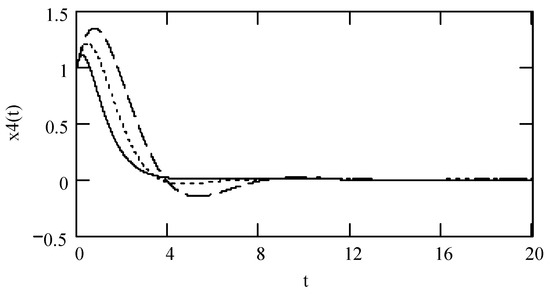
Figure 21. Plots of x₄(t) for ω = 1.3, m = 1, and k = 1 when (α, λ) = (1.3, 0.2) (solid line), (1.6, 0.4) (dotted line), and (1.9, 0.6) (dashed line).

Theorem 40 (Impulse response IV). 

Denote by h₄(t) the impulse response of a class IV fractional vibrator. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^{\alpha }{h}_4(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\lambda }{h}_4(t)}{d{t}^{\lambda }}}=\delta (t)$$

(184)

with zero initial conditions. Then,

$$h_4(t)={\displaystyle \frac{1}{m_{\mathrm{eq}4}{\omega }_{\mathrm{eqd}4}}}{e}^{-{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}t}\sin {\omega }_{\mathrm{eqd}4}t, t\ge 0.$$

(185)

Proof. 

The solution to (184) can be taken as the one to (186) below

$${\displaystyle \frac{d^2{h}_4(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}{\displaystyle \frac{d{h}_4(t)}{dt}}+{\omega }_{\mathrm{eqn}4}^2{h}_4(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}4}}}.$$

(186)

Thus, (185) holds. The proof ends. □

Some plots of h₄(t) are shown in Figure 22.

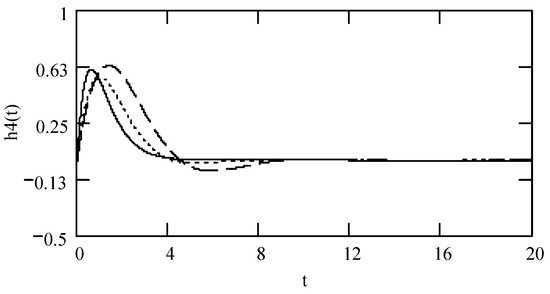
Figure 22. Plots of h₄(t) for ω = 1.3, m = 1, and k = 1 when (α, λ) = (1.3, 0.2) (solid line), (1.6, 0.4) (dotted line), and (1.9, 0.6) (dashed line).

Theorem 41 (Step response IV). 

Let g₄(t) be the unit step response of a class IV fractional vibrator. It is the solution to (187) in the form

$$m{\displaystyle \frac{d^{\alpha }{g}_4(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\lambda }{g}_4(t)}{d{t}^{\lambda }}}=u(t)$$

(187)

with zero initial conditions. Then,

$$g_4(t)={\displaystyle \frac{1}{k_{\mathrm{eq}4}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}4}^2}}}\cos \left({\omega }_{\mathrm{eqd}4}t-{\varphi }_4\right)\right], t\ge 0,$$

(188)

where

$${\varphi }_4={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}4}}{\sqrt{1-{\zeta }_{\mathrm{eq}4}^2}}}.$$

(189)

Proof. 

Substituting c = 0 into g₆(t) results in g₄(t) in (188) with (189). This completes the proof. □

Figure 23 indicates some of the plots of g₄(t).

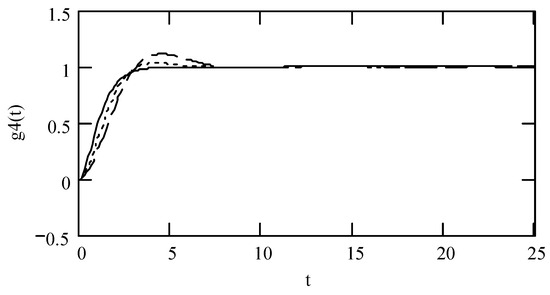
Figure 23. Plots of g₄(t) for ω = 1.3, m = 1, and k = 1 when (α, λ) = (1.3, 0.2) (solid line), (1.6, 0.4) (dotted line), and (1.9, 0.6) (dashed line).

Theorem 42 (Sinusoidal response IV). 

Let x_4zs(t) be the sinusoidal response of a class IV fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^{\alpha }{x}_{4\mathrm{zs}}(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\beta }{x}_{4\mathrm{zs}}(t)}{d{t}^{\beta }}}=A\cos \omega t,\\ x_{4\mathrm{zs}}(0)=0,x_{4\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(190)

Then,

$$x_{4\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}4}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}4}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}4}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}4}t\\ -\frac{{\varsigma }_{\mathrm{eq}4}}{\sqrt{1-{\varsigma }_{\mathrm{eq}4}^2}}\left({\omega }_{\mathrm{eqn}4}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}4}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}4}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}\omega \right)}^2}}.$$

(191)

Proof. 

The solution to (190) equals to the one to (192) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{4\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}4}{\omega }_{\mathrm{eqn}4}{\displaystyle \frac{d{x}_{4\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}4}^2{x}_{4\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}4}}},\\ x_{4\mathrm{zs}}(0)=0,x_{4\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(192)

Hence, (191) is true. This completes the proof. □

Figure 24 shows some plots of x_4zs(t).

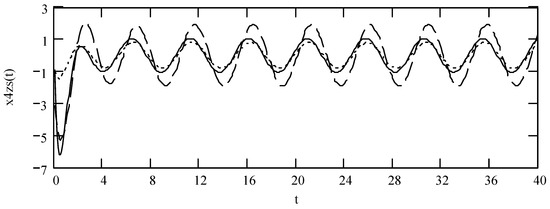
Figure 24. Plots of x_4zs(t) for ω = 1.3, m = 1, and k = 1 when (α, λ) = (1.3, 0.2) (solid line), (1.6, 0.5) (dotted line), and (1.9, 0.8) (dashed line).

6.5. Equivalent Logarithmic Decrement in Class IV Fractional Vibrators

Theorem 43 (Equivalent logarithmic decrement IV). 

Let t_i and t_i+1 be two successive time points of the free response x₄(t), where x₄(t) reaches its successive peak values of x₄(t_i) and x₄(t_i+1), respectively. Let Δ_eq4 be the equivalent logarithmic decrement in x₄(t). Then,

$${\Delta }_{\mathrm{eq}4}=\ln {\displaystyle \frac{x_4(t_i)}{x_4(t_{i+1})}}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}4}}{\sqrt{1-{\varsigma }_{\mathrm{eq}4}^2}}}={\displaystyle \frac{\pi \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}{\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\right]}}}}.$$

(193)

Proof. 

Substituting c = 0 into Δ_eq6 yields the above Δ_eq4 in (193). The proof ends. □

6.6. Quality Factor of Class IV Fractional Vibrators

Let Q_eq4 be the equivalent Q factor of class IV fractional vibrators. The equivalent motion equation of class IV fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}4}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}4}}}.$$

(194)

Theorem 44 (Equivalent Q factor IV). 

The quantity Q_eq4 is given by

$$Q_{\mathrm{eq}4}={\displaystyle \frac{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}}.$$

(195)

Proof. 

Substituting ζ_eq4 into (194) yields (195). The proof ends. □

6.7. Equivalent Frequency Bandwidth of Class IV Fractional Vibrators

Let B_eq4,0.707 be the equivalent frequency bandwidth of class IV fractional vibrators. As the equivalent motion equation of class IV fractional vibrators is in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}4,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}4}}{2\pi Q_{\mathrm{eq}4}}}.$$

(196)

Theorem 45 (Equivalent frequency bandwidth IV). 

The quantity B_eq4,0.707 is given by

$${\mathrm{B}}_{\mathrm{eq}4,0.707}={\displaystyle \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{-2\pi m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}.$$

(197)

Proof. 

Substituting ω_eqn4 and Q_eq4 into (196) produces (197). The proof is finished. □

6.8. More about Frequency Transfer Function of Class IV Fractional Vibrators

By using γ_eq4, ζ_eq4, and k_eq4, we have H₄(ω) in the form (198)

$$H_4(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}4}\left(1-{\gamma }_{\mathrm{eq}4}^2+i2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}\right)}}.$$

(198)

Since Re[H₄(ω)] is in the form (199)

$$\mathrm{Re}\left[H_4(\omega )\right]={\displaystyle \frac{1-{\gamma }_{\mathrm{eq}4}^2}{k_{\mathrm{eq}4}\sqrt{{\left(1-{\gamma }_{\mathrm{eq}4}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}\right)}^2}}},$$

(199)

and Im[H₄(ω)] is in the form (200)

$$\mathrm{Im}\left[H_4(\omega )\right]={\displaystyle \frac{-2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}}{k_{\mathrm{eq}4}\sqrt{{\left(1-{\gamma }_{\mathrm{eq}4}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}\right)}^2}}},$$

(200)

we have H₄(ω) expressed in the form of (201) below

$$H_4(\omega )=\mathrm{Re}\left[H_4(\omega )\right]+i\mathrm{Im}\left[H_4(\omega )\right].$$

(201)

Thus, the expression of |H₄(ω)| is in the form of (202) below

$$\left|H_4(\omega )\right|=\sqrt{{\left\{\mathrm{Re}\left[H_4(\omega )\right]\right\}}^2+{\left\{\mathrm{Im}\left[H_4(\omega )\right]\right\}}^2}.$$

(202)

Further, Arg[H₄(ω)] is expressed by (203)

$$\mathrm{Arg}\left[H_4(\omega )\right]={\tan }^{-1}{\displaystyle \frac{\mathrm{Im}\left[H_4(\omega )\right]}{\mathrm{Re}\left[H_4(\omega )\right]}}.$$

(203)

In engineering, we usually write H₄(ω) in the form of (204)

H₄(ω) = |H₄(ω)|exp[−φ₄(ω)].

(204)

Substituting γ_eq4, ζ_eq4, and k_eq4 into (202) yields |H₄(ω)| in the form of (205) below

$$\left|H_4(\omega )\right|={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{{\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\right)\right]}^2+{\gamma }^2{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}}}.$$

(205)

From the perspective of digital computations, we write φ₄(ω) by (206)

$${\phi }_4(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}4}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}4}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}\right)}^2}}}.$$

(206)

Figure 25 shows some plots of |H₄(ω)| and φ₄(ω).

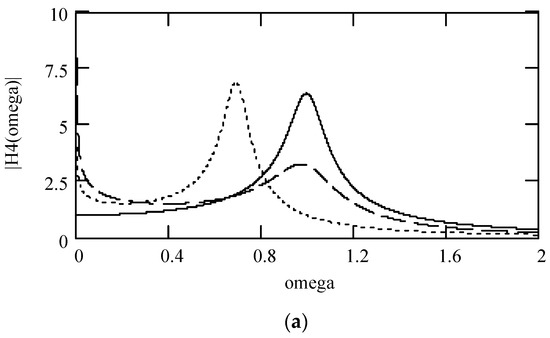
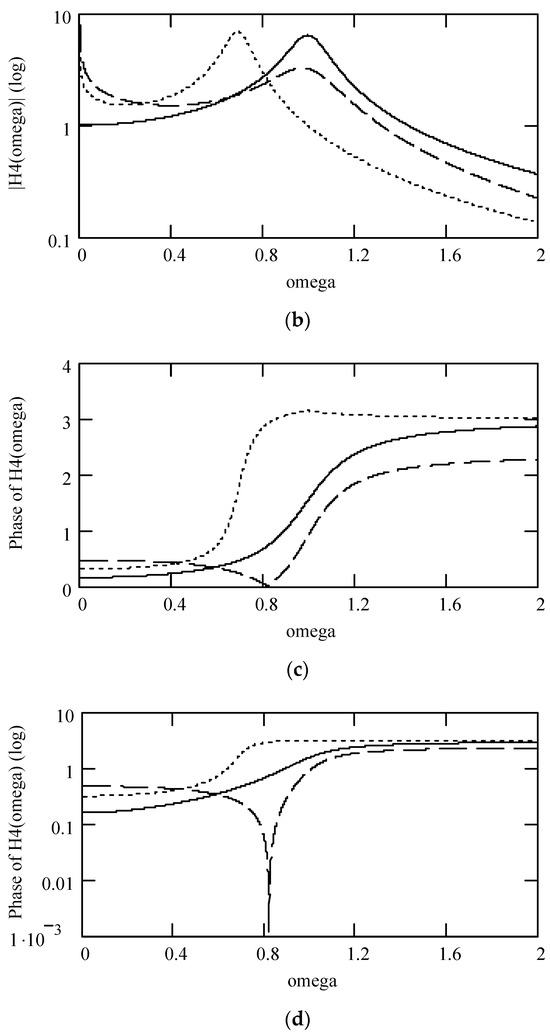
Figure 25. Plots of |H₄(ω)| and φ₄(ω) for m = 1 and k = 1 when (α, λ) = (1.9, 0.1) (solid line), (2.1, 0.2) (dotted line), and (2.5, 0.3) (dashed line). (a) |H₄(ω)|; (b) log|H₄(ω)|; (c) φ₄(ω); (d) logφ₄(ω).

7. Analytic Theory of Class V Fractional Vibrators

We explain a tutorial with respect to the analytic theory of class V fractional vibrators from six aspects: (1) the analytical expression for the frequency transfer function of a class V fractional vibrator in Theorem 46 in Section 7.1; (2) the equivalent motion equation of class V fractional vibrators in Theorem 47 in Section 7.2; (3) analytical expressions for the equivalent parameters of class V fractional vibrators in Section 7.3; (4) the analytical expressions of responses of class V fractional vibrators in Theorems 48–51 in Section 7.4, where the sinusoidal response expression is newly proposed; (5) the analytical expression of the equivalent logarithmic decrement in class V fractional vibrators in Theorem 52 in Section 7.5; (6) the analytical expression for the equivalent quality factor of class V fractional vibrators in Theorem 53 in Section 7.6; (7) furthermore, we put forward an analytical expression for the equivalent frequency bandwidth in class V fractional vibrators in Theorem 54 in Section 7.7.

7.1. Frequency Transfer Function of Class V Fractional Vibrator

Theorem 46 (Frequency transfer function V). 

Denote by H₅(ω) the frequency transfer function of a class V fractional vibrator. Then,

$$H_5(\omega )={\displaystyle \frac{1}{-m{\omega }^2+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+ik{\omega }^{\lambda }\sin \frac{\lambda \pi }{2}}}.$$

(207)

Proof. 

A class V fractional vibrator is a special case of a class VI fractional vibrator for α = 2 and c = 0. Therefore, substituting α = 2 and c = 0 into H₆(ω) yields (207). The proof ends. □

7.2. Equivalent Motion Equation of Class V Fractional Vibrator

Theorem 47 (Equivalent motion equation V). 

The motion equation of class V fractional vibrators is equivalently expressed by

$$m{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}{\displaystyle \frac{d{x}_5(t)}{dt}}+k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}{x}_5(t)=f(t).$$

(208)

Proof. 

As a class V fractional vibrator is a special case of class VI one for α = 2 and c = 0, replacing α by 2 and c with 0 in (18) yields (208). This finishes the proof. □

7.3. Equivalent Parameters of Class V Fractional Vibrator

Corollary 36 (Equivalent mass V). 

Let m_eq5 be the equivalent mass of class V fractional vibrators. Then,

m_eq5 = m.

(209)

Proof. 

The right side of the above expression is the coefficient of $x_5^{″}(t)$ in (208). Thus, (209) holds. The proof is finished. □

Corollary 37 (Equivalent damping V). 

Denote by c_eq5 the equivalent damping of class V fractional vibrators. Then,

$$c_{\mathrm{eq}5}=k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}.$$

(210)

Proof. 

Because the right side of the above expression is the coefficient of $x_5^{\prime }(t)$ in (208), (210) holds. The proof ends. □

Corollary 38 (Equivalent stiffness V). 

Let k_eq5 be the equivalent stiffness of class V fractional vibrators. Then,

$$k_{\mathrm{eq}5}=k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}.$$

(211)

Proof. 

As the right side of the above expression is the coefficient of x₅(t) in (208), (211) holds. The proof ends. □

Using m_eq5, c_eq5, and k_eq5 to write (208) produces (212) below

$$m_{\mathrm{eq}5}{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+c_{\mathrm{eq}5}{\displaystyle \frac{d{x}_5(t)}{dt}}+k_{\mathrm{eq}5}{x}_5(t)=f(t).$$

(212)

Corollary 39 (Equivalent damping ratio V). 

Denote by ζ_eq5 the equivalent damping ratio for a class V fractional vibrator. Define it by (213) below

$${\varsigma }_{\mathrm{eq}5}={\displaystyle \frac{c_{\mathrm{eq}5}}{2\sqrt{m_{\mathrm{eq}5}{k}_{\mathrm{eq}5}}}}.$$

(213)

Then,

$${\varsigma }_{\mathrm{eq}5}={\displaystyle \frac{{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(214)

Proof. 

Substituting α = 2 and c = 0 into ζ_eq6 produces the above ζ_eq5 in (214). The proof ends. □

Since ζ_eq5 > 1 is trivial in vibrations, |ζ_eq5| ≤ 1 is defaulted in what follows.

Corollary 40 (Equivalent damping free natural angular frequency V). 

Let ω_eqn5 be the equivalent damping free natural angular frequency of class V fractional vibrators. Define it by (215) below

$${\omega }_{\mathrm{eqn}5}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}5}}{m_{\mathrm{eq}5}}}}.$$

(215)

Then,

$${\omega }_{\mathrm{eqn}5}={\omega }_n\sqrt{{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}}.$$

(216)

Proof. 

Substituting α = 2 and c = 0 into ω_eqn6 produces the above ω_eqn5 in (216). The proof ends. □

Corollary 41 (Equivalent damped natural angular frequency V). 

Denote by ω_eqd5 the equivalent damped natural angular frequency of class V fractional vibrators. Define

$${\omega }_{\mathrm{eqd}5}={\omega }_{\mathrm{eqn}5}\sqrt{1-{\varsigma }_{\mathrm{eq}5}^2}.$$

(217)

Then,

$${\omega }_{\mathrm{eqd}5}={\omega }_n\sqrt{{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}}\sqrt{1-{\left({\displaystyle \frac{{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}\right)}^2}.$$

(218)

Proof. 

Substituting ω_eqn5 and ζ_eq5 into (217) results in (218). The proof ends. □

Corollary 42 (Equivalent frequency ratio V). 

Let γ_eq5 be the equivalent frequency ratio of class V fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}5}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}5}}}.$$

(219)

Then,

$${\gamma }_{\mathrm{eq}5}=\gamma \sqrt{{\displaystyle \frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(220)

Proof. 

Substituting ω_eqn5 into (219) produces (220). This finishes the proof. □

7.4. Responses of Class V Fractional Vibrator

Based on m_eq5, ζ_eq5, and ω_eqn5, we can write the motion equation of a class V fractional vibrator in the form of (221)

$${\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}{\displaystyle \frac{d{x}_5(t)}{dt}}+{\omega }_{\mathrm{eqn}5}^2{x}_5(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}5}}}.$$

(221)

Theorem 48 (Free response V). 

Let x₅(t) be the free response of a class V fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{x}_5(t)}{d{t}^{\lambda }}}=0,\\ x_5(0)=x_{50},x_5^{\prime }(0)=v_{50}.\end{array}\right.$$

(222)

Then,

$$x_5(t)=e^{-{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}t}\left(x_{50}\cos {\omega }_{\mathrm{eqd}5}t+{\displaystyle \frac{v_{50}+{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}{x}_{50}}{{\omega }_{\mathrm{eqd}5}}}\sin {\omega }_{\mathrm{eqd}5}t\right), t\ge 0.$$

(223)

Proof. 

The solution to (222) is equal to the one to (224) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}{\displaystyle \frac{d{x}_5(t)}{dt}}+{\omega }_{\mathrm{eqn}5}^2{x}_5(t)=0,\\ x_5(0)=x_{50},x_5^{\prime }(0)=v_{50}.\end{array}\right.$$

(224)

Thus, (223) holds. This finishes the proof. □

Figure 26 indicates some plots of x₅(t).

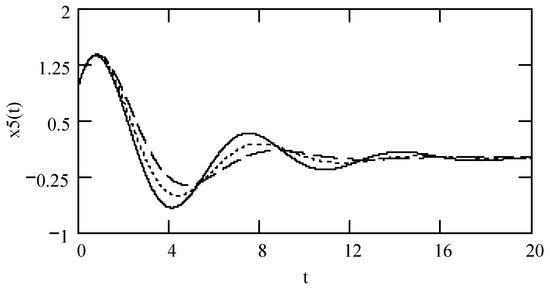
Figure 26. Plots of x₅(t) for ω = 1.3, m = 1, and k = 1 when λ = 0.3 (solid line), 0.4 (dot line), and 0.5 (dash line).

Theorem 49 (Impulse response V). 

Let h₅(t) be the impulse response of a class V fractional vibrator. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^2{h}_5(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{h}_5(t)}{d{t}^{\lambda }}}=\delta (t)$$

(225)

with zero initial conditions. Then,

$$h_5(t)={\displaystyle \frac{1}{m_{\mathrm{eq}5}{\omega }_{\mathrm{eqd}5}}}{e}^{-{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}t}\sin {\omega }_{\mathrm{eqd}5}t, t\ge 0.$$

(226)

Proof. 

The solution to (225) can be taken as the one to (227) below

$${\displaystyle \frac{d^2{h}_5(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}{\displaystyle \frac{d{h}_5(t)}{dt}}+{\omega }_{\mathrm{eqn}5}^2{h}_5(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}5}}}.$$

(227)

Thus, (226) holds. The proof ends. □

Some plots of h₅(t) are indicated in Figure 27.

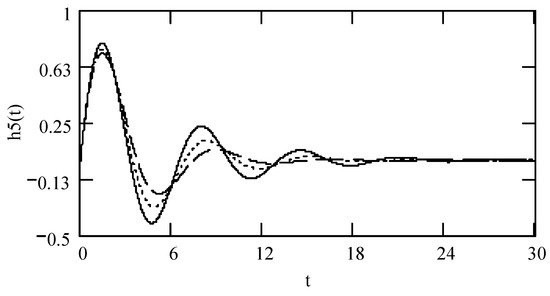
Figure 27. Plots of h₅(t) for ω = 1.3, m = 1, and k = 1 when λ = 0.3 (solid line), 0.4 (dotted line), and 0.5 (dashed line).

Theorem 50 (Step response V). 

Let g₅(t) be the unit step response of a class V fractional vibrator. It is the solution to (228)

$$m{\displaystyle \frac{d^2{g}_5(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{g}_5(t)}{d{t}^{\lambda }}}=u(t)$$

(228)

with zero initial conditions. Then,

$$g_5(t)={\displaystyle \frac{1}{k_{\mathrm{eq}5}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}5}^2}}}\cos \left({\omega }_{\mathrm{eqd}5}t-{\varphi }_5\right)\right],t\ge 0,$$

(229)

where

$${\varphi }_5={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}5}}{\sqrt{1-{\zeta }_{\mathrm{eq}5}^2}}}.$$

(230)

Proof. 

Substituting α = 2 and c = 0 into g₆(t) results in g₅(t) in (229) with (230). This finishes the proof. □

Figure 28 shows some plots of g₅(t).

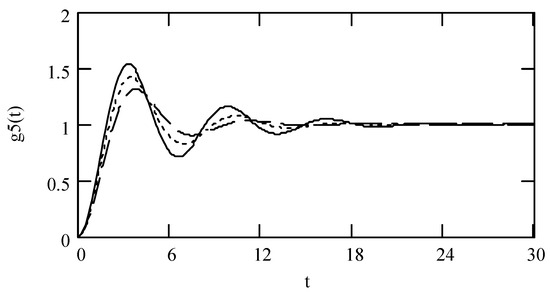
Figure 28. Plots of g₅(t) for ω = 1.3, m = 1, and k = 1 when λ = 0.3 (solid line), 0.4 (dotted line), and 0.5 (dashed line).

Theorem 51 (Sinusoidal response V). 

Denote by x_5zs(t) the sinusoidal response of a class V fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_{5\mathrm{zs}}(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{x}_{5\mathrm{zs}}(t)}{d{t}^{\lambda }}}=A\cos \omega t,\\ x_{5\mathrm{zs}}(0)=0,x_{5\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(231)

Then,

$$x_{5\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}5}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}5}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}5}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}5}t\\ -\frac{{\varsigma }_{\mathrm{eq}5}}{\sqrt{1-{\varsigma }_{\mathrm{eq}5}^2}}\left({\omega }_{\mathrm{eqn}5}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}5}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}5}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}\omega \right)}^2}}.$$

(232)

Proof. 

The solution to (231) equals to the one to (233) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{5\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}5}{\omega }_{\mathrm{eqn}5}{\displaystyle \frac{d{x}_{5\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}5}^2{x}_{5\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}5}}},\\ x_{5\mathrm{zs}}(0)=0,x_{5\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(233)

Thus, (232) holds. This finishes the proof. □

Figure 29 indicates some of the plots of x_5zs(t).

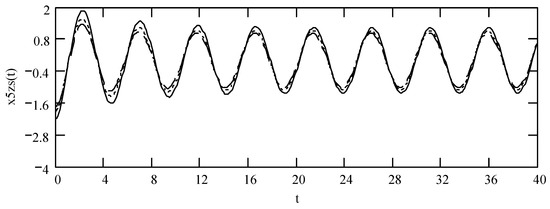
Figure 29. Plots of x_5zs(t) for ω = 1.3, m = 1, and k = 1 when λ = 0.3 (solid line), 0.4 (dotted line), and 0.5 (dashed line).

7.5. Equivalent Logarithmic Decrement in Class V Fractional Vibrators

Theorem 52 (Equivalent logarithmic decrement V). 

Let t_i and t_i+1 be two successive time points of the free response x₅(t), where x₅(t) reaches its successive peak values of x₅(t_i) and x₅(t_i+1), respectively. Let Δ_eq5 be the equivalent logarithmic decrement in x₅(t). Then,

$${\Delta }_{\mathrm{eq}5}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}5}}{\sqrt{1-{\varsigma }_{\mathrm{eq}5}^2}}}={\displaystyle \frac{\pi {\omega }_n\frac{{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{\sqrt{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}{\sqrt{1-\frac{{\left(k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}{4mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}}.$$

(234)

Proof. 

Substituting α = 2 c = 0 into Δ_eq6 yields the above Δ_eq5 in (234). The proof is finished. □

7.6. Quality Factor of Class V Fractional Vibrators

Let Q_eq5 be the equivalent Q factor of class V fractional vibrators. The equivalent motion equation of class V fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}5}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}5}}}.$$

(235)

Theorem 53 (Equivalent Q factor V). 

The quantity Q_eq5 is given by

$$Q_{\mathrm{eq}5}={\displaystyle \frac{\sqrt{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}{{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}}.$$

(236)

Proof. 

Substituting ζ_eq5 into (235) yields (236). The proof ends. □

7.7. Equivalent Frequency Bandwidth of Class V Fractional Vibrators

Let B_eq5,0.707 be the equivalent frequency bandwidth of class V fractional vibrators. As the equivalent motion equation of class V fractional vibrators is in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}5,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}5}}{2\pi Q_{\mathrm{eq}5}}}.$$

(237)

Theorem 54 (Equivalent frequency bandwidth V). 

The quantity B_eq5,0.707 is given by

$${\mathrm{B}}_{\mathrm{eq}5,0.707}={\displaystyle \frac{{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\pi }}.$$

(238)

Proof. 

Substituting ω_eqn5 and Q_eq5 into (237) yields (238). The proof is finished. □

7.8. More about Frequency Transfer Function of Class V Fractional Vibrators

By using γ_eq5, ζ_eq5, and k_eq5, we have (239) to express H₅(ω) by

$$H_5(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}5}\left(1-{\gamma }_{\mathrm{eq}5}^2+i2{\varsigma }_{\mathrm{eq}5}{\gamma }_{\mathrm{eq}5}\right)}}.$$

(239)

Writing H₅(ω) = |H₅(ω)|exp[−φ₅(ω)] results in (240) to express |H₅(ω)| by

$$\left|H_5(\omega )\right|={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{{\left({\omega }^{\lambda }\cos \frac{\lambda \pi }{2}-{\gamma }^2\right)}^2+{\gamma }^2{\left({\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}}}.$$

(240)

The phase of H₅(ω) is given by (241) below

$${\phi }_5(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}5}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}5}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}5}{\gamma }_{\mathrm{eq}5}\right)}^2}}}.$$

(241)

Figure 30 demonstrates some of the plots of |H₅(ω)| and φ₅(ω).

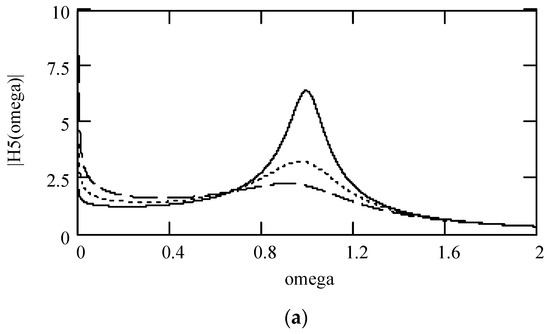
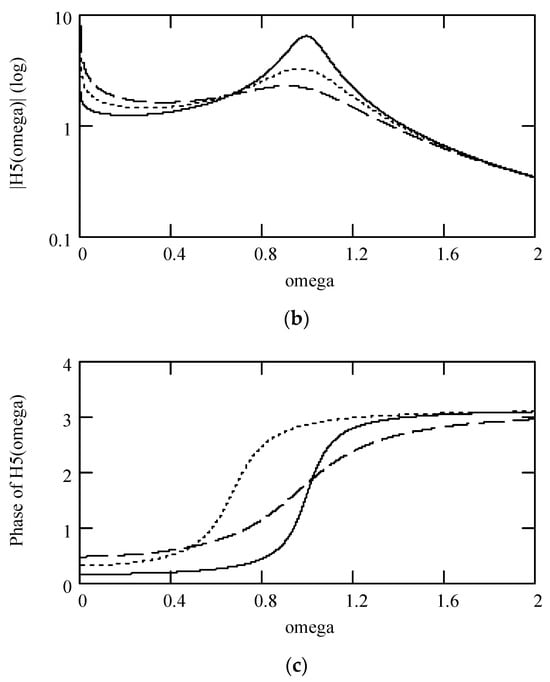
Figure 30. Plots of |H₅(ω)| and φ₅(ω) for m = 1 and k = 1 when λ = 0.1 (solid line), 0.2 (dotted line), and 0.3 (dashed line). (a) |H₅(ω)|; (b) log|H₅(ω)|; (c) φ₅(ω).

8. Analytic Theory of Class VII Fractional Vibrators

This section gives a tutorial with respect to the analytic theory of class VII fractional vibrators from seven aspects: (1) the analytical expression for the frequency transfer function of a class VII fractional vibrator in Theorem 55 in Section 8.1; (2) the equivalent motion equation of class VII fractional vibrators in Theorem 56 in Section 8.2; (3) analytical expressions for the equivalent parameters of class VII fractional vibrators in Section 8.3; (4) the analytical expressions of responses of class VII fractional vibrators in Theorems 57–60 in Section 8.4, where the sinusoidal response expression is first introduced; (5) the analytical expression of the equivalent logarithmic decrement in class VII fractional vibrators in Theorem 61 in Section 8.5; (6) the analytical expression for the equivalent quality factor of class VII fractional vibrators in Theorem 62 in Section 8.6; (7) moreover, we propose an analytical expression for the equivalent frequency bandwidth in class VII fractional vibrators in Theorem 63 in Section 8.7.

8.1. Frequency Transfer Function of Class VII Fractional Vibrator

Theorem 55 (Frequency transfer function VII). 

Let H₇(ω) be the frequency transfer function of a class VII fractional vibrator. Then,

$$\begin{array}{l}{H}_7(\omega )={\displaystyle \frac{1}{m{(i\omega )}^2+c{(i\omega )}^{\beta }+k{(i\omega )}^{\lambda }}}\\ ={\displaystyle \frac{1}{\left(-m{\omega }^2+c{\omega }^{\beta }\cos \frac{\beta \pi }{2}+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\right)+i\left(c{\omega }^{\beta }\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda }\sin \frac{\lambda \pi }{2}\right)}}.\end{array}$$

(242)

Proof. 

A class VII fractional vibrator is a special case of a class VI fractional vibrator in the case of α = 2. Thus, substituting α = 2 into H₆(ω) yields the above H₇(ω) in (242). The proof is finished. □

8.2. Equivalent Motion Equation of Class VII Fractional Vibrator

Theorem 56 (Equivalent motion equation VII). 

The motion equation of class VII fractional vibrators is equivalently expressed by

$$\begin{array}{l}\left(m-c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}\right){\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}\\ +\left(c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}\right){\displaystyle \frac{d{x}_7(t)}{dt}}+k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}{x}_7(t)=f(t).\end{array}$$

(243)

Proof. 

As a class VII fractional vibrator is a special case of a class VI one for α = 2, replacing α with 2 in (18) yields (243). This finishes the proof. □

8.3. Equivalent Parameters of Class VII Fractional Vibrator

Corollary 43 (Equivalent mass VII). 

Denote by m_eq7 the equivalent mass of class VII fractional vibrators. Then,

$$m_{\mathrm{eq}7}=m-c{\omega }^{\beta -2}\cos {\displaystyle \frac{\beta \pi }{2}}.$$

(244)

Proof. 

The right side of the above expression is the coefficient of $x_7^{″}(t)$ in (243). Thus, (244) holds. The proof ends. □

Corollary 44 (Equivalent damping VII). 

Let c_eq7 be the equivalent damping of class VII fractional vibrators. Then,

$$c_{\mathrm{eq}7}=c{\omega }^{\beta -1}\sin {\displaystyle \frac{\beta \pi }{2}}+k{\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}.$$

(245)

Proof. 

Because the right side of the above expression is the coefficient of $x_7^{\prime }(t)$ in (243), (245) is true. This finishes the proof. □

Corollary 45 (Equivalent stiffness VII). 

Denote by k_eq7 the equivalent stiffness of class VII fractional vibrators. Then,

$$k_{\mathrm{eq}7}=k{\omega }^{\lambda }\cos {\displaystyle \frac{\lambda \pi }{2}}.$$

(246)

Proof. 

The right side of the above expression is the coefficient of x₇(t) in (243); thus, (246) is true. The proof is finished. □

Using m_eq7, c_eq7, and k_eq7 to rewrite (243) yields the equation of motion in (247) below

$$m_{\mathrm{eq}7}{\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+c_{\mathrm{eq}7}{\displaystyle \frac{d{x}_7(t)}{dt}}+k_{\mathrm{eq}7}{x}_7(t)=f(t).$$

(247)

Corollary 46 (Equivalent damping ratio VII). 

Let ζ_eq7 be the equivalent damping ratio for a class VII fractional vibrator. Define it by (248) below

$${\varsigma }_{\mathrm{eq}7}={\displaystyle \frac{c_{\mathrm{eq}7}}{2\sqrt{m_{\mathrm{eq}7}{k}_{\mathrm{eq}7}}}}.$$

(248)

Then,

$${\varsigma }_{\mathrm{eq}7}={\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(249)

Proof. 

Substituting α = 2 into ζ_eq6 yields the above ζ_eq7 in (249). The proof ends. □

As ζ_eq7 > 1 is trivial in vibrations, |ζ_eq7| ≤ 1 is defaulted in what follows.

Corollary 47 (Equivalent damping free natural angular frequency VII). 

Denote by ω_eqn7 the equivalent damping free natural angular frequency of class VII fractional vibrators. Define it as (250)

$${\omega }_{\mathrm{eqn}7}=\sqrt{{\displaystyle \frac{k_{\mathrm{eq}7}}{m_{\mathrm{eq}7}}}}.$$

(250)

Then,

$${\omega }_{\mathrm{eqn}7}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}.$$

(251)

Proof. 

Substituting α = 2 into ω_eqn6 produces the above ω_eqn7 in (251) The proof ends. □

Corollary 48 (Equivalent damped natural angular frequency VII). 

Let ω_eqd7 be the equivalent damped natural angular frequency of class VII fractional vibrators. Define

$${\omega }_{\mathrm{eqd}7}={\omega }_{\mathrm{eqn}7}\sqrt{1-{\varsigma }_{\mathrm{eq}7}^2}.$$

(252)

Then,

$${\omega }_{\mathrm{eqd}7}=\sqrt{{\displaystyle \frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}\sqrt{1-{\left({\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}\right)}^2}.$$

(253)

Proof. 

Substituting ω_eqn7 and ζ_eq7 into (252) yields (253). The proof is finished. □

Corollary 49 (Equivalent frequency ratio VII). 

Denote by γ_eq7 the equivalent frequency ratio of class VII fractional vibrators. Define it by

$${\gamma }_{\mathrm{eq}7}={\displaystyle \frac{\omega }{{\omega }_{\mathrm{eqn}7}}}.$$

(254)

Then,

$${\gamma }_{\mathrm{eq}7}=\gamma \sqrt{{\displaystyle \frac{\left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}.$$

(255)

Proof. 

Substituting ω_eqn7 into (254) yields (255). The proof ends. □

8.4. Responses of Class VII Fractional Vibrator

Based on m_eq7, ζ_eq7, and ω_eqn7, we write the motion equation of a class VII fractional vibrator by (256) below

$${\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}{\displaystyle \frac{d{x}_7(t)}{dt}}+{\omega }_{\mathrm{eqn}7}^2{x}_7(t)={\displaystyle \frac{f(t)}{m_{\mathrm{eq}7}}}.$$

(256)

Theorem 57 (Free response VII). 

Denote by x₇(t) the free response of a class VII fractional vibrator. It is the solution to the following fractional differential equation

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_7(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_7(t)}{d{t}^{\lambda }}}=0,\\ x_7(0)=x_{70},x_7^{\prime }(0)=v_{70}.\end{array}\right.$$

(257)

Then,

$$x_7(t)=e^{-{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}t}\left(x_{70}\cos {\omega }_{\mathrm{eqd}7}t+{\displaystyle \frac{v_{70}+{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}{x}_{70}}{{\omega }_{\mathrm{eqd}7}}}\sin {\omega }_{\mathrm{eqd}7}t\right), t\ge 0.$$

(258)

Proof. 

The solution to (257) equals to the one to (259) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}{\displaystyle \frac{d{x}_7(t)}{dt}}+{\omega }_{\mathrm{eqn}7}^2{x}_7(t)=0,\\ x_7(0)=x_{70},x_7^{\prime }(0)=v_{70}.\end{array}\right.$$

(259)

Hence, (258) is true. This completes the proof. □

Figure 31 shows some plots of x₇(t).

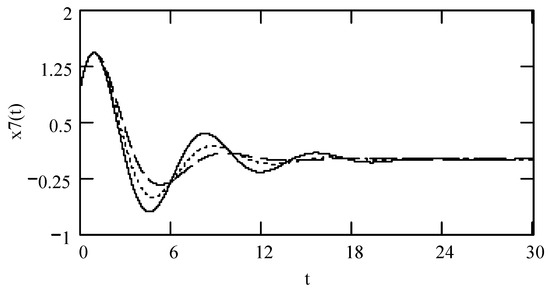
Figure 31. Plots of x₅(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (β, λ) = (1.9, 0.3) (solid line), (1.8, 0.4) (dotted line), and (1.7, 0.5) (dashed line).

Theorem 58 (Impulse response VII). 

Denote by h₇(t) the impulse response of a class VII fractional vibrator. It is the solution to the fractional differential equation given by

$$m{\displaystyle \frac{d^2{h}_7(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{h}_7(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{h}_7(t)}{d{t}^{\lambda }}}=\delta (t)$$

(260)

with zero initial conditions. Then,

$$h_7(t)={\displaystyle \frac{1}{m_{\mathrm{eq}7}{\omega }_{\mathrm{eqd}7}}}{e}^{-{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}t}\sin {\omega }_{\mathrm{eqd}7}t, t\ge 0.$$

(261)

Proof. 

The solution to (260) can be taken as the one to (262) below

$${\displaystyle \frac{d^2{h}_7(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}{\displaystyle \frac{d{h}_7(t)}{dt}}+{\omega }_{\mathrm{eqn}7}^2{h}_7(t)={\displaystyle \frac{\delta (t)}{m_{\mathrm{eq}7}}}.$$

(262)

Hence, (261) is true. The proof is finished. □

Some plots of h₇(t) are shown in Figure 32.

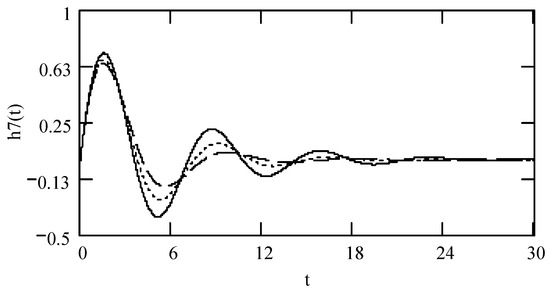
Figure 32. Plots of h₇(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (β, λ) = (1.9, 0.3) (solid line), (1.8, 0.4) (dotted line), and (1.7, 0.5) (dashed line).

Theorem 59 (Step response VII). 

Denote by g₇(t) the unit step response of a class VII fractional vibrator. It is the solution to (263) below

$$m{\displaystyle \frac{d^2{g}_7(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{g}_7(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{g}_7(t)}{d{t}^{\lambda }}}=u(t)$$

(263)

with zero initial conditions. Then,

$$g_7(t)={\displaystyle \frac{1}{k_{\mathrm{eq}7}}}\left[1-{\displaystyle \frac{e^{-{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}7}^2}}}\cos \left({\omega }_{\mathrm{eqd}7}t-{\varphi }_7\right)\right],t\ge 0,$$

(264)

where

$${\varphi }_7={\tan }^{-1}{\displaystyle \frac{{\varsigma }_{\mathrm{eq}7}}{\sqrt{1-{\zeta }_{\mathrm{eq}7}^2}}}.$$

(265)

Proof. 

Substituting α = 2 into g₆(t) produces (264) with (265). This completes the proof. □

Figure 33 illustrates some of the plots of g₇(t).

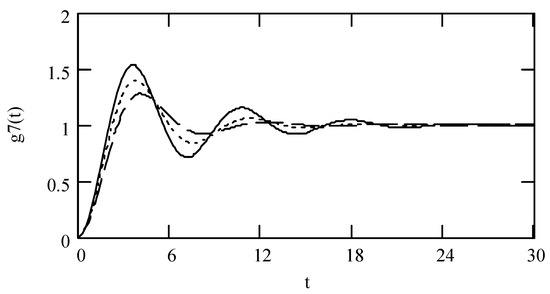
Figure 33. Plots of g₇(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (β, λ) = (1.9, 0.3) (solid line), (1.8, 0.4) (dotted line), and (1.7, 0.5) (dashed line).

Theorem 60 (Sinusoidal response VII). 

Let x_7zs(t) be the sinusoidal response of a class VII fractional vibrator. It results from

$$\left\{\begin{array}{c}m{\displaystyle \frac{d^2{x}_{7\mathrm{zs}}(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_{7\mathrm{zs}}(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_{7\mathrm{zs}}(t)}{d{t}^{\lambda }}}=A\cos \omega t,\\ x_{7\mathrm{zs}}(0)=0,x_{7\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(266)

Then,

$$x_{7\mathrm{zs}}(t)={\displaystyle \frac{1}{m{\omega }_{\mathrm{eqd}7}}}{\displaystyle \frac{A\left\{\begin{array}{l}\left({\omega }_{\mathrm{eqn}7}^2-{\omega }^2\right)\cos \omega t+2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}\omega \sin \omega t\\ +e^{-{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}t}\left[\begin{array}{l}\left({\omega }_{\mathrm{eqn}7}^2-{\omega }^2\right)\cos {\omega }_{\mathrm{eqd}7}t\\ -\frac{{\varsigma }_{\mathrm{eq}7}}{\sqrt{1-{\varsigma }_{\mathrm{eq}7}^2}}\left({\omega }_{\mathrm{eqn}7}^2+{\omega }^2\right)\sin {\omega }_{\mathrm{eqd}7}t\end{array}\right]\end{array}\right\}}{{\left({\omega }_{\mathrm{eqn}7}^2-{\omega }^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}\omega \right)}^2}}.$$

(267)

Proof. 

The solution to (266) is equal to the one to (268) below

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_{7\mathrm{zs}}(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{eq}7}{\omega }_{\mathrm{eqn}7}{\displaystyle \frac{d{x}_{7\mathrm{zs}}(t)}{dt}}+{\omega }_{\mathrm{eqn}7}^2{x}_{7\mathrm{zs}}(t)={\displaystyle \frac{A\cos \omega t}{m_{\mathrm{eq}7}}},\\ x_{7\mathrm{zs}}(0)=0,x_{7\mathrm{zs}}^{\prime }(0)=0.\end{array}\right.$$

(268)

Therefore, (267) is true. This completes the proof. □

Figure 34 shows some plots of x_7zs(t).

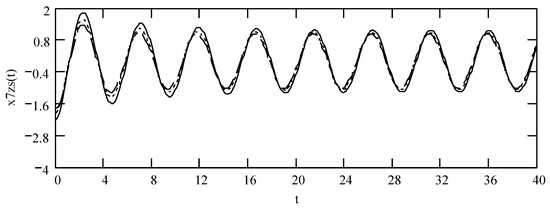
Figure 34. Plots of x_7zs(t) for ω = 1.3, m = 1, c = 0.2, and k = 1 when (β, λ) = (1.9, 0.3) (solid line), (1.8, 0.4) (dotted line), and (1.7, 0.5) (dashed line).

8.5. Equivalent Logarithmic Decrement in Class VII Fractional Vibrators

Theorem 61 (Equivalent logarithmic decrement VII). 

Let t_i and t_i+1 be two successive time points of the free response x₇(t), where x₇(t) reaches its successive peak values of x₇(t_i) and x₅(t_i+1), respectively. Let Δ_eq7 be the equivalent logarithmic decrement in x₇(t). Then,

$${\Delta }_{\mathrm{eq}7}={\displaystyle \frac{2\pi {\varsigma }_{\mathrm{eq}7}}{\sqrt{1-{\varsigma }_{\mathrm{eq}7}^2}}}={\displaystyle \frac{\pi \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}{\sqrt{1-\frac{{\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2}{4\left[\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\right]}}}}.$$

(269)

Proof. 

Substituting α = 2 into Δ_eq6 produces the above Δ_eq7 in (269). The proof ends. □

8.6. Quality Factor of Class VII Fractional Vibrators

Let Q_eq7 be the equivalent Q factor of class VII fractional vibrators. The equivalent motion equation of class VII fractional vibrators is in the standard form of conventional vibration systems. Hence, we define

$$Q_{\mathrm{eq}7}={\displaystyle \frac{1}{2{\varsigma }_{\mathrm{eq}7}}}.$$

(270)

Theorem 62 (Equivalent Q factor VII). 

The quantity Q_eq7 is given by

$$Q_{\mathrm{eq}7}={\displaystyle \frac{\sqrt{\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}}.$$

(271)

Proof. 

Substituting ζ_eq7 into (270) produces (271). The proof is finished. □

8.7. Equivalent Frequency Bandwidth of Class VII Fractional Vibrators

Let B_eq7,0.707 be the equivalent frequency bandwidth of class VII fractional vibrators. As the equivalent motion equation of class VII fractional vibrators is in the standard form of conventional vibration systems, we define

$${\mathrm{B}}_{\mathrm{eq}7,0.707}={\displaystyle \frac{{\omega }_{\mathrm{eqn}7}}{2\pi Q_{\mathrm{eq}7}}}.$$

(272)

Theorem 63 (Equivalent frequency bandwidth VII). 

The quantity B_eq7,0.707 is given by

$${\mathrm{B}}_{\mathrm{eq}7,0.707}={\displaystyle \frac{c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\pi \left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(273)

Proof. 

Substituting ω_eqn7 and Q_eq7 into (272) yields (273). The proof is finished. □

8.8. More about Frequency Transfer Function of Class VII Fractional Vibrators

By using γ_eq7, ζ_eq7, and k_eq7, we have (274) to express H₇(ω) in the form

$$H_7(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}7}\left(1-{\gamma }_{\mathrm{eq}7}^2+i2{\varsigma }_{\mathrm{eq}7}{\gamma }_{\mathrm{eq}7}\right)}}.$$

(274)

Writing H₇(ω) = |H₇(ω)|exp[−φ₇(ω)] yields (275) to express |H₇(ω)| by

$$\left|H_7(\omega )\right|={\displaystyle \frac{1}{k}}{\displaystyle \frac{1}{\sqrt{\begin{array}{l}{\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left(-1+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\gamma }^2{\left(2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2\end{array}}}}.$$

(275)

The phase of H₅(ω) is given by (276) in the form

$${\phi }_7(\omega )={\cos }^{-1}{\displaystyle \frac{1-{\gamma }_{\mathrm{eq}7}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}7}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}7}{\gamma }_{\mathrm{eq}7}\right)}^2}}}.$$

(276)

Figure 35 shows some of the plots of |H₇(ω)| and φ₇(ω).

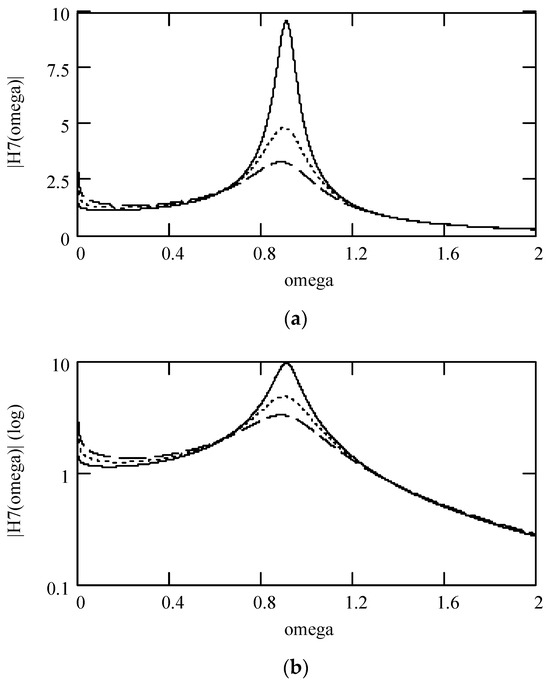
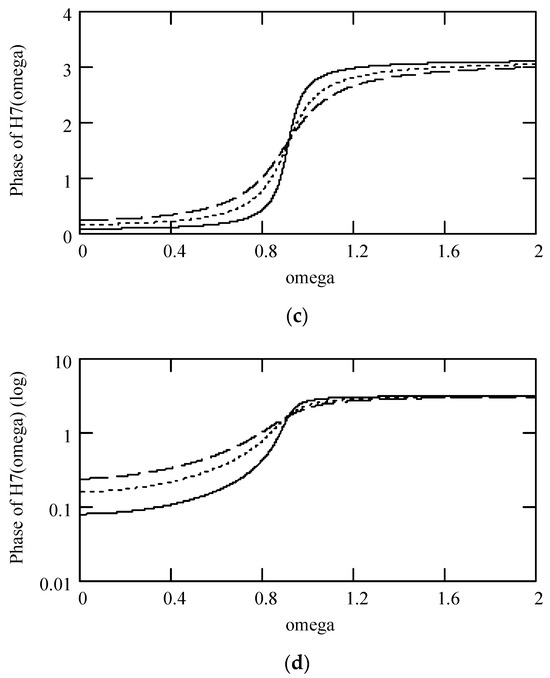
Figure 35. Plots of |H₇(ω)| and φ₇(ω) for m = 1, c = 0.2, and k = 1 when (β, λ) = (1.9, 0.05) (solid line), (1.8, 0.10) (dotted line), and (1.7, 0.15) (dashed line). (a) |H₇(ω)|; (b) log|H₇(ω)|; (c) φ₇(ω); (d) logφ₇(ω).

9. Application: Analytical Expression of Forced Response to Multi-Fractional Damped Euler–Bernoulli Beam

The Euler–Bernoulli beam plays a role in structural vibrations (Harris [71]). This is particularly true in ship structural vibrations (Palley et al. [72]; Lewis [73]). There are references regarding applications of fractional calculus to the Euler–Bernoulli beam, see, e.g., Alkhaldi et al. [29], Spanos and Malara [53], Ouzizi et al. [74], Lewandowski and Baum [75], Nešić et al. [76], Rossikhin and Shitikova [77], and Freundlich [78,79,80]. However, the closed form expression of forced response to a multi-fractional damped Euler–Bernoulli beam is rarely reported. By multi-fractional, we mean that inertial, internal, and external damping forces are of fractional orders. As an application of the analytic theory of fractional vibrations previously discussed, in this section, we review the analytic theory of fractional Euler–Bernoulli beams in Li [26].

9.1. Multi-Fractional Damped Euler–Bernoulli Beam

Consider a uniform beam of length l. Let A be its cross-sectional area. Let ρ be its material density. Let I be its cross-sectional moment of inertia. Let E be its elastic modulus. Then, EI is its bending rigidity. Denote by c_s and c internal and external damping, respectively. Denote by w(x, t) deflection. Let q(x, t) be driven force. Then, the motion equation of the conventional damped Euler–Bernoulli beam is expressed by

$${\displaystyle \frac{{\partial }^2}{\partial x^2}}\left(EI{\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}+c_{s}I{\displaystyle \frac{{\partial }^{3}w}{\partial x^2\partial t}}\right)+\rho A{\displaystyle \frac{{\partial }^{2}w}{\partial t^2}}+c{\displaystyle \frac{\partial w}{\partial t}}=q(x,t).$$

(277)

In (277), $c{\displaystyle \frac{\partial w}{\partial t}}$ is external damping force, $c_{s}I{\displaystyle \frac{{\partial }^{3}w}{\partial x^2\partial t}}$ is internal damping force, and $\rho A{\displaystyle \frac{{\partial }^{2}w}{\partial t^2}}$ is inertia force (Palley et al. [72], Lewis [73]). The forced response to (277) under the Rayleigh damping assumption is known (Palley et al. [72], Lewis [73]).

The above equation takes into account the Voigt assumption on materials about internal damping. Following Li [26], we describe the closed form of the forced response to the multi-fractional damped Euler–Bernoulli beam in the form (278)

$${\displaystyle \frac{{\partial }^2}{\partial x^2}}\left(EI{\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}+c_{s}I{\displaystyle \frac{{\partial }^{2+\lambda }w}{\partial x^2\partial t^{\lambda }}}\right)+\rho A{\displaystyle \frac{{\partial }^{\alpha }w}{\partial t^{\alpha }}}+c{\displaystyle \frac{{\partial }^{\beta }w}{\partial t^{\beta }}}=q(x,t), 1<\alpha <3,0<\beta <2,0<\lambda <2.$$

(278)

Precisely, the above stands for a beam with the fractional inertia force $\rho A{\displaystyle \frac{{\partial }^{\alpha }w}{\partial t^{\alpha }}},$ fractional internal damping force $c_{s}I{\displaystyle \frac{{\partial }^{2+\lambda }w}{\partial x^2\partial t^{\lambda }}},$ and fractional external damping force $c{\displaystyle \frac{{\partial }^{\beta }w}{\partial t^{\beta }}}.$

9.2. Closed Form Forced Response

Using separation of variables, we write the response by w(x, t) = φ(x)p(t). Substituting it into (278) produces

$$\begin{array}{l}{\displaystyle \sum _{j=1}^{\infty }\rho A{\phi }_j(x)\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+{\displaystyle \sum _{j=1}^{\infty }c{\phi }_j(x)\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\displaystyle \sum _{j=1}^{\infty }\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +{\displaystyle \sum _{j=1}^{\infty }\frac{d^2}{d{x}^2}\left[EI\frac{d^2{\phi }_j(x)}{d{x}^2}\right]p_j(t)}=q(x,t).\end{array}$$

(279)

In (279), p_j(t) is the jth order coordinate and φ_j(t) is the jth order vibration mode (j = 1, 2, …). Using the orthogonality of vibration modes φ_m(x) on both sides of the above equation produces the following

$$\begin{array}{l}{M}_j{\displaystyle \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+{\displaystyle \frac{M_{j}c}{\rho A}}{\displaystyle \frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[EI\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx{p}_j(t)}=Q_j(t),\end{array}$$

(280)

where $M_j=\rho A{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_j^2(x)}dx$ is the jth order generalized mass and Q_j(t) the jth order generalized force.

Using (281) below

$${\displaystyle \frac{d^2}{d{x}^2}}\left[EI{\displaystyle \frac{d^2{\phi }_j(x)}{d{x}^2}}\right]=\rho A{\omega }_{\mathrm{n}j}^2{\phi }_j(x),$$

(281)

where ${\omega }_{\mathrm{n}j}={\left({\displaystyle \frac{j\pi }{l}}\right)}^2\sqrt{{\displaystyle \frac{EI}{\rho A}}}$ is the jth order natural angular frequency; we rewrite (280) by

$$\begin{array}{l}{M}_j{\displaystyle \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+{\displaystyle \frac{M_{j}c}{\rho A}}{\displaystyle \frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +M_j{\omega }_{\mathrm{n}j}^2{p}_j(t)=Q_j(t).\end{array}$$

(282)

According to the Rayleigh damping assumption

c = ρAa,

(283)

where a is a coefficient with the unit of time since ρA is with the unit of mass, and

c_s = Eb,

(284)

where b is a coefficient with the unit of frequency as E is with the unit [N/m].

Substituting (283) and (284) into (282) and taking into account the orthogonality of vibration modes, we have (285) below

$$M_j{\displaystyle \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+M_{j}a{\displaystyle \frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+M_j{\omega }_{\mathrm{n}j}^{2}b{\displaystyle \frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}+M_j{\omega }_{\mathrm{n}j}^2{p}_j(t)=Q_j(t).$$

(285)

Therefore, we have a multi-fractional differential equation with respect to p_j(t) in the following form

$${\displaystyle \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+\left(a{\displaystyle \frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\omega }_{\mathrm{n}j}^{2}b{\displaystyle \frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\right)+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t),$$

(286)

where f_j(t) is given by (287) in the form

$$f_j(t)={\displaystyle \frac{Q_j(t)}{M_j}}.$$

(287)

According to the analytic theory of class VI fractional vibrators addressed in Section 2, (286) can be written by (288) in the form

$$\begin{array}{l}-\left(\cos {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -2}+a\cos {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -2}\right){\displaystyle \frac{d^2{p}_j(t)}{d{t}^2}}\\ +\left(\sin {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -1}+a\sin {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -1}\right){\displaystyle \frac{d{p}_j(t)}{dt}}+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t).\end{array}$$

(288)

As a matter of fact,

$$\begin{array}{l}{C}_j(t)\triangleq -\left(\cos {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -2}+a\cos {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -2}\right){\displaystyle \frac{d^2{p}_j(t)}{d{t}^2}}\\ +\left(\sin {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -1}+a\sin {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -1}\right){\displaystyle \frac{d{p}_j(t)}{dt}}+{\omega }_{\mathrm{n}j}^2{p}_j(t).\end{array}$$

(289)

Let

$$D_j(t)\triangleq {\displaystyle \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+\left(a{\displaystyle \frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\omega }_{\mathrm{n}j}^{2}b{\displaystyle \frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\right)+{\omega }_{\mathrm{n}j}^2{p}_j(t).$$

(290)

For (289) and (290), F[C_j(t) − D_j(t)] = 0, where F is the operator of Fourier transform.

Denote by m_e-EBj the jth equivalent mass in (286) in the form (291)

$$m_{\mathrm{e}-\mathrm{EB}j}=-\left(\cos {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -2}+a\cos {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -2}\right).$$

(291)

Let c_e-EBj be the jth equivalent damping in (286). It is given by (292) below

$$c_{\mathrm{e}-\mathrm{EB}j}=\sin {\displaystyle \frac{\alpha \pi }{2}}{\omega }^{\alpha -1}+a\sin {\displaystyle \frac{\beta \pi }{2}}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin {\displaystyle \frac{\lambda \pi }{2}}{\omega }^{\lambda -1}.$$

(292)

Using m_e-EBj and c_e-EBj, we have (293) to express the coordinate motion equation by

$$m_{\mathrm{e}-\mathrm{EB}j}{\displaystyle \frac{d^2{p}_j(t)}{d{t}^2}}+c_{\mathrm{e}-\mathrm{EB}j}{\displaystyle \frac{d{p}_j(t)}{dt}}+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t).$$

(293)

Denote by ζ_e-EBj the jth equivalent damping ratio regarding (286). Define it by ${\varsigma }_{\mathrm{e}-\mathrm{EB}j}={\displaystyle \frac{c_{\mathrm{e}-\mathrm{EB}j}}{2\sqrt{m_{\mathrm{e}-\mathrm{EB}j}}}}.$ Then, it is given by (294) in the form

$${\varsigma }_{\mathrm{e}-\mathrm{EB}j}={\displaystyle \frac{\sin \frac{\alpha \pi }{2}{\omega }^{\alpha -1}+a\sin \frac{\beta \pi }{2}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin \frac{\lambda \pi }{2}{\omega }^{\lambda -1}}{2\sqrt{-\left(\cos \frac{\alpha \pi }{2}{\omega }^{\alpha -2}+a\cos \frac{\beta \pi }{2}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos \frac{\lambda \pi }{2}{\omega }^{\lambda -2}\right)}}}.$$

(294)

Let ω_en-EBj be the jth equivalent damping free natural frequency regarding the system (286). It is given by (295) below

$${\omega }_{\mathrm{en}-\mathrm{EB}j}^2={\displaystyle \frac{{\omega }_{\mathrm{n}j}^2}{m_{\mathrm{e}-\mathrm{EB}j}}}.$$

(295)

From a view of vibration engineering, we are only interested in (296)

$$\left|{\varsigma }_{\mathrm{e}-\mathrm{EB}j}\right|\le 1.$$

(296)

Let ω_end-EBj be the jth equivalent damped natural frequency regarding the system (286). Then, the expression of ω_end-EBj is in the form (297) below

$${\omega }_{\mathrm{end}-\mathrm{EB}j}={\omega }_{\mathrm{en}-\mathrm{EB}j}\sqrt{1-{\varsigma }_{\mathrm{eEB}j}^2}.$$

(297)

Therefore, we rewrite (293) by

$${\displaystyle \frac{d^2{p}_j(t)}{d{t}^2}}+2{\varsigma }_{\mathrm{e}-\mathrm{EB}j}{\omega }_{\mathrm{en}-\mathrm{EB}j}{\displaystyle \frac{d{p}_j(t)}{dt}}+{\omega }_{\mathrm{en}-\mathrm{EB}j}^2{p}_j(t)={\displaystyle \frac{f_j(t)}{m_{\mathrm{e}-\mathrm{EB}j}}}.$$

(298)

Let h_j(t) be the jth impulse response function of the system (298). Then, it is expressed by (299) in the form

$$h_j(t)={\displaystyle \frac{1}{m_{\mathrm{e}-\mathrm{EB}j}{\omega }_{\mathrm{end}-\mathrm{EB}j}}}{e}^{-{\varsigma }_{\mathrm{e}-\mathrm{EB}j}{\omega }_{\mathrm{en}-\mathrm{EB}j}t}\sin {\omega }_{\mathrm{end}-\mathrm{EB}j}t, t>0.$$

(299)

Because of (300) below

$$p_j(t)=f_j(t)\ast h_j(t),$$

(300)

the zero-state forced response to a multi-fractional damped Euler–Bernoulli beam is expressed by (301) in the form

$$w(x,t)={\displaystyle \sum _{j=1}^{\infty }\frac{{\phi }_j(x)}{m_{\mathrm{e}-\mathrm{EB}j}{\omega }_{\mathrm{end}-\mathrm{EB}j}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-{\varsigma }_{\mathrm{e}-\mathrm{EB}j}{\omega }_{\mathrm{en}-\mathrm{EB}j}\tau }\sin {\omega }_{\mathrm{end}-\mathrm{EB}j}\tau f_j(t-\tau )}d\tau }.$$

(301)

9.3. Demonstration

Consider a free–free Euler–Bernoulli beam. Then, (302) below is the expression of φ_j(x)

$${\phi }_j(x)~{\displaystyle \frac{\mathrm{ch}{\mu }_{j}l-\cos {\mu }_{j}l}{\sin {\mu }_{j}l-\mathrm{sh}{\mu }_{j}l}}(\sin {\mu }_{j}x+\mathrm{sh}{\mu }_{j}x)+(\cos {\mu }_{j}x+\mathrm{ch}{\mu }_{j}x), j=1,2,\cdots$$

(302)

where one uses the identity in the form (303) below

$$\cos {\mu }_{j}l={\displaystyle \frac{1}{\mathrm{ch}{\mu }_{j}l}}.$$

(303)

Let f(t) = u(t). Figure 36 demonstrates the plots of w₁(x, t) = w1. Refer to [26] for more about applications and illustrations of fractional vibrations of class I-VII to beams.

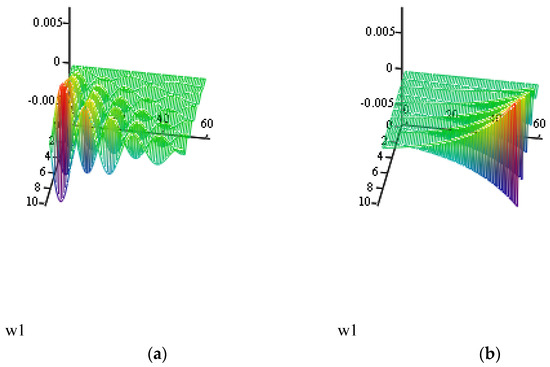
Figure 36. Plots of w₁(x, t) = w1 of a free-free damped Euler–Bernoulli beam when f_j(t) = u(t) and l = 10 for ω = 0.0314, a = 1, b = 1, E = 1, x = 0, …, 10, and t = 0, …, 60. (a) w1 for α = 1.8; β = λ = 1.2. (b) w1 for α = 1.8, β = 1.2, and λ = 0.1.

10. Application: Seven Classes of Fractionally Random Vibrations Driven by P-M Spectrum

The contributions given in this chapter are the analytic expressions of the power spectrum density (PSD) responses and cross-PSD responses to fractional vibrators from class I to class VII under the excitation with Pierson and Moskowitz (P-M) spectrum using elementary functions. The present results show that fractional orders, namely, α, β, and λ, have considerable effects on responses when ocean surface waves pass through those fractional vibration systems.

10.1. Background

Since the early literature by Crandall and Mark [81] in random vibrations, the topic of random vibrations has remained of interest to researchers. The literature regarding random vibrations is rich, see, e.g., Harris [71], Palley et al. [72], Lewis [73], Nakagawa and Ringo [82], Lalanne [83], Nigam [84], Preumont [85,86], Soong and Grigoriu [87], Thomson and Dahleh [88], Lutes and Sarkani [89], Elishakoff and Lyon [90], Jensen [91], Rothbart and Brown [92], Simiu and Scanlan [93], Ra [94], Dhanak and Xiros [95], Findeisen [96], Mukhopadhyay [97], and Cheli [98], just to mention a few. However, reports regarding fractionally random vibrations are rarely seen except Li [69]. In Li [69], the author addresses the power spectrum density (PSD) and cross-PSD of the responses of seven classes of fractional vibrations previously discussed when driven signals are fractional Gaussian noise, fractional Brownian motion, fractional Ornstein–Uhlenbeck process, and the von Kármán process. Nonetheless, the closed expressions of the PSD and cross-PSD responses of seven classes of fractional vibrations driven by the P-M spectrum are rarely seen.

Note that the P-M spectrum is widely used in the field of ocean engineering and ship building for describing fully developed ocean surface waves (Jensen [91], Lewis [99], Massel [100], Chairabarti [101], Li [102], and the final report of the 23rd International Towing Tank Conference [103]). Therefore, as an application of the analytic theory of fractional vibrations previously addressed, in this section, we present the novel results with respect to the analytic expressions of PSD and cross-PSD responses of seven classes of fractional vibrations driven by process with the Pierson and Moskowitz (P-M) spectrum, expecting that the present results may be useful for further explore ship structural vibrations.

The rest of the section is organized as follows. The power spectrum density (PSD) responses and cross-PSD responses to seven classes of fractional vibration systems under the excitation of P-M spectrum are given in Section 10.2, Section 10.3, Section 10.4, Section 10.5, Section 10.6, Section 10.7 and Section 10.8, respectively. The summary is given in Section 10.9.

10.2. Responses of Class I Fractional Vibrators Driven by P-M Spectrum

10.2.1. Computations

For facilitating discussions, we write the motion equation of a class I fractional vibrator in (304)

$$m{\displaystyle \frac{d^{\alpha }{x}_1(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d{x}_1(t)}{dt}}=f(t),$$

(304)

where f(t) is the driven force with the P-M spectrum and x₁(t) is the response.

Let S_ff(ω) be the PSD of f(t). Suppose f(t) follows the P-M spectrum. Then,

$$S_{ff}(\omega )=\alpha g^2{\omega }^{-5}{e}^{-\beta {\left({\displaystyle \frac{g}{V}}\right)}^4{\displaystyle \frac{1}{{\omega }^4}}}.$$

(305)

In (305), α = 8.1 × 10⁻³, β = 0.74, g is the acceleration of gravity (m/s²), and V is wind speed (m/s) at an elevation of 19.5 m above the sea surface. The unit of S is m²·s. Figure 37 indicates a plot of S_ff(ω) for V = 15.

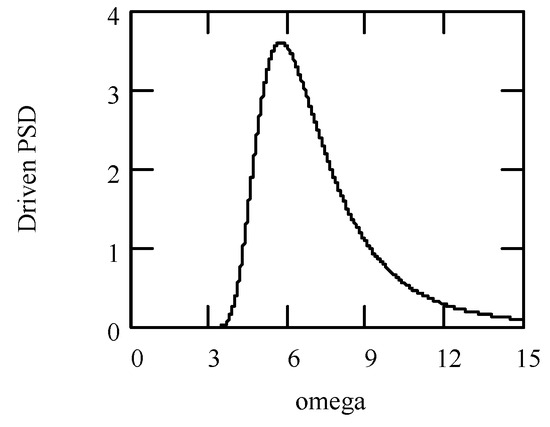
Figure 37. Plot of P-M spectrum.

Theorem 64 (PSD response I). 

Denote by S_xx1(ω) the PSD of the response x₁(t). Equation (306) is its expression

$$S_{xx1}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k^2\left[{\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|\right)}^2+{\left(\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}^2\right]}}.$$

(306)

Proof. 

Equation (307) expresses the relationship between S_xx1(ω) and S_xx1(ω) in the form

S_xx1(ω) = S_ff(ω)|H₁(ω)|².

(307)

Since

$$\left|H_1(\omega )\right|={\displaystyle \frac{1/k}{\sqrt{{\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|\right)}^2+{\left(\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}^2}}},$$

Theorem 64 holds. The proof is finished. □

Theorem 65 (Cross-PSD response I). 

Let S_fx1(ω) be the cross-PSD between f(t) and x₁(t). Equation (308) is its expression

$$S_{fx1}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|+i\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}}.$$

(308)

Proof. 

Note that

$$H_1(\omega )={\displaystyle \frac{1}{k\left(1-{\gamma }_{\mathrm{eq}1}^2+i2{\varsigma }_{\mathrm{eq}1}{\gamma }_{\mathrm{eq}1}\right)}}={\displaystyle \frac{1}{k\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|+i\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}}.$$

Equation (309) shows the relationship between S_fx1(ω) and S_ff(ω)

S_fx1(ω) = S_ff(ω)H₁(ω).

(309)

Thus, Theorem 65 is sound. This finishes the proof. □

In the time domain, the autocorrelation function (ACF) response is given by (310)

r_xx1(τ) = r_ff(τ)∗h₁(τ)∗h₁(−τ),

(310)

and the cross-correlation response is expressed by (311)

r_fx1(τ) = r_ff(τ)∗h₁(τ).

(311)

10.2.2. Effects of α on Responses

Figure 38 indicates some plots of |H₁(ω)|². Some plots of the PSD response S_xx1(ω) are shown in Figure 39.

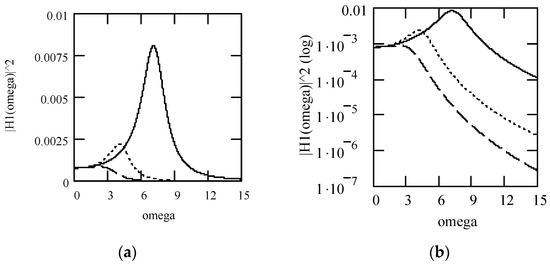
Figure 38. Plots of |H₁(ω)|² with α = 1.8 (solid), 2.4 (dotted), and 2.8 (dashed) when m = 1 and k = 36. (a) |H₁(ω)|²; (b) log|H₁(ω)|².

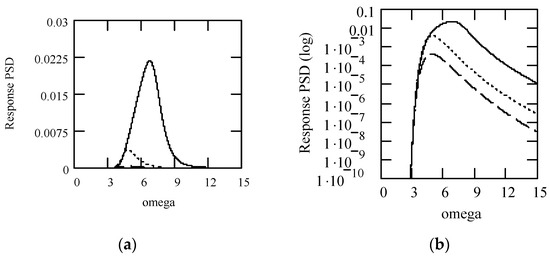
Figure 39. Plots of response PSD S_xx1(ω) with α = 1.8 (solid), 2.4 (dotted), and 2.8 (dashed) when m = 1, k = 36, and V = 15. (a) S_xx1(ω); (b) logS_xx1(ω).

When α = 2, a class I fractional vibrator reduces to be a conventional damping free vibrator. For α = 2, m = 1, c = 0.1, k = 36, and V = 15, a resonance occurs is indicated in Figure 40a. In Figure 41, we illustrate some plots of the cross-PSD response S_fx1(ω).

Figure 40. Resonance when with α = 2, m = 1, k = 36, and V = 15. (a) Plot of log|H₁(ω)|²; (b) plot of response PSD logS_xx1(ω).

Figure 41. Illustrations of cross-PSD response S_fx1(ω) with α = 1.8 (solid), 2.4 (dotted), and 2.8 (dashed) when m = 1, k = 36, and V = 15. (a) |S_fx1(ω)|; (b) log|S_fx1(ω)|; (c) Phase of S_fx1(ω). (d). Phase of S_fx1(ω) in log scale.

According to the random data generation used in Massel [100], Chairabarti [101], and Li [104], we illustrate some plots of driven signal f(t) and the response x₁(t) in Figure 42.

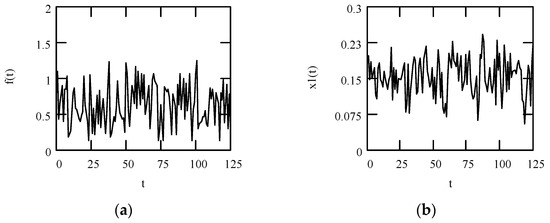
Figure 42. Plots of random series of driven signal and response signals when m = 1, k = 36, and V = 15: (a) Driven signal. (b) Response x₁(t) for α = 1.8. (c) Response x₁(t) for α = 2.4. (d) Response x₁(t) for α = 2.4 in log scale. (e) Response x₁(t) for α = 2.8. (f) Response x₁(t) for α = 2.8 in log scale.

There are noticeable effects of the fractional order α on the responses for class I fractional vibration systems driven by the P-M spectrum.

10.3. Responses of Class II Fractional Vibrators Driven by P-M Spectrum

10.3.1. Computation Methods

We write the equation of motion of a class II fractional vibrator as (312) for facilitating discussions

$$m{\displaystyle \frac{d^2{x}_2(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_2(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d{x}_2(t)}{dt}}=f(t),$$

(312)

where f(t) is the excitation with the P-M spectrum and x₂(t) is the system response.

Theorem 66 (PSD response II). 

Let S_xx2(ω) be the PSD of the response x₂(t). Equation (313) is its analytical expression

$$S_{xx2}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k^2\left\{{\left[1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2+{\left(\frac{2\varsigma {\omega }^{\beta }}{{\omega }_n}\sin \frac{\beta \pi }{2}\right)}^2\right\}}}.$$

(313)

Proof. 

Equation (314) gives the relationship between S_xx2(ω) and S_ff(ω)

S_xx2(ω) = S_ff(ω)|H₂(ω)|²,

(314)

where

$$\left|H_2(\omega )\right|={\displaystyle \frac{1/k}{\sqrt{{\left[1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2+{\left(\frac{2\varsigma {\omega }^{\beta }}{{\omega }_n}\sin \frac{\beta \pi }{2}\right)}^2}}}.$$

Thus, (313) is true and Theorem 66 is valid. This finishes the proof. □

Theorem 67 (Cross-PSD response II). 

Denote by S_fx2(ω) the cross-PSD between f(t) and x₂(t). Then, its expression is given by

$$S_{fx2}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k\left[1-{\gamma }^2\left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }}{{\omega }_n}\sin \frac{\beta \pi }{2}\right]}}.$$

(315)

Proof. 

Due to the relationship between S_fx2(ω) and S_ff(ω) in (316)

S_fx2(ω) = S_ff(ω)H₂(ω),

(316)

and

$$H_2(\omega )={\displaystyle \frac{1/k}{1-{\gamma }^2\left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}},$$

(315) is valid and Theorem 67 holds. The proof completes. □

In the time domain, one has the ACF response expressed by (317) below

rxx2(τ) = rff(τ)∗h2(τ)∗h2(−τ),

(317)

and the cross-correlation response is expressed by (318) below

r_fx2(τ) = r_ff(τ)∗h₂(τ).

(318)

10.3.2. Effects of β on Responses

Figure 43 shows some plots of |H₂(ω)|². Figure 44 indicates some plots of S_xx2(ω).

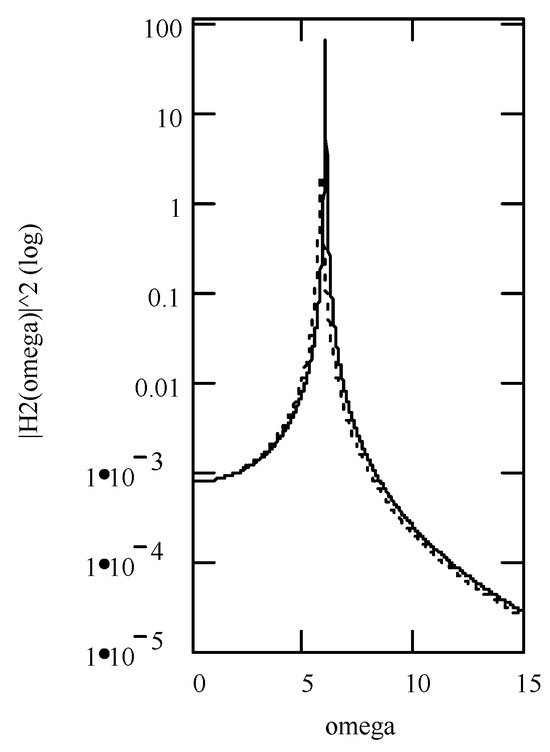
Figure 43. Plots of |H₂(ω)|² (log) with β = 0.4 (solid) and 1.8 (dotted) when m = 1, c = 0.1, and k = 36.

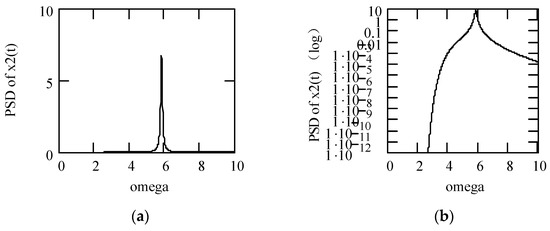
Figure 44. Plots of PSD response S_xx2(ω) with β = 1.8 when m = 1, c = 0.1, k = 36, and V = 15: (a) S_xx2(ω). (b) logS_xx2(ω).

When β = 1, a class II fractional vibrator becomes a conventional damping free vibrator. Figure 45 shows a resonance when β = 1. Figure 46 illustrates some plots of cross-PSD response S_fx2(ω).

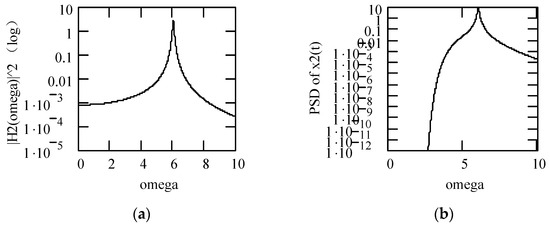
Figure 45. Resonance when with β = 1, m = 1, c = 0.1, k = 36, and V = 15: (a) log|H₂(ω)|². (b) logS_xx2(ω).

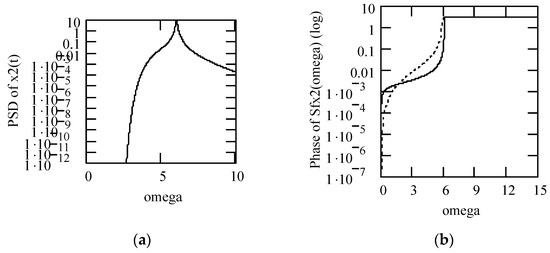
Figure 46. Plots of cross-PSD response S_fx2(ω) with β = 0.4 (solid) and 1.8 (dot) when m = 1, c = 0.1, k = 36, and V = 15: (a) log|S_fx2(ω)|. (b) Phase of S_fx2(ω) in log scale.

There are effects of β on the responses for class II fractional vibration systems. Figure 47 exhibits the effects of β on the fluctuation range of the response x₂(t).

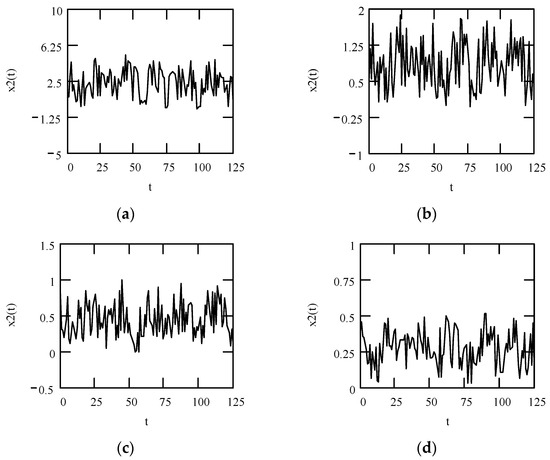
Figure 47. Simulated response series x₂(t) when m = 1, c = 0.1, k = 36, and V = 15: (a) x₂(t) for β = 0.4. (b) x₂(t) for β = 1. (c) x₂(t) for β = 1.4. (d) x₂(t) for β = 1.8.

10.4. Responses of Class III Fractional Vibrators Driven by P-M Spectrum

10.4.1. Computations

We write the motion equation of a class III fractional vibrator as (319) for facilitating discussions

$$m{\displaystyle \frac{d^{\alpha }{x}_3(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_3(t)}{d{t}^{\beta }}}+k{x}_3(t)=f(t),$$

(319)

where f(t) is the excitation with the P-M spectrum and x₃(t) is the response.

Theorem 68 (PSD response III). 

Let S_xx3(ω) be the PSD of the response x₃(t). Then, (320) is its expression

$$S_{xx3}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k^2\left\{\begin{array}{l}{\left[1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\left[\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\right]}^2\end{array}\right\}}}.$$

(320)

Proof. 

Note that S_xx3(ω) = S_ff(ω)|H₃(ω)|². In addition,

$$\begin{array}{l}{H}_3(\omega )={\displaystyle \frac{1}{k\left(1-{\gamma }_{\mathrm{eq}3}^2+i2{\varsigma }_{\mathrm{eq}3}{\gamma }_{\mathrm{eq}3}\right)}}\\ ={\displaystyle \frac{1/k}{1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}}.\end{array}$$

Thus, (320) is true and Theorem 68 holds. The proof is finished. □

Theorem 69 (Cross-PSD response III). 

Let S_fx3(ω) be the cross-PSD between f(t) and x₃(t). Then, (321) is its expression

$$S_{fx3}(\omega )={\displaystyle \frac{k^{-1}\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{\begin{array}{l}1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\end{array}}}.$$

(321)

Proof. 

As S_fx3(ω) = S_ff(ω)H₃(ω), we have (321) and Theorem 69 holds. The proof completes. □

In the time domain, we have the ACF response expressed by (322) in the form

r_xx3(τ) = r_ff(τ)∗h₃(τ)∗h₃(−τ),

(322)

and the cross-correlation response by (323) in the form

r_fx3(τ) = r_ff(τ)∗h₃(τ).

(323)

10.4.2. Effects of α and β on Responses

We illustrate some plots of |H₃(ω)|² in Figure 48. Figure 49 indicates some plots of response PSD S_xx3(ω). Some plots of cross-PSD response S_fx3(ω) are indicated in Figure 50.

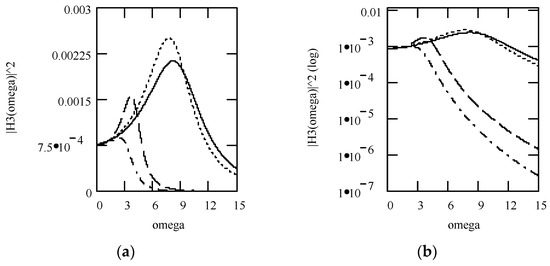
Figure 48. Plots of |H₃(ω)|² when m = 1, c = 0.1, and k = 36 for (α, β) = (1.6, 0.8) (solid), (1.6, 1.8) (dotted), (2.5, 0.8) (dashed), (2.8, 1.8) (dashed–dotted). (a) |H₃(ω)|²; (b) log|H₃(ω)|².

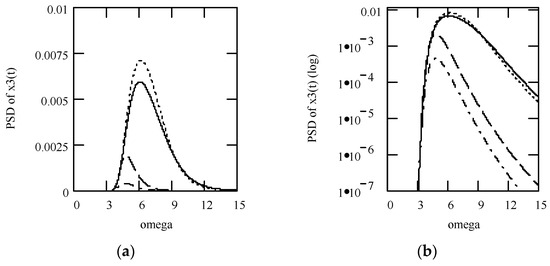
Figure 49. Plots of response PSD S_xx3(ω) when m = 1, c = 0.1, k = 36, and V = 15 for (α, β) = (1.6, 0.8) (solid), (1.6, 1.8) (dotted), (2.5, 0.8) (dashed), and (2.8, 1.8) (dashed–dotted). (a) S_xx3(ω); (b) logS_xx3(ω).

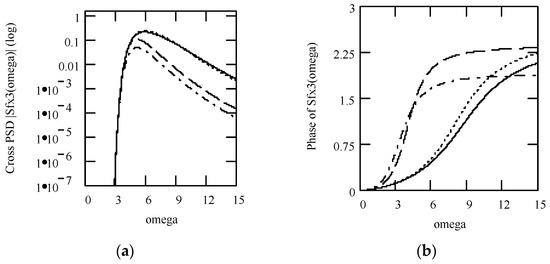
Figure 50. Plots of cross-PSD response S_fx3(ω) when m = 1, c = 0.1, k = 36, and V = 15 for (α, β) = (1.6, 0.8) (solid), (1.6, 1.8) (dotted), (2.5, 0.8) (dashed), and (2.8, 1.8) (dashed–dotted). (a) log|S_fx3(ω)|; (b) Phase of |S_fx3(ω)|.

Figure 49 and Figure 50 show that the effects of the fractional orders (α, β) on the responses of class III fractional vibrators are significant.

10.5. Responses of Class IV Fractional Vibrator Driven by P-M Spectrum

10.5.1. Computations

Equation (324) is the motion equation of a class IV fractional vibrator

$$m{\displaystyle \frac{d^{\alpha }{x}_4(t)}{d{t}^{\alpha }}}+k{\displaystyle \frac{d^{\lambda }{x}_4(t)}{d{t}^{\lambda }}}=f(t),$$

(324)

where f(t) is the driven signal with the P-M spectrum and x₄(t) is the response.

Theorem 70 (PSD response IV). 

Let S_xx4(ω) be the PSD of the response x₄(t). Then, (325) is its expression

$$S_{xx4}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k^2{\omega }^{2\lambda }{\cos }^2\frac{\lambda \pi }{2}\left[\begin{array}{l}{\left(1-{\gamma }^2\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\right)}^2\\ +4{\left(\gamma \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\alpha +\lambda -2}\left|\cos \frac{\alpha \pi }{2}\right|\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}^2\end{array}\right]}}.$$

(325)

Proof. 

Because S_xx4(ω) = S_ff(ω)|H₄(ω)|² and

$$\begin{array}{l}{H}_4(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}4}\left(1-{\gamma }_{\mathrm{eq}4}^2+i2{\varsigma }_{\mathrm{eq}4}{\gamma }_{\mathrm{eq}4}\right)}}\\ ={\displaystyle \frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(\begin{array}{l}1-{\gamma }^2\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\\ +i2\gamma \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\alpha +\lambda -2}\left|\cos \frac{\alpha \pi }{2}\right|\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\end{array}\right)}},\end{array}$$

(325) is true and Theorem 70 holds. This finishes the proof. □

Theorem 71 (Cross-PSD response IV). 

Denote by S_fx4(ω) the cross-PSD between f(t) and x₄(t). Then, its expression is given by

$$S_{fx4}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(\begin{array}{l}1-{\gamma }^2\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\\ +i2\gamma \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\alpha +\lambda -2}\left|\cos \frac{\alpha \pi }{2}\right|\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\end{array}\right)}}.$$

(326)

Proof. 

Performing the operation of S_fx4(ω) = S_ff(ω)H₄(ω) yields (326). The proof is finished. □

Calculating the inverse Fourier transform on the both sides of S_xx4(ω) = S_ff(ω)|H₄(ω)|² yields

r_xx4(τ) = r_ff(τ)∗h₄(τ)∗h₄(−τ).

(327)

In (327), r_xx4(τ) is the ACF of x₄(t). In addition, we have

r_fx4(τ) = r_ff(τ)∗h₄(τ).

(328)

In (328), r_fx4(τ) is the cross-correlation between f(t) and x₄(t). It is the cross-correlation response.

10.5.2. Effects of α and λ on Responses

We illustrate some plots of |H₄(ω)|² in Figure 51. Figure 52 indicates some plots of S_xx4(ω). Some plots of S_fx4(ω) are shown in Figure 53.

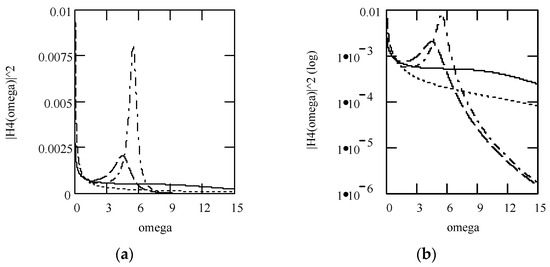
Figure 51. Plots of |H₄(ω)|² when m = 1, c = 0, and k = 36 for (α, λ) = (1.6, 0.2) (solid), (1.6, 0.4) (dotted), (2.5, 0.2) (dashed), and (2.5, 0.4) (dashed–dotted). (a) |H₄(ω)|²; (b) log|H₄(ω)|².

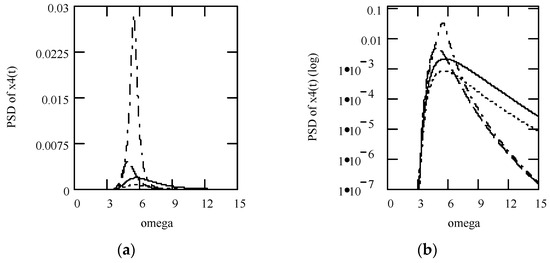
Figure 52. Plots of response PSD S_xx4(ω) when m = 1, c = 0, k = 36, and V = 15 for (α, λ) = (1.6, 0.2) (solid), (1.6, 0.4) (dotted), (2.5, 0.2) (dashed), and (2.5, 0.4) (dashed–dotted). (a) S_xx4(ω); (b) logS_xx4(ω).

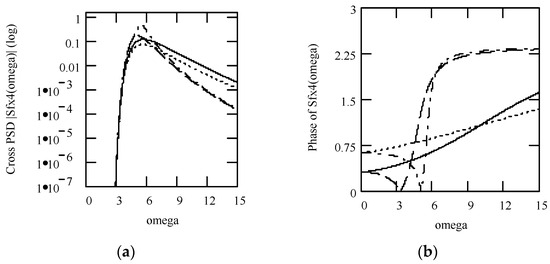
Figure 53. Plots of cross-PSD response S_fx4(ω) when m = 1, c = 0, k = 36, and V = 15 for (α, λ) = (1.6, 0.2) (solid), (1.6, 0.4) (dotted), (2.5, 0.2) (dashed), and (2.5, 0.4) (dashed–dotted). (a) log|S_fx4(ω)|; (b) phase of |S_fx4(ω)|.

Figure 52 and Figure 53 exhibit that the effects of fractional orders (α, λ) on the responses to class IV fractional vibrators driven by the P-M spectrum are noticeable.

10.6. Responses of Class V Fractional Vibrators Driven by P-M Spectrum

10.6.1. Computations

In the motion equation of a class V fractional vibrator (329)

$$m{\displaystyle \frac{d^2{x}_5(t)}{d{t}^2}}+k{\displaystyle \frac{d^{\lambda }{x}_5(t)}{d{t}^{\lambda }}}=f(t),$$

(329)

f(t) is the driven force with the P-M spectrum and x₅(t) is the response.

Theorem 72 (PSD response V). 

Denote by S_xx5(ω) the PSD of the response x₅(t). Then, (330) is its expression

$$S_{xx5}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k^2{\omega }^{2\lambda }{\cos }^2\frac{\lambda \pi }{2}\left[{\left(1-\frac{{\gamma }^2}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\right)}^2+4{\gamma }^2{\left(\frac{k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}^2\right]}}.$$

(330)

Proof. 

Considering

$$\begin{array}{l}{H}_5(\omega )={\displaystyle \frac{1}{k_{\mathrm{eq}5}\left(1-{\gamma }_{\mathrm{eq}5}^2+i2{\varsigma }_{\mathrm{eq}5}{\gamma }_{\mathrm{eq}5}\right)}}\\ ={\displaystyle \frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(1-\frac{{\gamma }^2}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}+i2\gamma \frac{k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}},\end{array}$$

and S_xx5(ω) = S_ff(ω)|H₅(ω)|², we have (330) and Theorem 72 holds. The proof is completed. □

Theorem 73 (Cross-PSD response V). 

Let S_fx5(ω) be the cross-PSD between f(t) and x₅(t). Then, (331) is its expression

$$S_{fx5}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(1-\frac{{\gamma }^2}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}+i2\gamma \frac{k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}}.$$

(331)

Proof. 

Doing S_fx5(ω) = S_ff(ω)H₅(ω) yields (331). This finishes the proof. □

In the time domain, one has the ACF response in the form of (332)

r_xx5(τ) = r_ff(τ)∗h₅(τ)∗h₅(−τ),

(332)

and the cross-correlation response in the form of (333)

r_fx5(τ) = r_ff(τ)∗h₅(τ).

(333)

10.6.2. Effects of λ on Responses

Figure 54 illustrates some plots of |H₅(ω)|². Figure 55 shows some plots of S_xx5(ω) and Figure 56 indicates some plots of S_fx5(ω).

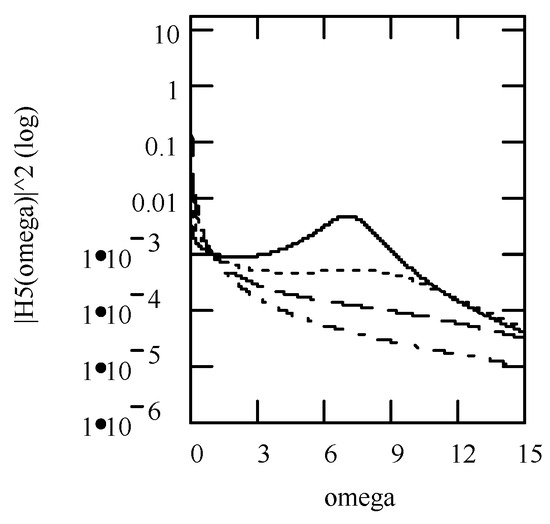
Figure 54. Plots of |H₅(ω)|² (log) when m = 1, c = 0, and k = 36 for λ = 0.2 (solid), 0.4 (dotted), 0.6 (dashed), and 0.8 (dashed–dotted).

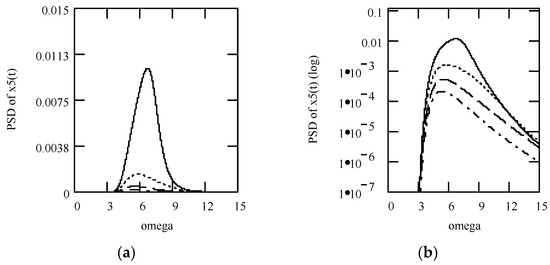
Figure 55. Plots of response PSD S_xx5(ω) when m = 1, c = 0, k = 36, and V = 15 for λ = 0.2 (solid), 0.4 (dotted), 0.6 (dashed), and 0.8 (dashed–dotted): (a) S_xx5(ω); (b) logS_xx5(ω).

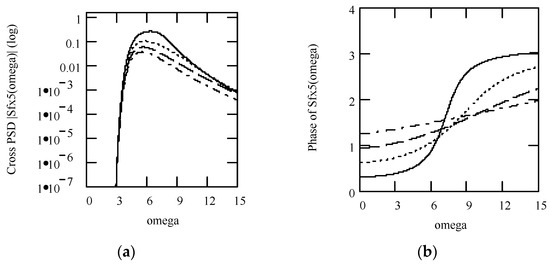
Figure 56. Plots of cross-PSD response S_fx5(ω) when m = 1, c = 0, k = 36, and V = 15 for λ = 0.2 (solid), 0.4 (dotted), 0.6) (dashed), and 0.8 (dashed–dotted): (a) log|S_fx5(ω)|; (b) phase of |S_fx5(ω)|.

Figure 55 and Figure 56 show that the effects of the fractional order λ on the responses to class V fractional vibration systems driven by the P-M spectrum are considerable.

10.7. Responses of Class VI Fractional Vibrators Driven by P-M Spectrum

10.7.1. Computations

Consider the motion equation of a class VI fractional vibrator below

$$m{\displaystyle \frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}}+c{\displaystyle \frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}}=f(t).$$

(334)

In (334), f(t) is the driven signal with the P-M spectrum and x₆(t) is the response.

Theorem 74 (PSD response VI). 

Let S_xx6(ω) be the PSD of the response x₆(t). Then, (335) is its expression

$$S_{xx6}(\omega )={\displaystyle \frac{1}{k^2}}{\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{\begin{array}{l}{\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\gamma }^2{\left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2\end{array}}}.$$

(335)

Proof. 

Performing the operation of S_xx6(ω) = S_ff(ω)|H₆(ω)|² produces (335). The proof ends. □

Theorem 75 (cross-PSD response VI). 

Denote by S_fx6(ω) the cross-PSD between f(t) and x₆(t). Then, (336) is its expression

$$S_{fx6}(\omega )={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k\left(\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right)}}.$$

(336)

Proof. 

Calculating S_fx6(ω) = S_ff(ω)H₆(ω) results in (336). The proof ends. □

In the time domain, we have (337) as the expression of the ACF response

r_xx6(τ) = r_ff(τ)∗h₆(τ)∗h₆(−τ),

(337)

and (338) as the expression of the cross-correlation response

r_fx6(τ) = r_ff(τ)∗h₆(τ).

(338)

10.7.2. Effects of α, β, and λ on Responses

Figure 57 is used to illustrate some plots of |H₆(ω)|², Figure 58 is used for some plots of S_xx6(ω), and Figure 59 for some of S_fx6(ω).

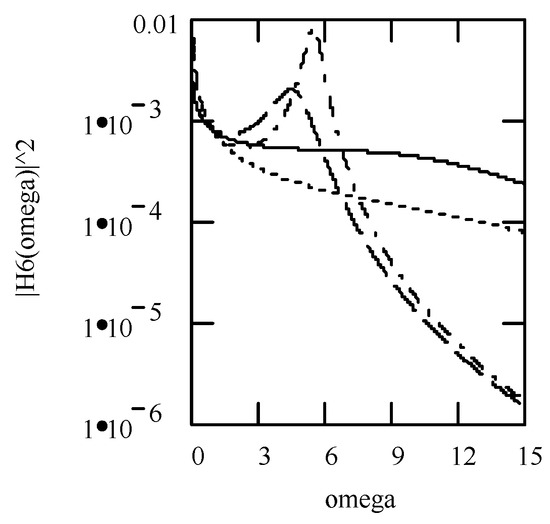
Figure 57. Plots of |H₆(ω)|² (log) when m = 1, c = 0.1, and k = 36 for (α, β, λ) = (1.6, 0.8, 0.2) (solid), (1.6, 1.8, 0.4) (dotted), (2.5, 0.4, 0.2) (dashed), and (2.5, 0.8, 0.4) (dashed–dotted).

Figure 58. Plots of response PSD S_xx6(ω) in log scale when m = 1, c = 0.1, k = 36, and V = 15 for (α, β, λ) = (1.6, 0.8, 0.2) (solid), (1.6, 1.8, 0.4) (dotted), (2.5, 0.4, 0.2) (dashed), and (2.5, 0.8, 0.4) (dashed–dotted).

Figure 59. Plots of cross-PSD response S_fx6(ω) when m = 1, c = 0.1, k = 36, and V = 15 for (α, β, λ) = (1.6, 0.8, 0.2) (solid), (1.6, 1.8, 0.4) (dotted), (2.5, 0.4, 0.2) (dashed), and (2.5, 0.8, 0.4) (dashed–dotted): (a) log|S_fx6(ω)|; (b) phase of |S_fx6(ω)|.

Figure 58 and Figure 59 show that the effects of the fractional orders (α, β, λ) on the responses of class VI fractional vibrators driven by the P-M spectrum are significant.

10.8. Responses of Class VII Fractional Vibrators Driven by P-M Spectrum

10.8.1. Computations

Equation (339) is the motion equation of a class VII fractional vibrator

$$m{\displaystyle \frac{d^2{x}_7(t)}{d{t}^2}}+c{\displaystyle \frac{d^{\beta }{x}_7(t)}{d{t}^{\beta }}}+k{\displaystyle \frac{d^{\lambda }{x}_7(t)}{d{t}^{\lambda }}}=f(t),$$

(339)

where f(t) is the excitation with the P-M spectrum and x₇(t) is the response.

Theorem 76 (PSD response VII). 

Denote by S_xx7(ω) the PSD of the response x₇(t). Then, (340) is its expression

$$S_{xx7}(\omega )={\displaystyle \frac{1}{k^2}}{\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{\begin{array}{l}{\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}-\gamma \left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\right]}^2\\ +{\gamma }^2{\left(2\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)}^2\end{array}}}.$$

(340)

Proof. 

Performing S_xx7(ω) = S_ff(ω)|H₇(ω)|² results in (340). This finishes the proof. □

Theorem 77 (Cross-PSD response VII). 

Let S_fx7(ω) be the cross-PSD between f(t) and x₇(t). Then, (341) is its expression

$$\begin{array}{l}{S}_{fx7}(\omega )\\ ={\displaystyle \frac{\alpha g^2{\omega }^{-5}{e}^{-\beta {\left(\frac{g}{V}\right)}^4\frac{1}{{\omega }^4}}}{k\left[{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}-\gamma \left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\gamma \left(2\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\right]}}.\end{array}$$

(341)

Proof. 

Doing S_fx7(ω) = S_ff(ω)H₇(ω) yields (341). The proof ends. □

In the time domain, one has the ACF response expressed by (342) below

r_xx7(τ) = r_ff(τ)∗h₇(τ)∗h₇(−τ),

(342)

and the cross-correlation response given by (343) below

r_fx7(τ) = r_ff(τ)∗h₇(τ).

(343)

10.8.2. Effects of β and λ on Responses

Figure 60 shows some plots of |H₇(ω)|². Figure 61 indicates some plots of S_xx7(ω). Figure 62 demonstrates some plots of S_fx7(ω).

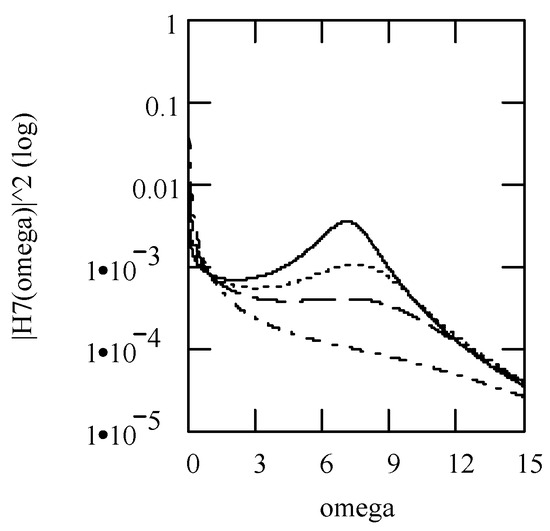
Figure 60. Plots of |H₇(ω)|² (log) when m = 1, c = 0.1, and k = 36, for (β, λ) = (0.5, 0.2) (solid), (0.5, 0.3) (dot), (1.5, 0.4) (dash), (1.5, 0.6) (dash dot).

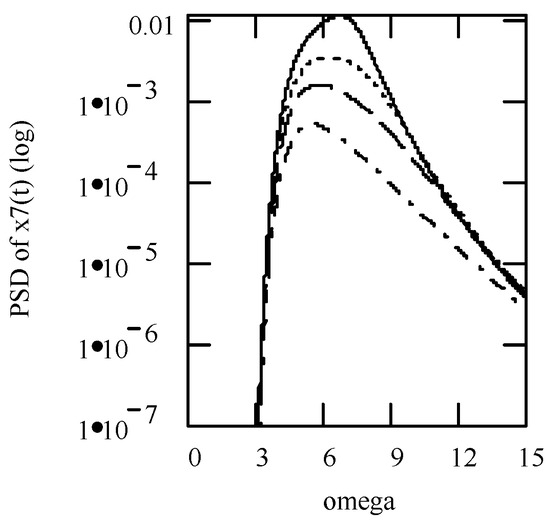
Figure 61. Plots of response PSD S_xx7(ω) in log scale when m = 1, c = 0.1, k = 36, and V = 15 for (β, λ) = (0.5, 0.2) (solid), (0.5, 0.3) (dot), (1.5, 0.4) (dash), (1.5, 0.6) (dash dot).

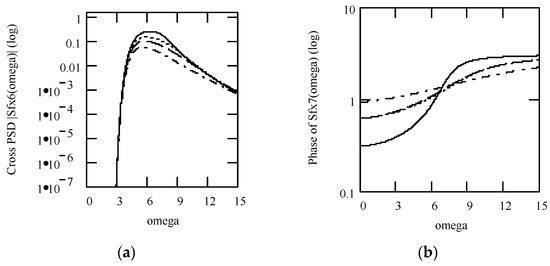
Figure 62. Plots of cross-PSD response S_fx7(ω) when m = 1, c = 0.1, k = 36, and V = 15 for (β, λ) = (0.5, 0.2) (solid), (0.5, 0.3) (dot), (1.5, 0.4) (dash), (1.5, 0.6) (dash dot). (a). log|S_fx7(ω)|. (b). Phase of |S_fx7(ω)| in log scale.

Figure 61 and Figure 62 indicate that there are significant effects of the fractional orders (β, λ) on the response x₇(t) under the excitation of the P-M spectrum.

10.9. Summary

We have presented the analytic expressions of the PSD and cross-PSD responses of fractional vibrators from class I to class VII in Theorems 64–77, respectively. We have shown that fractional orders of vibration systems, namely, α, β, and λ, have considerable effects on responses.

11. Application: Mathematical Explanation of Rayleigh Damping Assumption

In the field of structural mechanics, how to mathematically explain the Rayleigh damping assumption is a tough issue. We address two objectives in this section: One is to apply fractional vibrations to mathematically explain the Rayleigh damping assumption. The other is to show that a vibration system with the Rayleigh damping is with frequency-dependent mass, damping, and stiffness in reality.

11.1. Mathematical Explanation

Denote by c_r the damping assumed by Rayleigh for a system with the primary mass m and the primary stiffness k. Its standard form is given by

$$c_{\mathrm{r}}=am+bk,$$

(344)

where a and b are frequency-dependent parameters. To be precise, a is proportional to ω while b is inversely proportional to ω. In short, Rayleigh assumed that damping is proportional to m and k with the coefficients a and b (Harris [71], Palley et al. [72], Rayleigh [105]). We have already used (344) in Section 9. The literature with respect to applications of the Rayleigh damping assumption is rich, see, e.g., Trombetti and Silvestri [106], Poul and Zerva [107], Nåvik et al. [108], Park et al. [109], Hussein et al. [110], Sigmund and Jensen [111], Chen et al. [112], Battisti et al. [113], Cox et al. [114], Tisseur and Meerbergen [115], Chu et al. [116], Fay et al. [117], Naderian et al. [118], Tian et al. [119], Iovane and Nasedkin [120], Kouris et al. [121], Jin and Xia [122], DeWeaver and Nigam [123], Langley [124], Bhaskar [125], Horiuchi and Konno [126], Mohammad et al. [127], and Kim and Wiebe [128], just to mention a few.

According to the properties of a and b in (344), we rewrite it as (345) below

c_r = c_r(ω) = a(ω)m + b(ω)k.

(345)

We use (346) to express the above a(ω) and a(ω)

$$\begin{array}{l}a(\omega )={\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}},\\ b(\omega )={\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}.\end{array}$$

(346)

Thus, we have (347) to express c_r(ω) in the form

$$c_{\mathrm{r}}(\omega )=\left({\omega }^{\alpha -1}\sin {\displaystyle \frac{\alpha \pi }{2}}\right)m+\left({\omega }^{\lambda -1}\sin {\displaystyle \frac{\lambda \pi }{2}}\right)k.$$

(347)

The above is just the equivalent damping of class IV fractional vibrators (see Corollary 30 in Section 6). Therefore, the class IV fractional vibrators may yet provide us with a model to mathematically explain the famous Rayleigh damping assumption, referring to Li [26] for more explanations.

11.2. Frequency Dependency of Elements: A View from Rayleigh Damping Assumption

We call mass or damping or stiffness an element of a vibration system. When the damping of a vibration system follows c_r(ω), we denote its mass and stiffness by m = m_r(ω) and k = k_r(ω), respectively. As a matter of fact, m_r(ω) and k_r(ω) are, respectively, expressed by (348) and (349). To be precise,

$$m_{\mathrm{r}}=m_r(\omega )={\displaystyle \frac{c_{\mathrm{r}}(\omega )-b(\omega )k_r}{a(\omega )}},$$

(348)

and

$$k_r=k_r(\omega )={\displaystyle \frac{c_{\mathrm{r}}(\omega )-a(\omega )m_r}{b(\omega )}}.$$

(349)

Thus, m_r and k_r are also frequency-dependent. Consequently. When applying the Rayleigh damping assumption to a vibration system, we have the general form of the motion equation of a vibration system with frequency-dependent elements in the form (350) below

$$m_{\mathrm{r}}(\omega )x^{″}+c_{\mathrm{r}}(\omega )x^{\prime }+k_{\mathrm{r}}(\omega )x=f(t).$$

(350)

As a whole, we say that a system with the Rayleigh damping is with frequency-dependent mass and stiffness in addition to frequency-dependent damping c_r(ω).

12. Summary and Conclusions

Among seven classes of fractional vibrators that are listed in (1), (4), (6), (10), (11), (13), and (14) in Section 1, class VI is the general one. Thus, we start our review work from the class VI fractional vibrators in Section 2.

Regarding a class VI fractional vibrator, performing the Fourier transform on its fractional motion Equation (13) easily yields its frequency transfer function H₆(ω), see Theorem 2. Starting from H₆(ω), we can easily derive its equivalent motion Equation (18) in Theorem 2. Based on Theorem 2, for a class VI fractional vibrator, it is consequent for us to derive the analytical expressions of its equivalent mass (Corollary 1), equivalent damping (Corollary 2), equivalent stiffness (Corollary 3), equivalent damping ratio (Corollary 4), equivalent damping free natural angular frequency (Corollary 5), equivalent damped natural angular frequency (Corollary 6), and equivalent frequency ratio (Corollary 7). Therefore, based on the equivalent vibration parameters, it is natural for us to derive the analytical expressions of free response (Theorem 3), impulse response (Theorem 4), step response (Theorem 5), sinusoidal response (Theorem 6), equivalent logarithmic decrement (Theorem 7), equivalent Q factor (Theorem 8), and equivalent frequency bandwidth (Theorem 9).

Because class I (or II, III, IV, V, or VII) is a special case of class VI, the analytic theory of class I (or II, III, IV, V, or VII) with elementary functions is a consequent of that of class VI, which is, respectively, discussed in Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8.

Three applications of seven classes of fractional vibrations were discussed. Section 9 reviews the application to the analytical expression of the forced response to a damped Euler–Bernoulli beam. In Section 10, we presented the analytical expressions of power spectrum density response and cross-power spectrum density response of seven classes of fractional vibrations under the excitation with Pierson and Moskowitz spectrum. In Section 11, we reviewed a possible mathematical explanation of the Rayleigh damping assumption based on class IV fractional vibrators. In the case of the Rayleigh damping assumption, elements are frequency-dependent.

The analytical expressions of the frequency bandwidth in seven classes of fractional vibrators and the sinusoidal responses to fractional vibrators from class IV to VII are newly introduced in this paper. We have not reviewed the recent work by Li [129] on stationary responses using a fractional phasor.

The theory of fractional vibrations reviewed in this paper refers to a kind of nonlinear vibration. The nonlinearity of fractional vibrations can be explained from the point of view of fractional inertia or fractional damping or fractional stiffness; refer to Li [26] for details. Such a nonlinear vibration differs from the conventional nonlinear vibration described by, for example, the Duffing, van der Pol, or Duffing–van der Pol equation (Az-Zo’bi et al. [130]; Ren et al. [131]; El-Dib [132]; El-Nabulsi and Anukool [133]). From a structural mechanics perpective, vibration is strongly associated with the subject of fatigue (Harris [71]; Palley et al. [72]). Therefore, fractional fatigue may be an interesting issue to work on in future. In theory, the topic of fractional vibration symmetry/asymmetry would be interesting.