Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals

Abstract

The two-dimensional (2D) hydrogen atom is a fundamental atomic model that is important for various technologies based on 2D materials. Here, the atomic model is revisited to enhance understanding of the hydrogen wavefunctions. Unlike in previous studies, we propose an alternative expression of azimuthal wavefunctions, which are the eigenstates of the square of angular momentum and exhibit rotational symmetry. Remarkably, our expression leads to the rotation and oscillation along the azimuthal direction of the probability densities, which do not appear in the conventional wavefunctions. These behaviors are validated by the numerical results obtained through the 2D finite difference approach. Variation in oscillator strengths due to the rotation of wavefunctions is observed in our proposed 2D hydrogen wavefunctions, whereas those due to the conventional wavefunctions remain constant. More importantly, the proposed wavefunctions’ advantage is illustrating the orbital shapes of the planar hydrogen states, whose orientation is labeled here using Cartesian representation for the first time. This study can be applied to visualize the orbital characteristics of the states in quantum confinement with a radial potential.

1. Introduction

According to recent growing interest in the low-dimensional systems of single-layer and thin materials [1,2,3], the atomic model of the 2D hydrogen atom has gained significant importance as a foundational concept. It can be applied to describe donor atoms and excitons in thin semiconductors [4,5,6,7], both of which play a key role in various fields of science and technology. In quantum computing [8,9,10], individual donor atoms within a semiconductor can serve as qubits for quantum information processing. In single-electron transistors [11,12,13], donor atoms significantly influence the current–voltage characteristics of atomic devices. In 2D semiconductors [14,15,16], excitons bound by strong Coulomb interaction determine optical properties such as selection rules, circular dichroism, and efficient recombination. Therefore, the atomic model of the 2D hydrogen atom undoubtedly provides insight into and facilitates understanding of these technologies.

The theoretical framework regarding the 2D hydrogen atom has remained a subject of ongoing attention and further development for many decades [17,18,19]. It was first studied in 1967 by Zaslow and Zandler [20], who successfully solved the Schrödinger equation to obtain the exact eigenvalues and eigenfunctions of the 2D hydrogen atom. This planar atomic model has been revisited by Yang et al. [21], who conducted further investigations into the dipole matrix elements, Stark effect, optical transitions, and fine structures. Subsequently, the 2D hydrogen atom in various confinement potentials was investigated [22,23,24]. Stevanovic and Sen found that incidental degeneracy of the confined hydrogen states occurs at a particular radius of the infinite circular potential [22]. In the presence of a magnetic field and an electric field, the 2D hydrogen atom is explored numerically and analytically [25,26,27,28,29,30,31]. The explorations revealed that a tilted magnetic field can be used to manipulate the density of the hydrogen states [32]. The field also causes strong anisotropic distribution of the probability densities of the hydrogen states [33]. Meanwhile, an electric field leads to a decrease in the binding energy of the ground state and an increase in the oscillator strength of the 2D hydrogen atom [34]. Additionally, the effect of spin–orbit coupling on a 2D hydrogen atom has been reported; a large spin–orbit interaction results in the splitting of energy levels and the tight binding of an electron [35,36]. It is worth recognizing that the azimuthal wave function used in these previous studies is complex. Because it consists of real and imaginary components, plotting the complex wavefunction to visualize and understand the orbital shapes of the 2D hydrogen states is a struggle.

This work revisits the two-dimensional hydrogen atom. First, the planar hydrogen wavefunctions are investigated numerically using the 2D finite difference method. Surprisingly, the numerical results show that the spatial distribution of the probability densities (PDs) of most hydrogen states fluctuates along the azimuthal direction. This behavior has not been seen before in PDs due to the conventional analytical wavefunctions. Consequently, the new derivation of alternative azimuthal wavefunctions is presented here. Our proposed wavefunctions are confirmed by the excellent agreement with the numerical wavefunctions. The oscillator strength due to the proposed hydrogen wavefunctions is also explored and compared with the conventional wavefunctions. Moreover, our expression of the planar hydrogen states yields real-valued functions. These functions enable straightforward visualization of the orbital shapes and orientation, facilitating the first-ever labeling of $s$, $p$, $d$, and $f$ orbitals of the 2D hydrogen states using Cartesian representation.

2. Theoretical and Numerical Calculations

In the problem of the 2D hydrogen atom, the Schrödinger equation describing an electron trapped in a coulomb potential is given by

$$-{\displaystyle \frac{{ћ}^2}{2m_e}}{\nabla }^2\mathsf{\Psi }(r,\varphi )-{\displaystyle \frac{e^2}{4\pi {\epsilon }_{0}r}}\mathsf{\Psi }(r,\varphi )=E\mathsf{\Psi }(r,\varphi )$$

(1)

where $m_e$ is the electron mass, $e$ is the electron charge, and ${\epsilon }_0$ is the vacuum permittivity. $r$ and $\varphi$ are the radial distance and angle in polar coordinates. The exact solutions of Equation (1) are [21]

$$E_n=-{\displaystyle \frac{m_e{e}^4}{8{\pi }^2{\epsilon }_0^2{ћ}^2{\left(2n-1\right)}^2}},$$

(2)

and

$${\mathsf{\Psi }}_{nm}\left(r,\varphi \right)={\mathsf{\Phi }}_m^0\left(\varphi \right)R_{nm}\left(r\right)$$

(3)

where ${\mathsf{\Phi }}_m^0=e^{im\varphi }$ is the azimuthal part and $R_{nm}$ is the radial part of the 2D hydrogen wavefunctions. $n$ and $m$ are the principal quantum number and magnetic quantum number. Because the Hamiltonian and the momentum operator ${\hat{L}}_z$ commute each other, they have common eigenfunctions. As a result, $e^{im\varphi }$, the eigenfunction of ${\hat{L}}_z$, is conventionally chosen to be the azimuthal wavefunction, as discussed in many papers [37,38,39].

We first explore this problem by solving the Schrödinger equation numerically using the 2D finite difference method [4,40]. Here, the $xy$-plane is divided into a uniform squared grid with $a$ representing grid spacing. The positive charge of the nucleus is positioned at the origin, which is at the center of the plane, as seen in Figure S1 in the Supplementary Materials. Equation (1) can be rewritten in Cartesian coordinates using ${\nabla }^2={\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}$ and $r^2=x^2+y^2$, and expressed in discretized form as

$$-\left[{\displaystyle \frac{\left({\mathsf{\Psi }}_{i-1,j}-2{\mathsf{\Psi }}_{i,j}+{\mathsf{\Psi }}_{i+1,j}\right)}{{\tilde{a}}^2}}+{\displaystyle \frac{\left({\mathsf{\Psi }}_{i,j-1}-2{\mathsf{\Psi }}_{i,j}+{\mathsf{\Psi }}_{i,j+1}\right)}{{\tilde{a}}^2}}\right]-{\displaystyle \frac{2}{\sqrt{{\tilde{x}}^2+{\tilde{y}}^2}}}{\mathsf{\Psi }}_{i,j}={\displaystyle \frac{E}{E_0}}{\mathsf{\Psi }}_{i,j}.$$

(4)

Here,${\mathsf{\Psi }}_{i,j}$ is the wavefunction at the position $(i,j)$ in the $xy$-plane; $\tilde{a}=a/a_0$, $\tilde{x}=x/a_0$, $\tilde{y}=y/a_0$, and $E_0={ћ}^2/2m_e{a}_0^2$, where $a_0$ is the Bohr radius defined by $a_0=4\pi {\epsilon }_0{ћ}^2/m_e{e}^2$. The matrix eigenvalue problem corresponding to Equation (4) is shown in Note S1 in the Supplementary Materials and can be solved numerically to obtain the eigenenergies $E$ and eigenstates $\mathsf{\Psi }$.

In the next section, it will be demonstrated that the probability densities ${\left|{\mathsf{\Psi }}_{nm}\right|}^2$ due to the numerical method differ from those due to the analytical conventional calculation. To confirm the numerical results, the new derivation is presented here to obtain the alternative expression of azimuthal wavefunctions. Unlike previous studies, our proposed eigenfunctions originate from the commutation of the Hamiltonian with the square of the angular momentum ${\hat{L}}_z^2=-{ћ}^2{\displaystyle \frac{{\partial }^2}{\partial {\varphi }^2}}$, whose eigenvalue problem is $-{ћ}^2{\displaystyle \frac{{\partial }^2\mathsf{\Phi }}{\partial {\varphi }^2}}={(mћ)}^2\mathsf{\Phi }$. This is the second-order differential equation with constant coefficients, and its solution is

$${\mathsf{\Phi }}_m\left(\varphi \right)=C_m\cos (m\varphi )+D_m\sin (m\varphi )$$

(5)

where $C_m$ and $D_m$ are constants. Notice that our proposed ${\mathsf{\Phi }}_m$ in Equation (5) is generally not the eigenfunction of ${\hat{L}}_z$, but the conventional ${\mathsf{\Phi }}_m^0$ in Equation (3) is the eigenfunction of ${\hat{L}}_z^2$. Therefore, the commutation relation between ${\hat{L}}_z$ and ${\hat{L}}_z^2$ ($[{\hat{L}}_z,{\hat{L}}_z^2]=0$) can be represented by the Venn diagram in Figure 1. Note that the eigenfunctions of ${\hat{L}}_z^2$ in the blue region are concentrated and explored in this study.

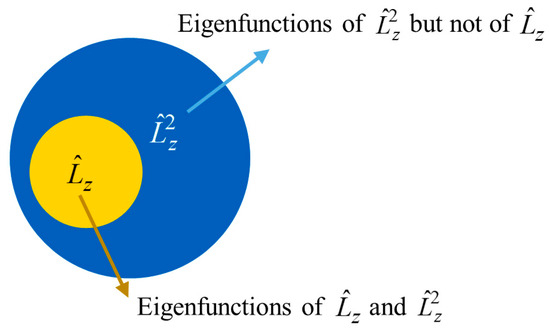
Figure 1. The Venn diagram of the eigenfunctions of ${\hat{L}}_z$ and ${\hat{L}}_z^2$.

The values of $C_m$ and $D_m$ in Equation (5) are determined from the normalization condition ${\displaystyle \underset{0}{\overset{2\pi }{\int }}{\mathsf{\Phi }}_m^{*}}{\mathsf{\Phi }}_{m}d\varphi =1$. It can be straightforwardly calculated that $C_{m=0}={\displaystyle \frac{1}{\sqrt{2\pi }}}$ for the states with $m=0$ and

$$C_m^2+D_m^2={\displaystyle \frac{1}{\pi }}$$

(6)

for the states with $m\ne 0$. Additionally, the values of the coefficients $C_m$ and $D_m$ are determined from the orthogonality of the eigenstates. To achieve the orthogonal set of eigenstates, it is shown in Appendix A that the state with momentum $m$ (${\mathsf{\Phi }}_m=C_m\cos (m\varphi )+D_m\sin (m\varphi )$) and the state with momentum $-m$ (${\mathsf{\Phi }}_{-m}=C_{-m}\cos \left(m\varphi \right)-D_{-m}\sin \left(m\varphi \right)$) are orthogonal when the coefficients satisfy the following relation:

$$C_m{C}_{-m}=D_m{D}_{-m}.$$

(7)

However, any two states with different values of $\left|m\right|$ are orthogonal regardless of the values of the coefficients.

In short, our calculation shows that the conventional azimuthal function ${\mathsf{\Phi }}_m^0$ in Equation (3) can be replaced by ${\mathsf{\Phi }}_m$ in Equation (5), where coefficients $C_m$ and $D_m$ must satisfy Equations (6) and (7), which are derived and presented here for the first time. It will be shown later that the possible values of these coefficients influence the physical properties of the 2D hydrogen states, such as rotation, orbital orientation, and optical transitions. For illustrating orbital shapes, the values of the coefficients $C_m$ and $D_m$ can be chosen to be 0 and $1/\sqrt{\pi }$ to obtain the azimuthal functions in the form of

$${\mathsf{\Phi }}_m(\varphi )=\left\{\begin{array}{lll}{\displaystyle \frac{1}{\sqrt{\pi }}}\cos (m\varphi )& \mathrm{for}& m>0\\ {\displaystyle \frac{1}{\sqrt{2\pi }}}& \mathrm{for}& m=0\\ {\displaystyle \frac{1}{\sqrt{\pi }}}\sin (m\varphi )& \mathrm{for}& m<0.\end{array}\right.$$

(8)

It will be demonstrated that the 2D hydrogen eigenfunctions ${\mathsf{\Psi }}_{nm}={\mathsf{\Phi }}_m{R}_{nm}$, where ${\mathsf{\Phi }}_m$ is defined in Equation (8), are convenient for labeling $s$, $p$, $d$, and $f$ orbitals in the next section.

3. Results and Discussion

Firstly, the solutions of the 2D hydrogen atom from the conventional analytical calculation shown in Equations (2) and (3) are compared with those from the numerical method. As shown in Table 1, the eigenenergies and the number of degenerate states in each energy level obtained from these two independent methods are in good agreement.

Table 1. Energy levels obtained from the analytical method and finite difference method, denoted by $E_n^{exact}$ and $E_n^{num}$, respectively. Note that there are 3, 5, and 7 degenerate states for the level $n$ = 2, 3, and 4.

$\mathit{n}$	${\mathit{E}}_{\mathit{n}}^{\mathit{e}\mathit{x}\mathit{a}\mathit{c}\mathit{t}}/{\mathit{E}}_0$	${\mathit{E}}_{\mathit{n}}^{\mathit{n}\mathit{u}\mathit{m}}/{\mathit{E}}_0$	Error (%)
1	−4.00000	−3.97619	0.59525
2	−0.44444	−0.44442	0.00450
	−0.44444	−0.44442	0.00450
	−0.44444	−0.44149	0.66376
3	−0.16000	−0.15998	0.01250
	−0.16000	−0.15993	0.04375
	−0.16000	−0.15987	0.08125
	−0.16000	−0.15987	0.08125
	−0.16000	−0.15872	0.80000
4	−0.08160	−0.08164	0.04901
	−0.08160	−0.08164	0.04901
	−0.08160	−0.08164	0.03676
	−0.08160	−0.08164	0.03676
	−0.08160	−0.08164	0.03676
	−0.08160	−0.08163	0.03676
	−0.08160	−0.08163	0.94363

(Note that the numerical method used does not directly identify degenerate states. However, by comparing the nearly identical numerical eigenenergies with exact analytical energy levels, we inferred that these correspond to degenerate states, as shown in Table 1.) However, the distributions of PDs $\left({\left|{\mathsf{\Psi }}_{nm}\right|}^2\right)$ of the states with $m\ne 0$ are different as seen in Figure 2 and Figure 3. Clearly, all of the conventional PDs in Figure 2 are independent of the azimuthal angle $\varphi$ because ${\left|{\mathsf{\Psi }}_{nm}\right|}^2$ results in the cancelation of the azimuthal eigenfunction $e^{im\varphi }$. In contrast, numerical PDs of the states with $m\ne 0$ in Figure 3 oscillate along the azimuthal direction and exhibit rotational symmetry. It appears that higher $n$ states show a greater diversity of orders of rotational symmetry. This indicates that the numerical wavefunctions lead to distinctive azimuthal behaviors and specific orders of rotational symmetry not present in the conventional wavefunctions. It should be noted that Equation (1) can also be solved using the variable-separable method, which is likely to yield results for the azimuthally dependent PDs and rotational symmetry similar to those obtained using the 2D finite difference method.

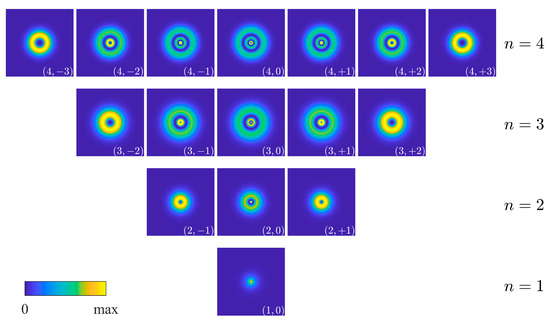
Figure 2. The distributions of PDs (${\left|\mathsf{\Psi }\right|}^2$) from the conventional calculation shown in Equation (3). $(n,m)$ represent the quantum numbers of each state. The degenerate states are presented in the same lines and their corresponding energy levels ($n$) are shown on the right-hand side. PDs of the states with $n=$ 1, 2, 3, and 4 are illustrated in squares with side lengths $5a_0$, $25a_0$, $45a_0$, and $95a_0$, respectively.

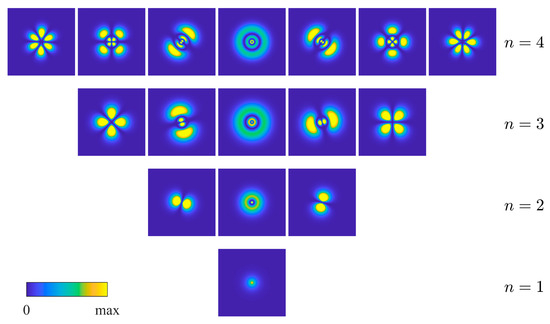
Figure 3. The distributions of PDs (${\left|\mathsf{\Psi }\right|}^2$) from the finite difference method. The degenerate states are presented in the same lines and their corresponding energy levels ($n$) are shown on the right-hand side. PDs of the states with $n=$ 1, 2, 3, and 4 are illustrated in squares with side lengths $5a_0$, $25a_0$, $45a_0$, and $95a_0$, respectively.

To confirm the numerical results, the eigenfunctions $\mathsf{\Psi }$ due to the finite difference method are further investigated and compared with the analytical eigenfunctions ${\mathsf{\Psi }}_{nm}$ with our proposed ${\mathsf{\Phi }}_m$, defined in Equation (5). We find that oscillating along the azimuthal direction of the numerical eigenfunctions depends on the number of grid points determined by $N$ (see Figure S1); several numerical eigenfunctions with $m\ne 0$ rotate unpredictably around the origin when the grid changes from $N$ = 1500 to $N$ = 2300, as seen in Figures S2–S5. For our analytic eigenfunctions ${\mathsf{\Psi }}_{nm}$, the rotating behavior is also found when the values of $C_m$ and $D_m$ in Equation (5) are varied. To illustrate this behavior, we have shown in Figure S6 that the eigenfunctions rotate clockwise when $C_m$ increases or $D_m$ decreases.

The eigenfunctions ${\mathsf{\Psi }}_{nm}$, where the azimuthal part ${\mathsf{\Phi }}_m$ is in the simple form as defined in Equation (8), are shown in Figure 4. One may notice that our analytical eigenfunctions in Figure 4 and the numerical eigenfunctions in Figures S2–S5 look very similar. To demonstrate that they are identical, the data of the numerical eigenfunctions $\left({\mathsf{\Psi }}_{i,j}\right)$ are fitted to the analytic eigenfunctions by varying $C_m$ and $D_m$ to obtain the maximum values of the coefficient of determination ($R^2$). As seen in Table 2, $R^2\ge 0.99$ for every eigenstate $\left(n,m\right)$ indicates that our analytic eigenfunctions fit the numerical eigenfunctions extremely well. Moreover, the coefficients $C_m$ and $D_m$ of the state $\left(n,m\right)$ and the state $\left(n,-m\right)$ in the table obey Equation (7). This means the numerical eigenstates $\left(n,m\right)$ and $\left(n,-m\right)$ are orthogonal to each other. These agreements between our analytical and numerical solutions verify that the results of these two independent approaches are correct. In fact, the sinusoidal functions of azimuthal wavefunctions have been presented in a few papers [41,42]. However, the wavefunctions are not in a general form; the values of $C_m$ and $D_m$ are specified. Thus, their expression cannot be used to verify the correctness and rotating behavior of the numerical wavefunctions.

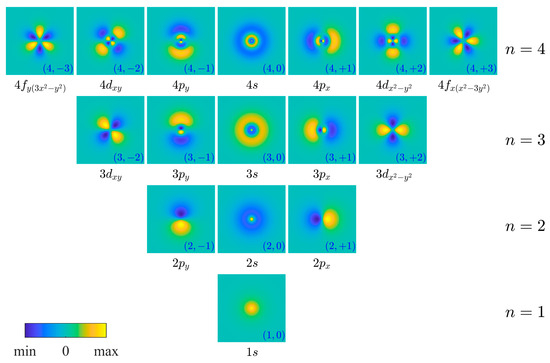
Figure 4. The eigenfunctions ${\mathsf{\Psi }}_{nm}$ with the azimuthal part ${\mathsf{\Phi }}_m$ described in Equation (8). The degenerate states are presented in the same lines and their corresponding energy levels ($n$) are shown on the right-hand side. PDs of the states with $n=$ 1, 2, 3, and 4 are illustrated in squares with side lengths $5a_0$, $25a_0$, $45a_0$, and $95a_0$, respectively. Cartesian representations of each orbital state are shown underneath each panel.

Table 2. The values of $R^2$ obtained by fitting the proposed eigenfunctions due to Equation (5) to the numerical eigenfunctions corresponding to the PDs in Figure 3, using the given values of $C_m$ and $D_m$.

Energy Level $(\mathit{n})$	Numerical Eigenfunctions	Analytic Eigenfunctions $(\mathit{n},\mathit{m})$		${\mathit{C}}_{\mathit{m}}$	${\mathit{D}}_{\mathit{m}}$	${\mathit{R}}^2$
1		(1,0)		$1/\sqrt{2\pi }$	0.0000	0.9997
2		(2,0)		$1/\sqrt{2\pi }$	0.0000	0.9998
		(2,+1)		−0.5407	0.1611	0.9999
		(2,−1)		−0.1611	0.5407	0.9999
3		(3,0)		$1/\sqrt{2\pi }$	0.0000	0.9989
		(3,+1)		0.5422	0.1560	0.9995
		(3,−1)		−0.1560	−0.5422	0.9995
		(3,+2)		−0.5642	0.0000	0.9998
		(3,−2)		0.0000	−0.5642	0.9999
4		(4,0)		$1/\sqrt{2\pi }$	0.0000	0.9981
		(4,+1)		0.4501	−0.3402	0.9904
		(4,−1)		−0.3402	0.4501	0.9904
		(4,+2)		−0.5642	0.0000	1.0000
		(4,−2)		0.0000	0.5642	1.0000
		(4,+3)		−0.5605	0.0644	0.9904
		(4,−3)		−0.0644	0.5605	0.9904

Next, the oscillator strength of our analytic eigenfunctions ${\mathsf{\Psi }}_{nm}$ is investigated and compared with that of the conventional eigenfunctions in Equation (3). This quantity indicates the probability of transition between states ${\mathsf{\Psi }}_{nm}$ and ${\mathsf{\Psi }}_{n^{\prime }{m}^{\prime }}$, defined by $P_{nm}^{n^{\prime }{m}^{\prime }}={\displaystyle \frac{2m_e(E_{n^{\prime }}-E_n)}{{ћ}^2}}{\left|{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\infty }{\mathsf{\Psi }}_{n^{\prime }{m}^{\prime }}^{*}x{\mathsf{\Psi }}_{nm}rdrd\varphi }}\right|}^2$ [43]. We first explore the transition from the ground state $(1,0)$ to the first-excited degenerate states $(2,-1)$, $(2,0)$, and $(2,1)$. Similar to the transition of the conventional eigenfunctions, the possible transition between our eigenfunctions is found when $\Delta m=1$. Therefore, $P_{10}^{2-1}$ and $P_{10}^{2+1}$ are presented in Figure 5. It is evident that they vary as a parabolic function with respect to $C_m$, which is further supported by the linear variation in the oscillator strengths, as shown in the inset where $C_m^2$ is varied. This relationship is also clearly derived from the definition of the oscillator strengths. Interestingly, although the values of $P_{10}^{2\pm 1}$ due to our analytic eigenfunctions are determined by coefficients $C_m$ and $D_m$, the summation of $P_{10}^{2-1}$ and $P_{10}^{2+1}$ is constant with a value of 0.2109 (yellow line). This value is equal to the summation due to the conventional eigenfunctions. Note that for the conventional eigenfunctions, $P_{10}^{2-1}$ = $P_{10}^{2+1}$ = 0.1055. After investigating the oscillator strength between the ground state and the excited states in other energy levels, we also find agreement between the summation due to our eigenfunctions and due to the conventional eigenfunctions, as shown in Table 3. While the summations of the oscillator strengths for the traditional wavefunctions and ours are the same, the variation in individual oscillator strengths indicates that the transitions between energy states proceed through distinct pathways or exhibit different intensities, challenging further experiments.

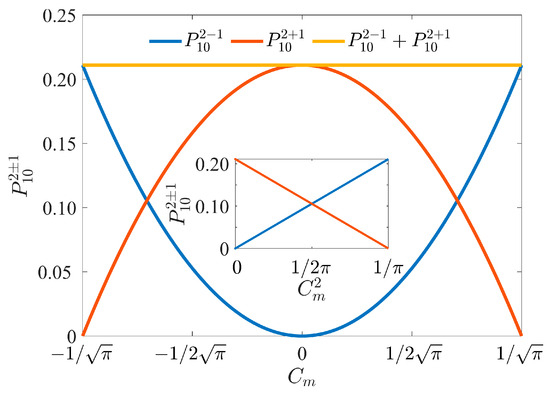
Figure 5. Variation in the oscillator strengths $P_{10}^{2-1}$ and $P_{10}^{2+1}$, and their summation when $C_m$ is varied. The inset shows the linear relationship between the oscillator strengths and $C_m^2$.

Table 3. Summation of the oscillator strengths $P_{10}^{n^{\prime }-1}$ and $P_{10}^{n^{\prime }+1}$ due to the conventional eigenfunctions and our proposed eigenfunctions for different values of $n^{\prime }$.

$\mathbf{Transition} \mathbf{between} \mathbf{States} (1,0)$$\mathbf{and} ({\mathit{n}}^{\prime },\pm 1)$	${\mathit{P}}_{10}^{{\mathit{n}}^{\prime }-1}$$+{\mathit{P}}_{10}^{{\mathit{n}}^{\prime }+1}$ Due to the Conventional Eigenfunctions	${\mathit{P}}_{10}^{{\mathit{n}}^{\prime }-1}$$+{\mathit{P}}_{10}^{{\mathit{n}}^{\prime }+1}$ Due to Our Proposed Eigenfunctions
$(1,0)\to (2,\pm 1)$	0.2109	0.2109
$(1,0)\to (3,\pm 1)$	0.0381	0.0381
$(1,0)\to (4,\pm 1)$	0.0132	0.0132

The advantage of our proposed wavefunctions is that they are appropriate for identifying orbital shapes labeled as $s$, $p$, $d$, and $f$, as well as for labeling the orientation of these shapes. Unlike the complex conventional wavefunctions, our 2D hydrogen wavefunctions are real-valued and clearly exhibit particular shapes, such as a circle, a ring, a dumbbell, and a cloverleaf, as seen in Figure 4. It should be noticed that these shapes look very similar to those in a 3D hydrogen atom [44]. For the 2D hydrogen atom, the azimuthal orbitals are characterized by their shapes and orientations, which are determined by the angular momentum quantum number $m$. The orbitals $s$, $p$, $d$, and $f$ are labeled for the states with $m=0, \pm 1, \pm 2, \pm 3,$ respectively, as seen in Figure 4. In a similar manner to a 3D hydrogen atom [45], the orientation of these orbitals can be labeled by transforming the azimuthal parts of the hydrogen wavefunctions into Cartesian coordinates on a circle with radius $r=1$, as shown in Table 4. (The proof of this transformation can be found in Appendix B.) Labeling the orbitals by Cartesian representation provides the interpretation of the orbital orientations. For example, as seen in Figure 4, the maxima and minima of $p_x\left(p_y\right)$-orbital states align along the $x\left(y\right)$-axis. The maxima and minima of $d_{x^2-y^2}$-orbital states align along the $x$- and $y$-axes, while those of $d_{xy}$-orbital states align between the $x$- and $y$-axes. It should be noted that all Cartesian representations of 2D hydrogen states shown in Table 4 duplicate some of those in 3D hydrogen states, except for those with a $z$-coordinate, such as $p_z$, $d_{xz}$, $d_{yz}$, and $f_{xyz}$, which only appear in the 3D hydrogen states [46].

Table 4. The azimuthal part for the 2D hydrogen states with angular momentum $m$ and their Cartesian representation.

Angular Momentum	Azimuthal Wavefunctions	Cartesian Representation on a Circle $\mathbf{with} \mathbf{a} \mathbf{Radius} \mathit{r}=1$	Orbitals with Labeling Orientation
$m=+1$	$\cos (\varphi )$	$x$	$p_x$
$m=-1$	$\sin (\varphi )$	$y$	$p_y$
$m=+2$	$\cos (2\varphi )$	$x^2-y^2$	$d_{x^2-y^2}$
$m=-2$	$\sin (2\varphi )$	$xy$	$d_{xy}$
$m=+3$	$\cos (3\varphi )$	$x(x^2-3y^2)$	$f_{x(x^2-3y^2)}$
$m=-3$	$\sin (3\varphi )$	$y(3x^2-y^2)$	$f_{y(3x^2-y^2)}$

In short, illustrating 2D hydrogen wavefunctions using our expression reveals the intuitive characteristics of orbital shapes and their orientations. Here, the hydrogen states are labeled by Cartesian representations for the first time, whereas the angular momentum $m$ was used in previous works [26,36,47]. Additionally, the azimuthal wavefunctions in Equation (5) can be applied to visualize the orbital characters of other quantum states confined in radial potentials, such as the Lennard-Jones potential [48] and the Woods–Saxon potential [49]. Our results, relevant to the concept of the optical transition between azimuthally dependent states, can also be applied to explain the transition in 2D systems with Coulomb potential, such as donor atoms and excitons in single-layer or thin materials [4,5,6,7].

4. Conclusions

In this study, we present alternative expressions of the azimuthal 2D hydrogen wavefunctions. Their probability densities corresponding to the states with $m\ne 0$ exhibit distinctive behavior; oscillating along the azimuthal direction is observed. This behavior is confirmed by the 2D finite difference method. After fitting the numerical wavefunctions to our proposed analytic wavefunctions, the values of $R^2$ are very close to one. Notably, although the summation of oscillator strengths from the ground state to excited degenerate states is identical for both the conventional and proposed wavefunctions, the wavefunction rotation causes a fundamental difference in optical mechanisms; the transitions between energy states happen through different pathways or with different intensities, suggesting new avenues for experimental verification and deeper understanding. Remarkably, the proposed wavefunctions are real-valued functions, providing an intuitive illustration of the orbital characteristics of the 2D hydrogen atom. Labeling the 2D hydrogen states using Cartesian representations suggests partial duplication in the orbital orientation between 2D and 3D hydrogen states. These results regarding orbital states provide a fundamental concept for describing science and technologies based on donor atoms and excitons in 2D materials.