Predictor Laplace Fractional Power Series Method for Finding Multiple Solutions of Fractional Boundary Value Problems
Abstract
1. Introduction
2. Preliminary and Notations
- .
- .
- .
- , for .
3. Predictor Laplace FPSM
- Assume the initial conditions .
- Apply the LT to Equation (4) to obtain
- Assume that and the LT of the nonlinear term can be formulated aswhere the parameter q is in the form such that , and and are fixed positive integers depending on the nonlinear terms.
- Set the for as , and for the other values.
- Multiply (9) by and take the limit to obtainThis gives for .
- Apply the inverse Laplace transform to Equation (8); the N-th order of the approximate solution becomeswhere is the vector .
- Substitute the solution into the conditions in Equation (5) to generate n-nonlinear algebraic equations.
- Solve the equations generated in Step 8 using an accurate method such as the Newton–Raphson method or the new optimal numerical root-solver [29] to determine all solutions for the unknown .
- Substitute the solutions for from Step 9 into to obtain the complete solution to Equation (4).
4. Applications
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Veeresha, P.; Prakasha, D.G.; Kumar, S. A fractional model for propagation of classical optical solitons by using nonsingular derivative. Math. Methods Appl. Sci. 2024, 45, 10609–10623. [Google Scholar] [CrossRef]
- Kumar, S. A new fractional modeling arising in engineering sciences and its analytical approximate solution. Alex. Eng. J. 2013, 52, 813–819. [Google Scholar] [CrossRef]
- Partohaghighi, M.; Akgül, A.; Guran, L.; Bota, M.F. Novel mathematical modelling of platelet-poor plasma arising in a blood coagulation system with the fractional Caputo–Fabrizio derivative. Symmetry 2022, 14, 1128. [Google Scholar] [CrossRef]
- Kumar, P.; Baleanu, D.; Erturk, V.S.; Inc, M.; Govindaraj, V. A delayed plant disease model with Caputo fractional derivatives. Adv. Contin. Discret. Models 2022, 1, 11. [Google Scholar] [CrossRef]
- Baleanu, D.; Qureshi, S.; Yusuf, A.; Soomro, A.; Osman, M.S. Bi-modal COVID-19 transmission with Caputo fractional derivative using statistical epidemic cases. Partial. Differ. Equations Appl. Math. 2024, 10, 100732. [Google Scholar] [CrossRef]
- Khuri, S.A. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 2002, 1, 141–155. [Google Scholar] [CrossRef]
- Ray, S.S. Analytical solution for the space fractional diffusion equation by two-step Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1295–1306. [Google Scholar]
- Chang, M.H. A decomposition solution for fins with temperature dependent surface heat flux. Int. J. Heat Mass Transf. 2005, 48, 1819–1824. [Google Scholar] [CrossRef]
- Alomari, A.K.; Awawdeh, F.; Tahat, N.; Ahmad, F.B.; Shatanawi, W. Multiple solutions for fractional differential equations: Analytic approach. Appl. Math. Comput. 2013, 219, 8893–8903. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Chung, J.D. A comparative study of fractional partial differential equations with the help of yang transform. Symmetry 2023, 15, 146. [Google Scholar] [CrossRef]
- Khader, M.M.; Babatin, M.M. On approximate solutions for fractional logistic differential equation. Math. Probl. Eng. 2013, 2013, 391901. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Aljarrah, H.; Alaroud, M.; Ishak, A.; Darus, M. Adaptation of residual-error series algorithm to handle fractional system of partial differential equations. Mathematics 2021, 9, 2868. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abdl-Rahim, H.R.; Ahmad, H.; Chu, Y.M. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena. Open Phys. 2020, 18, 799–805. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Albalawi, W.; Shah, R.; Nonlaopon, K.; El-Sherif, L.S.; El-Tantawy, S.A. Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations. Symmetry 2023, 15, 194. [Google Scholar] [CrossRef]
- Yadav, S.; Vats, R.K.; Rao, A. Constructing the fractional series solutions for time-fractional K-dV equation using Laplace residual power series technique. Opt. Quantum Electron. 2024, 56, 721. [Google Scholar] [CrossRef]
- Alaroud, M.; Aljarrah, H.; Alomari, A.K.; Ishak, A.; Darus, M. Explicit and approximate series solutions for nonlinear fractional wave-like differential equations with variable coefficients. Partial. Differ. Equations Appl. Math. 2024, 10, 100680. [Google Scholar] [CrossRef]
- Abdelhafeez, S.A.; Arafa, A.A.; Zahran, Y.H.; Osman, I.S.; Ramadan, M. Adapting Laplace residual power series approach to the Caudrey Dodd Gibbon equation. Sci. Rep. 2024, 14, 9772. [Google Scholar] [CrossRef]
- Alomari, A.K.; Alaroud, M.; Tahat, N.; Almalki, A. Extended Laplace power series method for solving nonlinear Caputo fractional Volterra integro-differential equations. Symmetry 2023, 15, 1296. [Google Scholar] [CrossRef]
- Alaroud, M.; Alomari, A.K.; Tahat, N.; Ishak, A. Analytical Computational Scheme for Multivariate Nonlinear Time-Fractional Generalized Biological Population Model. Fractal Fract. 2023, 7, 176. [Google Scholar] [CrossRef]
- Yahaya, R.I.; Md Arifin, N.; Pop, I.; Md Ali, F.; Mohamed Isa, S.S.P. Dual solutions for MHD hybrid nanofluid stagnation point flow due to a radially shrinking disk with convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 456–476. [Google Scholar] [CrossRef]
- Khan, M.; Ahmad, L.; Yasir, M.; Ahmed, J. Numerical analysis in thermally radiative stagnation point flow of cross nanofluid due to shrinking surface: Dual solutions. Appl. Nanosci. 2023, 13, 573–584. [Google Scholar] [CrossRef]
- Saleem, M.; Hussain, M. Dual solutions of Williamson-Casson fluid over a heated exponentially shrinking surface with stability analysis: A novel Catteneo-Christov heat flux model combination. Numer. Heat Transf. Part A Appl. 2024, 85, 114–136. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Magyari, E.; Shivanian, E. The homotopy analysis method for multiple solutions of nonlinear boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3530–3536. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shivanian, E. Prediction of multiplicity of solutions of nonlinear boundary value problems: Novel application of homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3830–3846. [Google Scholar] [CrossRef]
- Xu, H.; Liao, S.J. Dual solutions of boundary layer flow over an upstream moving plate. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 350–358. [Google Scholar] [CrossRef]
- Qureshi, S.; Chicharro, F.I.; Argyros, I.K.; Soomro, A.; Alahmadi, J.; Hincal, E. A New Optimal Numerical Root-Solver for Solving Systems of Nonlinear Equations Using Local, Semi-Local, and Stability Analysis. Axioms 2024, 13, 341. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shivanian, E. Predictor homotopy analysis method and its application to some nonlinear problems. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2456–2468. [Google Scholar] [CrossRef]
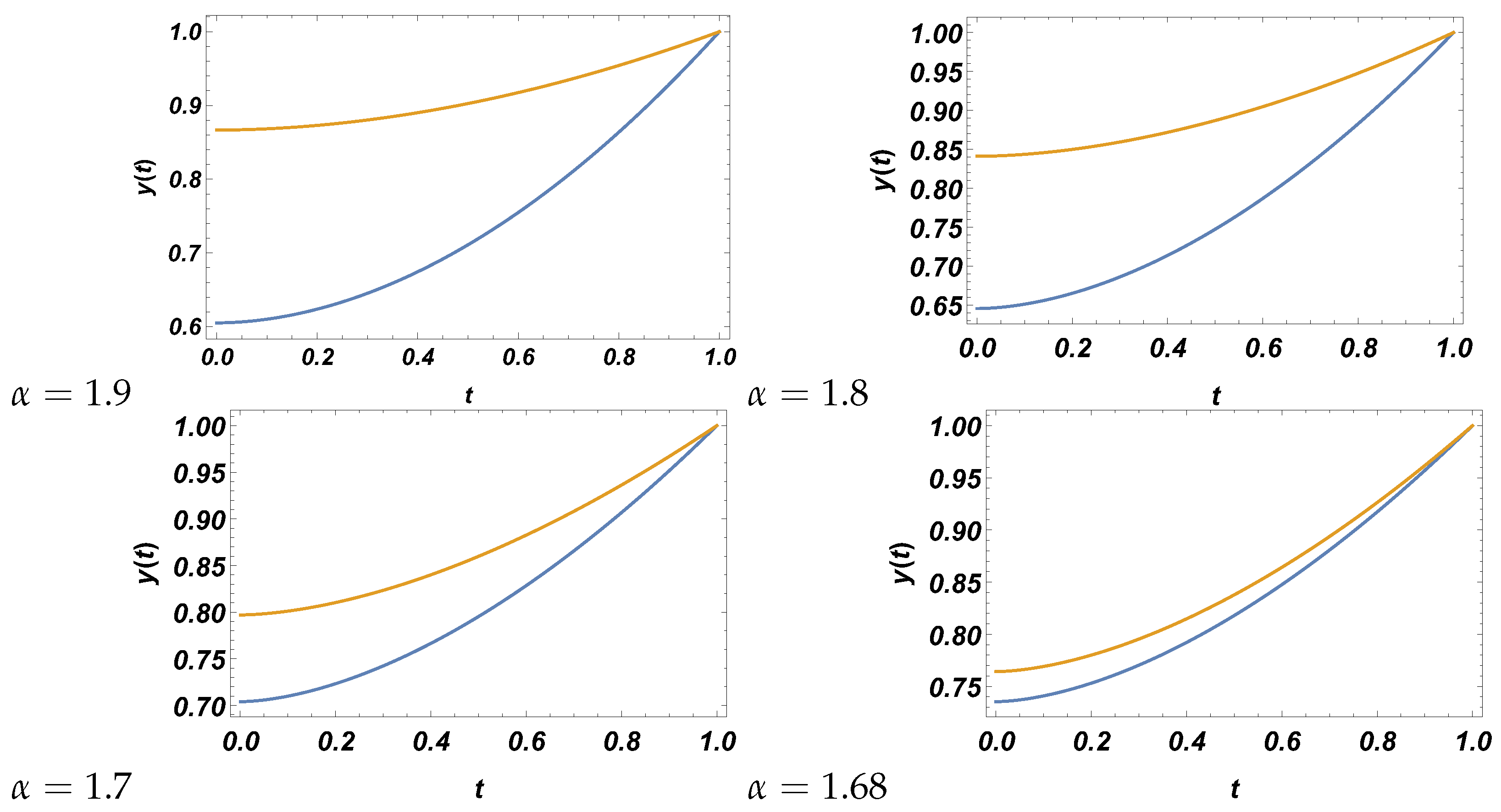
| n | ||||||
|---|---|---|---|---|---|---|
| 40 | 0.6052120962 | 0.8666280497 | 0.6454299587 | 0.8409846122 | 0.7040690899 | 0.7968988326 |
| 50 | 0.6052120962 | 0.8666280497 | 0.6454299587 | 0.8409846122 | 0.7040690899 | 0.7968988326 |
| 60 | 0.6052065265 | 0.8666339906 | 0.6454123301 | 0.8410056456 | 0.7039799571 | 0.7970001618 |
| 70 | 0.6052065265 | 0.8666339906 | 0.6454123301 | 0.8410056456 | 0.7039795681 | 0.7970000599 |
| 80 | 0.6052064987 | 0.8666339632 | 0.6454122363 | 0.8410055710 | 0.7039795681 | 0.7970000599 |
| 90 | 0.6052064987 | 0.8666339632 | 0.6454122364 | 0.8410055708 | 0.7039795696 | 0.7970000577 |
| 100 | 0.6052064987 | 0.8666339632 | 0.6454122364 | 0.8410055708 | 0.7039795696 | 0.7970000577 |
| n | ||||||
|---|---|---|---|---|---|---|
| 300 | −2.908126478 | 145.8780662 | −2.890668959 | 125.3769389 | −2.870259296 | 106.3892558 |
| 400 | −2.908126478 | 147.7398896 | −2.890668959 | 131.8532334 | −2.870259296 | 113.2663820 |
| 500 | −2.908126478 | 148.4348950 | −2.890668959 | 130.8731202 | −2.870259296 | 118.8103639 |
| 600 | −2.908126478 | 148.3813672 | −2.890668959 | 130.4388597 | −2.870259296 | 115.3101551 |
| 700 | −2.908126478 | 148.3654474 | −2.890668959 | 130.4794925 | −2.870259296 | 115.9764097 |
| 800 | −2.908126478 | 148.3669774 | −2.890668959 | 130.4985713 | −2.870259296 | 115.7959115 |
| 900 | −2.908126478 | 148.3668728 | −2.890668959 | 130.4956720 | −2.870259296 | 115.8171922 |
| 1000 | −2.908126478 | 148.3668434 | −2.890668959 | 130.4959435 | −2.870259296 | 115.8344660 |
| n | ||||||
|---|---|---|---|---|---|---|
| 300 | −138.0711661 | −3.101976104 | −118.1546084 | −3.123617677 | −100.1782084 | −3.149851401 |
| 400 | −139.3947405 | −3.101976104 | −122.1853108 | −3.123617677 | −109.4983522 | −3.149851401 |
| 500 | −139.7981285 | −3.101976104 | −121.7141473 | −3.123617677 | −107.3604086 | −3.149851401 |
| 600 | −139.7714048 | −3.101976104 | −121.5374888 | −3.123617677 | −106.3390332 | −3.149851401 |
| 700 | −139.7646425 | −3.101976104 | −121.5522702 | −3.123617677 | −106.524706 | −3.149851401 |
| 800 | −139.7651863 | −3.101976104 | −121.5578166 | −3.123617677 | −106.4873698 | −3.149851401 |
| 900 | −139.7651539 | −3.101976104 | −121.5571362 | −3.123617677 | −106.4913908 | −3.149851401 |
| 1000 | −139.7651461 | −3.101976104 | −121.5571918 | −3.123617677 | −106.4937748 | −3.149851401 |
| t | for | for | for | |||
|---|---|---|---|---|---|---|
| 0.00 | 1.48985 | −13.7152 | 1.48802 | −11.6233 | 1.48590 | −9.89024 |
| 0.25 | 1.39896 | −9.10445 | 1.39768 | −7.57271 | 1.39619 | −6.30149 |
| 0.50 | 1.12574 | 3.34540 | 1.12593 | 3.21957 | 1.12616 | 3.11011 |
| 0.75 | 0.66544 | 13.7643 | 0.667053 | 11.7956 | 0.668914 | 10.1577 |
| 1.00 | 3.04497 | 4.16334 | 9.49464 | 1.03251 | −5.60716 | 1.66533 |
| t | for | for | for | |||
|---|---|---|---|---|---|---|
| 0.00 | 15.2927 | 1.51121 | 13.205 | 1.51345 | 11.4798 | 1.51614 |
| 0.25 | 10.9479 | 1.41428 | 9.43037 | 1.41585 | 8.17621 | 1.41773 |
| 0.50 | −0.857015 | 1.12413 | −0.710199 | 1.12388 | −0.582739 | 1.12356 |
| 0.75 | −11.2594 | 0.646121 | −9.31746 | 0.644145 | −7.71311 | 0.6418 |
| 1.00 | 8.88178 | 2.93434 | −2.9976 | 1.78424 | −5.9952 | −1.09784 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alomari, A.-K.; Salameh, W.M.M.; Alaroud, M.; Tahat, N. Predictor Laplace Fractional Power Series Method for Finding Multiple Solutions of Fractional Boundary Value Problems. Symmetry 2024, 16, 1152. https://doi.org/10.3390/sym16091152
Alomari A-K, Salameh WMM, Alaroud M, Tahat N. Predictor Laplace Fractional Power Series Method for Finding Multiple Solutions of Fractional Boundary Value Problems. Symmetry. 2024; 16(9):1152. https://doi.org/10.3390/sym16091152
Chicago/Turabian StyleAlomari, Abedel-Karrem, Wael Mahmoud Mohammad Salameh, Mohammad Alaroud, and Nedal Tahat. 2024. "Predictor Laplace Fractional Power Series Method for Finding Multiple Solutions of Fractional Boundary Value Problems" Symmetry 16, no. 9: 1152. https://doi.org/10.3390/sym16091152
APA StyleAlomari, A.-K., Salameh, W. M. M., Alaroud, M., & Tahat, N. (2024). Predictor Laplace Fractional Power Series Method for Finding Multiple Solutions of Fractional Boundary Value Problems. Symmetry, 16(9), 1152. https://doi.org/10.3390/sym16091152







