Short-Distance Physics with Rare Kaon Decays
Abstract
1. Introduction
2.
2.1.
2.2.
3.
3.1. and
3.2.
- ) a direct CP-violating term: a purely short-distance effect contributing via the vector and axial Wilson coefficients and . It is proportional to the imaginary part of .
- ) an indirect CP-violating term: a long-distance dominated contribution of the single photon exchange via the vertex through -mixing. It is proportional to .
- ) an interference term from the above two contributions.
- ) a CP-conserving term: a long-distance-dominated contribution via two virtual photon exchanges.
4.
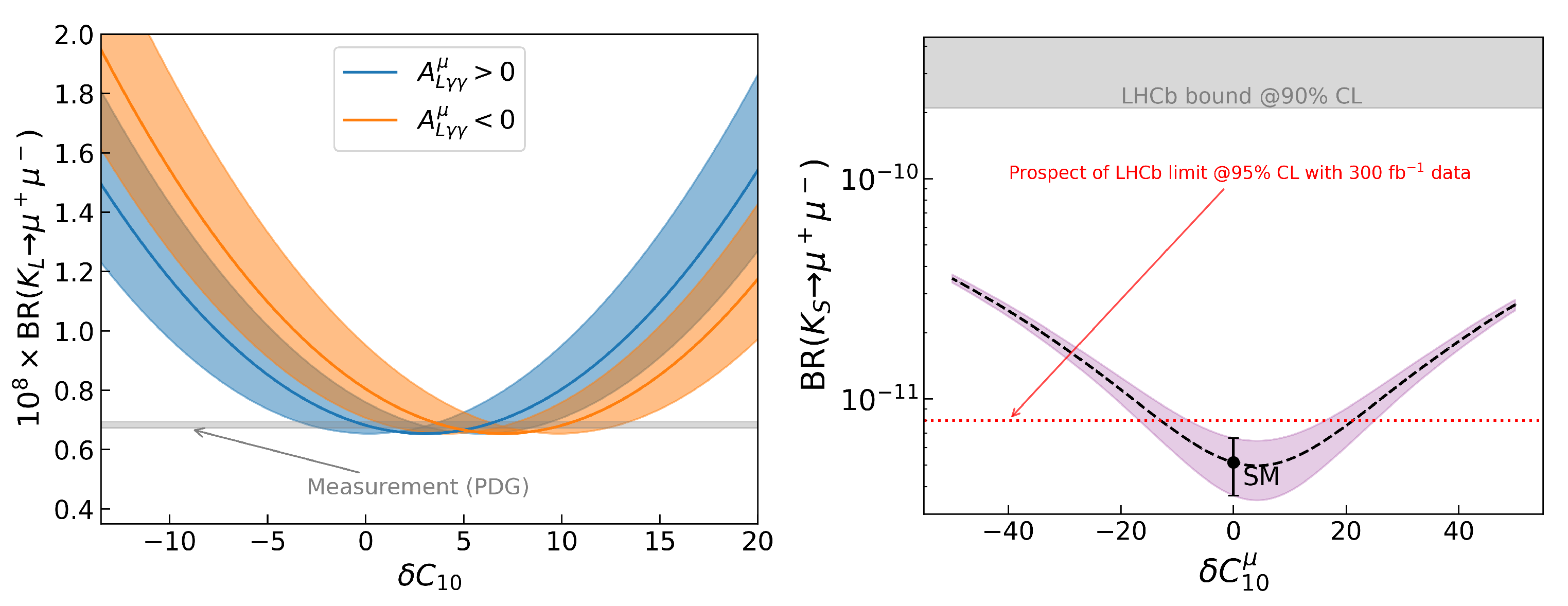
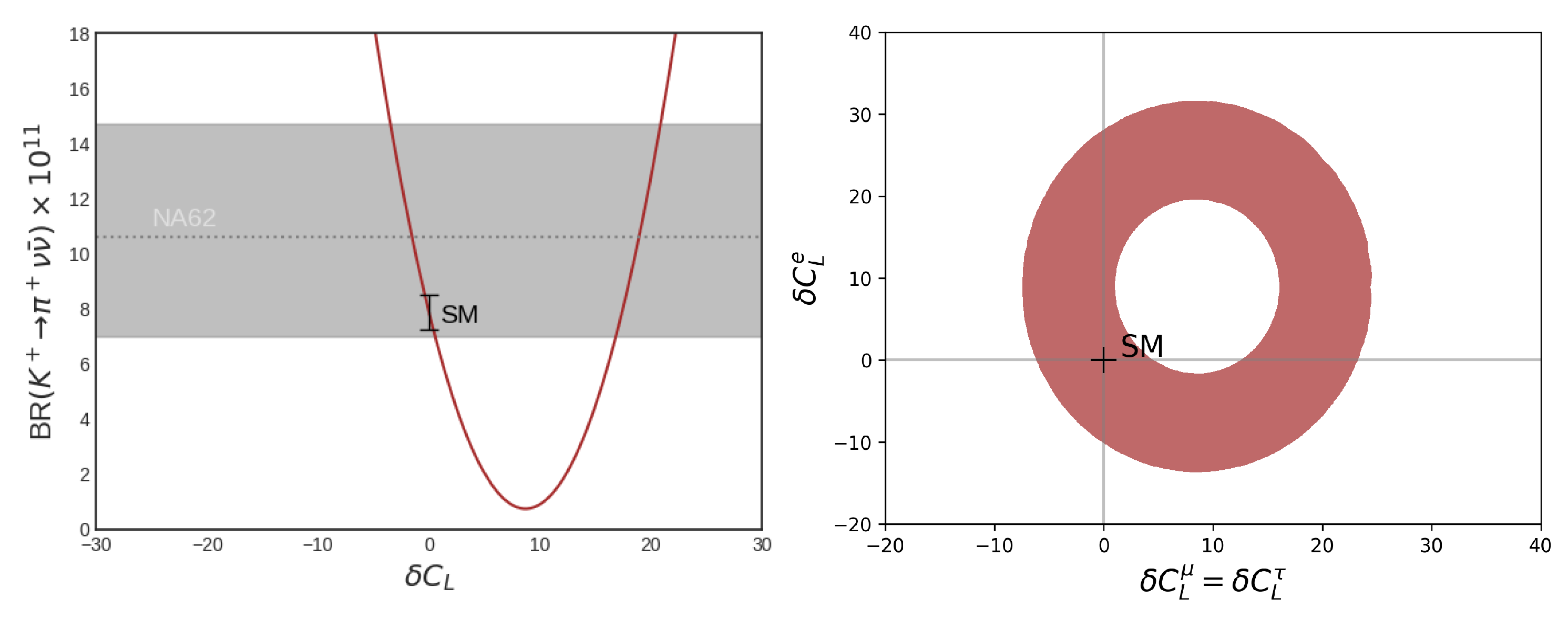
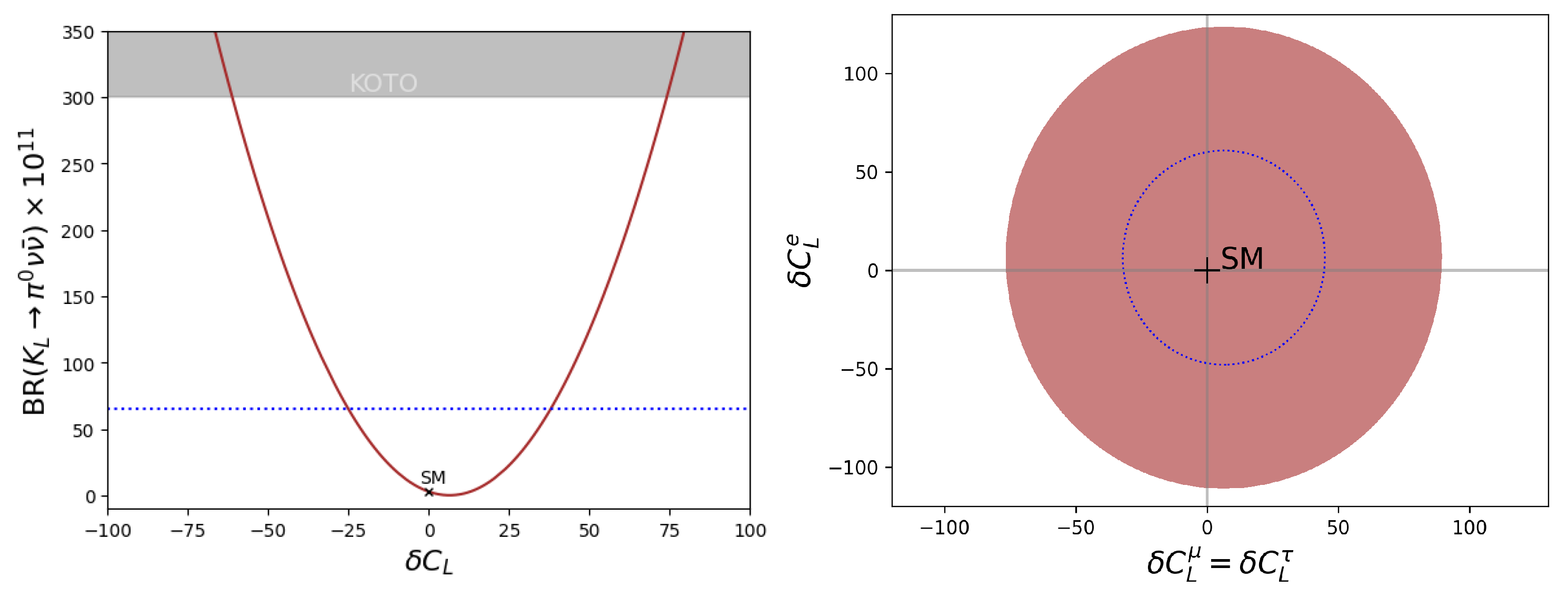
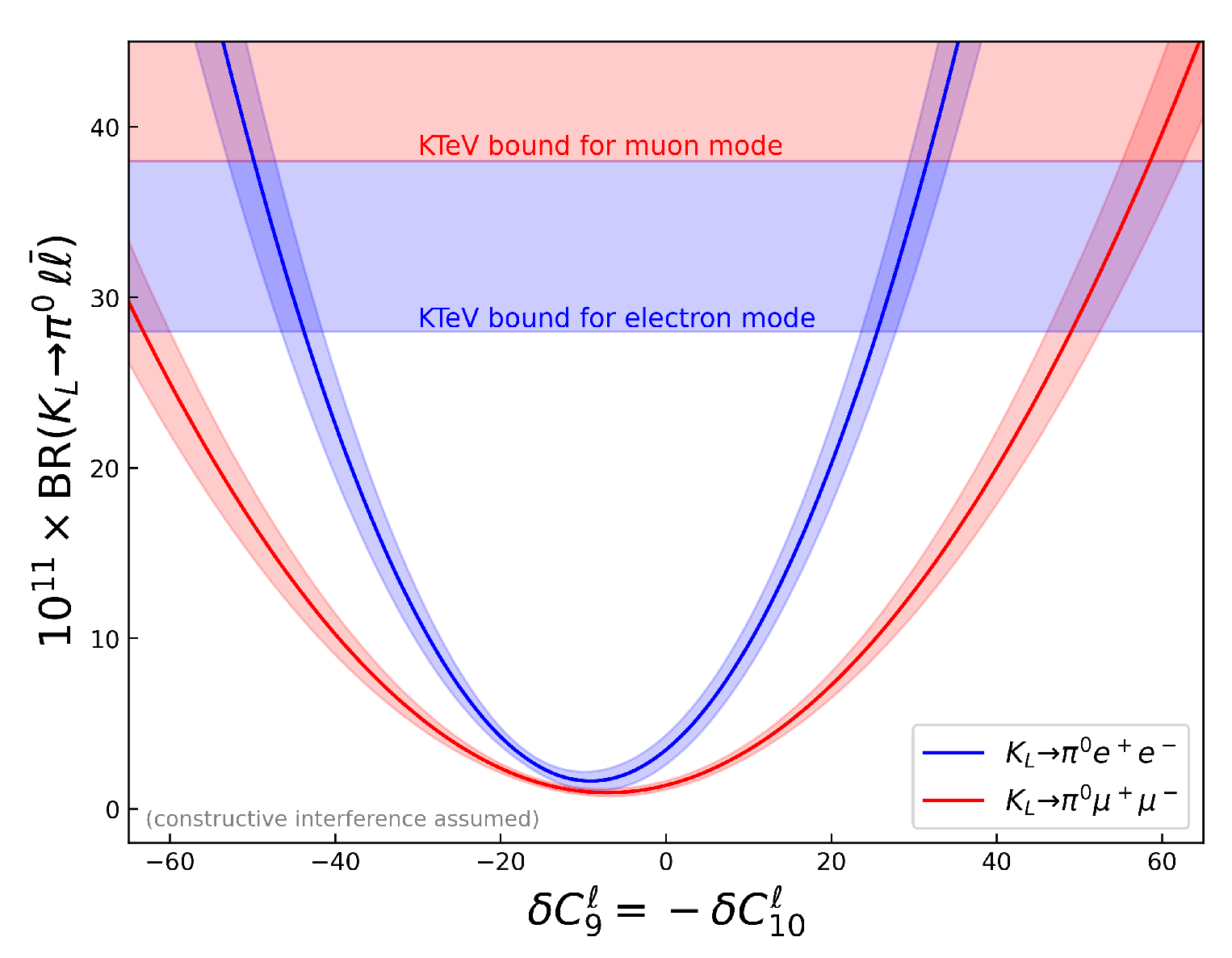
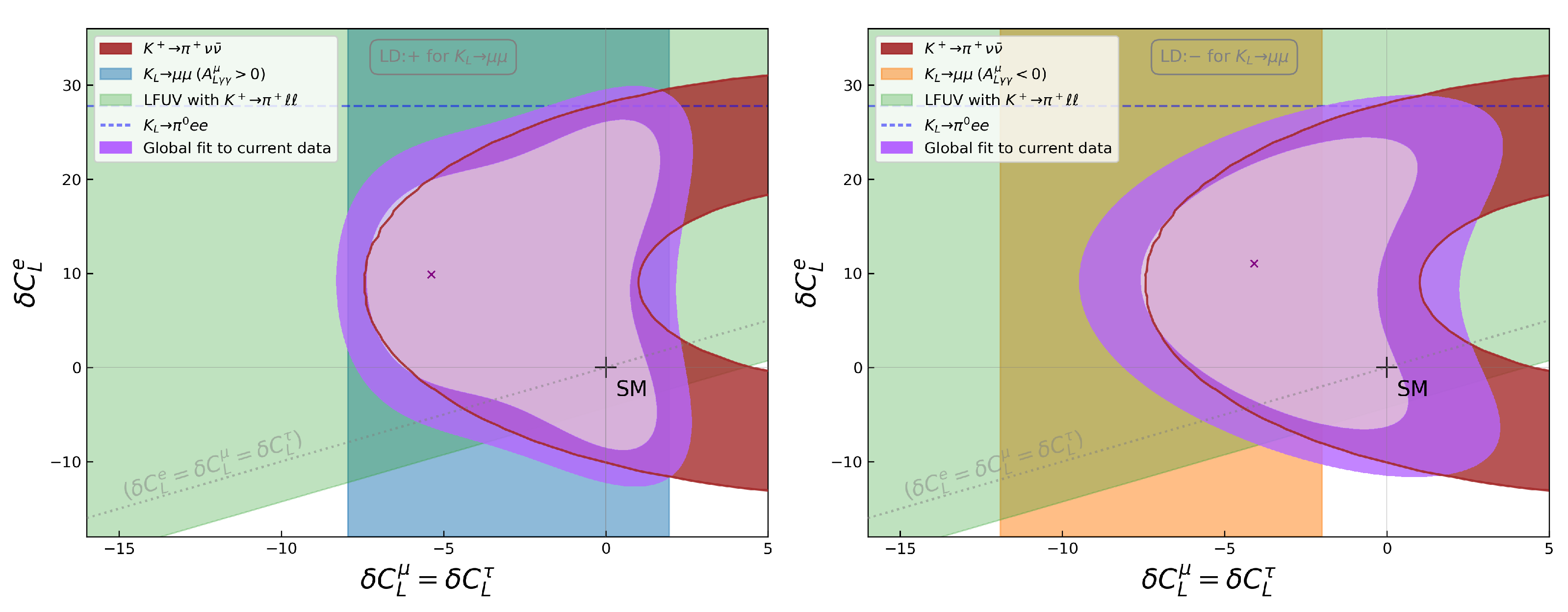
5. Global Picture
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Cabibbo, N. Unitary Symmetry and Leptonic Decays. Phys. Rev. Lett. 1963, 10, 531–533. [Google Scholar] [CrossRef]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the Meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak Interactions with Lepton-Hadron Symmetry. Phys. Rev. D 1970, 2, 1285–1292. [Google Scholar] [CrossRef]
- Littenberg, L.; Valencia, G. Rare and radiative kaon decays. Ann. Rev. Nucl. Part. Sci. 1993, 43, 729–792. [Google Scholar] [CrossRef]
- Pich, A. Chiral perturbation theory. Rept. Prog. Phys. 1995, 58, 563–610. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Isidori, G. CP violation in kaon decays. Int. J. Mod. Phys. A 1998, 13, 1–94. [Google Scholar] [CrossRef]
- Cirigliano, V.; Ecker, G.; Neufeld, H.; Pich, A.; Portoles, J. Kaon Decays in the Standard Model. Rev. Mod. Phys. 2012, 84, 399. [Google Scholar] [CrossRef]
- Bryman, D.; Marciano, W.J.; Tschirhart, R.; Yamanaka, T. Rare kaon and pion decays: Incisive probes for new physics beyond the standard model. Ann. Rev. Nucl. Part. Sci. 2011, 61, 331–354. [Google Scholar] [CrossRef]
- Ceccucci, A. Rare Kaon Decays. Ann. Rev. Nucl. Part. Sci. 2021, 71, 113–137. [Google Scholar] [CrossRef]
- Buras, A.J. New physics patterns in ε′/ε and εK with implications for rare kaon decays and ΔMK. J. High Energy Phys. 2016, 4, 071. [Google Scholar] [CrossRef]
- Bobeth, C.; Buras, A.J. Leptoquarks meet ε′/ε and rare Kaon processes. J. High Energy Phys. 2018, 2, 101. [Google Scholar] [CrossRef]
- Chobanova, V.; D’Ambrosio, G.; Kitahara, T.; Lucio Martinez, M.; Martinez Santos, D.; Fernandez, I.S.; Yamamoto, K. Probing SUSY effects in →μ+μ−. J. High Energy Phys. 2018, 5, 24. [Google Scholar] [CrossRef]
- Buras, A.J.; Buttazzo, D.; Girrbach-Noe, J.; Knegjens, R. K+→π+ν and KL→π0ν in the Standard Model: Status and perspectives. J. High Energy Phys. 2015, 11, 33. [Google Scholar] [CrossRef]
- Mescia, F.; Smith, C. Improved estimates of rare K decay matrix-elements from Kl3 decays. Phys. Rev. D 2007, 76, 034017. [Google Scholar] [CrossRef]
- Inami, T.; Lim, C.S. Effects of Superheavy Quarks and Leptons in Low-Energy Weak Processes KL→μ, K+→π+ν and K0↔0. Prog. Theor. Phys. 1981, 65, 297, Erratum in Prog. Theor. Phys. 1981, 65, 1772. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. QCD corrections to rare K and B decays for arbitrary top quark mass. Nucl. Phys. B 1993, 400, 225–239. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. The rare decays K→πν, B→Xν and B→l+l−: An Update. Nucl. Phys. B 1999, 548, 309–327. [Google Scholar] [CrossRef]
- Misiak, M.; Urban, J. QCD corrections to FCNC decays mediated by Z penguins and W boxes. Phys. Lett. B 1999, 451, 161–169. [Google Scholar] [CrossRef]
- Brod, J.; Gorbahn, M.; Stamou, E. Two-Loop Electroweak Corrections for the K→πν Decays. Phys. Rev. D 2011, 83, 034030. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. Two loop large mt electroweak corrections to K→πν for arbitrary Higgs boson mass. Phys. Rev. D 1998, 57, 216–223. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. The rare decays K+→π+ν and KL→μ+μ− beyond leading logarithms. Nucl. Phys. B 1994, 412, 106–142. [Google Scholar] [CrossRef]
- Buras, A.J.; Gorbahn, M.; Haisch, U.; Nierste, U. The Rare decay K+→π+ν at the next-to-next-to-leading order in QCD. Phys. Rev. Lett. 2005, 95, 261805. [Google Scholar] [CrossRef]
- Buras, A.J.; Gorbahn, M.; Haisch, U.; Nierste, U. Charm quark contribution to K+→π+ν at next-to-next-to-leading order. J. High Energy Phys. 2006, 11, 002, Erratum in J. High Energy Phys. 2012, 11, 167. [Google Scholar] [CrossRef][Green Version]
- Brod, J.; Gorbahn, M. Electroweak Corrections to the Charm Quark Contribution to K+→π+ν. Phys. Rev. D 2008, 78, 034006. [Google Scholar] [CrossRef]
- Isidori, G.; Unterdorfer, R. On the short distance constraints from KL,S→μ+μ−. J. High Energy Phys. 2004, 1, 009. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Quadt, A.; de Jong, P.; Demers, S.; Dobrescu, B.A.; D’Onofrio, M.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Hocker, A.; Lacker, H.; Laplace, S.; Le Diberder, F. A New approach to a global fit of the CKM matrix. Eur. Phys. J. C 2001, 21, 225–259. [Google Scholar] [CrossRef]
- Charles, J.; Hocker, A.; Lacker, H.; Laplace, S.; Le Diberder, F.R.; Malcles, J.; Ocariz, J.; Pivk, M.; Roos, L. CP violation and the CKM matrix: Assessing the impact of the asymmetric B factories. Eur. Phys. J. C 2005, 41, 1–131. [Google Scholar] [CrossRef]
- Bona, M.; Ciuchini, M.; Franco, E.; Lubicz, V.; Martinelli3, G.; Parodi4, F.; Pierini, M.; Roudeau, P.; Schiavi, C.; Silvestrini, L.; et al. The 2004 UTfit collaboration report on the status of the unitarity triangle in the standard model. J. High Energy Phys. 2005, 7, 28. [Google Scholar] [CrossRef]
- Bona, M.; Ciuchini, M.; Franco, E.; Lubicz, V.; Martinelli, G.; Parodi, F.; Pierini, M.; Roudeau, P.; Schiavi, C.; Silvestrini, L.; et al. Model-independent constraints on ΔF=2 operators and the scale of new physics. J. High Energy Phys. 2008, 3, 49. [Google Scholar] [CrossRef]
- Anzivino, G.; Cuendis, S.A.; Bernard, V.; Bijnens, J.; Bloch-Devaux, B.; Bordone, M.; Brizioli, F.; Brod, J.; Camalich, J.M.; Ceccucci, A.; et al. Workshop summary: Kaons@CERN 2023. Eur. Phys. J. C 2024, 84, 377. [Google Scholar] [CrossRef]
- Brod, J.; Gorbahn, M.; Stamou, E. Updated Standard Model Prediction for K→πν and ϵK. PoS 2021, BEAUTY2020, 056. [Google Scholar] [CrossRef]
- Buras, A.J.; Venturini, E. Searching for New Physics in Rare K and B Decays without |Vcb| and |Vub| Uncertainties. Acta Phys. Polon. B 2021, 53, 6-A1. [Google Scholar] [CrossRef]
- Cortina Gil, E.; Kleimenova, A.; Minucci, E.; Padolski, S.; Petrov, P.; Shaikhiev, A.; Volpe, R.; Numao, T.; Petrov, Y.; Velghe, B.; et al. Measurement of the very rare K+→π+ν decay. J. High Energy Phys. 2021, 6, 93. [Google Scholar] [CrossRef]
- NA62 Collaboration. NA62 Status Report to the CERN SPSC; Technical report; CERN: Geneva, Switzerland, 2023. [Google Scholar]
- D’Ambrosio, G.; Iyer, A.M.; Mahmoudi, F.; Neshatpour, S. Anatomy of kaon decays and prospects for lepton flavour universality violation. J. High Energy Phys. 2022, 9, 148. [Google Scholar] [CrossRef]
- Neshatpour, S.; D’Ambrosio, G.; Iyer, A.; Mahmoudi, F. Kaon rare decays: Theory overview. PoS 2024, WIFAI2023, 26. [Google Scholar] [CrossRef]
- Littenberg, L.S. The CP Violating Dacay →π0ν. Phys. Rev. D 1989, 39, 3322–3324. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.K.; Beckford, B.; Beechert, J.; Bryant, K.; Campbell, M.; Chen, S.H.; Comfort, J.; Dona, K.; Hara, N.; Haraguchi, H.; et al. Search for the KL→π0ν and KL→π0X0 decays at the J-PARC KOTO experiment. Phys. Rev. Lett. 2019, 122, 21802. [Google Scholar] [CrossRef]
- Grossman, Y.; Nir, Y. KL→π0ν beyond the standard model. Phys. Lett. B 1997, 398, 163–168. [Google Scholar] [CrossRef]
- Hsiung, Y.B. KOTO: Search for Direct CP Violating KL→π0ν Decays. PoS 2023, FPCP2023, 19. [Google Scholar] [CrossRef]
- Nanjo, H. KOTO II at J-PARC: Toward measurement of the branching ratio of KL→π0ν. J. Phys. Conf. Ser. 2023, 2446, 012037. [Google Scholar] [CrossRef]
- Aoki, K.; Fujioka, H.; Gogami, T.; Hidaka, Y.; Hiyama, E.; Honda, R.; Hosaka, A.; Ichikawa, Y.; Ieiri, M.; Isaka, M.; et al. Extension of the J-PARC Hadron Experimental Facility: Third White Paper. arXiv 2021, arXiv:2110.04462. [Google Scholar]
- Gilman, F.J.; Wise, M.B. K→πe+e− in the Six Quark Model. Phys. Rev. D 1980, 21, 3150. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Ecker, G.; Isidori, G.; Portoles, J. The Decays K→πl+l− beyond leading order in the chiral expansion. J. High Energy Phys. 1998, 8, 4. [Google Scholar] [CrossRef][Green Version]
- Ecker, G.; Pich, A.; de Rafael, E. K→πl+l− Decays in the Effective Chiral Lagrangian of the Standard Model. Nucl. Phys. B 1987, 291, 692–719. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Greynat, D.; Knecht, M. On the amplitudes for the CP-conserving K±(KS)→π±(π0)ℓ+ℓ− rare decay modes. J. High Energy Phys. 2019, 2, 49. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Greynat, D.; Knecht, M. Matching long and short distances at order O(αs) in the form factors for K→πℓ+ℓ−. Phys. Lett. B 2019, 797, 134891. [Google Scholar] [CrossRef]
- Boyle, P.A.; Erben, F.; Flynn, J.M.; Gülpers, V.; Hill, R.C.; Hodgson, R.; Jüttner, A.; hÓgáin, F.O.; Portelli, A.; Sachrajda, C.T. Simulating rare kaon decays K+→π+ℓ+ℓ− using domain wall lattice QCD with physical light quark masses. Phys. Rev. D 2023, 107, L011503. [Google Scholar] [CrossRef]
- Kambor, J.; Missimer, J.H.; Wyler, D. K→2π and K→3π decays in next-to-leading order chiral perturbation theory. Phys. Lett. B 1991, 261, 496–503. [Google Scholar] [CrossRef]
- Bijnens, J.; Dhonte, P.; Borg, F. K→3π decays in chiral perturbation theory. Nucl. Phys. B 2003, 648, 317–344. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Knecht, M.; Neshatpour, S. Determination of the structure of the K→πππ amplitudes from recent data. Phys. Lett. B 2022, 835, 137594. [Google Scholar] [CrossRef]
- Crivellin, A.; D’Ambrosio, G.; Hoferichter, M.; Tunstall, L.C. Violation of lepton flavor and lepton flavor universality in rare kaon decays. Phys. Rev. D 2016, 93, 074038. [Google Scholar] [CrossRef]
- Appel, R.; Atoyan, G.S.; Bassalleck, B.; Bergman, D.R.; Brown, D.N.; Cheung, N.; Eilerts, S.; Dhawan, S.; Do, H.; Egger, J.; et al. A New measurement of the properties of the rare decay K+→π+e+e−. Phys. Rev. Lett. 1999, 83, 4482–4485. [Google Scholar] [CrossRef]
- Batley, J.R.; Culling, A.J.; Kalmus, G.; Lazzeroni, C.; Munday, D.J.; Slater, M.W.; Bocquet, G.; Wotton, S.A.; Arcidiacono, R.; Bocquet, G.; et al. Precise measurement of the K±→π±e+e− decay. Phys. Lett. B 2009, 677, 246–254. [Google Scholar] [CrossRef]
- Cortina Gil, E.; Kleimenova, A.; Minucci, E.; Padolski, S.; Petrov, P.; Shaikhiev, A.; Volpe, R.; Numao, T.; Petrov, Y.; Velghe, B.; et al. A measurement of the K+→π+μ+μ− decay. J. High Energy Phys. 2022, 11, 11, Addendum in J. High Energy Phys. 2023, 6, 40. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Mahmoudi, F.; Neshatpour, S. Beyond the Standard Model prospects for kaon physics at future experiments. J. High Energy Phys. 2024, 2, 166. [Google Scholar] [CrossRef]
- NA62 Collaboration. ADDENDUM I TO P326 Continuation of the Physics Programme of the NA62 Experiment; Technical report; CERN: Geneva, Switzerland, 2019. [Google Scholar]
- NA62 Collaboration. NA62 Status Report to the CERN SPSC; Technical report; CERN: Geneva, Switzerland, 2024. [Google Scholar]
- Beder, D.S.; Dass, G.V. Leptonic Coupling Types in K+→π+ℓ+ℓ− Decays and the Question of Strangeness-Changing Semileptonic Neutral Currents. Phys. Lett. B 1975, 59, 444–450. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Iyer, A.M.; Mahmoudi, F.; Neshatpour, S. Exploring scalar contributions with K+→π+ℓ+ℓ−. Phys. Lett. B 2024, 855, 138824. [Google Scholar] [CrossRef]
- Batley, J.R.; Kalmus, G.E.; Lazzeroni, C.; Munday, D.J.; Patel, M.; Slater, M.W.; Wotton, S.A.; Arcidiacono, R.; Bocquet, G.; Ceccucci, A.; et al. Observation of the rare decay KS→π0e+e−. Phys. Lett. B 2003, 576, 43–54. [Google Scholar] [CrossRef]
- Batley, J.R.; Kalmus, G.E.; Lazzeroni, C.; Munday, D.J.; Patel, M.; Slater, M.W.; Wotton, S.A.; Arcidiacono, R.; Bocquet, G.; Ceccucci, A.; et al. Observation of the rare decay KS→π0μ+μ−. Phys. Lett. B 2004, 599, 197–211. [Google Scholar] [CrossRef]
- Chobanova, V.G.; Cid Vidal, X.; Dalseno, J.P.; Lucio Martinez, M.; Martinez Santos, D.; Renaudin, V. Sensitivity of LHCb and its upgrade in the measurement of B(→π0μ+μ−). 2016. Available online: http://cds.cern.ch/record/2195218 (accessed on 1 June 2024).
- Alves Junior, A.A.; Bettler, M.O.; Rodríguez, A.B.; Vidal, A.C.; Chobanova, V.; Vidal, X.C.; Contu, A.; D’Ambrosio, G.; Dalseno, J.; Dettori, F.; et al. Prospects for Measurements with Strange Hadrons at LHCb. J. High Energy Phys. 2019, 5, 48. [Google Scholar] [CrossRef]
- Buchalla, G.; D’Ambrosio, G.; Isidori, G. Extracting short distance physics from KL,S→π0e+e− decays. Nucl. Phys. B 2003, 672, 387–408. [Google Scholar] [CrossRef]
- Isidori, G.; Smith, C.; Unterdorfer, R. The Rare decay KL→π0μ+μ− within the SM. Eur. Phys. J. C 2004, 36, 57–66. [Google Scholar] [CrossRef][Green Version]
- Mescia, F.; Smith, C.; Trine, S. KL→π0e+e− and KL→π0μ+μ−: A Binary star on the stage of flavor physics. J. High Energy Phys. 2006, 8, 88. [Google Scholar] [CrossRef][Green Version]
- Martin, B.R.; De Rafael, E.; Smith, J. Neutral kaon decays into lepton pairs. Phys. Rev. D 1970, 2, 179–200. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Holstein, B.R.; Valencia, G. KL→π0e+e− as a Probe of CP Violation. Phys. Rev. D 1987, 35, 2769. [Google Scholar] [CrossRef]
- Ecker, G.; Pich, A.; de Rafael, E. Radiative Kaon Decays and CP Violation in Chiral Perturbation Theory. Nucl. Phys. B 1988, 303, 665–702. [Google Scholar] [CrossRef]
- Ecker, G.; Pich, A.; de Rafael, E. K0→π0γγ Decays in Chiral Perturbation Theory. Phys. Lett. B 1987, 189, 363–368. [Google Scholar] [CrossRef][Green Version]
- Sehgal, L.M. CP Violation in KL→π0e+e−: Interference of One Photon and Two Photon Exchange. Phys. Rev. D 1988, 38, 808. [Google Scholar] [CrossRef]
- Flynn, J.; Randall, L. The CP Conserving Long Distance Contribution to the Decay KL→π0e+e−. Phys. Lett. B 1989, 216, 221–226. [Google Scholar] [CrossRef]
- Cappiello, L.; D’Ambrosio, G. KL→π0γγ Decay in the Chiral Effective Lagrangian. Nuovo Cim. A 1988, 99, 155–161. [Google Scholar] [CrossRef]
- Morozumi, T.; Iwasaki, H. The CP Conserving Contribution in the Decays KL→π0γγ and KL→π0e+e−. Prog. Theor. Phys. 1989, 82, 371–379. [Google Scholar] [CrossRef][Green Version]
- Ecker, G.; Pich, A.; de Rafael, E. Vector Meson Exchange in Radiative Kaon Decays and Chiral Perturbation Theory. Phys. Lett. B 1990, 237, 481–487. [Google Scholar] [CrossRef]
- Savage, M.J.; Luke, M.E.; Wise, M.B. The Rare decays π0→e+e−, η→e+e− and η→μ+μ− in chiral perturbation theory. Phys. Lett. B 1992, 291, 481–483. [Google Scholar] [CrossRef][Green Version]
- Cappiello, L.; D’Ambrosio, G.; Miragliuolo, M. Corrections to K→πγγ from K→3π. Phys. Lett. B 1993, 298, 423–431. [Google Scholar] [CrossRef]
- Heiliger, P.; Sehgal, L.M. Analysis of the decay KL→π0γγ and expectations for the decays KL→π0e+e− and KL→π0μ+μ−. Phys. Rev. D 1993, 47, 4920–4938. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.G.; Ecker, G.; Pich, A. Unitarity and KL→π0γγ. Phys. Lett. B 1993, 304, 347–352. [Google Scholar] [CrossRef]
- Buras, A.J.; Lautenbacher, M.E.; Misiak, M.; Munz, M. Direct CP violation in KL→π0e+e− beyond leading logarithms. Nucl. Phys. B 1994, 423, 349–383. [Google Scholar] [CrossRef][Green Version]
- D’Ambrosio, G.; Portoles, J. Vector meson exchange contributions to K→πγγ and KL→γl+l−. Nucl. Phys. B 1997, 492, 417–454. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Gabbiani, F. KL→π0γe+e− and its relation to CP and chiral tests. Phys. Rev. D 1997, 56, 1605–1611. [Google Scholar] [CrossRef]
- Alavi-Harati, A.; Albuquerque, I.F.; Alexopoulos, T.; Arenton, M.; Arisaka, K.; Averitte, S.; Barker, A.R.; Bellantoni, L.; Bellavance, A.; Belz, J.; et al. Measurement of the decay KL→π0γγ. Phys. Rev. Lett. 1999, 83, 917–921. [Google Scholar] [CrossRef]
- Murakami, K.; Hemmi, Y.; Kurashige, H.; Matono, Y.; Nomura, T.; Sakamoto, H.; Sasao, N.; Suehiro, M.; Takeuchi, Y.; Fukushima, Y.; et al. Experimental search for the decay mode KL→π0γe+e−. Phys. Lett. B 1999, 463, 333–338. [Google Scholar] [CrossRef][Green Version]
- Alavi-Harati, A.; Alexopoulos, T.; Arenton, M.; Arisaka, K.; Averitte, S.; Barker, A.R.; Bellantoni, L.; Bellavance, A.; Belz, J.; Ben-David, R.; et al. First observation of the decay KL→π0e+e−γ. Phys. Rev. Lett. 2001, 87, 021801. [Google Scholar] [CrossRef]
- Diwan, M.V.; Ma, H.; Trueman, T.L. Muon decay asymmetries from →π0μ+μ− decays. Phys. Rev. D 2002, 65, 054020. [Google Scholar] [CrossRef]
- Gabbiani, F.; Valencia, G. KL→π0γγ and the bound on the CP conserving KL→π0e+e−. Phys. Rev. D 2001, 64, 094008. [Google Scholar] [CrossRef]
- Gabbiani, F.; Valencia, G. Vector meson contributions do not explain the rate and spectrum in KL→π0γγ. Phys. Rev. D 2002, 66, 074006. [Google Scholar] [CrossRef]
- Lai, A.; Marras, D.; Bevan, A.; Dosanjh, R.S.; Gershon, T.J.; Hay, B.; Kalmus, G.E.; Lazzeroni, C.; Munday, D.J.; Needham, M.D.; et al. Precise measurement of the decay KL→π0γγ. Phys. Lett. B 2002, 536, 229–240. [Google Scholar] [CrossRef]
- Isidori, G.; Martinelli, G.; Turchetti, P. Rare kaon decays on the lattice. Phys. Lett. B 2006, 633, 75–83. [Google Scholar] [CrossRef]
- Zhao, Y.; Christ, N.H. Calculating K→γγ using lattice QCD. PoS 2022, LATTICE2021, 451. [Google Scholar] [CrossRef]
- Bobeth, C.; Buras, A.J.; Celis, A.; Jung, M. Patterns of Flavour Violation in Models with Vector-Like Quarks. J. High Energy Phys. 2017, 04, 079. [Google Scholar] [CrossRef]
- Bruno, C.; Prades, J. Rare kaon decays in the 1/N(c) expansion. Z. Phys. C 1993, 57, 585–594. [Google Scholar] [CrossRef]
- Alavi-Harati, A.; Alexopoulos, T.; Arenton, M.; Barbosa, R.F.; Barker, A.R.; Barrio, M.; Bellantoni, L.; Bellavance, A.; Blucher, E.; Bock, G.J.; et al. Search for the rare decay KL→π0e+e−. Phys. Rev. Lett. 2004, 93, 021805. [Google Scholar] [CrossRef]
- Alavi-Harati, A.; Albuquerque, I.F.; Alexopoulos, T.; Arenton, M.; Arisaka, K.; Averitte, S.; Barker, A.R.; Bellantoni, L.; Bellavance, A.; Belz, J.; et al. Search for the Decay KL→π0μ+μ−. Phys. Rev. Lett. 2000, 84, 5279–5282. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. QCD corrections to the dZ vertex for arbitrary top quark mass. Nucl. Phys. B 1993, 398, 285–300. [Google Scholar] [CrossRef]
- Gorbahn, M.; Haisch, U. Charm Quark Contribution to KL→μ+μ− at Next-to-Next-to-Leading. Phys. Rev. Lett. 2006, 97, 122002. [Google Scholar] [CrossRef] [PubMed]
- Ecker, G.; Pich, A. The Longitudinal muon polarization in KL→μ+μ−. Nucl. Phys. B 1991, 366, 189–205. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Kitahara, T. Direct CP Violation in K→μ+μ−. Phys. Rev. Lett. 2017, 119, 201802. [Google Scholar] [CrossRef] [PubMed]
- Gomez Dumm, D.; Pich, A. Long distance contributions to the KL→μ+μ− decay width. Phys. Rev. Lett. 1998, 80, 4633–4636. [Google Scholar] [CrossRef]
- Knecht, M.; Peris, S.; Perrottet, M.; de Rafael, E. Decay of pseudoscalars into lepton pairs and large N(c) QCD. Phys. Rev. Lett. 1999, 83, 5230–5233. [Google Scholar] [CrossRef]
- Gerard, J.M.; Smith, C.; Trine, S. Radiative kaon decays and the penguin contribution to the ΔI=1/2 rule. Nucl. Phys. B 2005, 730, 1–36. [Google Scholar] [CrossRef]
- Hoferichter, M.; Hoid, B.L.; de Elvira, J.R. Improved Standard-Model prediction for KL→ℓ+ℓ−. J. High Energy Phys. 2024, 4, 71. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Constraints on the →μ+μ− Branching Fraction. Phys. Rev. Lett. 2020, 125, 231801. [Google Scholar] [CrossRef]
- Ashraf, M.U.; Cortina Gil, E.; Jerhot, J.; Lurkin, N.; Numao, T.; Velghe, B.; Wong, V.W.S.; Bryman, D.; Bician, L.; Hives, Z.; et al. High Intensity Kaon Experiments (HIKE) at the CERN SPS Proposal for Phases 1 and 2; CERN: Geneva, Switzerland, 2023. [Google Scholar]
- Dery, A.; Ghosh, M.; Grossman, Y.; Schacht, S. K→μ+μ− as a clean probe of short-distance physics. J. High Energy Phys. 2021, 07, 103. [Google Scholar] [CrossRef]
- Ambrose, D.; Arroyo, C.; Bachman, M.; de Cecco, P.; Connor, D.; Eckhause, M.; Ecklund, K.M.; Graessle, S.; Hancock, A.D.; Hartman, K.; et al. First observation of the rare decay mode →e+e−. Phys. Rev. Lett. 1998, 81, 4309–4312. [Google Scholar] [CrossRef]
- Ambrosino, F.; Antonelli, A.; Antonelli, M.; Archilli, F.; Beltrame, P.; Bencivenni, G.; Bertolucci, S.; Bini, C.; Bloise, C.; Bocchetta, S.; et al. Search for the KS→e+e− decay with the KLOE detector. Phys. Lett. B 2009, 672, 203–208. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Physics Case for an LHCb Upgrade II — Opportunities in Flavour Physics, and beyond, in the HL-LHC Era; Cornell University: Ithaca, NY, USA, 2018. [Google Scholar]
- Mahmoudi, F. SuperIso: A Program for calculating the isospin asymmetry of B→K*γ in the MSSM. Comput. Phys. Commun. 2008, 178, 745–754. [Google Scholar] [CrossRef]
- Mahmoudi, F. SuperIso v2.3: A Program for calculating flavor physics observables in Supersymmetry. Comput. Phys. Commun. 2009, 180, 1579–1613. [Google Scholar] [CrossRef]
- Mahmoudi, F. SuperIso v3.0, flavor physics observables calculations: Extension to NMSSM. Comput. Phys. Commun. 2009, 180, 1718–1719. [Google Scholar] [CrossRef]
- Neshatpour, S.; Mahmoudi, F. Flavour Physics with SuperIso. PoS 2021, TOOLS2020, 36. [Google Scholar] [CrossRef]
- Neshatpour, S.; Mahmoudi, F. Flavour Physics Phenomenology with SuperIso. PoS 2022, CompTools2021, 10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neshatpour, S. Short-Distance Physics with Rare Kaon Decays. Symmetry 2024, 16, 946. https://doi.org/10.3390/sym16080946
Neshatpour S. Short-Distance Physics with Rare Kaon Decays. Symmetry. 2024; 16(8):946. https://doi.org/10.3390/sym16080946
Chicago/Turabian StyleNeshatpour, Siavash. 2024. "Short-Distance Physics with Rare Kaon Decays" Symmetry 16, no. 8: 946. https://doi.org/10.3390/sym16080946
APA StyleNeshatpour, S. (2024). Short-Distance Physics with Rare Kaon Decays. Symmetry, 16(8), 946. https://doi.org/10.3390/sym16080946




