Abstract
A system of fractional differential equations (FDEs) with fractional derivatives of diverse orders is called an incommensurate system of FDEs. In this paper, the well-posedness of the initial value problem for incommensurate systems of FDEs is obtained on the space of continuous functions. Three different methods for this analysis are used and compared. The complexity of such analysis is reduced by new techniques. Strong existence results are obtained by weaker conditions. The uniqueness and the continuous dependency of the solution on initial values are investigated using the Gronwall inequality.
1. Introduction
The existence and uniqueness of a solution for dynamical systems depend on the space in which the solution is sought. In the analysis of such systems, it may become important to check whether the solutions belong to differentiability class (natural numbers with 0), (a local solution) or particularly (a global solution). This shows the regularity in the classical sense. In modern mathematics, the regularity of a dynamical system’s solutions refers to the existence of those solutions within a specific space. This space could be or the space of positive continuous functions. Both contexts address similar types of questions.
The existence of a solution to a system is insufficient for its application in practical models. The solution must be unique and continuous with respect to initial values. A system meeting these criteria is said to be well posed.
In this paper, we aim to study the well-posedness of the initial value problems for incommensurate systems of FDEs, which are as follows:
with the initial condition
on , where (real numbers), (natural numbers). Here, is the Caputo derivative of order defined as follows:
particularly for where stands for the Euler Gamma function. Supposing and we define the vector-order derivative as follows:
and the Riemann–Liouville integral is determined as follows:
Then, Equation (1) can be compactly written as
The initial condition of System (5) is given by
where
The main aim of this paper is to investigate the existence and uniqueness of the solutions of incommensurate FDEs described by Equations (5) and (6). Furthermore, to perform a complete analysis of well-posedness, the continuous dependency of the solution on the initial values is investigated.
The existence and uniqueness of commensurate fractional differential equations (FDEs) have been explored in [1,2,3]. However, to our knowledge, such studies have not been conducted for incommensurate FDEs (1) where in contrast to commensurate FDEs, may become mutually different. The complexity of these systems may contribute to this gap in research. Additionally, the interpretation of fractional derivatives remains somewhat ambiguous. We suggest that a useful interpretation of fractional derivatives is the rate of change with fading memory. This suggestion is clear by Definition (2).
Systems of commensurate fractional differential equations (FDEs) are significant and have various applications. For numerical solutions and applications of such systems, refer to [2,4]. We anticipate that systems of incommensurate FDEs will receive similar attention in the future as the concept of fractional derivative orders becomes better understood. Unlike commensurate systems, research on incommensurate FDE systems is currently sporadic. For instance, see [5,6,7]. Some applied papers, such as [7], do not distinguish between commensurate and incommensurate FDE systems. However, the term “incommensurate” does appear in some related works, such as [8,9].
Attempts for the existence and regularity of FDEs have a long history. Yu and Gao [10] obtained the regularity on based on the Schauder fixed-point theorem with the following conditions:
where and for . This theorem guarantees the existence of a solution on a suitable subspace of Daftardar-Gejji and Jafari [11] studied the existence and uniqueness of the solutions for non-autonomous systems of FDEs. Zhang [12] studied the existence of positive solutions. The well-posedness of FDEs has been extensively studied for diverse fractional derivatives and boundary conditions [13,14,15,16].
In this respect, this paper is considered to present a relatively comprehensive study on the solution’s regularity of systems of incommensurate FDEs in the space of continuous functions.
The significance of the space of continuous functions is further emphasized by the following remark:
Remark 1.
The existence results on follows from the existence of a solution on since
The exact solution of linear equations may be obtained with direct methods such as Laplace transform, and the obtained explicit solution determines the solution’s regularity. In contrast, the explicit solution of most nonlinear equations is not available, and fixed-point theorems play a major role in the analysis of such equations. For example, readers may refer to [17,18]. In this paper, we also use fixed-point theorems to perform the well–posedness analysis. However, it needs further development to obtain better results, which we discuss later.
Most analytical papers on existence results focus on one-dimensional equations, whereas the states of most applied systems reside in higher-dimensional Cartesian product spaces, such as . To conduct a similar analysis, we need to generalize the relevant theorems. For example, while the Arzelà–Ascoli theorem is stated for families of function on they are not stated for Cartesian product spaces Therefore, we dedicate a section to these generalizations.
The existence analysis is divided into three comparative parts. In the first and second parts, we utilize the Schauder and Banach fixed-point theorems, respectively. In the third part, we leverage the completeness of space . While the Banach fixed-point theorem ensures the uniqueness of the solution, other methods only ensure its existence. Therefore, we employ a different approach for proving uniqueness, leveraging the Gronwall inequality. Finally, we establish the continuity of the solution with respect to the initial value, thereby completing the well-posedness analysis for systems of incommensurate fractional differential equations (FDEs).
We encountered several challenges in this analysis due to the varying orders of fractional derivatives in each equation. One issue was the behavior of a maximum of before and after . Another problem was that the was not a monotone function on The innovation in our approach was to address these difficulties by transforming the equations to the interval We applied this method consistently in three parts of our investigation existence, uniqueness, and the dependency of continuity on initial values.
The innovation in our analysis is a major improvement compared with other analyses. First, it omits the restriction on the Lipschitz condition. For example, we no longer require the inequality (20) for well-posedness. Second, it extends the theorem for a global solution on instead of a local solution restricted by the Schauder terminal point (12).
Sophus Lie used symmetric analysis to find explicit solutions for ODEs by reducing the dimension of systems. In their book, Hashemi and Baleanu [19] performed a similar analysis for fractional differential equations. Our results with the invariant graph (self-mapping) as well as the dependency of the solutions to the initial value are fundamental for a better understanding of symmetry analysis.
In Section 2, we demonstrate that is a complete space and present a generalization of the Arzelà–Ascoli theorem. In Section 3 and Section 4, we establish the existence of a solution using the Schauder and Banach fixed-point theorems, respectively. In Section 5, we introduce the weaker conditions, directly. In Section 6, we prove that if a solution exists, it must be unique. In Section 7, we show that the solution continuously depends on the initial condition. Finally, in Section 8, we present an illustrative example.
2. Generalization of Preliminary Theorems on Cartesian Product Space
Most fixed-point theorems and related theorems apply well to subfamilies of but not to subfamilies of the Cartesian product Therefore, we carefully extended these theorems to apply to such spaces.
2.1. Completeness of and Generalization of Arzelà–Ascoli Theorem for Cartesian Space
Let us equip with the uniform/sup norm
We note that sup can be replaced with max, since we work on closed intervals The next theorem shows that this space is complete.
Theorem 1.
The space is complete (a Banach space).
Proof.
We know the space is complete concerning the uniform norm We provide the proof with a component-wise analysis. Suppose is a Cauchy sequence. Then, its components are Cauchy and hence there exists such that It is straightforward to show that which completes the proof. □
For the relative compactness of subfamily we need to generalize the Arzelà–Ascoli theorem for Cartesian spaces. First, we note the following lemma:
Definition 1.
Let G be a compact space. is relatively compact if it is bounded, i.e.,
and it is equicontinuous, i.e., for every there exists a such that
for all and such that
Lemma 1.
Let G be a compact metric space. is bounded and equicontinuous if
are bounded and equicontinuous for all
Proof.
The proof is straightforward. □
2.2. Compactness of Cartesian Product
Tychonoff’s theorem establishes the compactness of the product of compact topological spaces concerning the product topology. However, it is not evident that the product topology is identical to the topology produced with our introduced uniform/max norm. Therefore, we need to establish some theorems related to the studied Cartesian spaces.
Theorem 2
(Generalized Arzelà–Ascoli theorem). Let G be a compact metric space. is relatively compact if and only if it is bounded and equicontinuous concerning the norm .
Proof.
Let () be defined by (8). Then, each is bounded and equicontinuous. Thus, is a relatively compact set by the classical Arzelà–Ascoli theorem. Thus, is compact. Consequently,
Since the cartesian product of compact sets is a compact set, is compact, which completes the proof. □
2.3. Schauder and Banach Fixed-Point Theorems
Theorem 3
(Schauder fixed-point theorem). Let be a Banach space and compact, convex, and nonempty. If is a continuous operator, then it has a fixed point on .
Remark 2.
If is closed and relatively compact, then it is compact.
Theorem 4
(Banach fixed-point theorem). Let be a complete metric space and let be a contraction on Then, has a unique fixed point in
2.4. Transforming into Incommensurate Weakly Singular Volterra Integral Equation
3. Regularity Analysis with the Schauder Fixed-Point Theorem
For simplicity, we define the operator as follows:
and graph as follows:
for a given Supposing it is a simple fact from the real analysis that
is well defined, and Putting and
we define the Schauder terminal point as follows:
where Indeed, we guarantee the existence of a solution on For this aim, let
We have the following lemma on :
Lemma 2.
A mapping is self-mapping on i.e., if
Proof.
We can express the following theorem with the aim of Lemma 1:
Proof.
We show is a relatively compact set. Using Lemma 1, it is enough to show that
are relatively bounded and equicontinuous sets. Let Then, there exists such that and
for all Thus, is relatively bounded. On the other hand, from (10), if then Thus, is equicontinuous. Consequently, by the generalized Arzelà–Ascoli theorem is relatively compact. Since is compact, is compact. Finally, based on the Schauder fixed-point theorem, has a fixed point. □
4. An Existence Result Using the Banach Fixed-Point Theorem
The Banach fixed-point theorem guarantees the existence of a fixed point if the operator is contracting on complete space or Banach subspace. Contractiveness imposes a large restriction on source functions . Thus, the Banach fixed-point theorem cannot be applied to a large class of FDEs. Despite such restriction, the Banach fixed-point theorem is a constructive theory. It also introduces the solution by
for operator , and it provides unique results. However, we may obtain a better result for initial value problems without the Banach fixed-point theorem; for boundary value problems, the use of this theorem is inevitable in existence analysis. This section is devoted to the existence results based on the Banach fixed-point theorem. Using Equation (16), we know that and is a complete metric space by the induced metric of the norm . Thus, to provide the existence of a unique solution, we prove that is a contractive operator. Throughout this paper, we suppose
(HL) satisfies Lipschitz condition, i.e.,
Furthermore, we suppose
Theorem 6.
Proof.
Let Then,
and
Consequently,
Therefore, from Equation (20), it follows that is a contractive operator, and it has a unique fixed point. □
5. Existence Results with the Weaker Lipschitz Conditions
The Schauder fixed point guaranteed the existence of a solution in the restricted interval and the Banach fixed-point theorem guaranteed the existence of a unique solution on a restricted class of functions with smaller Lipschitz conditions. However, we know that for the second kind of weakly singular integral equations, the kernel’s Lipschitz continuity is enough to guarantee the existence of a unique solution. Thus, we may try direct methods for providing existing results. Let It is well defined since is continuous on In the next theorem, we prove the existence of a solution on [0, 1].
Theorem 7.
Suppose satisfies Condition (HL). Then, the incommensurate system (10) has a solution
Proof.
Suppose for For a sequence of functions obtained with (19), we have
From (22), we have
Similarly, there exists for such that
Let . Obviously, and for . Therefore,
Thanks to the fact that is increasing function for , and we can write
and hence by similar induction,
It follows from (10) that for all
However, it is obvious that the series
is a truncation of the Mittag–Leffler function [2]. Knowing the fact that the Mittag–Leffler function is the entire function [20], for each there exists such that for all and
and hence for all
Thus,
Therefore, is a Cauchy sequence in and there exists such that
Since
it is a matter of real analysis (uniform convergence theorem for fractional integrals) to show that
and hence
□
Theorem 8.
Suppose () satisfies Condition (HL). Then, the system of incommesurate FDEs (10) has a solution on
Proof.
From Theorem 7, System (10) has a solution on , say . We extend this solution on , ,..., . Here, we provide the proof for but the rest is similar. Suppose Then, System (10) can be written as follows:
Since for System (28) can be written as
Substituting , we obtain
and substituting and , we obtain
Renaming and we can write
Owing to Equation (29), it has a unique solution on by Theorem 7. □
Finally, we can extend our result to
Corollary 1.
Suppose satisfies Condition (HL). Then, the system of incommesurate FDEs (10) has a solution on
Proof.
Since in the previous theorem was arbitrary, the proof is straightforward. □
6. Uniqueness of the Solutions Based on Gronwall Inequality
The existence based on the Banach fixed-point theorem guarantees the uniqueness of solutions. However, other existence analyses in this paper do not guarantee the uniqueness of the solution. One of the modern mathematical methods to provide uniqueness theorems is to use Gronwall-type inequalities. Many extensions of Gronwall-type inequalities for fractional and weakly singular integrals are available in the literature [21,22]. Most of them can be applied here. We use the theorem established in [21].
Theorem 9
(Gronwall inequality). Let α and be positive numbers, and be a non-negative and locally integrable on , satisfying
Then,
where is the Mittag–Leffler function.
Theorem 10.
Suppose satisfies the condition Then, System (10) has a unique solution on
Proof.
The existence of a solution for system (10) on follows from Theorem (8). Suppose and are two solutions of System (10). Then, from
and from Hypothesis (HL), Equation (30) can be written as follows:
Since the right-hand side of System (31) is positive, we can write the following:
for . Suppose hence, for and
Therefore, by putting
we get
for Thus,
Setting and applying the Gronwall inequality, we obtain
Thus, for all and System (10) has a unique solution on . Now, we continue the proof on the interval The inequality (32) can be written as follows:
on Let us use our previous strategy. By substituting and () in (34), we obtain
Assume Thus,
Taking the maximum and defining
we obtain
It immediately results in and hence, for By a similar induction, for all , and thus □
7. Continuous Dependency to Initial Values
Let us emphasize the dependency of the solution on the initial value by the solution map In this section, we show that small changes in result in small changes in the solution . This means that the solution map is continuous with respect to the initial value. The next theorem explains this in detail.
Theorem 11.
Suppose () satisfies the condition (HL). Then, the solutions of System (5) are Lipschitz continuous conditions with respect to the initial values.
Proof.
Let and satisfy System (5). Then,
for and thus
Supposing
and
We obtain
Therefore, it follows from the Gronwall inequality that
In particular,
Now, suppose From Equation (36), we have
Substituting and in Equation (37), we obtain
for Thus,
and from the Gronwall inequality,
Rewriting with respect to we obtain
Similarly, inductions result in
for and
if is not an integer. Finally, setting
we obtain
which shows the solution of System (5) continuously depends on initial values. □
8. An Illustrative Example
The modeling of applied problems with commensurate FDEs has been extensively used in diverse branches of science. Inevitably, incommensurate FDEs will receive the same attention by increasing research on this topic and a better understanding of the concept of “memory”. Recently, incommensurate FDEs have been used in the structure of fractional Hopfield neural networks (FHNNs) [23,24]. In the following example, we incorporate our analysis into such systems.
Example 1
([23]). Consider a 3-D FHNN
where for (). Since
and for it is clear that values are Lipschitz continuous functions with respect to Indeed, condition (HL) satisfies with
Thus, based on Theorem 10, Equation (45) has a unique solution for all initial values Moreover, based on Theorem 11, the solution of Equation (45) is a Lipschitz continuous function with respect to the initial value
9. Conclusions
We applied the Schauder and Banach fixed-point theorems to provide existence results for systems of incommensurate FDEs. The Schauder fixed-point theorem guarantees the existence in a restrictive interval (the Schuader terminal point ), while the Banach fixed-point theorem limits the Lipschitz constant by condition (20). We could extend the result for any interval and continuous function that satisfies the Lipschitz condition. For this aim, we notice that the sequence of functions obtained by Picard iteration (19) is a Cauchy sequence on Thus, it is convergent on Indeed, we showed that the limit of this sequence is a solution. Then, we transformed the problem on into the same kind of problem on and thus guaranteed the solution on using the previous theorem. Similarly, we guaranteed the existence of a solution without extra conditions on Lipschitz constant on
One may wonder how to prove that obtained from (19) is a Cauchy sequence on However, the truth is that the behaves differently on and (see Figure 1). Therefore, we need different analyses for incommensurate FDEs, since it creates bifurcations that become larger and larger in other sequences, thus making the analysis complex and cumbersome. We should also note that the is not monotone on This brings another complexity to the analysis. Consequently, we solved these issues by transforming the incommensurate FDEs into a weakly singular Volterra integral equation on .
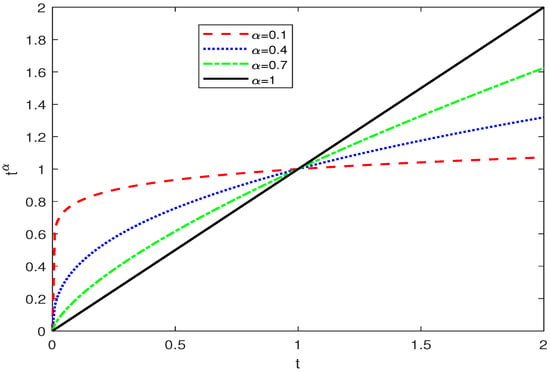
Figure 1.
for and for .
We applied the Gronwall inequality in combination with our suggested method to provide uniqueness and the dependency of the solution to the initial values. For general readers, the obtained theorems in this paper can be summarized and simplified as follows:
Theorem 12.
Let be Lipschitz continuous functions with respect to and . Then, the initial value problem for the system of incommensurate FDEs (1) has a unique solution, and the solution is continuous with respect to the initial values.
Theorem 12 generalizes well-posedness theorems for commensurate FDEs. Incommensurate FDEs are not studied systematically, and few papers are devoted to this particular topic. This topic should be further developed in many basic directions. For example, the analysis of existing positive solutions and the introduction of efficient numerical methods for this topic are rare, while there are numerous applications. We devote our time to this topic in future publications.
Author Contributions
Conceptualization, B.S. and D.B.; Methodology, B.S.; Validation, Y.-G.S. and D.B.; Formal analysis, Y.-G.S.; Investigation, B.S.; Resources, Y.-G.S.; Writing—original draft, B.S.; Supervision, D.B.; Funding acquisition, Y.-G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSF of Sichuan Province supporting Yong-Guo Shi, grant number 2023NSFSC0065.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Diethelm, K.; Ford, N.J. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Daftardar-Gejji, V.; Babakhani, A. Analysis of a system of fractional differential equations. J. Math. Anal. Appl. 2004, 293, 511–522. [Google Scholar] [CrossRef]
- Drapaca, C.S. A mathematical investigation of sex differences in Alzheimer’s disease. Fractal Fractional 2022, 6, 457. [Google Scholar] [CrossRef]
- Baleanu, D.; Shiri, B. Generalized fractional differential equations for past dynamic. AIMS Math. 2022, 7, 14394–14418. [Google Scholar] [CrossRef]
- Shiri, B.; Baleanu, D. Numerical solution of some fractional dynamical systems in medicine involving non-singular kernel with vector order. Results Nonlinear Anal. 2019, 2, 160–168. [Google Scholar]
- Das, S.; Gupta, P.K. A mathematical model on fractional Lotka–Volterra equations. J. Theor. Biol. 2011, 277, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tavazoei, M.; Asemani, M.H. On robust stability of incommensurate fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105–344. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Huang, J.; Gorbachev, S.; Aravind, R.V. Exploration on bifurcation for an incommensurate five-neuron fractional-order BAM neural network involving multiple delays. Phys. D Nonlinear Phenom. 2024, 460, 134047. [Google Scholar] [CrossRef]
- Yu, C.; Gao, G. Existence of fractional differential equations. J. Math. Anal. Appl. 2005, 310, 26–29. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. Analysis of a system of nonautonomous fractional differential equations involving Caputo derivatives. J. Math. Anal. Appl. 2007, 328, 1026–1033. [Google Scholar] [CrossRef]
- Zhang, S. The existence of a positive solution for a nonlinear fractional differential equation. J. Math. Anal. Appl. 2000, 252, 804–812. [Google Scholar] [CrossRef]
- Sheng, Y.; Zhang, T. The existence theory of solution in Sobolev space for fractional differential equations. Appl. Math. Lett. 2024, 149, 108896. [Google Scholar] [CrossRef]
- Saha, K.K.; Sukavanam, N.; Pan, S. Existence and uniqueness of solutions to fractional differential equations with fractional boundary conditions. Alex. Eng. J. 2023, 72, 147–155. [Google Scholar] [CrossRef]
- Matar, M.M.; Samei, M.E.; Etemad, S.; Amara, A.; Rezapour, S.; Alzabut, J. Stability Analysis and Existence Criteria with Numerical Illustrations to Fractional Jerk Differential System Involving Generalized Caputo Derivative. Qual. Theory Dyn. Syst. 2024, 23, 111. [Google Scholar] [CrossRef]
- Kou, C.; Zhou, H.; Yan, Y. Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis. Nonlinear Anal. Theory Methods 2011, 74, 5975–5986. [Google Scholar] [CrossRef]
- Turan, N.; Başarır, M.; Şahin, A. On the solutions of a nonlinear system of q-difference equations. Bound. Value Probl. 2024, 2024, 92. [Google Scholar] [CrossRef]
- Turan, N.; Başarır, M.; Şahin, A. On the solutions of the second-order (p, q)-difference equation with an application to the fixed-point theory. AIMS Math. 2024, 9, 10679–10697. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Baleanu, D. Lie Symmetry Analysis of Fractional Differential Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Paneva-Konovska, J. Series in Mittag-Leffler functions: Inequalities and convergent theorems. Fract. Calc. Appl. Anal.s 2010, 13, 403–414. [Google Scholar]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Webb, J.R. Weakly singular Gronwall inequalities and applications to fractional differential equations. J. Math. Anal. Appl. 2019, 471, 692–711. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Karoun, R.C.; Ouannas, A.; Horani, M.A.; Grassi, G. The effect of Caputo fractional variable difference operator on a discrete-time hopfield neural network with non-commensurate order. Fractal Fract. 2022, 6, 575. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).