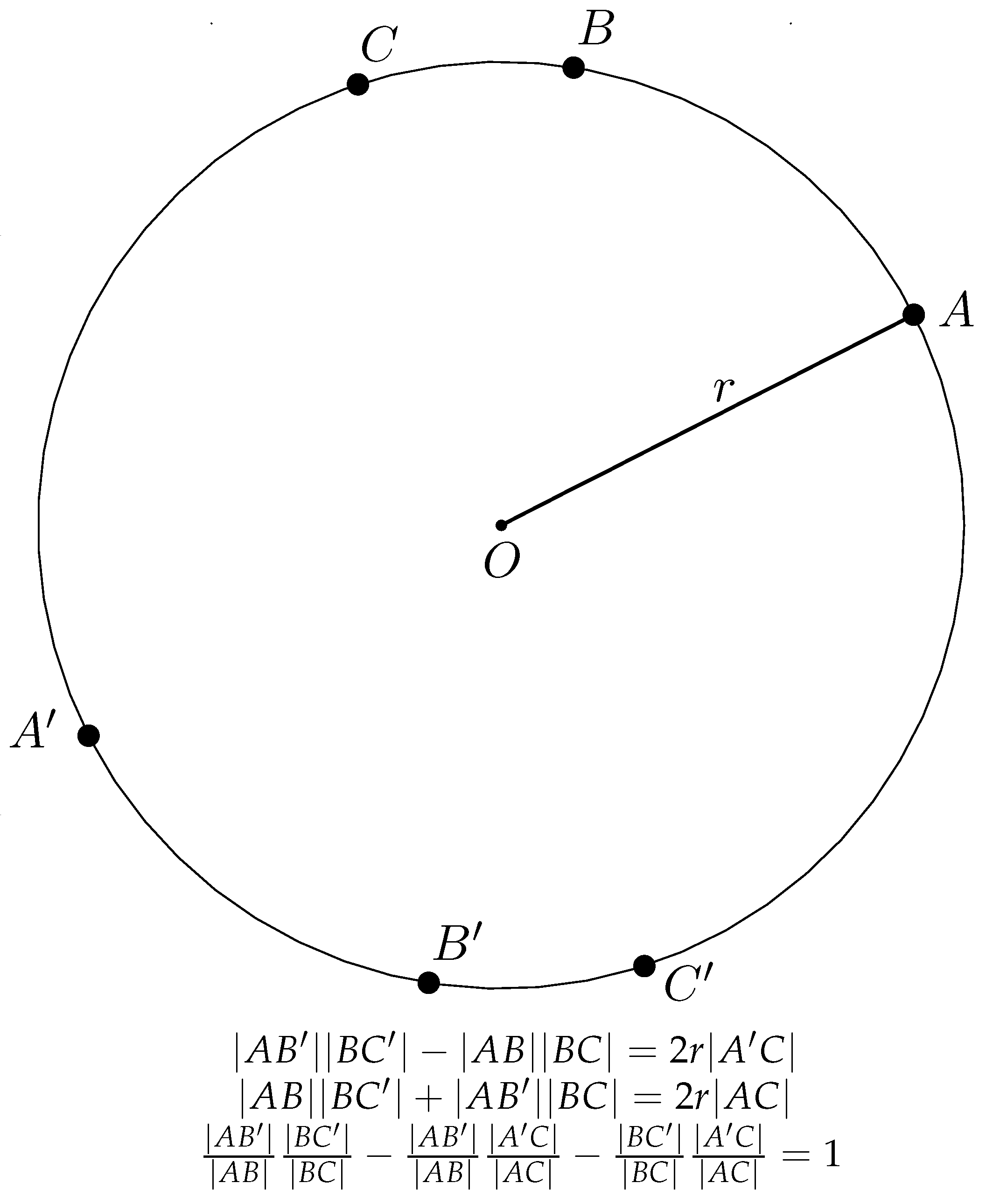1. Introduction
Einstein addition of relativistically admissible velocities, described in
Section 4, is neither commutative nor associative. Rather, it is both
gyrocommutative and
gyroassociative, giving rise to
gyrogroups,
gyrovector spaces and
gyrotrigonometry, which are fully analogous to groups, vector spaces and trigonometry, respectively. Einstein gyrovector spaces, in turn, form the algebraic setting for the Klein ball model of hyperbolic geometry, just as Euclidean vector spaces form the algebraic setting for the standard model of Euclidean geometry. Thus, in the resulting gyrolanguage, we prefix a gyro to terms that describe concepts in Euclidean geometry and algebra to mean the analogous concepts in hyperbolic geometry and nonassociative algebra. The prefix gyro stems from Thomas gyration, which is, in turn, the mathematical abstraction of a special relativistic effect known as Thomas precession. An attractive review of gyrogroups, gyrovector spaces and gyrotrigonometry, which stem from Einstein addition, is presented in [
1] (Sections 2–12).
Remarkably, every trigonometric identity in analytic Euclidean geometry can be viewed as a gyrotrigonometric identity in analytic hyperbolic geometry as well. The resulting
trigonometric–gyrotrigonometric duality plays an important role in this paper and is reviewed in [
1] (Section 11).
A trigonometric identity made up of sines of half angles is said to be
half-angled in trigonometry if viewed in Euclidean geometry or
half-gyroangled in gyrotrigonometry if viewed in hyperbolic geometry. Thus, for instance, the trigonometric identities (
1), (
4) and (
47) are half-angled when viewed in Euclidean geometry, and are half-gyroangled gyrotrigonometric identities when viewed in hyperbolic geometry. The importance of half-angled trigonometric identities in this article rests on the result that, simultaneously, they can be realized geometrically in both Euclidean and hyperbolic geometry. An iconic example is provided by the study of Ptolemy’s Theorem in both Euclidean and hyperbolic geometry in [
1,
2]. The present work is a continuation of the study in [
1] and, as such, is motivated by the study in [
1]. Accordingly, for a fruitful reading of this article, familiarity with [
1] is required.
The study of Ptolemy’s Theorem
- (1)
in Euclidean geometry in [
1];
- (2)
in the relativistic model of hyperbolic geometry in [
1];
- (3)
in the Poincaré ball model of hyperbolic geometry in [
2]
stems from the geometric realization of the half-angled trigonometric identity (or, simultaneously, the half-gyroangled gyrotrigonometric identity)
for any
such that
. Identity (
1) is viewed both trigonometrically (that is, within the framework of trigonometry) and gyrotrigonometrically (that is, within the framework of gyrotrigonometry). The resulting duality of trigonometry and gyrotrigonometry is reviewed in [
1] (Section 11).
Thus, remarkably, (
1) gives rise simultaneously to the Euclidean and to the hyperbolic Ptolemy’s Theorem, as shown in [
1], where the novel hyperbolic Ptolemy’s Theorem is established along with its well-known Euclidean counterpart.
Trigonometric identities are commonly viewed in analytic Euclidean geometry. However, they can be viewed in analytic hyperbolic geometry as well, where they are said to be
gyrotrigonometric identities, as explained in [
1]. Accordingly, if viewed in hyperbolic geometry, (
1) is said to be a
half-gyroangled gyrotrigonometric identity. Furthermore, we note the following observations in [
1,
2]:
- (1)
It is shown in [
1] that if viewed in Euclidean geometry, the half-angled trigonometric identity (
1) gives rise to the well-known Ptolemy’s Theorem in Euclidean geometry.
- (2)
It is shown in [
1] that if viewed in the relativistic model of hyperbolic geometry, the half-gyroangled gyrotrigonometric identity (
1) gives rise to the novel hyperbolic Ptolemy’s Theorem in the relativistic model of hyperbolic geometry. Remarkably, the relativistic model of hyperbolic geometry, in turn, is identical to the well-known Klein model of hyperbolic geometry [
3].
- (3)
It is shown in [
2] that if viewed in the Poincaré ball model of hyperbolic geometry, the half-gyroangled gyrotrigonometric identity (
1) gives rise to the novel hyperbolic Ptolemy’s Theorem in the Poincaré ball model of hyperbolic geometry.
The study of Ptolemy’s Theorem in both Euclidean geometry (where we recover the well-known Ptolemy’s Theorem) and hyperbolic geometry (where we discover a novel hyperbolic Ptolemy’s Theorem), presented in [
1,
2], is based on the geometric realization of the half-angled trigonometric identity (
1). The success of the process of geometric realization of a half-angled trigonometric identity simultaneously in both Euclidean and hyperbolic geometry in [
1,
2] motivates the exploration of the geometric realization of various half-angled trigonometric identities simultaneously in both Euclidean and hyperbolic geometries. To stimulate the exploration of geometric realization of half-angled trigonometric identities, in this article, we explore the geometric realization of the half-angled trigonometric identities (
4) and (
47).
Accordingly, the study of cyclic antipodal pairs in this article is based on the geometric realization of the half-angled trigonometric identity (
4). According to the
trigonometry–gyrotrigonometry duality, identity (
4) is simultaneously viewed both
- (1)
within the framework of trigonometry, as a half-angled trigonometric identity in Euclidean geometry;
- (2)
within the framework of gyrotrigonometry, as a half-gyroangled gyrotrigonometric identity in hyperbolic geometry.
As explained in [
1], a
gyroangle is a hyperbolic angle and
gyrotrigonometry is the hyperbolic trigonometry in the novel discipline known as
analytic hyperbolic geometry [
1,
4].
Any half-angled trigonometric identity admits a geometric realization in both Euclidean geometry and hyperbolic geometry. In this article, identity (
4) is realized geometrically (i) in Euclidean geometry, giving rise to the Four Cyclic Antipodal Pairs Theorem 1 in the Euclidean plane, and (ii) in hyperbolic geometry, giving rise to the Four Gyrocyclic Antipodal Pairs Theorem 2 in the relativistic model of the hyperbolic plane.
Finally, (i) in
Section 8, we realize geometrically the half-angled trigonometric identity (
47) in Euclidean geometry, obtaining the well known Euclidean Pythagorean identity; (ii) in
Section 9, we realize geometrically the half-gyroangled gyrotrigonometric identity (
47) in the relativistic model of hyperbolic geometry, obtaining a novel hyperbolic Pythagorean identity in Theorem 3.
2. Four Cyclic Antipodal Pairs
A cyclic antipodal pair of a circle in a Euclidean plane
is a pair
of points
that are the intersection of the circle with a diameter of the circle. Illustrating Theorem 1, a circle with four cyclic antipodal pairs is depicted in
Figure 1. The Euclidean distance
between two points
is given by
Equivalently,
is the Euclidean length of the segment
that joins points
A and
B. Contrastingly, in the context of hyperbolic geometry,
is a corresponding hyperbolic length, called
gyrolength, as in (
31).
Theorem 1. (A Four Cyclic Antipodal Pairs Theorem). Let be a circle in the Euclidean plane with radius r, centered at the origin , with four cyclic antipodal pairs , , and , such that the eight points are arbitrarily ordered counterclockwise (or clockwise), as shown in Figure 1. Then, the four cyclic antipodal pairs satisfy the identity Proof. Clearly, .
The proof of the theorem is based on the elegant half-angled trigonometric identity
which holds for all
that satisfy the condition
Noting that
, the trigonometric identity in (
4) and (
5) can readily be verified. When realized geometrically in
Figure 1, this trigonometric identity reveals its unexpected grace and elegance.
In order to realize (
4) and (
5) geometrically by a circle with four cyclic antipodal pairs in the Euclidean plane, shown in
Figure 1, we define the four
O-vertex angles in
Figure 1 as follows:
We note that
, as required by Condition (
5), since the points
are ordered counterclockwise.
Then, consequently, the remaining three
O-vertex angles in
Figure 1 are
Applying the law of cosines to triangle AOB in
Figure 1 yields
so that
Similarly to (
9), by means of (
6) and (
7), we obtain the following seven results for angles shown in
Figure 1:
The proof of the first equation in (
10) is given by Equation (
9) in triangle AOB in
Figure 1. The proof of each of the remaining equations in (
10) is similar.
Substituting the sines in (
10) into the half-angled trigonometric identity (
4) yields (
3), as desired. □
We say that (
3) realizes the half-angled trigonometric identity (
4) geometrically in the Euclidean plane.
The proof of Theorem 1 is motivated by the proof of Ptolemy’s Theorem in [
1]. In [
1,
2], Ptolemy’s Theorem is extended to hyperbolic geometry. Similarly, Theorem 1 can be extended to hyperbolic geometry as well, as we will see in
Section 6.
3. Special Cases
In the special case when
and, hence,
, the result (
3) of Theorem 1 descends to
Noting that
and
, (
11) yields
Formalizing the result in (
12), we obtain the result (
17) of Corollary 1.
In a second special case, when
and, hence,
, the result (
3) of Theorem 1 descends to
Equation (
13) gives rise to the elegant equation
Equation (
14) gives rise to the inequalities
and
Formalizing, we have the following Corollary.
Corollary 1. (A Three Cyclic Antipodal Pairs Theorem).
Let be a circle in the Euclidean plane with radius r, centered at , with three cyclic antipodal pairs , and . The six points are arbitrarily ordered counterclockwise (or clockwise), as shown in Figure 2. Proof. Equations (
17) and (
18) are proved, respectively, in (
12) and (
14). Equation (
19) follows from (
17) and (
18) by eliminating the term
between these two equations. □
In order to recover the Pythagorean theorem, we consider (
17) and (
19) in the special case when
and, hence,
. In this special case, (
17) descends to
implying
and (
19) descends to
Equations (
21) and (
22) recover the Pythagorean theorem
for right-angled triangles
, where
and
are any distinct pairs of cyclic antipodal pairs.
4. Einstein Addition, Gyrogroups, Gyrovector Spaces and the
Relativistic Model of Hyperbolic Geometry
In this section, we set the stage for the extension of Theorem 1 from Euclidean geometry to the relativistic model of hyperbolic geometry. The relativistic model of hyperbolic geometry, in turn, stems from Einstein addition, and is identical to the well-known Klein model of hyperbolic geometry [
3,
4].
Einstein addition
is a binary operation in the
s-ball
of the Euclidean
n-space
,
(
in physical applications), where
is an arbitrarily fixed positive constant that in physical applications represents the vacuum speed of light
. Einstein addition ⊕ is given by equation [
5] (p. 55)
for all
, where
is the gamma factor
For later reference, we note that it follows from (
26) that
so that
and, hence,
Einstein addition (
25) of relativistically admissible velocities was introduced by Einstein in his 1905 paper that founded the special theory of relativity, as explained in [
1].
Seemingly structureless, Einstein addition is neither commutative nor associative. Therefore, as F. Chatelin noted [
6], Einstein addition of 3-velocities (representing relativistically admissible velocities) was fully inconceivable: Einstein’s vision was greatly ahead of its time. A more understandable version of Special Relativity was conceived by Minkowski in 1907 by dressing up the Lorentz transformation group as a physical concept. This is the version adopted until today in physics textbooks. Einstein’s intuition was left dormant for 83 years until it was brought back to a new mathematical life in the seminal papers [
7,
8].
Since 1988, the author has crafted an algebraic language for hyperbolic geometry, which sheds a natural light on the physical theory of Special Relativity. In the resulting language, one prefixes a gyro to a classical term to mean the analogous term in hyperbolic geometry. As an example, the relativistic gyrotrigonometry of Einstein’s Special Relativity is developed in [
4] and employed to the study of the stellar aberration phenomenon in astronomy.
Being both gyrocommutative and gyroassociative, Einstein addition encodes a novel group-like object called a gyrogroup. Gyrogroup theory shares important analogies with group theory, as shown, for instance, in [
9,
10]. As such, Einstein addition provides a velocity–symmetry approach to special relativity theory.
Some gyrocommutative gyrogroups admit scalar multiplication, giving rise to gyrovector spaces. Einstein (Möbius) gyrovector spaces form the algebraic setting for the Klein (Poincaré) ball model of hyperbolic geometry with spectacular gains in clarity and simplicity, just as vector spaces form the algebraic setting for Euclidean geometry. In our work, the Poincaré ball model of hyperbolic geometry stems from
Möbius addition [
2] and the Klein model of hyperbolic geometry stems from Einstein addition [
1]. Hence, when studied analytically by means of Einstein addition, we refer to the Klein model as the relativistic model.
Each Einstein gyrovector plane and Möbius gyrovector plane admits its own gyrotrigonometry, which is fully analogous to the familiar trigonometry in the Euclidean plane.
An attractive review of gyrogroups, gyrovector spaces and gyrotrigonometry that Einstein addition encodes is available in [
1] (Sections 2–12). Familiarity with this review is necessary for a fruitful reading of the sequel.
5. The Law of Gyrocosines in the Relativistic Model of
Hyperbolic Geometry
The proof of Theorem 1 is based on the law of cosines of trigonometry. Accordingly, for translating Theorem 1 from Euclidean geometry into the relativistic model of hyperbolic geometry, we consider the law of gyrocosines of gyrotrigonometry in the relativistic model of hyperbolic geometry, which is reviewed in [
1] (Section 12).
Let
be a gyrotriangle in an Einstein gyrovector space
along with its standard notation shown in [
1] (Figure 4). According to [
11] (Section 7.3), the gyrotriangle
obeys the following three identities, each of which represents its
law of gyrocosines,
The elements
;
,
and
; and the gyroangles
in the law of gyrocosines (
30) are defined in [
1] (Figure 4)—that is,
,
,
. The gamma factors in (
30) are defined in (
26),
,
.
Note that
in (
30) is the
function of gyrotrigonometry, defined in [
1] (Equation (
35)) and illustrated in [
1] (Figure 3). The use of the symbol
to represent both (i) the cosine function of trigonometry and (ii) the gyrocosine function of gyrotrigonometry is justified by means of the
trigonometry–gyrotrigonometry duality, explained in [
1] (Section 11).
In
Section 2,
Figure 1 depicts a circle in a Euclidean plane
, along with its eight points
. Accordingly,
Figure 1 is viewed in a Euclidean plane.
In contrast, in this section, the same
Figure 1 is viewed in the relativistic model of a hyperbolic plane. As such, it depicts a gyrocircle in a hyperbolic plane
, along with its eight points
.
In full analogy with (
2), in the context of the relativistic model of hyperbolic geometry, we use the notation
for any
, where ⊕ denotes Einstein addition (
25) in
(reviewed in [
1]) and where
is the inverse of
A. Here,
represents the gyrodistance between
A and
B—that is, the hyperbolic distance between
A and
B in the relativistic model. Equivalently,
is the gyrolength of the gyrosegment
that joins the points
A and
B.
It should be noted that in the Euclidean limit,
, the hyperbolic
, given by (
31), descends to the Euclidean
, given by (
2), since
Let
be two points of a gyrocircle with gyroradius
r centered at
, as shown in
Figure 1. The gyroradius of the gyrocircle in
Figure 1 is given by
in the hyperbolic plane regulated by the Einstein gyrovector plane
.
Then, by the law of gyrocosines (
30) applied to gyrotriangle
in
Figure 1, we have
where we use the usual notations
and
,
.
Solving (
33) for
, noting (
27), yields
so that
and, hence,
Hence, finally, by means of (
29) we have
where we define
for any
.
Here, note that and represent the and the functions in the gyrotrigonometry of the relativistic model of hyperbolic geometry.
The result in (
37) is obtained by applying the law of gyrocosines to the
O-gyrovertex gyrotriangle
with the
O-gyrovertex gyroangle
. Expressing (
37) to all the
O-gyrovertex gyroangles in
Figure 1, which are
and
, where
, yields the following seven equations:
The proof of the first equation in (
39) follows from (
37). The proof of each of the remaining equations in (
39) is similar.
Substituting the sines in (
39) into the half-gyroangled gyrotrigonometric identity (
4) yields the equation
We say that (
40) realizes the half-gyroangled gyrotrigonometric identity (
4) geometrically in the relativistic model of the hyperbolic plane.
8. The Pythagorean Theorem Is Recovered
The study of half-angled trigonometric identities is rewarding since they admit geometric realizations associated with
cyclic points—that is, points on a circle—in both Euclidean and hyperbolic geometry. Accordingly, in this section, we explore a simple half-angled trigonometric identity, which we realize in both Euclidean geometry (in this section) and hyperbolic geometry (in
Section 9). Let us consider the trigonometric identity
Noting that
Equation (
45) can be written as a half-angled trigonometric identity,
In order to realize (
47) geometrically in the Euclidean plane, we consider
Figure 1 in a Euclidean plane with only the three points
on the circle
and the associated
O-vertex angles
and
. Then, by (
10),
Substituting the sines in (
48) into the half-angled trigonometric identity (
47) yields
thus recovering the Pythagorean theorem for the right-angled triangle
in
Figure 1 when viewed in a Euclidean plane.
It seems that exploring the half-angled trigonometric identity (
47) is pointless since it yields an expected, well-known result. But, we are not finished. In
Section 9, we will find that identity (
47), when viewed gyrotrigonometrically as a half-gyroangled gyrotrigonometric identity, does yield an interesting novel result in hyperbolic geometry.
9. A Hyperbolic Pythagorean Theorem
In
Section 8, we consider Identity (
47) trigonometrically as a half-angled trigonometric identity and, accordingly, we realize it geometrically in Euclidean geometry. In contrast, in this section, we consider Identity (
47) gyrotrigonometrically as a half-gyroangled gyrotrigonometric identity and, accordingly, we realize it geometrically in hyperbolic geometry. Consequently, in the same way that in
Section 8 we recover from Identity (
47) the well-known Pythagorean Theorem, in this section we discover from Identity (
47) a novel Hyperbolic Pythagorean Theorem. As such, the study in
Section 8 and
Section 9 illustrates the
trigonometry–gyrotrigonometry duality reviewed in [
1].
In order to realize (
47) geometrically in the relativistic model of the hyperbolic plane, we consider
Figure 1 in the relativistic model of the hyperbolic plane, with only the three points
on the gyrocircle
and the associated
O-vertex gyroangles
and
. Then, by (
39),
where
for any
.
Substituting the sines in (
50) into the half-gyroangled gyrotrigonometric identity (
47) yields the equation
It can be shown by means of (
51) and
that
. Hence, (
52) can be written as
for the gyrotriangle
when viewed in a hyperbolic plane, shown in
Figure 1.
Identity (
53) is a novel hyperbolic Pythagorean-like theorem in the relativistic model. A different way to obtain (
53) is presented in [
1] (Equation (63)). Note that the gyrotriangle
, shown in
Figure 1, associated with (
53), is not right-gyroangled. However, as in the Euclidean case, the gyrotriangle
is
gyrodiametric—that is, one of its sides coincides with a gyrodiameter of its circumgyrocircle (see [
1], Figure 7 and [
11], Figure 8.11).
Formalizing the result in (
53), we have the following theorem.
Theorem 3. (A Hyperbolic Pythagorean Theorem).
Let be a gyrotriangle of which the side coincides with a gyrodiameter of its circumgyrocircle in the relativistic model of the hyperbolic plane (Figure 1). Then, Additionally, the hyperbolic version of Theorem 3 in the Poincaré ball model of hyperbolic geometry appears in [
2] (Theorem 3).
10. Conclusions
Gyrotrigonometry is a novel discipline of hyperbolic trigonometry, reviewed in [
1]. Any trigonometric identity (viewed in analytic Euclidean geometry) can be considered as a gyrotrigonometric identity (viewed in analytic hyperbolic trigonometry).
The resulting concept of
trigonometry–gyrotrigonometry duality is reviewed in [
1]. For a fruitful reading of this article, familiarity with [
1] is required.
An iconic result that motivates the results of the present article is provided in [
1], where the famous Ptolemy’s Theorem is established in both Euclidean geometry (where it is well-known) and in hyperbolic geometry (where it is a novel result) by realizing the half-angled trigonometric identity (
1) in both Euclidean geometry and hyperbolic geometry. More specifically, in the iconic example in [
1],
- (1)
we realize the half-angled trigonometric identity (
1) within the framework of Euclidean geometry, obtaining the famous Ptolemy’s Theorem in Euclidean geometry;
- (2)
we realize the same identity (
1) as a gyrotrigonometric identity within the framework of hyperbolic geometry, obtaining the novel hyperbolic Ptolemy’s Theorem.
As in the iconic example of [
1], any half-angled trigonometric identity can be realized geometrically in both Euclidean geometry (as one commonly does) and hyperbolic geometry (as we do in [
1,
2] and in the present article). Hence, following the iconic example, it is interesting to explore the geometric realization in both Euclidean geometry and hyperbolic geometry of any half-angled trigonometric identity. Accordingly, we review the following:
- (1)
In
Section 2, we explore the realization of the half-angled trigonometric identity (
4) in Euclidean geometry, obtaining Theorem 1 along with interesting special cases in
Section 3.
- (2)
In
Section 6 and
Section 7, we explore the realization of the same half-angled trigonometric identity (
4) in hyperbolic geometry, obtaining Theorem 2;
Section 4 and
Section 5 present the preliminaries necessary for the transition from the Euclidean geometry in
Section 2 to the hyperbolic geometry in
Section 6;
- (3)
In
Section 8 and
Section 9, we explore the realization of the half-angled trigonometric identity (
47) in Euclidean geometry and in hyperbolic geometry, obtaining a hyperbolic Pythagorean identity in Theorem 3.
Finally, based on the methods presented in this article, interested readers can choose any half-angled trigonometric identity and explore its realization in both Euclidean geometry and hyperbolic geometry.