MultiFuzzTOPS: A Fuzzy Multi-Criteria Decision-Making Model Using Type-2 Soft Sets and TOPSIS
Abstract
1. Introduction
- Propose a novel fuzzy decision-making model MultiFuzzTOPS that employs multi-criteria decision-making, fuzzy logic, and soft sets such as type-2 soft sets (T2SS) and technique for order preference by similarity to ideal solution (TOPSIS).
- Optimize the proposed model to increase its accuracy by employing the normalized Hamming distance.
- Implement the proposed model and solve the pesticide selection problem in agriculture and food science.
- Validate the proposed model by comparative analysis.
2. Preliminaries and Literature Review
2.1. Preliminaries
2.1.1. TOPSIS Method
2.1.2. Soft Sets
2.1.3. Type-2 Soft Sets (T2SS)
2.2. Literature Review
- The comparison between the decision-making tools is not based on specific criteria that cause a conflict of opinion and inaccurate results.
- In the previous literature, the multi-criteria decision-making problem specified that the chosen parameters could be adjusted, which causes uncertainty due to the increased sample size.
- In the decision-making problem, uncertainty in obtaining weights is adjusted by a subjective and objective strategy. The consistency of the judgment is maintained by using Euclidean distances without taking into account the relationship among the attributes. The Euclidean distance has the disadvantage that it assumes a circular distribution of the sample centroids around the sample mean.
3. Proposed Fuzzy MultiFuzzTOPS Model Using Type-2 Soft Sets with TOPSIS
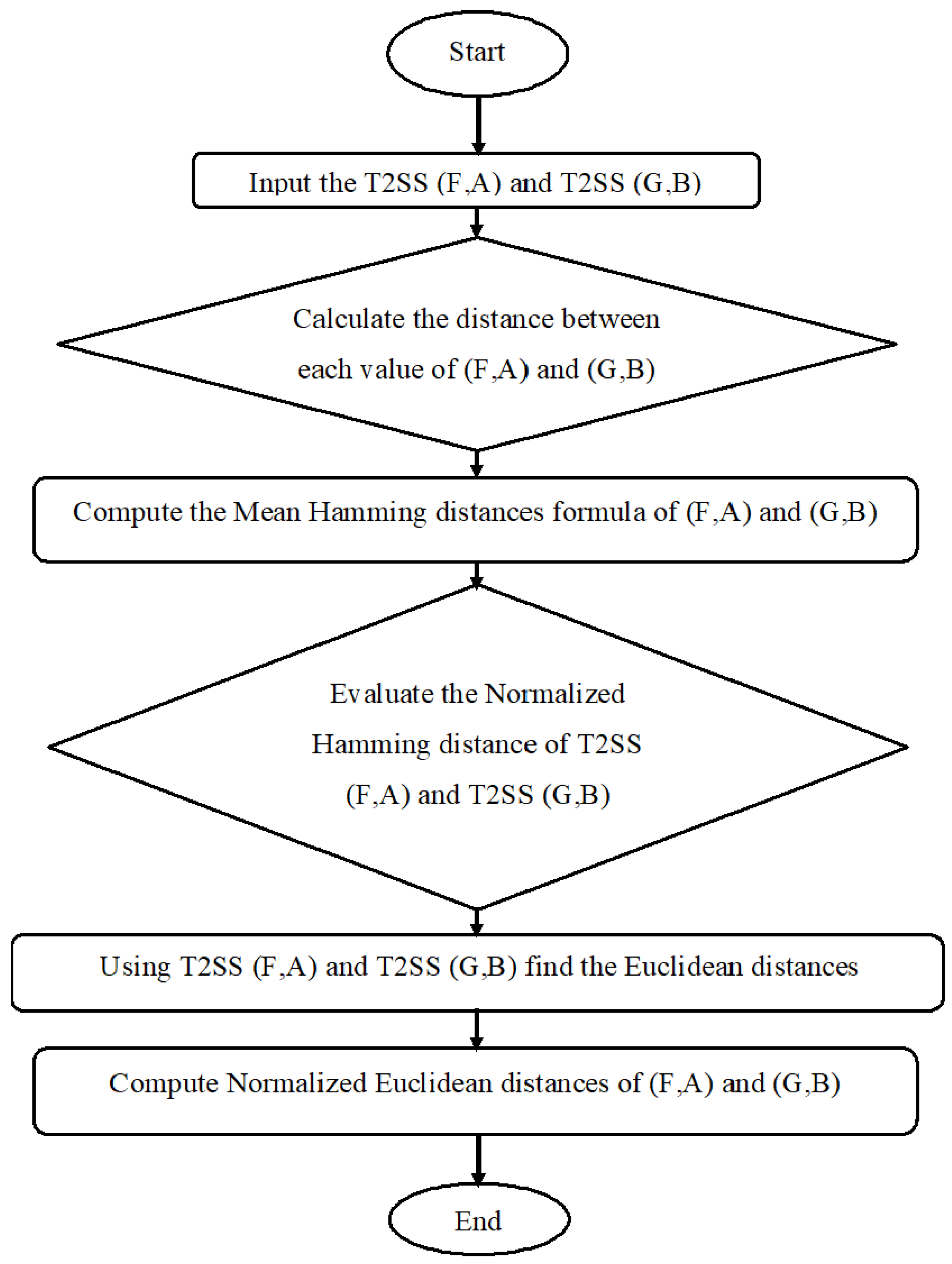
- Step 1:
- Input the T2SS, T2SS, T2SS and T2SS.
- Step 2:
- Compute a tabular representation of the .
- Step 3:
- Construct a weighted decision matrix for each of for the underlying parameters.
- Step 4:
- Compute the weighted decision matrix for each of for the primary parameters.
- Step 5:
- Combine all decision makers’ values in the final table.
- Step 6:
- Determine the positive ideal solution (PIS) and negative ideal solution (NIS).
- Step 7:
- Calculate the normalized Hamming distance.
- Step 8:
- Calculate the scores of alternatives with the help of positive and negative Hamming distances.
- Step 9:
- Rank the alternative by arranging the values in descending order.
3.1. Mathematical Problem Formulation
3.2. Pseudo-Code of the Fuzzy MultiFuzzTOPS Model
4. Numerical Computations
4.1. Selection Criteria
4.2. Implementation Details of Proposed MultiFuzzTOPS
5. Sensitivity and Comparative Analysis of Our Proposed Model
5.1. Sensitivity Analysis
Weights Assigned by the Decision Makers
5.2. Comparative Analysis
6. Real Life Applicability and Limitations of the Proposed Model
6.1. Real Life Applicability of the Proposed Model
6.2. Limitations of the Study
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- García-Zamora, D.; Labella, Á.; Ding, W.; Rodríguez, R.M.; Martínez, L. Large-scale group decision making: A systematic review and a critical analysis. IEEE/CAA J. Autom. Sin. 2022, 9, 949–966. [Google Scholar] [CrossRef]
- Yushuo, C.; Ling, D. A Framework for Assessment of Logistics Enterprises’ Safety Standardization Performance Based on Prospect Theory. J. Oper. Intell. 2024, 2, 153–166. [Google Scholar] [CrossRef]
- Jan, N.; Gwak, J.; Deveci, M.; Simic, V.; Antucheviciene, J. Mathematical analysis of big data analytics under bipolar complex fuzzy soft information. Appl. Soft Comput. 2024, 157, 111481. [Google Scholar] [CrossRef]
- Farooq, D. Application of Pythagorean Fuzzy Analytic Hierarchy Process for Assessing Driver Behavior Criteria Associated to Road Safety. J. Soft Comput. Decis. Anal. 2024, 2, 144–158. [Google Scholar] [CrossRef]
- Akber, S.M.A.; Khan, I.A.; Muhammad, S.S.; Mohsin, S.M.; Khan, I.A.; Shamshirband, S.; Chronopoulos, A.T. Data volume based data gathering in wsns using mobile data collector. In Proceedings of the 22nd International Database Engineering & Applications Symposium, Villa San Giovanni, Italy, 18–20 June 2018; pp. 199–207. [Google Scholar]
- Melek, A.B.; Gökmener, S.; Haspolat, E.; Çiçek, D.D.; Deveci, M.; Oğuz, E.; Khorasanchi, M. Fuzzy Einstein-based decision-making model for the evaluation of site selection criteria of floating photovoltaic system. Ocean Eng. 2024, 301, 117521. [Google Scholar] [CrossRef]
- Sriram, S.; Ramachandran, M.; Chinnasamy, S.; Mathivanan, G. A review on multi-criteria decision-making and its application. REST J. Emerg. Trends Model. Manuf. 2022, 7, 101–107. [Google Scholar]
- Hussain, A.; Liu, Y.; Ullah, K.; Rashid, M.; Senapati, T.; Moslem, S. Decision algorithm for picture fuzzy sets and Aczel Alsina aggregation operators based on unknown degree of wights. Heliyon 2024, 10, e27548. [Google Scholar] [CrossRef] [PubMed]
- Goswami, S.S.; Behera, D.K.; Afzal, A.; Razak Kaladgi, A.; Khan, S.A.; Rajendran, P.; Subbiah, R.; Asif, M. Analysis of a robot selection problem using two newly developed hybrid MCDM models of TOPSIS-ARAS and COPRAS-ARAS. Symmetry 2021, 13, 1331. [Google Scholar] [CrossRef]
- Lodi, A.; Sankaranarayanan, S.; Wang, G. A framework for fair decision-making over time with time-invariant utilities. Eur. J. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A modified CRITIC method to estimate the objective weights of decision criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Ullah, Z.; Elkadeem, M.R.; Wang, S.; Akber, S.M.A. Optimal planning of RDS considering PV uncertainty with different load models using artificial intelligence techniques. Int. J. Web Grid Serv. 2020, 16, 63–80. [Google Scholar] [CrossRef]
- Gulzar, K.; Tariq, O.; Mustafa, S.; Mohsin, S.M.; Kazmi, S.N.; Akber, S.M.A.; Abazeed, M.; Ali, M. A fuzzy analytic hierarchy process for usability requirements of online education systems. IEEE Access 2023, 11, 146076–146089. [Google Scholar] [CrossRef]
- Fan, V.Y. Multi-criteria decision analysis: Of politics, policy entrepreneurs, and processes. Cost Eff. Resour. Alloc. 2018, 16, 50. [Google Scholar] [CrossRef] [PubMed]
- Tsakalerou, M. GE/McKinsey matrices revisited: A mixed mode tool for multi-criteria decision analysis. Eur. J. Cont. Econ. Mgmt. 2015, 2, 92. [Google Scholar] [CrossRef]
- Jepson, P.C. Assessing environmental risks of pesticides. In Integrated Pest Management: Concepts, Strategies, Tactics and Case Studies; Cambridge University Press: Cambridge, UK, 2009; pp. 205–220. [Google Scholar]
- Radcliffe, E.B.; Hutchison, W.D.; Cancelado, R.E. Integrated Pest Management: Concepts, Strategies, Tactics and Case Studies; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Sherratt, T.N.; Jepson, P.C. A metapopulation approach to modelling the long-term impact of pesticides on invertebrates. J. Appl. Ecol. 1993, 30, 696–705. [Google Scholar] [CrossRef]
- Lewis, W.J.; Lenteren, J.C.V.; Phatak, S.C.; Iii, J.H.T. A total system approach to sustainable pest management. Proc. Natl. Acad. Sci. USA 1997, 94, 12243–12248. [Google Scholar] [CrossRef] [PubMed]
- Stern, V.; Smith, R.; van den Bosch, R.; Hagen, K. The integration of chemical and biological control of the spotted alfalfa aphid: The integrated control concept. Hilgardia 1959, 29, 81–101. [Google Scholar] [CrossRef]
- Chatterjee, R.; Majumdar, P.; Samanta, S.K. Type-2 soft sets. J. Intell. Fuzzy Syst. 2015, 29, 885–898. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.; Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Molodtsov, D. Soft set theory first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Bottani, E.; Rizzi, A. A fuzzy TOPSIS methodology to support outsourcing of logistics services. Supply Chain. Manag. Int. J. 2006, 11, 294–308. [Google Scholar] [CrossRef]
- Ashtiani, B.; Haghighirad, F.; Makui, A.; ali Montazer, G. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar] [CrossRef]
- Ghassemi, S.A.; Danesh, S. A hybrid fuzzy multi-criteria decision making approach for desalination process selection. Desalination 2013, 313, 44–50. [Google Scholar] [CrossRef]
- Balioti, V.; Tzimopoulos, C.; Evangelides, C. Multi-criteria decision making using TOPSIS method under fuzzy environment. Application in spillway selection. Proceedings 2018, 2, 637. [Google Scholar] [CrossRef]
- Gulzar, K.; Sang, J.; Ramzan, M.; Kashif, M. Fuzzy approach to prioritize usability requirements conflicts: An experimental evaluation. IEEE Access 2017, 5, 13570–13577. [Google Scholar] [CrossRef]
- Mustafa, S.; Fatimah, I.; Jun, Y.B. Modelling the logistic processes using fuzzy decision approach. Hacet. J. Math. Stat. 2019, 48, 552–563. [Google Scholar] [CrossRef]
- Mathew, M.; Chakrabortty, R.K.; Ryan, M.J. A novel approach integrating AHP and TOPSIS under spherical fuzzy sets for advanced manufacturing system selection. Eng. Appl. Artif. Intell. 2020, 96, 103988. [Google Scholar] [CrossRef]
- Lathamaheswari, M.; Nagarajan, D.; Kavikumar, J.; Broumi, S. Triangular interval type-2 fuzzy soft set and its application. Complex Intell. Syst. 2020, 6, 531–544. [Google Scholar] [CrossRef]
- Wan, S.; Yuan, H.; Dong, J. Decision making with incomplete interval multiplicative preference relations based on stochastic program and interval category. Inf. Sci. 2021, 570, 403–427. [Google Scholar] [CrossRef]
- Salsabeela, V.; John, S.J. TOPSIS techniques on Fermatean fuzzy soft sets. Aip Conf. Proc. 2021, 2336, 40022. [Google Scholar]
- Chu, T.C.; Le, T.H.P. Evaluating and selecting agricultural insurance packages through an AHP-based fuzzy TOPSIS Method. Soft Comput. 2022, 26, 7339–7354. [Google Scholar] [CrossRef]
- Mng’ong’o, B.G.; RAD, D.; Koloseni, D.; Balas, V.E. Application of fuzzy TOPSIS in assessing performance of agro-processed organic crops: A case of Sustainable Agriculture Tanzania (SAT) in Morogoro. J. Intell. Fuzzy Syst. 2022, 43, 1811–1826. [Google Scholar] [CrossRef]
- Mustafa, S.; Mahmood, S.; Salleh, Z. An application of fuzzy bipolar weighted correlation coefficient in decision-making problem. PLoS ONE 2023, 18, e0283516. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. [Google Scholar]
- Takeuti, G.; Titani, S. Intuitionistic fuzzy logic and intuitionistic fuzzy set theory. J. Symb. Log. 1984, 49, 851–866. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough set theory and its applications. J. Telecommun. Inf. Technol. 2002, 3, 7–10. [Google Scholar] [CrossRef]
- Alefeld, G.; Mayer, G. Interval analysis: Theory and applications. J. Comput. Appl. Math. 2000, 121, 421–464. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. An application of soft sets in a decision making problem. Comput. Math. Appl. 2002, 44, 1077–1083. [Google Scholar] [CrossRef]
- Feng, F.; Jun, Y.B.; Liu, X.; Li, L. An adjustable approach to fuzzy soft set based decision making. J. Comput. Appl. Math. 2010, 234, 10–20. [Google Scholar] [CrossRef]
- Ma, X.; Zhan, J.; Ali, M.I.; Mehmood, N. A survey of decision making methods based on two classes of hybrid soft set models. Artif. Intell. Rev. 2018, 49, 511–529. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Abdal, S.; Maalik, A.; Ali, B.; Zafar, Z.; Ahamad, M.I.; Younas, S.; Mariam, A.; Dayan, F. Application of TOPSIS method in decision making via soft set. Biomed. J. Sci. Tech. Res. 2020, 24, 18208–18215. [Google Scholar]
- Chatterjee, R.; Majumdar, P.; Samanta, S. Distance, entropy and similarity measures of Type-2 soft sets. arXiv 2016, arXiv:1612.06603. [Google Scholar]
- Hayat, K.; Ali, M.I.; Cao, B.Y.; Karaaslan, F. New results on type-2 soft sets. Hacet. J. Math. Stat. 2018, 47, 855–876. [Google Scholar] [CrossRef]

| Study | Publication Year | Technique | Limitation(s) |
|---|---|---|---|
| [26] | 2006 | Fuzzy TOPSIS method for logistic services | The selection tree need to be developed into a multi-tier hierarchy to address the relationships between the upper and lower tier |
| [27] | 2009 | Interval-valued fuzzy TOPSIS method | Proposed MCDM applies to unequal weights. This could introduce bias or skew the results. |
| [45] | 2010 | Soft sets theory to solve a decision problem | Uncertainty in multi-criteria decision-making |
| [28] | 2013 | Fuzzy AHP and TOPSIS methods | Ineffective MCDM process caused by uncertainty because of increased sample size |
| [21] | 2015 | Type-2 soft sets | Relationship among decision-making attributes is not considered |
| [48] | 2016 | Proposed new distance measures | Effectiveness and accuracy of may be a limitation depending on the context of application |
| [30] | 2017 | A new framework using fuzzy logic focusing on mapping attributes of usability requirements | Lack of criteria for the prioritization of conflicting usability requirements attributes |
| [49] | 2018 | Type-2 soft sets using de Morgan’s law | Parameters adjustment affects the multi-criteria decision-making |
| [29] | 2018 | Multi-criteria TOPSIS method under fuzzy along with the analytic hierarchy process | Uncertainty in decision-making |
| [31] | 2019 | Multi-criteria structural model on the basis of logistic processes | Parameters adjustment leads to uncertainty |
| [47] | 2020 | Soft sets and the TOPSIS method | Parameters adjustment leads to uncertainty caused and relationship among attributes is not considered |
| [32] | 2020 | A novel algorithm that integrates AHP and TOPSIS under a spherical fuzzy set | Integration of AHP and TOPSIS with a spherical fuzzy set increases the complexity |
| [33] | 2020 | A triangular interval type-2 fuzzy soft weighted arithmetic operator | Lack of generalization as it is specific to decision-making problems for profit analysis. |
| [34] | 2021 | Decision-making with incomplete interval multiplicative preference relation | Increase in uncertainties as the sample size grows |
| [35] | 2021 | Extend TOPSIS with a Fermatean fuzzy soft set | Lack of any particular criteria for decision-making |
| [36] | 2022 | FAHP algorithm to solve MCDM problems | Does not consider the relationship among attributes |
| [37] | 2022 | Fuzzy TOPSIS method to evaluate the performance of agricultural crops | Increase in sample size leads to uncertainties |
| [38] | 2023 | Bipolar fuzzy sets used to cover the positive and negative aspects of a specific symptom | No specific criteria for decision-making |
| Our | 2024 | Proposed FMCDM using type-2 soft sets with TOPSIS | - |
| Acronym | Description |
|---|---|
| Attributes of primary parameters | |
| Attributes of underlying parameters in type-2 soft sets | |
| Attributes of underlying parameters in type-2 soft sets | |
| Triazoles spray | |
| Strobilurin spray | |
| Mancozeb spray | |
| Propiconazole spray | |
| Primary parameters | |
| P | Production effect |
| T | Time of reaction |
| E | Environment effect |
| Effect on human health | |
| Underlying parameters | |
| s | Soil effect |
| Effect on water | |
| Animal life effect | |
| C | Cost of Sprays |
| T2SS | Type-2 soft sets |
| FMCDM | Fuzzy multi-criteria decision-making |
| TOPSIS | Technique for order preference by similarity to ideal solution |
| MultiFuzzTOPS | A fuzzy multi-criteria decision-making model using type-2 soft sets and TOPSIS |
| Decision Maker 1 () | Decision Maker 2 () | ||||||
|---|---|---|---|---|---|---|---|
| Primary Parameters | Underlying Parameters | Primary Parameters | Underlying Parameters | ||||
| Weights | Weights | Weights | Weights | ||||
| P | 0.4 | S | 0.1 | P | 0.35 | S | 0.45 |
| T | 0.3 | EW | 0.2 | T | 0.45 | EW | 0.25 |
| E | 0.1 | AL | 0.5 | E | 0.1 | AL | 0.01 |
| EH | 0.2 | C | 0.3 | EH | 0.1 | C | 0.29 |
| Decision Maker 3 () | Decision Maker 4 () | ||||||
| Primary Parameters | Underlying Parameters | Primary Parameters | Underlying Parameters | ||||
| Weights | Weights | Weights | Weights | ||||
| P | 0.5 | S | 0.7 | P | 0.55 | S | 0.2 |
| T | 0.35 | EW | 0.01 | T | 0.2 | EW | 0.8 |
| E | 0.05 | AL | 0.1 | E | 0.04 | AL | 0.22 |
| EH | 0.1 | C | 0.19 | EH | 0.21 | C | 0.5 |
| Weights | 0.1 | 0.2 | 0.5 | 0.3 | |
|---|---|---|---|---|---|
| Sprays/Underlying Parameters | S | EW | AL | C | Scores |
| 0 | 1 | 0 | 0 | 0.2 | |
| 0 | 0 | 1 | 0 | 0.5 | |
| 1 | 0 | 0 | 0 | 0.1 | |
| 0 | 1 | 0 | 0 | 0.2 |
| Weights | 0.45 | 0.25 | 0.01 | 0.29 | |
|---|---|---|---|---|---|
| Sprays/Underlying Parameters | S | EW | AL | C | Scores |
| 0 | 0 | 1 | 0 | 0.01 | |
| 0 | 1 | 0 | 0 | 0.25 | |
| 0 | 1 | 0 | 0 | 0.25 | |
| 0 | 0 | 0 | 1 | 0.29 |
| Weights | 0.7 | 0.01 | 0.1 | 0.19 | |
|---|---|---|---|---|---|
| Sprays/Underlying Parameters | S | EW | AL | C | Scores |
| S1 | 0 | 0 | 0 | 1 | 0.19 |
| S2 | 1 | 0 | 0 | 0 | 0.7 |
| S3 | 0 | 0 | 1 | 0 | 0.1 |
| S4 | 0 | 0 | 1 | 0 | 0.1 |
| Weights | 0.2 | 0.8 | 0.22 | 0.5 | |
|---|---|---|---|---|---|
| Sprays/Underlying Parameters | S | EW | AL | C | Scores |
| S1 | 1 | 0 | 0 | 0 | 0.2 |
| S2 | 0 | 0 | 1 | 0 | 0.22 |
| S3 | 0 | 0 | 1 | 1 | 0.72 |
| S4 | 1 | 0 | 0 | 0 | 0.2 |
| Sprays/Decision Maker | D1 | D2 | D3 | D4 |
|---|---|---|---|---|
| 0.19 | 0.8855 | 0.1045 | 0.347 | |
| 0.37 | 0.3565 | 0.6655 | 0.457 | |
| 0.26 | 0.4055 | 0.195 | 0.5142 | |
| 0.3 | 0.9395 | 0.1135 | 0.3098 |
| Sprays | PIS | NIS |
|---|---|---|
| 0.8855 | 0.1045 | |
| 0.6655 | 0.3565 | |
| 0.5142 | 0.195 | |
| 0.9395 | 0.1135 |
| Sprays | HPD | HND |
|---|---|---|
| 0.031484 | 0.017328 | |
| 0.012703 | 0.006609 | |
| 0.010658 | 0.009292 | |
| 0.032738 | 0.018888 |
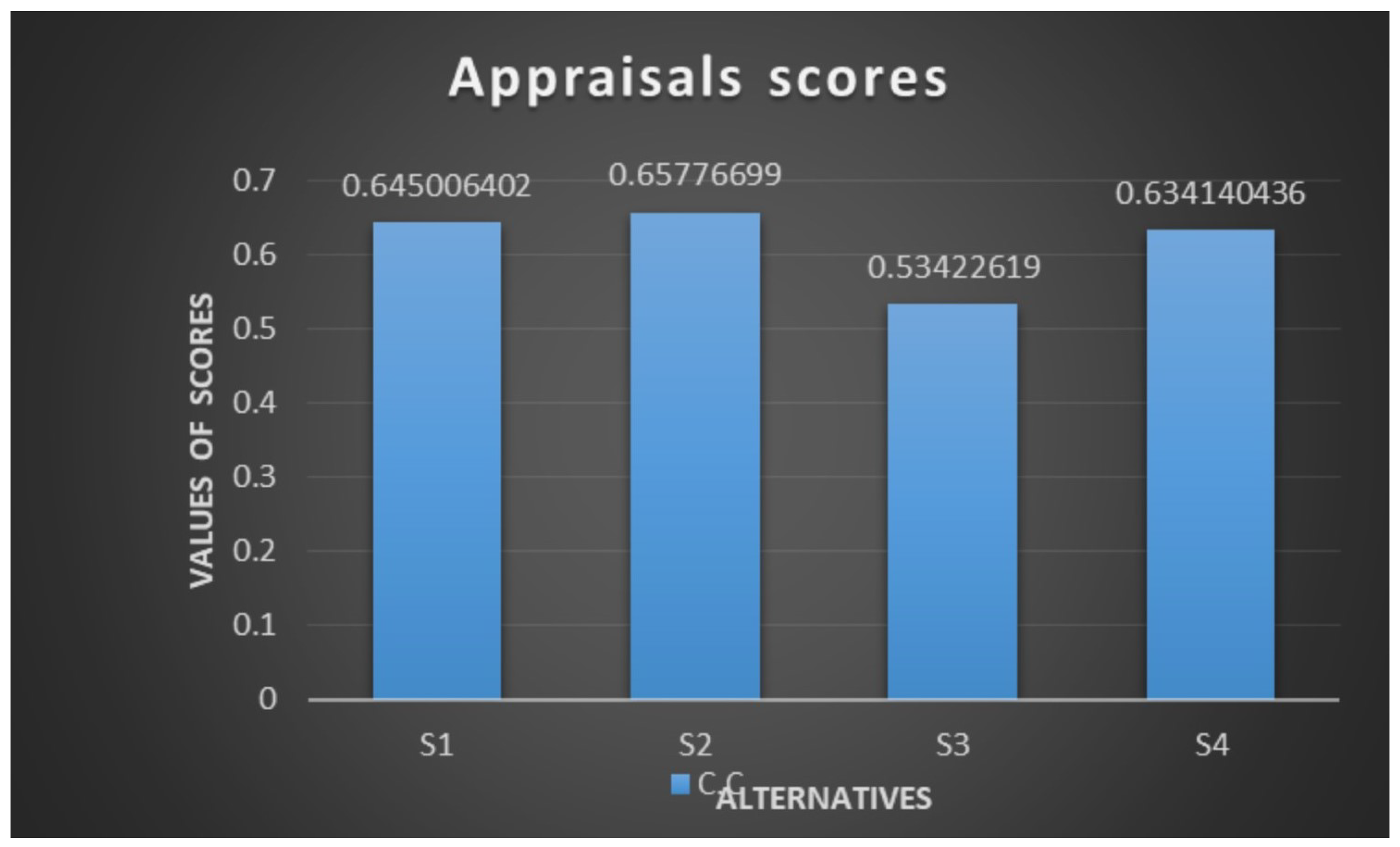
| Sprays | CC | Rank |
|---|---|---|
| 0.645006 | 2 | |
| 0.657767 | 1 | |
| 0.534226 | 4 | |
| 0.63414 | 3 |
| Decision Maker 1 () | Decision Maker 2 () | ||||||
|---|---|---|---|---|---|---|---|
| Primary Parameters | Underlying Parameters | Primary Parameters | Underlying Parameters | ||||
| Weights | Weights | Weights | Weights | ||||
| P | 0.19 | S | 0.45 | P | 0.3 | S | 0.1 |
| T | 0.1 | EW | 0.1 | T | 0.5 | EW | 0.5 |
| E | 0.01 | AL | 0.35 | E | 0.2 | AL | 0.35 |
| EH | 0.007 | C | 0.1 | EH | 0.1 | C | 0.05 |
| Decision Maker 3 () | Decision Maker 4 () | ||||||
| Primary Parameters | Underlying Parameters | Primary Parameters | Underlying Parameters | ||||
| Weights | Weights | Weights | Weights | ||||
| P | 0.22 | S | 0.7 | P | 0.45 | S | 0.2 |
| T | 0.1 | EW | 0.01 | T | 0.25 | EW | 0.8 |
| E | 0.46 | AL | 0.1 | E | 0.01 | AL | 0.22 |
| EH | 0.2 | C | 0.19 | EH | 0.29 | C | 0.05 |
| Reference | Technique | Conflict of Opinion | Inaccuracy of Results | Sub-Attributes on a Priority Basis | Loss of Data |
|---|---|---|---|---|---|
| [21] | Type-2 Soft sets | ✓ | ✓ | X | X |
| [49] | Type-2 Soft sets | ✓ | ✓ | ✓ | X |
| [47] | TOPSIS with soft sets technique | ✓ | ✓ | X | ✓ |
| Our proposed MultiFuzzTOPS model | TOPSIS with type-2 soft sets | X | X | ✓ | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoor, S.; Mustafa, S.; Gulzar, K.; Gulzar, A.; Kazmi, S.N.; Akber, S.M.A.; Bukhsh, R.; Aslam, S.; Mohsin, S.M. MultiFuzzTOPS: A Fuzzy Multi-Criteria Decision-Making Model Using Type-2 Soft Sets and TOPSIS. Symmetry 2024, 16, 655. https://doi.org/10.3390/sym16060655
Manzoor S, Mustafa S, Gulzar K, Gulzar A, Kazmi SN, Akber SMA, Bukhsh R, Aslam S, Mohsin SM. MultiFuzzTOPS: A Fuzzy Multi-Criteria Decision-Making Model Using Type-2 Soft Sets and TOPSIS. Symmetry. 2024; 16(6):655. https://doi.org/10.3390/sym16060655
Chicago/Turabian StyleManzoor, Shumaila, Saima Mustafa, Kanza Gulzar, Asim Gulzar, Sadia Nishat Kazmi, Syed Muhammad Abrar Akber, Rasool Bukhsh, Sheraz Aslam, and Syed Muhammad Mohsin. 2024. "MultiFuzzTOPS: A Fuzzy Multi-Criteria Decision-Making Model Using Type-2 Soft Sets and TOPSIS" Symmetry 16, no. 6: 655. https://doi.org/10.3390/sym16060655
APA StyleManzoor, S., Mustafa, S., Gulzar, K., Gulzar, A., Kazmi, S. N., Akber, S. M. A., Bukhsh, R., Aslam, S., & Mohsin, S. M. (2024). MultiFuzzTOPS: A Fuzzy Multi-Criteria Decision-Making Model Using Type-2 Soft Sets and TOPSIS. Symmetry, 16(6), 655. https://doi.org/10.3390/sym16060655








