Abstract
Quantum mechanics of unitary systems is considered in quasi-Hermitian representation and in the dynamical regime in which one has to take into account the ubiquitous presence of perturbations, random or specific. In this paper, it is shown that multiple technical obstacles encountered in such a context can be circumvented via just a mild amendment of the so-called Rayleigh–Schrödinger perturbation–expansion approach. In particular, the quasi-Hermitian formalism characterized by an enhancement of flexibility is shown to remain mathematically tractable while, on the phenomenological side, opening several new model-building horizons. It is emphasized that they include, i.a., the study of generic random perturbations and/or of multiple specific non-Hermitian toy models. In parallel, several paradoxes and open questions are shown to survive.
1. Introduction
The exact or approximate solutions of the time-independent Schrödinger equation
play a key role in our understanding of the structure of quantum bound states or resonances. Often, it is believed that up to some truly exotic exceptions the division line which separates the case of bound states from the case of resonances also separates Equation (1) in which H is Hermitian from Equation (1) and in which H is non-Hermitian. Incidentally, the latter belief has been shattered after 1998 when Bender with Boettcher [1] revealed that the class of the “anomalous” non-Hermitian Equation (1) yielding bound states can be larger than expected, also incorporating certain models in which the Hamiltonians have the form of superposition of the most common kinetic energy ∼ with an equally standard (but complex) local interaction potential.
In the latter models, widely known as “–symmetric” [2,3,4,5,6], the manifest non-Hermiticity of the Hamiltonian
has been found to coexist with the reality of the spectrum. Thus, it was immediate to conclude that the unitarity of the evolution can be guaranteed not only in the conventional textbook spirit (i.e., via the self-adjointness of the Hamiltonian [7]), but also under certain additional technical conditions [8], via the Dieudonné’s [9] quasi-Hermiticity requirement
One can then speak about quantum mechanics of unitary systems which are slightly modified and reformulated in the so-called quasi-Hermitian representation.
In this framework, one of the most important features of the modification may be seen in its innovative approach to the concept of perturbation, which is found to be, in this setting, counterintuitive. This is for three reasons. The first one is that in this formalism (cf., e.g., its reviews in [10] or [11]), we are allowed to change the physical Hilbert-space norm. Thus, in a preselected “perturbed” Hamiltonian the size (and, hence, influence) of the perturbation cannot always be kept under reliable control. Often, an enhanced sensitivity to perturbations is observed. For this reason, in open quantum systems, a few more remarks on this subtlety will be added below.
The second reason and paradox emerges when we consider just a closed quantum system in which the influence of is guaranteed to be small. Still, the correct probabilistic interpretation of the system remains ambiguous, mainly again due to the non-uniqueness of the physical Hilbert-space inner-product metric (again, a more detailed support of this observation will be given below).
Thirdly, even if we decide to ignore the latter ambiguity and even if we pick up just any one of the eligible metrics (which would reduce the scope of the theory in a not quite predictable manner of course), such a choice of the geometry of the physical Hilbert space would still vary with . This is, probably, the most challenging problem that is also to be addressed in our present paper.
Preliminarily we may notice and emphasize that in the language of mathematics, the problem may be formulated easily because the underlying auxiliary, unitarity-of-evolution-guaranteeing operator (if it exists [8]) can be perceived as representing just an invertible and positive definite ad hoc physical-Hilbert-space inner-product metric, . In the related reformulation of quantum theory, all of the measurable predictions only require, therefore, the evaluation of the following metric-dependent matrix elements:
The knowledge of the wave function and of the operator A representing an observable of interest must be complemented here by the guarantee of observability of course [8,10].
One of the most influential sources of interest in certain special classes of non-Hermitian Hamiltonians with real spectra lied in quantum field theory [12] and, in particular, in the role played there by perturbation theory [13,14,15]. One of the most important subsets of the underlying phenomenological Hamiltonians H is formed, therefore, by the one-parametric families
where is a complex number and where the component V representing the perturbation should not be, in some sense, too large [15].
Under this assumption, a powerful tool of the construction of the solutions of Equation (1) lies in the use of power-series ansatzs
and
A serious obstacle emerges when we turn our attention to the unconventional quasi-Hermitian models. In light of Equation (2), the metric will become manifestly – dependent in general, . In contrast to the conventional perturbation-expansion constructions, it becomes necessary to complement the standard pair (5) and (6) of the Rayleigh–Schrödinger perturbation–expanison ansatzs by their new, operator–expansion partner, say, of the power-series form
This means that the non-Hermiticity (4) of Hamiltonian makes a consequent implementation of the Rayleigh–Schrödinger perturbation-expansion approach to the quasi-Hermitian bound state quantum physics complicated.
The consequent theory requires an explicit or implicit reference to as many as five separate but mutually interrelated Hilbert spaces in general (cf. [16]). The main theoretical benefit of such a five-Hilbert-space reformulation of quantum mechanics lies in an exhaustive classification of admissible perturbations. In this sense, our present paper can be read as a more pragmatically oriented follow up of [16].
As an introduction, a few basic features of the theory may be found summarized in Appendix A, Appendix B, Appendix C and Appendix D. With this background in mind, Section 2 will add two illustrative examples explaining not only an overall motivation of using non-Hermitian Hamiltonians but also the existence of the deep mathematical differences between the use of perturbation expansions in the closed and open quantum systems.
In Section 3, we will turn our attention to the physical consequences of these differences. We will point out that in the related literature the necessity of an unambiguous separation of the closed-system quantum physics from the open-system quantum physics is not always sufficiently carefully observed. This note will be complemented by an outline of the role of random perturbations in realistic models. A critique of a few recent results will be given in which the depth of the difference between the closed and open systems has been underestimated. This will be followed by a clarification of one of the related paradoxes connected with the usage of the concept of the so-called pseudospectra [17]. For the description of the influence of the random perturbations, the usefulness of the concept of pseudospectra remains strictly restricted to the studies of the open quantum systems. In the quasi-Hermitian models, the transition from spectra to pseudospectra cannot be recommended because it does not lead to any enrichment of the information about the dynamics of the underlying closed quantum systems.
In Section 4, we will finally return to the quasi-Hermitian perturbation theory. We will recall the mathematical challenge represented by the necessity of the construction of an additional operator expansion (7). In the climax of our paper, we will offer a new, alternative, upgraded formulation of the quasi-Hermitian version of the Rayleigh–Schrödinger perturbation series in which the latter necessity will be circumvented.
An extensive discussion and summary of our results will be presented in the last two sections, Section 5 and Section 6. The essence of the innovation (and, first of all, of a significant simplification of the formalism) will be shown to lie in an implementation of the biorthogonal-basis ideas [18] as taken from their application in a different, non-stationary quantum dynamics context [19].
2. Merits of Non-Hermitian Hamiltonians
From a purely pragmatic point of view, Schrödinger Equation (1) can be perceived as a linear eigenvalue problem in which, in the majority of applications, the possible non-Hermiticity of the Hamiltonian would make the construction of solutions less stable and technically more difficult. This is a generic statement which is well known [11,17]. People often seem surprised when they encounter a quantum system for which the technically friendliest representation of Hamiltonian happens to be non-Hermitian.
2.1. Dyson-Inspired Simplifications of Schrödinger Equations
A compact account of history of the recent quick enhancement of interest in the closed and stable quantum systems controlled by an “anomalous” Hamiltonian can be found in [11]. The emergence of such a class of models can look, at first sight, surprising. Nevertheless, one of the oldest demonstrations of the technical advantages of using a non-Hermitian H emerged many years ago, viz., during Dyson’s entirely pragmatic, well-motivated, and purely numerical study of a specific real-world many-body problem [20].
An impact of the latter quantum-many-body result remained, for a couple of years, restricted just to nuclear physics [21]. The idea only acquired a new life and broader response after Bender with Milton [12] revealed that the study of non-Hermitian models may be also of immediate relevance in quantum field theory.
In such a broadened methodical context, a particularly elementary and fully non-numerical sample of such a Hamiltonian has been proposed, in 2006, by Jones with Mateo [22]. Via an exactly solvable toy model, these authors demonstrated that, in some cases, given a conventional self-adjoint Hamiltonian , one can profit from its replacement by an isospectral alternative , which is non-Hermitian. Indeed, the former operator where the potential contained two components
could be perceived as more complicated than their avatar with
containing just the single interaction term. Moreover, the single-term potential (9) is symmetric with respect to the product of parity and time-reversal, i.e., in comparison, it is less complicated than its left–right-asymmetric two-term partner (8). One can really speak about a simplification , in principle at least.
Both of the latter Hamiltonians predict the same real (i.e., measurable and stable) bound-state spectrum which is discrete and bounded from below. The conventional one, viz., operator is self-adjoint while its non-Hermitian avatar is merely quasi-Hermitian (cf. definition (2)). From an experimentalist’s point of view the isospectrality of the two alternative Hamiltonians makes the two representations of the same closed quantum system indistinguishable. For mathematicians, the differences are also not too deep because the main source of difference, viz., the inner-product metric needed in Equation (2), has been found, in [22], in an exact, closed and really elementary operator form
This makes the non-Hermiticity of just a minor, easily surmounted complication.
2.2. Analytic Continuations and Non-Unitary Open Systems
From the point of view of experimental physics, the truly exceptional exact solvability of the Jones’ and Mateo’s interaction (9) is not so impressive because the coordinate x is complex (see its definition in [22]). This makes the standard probabilistic interpretation of the “simplified” system unclear because the value of x (tentatively treated as the position of a particle) ceases to be a measurable quantity.
A new physics has to be then sought in a return to differential Schrödinger equations in which the coordinate x remains real. In the light of the paradox (or rather of the danger) of the non-observability of coordinates, one is forced to consider the asymptotically less anomalous potentials in which the line of coordinate x could still be kept real. One of such illustrative examples can be found in our older paper [23] where we studied the perturbation expansions (5) of the energies generated by the two-parametric imaginary cubic oscillator Hamiltonian
Indeed, such a differential–operator model is still non-Hermitian and – symmetric, i.e., it is formally closely analogous to Equation (9). Moreover, knowing that after identification , i.e., in the weak-coupling regime, the conventional small-anharmonicity expansions would diverge, we were able to transfer the role of a small parameter to the other coupling and choose . As a consequence, we achieved a very good convergence of our resulting perturbative strong-coupling series (5) for the energies.
Later, we found a complementary inspiration in [24] in which Bender and Dunne set and and studied the alternative, divergent but resummable weak-coupling expansion. They were interested in just the ground state energy, and they managed to construct the Rayleigh–Schrödinger perturbation series
up to very large orders by having evaluated the necessary integer-valued coefficients non-numerically,
At , they managed to fit these coefficients using an amazing asymptotic formula
Via an appropriate resummation of the divergent series (12), this enabled them to obtain, at any not too large real coupling , a very good (they even wrote “excellent”) agreement with the known and real numerical value of the ground-state energy .
As a climax of the story, Bender and Dunne also proposed a phenomenologically meaningful physical output of their considerations. For this purpose, they re-interpreted their asymptotic estimate (14) as a support of the possibility and consistency of an analytic continuation of the function to the (cut) complex plane of . On these grounds, they were able to evaluate the imaginary part of and to interpret the result as a prediction of a measurable decay width of another quantum system described by an analytically continued Hamiltonian
(cf. Eq. Nr. 5 in [24]). In other words, the initial non-Hermitian operator (11) has been reinterpreted, via analytic continuation, as a more or less standard physical quantum Hamiltonian supporting an unstable (but still observable) ground state.
2.3. Dyson Maps and the Modified Concept of Locality
In the overall framework of quasi-Hermitian quantum mechanics (QHQM) of closed systems as formulated, in the Schrödinger picture, by Scholtz et al. [8], we paid attention, in our recent paper [16], to the consistent applicability of the theory in the presence of perturbations. We pointed out that even in the non-perturbative version of the theory it made sense to realize the description using three separate Hilbert spaces (cf. diagram Nr. (10) in [16] or Equation (A1) in Appendix A).
One of these spaces is denoted here by symbol . By assumption, it is just a hypothetical and, for practical purposes, inaccessible space. Only the other two are relevant, both hosting operator H and differing just by the respective forms of inner products. The first space (viz., ) is just auxiliary and unphysical. The second one (denoted here as ) is physical and, for this reason, a unitary equivalent to , with the equivalence mediated by a mapping .
The latter (often called Dyson [25]) mapping is related to the metric by formula
In a way dating back to the Dyson’s paper [20], the key message as delivered by our paper [16] is that after one makes the Hamiltonian – dependent and after one implements the perturbation-expansion philosophy, one has to distinguish between the “physics” (represented by the perturbed at any ) and “mathematics” (represented by the exactly solvable ). In other words, both of the Hamiltonian-supporting Hilbert spaces and become – dependent.
Incidentally, at both and , the knowledge of factorization (16) would enable us to return also to the above-mentioned toy-model interaction (9) in which the “false coordinate” appeared to be complex, . Due to the exact solvability of the model and due to the extreme simplicity of the related metric (10), one could also introduce a closed-form Dyson-map operator
and define a correct (i.e., by construction, quasi-Hermitian) coordinate-representing operator acting in and using formula
This is the definition of a suitable (albeit a bit artificial) observable tractable as a coordinate. From the point of view of consistency of the theory, the choice of the self-adjoint (or, directly, of the quasi-Hermitian ) is more or less arbitrary.
The relation (18) can itself be re-read as the closest analogue of connection between the more common energy-operators alias Hamiltonians (cf. relation (A2) in Appendix B). Such a constraint can be complemented by some additional phenomenological requirements. For example, it is possible to start from the “inaccessible” textbook Hilbert space and choose the left-hand side “input information” as a diagonal operator with the equidistant spectrum simulating the position on a one-dimensional discrete lattice or on its suitable continuous-spectrum limit [26,27].
3. Norm-Ambiguity Paradox and Its Consequences
A concise outline of the non-Hermitian but unitary theory of closed systems is relocated to Appendix A, Appendix B, Appendix C and Appendix D. Using the notation of diagram (A1) in Appendix A, let us now emphasize that in most applications the information about dynamics is carried just by the Hamiltonian H acting in an auxiliary Hilbert space in which . As a consequence, the choice of metric , compatible with the quasi-Hermiticity condition (2), remains non-unique [8]. The relevant (i.e., physical, – dependent) size of the perturbations V in (4) is, therefore, indeterminate.
This is a paradox, the relevance of which becomes particularly serious in the realistic models of quantum systems in which one cannot ignore the possible occurrence of random, uncontrolled, statistically distributed perturbations.
3.1. Random Perturbations and Pseudospectra
In the most common textbook version of quantum mechanics of the perturbed unitary systems living in , the evolution is generated by the perturbed Hamiltonians, which are self-adjoint.
(see [28] or Equation (A2) in Appendix B). The stability of the system may then be tested using all perturbations, the norm of which is bounded, . For this purpose, the spectra of the perturbed Hamiltonians could be calculated using the – dependent Schrödinger equation in ,
plus, say, the Rayleigh–Schrödinger perturbation-series ansatz (5).
As a result, one would obtain, in principle at least, a union of all of the possible perturbed spectra, i.e., the set
which should lie, for stable systems, just inside a small vicinity of , i.e., of the unperturbed spectrum. In such a setting, it is recommended to recall the Roch’s and Silberman’s observation [29] that the set (20) coincides with the so-called pseudospectrum of , i.e., with the set that is defined as the following union of the spectrum and of the domain in which the resolvent of remains large [17],
One can cite [30] and conclude that “if is self-adjoint …”, the pseudospectra “give no additional information”.
3.2. Norms in Non-Hermitian Models
Let us repeat that as long as the Hamiltonians in question are kept self-adjoint, the Roch’s and Silberman’s observation simplifies the analysis of the influence of random perturbations because it just shows that the smallness of perturbations immediately implies that at the sufficiently small the difference between the sets (pseudospectrum) and (spectrum) becomes negligible.
The situation becomes thoroughly different when a quantum Hamiltonian H is chosen “highly non-self-adjoint” because then, “the pseudospectrum is typically much larger than the –neighborhood of the spectrum”. There is a subtlety in such a proposition (cited from [30]) because in the context of the general non-Hermitian Schrödinger Equation (1), one has to distinguish, in a way already emphasized in the Introduction, between its open-system and closed-system interpretations.
In the former, “resonances-describing” subcase, we would have to complement Equation (1) by the specification of the conventional Hilbert space endowed with the usual, metric-independent norm. In diagram (A1), such a space is denoted by the dedicated symbol , with the norm of V denoted as as usual. Hence, in such a case (not, by the way, of our present immediate interest), we may formally set and in Appendix A.
In the other, “bound-states-describing” subcase (which is of our present interest) we may still follow the same conventions as introduced in Appendix A. Thus, with and with we have to treat Schrödinger Equation (1) as living in an amended, physical Hilbert space .
Unless one asks questions about norms, only the dual versions of the vector spaces and are different. Still, precisely the difference between the operator norm of V in (denoted as usual, ) and in (to be denoted differently, say, as ) becomes one of the most essential aspects of the respective alternative definitions of the Hilbert-space-dependent pseudospectra.
3.3. Pseudospectra in Quasi-Hermitian Models
As long as we are not going to study resonances, we may just restrict our attention to the random perturbations in quasi-Hermitian (i.e., by definition, in the hiddenly unitary) closed quantum systems. In principle, their description in the alternative physical Hilbert spaces and is then equivalent. In practice, nevertheless, one may observe that the predictions of the measurements as constructed in the textbook Hilbert-space representation are impractical and less user-friendly. Then, we are forced to treat the knowledge of the union (20) of the perturbed spectra in as “technically inaccessible”.
After we decide to move to , we must also remember that the corresponding physical norm of perturbations becomes different and, first of all, dependent. The key and meaningful question to ask is then the question about the structure of the union
of the spectra of all of the slightly but randomly perturbed systems living in .
The above-cited theorem can be recalled again. After one defines the pseudospectrum
in , one immediately obtains the Roch–Silberman relationship
This is our desired ultimate formula. In the correct and physical Hilbert space in which the Hamiltonian is made self-adjoint, this formula defines the sensitivity to perturbations in terms of the correct physical pseudospectrum (23). Its explicit numerical construction is facilitated and made useful. Obviously, once we require our random perturbations to be small in , we may again recall Proposition Nr. 3 in [30] and conclude that in full parallel with the Hermitian models also in the quasi-Hermitian picture of dynamics the spectrum and pseudospectrum carry equivalent information about the sensitivity of bound states to perturbations,
At the small values of , the pseudospectrum is formed just by a small vicinity of the spectrum. In the terminology of [30], such a pseudospectrum is “trivial” because small random perturbations cannot destroy the stability of the underlying closed quantum system.
4. Amended Rayleigh–Schrödinger Construction
Let us temporarily return to the open-system theory where one does not need to define any nontrivial inner-product metric because the evolution is non-unitary (cf., e.g., monographs [31] or [32]). In Section 2, we recalled, for illustration, the work in [24] as a typical sample of a more traditional approach. Bender and Dunne used there a Hamiltonian (11) for the purposes of the description of a complicated physical phenomenon. The physical Hamiltonian itself, as sampled by Equation (15), has only been deduced after an analytic-continuation redefinition of the model.
In our present paper, our strategy is different, with our attention restricted to the unitary, closed and stable quantum systems in which the unitarity of evolution coexists with the non-Hermiticity of H. In this setting, we intend to describe an amendment of the QHQM perturbation-expansion recipe in which the metric-related technical obstacles will be circumvented using a reformulation of the theory as recently proposed, in a different context, in [19].
4.1. The Choice-of-Space Problem Revisited
The requirement of unitarity of the evolution may make the QHQM perturbation theory discouragingly complicated, mainly due to the operator–expansion nature of the newly emerging series (7) representing the metric. In a way outlined in Appendix C, the theory has to be formulated in as many as five Hilbert spaces (cf. our present diagram (A13) or analogous diagram Nr. (20) in [16]). The standard, reference-providing space of textbooks has to be accompanied by the doublet of the preferred representation spaces, viz., by pertaining to the ultimate dynamical scenario and by representing the solvable unperturbed system. The remaining pair of their amended physical partners consists of the predictions-offering (carrying the ultimate picture of physics) and (i.e., its unperturbed partner).
The five-Hilbert-space pattern looks complicated. Concerning its applicability, one has to be a bit skeptical. In what follows, we intend to show that a fairly efficient remedy of the skepticism can be based on a more or less straightforward reformulation of the theory in which the specification of the metric will be re-interpreted as an upgraded form of transition from to the correct physical Hilbert space . A motivation of our present modification of the theory lies in an undeniable appeal of the Rayleigh–Schrödinger perturbation-approximation philosophy, which may be characterized, in the conventional textbook setting, by its enormous technical simplicity. In this sense, we intend to show that this simplicity need not get lost after one moves to the innovative QHQM framework.
Our attention will be concentrated upon the mathematical consistency aspects of the theory. We will emphasize that it is possible to overcome the most unpleasant conceptual complications emerging when one deals with a realistic quasi-Hermitian Hamiltonian of a unitary quantum system which is allowed to vary with a parameter. The theory will be re-analyzed in a way inspired by several publications, a sample of which is recalled in Appendix C.
Attention will be paid to the models in which the parameter-dependence remains weak and tractable by the techniques of perturbation theory [15]. In the first step of amendment of the conventional approaches, we will modify the very concept of a state, keeping in mind that in conventional textbooks, the state is usually characterized by aket–vector element of a physical Hilbert space (i.e., by ). The most immediate inspiration of a change in such a definition may be deduced from Equation (3), in which it is sufficient to abbreviate
or, after the Hermitian conjugation in our mathematical representation space,
These abbreviations enable us to rewrite Equation (3) in a more compact form,
out of which the metric seems to have “disappeared”.
An easy resolution of such an apparent paradox is that we moved back from auxiliary to physical . After some elementary algebra, we also reveal that the parallels between the “old” ket vectors and their “new” partners of Equation (27) (which could be called “ketkets”) can even be extended, yielding an identically satisfied “parallel” eigenvalue problem
(with the same real spectrum of course) or, after the mere Hermitian conjugation in , equivalently,
Now, we are prepared to realize that for vectors, the “physical” Hermitian conjugation as defined, hypothetically, in the “hidden” Hilbert space just replaces the ket by the “brabra” .
To summarize, we come to the conclusion that in the correct physical Hilbert space , the most natural representation of an –th bound state of the quantum system in question will not be provided by any ket but rather by the elementary projector
The main advantage of such an upgrade of conventions is two-fold. First, formula (31) remains the same in both of the Hilbert-space representations in and in , and second, using the standard definition
of the probability density, one immediately rediscovers the above-mentioned equivalent measurement-predicting prescription (3). Moreover, the use of formula also opens the way from pure states to mixed states and quantum statistical physics [33,34,35].
4.2. Rayleigh–Schrödinger Construction Revisited
In the light of our preceding considerations, the essence of our present innovation of the QHQM Rayleigh–Schrödinger construction of the series (5)–(7) [with an implicit reference to the “measurement-prediction” Formula (3) alias (28) alias (32)] can be seen to lie simply in the replacement of the almost prohibitively complicated operator–expansion formula (7) by the alternative and formally sufficient new ketket-expansion ansatz
In other words, we will still have to start from the entirely conventional decomposition (4) of the Hamiltonian and from the related order-by-order re-arrangement
of our initial perturbed form of Schrödinger Equation (1). The innovation only comes when we reject the recipe of our previous proposal [16] (based on the reconstruction of via the clumsy power-series ansatz (7)) as unnecessarily (and, what is worse, more or less prohibitively) complicated.
In our present upgraded recipe, one simply complements Equation (34) by its associated partner for ketkets,
Obviously, an enormous simplification of the construction of the measurable predictions (32) is achieved. Indeed, in comparison with the complicated formulae in [16], the construction of the necessary recurrences for the sequence of corrections becomes immediate, making use only of the slightly upgraded projector
and leading to the easily deduced formulae for the energies, say,
as well as to the kets
(etc.) and, analogously, for the ketkets,
etc.
Summarizing, one only has to remind the readers that the full-fledged version of the present amended QHQM perturbation theory is only needed when we really have to predict the results of measurements of the observable represented by a preselected operator A. In applications, we are often interested in just the evaluation of only one of the values of the energy (which is, moreover, defined as one of the eigenvalues of the Hamiltonian). In practice, such a value is often known to be real. In such a case, naturally, what is needed is just the more or less standard construction of the single power series (5). We may conclude that precisely such simplified calculations were performed in papers [23,24], with the details recalled in Section 2 and in Section 2.2 above.
5. Discussion
5.1. Key Role Played by the Proof of Reality of Spectrum
In the early studies of non-Hermitian Hamiltonians with real spectra [1,2,12,36], the authors admitted that the non-Hermiticity of could make the standard probabilistic closed-system interpretation of the states questionable. For example, Bender and Dunne [24] circumvented the problem by claiming that their expansion (12) offers only “strong evidence” that the quantity is an analytic function, which can be continued to the cut complex plane of couplings .
Later, emphasis has been shifted to the requirement of the reality alias potential observability of the would-be bound-state energy-level spectrum of H representing a necessary condition of existence of an amended inner product. A direct and truly innovative closed-system physical interpretation of models started to be sought in the reconstruction of metric [3,10].
In the context of QHQM perturbation theory, for several reasons (some of which have been discussed above), the necessity of the proof of the reality of the energy spectra also acquired a new urgency. In its analysis, as performed in our preceding paper [16], we emphasized that the scope of the QHQM perturbation theory is in fact “too broad”. In comparison with the constructive strategy of conventional textbooks (where the trivial physical inner-product metric is chosen in advance), the more flexible QHQM theoretical framework forced us to admit that our must be treated as perturbation dependent. The two conventional Rayleigh–Schrödinger power series (5) and (6) had to be complemented by the third item (7) representing the metric and making the construction of the model (i.e., of its correct physical Hilbert space) almost prohibitively difficult.
In this context, one of our present main results is that we managed to simplify the construction by replacing the difficult operator expansion (7) by its mere ketket–vector alternative (33). Nevertheless, even after such an upgrade of the recipe the (rarely easy!) proof of the reality of the spectrum will still keep playing the most important role of a necessary preparatory step in applications.
5.2. The Requirement of Completeness of the Set of Observables
We achieved a simplification of the non-Hermitian version of the Rayleigh–Schrödinger formalism by making the operator–expansion (7) of the metric “invisible”. The price to pay was the loss of insight into the correspondence between the reality of spectrum and the choice of the class of admissible perturbations. In fact, the study of this correspondence is nontrivial, requiring, probably, a return to the study of explicit expansions (7).
The question remains to be kept in mind as a truly interesting and challenging future project, nevertheless. One of the reasons is that it is closely related to the paradox of the ambiguity of the metric. Indeed, it is well known that the operator endowing a given Hamiltonian H with a self-adjoint status in need not be unique. As a consequence, even the norm of perturbation V in ansatz (4) can vary so that also the conventional condition of its “sufficient smallness” could be difficult, if not impossible, to prove.
The ambiguity of has been identified in [8], resulting from an incompleteness of our information about the system’s dynamics. Indeed, the emergence of any independent candidate for an observable (which would have to be quasi-Hermitian with respect to the same metric, ) would suppress the ambiguity of whenever such a candidate appears not to be reducible to a function of H, . This means that a unique will be obtained only after one specifies a complete set of irreducible observables and and, perhaps, , etc. [8].
In a way discussed in [8], one is usually forced to work with only an incomplete irreducible set of preselected observables . This means that the ambiguity of the metric can only rarely be fully suppressed. One may try to circumvent the problem by making a more or less arbitrary choice of one of the eligible metrics. The same strategy is, after all, widely accepted in the conventional textbooks using trivial .
In the framework of unconventional QHQM, an exhaustive explanation of the problem of the ambiguity of the norm can already be found in [8], where one reads that the variability of our choice of the metric just reflects an incompleteness of the input information about dynamics. This means that such an ambiguity disappears when our knowledge of H becomes complemented by the knowledge of a sufficiently large (i.e., in mathematical language, “irreducible”) set of some further operator candidates for the observables.
In this sense, we arrive at a new paradox. Either we postulate such a knowledge or not. Naturally, the abstract theory would only be fully satisfactory in the former case. In such a case, nevertheless, the dependence of the Hamiltonian and metric would be inherited by an induced and strongly counterintuitive dependence of all of the further (i.e., necessarily quasi-Hermitian) observables with .
5.3. The Coordinate-Non-Observability Paradox
Among all of the differential–operator candidates for a closed-system quantum Hamiltonian possessing a real energy-like spectrum as sampled by Equation (11) above, one of the most interesting alternative models was studied by Buslaev and Grecchi [2]. One of the truly striking features of their model (which made it qualitatively different from Equation (11)) was that for the purposes of its mathematical consistency it was necessary to keep the “coordinate” complex (i.e., , in the asymptotic domain at least). This is a contradictory situation because such a variable cannot in fact be interpreted as an observable quantity.
The puzzle has been clarified by an explicit reference to perturbation theory in combination with the techniques of analytic continuation. In a way discussed also in Section 2 above, Buslaev and Grecchi revealed a hidden, perturbation-series-mediated connection between their manifestly non-Hermitian “complex-coordinate” oscillator and the safely self-adjoint Hamiltonian
describing an entirely conventional quartic anharmonic oscillator [14,37]. They were aware of the divergence of the related Rayleigh–Schrödinger perturbation series (5), but their analysis revealed the existence of an intimate relationship between operator (42) (defined as self-adjoint in the most common physical Hilbert space ) and its specific non-Hermitian isospectral descendant.
In [2], the same idea has been shown to work also in application to another, multiparametric multiplet of ordinary differential Hamiltonian-like operators with (with, incidentally, ). A special status has been again enjoyed by the element which was required, in the most conventional Hilbert space , to be self-adjoint. The last element of the sequence appeared to be non-Hermitian but parity-time-symmetric alias – symmetric. For our present purposes, we may abbreviate (i.e., drop the last subscript) and notice that the above-mentioned Jones and Mateo isospectrality relationship finds a direct analogue in formula
This is not too surprising because the Jones and Mateo Hamiltonian is just a parameter-free special case of the Buslaev and Grechi multiparametric operator . Thus, after a multiparametric generalization of Jones’ and Mateo’s Dyson operator (17), a new light could be thrown upon the concept of locality in non-Hermitian physics (cf. [38] and also formula (18) in Section 2.3 above).
Incidentally, Jones’ and Mateo’s “direction of simplification” becomes inverted since the evolution controlled by has to be reclassified as a more complicated picture of dynamics. Still, the message which survives is that the physical interpretation is directly provided by the Rayleigh–Schrödinger perturbation series of Equation (5).
5.4. A Detour to Meaningful Complex Spectra
In the conventional applications of perturbation theory, one starts from the knowledge of a preselected family of Hamiltonians
in which the unperturbed operator is assumed maximally user-friendly or even, often, diagonal. The specification of the admissible perturbations is then rather routine, made in accordance with both the phenomenological and mathematical model-building needs [15]. Family (43) is chosen, in most textbooks, as a mere sum of two self-adjoint operators.
We have already emphasized that once one admits a manifest non-Hermiticity of one or both of the operator components of the Hamiltonian in an auxiliary Hilbert space ,
the technical costs of such a weakening of the conventional assumptions may be high (cf. [3,8,10,11,39,40]). Even when one decides to keep the working Hilbert space perturbation-independent, , a number of challenging questions survive. One of the most important ones follows from the possible loss of the reality of eigenvalues,
Then, one has to accept the open-system philosophy and to treat the Rayleigh–Schrödinger expansions just as an ansatz which could work even when and even when the series is divergent.
The feasibility of such an alternative model-building strategy has been confirmed, e.g., by Caliceti et al. [36] (cf. also a more recent review of the field in [41]). In essence, the latter authors revealed that in a number of specific toy models the conventional ansatz (45) may still serve as a productive constructive tool, yielding, at the small and real coupling constants, the real (i.e., energy-like) as well as complex (i.e., resonance-representing) low-lying spectra after standard resummation.
5.5. Real Spectra and the Paradox of Emergent Instabilities
The reality of spectra of the Hamiltonians has independently been noticed in the context of quantum field theory [12]. This attracted the attention of the physics community to the applicability of expansions (45) in the non-Hermitian setting of Equation (44). The authors of the innovated studies of imaginary cubic anharmonic-oscillator Hamiltonians
identified either (say, in the “strong-coupling expansions” of Ref. [23]) or (say, in the “weak-coupling expansions” in [24]).
Even when having the strictly real bound-state-like spectra, the latter model-building efforts were criticized by mathematicians [17,30]. They recommended a replacement of the mere search for eigenvalues (characterized as “fragile”) by a more ambitious construction of pseudospectra. We have to point out that the mathematically well-founded latter recommendation has been based on a conceptual misunderstanding. Fortunately, a disentanglement of the misunderstanding was straightforward. It proved sufficient to distinguish between the closed and open systems and to show that the construction of pseudospectra only makes sense (and offers new information) in the latter case (for more details, see also Section 3 above).
From a purely mathematical point of view, one should not be too surprised by the latter conclusion and, in particular, by the “wild” [30] behavior of open systems exhibiting emergent instabilities because the theory behind the closed systems is different. For them, the constructions and predictions obtained in the two alternative “physical” Hilbert spaces and are, by definition, equivalent. Thus, no paradox can be seen in the existence of the mechanism due to which the pseudospectra of closed systems remain well behaved even when the representation of dynamics itself is non-Hermitian.
Another, even more straightforward explanation of the existence of the emergent open-system instabilities becomes best visible when the system in question happens to lie close to a Kato’s exceptional-point singularity [42,43,44]. In such a vicinity, indeed, the operator of metric becomes singular and dominated by a projector [45]. Perturbations , which are small with respect to the correct physical Hilbert-space norm (in our present notation this means that ) may still be, simultaneously, very large with respect to the conventional open-system norm as defined in the standard regular limit of (i.e., ). As a consequence, perturbations may be expected to lead to the “wild” forms of pseudospectrs (20) as sampled, via a number of elementary examples, in [30].
5.6. Ultimate Challenge: Models Where the Metric Does Not Exist
To a compact introduction in the overall QHQM theory, as provided in Appendix A, it makes sense to add that a truly enormous increase in the popularity of the formalism has been inspired by Bender’s and Boettcher’s claim [1] that the reality of spectra is a phenomenon which can be observed in an unexpectedly broad class of models which are not only phenomenologically attractive but also mathematically user-friendly. These results set the scene for an intensive subsequent study. It is of no surprise that whenever an operator H proves non-Hermitian (in ) while its spectrum is “bound-state-like” (i.e., real, discrete, and bounded from below), one feels tempted to consider the possibility of its quantum quasi-Hermitian Hamiltonian-operator interpretation.
In [1], the temptation has been further supported by the detailed analysis of the specific ordinary differential Hamiltonian-like operators
These operators are, in general, complex and manifestly non-Hermitian but still possessing the strictly real and discrete bound-state-like spectra. On these grounds, Bender and Boettcher conjectured that such operators could be treated as Hamiltonians in certain unconventional, “analytically continued” quantum theories.
In 2012, Siegl and Krejčiřík [46] opposed the claim. Using the rigorous methods of functional analysis, they proved that for at least some of the toy models where H had the elementary differential–operator form (47), an acceptable metric which would satisfy relation (2) does not exist at all. This weakened the enthusiasm because at least some of the local interaction benchmark models cannot be endowed with any admissible physical-Hilbert space .
One of the ways of circumventing such a mathematical disproof of quasi-Hermiticity has been found in a transition to the open system reinterpretation of the models [5]. As a benefit, such a change of strategy simplified the mathematics because one could simply set . A return to the old open-system philosophy behind models (47) appeared even productive in mathematics. In a way outlined in Section 5.5 above, it led to the discovery of certain unexpected spurious approximate solutions of Equation (1) emerging at the energies which were far from the spectrum [30]. Thus, it was immediate to conclude that in place of the spectrum, the much more useful descriptive tool can be sought in the pseudospectra.
In a way which we described in Section 3 above, the pseudospectra directly characterize the influence of random perturbations upon dynamics of the systems. Incidentally, their analysis has been shown to make sense only in the open-system cases in which the spectra of H are not real. As long as at some n, the Hamiltonian cannot be Hermitian, . Thus, we may set and identify . In contrast, the knowledge of pseudospecta is not needed in the other, stable-bound-state scenario, partially because the implication cannot be inverted.
It is possible to conclude that for the closed systems with the Hamiltonians sampled by Equation (47), the question of their acceptability is still open. The reason is that the physical Hilbert space defined in terms of the correct inner-product metric need not exist. Thus, whenever we decide to stay inside the QHQM theory and require that
we must keep in mind that the status of many popular illustrative examples has to be reconsidered as inconclusive, with an acceptable physical interpretation being still sought in several new directions [47,48,49,50,51,52,53,54,55].
In fact, Scholtz et al. [8], were probably already aware of the similar mathematical subtlety because they complemented the quasi-Hermiticity requirement (2) by a few further consistency-supporting sufficient conditions. Among them, the most prominent amendment of the theory seems to be their mysterious requirement of the boundedness of H. Unmotivated and counterintuitive as it might have looked in the past, it was probably one of the lucky parts of the formulation of QHQM by Scholtz et al. [8] because, in retrospect, it excludes the contradictory differential unbounded-operator models (47) as unacceptable.
6. Summary
In the textbooks on quantum theory, the authors have to distinguish between the models supporting, and not supporting, the presence of resonances. The notion of perturbation plays a fundamental role in both of these implementations of the theory. This is for two reasons. The first one is realistic: Whenever one tries to prepare and study a quantum system, stable or unstable, it is hardly possible to achieve its absolute isolation from an uncontrolled environment. One has to guarantee the negligibility of influence of such an environment using, typically, non-Hermitian Hamiltonians and open-system models with complex spectra and random perturbations.
The second reason is mathematical: Even if we manage to guarantee that the system in question is, up to negligible errors, isolated, perturbation theory re-appears as a powerful tool suitable for calculations and for an efficient evaluation of predictions. Naturally, a consistency of perturbation-related constructions needs a guarantee of a “sufficient smallness” of the perturbation. Such a guarantee is a task, an explicit formulation of which depends on the model-building details. Our present attention has mainly been devoted, therefore, to the physics of stable bound states (and just marginally to unstable resonances) in a way motivated by the recently increasing popularity of the so-called non-Hermitian Schrödinger representations of the stable and unitary quantum systems.
In the literature, the presentation of this subject may be found accompanied by the emergence of multiple new and unanswered questions. In our paper, we picked up a few of such questions which we were able to answer. Basically, our answers may be separated in several groups. In the first one, we felt inspired by the authors who studied the pseudospectra. We imagined that in such an area of research the application of innovative mathematics is not always accompanied by a clear explanation of physics. In this setting, we conjectured that a key to the resolution of certain emerging apparent paradoxes can be found in distinguishing, more consequently, between the traditional non-Hermitian quantum models with (for the study of which the pseudospectra have been found truly indispensable [17]) and the more recent and sophisticated closed-system theories in which the specification of the correct inner-product metric proves nontrivial and Hamiltonian-dependent, .
In this way, we managed to explain that in certain applications (sampled by the random-perturbation studies) there is practically no difference between the use of the QHQM and standard quantum mechanics. A slightly different conclusion has been achieved when we turned attention to a more explicit study of the Rayleigh–Schrödinger perturbation expansions. The differences, not too well visible in the mere calculations of energies [23,24], appeared immediately deeply relevant when one becomes interested in practically any other observable quality/quantity of the system.
The latter feature of the theory has already been observed (and not found to be too welcome) in our preceding paper [16]. Our detailed analysis of the structure of the QHQM-version of perturbation theory led us there to a few rather skeptical conclusions concerning the applicability of the formalism in its full generality. In our present paper, we managed to show that the strength of the latter discouraging results can perceivably be weakened when one reconsiders the theory and after one reduces its scope to just the description of its experimentally verifiable predictions.
In this spirit, we proposed replacing the next-to-prohibitively difficult operator-valued solution of Equation (2) (specifying the perturbation-dependent metric needed in Equation (3)) by the vector-valued solution of Equation (29) entering the modified form (28)) of the same prediction which is, even by itself, much easier to evaluate.
In conclusion, it is probably worth adding that along the same methodical lines one could also get beyond the framework of the Schrödinger picture in which the opereators of observables are mostly assumed time independent, . In the future, perhaps, the same methodical ideas might prove applicable also in the non-stationary context and models and in the interaction-picture extension of the hiddenly unitary-evolution formalism as proposed a couple of years ago in [56].
Funding
This research received no external funding.
Data Availability Statement
No new data were created in this study.
Acknowledgments
The author was supported by Faculty of Science of University of Hradec Kralove.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Quantum Mechanics in Quasi-Hermitian Representation
A comprehensive outline of the formulation of unitary quantum mechanics in which the conventional requirement of Hermiticity of the Hamiltonian is replaced by an apparently weaker, metric-dependent quasi-Hermiticity constraint (2) can be found not only in the older review by Scholtz et al. [8] but also in a few newer papers (e.g., [3,10,57]) and books (e.g., [4,11]). In the interpretation of review [39], the formalism is based on the simultaneous use of a triplet of Hilbert spaces (say, ) connected by the Dyson-inspired [20] mutual correspondences, as displayed in the following diagram:
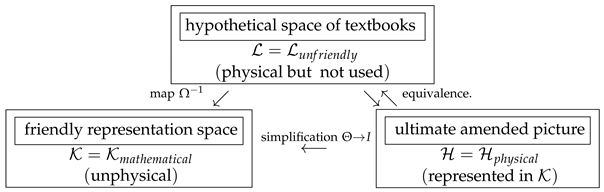

In such an arrangement, by assumption, the two lower-line Hilbert spaces and coincide as linear modules or vector-space sets of the ket–vector elements . Thus, we can write and/or and treat the Hamiltonian H (carrying the input information about dynamics) as an operator defined and acting in both of these two spaces.
The difference between and lies in two conventions. First, the former, auxiliary, manifestly unphysical Hilbert space is definitely preferred as the more user-friendly one. The standard Dirac’s notation is applied to the bra–vector elements of its dual marked by a prime, . Second, the correct physical Hilbert space is only treated as represented in using the mere change of the inner product,
The bra–vector elements of the dual physical vector space are, in the notation of Ref. [58], denoted as “brabras”, . They have the metric-dependent representation
in . Thus, we can treat these brabras as the Hermitian conjugates of the kets in the physical Hilbert space . In parallel, we can also introduce the “ketkets” as the Hermitian conjugates of the brabras with respect to the simpler, conventional inner-products in the unphysical but preferred representation-Hilbert-space .
Appendix B. Rayleigh–Schrödinger Construction in
A factorization of the metric enables us to define the textbook –space self-adjoint avatar of our Hamiltonian
It acts in the upper component of diagram (A1), which is just the conventional physical Hilbert space of textbooks. The latter Hilbert space can be perceived as the set of the “spiked-ket” elements and of their Hermitian-conjugate “spiked-bra” duals . By definition, the hypothetical and practically inaccessible operator is an –space image of our preselected Hamiltonian H. Hence, the the above-mentioned links of to the other two spaces imply that the Hermiticity of in is equivalent to the (hidden) Hermiticity of our H in . In contrast, the same operator H is non-Hermitian in the mathematical manipulation space .
In the context of perturbation theory with in Schrödinger equation
the standard power-series ansatz for energies (5) is complemented by its wave-function analogue
The Hermiticity (A2) is then an important mathematical advantage. In particular, this property enables us to treat the unperturbed Schrödinger equation
as a standard eigenvalue problem, preferably solvable in closed form. Next, we may recall any textbook and write down the first-order-approximation extension of Equation (A5),
as well as its second-order extension
etc. In this manner, we may reconstruct the sequence of the corrections to the energy,
(etc.) as well as the analogous sequence of the corrections to the wave-function ket–vectors
(etc.) where the symbol
denotes an elementary projector “out of model space”.
Appendix C. Open Questions behind Quasi-Hermitian Perturbations
In the ultimate physical Hilbert space in which H is self-adjoint, it would be possible to introduce a dedicated superscript marking the space-characterizing conjugation and to rewrite Equation (2) as follows,
Nevertheless, once we move to the preferred representation space , the latter notation becomes redundant because the relation finds its rephrasing in the quasi-Hermiticity constraint (2) in .
In applications, we have to re-read Equation (2) as restricting an assignment of metric to a preselected non-Hermitian operator H. Such a metric will necessarily vary with the Hamiltonian in general, . The same observation applies to its Dyson-map factor, . Both of these comments have already been formulated in [16]. We pointed out there that whenever one decides to consider any one-parametric family of Hamiltonians (including also the perturbed Hamiltonians of Equation (4) as a special case), the physical meaning of the quantum system can only be deduced from its textbook probabilistic interpretation in at every .
This means that the change in the parameter will imply the change of diagram (A1). The independence of the unperturbed and perturbed versions of Schrödinger Equation (1) lead to the necessity of working, at every non-vanishing parameter , with as many as six separate Hilbert spaces. Even though we can merge and use the single textbook space for reference, the union of the two respective diagrams (A1) with and still has to be replaced by their five-Hilbert-space concatenation.
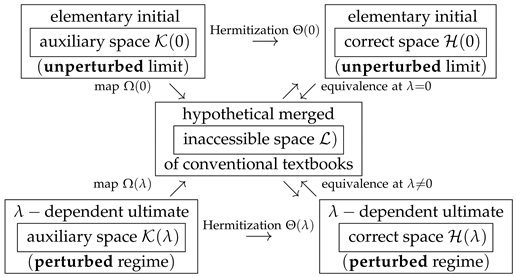

In [16], we emphasized that the general QHQM formalism remains consistent and applicable even when the –dependence of the Hilbert space metric is not smooth. Nevertheless, we proposed that for the perturbed models of Equation (4) characterized by a smooth –dependence of the Hamiltonian, it makes sense to also postulate the analyticity of . Still, our concluding comments concerning the practical feasibility of the calculations were skeptical. In contrast, one of the key messages, as delivered by our present paper, can be seen in a significant suppression of the latter skepticism.
Appendix D. Biorthonormalized Unperturbed Bases
In Hilbert space , our Hamiltonians are assumed non-Hermitian, . In Section 4, we emphasized that we therefore have to complement the conventional Schrödinger equation (i.e., Equation (1) for the ket vectors) by its conjugate partner specifying their –space duals. This goal is achieved either via Equation (30) for the “brabra” vectors or, equivalently, via Equation (29) for the “ketket” vectors.
Temporarily let us simplify the mathematics and assume that dim [59]. Then, for the reasons explained in diagram (A13) of Appendix C, we must distinguish between the equations at (the unperturbed limit) and at (the perturbed regime). In the former case, let us now rewrite both of the Schrödinger equations in a more compact notation,
In the framework of perturbation theory in its most elementary form, the solutions of such an advanced, “doubled” quasi-Hermitian bound-state problem are usually assumed available in closed form. We will also require that all of the unperturbed eigenvectors form a biorthonormalized set (i.e., one has ), which is complete. Thus, we will have, at our disposal, the spectral decomposition of the identity operator,
Formally, one can even postulate the validity of a spectral representation of the unperturbed Hamiltonian,
Finally, recalling [58], one can write down also the multiparametric definition
of all of the metrics which would be formally compatible with the Dieudonné’s quasi-Hermiticity constraint (2) at . In parallel, the related Dyson-map factor appearing in Equation (16) and in diagrams (A1) and/or (A13), as well as in the explicit definition of the elements of the hypothetical space of textbooks can be formally represented by the sum
Depending on the representation, one can insert here or .
References
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Buslaev, V.; Grecchi, V. Equivalence of unstable anharmonic oscillators and double wells. J. Phys. A Math. Gen. 1993, 26, 5541–5549. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018; (with contributions from Dorey, P.E.; Dunning, C.; Fring, A.; Hook, D.W.; Jones, H.F.; Kuzhel, S.; Levai, G.; Tateo, R.). [Google Scholar]
- Christodoulides, D.; Yang, J.-K. (Eds.) Parity-Time Symmetry and Its Applications; Springer: Singapore, 2018. [Google Scholar]
- Bagchi, B.; Ghosh, R.; Sen, S. Analogue Hawking Radiation as a Tunneling in a Two-Level PT-Symmetric System. Entropy 2023, 25, 1202. [Google Scholar] [CrossRef]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643–648. [Google Scholar] [CrossRef]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Dieudonne, J. Quasi-Hermitian Operators. In Proceedings of the International Symposium on Linear Spaces, Jerusalem, Israel, 5–12 July 1960; Pergamon: Oxford, UK, 1961; pp. 115–122. [Google Scholar]
- Mostafazadeh, A. Pseudo-Hermitian Representation of Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bender, C.M.; Milton, K.A. Nonperturbative Calculation of Symmetry Breaking in Quantum Field Theory. Phys. Rev. D 1997, 55, R3255. [Google Scholar] [CrossRef]
- Bender, C.M.; Wu, T.T. Anharmonic Oscillator. Phys. Rev. 1969, 184, 1231–1260. [Google Scholar] [CrossRef]
- Turbiner, A.; del Valle, D.C. Anharmonic oscillator: A solution. J. Phys. A Math. Theor. 2021, 54, 295404. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Znojil, M. Theory of response to perturbations in non-hermitian systems using five-Hilbert-space reformulation of unitary quantum mechanics. Entropy 2020, 22, 80. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Embree, M. Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Brody, D.C. Biorthogonal quantum mechanics. J. Phys. A Math. Theor. 2013, 47, 035305. [Google Scholar] [CrossRef]
- Znojil, M. Quasi-Hermitian formulation of quantum mechanics using two conjugate Schroedinger equations. Axioms 2023, 12, 644. [Google Scholar] [CrossRef]
- Dyson, F.J. General theory of spin-wave interactions. Phys. Rev. 1956, 102, 1217. [Google Scholar] [CrossRef]
- Janssen, D.; Dönau, F.; Frauendorf, S.; Jolos, R.V. Boson description of collective states. Nucl. Phys. A 1971, 172, 145–165. [Google Scholar] [CrossRef]
- Jones, H.F.; Mateo, J. An Equivalent Hermitian Hamiltonian for the non-Hermitian −x4 Potential. Phys. Rev. D 2006, 73, 085002. [Google Scholar] [CrossRef]
- Fernández, F.; Guardiola, R.; Ros, J.; Znojil, M. Strong-coupling expansions for the PT-symmetric oscillators V(r) = aix + b(ix)2 + c(ix)3. J. Phys. A Math. Gen. 1998, 31, 10105–10112. [Google Scholar] [CrossRef]
- Bender, C.M.; Dunne, G.V. Large-order perturbation theory for a non-Hermiitan PT-symmetric Hamiltonian. J. Math. Phys. 1999, 40, 4616–4621. [Google Scholar] [CrossRef]
- Koukoutsis, E.; Hizanidis, K.; Ram, A.K.; Vahala, G. Dyson maps and unitary evolution for Maxwell equations in tensor dielectric media. Phys. Rev. A 2023, 107, 042215. [Google Scholar] [CrossRef]
- Jones, H.F. Interface between Hermitian and non-Hermitian Hamiltonians in a model calculation. Phys. Rev. D 2008, 78, 065032. [Google Scholar] [CrossRef]
- Znojil, M. Scattering theory using smeared non-Hermitian potentials. Phys. Rev. D 2009, 80, 045009. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Roch, S.; Silberman, B. C∗-algebra techniques in numerical analysis. J. Oper. Theory 1996, 35, 241–280. [Google Scholar]
- Krejčiřík, D.; Siegl, P.; Tater, M.; Viola, J. Pseudospectra in non-Hermitian quantum mechanics. J. Math. Phys. 2015, 56, 103513. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A Math. Theor. 2009, 42, 153001. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge Univ. Press: Cambridge, UK, 2011. [Google Scholar]
- Jakubský, V. Thermodynamics of Pseudo-Hermitian Systems in Equilibrium. Mod. Phys. Lett. A 2007, 22, 1075–1084. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef]
- Moise, A.A.A.; Cox, G.; Merkli, M. Entropy and entanglement in a bipartite quasi-Hermitian system and its Hermitian counterparts. Phys. Rev. A 2023, 108, 012223. [Google Scholar] [CrossRef]
- Caliceti, E.; Graffi, S.; Maioli, M. Perturbation theory of odd anharmonic oscillators. Commun. Math. Phys. 1980, 75, 51–66. [Google Scholar] [CrossRef]
- Eremenko, A.; Gabrielov, A. Analytic continuation of eigenvalues of a quartic oscillator. Commun. Math. Phys. 2009, 287, 431. [Google Scholar] [CrossRef]
- Liu, Y.X.; Jiang, X.P.; Cao, J.P.; Chen, S. Non-Hermitian mobility edges in one-dimensional quasicrystals with parity-time symmetry. Phys. Rev. B 2020, 101, 174205. [Google Scholar] [CrossRef]
- Znojil, M. Three-Hilbert-space formulation of Quantum Mechanics. Symmetry Integr. Geom. Methods Appl. SIGMA 2009, 5, 001. [Google Scholar] [CrossRef]
- Ju, C.Y.; Miranowicz, A.; Chen, Y.N.; Chen, G.Y.; Nori, F. Emergent parallel transport and curvature in Hermitian and non-Hermitian quantum mechanics. Quantum 2024, 8, 1277. [Google Scholar] [CrossRef]
- Caliceti, E.; Graffi, S. Criteria for the Reality of the Spectrum of PT-Symmetric Schrödudinger Operators. In Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Bagarello, F., Gazeau, J.-P., Szafraniec, F., Znojil, M., Eds.; Wiley: Hoboken, NJ, USA, 2015; Chapter 4; pp. 189–240. [Google Scholar]
- Zezyulin, D.A.; Kartashov, Y.V.; Konotop, V.V. Metastable two-component solitons near an exceptional point. Phys. Rev. A 2021, 104, 023504. [Google Scholar] [CrossRef]
- Bagchi, B.; Ghosh, R.; Sen, S. Exceptional point in a coupled Swanson system. Europhys. Lett. 2022, 137, 50004. [Google Scholar] [CrossRef]
- Guria, C.; Zhong, Q.; Ozdemir, S.K.; Patil, Y.S.S.; El-Ganainy, R.; Harris, J.G.E. Resolving the topology of encircling multiple exceptional points. Nat. Commun. 2024, 15, 1369. [Google Scholar] [CrossRef] [PubMed]
- Henry, R.A.; Batchelor, M.T. Exceptional points in the Baxter-Fendley free parafermion model. Scipost Phys. 2023, 15, 016. [Google Scholar] [CrossRef]
- Siegl, P.; Krejčiřík, D. On the metric operator for the imaginary cubic oscillator. Phys. Rev. D 2012, 86, 121702. [Google Scholar] [CrossRef]
- Berry, M.V. Physics of Nonhermitian Degeneracies. Czech. J. Phys. 2004, 54, 1039–1047. [Google Scholar] [CrossRef]
- Bagarello, F.; Fring, A. A non selfadjoint model on a two dimensional noncommutative space with unbound metric. Phys. Rev. A 2013, 88, 042119. [Google Scholar] [CrossRef]
- Krejčiřík, D.; Siegl, P. Elements of spectral theory without the spectral theorem. In Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Bagarello, F., Gazeau, J.-P., Szafraniec, F., Znojil, M., Eds.; Wiley: Hoboken, NJ, USA, 2015; Chapter 5; pp. 241–292. [Google Scholar]
- Günther, U.; Stefani, F. IR-truncated PT-symmetric ix3 model and its asymptotic spectral scaling graph. arXiv 2019, arXiv:1901.08526. [Google Scholar]
- Ramirez, R.; Reboiro, M.; Tielas, D. Exceptional Points from the Hamiltonian of a hybrid physical system: Squeezing and anti-Squeezing. Eur. Phys. J. D 2020, 74, 193. [Google Scholar] [CrossRef]
- Brody, D.C.; Hughston, L.P. Quantum measurement of space-time events. J. Phys. A Math. Theor. 2021, 54, 235304. [Google Scholar] [CrossRef]
- Alase, A.; Karuvade, S.; Scandolo, C.M. The operational foundations of PT-symmetric and quasi-Hermitian quantum theory. J. Phys. A Math. Theor. 2022, 55, 244003. [Google Scholar] [CrossRef]
- Feinberg, J.; Riser, B. Pseudo-Hermitian random-matrix models: General formalism. Nucl. Phys. 2022, B 975, 115678. [Google Scholar] [CrossRef]
- Semorádová, I.; Siegl, P. Diverging eigenvalues in domain truncations of Schroedinger operators with complex potentials. SIAM J. Math. Anal. 2022, 54, 5064–5101. [Google Scholar] [CrossRef]
- Znojil, M. Time-dependent version of cryptohermitian quantum theory. Phys. Rev. D 2008, 78, 085003. [Google Scholar] [CrossRef]
- Wang, W.H.; Chen, Z.L.; Li, W. The metric operators for pseudo-Hermitian Hamiltonian. ANZIAM J. 2023, 65, 215–228. [Google Scholar] [CrossRef]
- Znojil, M. On the role of the normalization factors κn and of the pseudo-metric P in crypto-Hermitian quantum models. Symmetry Integr. Geom. Methods Appl. SIGMA 2008, 4, 001. [Google Scholar] [CrossRef]
- Ballesteros, A.; Ramírez, R.; Reboiro, M. Non-standard quantum algebras and finite dimensional PT-symmetric systems. J. Phys. A Math. Theor. 2024, 57, 035202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).