Dynamics of a Stochastic SVEIR Epidemic Model with Nonlinear Incidence Rate
Abstract
1. Introduction
2. Preliminaries
- (i)
- Within the open domain U and its neighborhood, the minimum eigenvalue of the diffusion matrix remains bounded away from zero.
- (ii)
- For any , the average time τ for a trajectory originating from x to each the set U is finite. Additionally, for every compact .
3. Theoretical Analysis
3.1. Extinction of the Stochastic Epidemic Model (3)
3.2. Stationary Distribution and Ergodicity of the Stochastic Model (3)
- (i)
- (ii)
4. Numerical Simulations and Data Interpretation
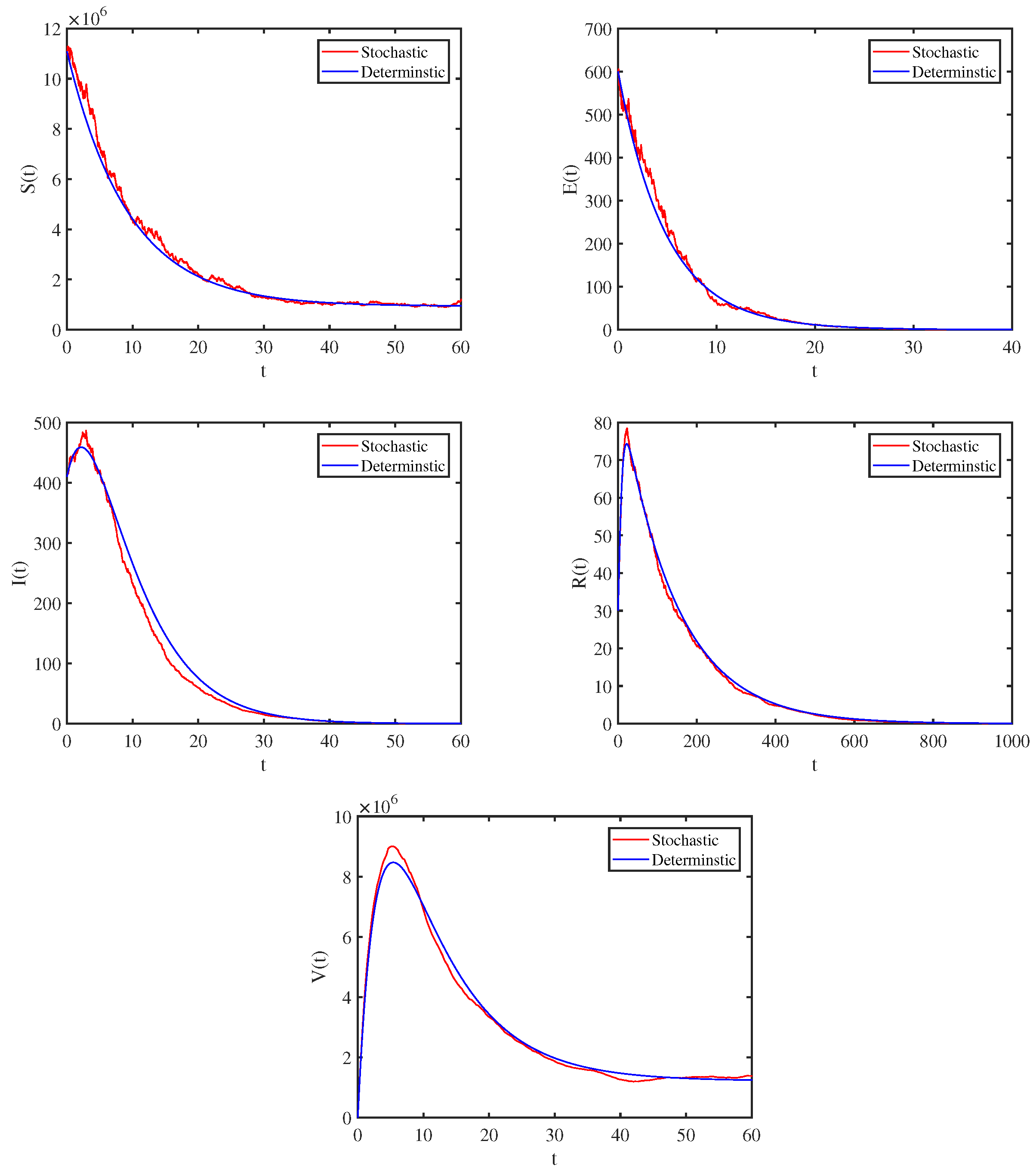
4.1. Model Validation
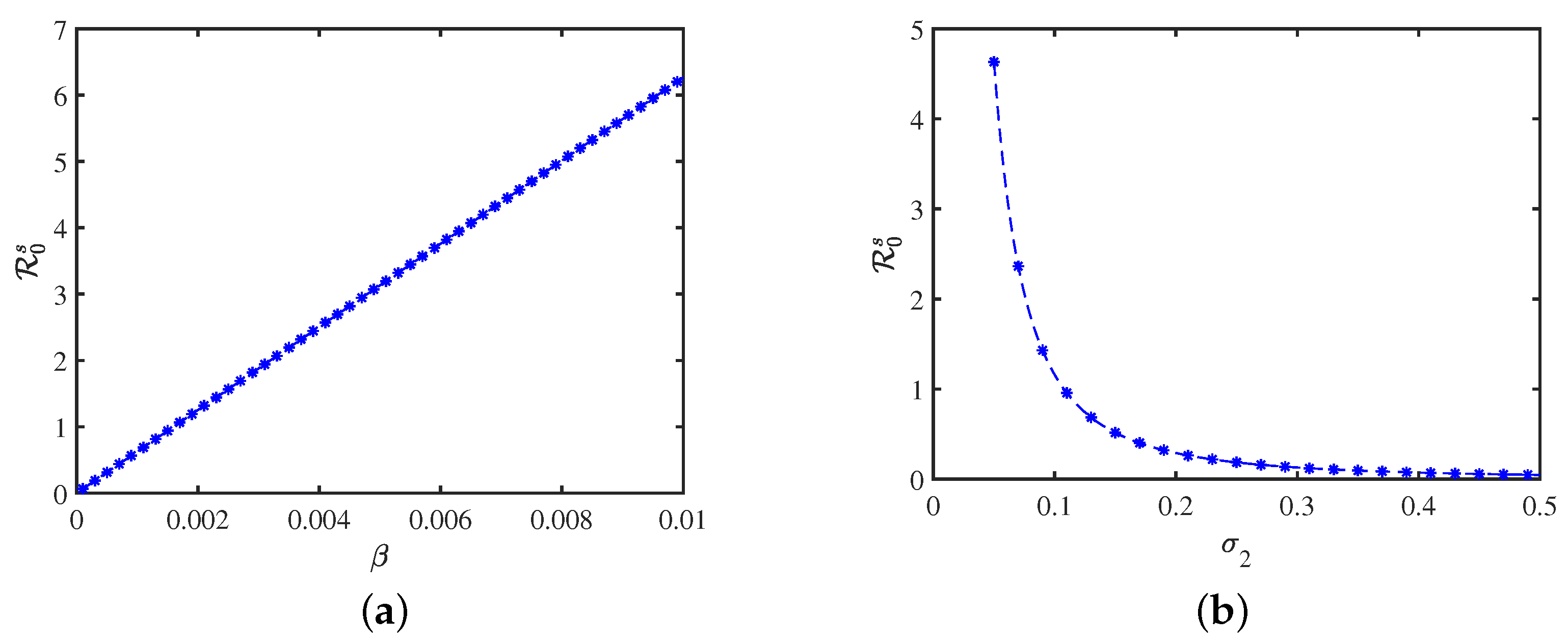
4.2. Sensitivity Analysis of and
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naheed, A.; Singh, M.; Lucy, D. Numerical study of SARS epidemic model with the inclusion of diffusion in the system. Appl. Math. Comput. 2014, 229, 480–498. [Google Scholar] [CrossRef] [PubMed]
- Huo, H.F.; Feng, L.X. Global stability for an HIV/AIDS epidemic model with different latent stages and treatment. Appl. Math. Model. 2013, 37, 1480–1489. [Google Scholar] [CrossRef]
- Pongsumpun, P.; Tang, I.M. Dynamics of a new strain of the H1N1 influenza a virus incorporating the effects of repetitive contacts. Comput. Math. Methods Med. 2014, 2014, 487974. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sen, M.; Ibeas, A. On an SE(Is)(Ih)AR epidemic model with combined vaccination and antiviral controls for COVID-19 pandemic. Adv. Differ. Equ. 2021, 2021, 92. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, L.; Wang, X. Modelling and stability of epidemic model with free-living pathogens growing in the environment. J. Appl. Anal. Comput. 2020, 10, 55–70. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, Y.F. Stability Analysis of a Reaction-Diffusion Heroin Epidemic Model. Complexity 2020, 2020, 3781425. [Google Scholar] [CrossRef]
- Wang, X. An SIRS Epidemic Model with Vital Dynamics and a Ratio-Dependent Saturation Incidence Rate. Discret. Dyn. Nat. Soc. 2015, 2015, 720682. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Global stability of an SIR epidemic model with time delays. J. Math. Biol. 1995, 33, 250. [Google Scholar] [CrossRef] [PubMed]
- Ruan, S.; Wang, W. Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equ. 2003, 188, 135–163. [Google Scholar] [CrossRef]
- Xiang, H.; Wang, Y.; Huo, H. Analysis of the binge drinking models with demographics and nonlinear infectivity on networks. J. Appl. Anal. Comput. 2018, 8, 1535–1554. [Google Scholar] [CrossRef]
- Rui, X.; Ma, Z. Global stability of a delayed SEIRS epidemic model withsaturation incidence rate. Nonlinear Dyn. 2010, 61, 229–239. [Google Scholar] [CrossRef]
- Alexander, M.; Moghadas, S. Bifurcation analysis of an SIRS epidemic model with generalized incidence. SIAM J. Appl. Math. 2005, 65, 1794–1816. [Google Scholar] [CrossRef]
- Watmough, J.; Mccluskey, C.; Gumel, A. An SVEIR model for assessing potential impact of an imperfect anti-SARS vaccine. Math. Biosci. Eng. 2006, 3, 485–512. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Badshah, Q.; Islam, S.; Khan, I.; Khan, S.A. Global dynamics of SEIRS epidemic model with non-linear generalized incidences and preventive vaccination. Adv. Differ. Equ. 2015, 2015, 88. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, Y.; Khan, S.; Islam, S. Global stability and vaccination of an SEIVR epidemic model with saturated incidence rate. Int. J. Biomath. 2016, 9, 59–83. [Google Scholar] [CrossRef]
- Liu, X.; Yang, L. Stability analysis of an SEIQV epidemic model with saturated incidence rate. Nonlinear Anal. Real World Appl. 2012, 13, 2671–2679. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, C.; Jiang, X. Global stability of an SEIQV epidemic model with general incidence rate. Int. J. Biomath. 2015, 8, 1550020. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, X. Backward bifurcation of an epidemic model with saturated treatment function. J. Math. Anal. Appl. 2008, 348, 433–443. [Google Scholar] [CrossRef]
- Kyrychko, Y.N.; Blyuss, K.B. Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate. Nonlinear Anal. Real World Appl. 2005, 6, 495–507. [Google Scholar] [CrossRef]
- Farrington, C.P. On vaccine efficacy and reproduction numbers. Math. Biosci. 2003, 185, 89–109. [Google Scholar] [CrossRef]
- Agaba, G.O.; Kyrychko, Y.N.; Blyuss, K.B. Dynamics of vaccination in a time-delayed epidemic model with awareness. Math. Biosci. 2017, 294, 92. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gao, D.P.; Huang, N.J.; Kang, S.M.; Zhang, C. Global stability analysis of an SVEIR epidemic model with general incidence rate. Bound. Value Probl. 2018, 2018, 42. [Google Scholar] [CrossRef] [PubMed]
- Rao, F.; Mandal, P.; Kang, Y. Complicated endemics of an SIRS model with a generalized incidence under preventive vaccination and treatment controls. Appl. Math. Model. 2019, 67, 38–61. [Google Scholar] [CrossRef]
- Liu, X.; Takeuchi, Y.; Iwami, S. SVIR epidemic models with vaccination strategies. J. Theor. Biol. 2008, 253, 1–11. [Google Scholar] [CrossRef] [PubMed]
- He, Z.L.; Nie, L.F. The Effect of Pulse Vaccination and Treatment on SIR Epidemic Model with Media Impact. Discret Dyn. Nat. Soc. 2015, 2015, 3129–3132. [Google Scholar] [CrossRef]
- Zhang, T. Permanence and extinction in a nonautonomous discrete SIRVS epidemic model with vaccination. Appl. Math. Comput. 2015, 271, 716–729. [Google Scholar] [CrossRef]
- Spencer, S. Stochastic Epidemic Models for Emerging Diseases. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2008. [Google Scholar]
- Beddington, J.R.; May, R.M. Harvesting Natural Populations in a Randomly Fluctuating Environment. Science 1977, 197, 463–465. [Google Scholar] [CrossRef] [PubMed]
- Gard, T.C. Introduction to Stochastic Differential Equations; Marcel Dekker Inc.: New York, NY, USA, 1988; Volume 84, p. 19. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Jiang, D.; Shi, N.; Li, X. Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation. J. Math. Anal. Appl. 2008, 340, 588–597. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L. Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence. Stat. Probab. Lett. 2013, 83, 960–968. [Google Scholar] [CrossRef]
- Chen, C.; Kang, Y. The asymptotic behavior of a stochastic vaccination model with backward bifurcation. Appl. Math. Model. 2016, 40, 6051–6068. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Shi, N.; Hayat, T.; Alsaedi, A. Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence. Physica A Stat. Mech. Its Appl. 2017, 469, 510–517. [Google Scholar] [CrossRef]
- Zhang, X.; Huo, H.; Xiang, H.; Meng, X. Dynamics of the deterministic and stochastic SIQS epidemic model with non-linear incidence. Appl. Math. Comput. 2014, 243, 546–558. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Xing, Y. Dynamics of a stochastic heroin epidemic model. J. Comput. Appl. Math. 2019, 351, 260–269. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, S.; Zhang, X. Asymptotic behavior of a stochastic virus dynamics model with intracellular delay and humoral immunity. J. Appl. Anal. Comput. 2019, 9, 1425–1442. [Google Scholar] [CrossRef]
- Cai, Y.L.; Kang, Y.; Wang, W.M. A stochastic SIRS epidemic model with nonlinear incidence rate. Appl. Math. Comput. 2017, 305, 221–240. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Mao, X.; Marion, G.; Renshaw, E. Environmental Brownian noise suppresses explosions in population dynamics. Stoch. Process. Their Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Zhang, X.B.; Liu, R.J. The stationary distribution of a stochastic SIQS epidemic model with varying total population size. Appl. Math. Lett. 2020, 116, 106974. [Google Scholar] [CrossRef]
- Zhang, X.B.; Zhang, X.H. The threshold of a deterministic and a stochastic SIQS epidemic model with varying total population size. Appl. Math. Model. 2021, 91, 749–767. [Google Scholar] [CrossRef]
- Britton, T. Stochastic epidemic models: A survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef]
- Ball, F.; Neal, P. A general model for stochastic SIR epidemics with two levels of mixing. Math. Biosci. 2002, 180, 73–102. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Jiang, D.; Shi, N.; Ji, C. The ergodicity and extinction of stochastically perturbed SIR and SEIR epidemic models with saturated incidence. J. Math. Anal. Appl. 2017, 388, 248–271. [Google Scholar] [CrossRef]
- Khasminiskii, R.Z. Stochastic Stability of Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, X.; Huo, H.; Xiang, H.; Shi, Q.; Li, D. The threshold of a stochastic SIQS epidemic model. Physica A Stat. Mech. Its Appl. 2017, 482, 362–374. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Applications; Harcourt Brace Jovanovich: Orlando, FL, USA, 1988. [Google Scholar]
- Zhu, C.; Yin, G. Asymptotic properties of hybrid diffusion systems. SIAM J. Control Optim. 2007, 46, 1155–1179. [Google Scholar] [CrossRef]
- Sinan, M.; Ali, A.; Shah, K.; Assiri, T.A.; Nofal, T.A. Stability Analysis and Optimal Control of COVID-19 Pandemic SEIQR Fractional Mathematical Model with Harmonic Mean Type Incidence Rate and Treatment. Results Phys. 2021, 22, 103873. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Li, M.; Hao, Y.; Liu, Z.; Hu, L.; Wang, L. The introduction of population migration to SEIAR for COVID-19 epidemic modeling with an efficient intervention strategy-ScienceDirect. Inf. Fusion 2020, 64, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Al Kaabi, N.; Zhang, Y.; Xia, S.; Yang, Y.; Al Qahtani, M.M.; Abdulrazzaq, N.; Nusair, M.A.; Hassany, M.; Jawad, J.S.; Abdalla, J.; et al. Effect of 2 Inactivated SARS-CoV-2 Vaccines on Symptomatic COVID-19 Infection in Adults: A Randomized Clinical Trial. JAMA 2021, 326, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Tang, S.; Chen, Y.; Feng, X.; Xiao, Y.; Xu, Z. When will be the resumption of work in Wuhan and its surrounding areas during COVID-19 epidemic? A data-driven network modeling analysis. Sci. Sin. Math. 2020, 50, 969–978. (In Chinese) [Google Scholar]


| Parameter | Description |
|---|---|
| A | The recruitment rate of new individuals |
| The contact rate or the rate of transfer of virus from an infectious individual to the susceptible | |
| The natural mortality rate | |
| The rate at which the vaccinated individuals lose their immunity and join the susceptible class | |
| The vaccination rate coefficient | |
| The rate at which exposed individuals become infectious | |
| The recovery rate of the infectious individuals | |
| The disease-related death rate of infectious individuals | |
| a | The proportion constant related to susceptible individuals |
| b | The proportion constant related to infectious individuals |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, L.; Zhang, X.-B. Dynamics of a Stochastic SVEIR Epidemic Model with Nonlinear Incidence Rate. Symmetry 2024, 16, 467. https://doi.org/10.3390/sym16040467
Wang X, Zhang L, Zhang X-B. Dynamics of a Stochastic SVEIR Epidemic Model with Nonlinear Incidence Rate. Symmetry. 2024; 16(4):467. https://doi.org/10.3390/sym16040467
Chicago/Turabian StyleWang, Xinghao, Liang Zhang, and Xiao-Bing Zhang. 2024. "Dynamics of a Stochastic SVEIR Epidemic Model with Nonlinear Incidence Rate" Symmetry 16, no. 4: 467. https://doi.org/10.3390/sym16040467
APA StyleWang, X., Zhang, L., & Zhang, X.-B. (2024). Dynamics of a Stochastic SVEIR Epidemic Model with Nonlinear Incidence Rate. Symmetry, 16(4), 467. https://doi.org/10.3390/sym16040467





