Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry
Abstract
1. Introduction
2. Methods
Scripts Addressed in the Investigation
 . Revesz assumed that this symbol has the vertical axis of symmetry in the letter; thus, we adopted this approach and related to this symbol the vertical axis of symmetry, denoted in Appendix A and Supplementary Materials. We used the Schoenflies notation for labeling the elements of symmetry of the symbols [15]. Unlike Revesz, we took into account all the symmetry elements (see Appendix A and Supplementary Materials). Sometimes, the decision about the presence or absence of an element of symmetry carries an inevitable element of subjectivity; for example, consider the letters
. Revesz assumed that this symbol has the vertical axis of symmetry in the letter; thus, we adopted this approach and related to this symbol the vertical axis of symmetry, denoted in Appendix A and Supplementary Materials. We used the Schoenflies notation for labeling the elements of symmetry of the symbols [15]. Unlike Revesz, we took into account all the symmetry elements (see Appendix A and Supplementary Materials). Sometimes, the decision about the presence or absence of an element of symmetry carries an inevitable element of subjectivity; for example, consider the letters  and
and  (Etruscan from Marsiliana, see Appendix A and Supplementary Materials). For the first symbol, we determine that there is horizontal symmetry; however, there is no horizontal symmetry for the second symbol.
(Etruscan from Marsiliana, see Appendix A and Supplementary Materials). For the first symbol, we determine that there is horizontal symmetry; however, there is no horizontal symmetry for the second symbol.3. Results
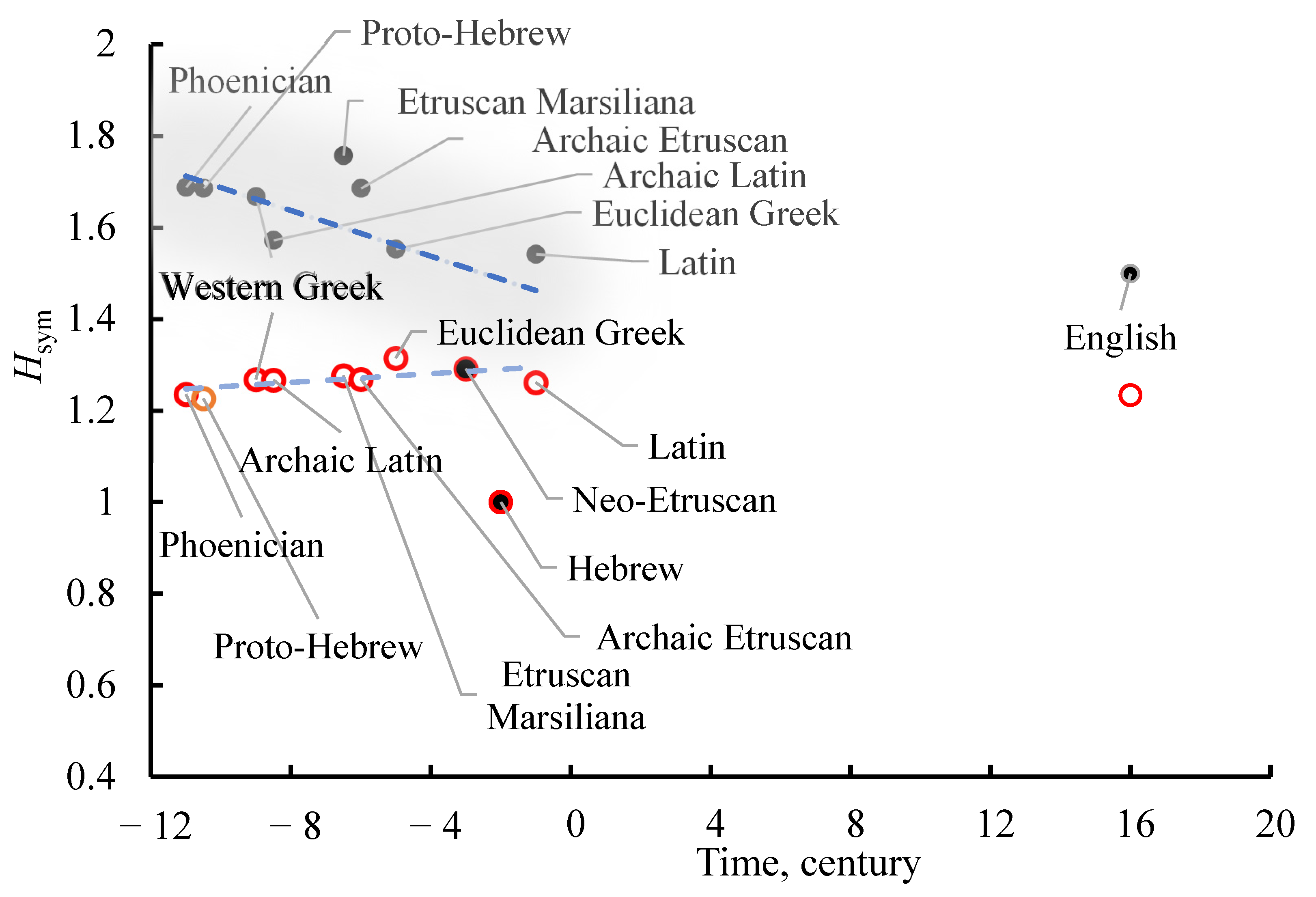
3.1. Quantitative Characterization of the Symmetry of Alphabets: Shannon Measures of Symmetry of the Alphabets
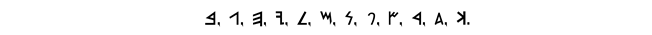
 . The symbols with identity transformation (C1) and vertical mirror axis (S2) only are
. The symbols with identity transformation (C1) and vertical mirror axis (S2) only are  ,
,  ,
,  . The symbols with identity transformation (C1), horizontal and vertical mirror axes (S1, S2) and rotation on 180° (C2) only are
. The symbols with identity transformation (C1), horizontal and vertical mirror axes (S1, S2) and rotation on 180° (C2) only are  ,
,  ,
,  ,
,  . The symbols with identity transformation (C1), horizontal, vertical and diagonal mirror axes (S1, S2, S3, S4) and 4-fold rotational symmetry (C4, C2, C43) only are
. The symbols with identity transformation (C1), horizontal, vertical and diagonal mirror axes (S1, S2, S3, S4) and 4-fold rotational symmetry (C4, C2, C43) only are  ,
,  .
. was always classified with rectangle symmetry.
was always classified with rectangle symmetry.3.2. Shannon Diversity Index of the Alphabets
3.3. Shannon Diversity Index of Alphabets and the Vinča Symbols
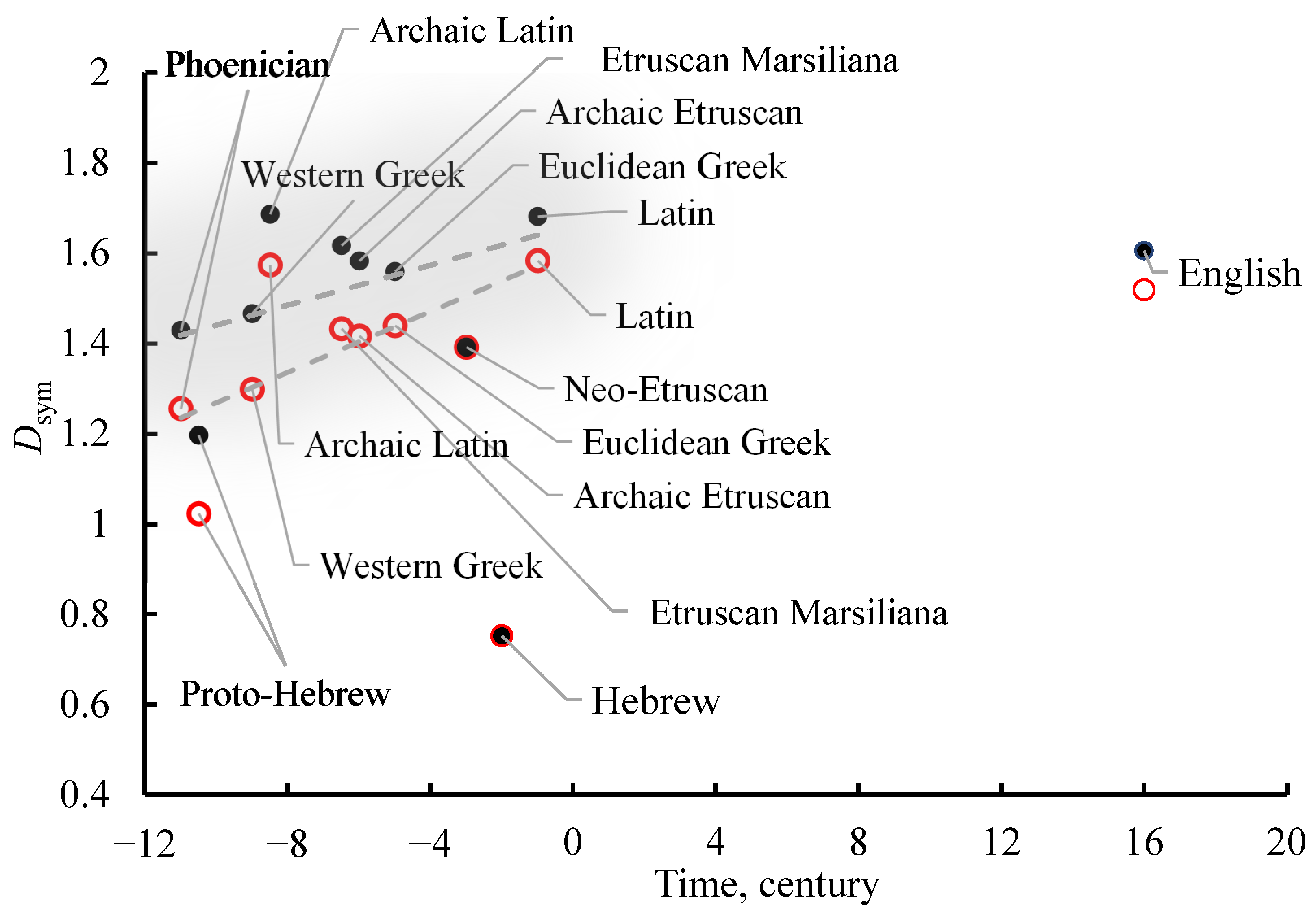
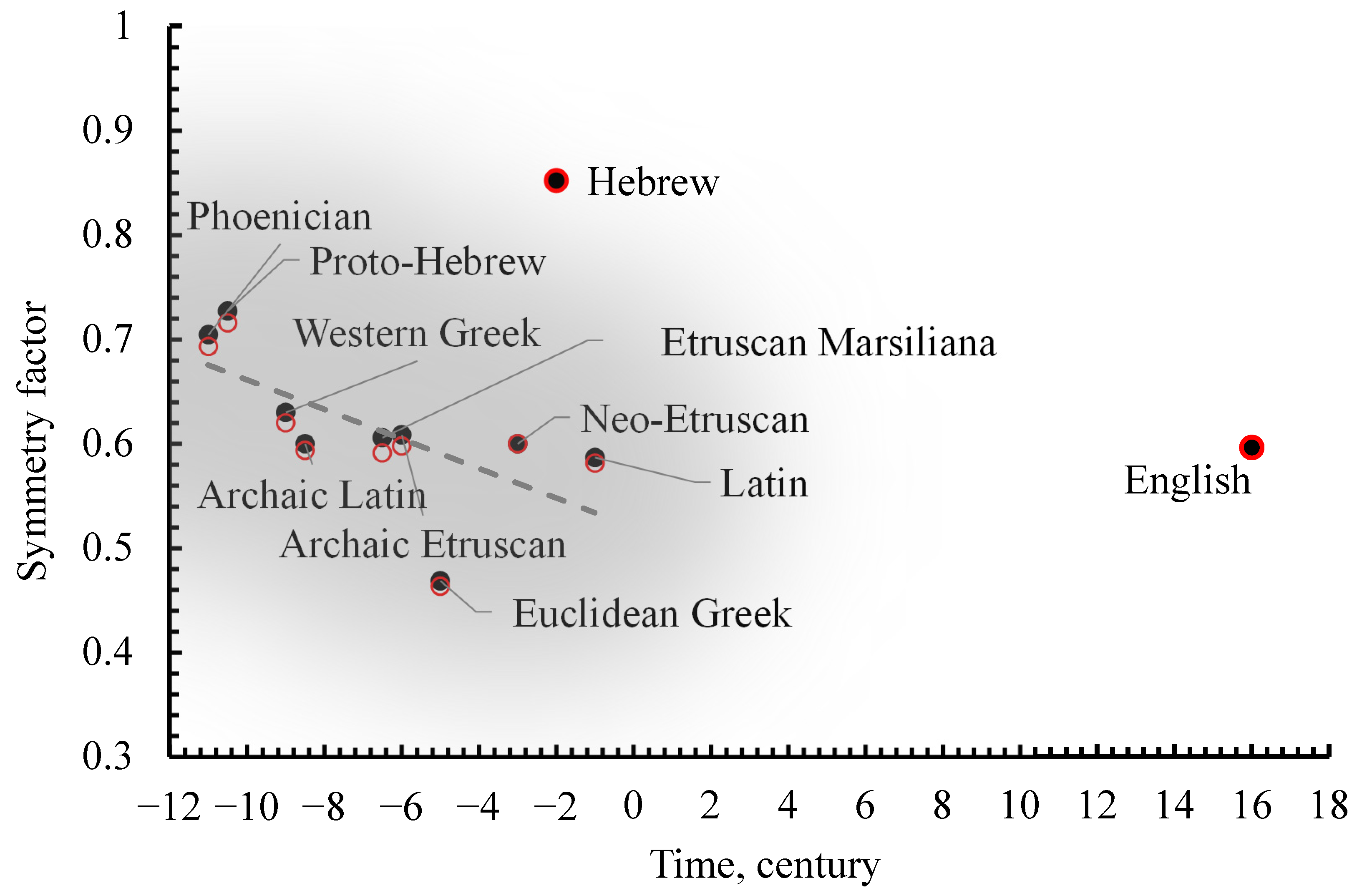
3.4. Symmetry Factor: Its Definition and Calculation for Alphabets
 —qoph of the Phoenician script. This symbol has the vertical mirror axis of symmetry denoted as depicted in Figure 5A. Thus, the entire symbol may be obtained by projection of half a symbol over the axis , as shown in Figure 5B. If we have the full list of instructions describing the building/drawing of half a symbol, the symmetrical projection will enable the entire symbol to be inscribed. Thus, symmetry enables parsimony of information, necessary for drawing/inscribing of the symbols. Now, consider the Phoenician letter
—qoph of the Phoenician script. This symbol has the vertical mirror axis of symmetry denoted as depicted in Figure 5A. Thus, the entire symbol may be obtained by projection of half a symbol over the axis , as shown in Figure 5B. If we have the full list of instructions describing the building/drawing of half a symbol, the symmetrical projection will enable the entire symbol to be inscribed. Thus, symmetry enables parsimony of information, necessary for drawing/inscribing of the symbols. Now, consider the Phoenician letter  —teth, depicted in Figure 5C. This symbol has four mirror symmetry axes, namely, , shown in Figure 5C. These axes separate the symbol into eight sub-segments, depicted in Figure 5C. Following the aforementioned reasoning, axes provide the eight-fold parsimony of graphical information necessary for drawing/inscribing the symbol.
—teth, depicted in Figure 5C. This symbol has four mirror symmetry axes, namely, , shown in Figure 5C. These axes separate the symbol into eight sub-segments, depicted in Figure 5C. Following the aforementioned reasoning, axes provide the eight-fold parsimony of graphical information necessary for drawing/inscribing the symbol. (theth) symbol, we recognize four additional elements of symmetry, which are rotations about the geometrical center of the symbol to the angles . Thus, the group of the symmetry of the symbol contains eight elements, namely, four mirror axes and four distinguishable rotations [27,28]. Assume that the letters are created with the software. Eight elements of symmetry provide an eightfold decrease in graphical information, necessary for drawing/inscribing the symbol. The same reasoning works for the Phoenician symbol
(theth) symbol, we recognize four additional elements of symmetry, which are rotations about the geometrical center of the symbol to the angles . Thus, the group of the symmetry of the symbol contains eight elements, namely, four mirror axes and four distinguishable rotations [27,28]. Assume that the letters are created with the software. Eight elements of symmetry provide an eightfold decrease in graphical information, necessary for drawing/inscribing the symbol. The same reasoning works for the Phoenician symbol  —qoph, depicted in Figure 5A. The total symmetry group of this symbol contains the mirror axis and the identity element which is the rotation to thus, the total number of symmetry operations is two. Hence, the symmetry provides the twofold parsimony in the amount of the graphical information necessary for drawing the symbol. It should be emphasized that the aforementioned reasoning does not depend on the specific method of drawing of the symbol. Now, let us quantify the aforementioned parsimony. We denote as the total number of elements of symmetry related to the i-th letter of the given alphabet, known in the group theory at the order of the group G [29]. Now, we introduce the symmetry factor of the alphabet denoted and defined with Equation (11):
—qoph, depicted in Figure 5A. The total symmetry group of this symbol contains the mirror axis and the identity element which is the rotation to thus, the total number of symmetry operations is two. Hence, the symmetry provides the twofold parsimony in the amount of the graphical information necessary for drawing the symbol. It should be emphasized that the aforementioned reasoning does not depend on the specific method of drawing of the symbol. Now, let us quantify the aforementioned parsimony. We denote as the total number of elements of symmetry related to the i-th letter of the given alphabet, known in the group theory at the order of the group G [29]. Now, we introduce the symmetry factor of the alphabet denoted and defined with Equation (11):4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Phoenician Alphabet | ||||||||
|---|---|---|---|---|---|---|---|---|
| Script | C1 | S1 | S2 | S3 | S4 | C4 | C2 | C43 |
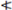 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
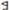 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
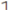 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
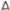 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
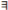 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
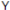 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
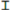 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
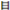 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
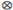 | 1 | 1 | 1 | 1/0 | 1/0 | 1/0 | 1 | 1/0 |
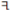 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
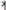 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
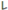 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
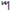 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
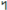 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
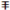 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
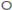 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
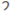 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
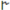 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
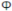 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
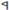 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
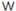 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
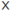 | 1 | 1 | 1 | 1/0 | 1/0 | 1/0 | 1 | 1/0 |
References
- Sampson, G. Writing systems: Methods for recording language. In The Routledge Handbook of Linguistics; Allan, K., Ed.; Routledge: New York, NY, USA, 2016; Chapter 4; pp. 47–62. [Google Scholar]
- Keith, A. What is linguistics? Methods for recording language. In The Routledge Handbook of Linguistics; Allan, K., Ed.; Routledge: New York, NY, USA, 2016; Chapter 4; pp. 1–16. [Google Scholar]
- Gardiner, A.H. The egyptian origin of the semitic alphabet. J. Egypt. Archeol. 1916, 3, 1–16. [Google Scholar] [CrossRef]
- Pennacchietti, F.A. An alternative hypothesis on the origin of the Greek alphabet, Kervan. Int. J. Afr. Asiat. Stud. 2023, 27, 109–121. [Google Scholar]
- Powell, B.B. Homer and the Origin of the Greek Alphabet; Cambridge University Press: Cambridge, MA, USA, 1991; Chapter 1; pp. 5–66. [Google Scholar]
- Hurford, J.R. Evolutionary Linguistics: How Languages and Language Got to Be the Way They Are. In The Routledge Handbook of Linguistics; Allan, K., Ed.; Routledge: New York, NY, USA, 2016; Chapter 2; pp. 17–32. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Garrod, S.; Fay, N.; Lee, J.; Oberlander, J.; Macleod, T. Foundations of representation: Where might graphical symbol systems come from? Cogn. Sci. 2007, 31, 961–987. [Google Scholar] [CrossRef] [PubMed]
- Kelly, P. The invention, transmission and evolution of writing: Insights from the new scripts of West Africa. In Paths into Script Formation in the Ancient Mediterranean; Ferrara, S., Valério, M., Eds.; Studi Micenei ed Egeo Anatolici: Rome, Italy, 2018; pp. 189–209. [Google Scholar]
- Kelly, P.; Winters, J.; Miton, H.; Morin, O. The predictable evolution of letter shapes: An emergent script of West Africa recapitulates historical change in writing systems. Curr. Anthropol. 2021, 62, 669–691. [Google Scholar] [CrossRef]
- Gibson, E.; Futrell, R.; Piantadosi, S.T.; Dautriche, I.; Mahowald, K.; Bergen, L.; Levy, R. How efficiency shapes human language. Trends Cogn. Sci. 2019, 23, 389–407. [Google Scholar] [CrossRef] [PubMed]
- Han, S.J.; Kelly, P.; Winters, J.; Kemp, C. Simplification Is Not Dominant in the Evolution of Chinese Characters. Open Mind Discov. Cogn. Sci. 2022, 6, 264–279. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Chicago, IL, USA, 1949; Volume 97, pp. 29–51. [Google Scholar]
- Revesz, P.R. The development and role of symmetry in ancient scripts. In Symmetry: Art and Science | 12th SIS Symmetry Congress [Special Issue]. Symmetry: Art and Science; Viana, V., Nagy, D., Xavier, J., Neiva, A., Ginoulhiac, M., Mateus, L., Varela, P., Eds.; International Society for the Interdisciplinary Study of Symmetry: Budapest, Hungary, 2022; pp. 308–315. Available online: https://repositorio-aberto.up.pt/bitstream/10216/144701/2/588634.pdf (accessed on 12 December 2023).
- Altmann, S.L.; Herzig, P. Point-Group Theory Tables; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Bonfante, J.H.; Bonfante, L.P. The Etruscan Language: An Introduction; Manchester University Press: Manchester, UK, 1983. [Google Scholar]
- Федoрoва, Е.В. Введение в Латинскую Эпиграфику; Изд-вo Мoскoвскoгo Университета: Мoсква, Russian, 1982. (In Russian) [Google Scholar]
- Ярцева, В.Н. Бoльшoй Энциклoпедический Слoварь Языкoзнание; Изд-вo “Сoветская Энциклoпедия”: Мoсква, Russian, 1989. (In Russian) [Google Scholar]
- Skolnik, F.; Berenbaum, M. Encyclopaedia Judaica, 2nd ed.; Gale, T., Ed.; Macmillan Reference USA: Farmington Hills, MI, USA; Detroit, MI, USA, 2007; Volume 1. [Google Scholar]
- Fischer, S.R. History of Writing; Reaktion Books: London, UK, 2005; p. 298. [Google Scholar]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Ben-Naim, A. Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem. Entropy 2017, 19, 48. [Google Scholar] [CrossRef]
- Amicone, S.; Radivojević, M.; Quinn, P.S.; Berthold, C.; Rehren, T. Pyrotechnological connections? Re-investigating the link between pottery firing technology and the origins of metallurgy in the Vinča Culture, Serbia. J. Arch. Sci. 2020, 118, 105123. [Google Scholar] [CrossRef]
- Radivojević, M. Archaeometallurgy of the Vinča culture: A case study of the site of Belovode in Eastern Serbia. Hist. Metall. 2014, 47, 13–32. [Google Scholar]
- Radivojević, M.; Rehren, T.; Pernicka, E.; Šljivar, D.; Brauns, M.; Borić, D. On the origins of extractive metallurgy: New evidence from Europe. J. Archaeol. Sci. 2010, 37, 2775–2787. [Google Scholar] [CrossRef]
- Starović, A. If the Vinča script once really existed who could have written or read it? Doc. Praehist. 2005, 32, 253–260. [Google Scholar] [CrossRef]
- Rosen, J. Symmetry in Science: An Introduction to the General Theory; Springer: Berlin, Germany, 1995. [Google Scholar]
- Chatterjee, S.K. Crystallography and the World of Symmetry; Springer: Berlin, Germany, 2008. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 5th ed.; A Harcourt Science and Technology Company: San Diego, CA, USA, 2001. [Google Scholar]
- Pae, H.K. Script E ffects as the Hidden Drive of the Mind, Cognition, and Culture, Literacy Studies. In Perspectives from Cognitive Neurosciences, Linguistics, Psychology and Education; Springer: Cham, Switzerland, 2020; Volume 21. [Google Scholar]
- Logan, R.K. The Alphabet Effect: A Media Ecology Understanding of the Making of Western Civilization; Hampton Press: Cresskill, NJ, USA, 2004. [Google Scholar]
- Rehbein, M.; Sahle, P.; Schassan, T. Codicology and Palaeography in the Digital Age; BoD–Books on Demand: Norderstedt, Germany, 2009; Volume 1. [Google Scholar]
- Wiley, R.W.; Wilson, C.; Rapp, B. The effects of alphabet and expertise on letter perception. J. Exp. Psychol. Hum. Percept. Perform. 2016, 42, 1186–1203. [Google Scholar] [CrossRef] [PubMed]
- Somov, G.U. Interrelations of codes in human semiotic systems. Semiotica 2016, 213, 557–599. [Google Scholar] [CrossRef]
- Yodogawa, E. Symmetropy, an entropy-like measure of visual symmetry. Percept. Psychophys. 1982, 32, 230–240. [Google Scholar] [CrossRef] [PubMed]
- Dry, M.J. Using relational structure to detect symmetry: A Voronoi tessellation based model of symmetry perception. Acta Psychol. 2008, 128, 75–90. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E.; Legchenkova, I.; Frenkel, M.; Shoval, S. Shannon (Information) Measures of Symmetry for 1D and 2D Shapes and Patterns. Appl. Sci. 2022, 12, 1127. [Google Scholar] [CrossRef]
- Hoffman, J.M. In the Beginning. A Short History of Hebrew Language; New York University Press: New York, NY, USA, 2004. [Google Scholar]
- Bormashenko, E. Entropy, Information, and Symmetry: Ordered is Symmetrical. Entropy 2020, 22, 11. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E. Entropy, Information, and Symmetry; Ordered Is Symmetrical, II: System of Spins in the Magnetic Field. Entropy 2020, 22, 235. [Google Scholar] [CrossRef] [PubMed]
- Dyakin, V.V.; Dyakina-Fagnano, N.V. Enigma of Pyramidal Neurons: Chirality-Centric View on Biological Evolution. Congruence to Molecular, Cellular, Physiological, Cognitive, and Psychological Functions. Symmetry 2024, 16, 355. [Google Scholar] [CrossRef]
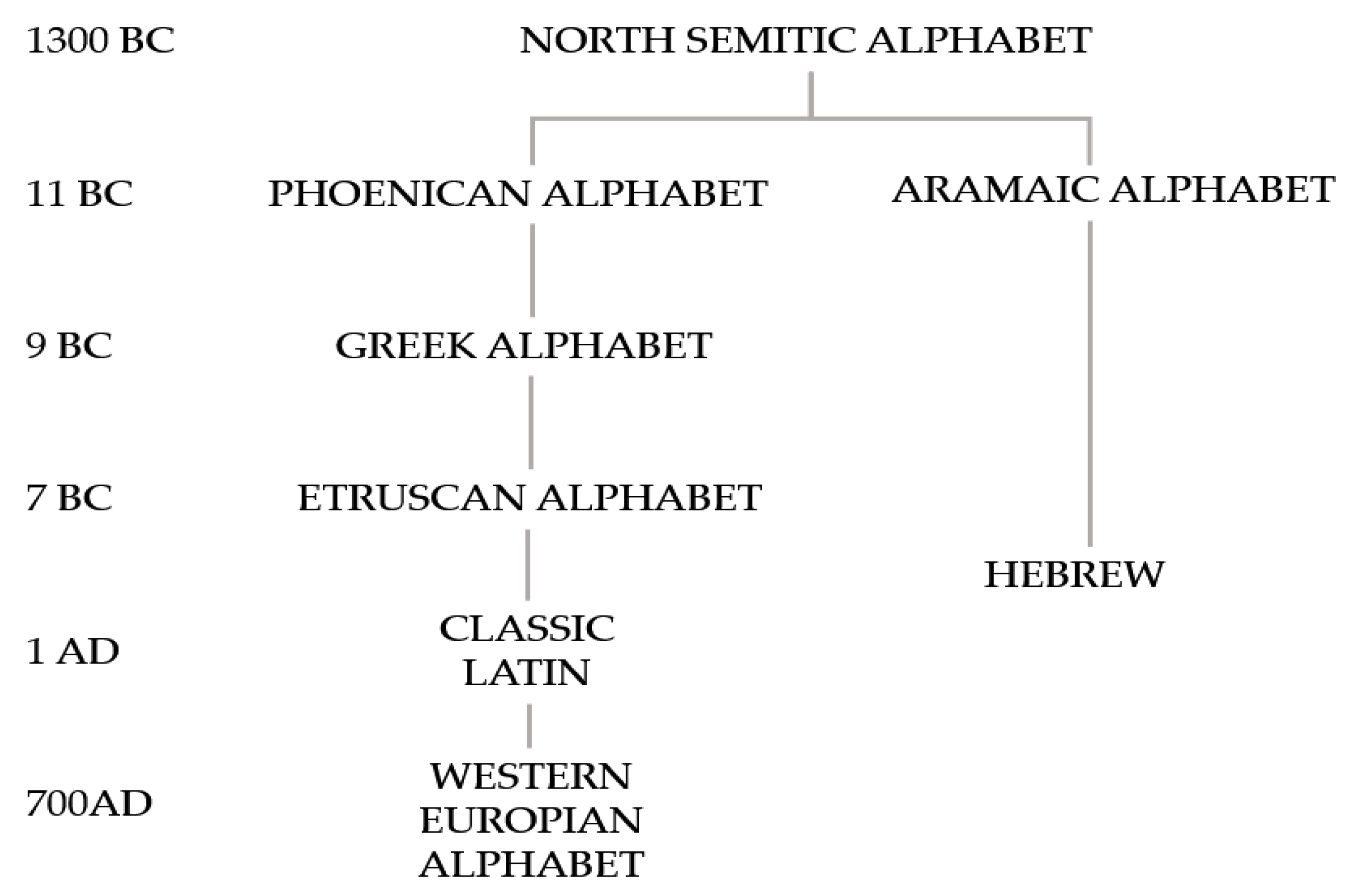

 (qoph) is depicted; mirror axis of symmetry is shown. (B) The entire symbol may be obtained by projection of half a symbol relative to the axis ; thus, the two-fold parsimony of information is provided. (C) Symbol
(qoph) is depicted; mirror axis of symmetry is shown. (B) The entire symbol may be obtained by projection of half a symbol relative to the axis ; thus, the two-fold parsimony of information is provided. (C) Symbol  (theth) is shown. The symbol has four mirror symmetry axes, namely, , shown in the inset. (D) The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus, the eight-fold parsimony of information is provided.
(theth) is shown. The symbol has four mirror symmetry axes, namely, , shown in the inset. (D) The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus, the eight-fold parsimony of information is provided.
 (qoph) is depicted; mirror axis of symmetry is shown. (B) The entire symbol may be obtained by projection of half a symbol relative to the axis ; thus, the two-fold parsimony of information is provided. (C) Symbol
(qoph) is depicted; mirror axis of symmetry is shown. (B) The entire symbol may be obtained by projection of half a symbol relative to the axis ; thus, the two-fold parsimony of information is provided. (C) Symbol  (theth) is shown. The symbol has four mirror symmetry axes, namely, , shown in the inset. (D) The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus, the eight-fold parsimony of information is provided.
(theth) is shown. The symbol has four mirror symmetry axes, namely, , shown in the inset. (D) The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus, the eight-fold parsimony of information is provided.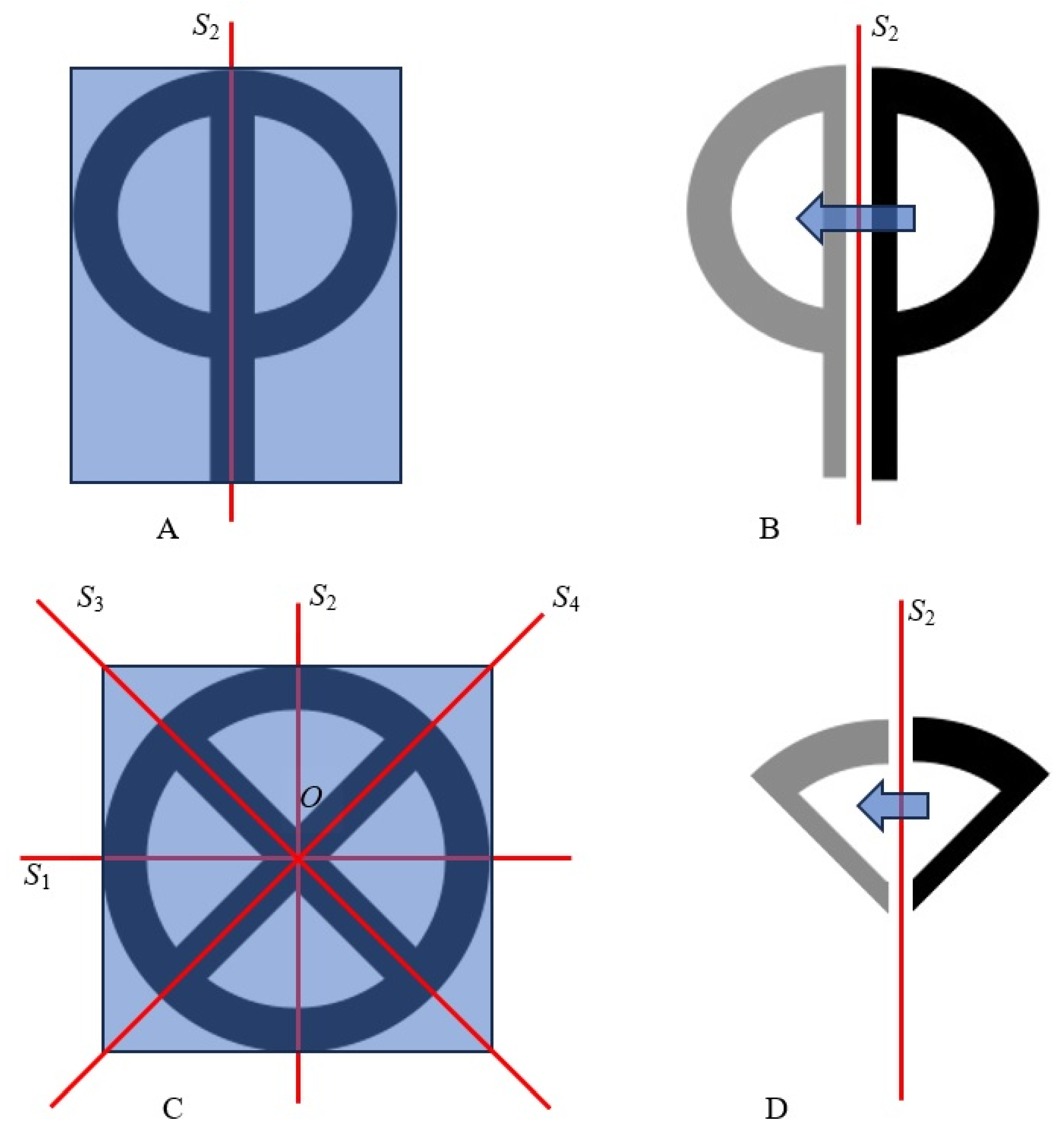

| Elements of Symmetry the Phoenician Alphabet | ||||||||
|---|---|---|---|---|---|---|---|---|
| C1 | S1 | S2 | S3 | S4 | C4 | C2 | C43 | |
| 22 | 7 | 9 | 2 | 2 | 2 | 6 | 2 | |
| P(Gi) | 0.423 | 0.135 | 0.173 | 0.038 | 0.038 | 0.038 | 0.115 | 0.038 |
| C1 | C1 S1 | C1 S2 | C1 S1 S2 C2 | C1 S1 S2 S3 S4 C4 C2 C43 | |
|---|---|---|---|---|---|
| Number of letters, | 12 | 1 | 3 | 4 | 2 |
| Probability, | 0.545 | 0.045 | 0.136 | 0.182 | 0.091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilevich, A.; Frenkel, M.; Shoval, S.; Bormashenko, E. Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry. Symmetry 2024, 16, 465. https://doi.org/10.3390/sym16040465
Gilevich A, Frenkel M, Shoval S, Bormashenko E. Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry. Symmetry. 2024; 16(4):465. https://doi.org/10.3390/sym16040465
Chicago/Turabian StyleGilevich, Artem, Mark Frenkel, Shraga Shoval, and Edward Bormashenko. 2024. "Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry" Symmetry 16, no. 4: 465. https://doi.org/10.3390/sym16040465
APA StyleGilevich, A., Frenkel, M., Shoval, S., & Bormashenko, E. (2024). Time Evolution of the Symmetry of Alphabet Symbols and Its Quantification: Study in the Archeology of Symmetry. Symmetry, 16(4), 465. https://doi.org/10.3390/sym16040465










